No CrossRef data available.
Article contents
REPRESENTING AN ELEMENT IN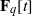 
${\mathbf{F} }_{q} [t] $ AS THE SUM OF TWO IRREDUCIBLES
Part of:
Finite fields and commutative rings (number-theoretic aspects)
Algebraic number theory: global fields
Published online by Cambridge University Press: 23 May 2013
Abstract
A monic polynomial in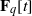 
${\mathbf{F} }_{q} [t] $ of degree 
$n$ over a finite field 
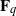${\mathbf{F} }_{q} $ of odd characteristic can be written as the sum of two irreducible monic elements in 
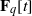${\mathbf{F} }_{q} [t] $ of degrees 
$n$ and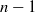 
$n- 1$ if 
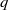$q$ is larger than a bound depending only on 
$n$. The main tool is a sufficient condition for simultaneous primality of two polynomials in one variable 
$x$ with coefficients in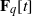 
${\mathbf{F} }_{q} [t] $.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2013
References
Bender, A. O., Decompositions into sums of two irreducibles in 
${\mathbf{F} }_{q} [t] $. C. R. Math. Acad. Sci. Paris 346 (17–18) (2008), 931–934; also available from http://dx.doi.org/10.1016/j.crma.2008.07.025.CrossRefGoogle Scholar
${\mathbf{F} }_{q} [t] $. C. R. Math. Acad. Sci. Paris 346 (17–18) (2008), 931–934; also available from http://dx.doi.org/10.1016/j.crma.2008.07.025.CrossRefGoogle ScholarBender, A. O. and Wittenberg, O., A potential analogue of Schinzel’s hypothesis for polynomials with coefficients in ${\mathbf{F} }_{q} [t] $. Int. Math. Res. Not. 36 (2005), 2237–2248; also available from http://arxiv.org/abs/math/0412303.CrossRefGoogle Scholar
${\mathbf{F} }_{q} [t] $. Int. Math. Res. Not. 36 (2005), 2237–2248; also available from http://arxiv.org/abs/math/0412303.CrossRefGoogle ScholarCar, M., Le problème de Goldbach pour l’anneau des polynômes sur un corps fini. C. R. Acad. Sci. Paris, Sér. A-B 273 (1971), A201–A204.Google Scholar
Car, M., Le théorème de Chen pour ${\mathbf{F} }_{q} [X] $. Dissertationes Math. (Rozprawy Mat.) 223 (1984), Polska Akademia Nauk. Instytut Matematyczny.Google Scholar
${\mathbf{F} }_{q} [X] $. Dissertationes Math. (Rozprawy Mat.) 223 (1984), Polska Akademia Nauk. Instytut Matematyczny.Google ScholarCar, M., The generalized polynomial Goldbach problem. J. Number Theory 57 (1) (1996), 22–49.CrossRefGoogle Scholar
Chen, J.-R., On the representation of a larger even integer as the sum of a prime and the product of at most two primes. Sci. Sinica 16 (2) (1973), 157–176; also available in Y. Wang (ed.), The Goldbach Conjecture, 2nd edn., World Scientific Publishing (Singapore, 2002).Google Scholar
Cherly, J., A lower bound theorem in ${\mathbf{F} }_{q} [x] $. J. Reine Angew. Math. 303/304 (1978), 253–264.Google Scholar
${\mathbf{F} }_{q} [x] $. J. Reine Angew. Math. 303/304 (1978), 253–264.Google ScholarDavenport, H., Multiplicative Number Theory, 3rd edn. (Graduate Texts in Mathematics 74), Springer (New York, NY, 2000), revised by Hugh L. Montgomery.Google Scholar
Effinger, G. W. and Hayes, D. R., A complete solution to the polynomial 3-primes problem. Bull. Amer. Math. Soc. (N.S.) 24 (2) (1991), 363–369.CrossRefGoogle Scholar
Effinger, G. W. and Hayes, D. R., Additive Number Theory of Polynomials over a Finite Field, Oxford University Press (New York, NY, 1991).CrossRefGoogle Scholar
Eisenbud, D., Commutative Algebra with a View Toward Algebraic Geometry (Graduate Texts in Mathematics 150), Springer (New York, NY, 1995).Google Scholar
Euler, L., Letter to Christian Goldbach dated 30th June 1742. In Leonhard Euler und Christian Goldbach: Briefwechsel 1729–1764 (eds Juskevic, A. P.
and
Winter, E.),Akademie (Berlin, 1965), also available as Lettre XLIV from http://www.math.dartmouth.edu/~euler/correspondence/letters/OO0766.pdf.Google Scholar
Fantechi, B., Göttsche, L., Illusie, L., Kleiman, S. L., Nitsure, N. and Vistoli, A., Fundamental Algebraic Geometry, Grothendieck’s fga explained (Mathematical Surveys and Monographs 123), American Mathematical Society (Providence, RI, 2005).Google Scholar
Gelfand, I. M., Kapranov, M. and Zelevinsky, A., Discriminants, Resultants and Multidimensional Determinants, Birkhäuser (Boston, MA, 1994).CrossRefGoogle Scholar
Geyer, W.-D. and Jarden, M., Bounded realization of $l$-groups over global fields. Nagoya Math. J. 150 (1998), 13–62.Google Scholar
$l$-groups over global fields. Nagoya Math. J. 150 (1998), 13–62.Google ScholarGoldbach, C., Letter to Leonhard Euler dated 7th June 1742. In Leonhard Euler und Christian Goldbach: Briefwechsel 1729–1764 (eds Juskevic, A. P.
and
Winter, E.),Akademie (Berlin, 1965), http://www.math.dartmouth.edu/~euler/correspondence/letters/OO0765.pdf.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique (rédigés avec la collaboration de Jean Dieudonné): IV. Étude locale des schémas et des morphismes de schémas, II. Publ. Math. Inst. Hautes Études Sci. 24 (1965), 5–231.Google Scholar
Hayes, D. R., A polynomial analog of the Goldbach conjecture. Bull. Amer. Math. Soc. 69 (1963), 115–116; Correction ibid. 493.CrossRefGoogle Scholar
Homma, M., Funny plane curves in characteristic $p\gt 0$. Comm. Algebra 15 (7) (1987), 1469–1501.Google Scholar
$p\gt 0$. Comm. Algebra 15 (7) (1987), 1469–1501.Google ScholarHurwitz, A., Über Riemann’sche Flächen mit gegebenen Verzweigungspunkten. Math. Ann. 39 (1891), 1–60; and Math. Werke, Band 1/XXI, Birkhäuser (Basel, 1932).CrossRefGoogle Scholar
Jouanolou, J.-P., Le formalisme du résultant. Adv. Math. 90 (2) (1991), 117–263.CrossRefGoogle Scholar
Lorenzini, D., An Invitation to Arithmetic Geometry, American Mathematical Society (Providence, RI, 1996).CrossRefGoogle Scholar
Nathanson, M. B., Additive Number Theory: the Classical Bases (Graduate Texts in Mathematics 164), Springer (New York, NY, 1996).CrossRefGoogle Scholar
Pollack, P., Prime polynomials over finite fields, PhD Thesis, Dartmouth College, 2008.Google Scholar
Pollack, P., The exceptional set in the polynomial Goldbach problem. Int. J. Number Theory 7 (3) (2011), 579–591.CrossRefGoogle Scholar
Schmidt, W. M., Equations Over Finite Fields: An Elementary Approach (Lecture Notes in Mathematics 536), Springer (Heidelberg, 1976).Google Scholar
Serre, J.-P., Topics in Galois Theory, Jones and Bartlett Publishers (Boston, MA, 1992).Google Scholar
Vinogradov, I. M., Representation of an odd number as a sum of three primes. Dokl. Akad. Nauk SSSR 15 (6–7) (1937), 291–294.Google Scholar