Hostname: page-component-848d4c4894-nr4z6 Total loading time: 0 Render date: 2024-05-28T11:32:18.226Z Has data issue: false hasContentIssue false
  • English
  • Français

Some metrical properties of continued fractions

Published online by Cambridge University Press:  26 February 2010

G. Ramharter
G. Ramharter
Affiliation:
Institut fuer Analysis, Techn. Universitaet Wien, A-1040 Wien, Gusshausstrasse 27–29, Austria
Get access

Extract

§1. Let E = E(A) be the set of real numbers x ε (0, 1) whose regular continued fraction expansion

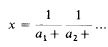
contains only partial denominators ai from a given set A of positive integers. For finite A the (Hausdorff-) dimensional numbers dim E have been studied by I. J. Good ‘2’ and T. W. Cusick ‘1’. C. A. Rogers ‘8’ introduced a natural probability measure on E. He showed that excluding sets with measure between 0 and 1 (in the strict sense) from E does not reduce the dimensionality more than excluding sets of measure zero, and that the minimal (“essential”) dimensions ess dim E arising in this way is smaller than dim E, at least for A = {1,…, r} when r = 2 or r is sufficiently large.

Type
Research Article
Information
Mathematika , Volume 30 , Issue 1 , June 1983 , pp. 117 - 132
Copyright
Copyright © University College London 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Cusick, T. W.. Continuants with bounded digits. Mathematika, 24 (1977), 166–172.CrossRefGoogle Scholar
2.Good, I. J.. The fractional dimension theory of continued fractions. Proc. Camb. Phil. Soc, 37 (1941), 199–228.CrossRefGoogle Scholar
3.Kaufman, R.. Continued fractions and Fourier transforms. Mathematika, 27 (1980), 262–267.CrossRefGoogle Scholar
4.Lévy, P.. Sur les lois de probabilité dont dépendent les quotients complets et incomplets d'une fraction continue. Bulletin Soc. Math. France, 57 (1929), 178–194.CrossRefGoogle Scholar
5.Motzkin, T. S. and Straus, E. G.. Some combinatorial extremum problems. Proc. Amer. Math. Soc, 7 (1956), 1014–1021.CrossRefGoogle Scholar
6.Ramharter, G.. Über Asymmetrische Diophantische Approximationen. J. Number Th., 14 (1982), 269–279.CrossRefGoogle Scholar
7.Ramharter, G.. Extremal values of continuants. Proc. Amer. Math. Soc. (To appear).Google Scholar
8.Rogers, C. A.. Some sets of continued fractions. Proc. London Math. Soc. (3), 14 (1964), 29–44.CrossRefGoogle Scholar