Hostname: page-component-848d4c4894-ttngx Total loading time: 0 Render date: 2024-05-19T06:15:36.017Z Has data issue: false hasContentIssue false
  • English
  • Français

A Steiner type formula for convex functions

Part of: General convexity

Published online by Cambridge University Press:  26 February 2010

Andrea Colesanti
Andrea Colesanti
Affiliation:
Dipartimento di Matematica “U. Dini”, Università degli Studi di Firenze, Viale Morgagni 67/A, 50134 Firenze, Italy.
Get access

Abstract

Given a convex function u, defined in an open bounded convex subset Ω of ℝn, we consider the set

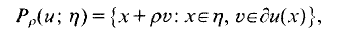
where η is a Borel subset of Ω,ρ is nonnegative, and ∂u(x) denotes the subgradient (or subdifferential) of u at x. We prove that Pp(u; η) is a Borel set and its n-dimensional measure is a polynomial of degree n with respect to ρ. The coefficients of this polynomial are nonnegative measures defined on the Borel subsets of Ω. We find an upper bound for the values attained by these measures on the sublevel sets of u. Such a bound depends on the quermassintegrals of the sublevel set and on the Lipschitz constant of u. Finally we prove that one of these measures coincides with the Lebesgue measure of the image under the subgradient map of u.

MSC classification

Secondary: 52A22: Random convex sets and integral geometry
Type
Research Article
Information
Mathematika , Volume 44 , Issue 1 , June 1997 , pp. 195 - 214
Copyright
Copyright © University College London 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

A.Ash, R. B., Measure, Integration and Functional Analysis (Academic Press, New York, 1972).Google Scholar
B.Bakelman, I. J.. Geometric inequalities and existence theorems for convex generalized solutions of tt-dimensional Monge Ampere equations. In: Geometric Analysis and Nonlinear Partial Differential Equations. Bakelman, I. J., ed. (Marcel Dekker, New York, 1993), pp. 287–87.Google Scholar
CH.Colesanti, A. and Huz, D.. Steiner type formulae and weighted measures of singularities for semi-convex functions. Preprint (1996).Google Scholar
CY.Cheng, S. Y. and Yau, S. T.. On the regularity of the Monge Ampere equation det (∂2u)/(∂x, ∂x j)=f(x, u). Comm. Pure Appl. Math. 30 (1977), 41–68.CrossRefGoogle Scholar
R.Reilly, R. C.. On the Hessian of a function and the curvature of its graph. Michigan Math., J., 20 (1973), 373–383.Google Scholar
S.Schneider, R.. Convex Bodies: the Brunn Minkowski Theory (University Press, Cambridge, 1993).CrossRefGoogle Scholar