Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-05-19T04:46:59.472Z Has data issue: false hasContentIssue false
  • English
  • Français

The Szendrei expansion of a semigroup

Part of: Semigroups

Published online by Cambridge University Press:  26 February 2010

John Fountain  and
Gracinda M. S. Gomes
John Fountain
Affiliation:
Department of Mathematics, University of York, Heslington, York, YO1 5DD
Gracinda M. S. Gomes
Affiliation:
Departamento de Matemàtica, Faculdade de Ciências, Universidade de Lisboa, 1700 Lisboa, Portugal.
Get access

Extract

In the terminology of Birget and Rhodes [3], an expansion is a functor F from the category of semigroups into some special category of semigroups such that there is a natural transformation η from F to the identity functor for which ηs is surjective for every semigroup S. The three expansions 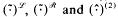introduced in [3] have proved to be of particular interest when applied to groups. In fact, as shown in [4], 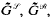Ĝ(2) are isomorphic for any group G, 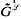is an E-unitary inverse monoid and the kernel of the homomorphism ηG is the minimum group congruence on 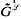. Furthermore, if G is the free group on A, then the “cut-down to generators” 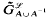which is a subsemigroup of 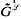is the free inverse semigroup on A. Essentially the same result was given by Margolis and Pin [12].

MSC classification

Secondary: 20M50: Connections of semigroups with homological algebra and category theory
Type
Research Article
Information
Mathematika , Volume 37 , Issue 2 , December 1990 , pp. 251 - 260
Copyright
Copyright © University College London 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Batbedat, A.. Les demi-groupes idunaires ou gamma-demi-groupes, Cahiers Mathématiques 20 (Montpellier, 1981).Google Scholar
2. Birget, J.-C.. Iteration of expansions–unambiguous semigroups. J. Pure Appl. Algebra, 34 (1984), 1–55.CrossRefGoogle Scholar
3. Birget, J.-C. and Rhodes, J.. Almost finite expansions of arbitrary semigroups. J. Pure Appl. Algebra, 32 (1984), 239–287.CrossRefGoogle Scholar
4. Birget, J.-C. and Rhodes, J.. Group theory via global semigroup theory. J. Algebra, 120 (1989), 284–300.CrossRefGoogle Scholar
5. Fountain, J.. Free right type A semigroups. To appear in Glasgow Math. J.Google Scholar
6. Fountain, J.. A class of right PP monoids. Quart J. Math. Oxford, 28 (1977), 285–300.CrossRefGoogle Scholar
7. Fountain, J.. Adequate semigroups. Proc. Edinb. Math. Soc., 22 (1979), 113–125.CrossRefGoogle Scholar
8. Giraldes, E. and Howie, J. M.. Semigroups of high rank. Proc. Edinb. Math. Soc., 28 (1985), 13–34.CrossRefGoogle Scholar
9. Hall, T. E.. 4Almost commutative bands. Glasgow Math. J., 13 (1972), 176–178.CrossRefGoogle Scholar
10. Howie, J. M.. An Introduction to Semigroup Theory (Academic Press, 1976).Google Scholar
11. McAlister, D. B.. One-to-one partial right translations of a right cancellative semigroup. J. Algebra, 43 (1976), 231–251.CrossRefGoogle Scholar
12. Margolis, S. W. and Pin, J.-E.. Expansions, free inverse semigroups and Schutzenberger products. J. Algebra, 110 (1987), 298–305.CrossRefGoogle Scholar
13. Meakin, J.. Regular expansions of semigroups. Simon Stevin, 60 (1986), 241–255.Google Scholar
14. Pastijn, F.. A representation of a semigroup by a semigroup of matrices over a group with zero. Semigroup Forum, 10 (1975), 238–249.CrossRefGoogle Scholar
15. Szendrei, M. B.. A note on Birget-Rhodes' expansion of groups. J. Pure Appl. Algebra, 58 (1989), 93–99.CrossRefGoogle Scholar