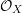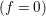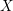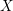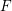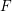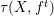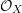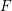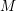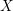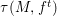Introduction
To keep notation simple in this introduction let ![]() $X=\text{Spec}\,k[x_{1},\ldots ,x_{n}]$ be the affine
$X=\text{Spec}\,k[x_{1},\ldots ,x_{n}]$ be the affine ![]() $n$-space over an algebraically closed field
$n$-space over an algebraically closed field ![]() $k$. Denote the polynomial ring by
$k$. Denote the polynomial ring by ![]() $R=k[x_{1},\ldots ,x_{n}]$ and fix an equation
$R=k[x_{1},\ldots ,x_{n}]$ and fix an equation ![]() $f\in R$ defining a hypersurface in
$f\in R$ defining a hypersurface in ![]() $X$. We denote by
$X$. We denote by ![]() ${\it\gamma}:\text{Spec}\,R\rightarrow \text{Spec}\,R[t]$ the graph embedding of
${\it\gamma}:\text{Spec}\,R\rightarrow \text{Spec}\,R[t]$ the graph embedding of ![]() $f$ given by sending
$f$ given by sending ![]() $t$ to
$t$ to ![]() $f$.
$f$.
If ![]() $k=\mathbb{C}$ one has the Bernstein–Sato Polynomial of
$k=\mathbb{C}$ one has the Bernstein–Sato Polynomial of ![]() $f$ which is an important measure of the singularities of the hypersurface defined by
$f$ which is an important measure of the singularities of the hypersurface defined by ![]() $f=0$. It is defined to be the nonzero monic polynomial of minimal degree among those
$f=0$. It is defined to be the nonzero monic polynomial of minimal degree among those ![]() $b(s)\in k[s]$ such that
$b(s)\in k[s]$ such that
for some differential operator ![]() $P\in {\mathcal{D}}_{R}[s]=k[x_{1},\ldots ,x_{n},\partial _{x_{1}},\ldots ,\partial _{x_{n}}][s]$.
$P\in {\mathcal{D}}_{R}[s]=k[x_{1},\ldots ,x_{n},\partial _{x_{1}},\ldots ,\partial _{x_{n}}][s]$.
Kashiwara and Malgrange interpret in [Reference Kashiwara16] and [Reference Malgrange21] the Bernstein–Sato polynomial as the minimal polynomial of the action of the Euler operator ![]() $\frac{\partial }{\partial t}t$ on a graded piece of the
$\frac{\partial }{\partial t}t$ on a graded piece of the ![]() $V$-filtration of the
$V$-filtration of the ![]() ${\mathcal{D}}_{R}$-module pushforward
${\mathcal{D}}_{R}$-module pushforward ![]() ${\it\gamma}_{+}R$ along the graph embedding. In fact, a key point in the work of Kashiwara and Malgrange is the construction of said
${\it\gamma}_{+}R$ along the graph embedding. In fact, a key point in the work of Kashiwara and Malgrange is the construction of said ![]() $V$-filtration in a much more general context, namely for regular holonomic
$V$-filtration in a much more general context, namely for regular holonomic ![]() ${\mathcal{D}}_{R}$-modules, which they achieve by their theory of
${\mathcal{D}}_{R}$-modules, which they achieve by their theory of ![]() $b$-functions, which generalizes the Bernstein–Sato polynomial for a hypersurface equation recalled above. By work of Budur and Saito [Reference Budur and Saito12] from the
$b$-functions, which generalizes the Bernstein–Sato polynomial for a hypersurface equation recalled above. By work of Budur and Saito [Reference Budur and Saito12] from the ![]() $V$-filtration on the
$V$-filtration on the ![]() ${\mathcal{D}}_{R[t]}$-module
${\mathcal{D}}_{R[t]}$-module ![]() ${\it\gamma}_{+}R$, one can reconstruct the filtration of multiplier ideals
${\it\gamma}_{+}R$, one can reconstruct the filtration of multiplier ideals ![]() ${\mathcal{J}}(R,f^{t})\subseteq R$ for
${\mathcal{J}}(R,f^{t})\subseteq R$ for ![]() $0<t\leqslant 1$. This shows, in particular, that the jumping numbers of the multiplier ideal filtration between
$0<t\leqslant 1$. This shows, in particular, that the jumping numbers of the multiplier ideal filtration between ![]() $0$ and
$0$ and ![]() $1$ are zeros of the Bernstein–Sato polynomial.
$1$ are zeros of the Bernstein–Sato polynomial.
A consequence of the existence of the Bernstein–Sato Polynomial is that the ![]() ${\mathcal{D}}_{R}$-module
${\mathcal{D}}_{R}$-module ![]() $R_{f}$ is generated by
$R_{f}$ is generated by ![]() $1/f$ if (and only if) the reduced Bernstein–Sato Polynomial
$1/f$ if (and only if) the reduced Bernstein–Sato Polynomial ![]() $(x+1)^{-1}b(s)$ does not have negative integral roots [Reference Torrelli27]. However, if
$(x+1)^{-1}b(s)$ does not have negative integral roots [Reference Torrelli27]. However, if ![]() $k$ is a field of positive characteristic
$k$ is a field of positive characteristic ![]() $p>0$, then it is shown in [Reference Alvarez-Montaner, Blickle and Lyubeznik1] that the
$p>0$, then it is shown in [Reference Alvarez-Montaner, Blickle and Lyubeznik1] that the ![]() ${\mathcal{D}}_{R}$-module
${\mathcal{D}}_{R}$-module ![]() $R_{f}$ is always generated by
$R_{f}$ is always generated by ![]() $1/f$. Hence, there cannot be a theory of Bernstein–Sato polynomials in positive characteristic with the same defining property. This observation is just one example for the fact that
$1/f$. Hence, there cannot be a theory of Bernstein–Sato polynomials in positive characteristic with the same defining property. This observation is just one example for the fact that ![]() ${\mathcal{D}}$-module theory in positive characteristic is quite different from the complex case.
${\mathcal{D}}$-module theory in positive characteristic is quite different from the complex case.
However, by taking the interpretation of the Bernstein–Sato polynomial as the minimal polynomial of an action of the Euler operator (due to Kashiwara and Malgrange) as his point of departure, Mustaţă defines in [Reference Mustaţă23] a family of Bernstein–Sato polynomials for a hypersurface ![]() $f=0$ over a field of positive characteristic. Contrary to the complex analytic case it is not enough to consider the action of the Euler operator alone; instead one has to also consider all higher divided power Euler operators
$f=0$ over a field of positive characteristic. Contrary to the complex analytic case it is not enough to consider the action of the Euler operator alone; instead one has to also consider all higher divided power Euler operators ![]() ${\it\vartheta}_{i}=\partial _{t}^{[p^{i}]}t^{p^{i}}$ at once.Footnote 1
${\it\vartheta}_{i}=\partial _{t}^{[p^{i}]}t^{p^{i}}$ at once.Footnote 1
More precisely, for ![]() $e\geqslant 1$ let
$e\geqslant 1$ let ![]() $M_{f}^{e}$ be the
$M_{f}^{e}$ be the ![]() ${\mathcal{D}}_{R}^{e}[{\it\vartheta}_{1},\ldots ,{\it\vartheta}_{p^{e-1}}]$-module generated by the image of
${\mathcal{D}}_{R}^{e}[{\it\vartheta}_{1},\ldots ,{\it\vartheta}_{p^{e-1}}]$-module generated by the image of ![]() ${\it\gamma}_{\ast }R$ in
${\it\gamma}_{\ast }R$ in ![]() ${\it\gamma}_{+}R$, where
${\it\gamma}_{+}R$, where ![]() ${\mathcal{D}}_{R}^{e}$ is the subring consisting of those differential operators which are linear over
${\mathcal{D}}_{R}^{e}$ is the subring consisting of those differential operators which are linear over ![]() $R^{p^{e}}$. The Euler operators
$R^{p^{e}}$. The Euler operators ![]() ${\it\vartheta}_{i}$ act on the quotient
${\it\vartheta}_{i}$ act on the quotient ![]() $M_{f}^{e}/tM_{f}^{e}$ for
$M_{f}^{e}/tM_{f}^{e}$ for ![]() $1\leqslant i\leqslant e-1$ with eigenvalues in
$1\leqslant i\leqslant e-1$ with eigenvalues in ![]() $\mathbb{F}_{p}$. The
$\mathbb{F}_{p}$. The ![]() $e$th Bernstein–Sato polynomial as introduced by Mustaţă encodes the common eigenvalues of these operators. Furthermore, Mustaţă proved that the information of these eigenvalues (suitably lifted to
$e$th Bernstein–Sato polynomial as introduced by Mustaţă encodes the common eigenvalues of these operators. Furthermore, Mustaţă proved that the information of these eigenvalues (suitably lifted to ![]() $\mathbb{Q}$) is equivalent to the data of the
$\mathbb{Q}$) is equivalent to the data of the ![]() $F$-jumping numbers of the test ideal filtration
$F$-jumping numbers of the test ideal filtration ![]() ${\it\tau}(R,f^{t})$ of
${\it\tau}(R,f^{t})$ of ![]() $f$ in the range
$f$ in the range ![]() $(0,1]$. As the test ideal can be viewed as a positive characteristic analog of the multiplier ideal this statement is a characteristic
$(0,1]$. As the test ideal can be viewed as a positive characteristic analog of the multiplier ideal this statement is a characteristic ![]() $p$ version of the result of Budur and Saito that the jumping numbers of the multiplier ideal are zeroes of the classical Bernstein–Sato polynomial as alluded to above.
$p$ version of the result of Budur and Saito that the jumping numbers of the multiplier ideal are zeroes of the classical Bernstein–Sato polynomial as alluded to above.
Work of Axel Stäbler in [Reference Stäbler25] suggests that in positive characteristic the test module filtration itself is a suitable analog of the ![]() $V$-filtration: For one thing there is a certain axiomatic characterization of the test module filtration similar to that of the
$V$-filtration: For one thing there is a certain axiomatic characterization of the test module filtration similar to that of the ![]() $V$-filtration but also different in the sense that the action of the differential operators is replaced by a (right) action of the Frobenius. Furthermore, a certain associated graded piece of the test module filtration corresponds, via an analog of the Riemann–Hilbert correspondence, to a functor on perverse constructible sheaves of
$V$-filtration but also different in the sense that the action of the differential operators is replaced by a (right) action of the Frobenius. Furthermore, a certain associated graded piece of the test module filtration corresponds, via an analog of the Riemann–Hilbert correspondence, to a functor on perverse constructible sheaves of ![]() $\mathbb{F}_{p}$-vector spaces that has several of the desirable properties of nearby cycles in the
$\mathbb{F}_{p}$-vector spaces that has several of the desirable properties of nearby cycles in the ![]() $\ell \neq p$-case. This relationship between nearby cycles and
$\ell \neq p$-case. This relationship between nearby cycles and ![]() ${\mathcal{D}}$-modules in characteristic
${\mathcal{D}}$-modules in characteristic ![]() $0$ was the motivation behind the construction of the
$0$ was the motivation behind the construction of the ![]() $V$-filtration for holonomic
$V$-filtration for holonomic ![]() ${\mathcal{D}}$-modules as a way to realize the nearby cycles functor for constructible
${\mathcal{D}}$-modules as a way to realize the nearby cycles functor for constructible ![]() $\mathbb{C}$-sheaves on the
$\mathbb{C}$-sheaves on the ![]() ${\mathcal{D}}$-module side.
${\mathcal{D}}$-module side.
What we achieve in the present paper is to also generalize Mustaţă’s theory of Bernstein–Sato polynomials to this more general context where the test module filtration is defined and well behaved as in [Reference Stäbler25]. In order to state our results let us recall some background on Cartier modules and their test modules from [Reference Blickle6].
Let us from now on assume that ![]() $R$ is an
$R$ is an ![]() $F$-finite Noetherian ring of positive characteristic
$F$-finite Noetherian ring of positive characteristic ![]() $p$. A Cartier module
$p$. A Cartier module ![]() $M$ (over
$M$ (over ![]() $R$) is an
$R$) is an ![]() $R$-module together with an
$R$-module together with an ![]() $R$-linear map
$R$-linear map ![]() ${\it\kappa}:F_{\ast }M\rightarrow M$, where
${\it\kappa}:F_{\ast }M\rightarrow M$, where ![]() $F:R\rightarrow R$ is the absolute Frobenius given by
$F:R\rightarrow R$ is the absolute Frobenius given by ![]() $x\mapsto x^{p}$. A Cartier submodule of
$x\mapsto x^{p}$. A Cartier submodule of ![]() $M$ is an
$M$ is an ![]() $R$-submodule
$R$-submodule ![]() $N$ such that
$N$ such that ![]() ${\it\kappa}(N)\subseteq N$. We say that
${\it\kappa}(N)\subseteq N$. We say that ![]() $M$ is
$M$ is ![]() $F$-pure if
$F$-pure if ![]() ${\it\kappa}$ is surjective. We call
${\it\kappa}$ is surjective. We call ![]() $M$
$M$![]() $F$-regular if
$F$-regular if ![]() $M$ is
$M$ is ![]() $F$-pure and if for any Cartier submodule
$F$-pure and if for any Cartier submodule ![]() $N$ of
$N$ of ![]() $M$ which after localizing at every generic point of
$M$ which after localizing at every generic point of ![]() $\text{Supp}M$ agrees with
$\text{Supp}M$ agrees with ![]() $M$ we have
$M$ we have ![]() $N=M$.
$N=M$.
Let ![]() $M$ be an
$M$ be an ![]() $F$-regular Cartier module which as an
$F$-regular Cartier module which as an ![]() $R$-module is finitely generated. Let
$R$-module is finitely generated. Let ![]() $f$ be a nonzero divisor on
$f$ be a nonzero divisor on ![]() $M$. Then the test module with respect to the ideal
$M$. Then the test module with respect to the ideal ![]() $(f)\subseteq R$ and
$(f)\subseteq R$ and ![]() $t\in \mathbb{R}_{{\geqslant}0}$ is
$t\in \mathbb{R}_{{\geqslant}0}$ is
where ![]() ${\mathcal{C}}$ is the algebra generated for
${\mathcal{C}}$ is the algebra generated for ![]() $n\geqslant 1$ by the
$n\geqslant 1$ by the ![]() ${\it\kappa}^{n}f^{\lceil tp^{n}\rceil }$ and
${\it\kappa}^{n}f^{\lceil tp^{n}\rceil }$ and ![]() $\underline{M}_{{\mathcal{C}}}=({\mathcal{C}}_{+})^{h}M$ for all
$\underline{M}_{{\mathcal{C}}}=({\mathcal{C}}_{+})^{h}M$ for all ![]() $h\gg 0$ is the stable image (cf. [Reference Blickle6, Proposition 2.13]). It follows from [Reference Blickle6, Theorem 3.11], [Reference Stäbler25, Lemma 3.1] that the definition we give here is in fact equivalent to the definition of test modules in [Reference Blickle6]. Moreover, we simplify the description of the test module in Section 4.
$h\gg 0$ is the stable image (cf. [Reference Blickle6, Proposition 2.13]). It follows from [Reference Blickle6, Theorem 3.11], [Reference Stäbler25, Lemma 3.1] that the definition we give here is in fact equivalent to the definition of test modules in [Reference Blickle6]. Moreover, we simplify the description of the test module in Section 4.
Test modules form a decreasing filtration of ![]() $R$-submodules of
$R$-submodules of ![]() $M$, that is,
$M$, that is, ![]() ${\it\tau}(M,f^{s})\subseteq {\it\tau}(M,f^{t})$ for
${\it\tau}(M,f^{s})\subseteq {\it\tau}(M,f^{t})$ for ![]() $s\geqslant t$. This filtration is right continuous, that is, for
$s\geqslant t$. This filtration is right continuous, that is, for ![]() ${\it\varepsilon}\ll 1$ one has
${\it\varepsilon}\ll 1$ one has ![]() ${\it\tau}(M,f^{t})={\it\tau}(M,f^{t+{\it\varepsilon}})$. An element
${\it\tau}(M,f^{t})={\it\tau}(M,f^{t+{\it\varepsilon}})$. An element ![]() $t\in \mathbb{Q}$ such that for all
$t\in \mathbb{Q}$ such that for all ![]() ${\it\varepsilon}>0$ one has
${\it\varepsilon}>0$ one has ![]() ${\it\tau}(M,f^{t})\neq {\it\tau}(M,f^{t-{\it\varepsilon}})$ is called an
${\it\tau}(M,f^{t})\neq {\it\tau}(M,f^{t-{\it\varepsilon}})$ is called an ![]() $F$-jumping number (of the test module filtration along
$F$-jumping number (of the test module filtration along ![]() $f$). Test module filtrations satisfy the so-called Briançon–Skoda theorem, namely for any
$f$). Test module filtrations satisfy the so-called Briançon–Skoda theorem, namely for any ![]() $t\geqslant 1$ one has
$t\geqslant 1$ one has ![]() ${\it\tau}(M,f^{t})=f{\it\tau}(M,f^{t-1})$. In particular, it suffices to control the
${\it\tau}(M,f^{t})=f{\it\tau}(M,f^{t-1})$. In particular, it suffices to control the ![]() $F$-jumping numbers in the range
$F$-jumping numbers in the range ![]() $(0,1]$. Moreover, if
$(0,1]$. Moreover, if ![]() $R$ is essentially of finite type over an
$R$ is essentially of finite type over an ![]() $F$-finite field then the set of
$F$-finite field then the set of ![]() $F$-jumping numbers in
$F$-jumping numbers in ![]() $(0,1]$ is finite [Reference Blickle6, Corollary 4.19] and all
$(0,1]$ is finite [Reference Blickle6, Corollary 4.19] and all ![]() $F$-jumping numbers are rational (the rationality is a formal consequence of the finiteness similar to the argument in [Reference Blickle, Mustaţă and Smith9, Theorem 3.1]).
$F$-jumping numbers are rational (the rationality is a formal consequence of the finiteness similar to the argument in [Reference Blickle, Mustaţă and Smith9, Theorem 3.1]).
Similar to Mustaţă’s approach in [Reference Mustaţă23] we use the graph embedding along the fixed hypersurface ![]() $f=0$ to define a family of Bernstein–Sato polynomials
$f=0$ to define a family of Bernstein–Sato polynomials ![]() $b_{f,M}^{e}(s)\in \mathbb{Q}[s]$. This will be done by exploiting a system of right
$b_{f,M}^{e}(s)\in \mathbb{Q}[s]$. This will be done by exploiting a system of right ![]() ${\mathcal{D}}_{R}^{e}$-modules which arises from the Cartier module structure of
${\mathcal{D}}_{R}^{e}$-modules which arises from the Cartier module structure of ![]() $M$. This is explained in the following sections. Our main result can now be stated as follows:
$M$. This is explained in the following sections. Our main result can now be stated as follows:
Theorem 5.4.
Let ![]() $R$ be regular essentially of finite type over an
$R$ be regular essentially of finite type over an ![]() $F$-finite field. Let
$F$-finite field. Let ![]() $(M,{\it\kappa})$ be an
$(M,{\it\kappa})$ be an ![]() $F$-regular Cartier module and
$F$-regular Cartier module and ![]() $f\in R$ a nonzero divisor on
$f\in R$ a nonzero divisor on ![]() $M$. The roots of the Bernstein–Sato polynomials
$M$. The roots of the Bernstein–Sato polynomials ![]() $b_{M,f}^{e}(s)$ are given for
$b_{M,f}^{e}(s)$ are given for ![]() $e$ sufficiently large by
$e$ sufficiently large by ![]() $\frac{\lceil {\it\lambda}p^{e}\rceil -1}{p^{e}}$, where
$\frac{\lceil {\it\lambda}p^{e}\rceil -1}{p^{e}}$, where ![]() ${\it\lambda}$ varies over the
${\it\lambda}$ varies over the ![]() $F$-jumping numbers of the test module filtration
$F$-jumping numbers of the test module filtration ![]() ${\it\tau}(M,f^{t})$ for
${\it\tau}(M,f^{t})$ for ![]() $t\in (0,1]$.
$t\in (0,1]$.
The crucial point is that the a priori infinite collection of Bernstein–Sato polynomials ![]() $b_{M,f}^{e}(s)$ for
$b_{M,f}^{e}(s)$ for ![]() $e\geqslant 0$ is completely determined by a finite collection of rational numbers, namely the jumping numbers of the test module filtration attached to
$e\geqslant 0$ is completely determined by a finite collection of rational numbers, namely the jumping numbers of the test module filtration attached to ![]() $(M,f)$.
$(M,f)$.
In conclusion we would like to draw the reader’s attention to the recent work of Stadnik [Reference Stadnik26] who also addresses the problem of extending Mustaţă’s Bernstein–Sato polynomials to a more general context. Stadnik, however, works in the context of Emerton and Kisin’s category of unit ![]() $R[F]$-modules [Reference Emerton and Kisin14]. In order to prove his existence result for
$R[F]$-modules [Reference Emerton and Kisin14]. In order to prove his existence result for ![]() $b$-functions he essentially has to reconstruct a theory of test ideals in this context, which he coins list-test-ideals in [Reference Stadnik26]. It was one motivation of the authors of the present paper to point out that, by working in the essentially equivalent theory of Cartier modules (more precisely Cartier crystals, see [Reference Blickle and Böckle7, Section 5.2]) one can rely on the already existing theory of test modules. By further replacing left
$b$-functions he essentially has to reconstruct a theory of test ideals in this context, which he coins list-test-ideals in [Reference Stadnik26]. It was one motivation of the authors of the present paper to point out that, by working in the essentially equivalent theory of Cartier modules (more precisely Cartier crystals, see [Reference Blickle and Böckle7, Section 5.2]) one can rely on the already existing theory of test modules. By further replacing left ![]() ${\mathcal{D}}_{R}$-modules by right
${\mathcal{D}}_{R}$-modules by right ![]() ${\mathcal{D}}_{R}$-modules there is a natural construction of the Bernstein–Sato polynomials with the desired link to the
${\mathcal{D}}_{R}$-modules there is a natural construction of the Bernstein–Sato polynomials with the desired link to the ![]() $F$-jumping numbers of the test module filtration. We show in Section 6 that Stadnik’s
$F$-jumping numbers of the test module filtration. We show in Section 6 that Stadnik’s ![]() $b$-functions are precisely the limit over our Bernstein–Sato polynomials
$b$-functions are precisely the limit over our Bernstein–Sato polynomials ![]() $b_{M,f}^{e}(s)$.
$b_{M,f}^{e}(s)$.
1  ${\mathcal{D}}$-modules in positive characteristic
${\mathcal{D}}$-modules in positive characteristic
Throughout this article we assume all rings to contain a field of prime characteristic ![]() $p>0$. The absolute Frobenius homomorphism given by sending
$p>0$. The absolute Frobenius homomorphism given by sending ![]() $r\mapsto r^{p}$ is denoted by
$r\mapsto r^{p}$ is denoted by ![]() $F:R\rightarrow F_{\ast }R$. For an
$F:R\rightarrow F_{\ast }R$. For an ![]() $R$-module
$R$-module ![]() $M$ we denote by
$M$ we denote by ![]() $F_{\ast }^{e}M$ the
$F_{\ast }^{e}M$ the ![]() $R$-module whose underlying abelian group is
$R$-module whose underlying abelian group is ![]() $M$ but with multiplication given by
$M$ but with multiplication given by ![]() $r\cdot m=r^{p^{e}}m$. The ring
$r\cdot m=r^{p^{e}}m$. The ring ![]() $R$ is called
$R$ is called ![]() $F$-finite if
$F$-finite if ![]() $F_{\ast }R$ is a finite
$F_{\ast }R$ is a finite ![]() $R$-module; in other words, the Frobenius morphism on
$R$-module; in other words, the Frobenius morphism on ![]() $\text{Spec}\,R$ is a finite map.
$\text{Spec}\,R$ is a finite map.
Given a ring ![]() $R$ we denote by
$R$ we denote by ![]() ${\mathcal{D}}_{R}$ the ring of (absolute)
${\mathcal{D}}_{R}$ the ring of (absolute) ![]() $\mathbb{Z}$-linear differential operators in the sense of Grothendieck [Reference Grothendieck and Dieudonné15]. Given a polynomial ring
$\mathbb{Z}$-linear differential operators in the sense of Grothendieck [Reference Grothendieck and Dieudonné15]. Given a polynomial ring ![]() $R[t]$, we write
$R[t]$, we write ![]() $\partial _{t}^{[m]}:R[t]\rightarrow R[t]$ for the
$\partial _{t}^{[m]}:R[t]\rightarrow R[t]$ for the ![]() $R$-linear differential operator which sends
$R$-linear differential operator which sends ![]() $t^{n}$ to
$t^{n}$ to ![]() $\binom{n}{m}t^{n-m}$ with the usual convention that
$\binom{n}{m}t^{n-m}$ with the usual convention that ![]() $\binom{n}{m}=0$ for
$\binom{n}{m}=0$ for ![]() $m>n$. We introduce the notation
$m>n$. We introduce the notation
for the ![]() $R$-linear operators which are given by sending
$R$-linear operators which are given by sending ![]() $t^{n}\mapsto \binom{n}{m}t^{n}$ and
$t^{n}\mapsto \binom{n}{m}t^{n}$ and ![]() $t^{n}\mapsto \binom{n+m}{m}t^{n}$, respectively. The operator
$t^{n}\mapsto \binom{n+m}{m}t^{n}$, respectively. The operator ![]() ${\it\theta}_{m}$ is called the (divided power) Euler operator of order
${\it\theta}_{m}$ is called the (divided power) Euler operator of order ![]() $m$.
$m$.
As ![]() $R$ is a ring of prime characteristic
$R$ is a ring of prime characteristic ![]() $p>0$ one has the
$p>0$ one has the ![]() $p$-filtration of its ring of differential operators, see [Reference Chase13]. The ring of (absolute) differential operators
$p$-filtration of its ring of differential operators, see [Reference Chase13]. The ring of (absolute) differential operators ![]() ${\mathcal{D}}_{R}$ is the direct limit of rings
${\mathcal{D}}_{R}$ is the direct limit of rings
called the differential operators of level ![]() $e$. Indeed, the inclusion from
$e$. Indeed, the inclusion from ![]() ${\mathcal{D}}_{R}^{e}\rightarrow {\mathcal{D}}_{R}^{e+1}$ is the composition of the natural map
${\mathcal{D}}_{R}^{e}\rightarrow {\mathcal{D}}_{R}^{e+1}$ is the composition of the natural map ![]() $\text{End}_{R}(F_{\ast }^{e}R)\rightarrow F_{\ast }\,\text{End}_{R}(F_{\ast }^{e}R)$ followed by
$\text{End}_{R}(F_{\ast }^{e}R)\rightarrow F_{\ast }\,\text{End}_{R}(F_{\ast }^{e}R)$ followed by ![]() $F_{\ast }\,\text{End}_{R}(F_{\ast }^{e}R)\rightarrow \text{End}_{R}(F_{\ast }^{e+1}R)$. The direct limit over these maps yields
$F_{\ast }\,\text{End}_{R}(F_{\ast }^{e}R)\rightarrow \text{End}_{R}(F_{\ast }^{e+1}R)$. The direct limit over these maps yields ![]() ${\mathcal{D}}_{R}$.
${\mathcal{D}}_{R}$.
If one uses ![]() $R^{p}\subseteq R$ instead of
$R^{p}\subseteq R$ instead of ![]() $R\rightarrow F_{\ast }R$ then one obtains the more familiar but equivalent description
$R\rightarrow F_{\ast }R$ then one obtains the more familiar but equivalent description ![]() ${\mathcal{D}}_{R}^{e}=\text{End}_{R^{p^{e}}}(R)$ and the union over these is
${\mathcal{D}}_{R}^{e}=\text{End}_{R^{p^{e}}}(R)$ and the union over these is ![]() ${\mathcal{D}}_{R}$. Also note that if
${\mathcal{D}}_{R}$. Also note that if ![]() $R[t]$ is a polynomial ring over
$R[t]$ is a polynomial ring over ![]() $R$ then we have an inclusion
$R$ then we have an inclusion ![]() ${\mathcal{D}}_{R}\rightarrow {\mathcal{D}}_{R[t]}$. Indeed,
${\mathcal{D}}_{R}\rightarrow {\mathcal{D}}_{R[t]}$. Indeed, ![]() $F_{\ast }R[t]=\bigoplus _{i=0}^{p^{e}-1}F_{\ast }Rt^{i}$ and given
$F_{\ast }R[t]=\bigoplus _{i=0}^{p^{e}-1}F_{\ast }Rt^{i}$ and given ![]() $P\in {\mathcal{D}}_{R}^{e}$ we have an extension
$P\in {\mathcal{D}}_{R}^{e}$ we have an extension ![]() $P^{\prime }$ by sending
$P^{\prime }$ by sending ![]() $bt^{i}$ to
$bt^{i}$ to ![]() $P(b)t^{i}$ for
$P(b)t^{i}$ for ![]() $i\geqslant 0$.
$i\geqslant 0$.
We denote by Mod-![]() ${\mathcal{D}}_{R}^{e}$ the category of right
${\mathcal{D}}_{R}^{e}$ the category of right ![]() ${\mathcal{D}}_{R}^{e}$-modules and by Mod-
${\mathcal{D}}_{R}^{e}$-modules and by Mod-![]() $R$ the category of right
$R$ the category of right ![]() $R$-modules.
$R$-modules.
We recall a theorem of Lucas [Reference Lucas19, § XXI] which states that given natural numbers ![]() $n,m$ with
$n,m$ with ![]() $p$-adic expansions
$p$-adic expansions ![]() $n=\sum _{i=0}^{s}a_{i}p^{i}$ and
$n=\sum _{i=0}^{s}a_{i}p^{i}$ and ![]() $m=\sum _{i=0}^{s}b_{i}p^{i}$ with
$m=\sum _{i=0}^{s}b_{i}p^{i}$ with ![]() $a_{i},b_{i}\in \{0,\ldots ,p-1\}$ one has
$a_{i},b_{i}\in \{0,\ldots ,p-1\}$ one has
In particular, it is a crucial ingredient in some proofs of the following relations among the differential operators in positive characteristic which we recall for the convenience of the reader.
Lemma 1.1. Let ![]() $R$ be a regular and
$R$ be a regular and ![]() $F$-finite ring and
$F$-finite ring and ![]() $R[t]$ the polynomial ring over
$R[t]$ the polynomial ring over ![]() $R$ in one variable. Then the following hold:
$R$ in one variable. Then the following hold:
(a)
 $[\partial _{t}^{[p^{i}]},t^{p^{i}}]=1$ which just means
$[\partial _{t}^{[p^{i}]},t^{p^{i}}]=1$ which just means  ${\it\vartheta}_{i}=1+{\it\theta}_{i}$.
${\it\vartheta}_{i}=1+{\it\theta}_{i}$.(b)
 $\frac{(sr)!}{(s!)^{r}}\partial _{t}^{[sr]}=(\partial _{t}^{[s]})^{r}$.
$\frac{(sr)!}{(s!)^{r}}\partial _{t}^{[sr]}=(\partial _{t}^{[s]})^{r}$.(c)
 $\prod _{j=1}^{r}({\it\theta}_{p^{e}}+j)=(\partial _{t}^{[p^{e}]})^{r}(t^{p^{e}})^{r}$.
$\prod _{j=1}^{r}({\it\theta}_{p^{e}}+j)=(\partial _{t}^{[p^{e}]})^{r}(t^{p^{e}})^{r}$.(d)
 $[t,{\it\theta}_{p^{i}}]=-{\it\theta}_{p^{i}-1}t-t$ for all
$[t,{\it\theta}_{p^{i}}]=-{\it\theta}_{p^{i}-1}t-t$ for all  $i$.
$i$.(e)
 $[{\it\theta}_{i},{\it\theta}_{j}]=0$ for all
$[{\it\theta}_{i},{\it\theta}_{j}]=0$ for all  $i,j$.
$i,j$.(f)
 $[t,{\it\theta}_{m}](t^{n})=-\binom{n}{m-1}t^{n+1}$.
$[t,{\it\theta}_{m}](t^{n})=-\binom{n}{m-1}t^{n+1}$.(g)
 ${\it\theta}_{m}\in {\mathcal{D}}_{R}^{e}[{\it\theta}_{1},{\it\theta}_{p},\ldots ,{\it\theta}_{p^{e-1}}]$ for all
${\it\theta}_{m}\in {\mathcal{D}}_{R}^{e}[{\it\theta}_{1},{\it\theta}_{p},\ldots ,{\it\theta}_{p^{e-1}}]$ for all  $m<p^{e}$.
$m<p^{e}$.(h)
 ${\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]t=t{\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]$.
${\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]t=t{\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]$.
Proof. (a) and (b) are proven in [Reference Mustaţă23, Lemma 4.1], and (c), (d), (e), (f) follow from (a) and [Reference Mustaţă23, Lemma 4.1], (g) follows from [Reference Mustaţă23, Remark 6.3] and (a). For (h) we argue along the lines of [Reference Mustaţă23, Lemma 6.4]. The inclusion from right to left follows from (d) and (g). The other inclusion follows similarly using (f). ◻
2 From Cartier modules to right  ${\mathcal{D}}$-modules
${\mathcal{D}}$-modules
In this section, we recall the construction of the functor from Cartier modules to (right) ![]() ${\mathcal{D}}_{R}$-modules.
${\mathcal{D}}_{R}$-modules.
Throughout we assume that ![]() $R$ is an
$R$ is an ![]() $F$-finite regular ring and that all modules considered are finitely generated. By definition, a Cartier module
$F$-finite regular ring and that all modules considered are finitely generated. By definition, a Cartier module ![]() $M$ is an
$M$ is an ![]() $R$-module
$R$-module ![]() $M$ together with an
$M$ together with an ![]() $R$-linear map
$R$-linear map ![]() ${\it\kappa}:F_{\ast }M\rightarrow M$. This is equivalent to the data of an
${\it\kappa}:F_{\ast }M\rightarrow M$. This is equivalent to the data of an ![]() $R$-module and an
$R$-module and an ![]() $R$-linear map
$R$-linear map ![]() $C:M\rightarrow F^{!}M=\text{Hom}_{R}(F_{\ast }R,M)$ (
$C:M\rightarrow F^{!}M=\text{Hom}_{R}(F_{\ast }R,M)$ (![]() $C$ is just the adjoint of
$C$ is just the adjoint of ![]() ${\it\kappa}$ — see [Reference Blickle and Böckle7, Proposition 2.18]). Iterating this map we obtain a directed system
${\it\kappa}$ — see [Reference Blickle and Böckle7, Proposition 2.18]). Iterating this map we obtain a directed system ![]() $M\rightarrow F^{!}M\rightarrow \cdots \rightarrow {F^{e}}^{!}M$. We have
$M\rightarrow F^{!}M\rightarrow \cdots \rightarrow {F^{e}}^{!}M$. We have
Proposition 2.1. Let ![]() $(M,{\it\kappa})$ be a Cartier module. Then the limit
$(M,{\it\kappa})$ be a Cartier module. Then the limit ![]() ${\mathcal{M}}$ over the maps
${\mathcal{M}}$ over the maps ![]() $M\rightarrow {F^{e}}^{!}M$ yields an isomorphism
$M\rightarrow {F^{e}}^{!}M$ yields an isomorphism ![]() ${\mathcal{M}}\rightarrow F^{!}{\mathcal{M}}$ which endows
${\mathcal{M}}\rightarrow F^{!}{\mathcal{M}}$ which endows ![]() ${\mathcal{M}}$ with a right
${\mathcal{M}}$ with a right ![]() ${\mathcal{D}}_{R}$-module structure.
${\mathcal{D}}_{R}$-module structure.
Proof. It is easy to see that the ![]() $C^{e}$ induce a map
$C^{e}$ induce a map ![]() ${\mathcal{M}}\rightarrow {F^{e}}^{!}{\mathcal{M}}$ which is an isomorphism for all
${\mathcal{M}}\rightarrow {F^{e}}^{!}{\mathcal{M}}$ which is an isomorphism for all ![]() $e\geqslant 0$. Each
$e\geqslant 0$. Each ![]() ${F^{e}}^{!}M$ is naturally a right
${F^{e}}^{!}M$ is naturally a right ![]() ${\mathcal{D}}_{R}^{e}$-module by premultiplication. This induces a right
${\mathcal{D}}_{R}^{e}$-module by premultiplication. This induces a right ![]() ${\mathcal{D}}_{R}$-module structure in the limit.◻
${\mathcal{D}}_{R}$-module structure in the limit.◻
It is well known that if ![]() $R$ is smooth over a perfect field
$R$ is smooth over a perfect field ![]() $k$ then the top-dimensional differential forms
$k$ then the top-dimensional differential forms ![]() ${\it\omega}_{R/k}$ are naturally equipped with a right
${\it\omega}_{R/k}$ are naturally equipped with a right ![]() ${\mathcal{D}}_{R}$-module structure and
${\mathcal{D}}_{R}$-module structure and ![]() ${\it\omega}_{R/k}$ induces an equivalence between left and right
${\it\omega}_{R/k}$ induces an equivalence between left and right ![]() ${\mathcal{D}}_{R}$-modules (see [Reference Berthelot3, Chapitre 1]).
${\mathcal{D}}_{R}$-modules (see [Reference Berthelot3, Chapitre 1]).
If ![]() $k$ is only
$k$ is only ![]() $F$-finite but not perfect then the situation is more complicated. We proceed as follows. Fix, once and for all, an isomorphism
$F$-finite but not perfect then the situation is more complicated. We proceed as follows. Fix, once and for all, an isomorphism ![]() $k\rightarrow F^{!}k$. If
$k\rightarrow F^{!}k$. If ![]() $R$ is regular essentially of finite type over
$R$ is regular essentially of finite type over ![]() $k$ with structural morphism
$k$ with structural morphism ![]() $f:\text{Spec}\,R\rightarrow k$ then we set
$f:\text{Spec}\,R\rightarrow k$ then we set ![]() ${\it\omega}_{R}:=f^{!}k$ and we get an induced isomorphism
${\it\omega}_{R}:=f^{!}k$ and we get an induced isomorphism ![]() ${\it\omega}_{R}\rightarrow F^{!}{\it\omega}_{R}$ (note that
${\it\omega}_{R}\rightarrow F^{!}{\it\omega}_{R}$ (note that ![]() $F$ is the absolute Frobenius morphism)Footnote 2. This isomorphism endows
$F$ is the absolute Frobenius morphism)Footnote 2. This isomorphism endows ![]() ${\it\omega}_{R}$ with a right
${\it\omega}_{R}$ with a right ![]() ${\mathcal{D}}_{R}$-module structure and after this choice one has an equivalence between right and left
${\mathcal{D}}_{R}$-module structure and after this choice one has an equivalence between right and left ![]() ${\mathcal{D}}_{R}$-modules that is obtained by tensoring with
${\mathcal{D}}_{R}$-modules that is obtained by tensoring with ![]() ${\it\omega}_{R}^{-1}$.
${\it\omega}_{R}^{-1}$.
In particular, since direct limits commute with tensor products the category of ![]() ${\mathcal{D}}_{R}$-modules obtained in Proposition 2.1 (together with the fixed isomorphism) is equivalent to the category of unit
${\mathcal{D}}_{R}$-modules obtained in Proposition 2.1 (together with the fixed isomorphism) is equivalent to the category of unit ![]() $R[F]$-modules of Emerton and Kisin (see [Reference Blickle5, Theorem 2.27]). Moreover, if we restrict the functor
$R[F]$-modules of Emerton and Kisin (see [Reference Blickle5, Theorem 2.27]). Moreover, if we restrict the functor ![]() $M\mapsto \text{colim}_{e}{F^{e}}^{!}M$ to the category of minimal Cartier modules (or equivalently, if we descend it to Cartier crystals — see [Reference Blickle and Böckle7] and [Reference Blickle and Böckle8] for these notions) then it is also fully faithful.
$M\mapsto \text{colim}_{e}{F^{e}}^{!}M$ to the category of minimal Cartier modules (or equivalently, if we descend it to Cartier crystals — see [Reference Blickle and Böckle7] and [Reference Blickle and Böckle8] for these notions) then it is also fully faithful.
Since test modules are naturally attached to Cartier modules it seems more natural to work with right-![]() ${\mathcal{D}}_{R}$ modules when studying test module filtrations and Bernstein–Sato polynomials. In fact, using this approach we can employ the ordinary higher Euler operators (i.e.
${\mathcal{D}}_{R}$ modules when studying test module filtrations and Bernstein–Sato polynomials. In fact, using this approach we can employ the ordinary higher Euler operators (i.e. ![]() $t^{p^{i}}\partial _{t}^{[p^{i}]}$ instead of
$t^{p^{i}}\partial _{t}^{[p^{i}]}$ instead of ![]() $\partial _{t}^{[p^{i}]}t^{p^{i}}$) and avoid a sign change in the definition of Bernstein–Sato polynomials compared to [Reference Mustaţă23].
$\partial _{t}^{[p^{i}]}t^{p^{i}}$) and avoid a sign change in the definition of Bernstein–Sato polynomials compared to [Reference Mustaţă23].
Note that the case Mustaţă considered in [Reference Mustaţă23] corresponds in our setting to the Cartier module ![]() ${\it\omega}_{R}$ with the (chosen) isomorphism
${\it\omega}_{R}$ with the (chosen) isomorphism ![]() ${\it\omega}_{R}\rightarrow F^{!}{\it\omega}_{R}$. In terms of constructible sheaves on the étale site this corresponds, via the Riemann–Hilbert correspondence of [Reference Emerton and Kisin14] and [Reference Blickle and Böckle7, Theorem 5.15], to the case of the constant sheaf.
${\it\omega}_{R}\rightarrow F^{!}{\it\omega}_{R}$. In terms of constructible sheaves on the étale site this corresponds, via the Riemann–Hilbert correspondence of [Reference Emerton and Kisin14] and [Reference Blickle and Böckle7, Theorem 5.15], to the case of the constant sheaf.
For left ![]() ${\mathcal{D}}_{R}^{e}$-modules one has, as a special case of Morita equivalence, an equivalence with
${\mathcal{D}}_{R}^{e}$-modules one has, as a special case of Morita equivalence, an equivalence with ![]() $R$-Mod for all
$R$-Mod for all ![]() $e\geqslant 0$ (see e.g. [Reference Blickle4, Proposition 3.8 and Corollary 3.10]). A similar statement holds for right modules:
$e\geqslant 0$ (see e.g. [Reference Blickle4, Proposition 3.8 and Corollary 3.10]). A similar statement holds for right modules:
Proposition 2.2. Let ![]() $R$ be an
$R$ be an ![]() $F$-finite regular ring. Then the functor
$F$-finite regular ring. Then the functor ![]() ${F^{e}}^{!}(-)=\text{Hom}_{R}(F_{\ast }^{e}R,-)$ induces an equivalence between Mod-
${F^{e}}^{!}(-)=\text{Hom}_{R}(F_{\ast }^{e}R,-)$ induces an equivalence between Mod-![]() $R$ and Mod-
$R$ and Mod-![]() ${\mathcal{D}}_{R}^{e}$. Its inverse is given by
${\mathcal{D}}_{R}^{e}$. Its inverse is given by ![]() $-\otimes _{\text{End}_{R}(F_{\ast }^{e}R)}F_{\ast }^{e}R$. In particular,
$-\otimes _{\text{End}_{R}(F_{\ast }^{e}R)}F_{\ast }^{e}R$. In particular, ![]() ${F^{e}}^{!}$ reflects isomorphisms.
${F^{e}}^{!}$ reflects isomorphisms.
Proof. By the assumptions on ![]() $R$ we obtain that
$R$ we obtain that ![]() $F_{\ast }^{e}R$ is a finitely generated locally free
$F_{\ast }^{e}R$ is a finitely generated locally free ![]() $R$-module. Note that
$R$-module. Note that ![]() ${F^{e}}^{!}M=\text{Hom}(F_{\ast }^{e}R,M)$ viewed as an
${F^{e}}^{!}M=\text{Hom}(F_{\ast }^{e}R,M)$ viewed as an ![]() $R$-module via the ring isomorphism
$R$-module via the ring isomorphism ![]() $R\rightarrow F_{\ast }^{e}R$ and acting on the first factor is isomorphic to
$R\rightarrow F_{\ast }^{e}R$ and acting on the first factor is isomorphic to ![]() ${F^{e}}^{\ast }M\otimes _{F_{\ast }^{e}R}{F^{e}}^{!}R\cong M\otimes _{R}{F^{e}}^{!}R$ by [Reference Blickle and Böckle7, Lemma 5.7]. Since
${F^{e}}^{\ast }M\otimes _{F_{\ast }^{e}R}{F^{e}}^{!}R\cong M\otimes _{R}{F^{e}}^{!}R$ by [Reference Blickle and Böckle7, Lemma 5.7]. Since ![]() ${F^{e}}^{!}R=\text{Hom}_{R}(F_{\ast }^{e}R,R)$ the claimed equivalence is just a case of Morita equivalence (cf. e.g. [Reference Lam18, Theorem 18.24]).
${F^{e}}^{!}R=\text{Hom}_{R}(F_{\ast }^{e}R,R)$ the claimed equivalence is just a case of Morita equivalence (cf. e.g. [Reference Lam18, Theorem 18.24]).
As ![]() ${F^{e}}^{!}$ induces an equivalence it is fully faithful and hence reflects isomorphisms.◻
${F^{e}}^{!}$ induces an equivalence it is fully faithful and hence reflects isomorphisms.◻
3 Bernstein–Sato polynomials
In this section, we introduce our notion of Bernstein–Sato polynomial after transferring some results of Mustaţă in [Reference Mustaţă23] to our right ![]() ${\mathcal{D}}$-module situation.
${\mathcal{D}}$-module situation.
If ![]() $k$ is perfect and
$k$ is perfect and ![]() $\text{Spec}\,R$ is smooth most of the results in this section follow formally once one observes that given a right
$\text{Spec}\,R$ is smooth most of the results in this section follow formally once one observes that given a right ![]() ${\mathcal{D}}_{R}[t]$-module the operator
${\mathcal{D}}_{R}[t]$-module the operator ![]() $t^{p^{e}}\partial _{t}^{[p^{e}]}$ acts via
$t^{p^{e}}\partial _{t}^{[p^{e}]}$ acts via ![]() $-\partial _{t}^{[p^{e}]}t^{p^{e}}$ on the left module obtained by tensoring with
$-\partial _{t}^{[p^{e}]}t^{p^{e}}$ on the left module obtained by tensoring with ![]() ${\it\omega}_{R[t]/k}^{-1}$ [Reference Berthelot3, 1.3.4].
${\it\omega}_{R[t]/k}^{-1}$ [Reference Berthelot3, 1.3.4].
Lemma 3.1. Let ![]() $R$ be regular and
$R$ be regular and ![]() $F$-finite and let
$F$-finite and let ![]() $R[t]$ be the polynomial ring in one variable over
$R[t]$ be the polynomial ring in one variable over ![]() $R$. Given a right
$R$. Given a right ![]() ${\mathcal{D}}_{R[t]}^{e}$-module
${\mathcal{D}}_{R[t]}^{e}$-module ![]() $M$, there is a unique decomposition as
$M$, there is a unique decomposition as ![]() ${\mathcal{D}}_{R}^{e}$-modules
${\mathcal{D}}_{R}^{e}$-modules
where for ![]() $1\leqslant l\leqslant e$ the operator
$1\leqslant l\leqslant e$ the operator ![]() ${\it\theta}_{p^{l-1}}$ acts on
${\it\theta}_{p^{l-1}}$ acts on ![]() $M_{i}$ via
$M_{i}$ via ![]() $i_{l}$. This decomposition is preserved by
$i_{l}$. This decomposition is preserved by ![]() ${\mathcal{D}}_{R[t]}^{e}$-morphisms. The same statement holds for
${\mathcal{D}}_{R[t]}^{e}$-morphisms. The same statement holds for ![]() ${\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]$-modules.
${\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]$-modules.
Proof. This works similarly to [Reference Mustaţă23, Proposition 4.2]. More precisely, one has
for all ![]() $e\geqslant 0$. Indeed, by Lemma 1.1 it suffices to show that
$e\geqslant 0$. Indeed, by Lemma 1.1 it suffices to show that ![]() $(\partial _{t}^{[p^{e}]})^{p}=0$. This in turn follows from (b) since
$(\partial _{t}^{[p^{e}]})^{p}=0$. This in turn follows from (b) since ![]() $\frac{p^{e+1}!}{(p^{e}!)^{p}}$ is divisible by
$\frac{p^{e+1}!}{(p^{e}!)^{p}}$ is divisible by ![]() $p$. Using this and the fact that
$p$. Using this and the fact that ![]() $[{\it\theta}_{i},{\it\theta}_{j}]=0$ the existence of such a decomposition follows. The remaining statements follow easily.◻
$[{\it\theta}_{i},{\it\theta}_{j}]=0$ the existence of such a decomposition follows. The remaining statements follow easily.◻
Given ![]() $M$ we refer to the decomposition of Lemma 3.1 as the eigenspace decomposition of
$M$ we refer to the decomposition of Lemma 3.1 as the eigenspace decomposition of ![]() $M$(with respect to the Euler operators).
$M$(with respect to the Euler operators).
Note that if ![]() $M$ is a right
$M$ is a right ![]() ${\mathcal{D}}_{R[t]}^{e}$-module then it is in particular a right
${\mathcal{D}}_{R[t]}^{e}$-module then it is in particular a right ![]() ${\mathcal{D}}_{R[t]}^{e-1}$-module. Hence,
${\mathcal{D}}_{R[t]}^{e-1}$-module. Hence, ![]() $M$ admits eigenspace decompositions with respect to
$M$ admits eigenspace decompositions with respect to ![]() ${\mathcal{D}}_{R[t]}^{e}$ and with respect to
${\mathcal{D}}_{R[t]}^{e}$ and with respect to ![]() ${\mathcal{D}}_{R[t]}^{e-1}$ and these are compatible. That is, if
${\mathcal{D}}_{R[t]}^{e-1}$ and these are compatible. That is, if ![]() $M_{(i_{1},\ldots ,i_{e-1})}$ is an eigenspace for the
$M_{(i_{1},\ldots ,i_{e-1})}$ is an eigenspace for the ![]() ${\it\theta}_{p^{l}-1}$ with
${\it\theta}_{p^{l}-1}$ with ![]() $1\leqslant l\leqslant e-1$ then
$1\leqslant l\leqslant e-1$ then
is an eigenspace decomposition with respect to the ![]() ${\it\theta}_{p^{l}-1}$ for
${\it\theta}_{p^{l}-1}$ for ![]() $1\leqslant l\leqslant e$. Again, a similar statement holds for right
$1\leqslant l\leqslant e$. Again, a similar statement holds for right ![]() ${\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]$-modules.
${\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]$-modules.
Given a morphism ![]() $f:\text{Spec}\,S\rightarrow \text{Spec}\,R$ of regular schemes and a right
$f:\text{Spec}\,S\rightarrow \text{Spec}\,R$ of regular schemes and a right ![]() ${\mathcal{D}}_{S}$ module
${\mathcal{D}}_{S}$ module ![]() $M$ one defines the pushforward
$M$ one defines the pushforward ![]() $f_{+}M$ as
$f_{+}M$ as ![]() $f_{\ast }(M\otimes _{{\mathcal{D}}_{S}}S)\otimes _{R}{\mathcal{D}}_{R}$. We thus have a natural map
$f_{\ast }(M\otimes _{{\mathcal{D}}_{S}}S)\otimes _{R}{\mathcal{D}}_{R}$. We thus have a natural map ![]() $f_{\ast }M\rightarrow f_{+}M$. By abuse of notation we denote the image of
$f_{\ast }M\rightarrow f_{+}M$. By abuse of notation we denote the image of ![]() $f_{\ast }M$ under this map again by
$f_{\ast }M$ under this map again by ![]() $f_{\ast }M$. Similarly, we define the pushforward
$f_{\ast }M$. Similarly, we define the pushforward ![]() $f_{+}M$ for a right
$f_{+}M$ for a right ![]() ${\mathcal{D}}_{S}^{e}$-module as
${\mathcal{D}}_{S}^{e}$-module as ![]() $f_{\ast }(M\otimes _{{\mathcal{D}}_{S}^{e}}S)\otimes _{R}{\mathcal{D}}_{R}^{e}$.
$f_{\ast }(M\otimes _{{\mathcal{D}}_{S}^{e}}S)\otimes _{R}{\mathcal{D}}_{R}^{e}$.
Our next goal is to describe this natural map in the setting where we identify ![]() ${\mathcal{D}}_{R}^{e}$ with
${\mathcal{D}}_{R}^{e}$ with ![]() $\text{End}_{R}(F_{\ast }^{e}R)$. We first need a
$\text{End}_{R}(F_{\ast }^{e}R)$. We first need a
Lemma 3.2. Let ![]() $R$ be regular and
$R$ be regular and ![]() $F$-finite and
$F$-finite and ![]() $M$ a (right)
$M$ a (right) ![]() $R$-module. Then
$R$-module. Then ![]() $F_{\ast }^{e}M\otimes _{F_{\ast }^{e}R}\text{End}_{R}(F_{\ast }^{e}R)\rightarrow \text{Hom}_{R}(F_{\ast }^{e}R,M),m\otimes {\it\varphi}\mapsto [r\mapsto m{\it\varphi}(r)]$ is an isomorphism of
$F_{\ast }^{e}M\otimes _{F_{\ast }^{e}R}\text{End}_{R}(F_{\ast }^{e}R)\rightarrow \text{Hom}_{R}(F_{\ast }^{e}R,M),m\otimes {\it\varphi}\mapsto [r\mapsto m{\it\varphi}(r)]$ is an isomorphism of ![]() $\text{End}_{R}(F_{\ast }^{e}R)$-modules.
$\text{End}_{R}(F_{\ast }^{e}R)$-modules.
Proof. The module structure on ![]() $F_{\ast }^{e}M\otimes _{F_{\ast }^{e}R}\text{End}_{R}(F_{\ast }^{e}R)$ is given by multiplication from the right and the one on
$F_{\ast }^{e}M\otimes _{F_{\ast }^{e}R}\text{End}_{R}(F_{\ast }^{e}R)$ is given by multiplication from the right and the one on ![]() $\text{Hom}_{R}(F_{\ast }^{e}R,M)$ is given by premultiplication. Bijectivity is local so that we may assume that
$\text{Hom}_{R}(F_{\ast }^{e}R,M)$ is given by premultiplication. Bijectivity is local so that we may assume that ![]() $F_{\ast }^{e}R$ is a free
$F_{\ast }^{e}R$ is a free ![]() $R$-module (use [Reference Kunz17, Theorem 2.1]). Fix a basis
$R$-module (use [Reference Kunz17, Theorem 2.1]). Fix a basis ![]() $b_{1},\ldots ,b_{n}$ and let
$b_{1},\ldots ,b_{n}$ and let ![]() ${\it\delta}_{i}:F_{\ast }^{e}R\rightarrow F_{\ast }^{e}R$ be the projection onto the
${\it\delta}_{i}:F_{\ast }^{e}R\rightarrow F_{\ast }^{e}R$ be the projection onto the ![]() $i$th basis vector. We define a map
$i$th basis vector. We define a map ![]() $\text{Hom}_{R}(F_{\ast }^{e}R,M)\rightarrow F_{\ast }^{e}M\otimes _{F_{\ast }^{e}R}\text{End}_{R}(F_{\ast }^{e}R),{\it\varphi}\mapsto \sum _{i}{\it\varphi}(b_{i})\otimes {\it\delta}_{i}$ which is a two-sided inverse.◻
$\text{Hom}_{R}(F_{\ast }^{e}R,M)\rightarrow F_{\ast }^{e}M\otimes _{F_{\ast }^{e}R}\text{End}_{R}(F_{\ast }^{e}R),{\it\varphi}\mapsto \sum _{i}{\it\varphi}(b_{i})\otimes {\it\delta}_{i}$ which is a two-sided inverse.◻
Proposition 3.3. Let ![]() $f:\text{Spec}\,S\rightarrow \text{Spec}\,R$ be a morphism of regular
$f:\text{Spec}\,S\rightarrow \text{Spec}\,R$ be a morphism of regular ![]() $F$-finite schemes and let
$F$-finite schemes and let ![]() $M$ be an
$M$ be an ![]() $S$-module. Let
$S$-module. Let ![]() $\text{Hom}_{S}(F_{\ast }^{e}S,M)$ be a right
$\text{Hom}_{S}(F_{\ast }^{e}S,M)$ be a right ![]() ${\mathcal{D}}_{S}^{e}$-module via the action on the first factor. Then
${\mathcal{D}}_{S}^{e}$-module via the action on the first factor. Then ![]() $f_{+}\,\text{Hom}_{S}(F_{\ast }^{e}S,M)$ is naturally isomorphic to
$f_{+}\,\text{Hom}_{S}(F_{\ast }^{e}S,M)$ is naturally isomorphic to ![]() ${F^{e}}^{!}f_{\ast }M$. Under this identification the natural map
${F^{e}}^{!}f_{\ast }M$. Under this identification the natural map
is given by the composition of the canonical maps
with the map
Proof. By definition the pushforward ![]() $f_{+}\,\text{Hom}_{S}(F_{\ast }^{e}S,M)$ is given as
$f_{+}\,\text{Hom}_{S}(F_{\ast }^{e}S,M)$ is given as
Note that the right ![]() $F_{\ast }^{e}R$-module structure on the term
$F_{\ast }^{e}R$-module structure on the term ![]() $F_{\ast }^{e}f_{\ast }(\ldots )$ is given by
$F_{\ast }^{e}f_{\ast }(\ldots )$ is given by ![]() $({\it\psi}\otimes s)\cdot r={\it\psi}\otimes sf(r)$. By Proposition 2.2 the whole expression is isomorphic to
$({\it\psi}\otimes s)\cdot r={\it\psi}\otimes sf(r)$. By Proposition 2.2 the whole expression is isomorphic to ![]() $F_{\ast }^{e}f_{\ast }M\otimes _{F_{\ast }^{e}R}\text{End}_{R}(F_{\ast }^{e}R)$. Using Lemma 3.2 above we obtain that
$F_{\ast }^{e}f_{\ast }M\otimes _{F_{\ast }^{e}R}\text{End}_{R}(F_{\ast }^{e}R)$. Using Lemma 3.2 above we obtain that ![]() $F_{\ast }^{e}f_{\ast }M\otimes _{F_{\ast }^{e}R}\text{End}_{R}(F_{\ast }^{e}R)\rightarrow \text{Hom}_{R}(F_{\ast }^{e}R,f_{\ast }M)$ is an isomorphism. One readily checks that the natural map is given by the formula above.◻
$F_{\ast }^{e}f_{\ast }M\otimes _{F_{\ast }^{e}R}\text{End}_{R}(F_{\ast }^{e}R)\rightarrow \text{Hom}_{R}(F_{\ast }^{e}R,f_{\ast }M)$ is an isomorphism. One readily checks that the natural map is given by the formula above.◻
Next we show that this isomorphism is compatible with direct limits. We first need a general Lemma.
Lemma 3.4. Let ![]() $I$ be a directed system and let
$I$ be a directed system and let ![]() $M_{i},N_{i}$ be
$M_{i},N_{i}$ be ![]() $R_{i}$-modules such that
$R_{i}$-modules such that ![]() $M_{i},N_{i}$ and
$M_{i},N_{i}$ and ![]() $R_{i}$ are filtered by
$R_{i}$ are filtered by ![]() $I$. Write
$I$. Write ![]() $M=\text{colim}_{i}\,M_{i}$,
$M=\text{colim}_{i}\,M_{i}$, ![]() $N=\text{colim}_{i}\,N_{i}$ and
$N=\text{colim}_{i}\,N_{i}$ and ![]() $R=\text{colim}_{i}\,R_{i}$. Then one has an isomorphism
$R=\text{colim}_{i}\,R_{i}$. Then one has an isomorphism ![]() $\text{colim}_{i}(M_{i}\otimes _{R_{i}}N_{i})\rightarrow M\otimes _{R}N$.
$\text{colim}_{i}(M_{i}\otimes _{R_{i}}N_{i})\rightarrow M\otimes _{R}N$.
Proof. We have ![]() $R_{i}$-bilinear maps
$R_{i}$-bilinear maps ![]() $M_{i}\times N_{i}\rightarrow M\otimes _{R}N$ which induce, by the universal properties of the limit and the tensor product, an
$M_{i}\times N_{i}\rightarrow M\otimes _{R}N$ which induce, by the universal properties of the limit and the tensor product, an ![]() $R$-linear map
$R$-linear map ![]() $\text{colim}_{i}\,M_{i}\otimes _{R_{i}}N_{i}\rightarrow M\otimes N,[m_{i}\otimes n_{i}]\mapsto [m_{i}]\otimes [n_{i}]$.
$\text{colim}_{i}\,M_{i}\otimes _{R_{i}}N_{i}\rightarrow M\otimes N,[m_{i}\otimes n_{i}]\mapsto [m_{i}]\otimes [n_{i}]$.
On the other hand, the maps ![]() $M_{i}\times N_{i}\rightarrow \text{colim}_{i}\,M_{i}\otimes _{R_{i}}N_{i},(m_{i},n_{i})\mapsto [m_{i}\otimes n_{i}]$ induce an
$M_{i}\times N_{i}\rightarrow \text{colim}_{i}\,M_{i}\otimes _{R_{i}}N_{i},(m_{i},n_{i})\mapsto [m_{i}\otimes n_{i}]$ induce an ![]() $R$-bilinear map
$R$-bilinear map ![]() $M\times N\rightarrow \text{colim}_{i}\,M_{i}\otimes _{R_{i}}N_{i}$. This in turn induces an
$M\times N\rightarrow \text{colim}_{i}\,M_{i}\otimes _{R_{i}}N_{i}$. This in turn induces an ![]() $R$-linear map
$R$-linear map ![]() $M\otimes N\rightarrow \text{colim}_{i}\,M_{i}\otimes _{R_{i}}N_{i}$ which is an inverse to the map constructed above.◻
$M\otimes N\rightarrow \text{colim}_{i}\,M_{i}\otimes _{R_{i}}N_{i}$ which is an inverse to the map constructed above.◻
Proposition 3.5. Let ![]() $f:\text{Spec}\,S\rightarrow \text{Spec}\,R$ be a morphism of regular
$f:\text{Spec}\,S\rightarrow \text{Spec}\,R$ be a morphism of regular ![]() $F$-finite schemes and assume that
$F$-finite schemes and assume that ![]() $(M,{\it\kappa})$ is a Cartier module on
$(M,{\it\kappa})$ is a Cartier module on ![]() $\text{Spec}\,S$ and denote its limit over the
$\text{Spec}\,S$ and denote its limit over the ![]() $C^{e}$ by
$C^{e}$ by ![]() ${\mathcal{M}}$. Then
${\mathcal{M}}$. Then ![]() $f_{+}{\mathcal{M}}$ is naturally isomorphic to
$f_{+}{\mathcal{M}}$ is naturally isomorphic to ![]() $\text{colim}\,{F^{e}}^{!}f_{\ast }M\cong \text{colim}\,f_{+}{F^{e}}^{!}M$.
$\text{colim}\,{F^{e}}^{!}f_{\ast }M\cong \text{colim}\,f_{+}{F^{e}}^{!}M$.
Proof. The first claimed isomorphism is obtained by applying Lemma 3.4 twice.
For the second claimed isomorphism note that by Proposition 3.3 we have isomorphisms ![]() $f_{+}{F^{e}}^{!}M\rightarrow {F^{e}}^{!}f_{\ast }M$. Moreover, we have a commutative diagram
$f_{+}{F^{e}}^{!}M\rightarrow {F^{e}}^{!}f_{\ast }M$. Moreover, we have a commutative diagram
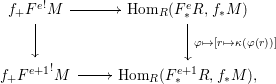
where the left vertical map is given by tensoring ![]() ${\it\varphi}\mapsto [s\mapsto {\it\kappa}({\it\varphi}(s))]$ with the natural maps
${\it\varphi}\mapsto [s\mapsto {\it\kappa}({\it\varphi}(s))]$ with the natural maps ![]() $F_{\ast }^{e}S\rightarrow F_{\ast }^{e+1}S$ and
$F_{\ast }^{e}S\rightarrow F_{\ast }^{e+1}S$ and ![]() ${\mathcal{D}}_{S}^{e}\rightarrow {\mathcal{D}}_{S}^{e+1}$.◻
${\mathcal{D}}_{S}^{e}\rightarrow {\mathcal{D}}_{S}^{e+1}$.◻
Lemma 3.6. Let ![]() $R$ be regular and
$R$ be regular and ![]() $F$-finite and
$F$-finite and ![]() $f\in R$. Denote by
$f\in R$. Denote by ![]() ${\it\gamma}:\text{Spec}\,R\rightarrow \text{Spec}\,R[t]$ the graph embedding along
${\it\gamma}:\text{Spec}\,R\rightarrow \text{Spec}\,R[t]$ the graph embedding along ![]() $f$ and let
$f$ and let ![]() $M$ be a right
$M$ be a right ![]() ${\mathcal{D}}_{R}$-module. Then the quotient
${\mathcal{D}}_{R}$-module. Then the quotient
is a right ![]() ${\mathcal{D}}_{R}^{e}[{\it\theta}_{1},{\it\theta}_{p},\ldots ,{\it\theta}_{p^{e-1}}]$-module.
${\mathcal{D}}_{R}^{e}[{\it\theta}_{1},{\it\theta}_{p},\ldots ,{\it\theta}_{p^{e-1}}]$-module.
Proof. The claim follows from Lemma 1.1 (i) and ![]() $({\it\gamma}_{\ast }M)t={\it\gamma}_{\ast }(Mf)$.◻
$({\it\gamma}_{\ast }M)t={\it\gamma}_{\ast }(Mf)$.◻
Definition 3.7. With the notation of Lemma 3.6 let ![]() ${\rm\Gamma}_{f}^{e}\subseteq \{0,\ldots ,p-1\}^{e}$ be the set of those
${\rm\Gamma}_{f}^{e}\subseteq \{0,\ldots ,p-1\}^{e}$ be the set of those ![]() $i=(i_{1},\ldots ,i_{e})\in \mathbb{F}_{p}^{e}$ for which the eigenspace
$i=(i_{1},\ldots ,i_{e})\in \mathbb{F}_{p}^{e}$ for which the eigenspace ![]() $N_{i}$ of
$N_{i}$ of ![]() $N$ (as constructed in Lemma 3.1) is nontrivial. Then we define the
$N$ (as constructed in Lemma 3.1) is nontrivial. Then we define the ![]() $e$th Bernstein–Sato polynomial of
$e$th Bernstein–Sato polynomial of ![]() $M$ as
$M$ as
where we liftFootnote 3 elements of ![]() $\mathbb{F}_{p}=\{0,\ldots ,p-1\}$ to
$\mathbb{F}_{p}=\{0,\ldots ,p-1\}$ to ![]() $\mathbb{Z}$.
$\mathbb{Z}$.
Note that since we are working with right modules rather then left modules we do not need to invert the sign of the eigenvalues as in [Reference Mustaţă23]. More precisely, Mustaţă considers the action of ![]() $\partial ^{[p^{l}]}t^{p^{l}}$ on the left
$\partial ^{[p^{l}]}t^{p^{l}}$ on the left ![]() ${\mathcal{D}}_{R}^{e}[{\it\vartheta}_{1},\ldots ,{\it\vartheta}_{p^{e-1}}]$-module
${\mathcal{D}}_{R}^{e}[{\it\vartheta}_{1},\ldots ,{\it\vartheta}_{p^{e-1}}]$-module
and if ![]() $(i_{1},\ldots ,i_{e})$ is an eigenvalue for the left action then
$(i_{1},\ldots ,i_{e})$ is an eigenvalue for the left action then ![]() $\frac{-i_{e}}{p}+\cdots +\frac{-i_{1}}{p^{e}}$ is encoded as a zero in a Bernstein–Sato polynomial. As pointed out at the beginning of Section 3 these Bernstein–Sato polynomials coincide with the one defined in 3.7 provided
$\frac{-i_{e}}{p}+\cdots +\frac{-i_{1}}{p^{e}}$ is encoded as a zero in a Bernstein–Sato polynomial. As pointed out at the beginning of Section 3 these Bernstein–Sato polynomials coincide with the one defined in 3.7 provided ![]() $R$ is smooth over a perfect field
$R$ is smooth over a perfect field ![]() $k$. In fact, Theorem 5.4 and [Reference Mustaţă23, Theorem 6.7] show that the polynomials coincide for
$k$. In fact, Theorem 5.4 and [Reference Mustaţă23, Theorem 6.7] show that the polynomials coincide for ![]() $R$ regular essentially of finite type over an
$R$ regular essentially of finite type over an ![]() $F$-finite field and
$F$-finite field and ![]() $e\gg 0$.
$e\gg 0$.
Remark 3.8. We comment on our definition of Bernstein–Sato polynomial and its relation to the definition over the complex numbers. Let ![]() $X=\mathbb{A}_{\mathbb{C}}^{n+1}$. Then
$X=\mathbb{A}_{\mathbb{C}}^{n+1}$. Then ![]() ${\mathcal{D}}_{X}$ is just the Weyl algebra
${\mathcal{D}}_{X}$ is just the Weyl algebra ![]() $\mathbb{C}[x_{1},\ldots ,x_{n+1},\partial _{1},\ldots ,\partial _{n+1}]$ with the usual relation
$\mathbb{C}[x_{1},\ldots ,x_{n+1},\partial _{1},\ldots ,\partial _{n+1}]$ with the usual relation ![]() $[\partial _{i},x_{j}]={\it\delta}_{ij}$. Assume that the hypersurface is given by
$[\partial _{i},x_{j}]={\it\delta}_{ij}$. Assume that the hypersurface is given by ![]() $t=x_{n+1}$. Then for a regular holonomic quasi-unipotent
$t=x_{n+1}$. Then for a regular holonomic quasi-unipotent ![]() ${\mathcal{D}}_{X}$-module
${\mathcal{D}}_{X}$-module ![]() $M$ the
$M$ the ![]() $V$-filtration along
$V$-filtration along ![]() $t$ is a decreasing
$t$ is a decreasing ![]() $\mathbb{Q}$-indexed filtration with certain properties (see [Reference Budur, Bogomolov and Tschinkel11] for a definition).
$\mathbb{Q}$-indexed filtration with certain properties (see [Reference Budur, Bogomolov and Tschinkel11] for a definition).
In particular, one has (cf. [Reference Sabbah24, Proposition 2.1.7]) ![]() $V^{k}M=V^{k}({\mathcal{D}}_{R})V^{0}(M)$ for
$V^{k}M=V^{k}({\mathcal{D}}_{R})V^{0}(M)$ for ![]() $k\leqslant 0$ but
$k\leqslant 0$ but ![]() $V^{k}M=V^{k-1}({\mathcal{D}}_{R})V^{1}(M)$ only for
$V^{k}M=V^{k-1}({\mathcal{D}}_{R})V^{1}(M)$ only for ![]() $k\geqslant 1$.Footnote 4 Here
$k\geqslant 1$.Footnote 4 Here ![]() $V^{k}({\mathcal{D}}_{X})$ is the
$V^{k}({\mathcal{D}}_{X})$ is the ![]() $V$-filtration on
$V$-filtration on ![]() ${\mathcal{D}}_{X}$ which is given by
${\mathcal{D}}_{X}$ which is given by
and by
where ![]() ${\mathcal{D}}_{X,-k}$ are the differential operators of order
${\mathcal{D}}_{X,-k}$ are the differential operators of order ![]() ${\leqslant}-k$. Finally,
${\leqslant}-k$. Finally, ![]() $V^{0}({\mathcal{D}}_{X})$ is given by
$V^{0}({\mathcal{D}}_{X})$ is given by ![]() $\{\sum _{n\geqslant m}f(x)\partial _{x}^{{\it\alpha}}t^{n}\partial _{t}^{m}\,|\,f\in \mathbb{C}[x_{1},\ldots ,x_{n}]\}$.
$\{\sum _{n\geqslant m}f(x)\partial _{x}^{{\it\alpha}}t^{n}\partial _{t}^{m}\,|\,f\in \mathbb{C}[x_{1},\ldots ,x_{n}]\}$.
The Bernstein–Sato polynomial of ![]() $M$ is now defined as the monic minimal polynomial
$M$ is now defined as the monic minimal polynomial ![]() $b\in \mathbb{C}[s]$ such that
$b\in \mathbb{C}[s]$ such that ![]() $b(t\partial _{t}+k)V^{k}M\subseteq V^{k+1}M$ for all
$b(t\partial _{t}+k)V^{k}M\subseteq V^{k+1}M$ for all ![]() $k\in \mathbb{Z}$. By the above it is actually sufficient to construct a Bernstein–Sato polynomial that satisfies the above identity for
$k\in \mathbb{Z}$. By the above it is actually sufficient to construct a Bernstein–Sato polynomial that satisfies the above identity for ![]() $k=-1,0,1$.
$k=-1,0,1$.
Since in characteristic ![]() $p>0$ the Briançon–Skoda theorem [Reference Blickle6, Theorem 4.21] always yields
$p>0$ the Briançon–Skoda theorem [Reference Blickle6, Theorem 4.21] always yields ![]() $f^{n}{\it\tau}(M,f^{t-n})={\it\tau}(M,f^{t})$ for
$f^{n}{\it\tau}(M,f^{t-n})={\it\tau}(M,f^{t})$ for ![]() $t\geqslant n$ our definition can be seen as an analog of the one over the complex numbers since we only need to control the range
$t\geqslant n$ our definition can be seen as an analog of the one over the complex numbers since we only need to control the range ![]() $k=0$.
$k=0$.
4 Test modules and  ${\mathcal{D}}$-modules
${\mathcal{D}}$-modules
In this section, we relate test modules of a Cartier module ![]() $M$ over a regular
$M$ over a regular ![]() $F$-finite ring
$F$-finite ring ![]() $R$ with certain right
$R$ with certain right ![]() ${\mathcal{D}}_{R}^{e}$ submodules of
${\mathcal{D}}_{R}^{e}$ submodules of ![]() ${F^{e}}^{!}M$. First, we need several technical lemmata concerning test modules.
${F^{e}}^{!}M$. First, we need several technical lemmata concerning test modules.
Lemma 4.1. Let ![]() $R$ be essentially of finite type over an
$R$ be essentially of finite type over an ![]() $F$-finite field,
$F$-finite field, ![]() $(M,{\it\kappa})$ an
$(M,{\it\kappa})$ an ![]() $F$-pure coherent Cartier module,
$F$-pure coherent Cartier module, ![]() $t\in \mathbb{Q}_{{\geqslant}0}$ and let
$t\in \mathbb{Q}_{{\geqslant}0}$ and let ![]() $f$ be an
$f$ be an ![]() $M$-regular element. Then one has
$M$-regular element. Then one has ![]() ${\it\kappa}^{e}f^{\lceil tp^{e}\rceil }f^{l}M\subseteq {\it\kappa}^{e+1}f^{\lceil tp^{e+1}\rceil }f^{l}M$ for all
${\it\kappa}^{e}f^{\lceil tp^{e}\rceil }f^{l}M\subseteq {\it\kappa}^{e+1}f^{\lceil tp^{e+1}\rceil }f^{l}M$ for all ![]() $l\geqslant 0$. In particular, for
$l\geqslant 0$. In particular, for ![]() $e\gg 0$ depending on
$e\gg 0$ depending on ![]() $l$ equality holds.
$l$ equality holds.
Proof. First of all, for any ![]() $l$ we have
$l$ we have
where we used that ![]() ${\it\kappa}$ is surjective since
${\it\kappa}$ is surjective since ![]() $M$ is
$M$ is ![]() $F$-pure.
$F$-pure.
Next, we have
where we used the previous observation with ![]() $n=1$ for the last inclusion. Applying
$n=1$ for the last inclusion. Applying ![]() ${\it\kappa}^{e}$ on both sides yields the claimed inclusion. Since
${\it\kappa}^{e}$ on both sides yields the claimed inclusion. Since ![]() $M$ is coherent the ascending chain
$M$ is coherent the ascending chain ![]() ${\it\kappa}^{e}f^{\lceil tp^{e}\rceil }f^{l}M$ stabilizes.◻
${\it\kappa}^{e}f^{\lceil tp^{e}\rceil }f^{l}M$ stabilizes.◻
Remark 4.2. With the notation of Lemma 4.1 if ![]() $t=\frac{m}{p^{s}}$ and
$t=\frac{m}{p^{s}}$ and ![]() $n\geqslant s$ is such that
$n\geqslant s$ is such that ![]() ${\it\kappa}^{n}f^{l}M=M$ then equality holds for any
${\it\kappa}^{n}f^{l}M=M$ then equality holds for any ![]() $e\geqslant 2n$. Indeed,
$e\geqslant 2n$. Indeed,
which is independent of ![]() $e$.
$e$.
If ![]() $R$ is a polynomial ring and
$R$ is a polynomial ring and ![]() $M$ is given explicitly by a presentation
$M$ is given explicitly by a presentation ![]() $R^{a}\rightarrow R^{b}\rightarrow M$ then we expect that it should be possible to determine
$R^{a}\rightarrow R^{b}\rightarrow M$ then we expect that it should be possible to determine ![]() $e$ explicitly for a given hypersurface
$e$ explicitly for a given hypersurface ![]() $f$.
$f$.
Lemma 4.3. Let ![]() $R$ be essentially of finite type over an
$R$ be essentially of finite type over an ![]() $F$-finite field, let
$F$-finite field, let ![]() $(M,{\it\kappa})$ be an
$(M,{\it\kappa})$ be an ![]() $F$-regular coherent Cartier module,
$F$-regular coherent Cartier module, ![]() $t\in \mathbb{Z}[\frac{1}{p}]$ and let
$t\in \mathbb{Z}[\frac{1}{p}]$ and let ![]() $f$ be an
$f$ be an ![]() $M$-regular element. Consider the Cartier algebra
$M$-regular element. Consider the Cartier algebra ![]() ${\mathcal{C}}$ generated in degree
${\mathcal{C}}$ generated in degree ![]() $e\geqslant 1$ by
$e\geqslant 1$ by ![]() ${\it\kappa}^{e}f^{\lceil tp^{e}\rceil }$. Then
${\it\kappa}^{e}f^{\lceil tp^{e}\rceil }$. Then ![]() $\underline{M}_{{\mathcal{C}}}={\it\kappa}^{e}f^{\lceil tp^{e}\rceil }M$ for all
$\underline{M}_{{\mathcal{C}}}={\it\kappa}^{e}f^{\lceil tp^{e}\rceil }M$ for all ![]() $e\gg 0$.
$e\gg 0$.
Proof. The calculation
with ![]() $0\leqslant r=\lceil tp^{a^{\prime }}\rceil +\lceil tp^{a}\rceil p^{a^{\prime }}-\lceil tp^{a+a^{\prime }}\rceil$ shows that
$0\leqslant r=\lceil tp^{a^{\prime }}\rceil +\lceil tp^{a}\rceil p^{a^{\prime }}-\lceil tp^{a+a^{\prime }}\rceil$ shows that ![]() ${\mathcal{C}}$ is in indeed a Cartier algebra. Applying Lemma 4.1 with
${\mathcal{C}}$ is in indeed a Cartier algebra. Applying Lemma 4.1 with ![]() $l=0$ shows that
$l=0$ shows that ![]() ${\it\kappa}^{e}f^{\lceil tp^{e}\rceil }M\subseteq {\it\kappa}^{e+1}f^{\lceil tp^{e+1}\rceil }M$ (with equality for
${\it\kappa}^{e}f^{\lceil tp^{e}\rceil }M\subseteq {\it\kappa}^{e+1}f^{\lceil tp^{e+1}\rceil }M$ (with equality for ![]() $e\gg 0$) so that for all
$e\gg 0$) so that for all ![]() $e\gg 0$ we have
$e\gg 0$ we have ![]() ${\it\kappa}^{e}f^{\lceil tp^{e}\rceil }M={\mathcal{C}}_{+}M$.
${\it\kappa}^{e}f^{\lceil tp^{e}\rceil }M={\mathcal{C}}_{+}M$.
By [Reference Blickle6, Proposition 2.13 and Corollary 2.14], one has ![]() $\underline{M}_{{\mathcal{C}}}=({\mathcal{C}}_{+})^{h}M$ for all
$\underline{M}_{{\mathcal{C}}}=({\mathcal{C}}_{+})^{h}M$ for all ![]() $h\gg 0$. Fix such an
$h\gg 0$. Fix such an ![]() $h$ and
$h$ and ![]() $e$ as above. Then the inclusion from left to right follows by the same argument as above.
$e$ as above. Then the inclusion from left to right follows by the same argument as above.
For the other inclusion we have to prove that ![]() ${\mathcal{C}}_{+}{\it\kappa}^{e}f^{\lceil tp^{e}\rceil }M\supseteq {\it\kappa}^{e}f^{\lceil tp^{e}\rceil }M$ for
${\mathcal{C}}_{+}{\it\kappa}^{e}f^{\lceil tp^{e}\rceil }M\supseteq {\it\kappa}^{e}f^{\lceil tp^{e}\rceil }M$ for ![]() $e\gg 0$. We use the assumption on
$e\gg 0$. We use the assumption on ![]() $t$ and write
$t$ and write ![]() $t=\frac{m}{p^{s}}$ with
$t=\frac{m}{p^{s}}$ with ![]() $m\in \mathbb{Z}$ and assume that
$m\in \mathbb{Z}$ and assume that ![]() $e\geqslant s$. We consider elements of the form
$e\geqslant s$. We consider elements of the form ![]() ${\it\kappa}^{e^{\prime }}f^{\lceil tp^{e^{\prime }}\rceil }\in {\mathcal{C}}_{+}$. For
${\it\kappa}^{e^{\prime }}f^{\lceil tp^{e^{\prime }}\rceil }\in {\mathcal{C}}_{+}$. For ![]() $e^{\prime }\geqslant e$ we compute
$e^{\prime }\geqslant e$ we compute
where for the last equality we used the ![]() $F$-regularity of
$F$-regularity of ![]() $(M,{\it\kappa})$ (see [Reference Stäbler25, Proposition 5.2] and Lemma 4.1) possibly choosing a larger
$(M,{\it\kappa})$ (see [Reference Stäbler25, Proposition 5.2] and Lemma 4.1) possibly choosing a larger ![]() $e^{\prime }$.◻
$e^{\prime }$.◻
Next, we prove a variant of [Reference Blickle, Mustaţă and Smith10, Lemma 2.1] for modules.
Lemma 4.4. Let ![]() $R$ be essentially of finite type over an
$R$ be essentially of finite type over an ![]() $F$-finite field. Let
$F$-finite field. Let ![]() $(M,{\it\kappa})$ be an
$(M,{\it\kappa})$ be an ![]() $F$-regular coherent Cartier module,
$F$-regular coherent Cartier module, ![]() $f\in R$ a nonzero divisor on
$f\in R$ a nonzero divisor on ![]() $M$ and
$M$ and ![]() $t\in \mathbb{Z}[\frac{1}{p}]$. Then for all
$t\in \mathbb{Z}[\frac{1}{p}]$. Then for all ![]() $e\gg 0$ we have
$e\gg 0$ we have ![]() ${\it\tau}(M,f^{t})={\it\kappa}^{e}(f^{tp^{e}}M)$.
${\it\tau}(M,f^{t})={\it\kappa}^{e}(f^{tp^{e}}M)$.
Proof. First of all, note that ![]() $M_{f}$ is
$M_{f}$ is ![]() $F$-regular with respect to the Cartier algebra
$F$-regular with respect to the Cartier algebra ![]() ${\mathcal{C}}$ generated by the
${\mathcal{C}}$ generated by the ![]() ${\it\kappa}^{e}f^{\lceil tp^{e}\rceil }$. By [Reference Blickle6, Theorem 3.11], we thus have
${\it\kappa}^{e}f^{\lceil tp^{e}\rceil }$. By [Reference Blickle6, Theorem 3.11], we thus have
By Lemma 4.3 we may replace ![]() $\underline{M}_{{\mathcal{C}}}$ by
$\underline{M}_{{\mathcal{C}}}$ by ![]() ${\it\kappa}^{e}f^{tp^{e}}M$ for any sufficiently large
${\it\kappa}^{e}f^{tp^{e}}M$ for any sufficiently large ![]() $e$. As seen in the proof of Lemma 4.3 we have
$e$. As seen in the proof of Lemma 4.3 we have ![]() ${\mathcal{C}}_{n}={\it\kappa}^{n}f^{\lceil tp^{n}\rceil }R$.
${\mathcal{C}}_{n}={\it\kappa}^{n}f^{\lceil tp^{n}\rceil }R$.
We compute
and for ![]() $tp^{n}\in \mathbb{Z}$ equality holds. In particular, using Lemma 4.1 we obtain that
$tp^{n}\in \mathbb{Z}$ equality holds. In particular, using Lemma 4.1 we obtain that
Finally, we have for ![]() $n\gg 0$ and suitable
$n\gg 0$ and suitable ![]() $e^{\prime }$
$e^{\prime }$
where the last equality is due to the ![]() $F$-regularity of
$F$-regularity of ![]() $(M,{\it\kappa})$.◻
$(M,{\it\kappa})$.◻
Remark 4.5. In particular, if ![]() $t=\frac{m}{p^{s}}\in \mathbb{Z}[\frac{1}{p}]$ we may write
$t=\frac{m}{p^{s}}\in \mathbb{Z}[\frac{1}{p}]$ we may write ![]() $t=\frac{mp^{e-s}}{p^{e}}$ so that
$t=\frac{mp^{e-s}}{p^{e}}$ so that ![]() ${\it\tau}(M,f^{t})={\it\kappa}^{e}(f^{m^{\prime }}M)$, where
${\it\tau}(M,f^{t})={\it\kappa}^{e}(f^{m^{\prime }}M)$, where ![]() $m^{\prime }=mp^{e-s}$.
$m^{\prime }=mp^{e-s}$.
Also note that by right continuity (i.e. ![]() ${\it\tau}(M,f^{t})={\it\tau}(M,f^{t+{\it\varepsilon}})$ for small
${\it\tau}(M,f^{t})={\it\tau}(M,f^{t+{\it\varepsilon}})$ for small ![]() ${\it\varepsilon}>0$) we may always assume that
${\it\varepsilon}>0$) we may always assume that ![]() $t\in \mathbb{Z}[\frac{1}{p}]$ if we want to compute test modules.
$t\in \mathbb{Z}[\frac{1}{p}]$ if we want to compute test modules.
Given a ![]() ${\it\kappa}$-module
${\it\kappa}$-module ![]() $M$ we have a natural map (the adjoint of
$M$ we have a natural map (the adjoint of ![]() ${\it\kappa}$)
${\it\kappa}$) ![]() $C:M\rightarrow F^{!}M,m\mapsto (r\mapsto {\it\kappa}(rm))$ and if
$C:M\rightarrow F^{!}M,m\mapsto (r\mapsto {\it\kappa}(rm))$ and if ![]() $N$ is an
$N$ is an ![]() $R$-submodule of
$R$-submodule of ![]() $M$ we may consider the right
$M$ we may consider the right ![]() ${\mathcal{D}}_{R}^{e}$-submodule of
${\mathcal{D}}_{R}^{e}$-submodule of ![]() ${F^{e}}^{!}M$ generated by
${F^{e}}^{!}M$ generated by ![]() $N$ which by definition is
$N$ which by definition is ![]() $C^{e}(N)\cdot {\mathcal{D}}_{R}^{e}$.
$C^{e}(N)\cdot {\mathcal{D}}_{R}^{e}$.
Lemma 4.6. Let ![]() $R$ be regular and
$R$ be regular and ![]() $F$-finite. Let
$F$-finite. Let ![]() $M$ be a coherent
$M$ be a coherent ![]() ${\it\kappa}$-module and let
${\it\kappa}$-module and let ![]() $N$ be an
$N$ be an ![]() $R$-submodule of
$R$-submodule of ![]() $M$. Then
$M$. Then ![]() ${F^{e}}^{!}{\it\kappa}^{e}(F_{\ast }^{e}N)$ is the right
${F^{e}}^{!}{\it\kappa}^{e}(F_{\ast }^{e}N)$ is the right ![]() ${\mathcal{D}}_{R}^{e}$-submodule of
${\mathcal{D}}_{R}^{e}$-submodule of ![]() ${F^{e}}^{!}M$ generated by the image of
${F^{e}}^{!}M$ generated by the image of ![]() $N$ in
$N$ in ![]() ${F^{e}}^{!}M$.
${F^{e}}^{!}M$.
Proof. Clearly, ![]() ${F^{e}}^{!}{\it\kappa}^{e}(F_{\ast }^{e}N)$ is a right
${F^{e}}^{!}{\it\kappa}^{e}(F_{\ast }^{e}N)$ is a right ![]() ${\mathcal{D}}_{R}^{e}$-submodule of
${\mathcal{D}}_{R}^{e}$-submodule of ![]() ${F^{e}}^{!}M$. So one inclusion is dealt with once we show that
${F^{e}}^{!}M$. So one inclusion is dealt with once we show that ![]() $C^{e}(N)\subseteq {F^{e}}^{!}{\it\kappa}^{e}(F_{\ast }^{e}N)$. If
$C^{e}(N)\subseteq {F^{e}}^{!}{\it\kappa}^{e}(F_{\ast }^{e}N)$. If ![]() $n\in N$ then
$n\in N$ then ![]() $C^{e}(n):F_{\ast }^{e}R\rightarrow M,r\mapsto {\it\kappa}^{e}(rn)$ and
$C^{e}(n):F_{\ast }^{e}R\rightarrow M,r\mapsto {\it\kappa}^{e}(rn)$ and ![]() $C^{e}(rn)\in {\it\kappa}^{e}(F_{\ast }^{e}N)$ for all
$C^{e}(rn)\in {\it\kappa}^{e}(F_{\ast }^{e}N)$ for all ![]() $r\in F_{\ast }^{e}R$.
$r\in F_{\ast }^{e}R$.
For the other inclusion we may assume that ![]() $R$ is local. Hence,
$R$ is local. Hence, ![]() $F_{\ast }^{e}R$ is free of rank
$F_{\ast }^{e}R$ is free of rank ![]() $s=p^{e\dim R}$ since
$s=p^{e\dim R}$ since ![]() $R$ is regular and
$R$ is regular and ![]() $F$-finite (see [Reference Kunz17, Theorem 2.1]). Fix a basis
$F$-finite (see [Reference Kunz17, Theorem 2.1]). Fix a basis ![]() $b_{1},\ldots ,b_{s}$ of
$b_{1},\ldots ,b_{s}$ of ![]() $F_{\ast }^{e}R$ and let
$F_{\ast }^{e}R$ and let ![]() ${\it\varphi}:F_{\ast }^{e}R\rightarrow {\it\kappa}^{e}(F_{\ast }^{e}N)$ be an element of
${\it\varphi}:F_{\ast }^{e}R\rightarrow {\it\kappa}^{e}(F_{\ast }^{e}N)$ be an element of ![]() ${F^{e}}^{!}{\it\kappa}^{e}(F_{\ast }^{e}N)$. Each
${F^{e}}^{!}{\it\kappa}^{e}(F_{\ast }^{e}N)$. Each ![]() ${\it\varphi}(b_{i})$ is of the form
${\it\varphi}(b_{i})$ is of the form ![]() ${\it\kappa}^{e}(n_{i})$ for some
${\it\kappa}^{e}(n_{i})$ for some ![]() $n_{i}\in N$. We then can write
$n_{i}\in N$. We then can write ![]() ${\it\varphi}$ as
${\it\varphi}$ as ![]() $\sum _{i=1}^{s}{\it\psi}_{i}\circ p_{i}$, where
$\sum _{i=1}^{s}{\it\psi}_{i}\circ p_{i}$, where ![]() $p_{i}:F_{\ast }^{e}R\rightarrow F_{\ast }^{e}R,p_{i}(b_{j})={\it\delta}_{ij}$ and
$p_{i}:F_{\ast }^{e}R\rightarrow F_{\ast }^{e}R,p_{i}(b_{j})={\it\delta}_{ij}$ and ![]() ${\it\psi}_{i}(r)={\it\kappa}^{e}(rn_{i})$. Then
${\it\psi}_{i}(r)={\it\kappa}^{e}(rn_{i})$. Then ![]() $p_{i}\in {\mathcal{D}}_{R}^{e}$ and
$p_{i}\in {\mathcal{D}}_{R}^{e}$ and ![]() ${\it\psi}_{i}\in C^{e}(N)$ as desired.◻
${\it\psi}_{i}\in C^{e}(N)$ as desired.◻
Example 4.7. Let ![]() $M$ be a Cartier module on
$M$ be a Cartier module on ![]() $R$ and let
$R$ and let ![]() ${\it\gamma}:\text{Spec}\,R\rightarrow \text{Spec}\,R[t]$ be the graph embedding along
${\it\gamma}:\text{Spec}\,R\rightarrow \text{Spec}\,R[t]$ be the graph embedding along ![]() $f$. Then one has, in general, a proper inclusion
$f$. Then one has, in general, a proper inclusion ![]() ${\it\gamma}_{\ast }(C^{e}(M)){\mathcal{D}}_{R}^{e}\subseteq {\it\gamma}_{\ast }(C^{e}(M){\mathcal{D}}_{R}^{e}){\mathcal{D}}_{R}^{e}$. Here we let
${\it\gamma}_{\ast }(C^{e}(M)){\mathcal{D}}_{R}^{e}\subseteq {\it\gamma}_{\ast }(C^{e}(M){\mathcal{D}}_{R}^{e}){\mathcal{D}}_{R}^{e}$. Here we let ![]() ${\mathcal{D}}_{R}^{e}$ act via the inclusion
${\mathcal{D}}_{R}^{e}$ act via the inclusion ![]() ${\mathcal{D}}_{R}^{e}\rightarrow {\mathcal{D}}_{R[t]}^{e}$. Also note that
${\mathcal{D}}_{R}^{e}\rightarrow {\mathcal{D}}_{R[t]}^{e}$. Also note that ![]() $C^{e}(M){\mathcal{D}}_{R}^{e}={F^{e}}^{!}M$.
$C^{e}(M){\mathcal{D}}_{R}^{e}={F^{e}}^{!}M$.
As an example for this let ![]() $R=k[y]$ and
$R=k[y]$ and ![]() $M=R$ with twisted Cartier structure
$M=R$ with twisted Cartier structure ![]() ${\it\kappa}\cdot y$, where
${\it\kappa}\cdot y$, where ![]() ${\it\kappa}(y^{i})={\it\delta}_{i(p-1)}$ for
${\it\kappa}(y^{i})={\it\delta}_{i(p-1)}$ for ![]() $0\leqslant i\leqslant p-1$. Then
$0\leqslant i\leqslant p-1$. Then ![]() ${F^{e}}^{!}R$ contains
${F^{e}}^{!}R$ contains ![]() ${\it\kappa}^{e}$ and we claim that this is not contained in
${\it\kappa}^{e}$ and we claim that this is not contained in ![]() ${\it\gamma}_{\ast }(C^{e}(M)){\mathcal{D}}_{R}^{e}$. Indeed, any element
${\it\gamma}_{\ast }(C^{e}(M)){\mathcal{D}}_{R}^{e}$. Indeed, any element ![]() ${\it\psi}$ in
${\it\psi}$ in ![]() ${\it\gamma}_{\ast }(C^{e}(M)){\mathcal{D}}_{R}^{e}$ is of the form
${\it\gamma}_{\ast }(C^{e}(M)){\mathcal{D}}_{R}^{e}$ is of the form
where ![]() $P_{l}\in {\mathcal{D}}_{R}^{e}$ and we used that
$P_{l}\in {\mathcal{D}}_{R}^{e}$ and we used that ![]() $({\it\kappa}y)^{e}={\it\kappa}^{e}y^{1+p+\cdots +p^{e-1}}$. Here
$({\it\kappa}y)^{e}={\it\kappa}^{e}y^{1+p+\cdots +p^{e-1}}$. Here ![]() ${\it\kappa}^{e}$ is given by acting on basis elements
${\it\kappa}^{e}$ is given by acting on basis elements ![]() $y^{i}t^{j}\mapsto 1$ if
$y^{i}t^{j}\mapsto 1$ if ![]() $i+j=p^{e}-1$ and
$i+j=p^{e}-1$ and ![]() $0$ else. To see the claim let now
$0$ else. To see the claim let now ![]() $i=0$ and
$i=0$ and ![]() $j=p^{e}-1$. Then we can write
$j=p^{e}-1$. Then we can write ![]() ${\it\psi}(t^{p^{e}-1})$ as
${\it\psi}(t^{p^{e}-1})$ as ![]() $y\cdot \sum \ldots$ and clearly this cannot evaluate to
$y\cdot \sum \ldots$ and clearly this cannot evaluate to ![]() $1$. Hence, the inclusion is strict.
$1$. Hence, the inclusion is strict.
Combining the two previous lemmata we obtain the following
Corollary 4.8. Let ![]() $R$ be regular and essentially of finite type over an
$R$ be regular and essentially of finite type over an ![]() $F$-finite field. Let
$F$-finite field. Let ![]() $(M,{\it\kappa})$ be an
$(M,{\it\kappa})$ be an ![]() $F$-regular Cartier module and let
$F$-regular Cartier module and let ![]() $f\in R$ be a nonzero divisor on
$f\in R$ be a nonzero divisor on ![]() $M$ and
$M$ and ![]() $t\in \mathbb{Z}[\frac{1}{p}]$. Then for
$t\in \mathbb{Z}[\frac{1}{p}]$. Then for ![]() $e\gg 0$ and
$e\gg 0$ and ![]() $t=\frac{m}{p^{e}}$ we have
$t=\frac{m}{p^{e}}$ we have ![]() ${F^{e}}^{!}{\it\tau}(M,f^{t})=C^{e}(f^{m}M)\cdot {\mathcal{D}}_{R}^{e}$.
${F^{e}}^{!}{\it\tau}(M,f^{t})=C^{e}(f^{m}M)\cdot {\mathcal{D}}_{R}^{e}$.
5 Test modules and Bernstein–Sato polynomials
In this section, we prove the main result of this paper. That is, we show that the roots of the Bernstein–Sato polynomials for ![]() $e$ sufficiently large are precisely the
$e$ sufficiently large are precisely the ![]() $F$-jumping numbers in the range
$F$-jumping numbers in the range ![]() $(0,1]$ of the test module filtration.
$(0,1]$ of the test module filtration.
Recall that given a morphism ![]() ${\it\gamma}:\text{Spec}\,R\rightarrow \text{Spec}\,R[t]$ and a right
${\it\gamma}:\text{Spec}\,R\rightarrow \text{Spec}\,R[t]$ and a right ![]() ${\mathcal{D}}_{R}^{e}$-module
${\mathcal{D}}_{R}^{e}$-module ![]() $M$ we denote the image of the natural map
$M$ we denote the image of the natural map ![]() ${\it\gamma}_{\ast }M\rightarrow {\it\gamma}_{+}M$ again by
${\it\gamma}_{\ast }M\rightarrow {\it\gamma}_{+}M$ again by ![]() ${\it\gamma}_{\ast }M$. In particular,
${\it\gamma}_{\ast }M$. In particular, ![]() ${\it\gamma}_{\ast }M$ is then contained in
${\it\gamma}_{\ast }M$ is then contained in ![]() $\text{Hom}_{R[t]}(F_{\ast }^{e}R[t],{\it\gamma}_{\ast }M)$ (see Proposition 3.3).
$\text{Hom}_{R[t]}(F_{\ast }^{e}R[t],{\it\gamma}_{\ast }M)$ (see Proposition 3.3).
Lemma 5.1. Let ![]() $R$ be a regular
$R$ be a regular ![]() $F$-finite ring and
$F$-finite ring and ![]() $(M,{\it\kappa})$ a Cartier module with adjoint
$(M,{\it\kappa})$ a Cartier module with adjoint ![]() $C$. Let
$C$. Let ![]() $f\in R$ and denote by
$f\in R$ and denote by ![]() ${\it\gamma}:\text{Spec}\,R\rightarrow \text{Spec}\,R[t]$ the graph embedding along
${\it\gamma}:\text{Spec}\,R\rightarrow \text{Spec}\,R[t]$ the graph embedding along ![]() $f$. Then we have an eigenspace decomposition
$f$. Then we have an eigenspace decomposition
where
is the projection onto the eigenspace.
Proof. We denote ![]() $({\it\gamma}_{\ast }C^{e}(M)){\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]$ by
$({\it\gamma}_{\ast }C^{e}(M)){\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]$ by ![]() $N$ and its eigenspaces by
$N$ and its eigenspaces by ![]() $N_{i}$. First of all, note that Lucas’ theorem shows that
$N_{i}$. First of all, note that Lucas’ theorem shows that ![]() ${\it\pi}_{i}$ is the projection onto the eigenspace
${\it\pi}_{i}$ is the projection onto the eigenspace ![]() $i_{1},\ldots ,i_{e}$ for the
$i_{1},\ldots ,i_{e}$ for the ![]() ${\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}$.
${\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}$.
Assume that ![]() ${\it\varphi}\in N_{i}$. Then viewing
${\it\varphi}\in N_{i}$. Then viewing ![]() ${\it\varphi}$ as an element of
${\it\varphi}$ as an element of ![]() $\text{Hom}_{R[t]}(F_{\ast }^{e}R[t],{\it\gamma}_{\ast }M)$ we have
$\text{Hom}_{R[t]}(F_{\ast }^{e}R[t],{\it\gamma}_{\ast }M)$ we have ![]() ${\it\varphi}(rt^{m})=0$ for
${\it\varphi}(rt^{m})=0$ for ![]() $m\neq i_{1}+i_{2}p+\cdots +i_{e}p^{e-1}$ so that
$m\neq i_{1}+i_{2}p+\cdots +i_{e}p^{e-1}$ so that ![]() ${\it\varphi}$ factors through
${\it\varphi}$ factors through ![]() ${\it\pi}_{i}$.
${\it\pi}_{i}$.
In the other direction note that given ![]() ${\it\varphi}\in N$ we have
${\it\varphi}\in N$ we have ![]() ${\it\varphi}=\sum _{i\in \mathbb{F}_{p}^{e}}{\it\varphi}\circ {\it\pi}_{i}$ which is a decomposition of
${\it\varphi}=\sum _{i\in \mathbb{F}_{p}^{e}}{\it\varphi}\circ {\it\pi}_{i}$ which is a decomposition of ![]() ${\it\varphi}$ in the ambient module
${\it\varphi}$ in the ambient module ![]() $({\it\gamma}_{\ast }F^{!}M){\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]$ as eigenvectors. Since this decomposition is preserved by morphisms (see Lemma 3.1) the above has to be the decomposition of
$({\it\gamma}_{\ast }F^{!}M){\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]$ as eigenvectors. Since this decomposition is preserved by morphisms (see Lemma 3.1) the above has to be the decomposition of ![]() ${\it\varphi}$ in
${\it\varphi}$ in ![]() $N$ as well.◻
$N$ as well.◻
Proposition 5.2. Let ![]() $R$ be a regular
$R$ be a regular ![]() $F$-finite ring and
$F$-finite ring and ![]() $(M,{\it\kappa})$ a Cartier module with adjoint
$(M,{\it\kappa})$ a Cartier module with adjoint ![]() $C$. Let
$C$. Let ![]() $f\in R$ and denote by
$f\in R$ and denote by ![]() ${\it\gamma}:\text{Spec}\,R\rightarrow \text{Spec}\,R[t]$ the graph embedding along
${\it\gamma}:\text{Spec}\,R\rightarrow \text{Spec}\,R[t]$ the graph embedding along ![]() $f$. Then the
$f$. Then the ![]() $(i_{1},\ldots ,i_{e})$-eigenspace of
$(i_{1},\ldots ,i_{e})$-eigenspace of ![]() $({\it\gamma}_{\ast }C^{e}(M)){\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]$ is isomorphic to
$({\it\gamma}_{\ast }C^{e}(M)){\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]$ is isomorphic to ![]() $C^{e}(f^{i_{1}+i_{2}p+\cdots i_{e}p^{e-1}}M)\cdot {\mathcal{D}}_{R}^{e}$ as a right
$C^{e}(f^{i_{1}+i_{2}p+\cdots i_{e}p^{e-1}}M)\cdot {\mathcal{D}}_{R}^{e}$ as a right ![]() ${\mathcal{D}}_{R}^{e}$-module.
${\mathcal{D}}_{R}^{e}$-module.
Proof. We write ![]() $m=i_{1}+i_{2}p+\cdots +i_{e}p^{e-1}$. Clearly, the right
$m=i_{1}+i_{2}p+\cdots +i_{e}p^{e-1}$. Clearly, the right ![]() ${\mathcal{D}}_{R}^{e}$-submodule
${\mathcal{D}}_{R}^{e}$-submodule ![]() $F_{\ast }^{e}R\cdot t^{m}$ of
$F_{\ast }^{e}R\cdot t^{m}$ of ![]() $F_{\ast }^{e}R[t]$ is isomorphic to
$F_{\ast }^{e}R[t]$ is isomorphic to ![]() $F_{\ast }^{e}R$ by sending
$F_{\ast }^{e}R$ by sending ![]() $t^{m}$ to
$t^{m}$ to ![]() $1$. In particular, we have a commutative diagram
$1$. In particular, we have a commutative diagram
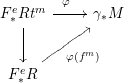
for any element ![]() ${\it\varphi}$ of the eigenspace. This induces the desired isomorphism of right
${\it\varphi}$ of the eigenspace. This induces the desired isomorphism of right ![]() ${\mathcal{D}}_{R}^{e}$-modules.◻
${\mathcal{D}}_{R}^{e}$-modules.◻
Corollary 5.3. The quotient
is a right ![]() ${\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e}-1}]$-module and the
${\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e}-1}]$-module and the ![]() $(i_{1},\ldots ,i_{e})$-eigenspace of the quotient is isomorphic to
$(i_{1},\ldots ,i_{e})$-eigenspace of the quotient is isomorphic to
as a right ![]() ${\mathcal{D}}_{R}^{e}$-module.
${\mathcal{D}}_{R}^{e}$-module.
Proof. The first claim is just Lemma 3.6. Since the eigenspace decomposition is preserved by the canonical projection we get the desired isomorphism on the quotient by Proposition 5.2. ◻
Following [Reference Mustaţă23] we introduce some notation. Namely, given ![]() ${\it\lambda}\in (0,1]$ we can write it uniquely as
${\it\lambda}\in (0,1]$ we can write it uniquely as
with all ![]() $c_{i}({\it\lambda})\in \{0,\ldots ,p-1\}$, and such that infinitely many of them are nonzero. Moreover, one obtains for every
$c_{i}({\it\lambda})\in \{0,\ldots ,p-1\}$, and such that infinitely many of them are nonzero. Moreover, one obtains for every ![]() $e\geqslant 1$ that
$e\geqslant 1$ that
We are now ready to state and prove our main result:
Theorem 5.4. Let ![]() $R$ be regular essentially of finite type over an
$R$ be regular essentially of finite type over an ![]() $F$-finite field. Let
$F$-finite field. Let ![]() $(M,{\it\kappa})$ be an
$(M,{\it\kappa})$ be an ![]() $F$-regular Cartier module and
$F$-regular Cartier module and ![]() $f\in R$ a nonzero divisor on
$f\in R$ a nonzero divisor on ![]() $M$. The roots of the Bernstein–Sato polynomials
$M$. The roots of the Bernstein–Sato polynomials ![]() $b_{M,f}^{e}(s)$ are given for
$b_{M,f}^{e}(s)$ are given for ![]() $e$ sufficiently large by
$e$ sufficiently large by ![]() $\frac{\lceil {\it\lambda}p^{e}\rceil -1}{p^{e}}$, where
$\frac{\lceil {\it\lambda}p^{e}\rceil -1}{p^{e}}$, where ![]() ${\it\lambda}$ varies over the
${\it\lambda}$ varies over the ![]() $F$-jumping numbers of the test module filtration
$F$-jumping numbers of the test module filtration ![]() ${\it\tau}(M,f^{t})$ for
${\it\tau}(M,f^{t})$ for ![]() $t\in (0,1]$.
$t\in (0,1]$.
Proof. By definition ![]() ${\it\lambda}\in (0,1]$ is an
${\it\lambda}\in (0,1]$ is an ![]() $F$-jumping number if and only if for all
$F$-jumping number if and only if for all ![]() $e\gg 0$ we have
$e\gg 0$ we have
Using the fact that ![]() ${F^{e}}^{!}$ is fully faithful (Proposition 2.2) this inequality is equivalent to
${F^{e}}^{!}$ is fully faithful (Proposition 2.2) this inequality is equivalent to
for all ![]() $e\gg 0$. We write
$e\gg 0$. We write ![]() $\lceil {\it\lambda}p^{e}\rceil -1=i_{1}+i_{2}p+\cdots +i_{e}p^{e-1}$. Then by Corollary 4.8 the above means that
$\lceil {\it\lambda}p^{e}\rceil -1=i_{1}+i_{2}p+\cdots +i_{e}p^{e-1}$. Then by Corollary 4.8 the above means that
for all ![]() $e\gg 0$. Finally, by Corollary 5.3 this is equivalent to
$e\gg 0$. Finally, by Corollary 5.3 this is equivalent to ![]() $\frac{\lceil {\it\lambda}p^{e}\rceil -1}{p^{e}}$ being a zero of
$\frac{\lceil {\it\lambda}p^{e}\rceil -1}{p^{e}}$ being a zero of ![]() $b_{M,f}^{e}(s)$ for all
$b_{M,f}^{e}(s)$ for all ![]() $e\gg 0$.◻
$e\gg 0$.◻
(a) We recall that there are only finitely many
 $F$-jumping numbers in
$F$-jumping numbers in  $(0,1]$ and that they are all rational. In particular, the limit over the
$(0,1]$ and that they are all rational. In particular, the limit over the  $b_{M,f}^{e}(s)$ for
$b_{M,f}^{e}(s)$ for  $e\rightarrow \infty$ is a polynomial with rational roots.
$e\rightarrow \infty$ is a polynomial with rational roots.(b) The case where
 $M$ is locally constant (and
$M$ is locally constant (and  $R$ is smooth over a perfect field), that is, when there exists a finite étale morphism
$R$ is smooth over a perfect field), that is, when there exists a finite étale morphism  ${\it\varphi}:\text{Spec}\,S\rightarrow \text{Spec}\,R$ such that
${\it\varphi}:\text{Spec}\,S\rightarrow \text{Spec}\,R$ such that  ${\it\varphi}^{\ast }M\cong {\it\omega}_{S}^{n}$ can also be directly deduced from the constant case treated in [Reference Mustaţă23]. This essentially boils down to the fact that differential operators along étale morphisms are well behaved (one obtains an inclusion
${\it\varphi}^{\ast }M\cong {\it\omega}_{S}^{n}$ can also be directly deduced from the constant case treated in [Reference Mustaţă23]. This essentially boils down to the fact that differential operators along étale morphisms are well behaved (one obtains an inclusion  ${\mathcal{D}}_{R}^{e}\rightarrow {\mathcal{D}}_{S}^{e}$ and the natural map
${\mathcal{D}}_{R}^{e}\rightarrow {\mathcal{D}}_{S}^{e}$ and the natural map  $M\rightarrow {\it\varphi}^{!}M$ is
$M\rightarrow {\it\varphi}^{!}M$ is  ${\mathcal{D}}_{R}^{e}$-linear — see [Reference Másson22, Theorem 2.2.5, Corollary 2.2.6] for the first statement. The latter may be extracted from [Reference Másson22, Theorem 2.2.10] and [Reference Berthelot3, 2.1.3]). Then one uses [Reference Stäbler25, Theorem 8.5] to see that the
${\mathcal{D}}_{R}^{e}$-linear — see [Reference Másson22, Theorem 2.2.5, Corollary 2.2.6] for the first statement. The latter may be extracted from [Reference Másson22, Theorem 2.2.10] and [Reference Berthelot3, 2.1.3]). Then one uses [Reference Stäbler25, Theorem 8.5] to see that the  $F$-jumping numbers of
$F$-jumping numbers of  $M$ are the same as that of
$M$ are the same as that of  ${\it\omega}_{S}$. In fact, writing this up precisely was the original motivation for this paper.
${\it\omega}_{S}$. In fact, writing this up precisely was the original motivation for this paper.(c) Note that Mustaţă’s result [Reference Mustaţă23, Theorem 6.7] is valid for any
 $e\geqslant 1$ while we only obtain a result for
$e\geqslant 1$ while we only obtain a result for  $e\gg 0$.
$e\gg 0$.
6 A comparison with Stadnik’s  $b$-functions
$b$-functions
The goal of this section is to point out the relation of our Bernstein–Sato polynomials to the ![]() $b$-functions of Stadnik defined in [Reference Stadnik26, Definition 4.4]. Stadnik works in the context of unit
$b$-functions of Stadnik defined in [Reference Stadnik26, Definition 4.4]. Stadnik works in the context of unit ![]() $R[F]$-modules which were introduced by Lyubeznik [Reference Lyubeznik20] and Emerton–Kisin [Reference Emerton and Kisin14]. We briefly recall the relevant notions. A unit
$R[F]$-modules which were introduced by Lyubeznik [Reference Lyubeznik20] and Emerton–Kisin [Reference Emerton and Kisin14]. We briefly recall the relevant notions. A unit ![]() $R[F]$-module is an
$R[F]$-module is an ![]() $R$-module
$R$-module ![]() ${\mathcal{M}}$ equipped with a structural isomorphism
${\mathcal{M}}$ equipped with a structural isomorphism ![]() ${\it\theta}:F^{\ast }{\mathcal{M}}\xrightarrow[]{\cong }{\mathcal{M}}$. A root of
${\it\theta}:F^{\ast }{\mathcal{M}}\xrightarrow[]{\cong }{\mathcal{M}}$. A root of ![]() ${\mathcal{M}}$ is an
${\mathcal{M}}$ is an ![]() $R$-module
$R$-module ![]() $M$ together with an injective
$M$ together with an injective ![]() $R$-linear map
$R$-linear map ![]() ${\rm\Phi}:M\rightarrow F^{\ast }M$ such that
${\rm\Phi}:M\rightarrow F^{\ast }M$ such that ![]() $\text{colim}_{e}\,{F^{e}}^{\ast }M$ and
$\text{colim}_{e}\,{F^{e}}^{\ast }M$ and ![]() ${\mathcal{M}}$ are isomorphic as unit
${\mathcal{M}}$ are isomorphic as unit ![]() $R[F]$-modules. In particular, if
$R[F]$-modules. In particular, if ![]() $M$ is a root for
$M$ is a root for ![]() ${\mathcal{M}}$ then
${\mathcal{M}}$ then ![]() ${\it\gamma}_{\ast }M\otimes {\it\omega}_{R[t]/R}^{-1}$ is a root for
${\it\gamma}_{\ast }M\otimes {\it\omega}_{R[t]/R}^{-1}$ is a root for ![]() ${\it\gamma}_{+}{\mathcal{M}}$, where
${\it\gamma}_{+}{\mathcal{M}}$, where ![]() ${\it\gamma}:\text{Spec}\,R\rightarrow \text{Spec}\,R[t]$ is the graph embedding for some hypersurface
${\it\gamma}:\text{Spec}\,R\rightarrow \text{Spec}\,R[t]$ is the graph embedding for some hypersurface ![]() $f$ (Proposition 3.5 above shows that
$f$ (Proposition 3.5 above shows that ![]() ${\it\gamma}_{+}$ is the
${\it\gamma}_{+}$ is the ![]() ${\mathcal{D}}$-module pushforward and [Reference Emerton and Kisin14, 14.3.10, 15.2] shows that the
${\mathcal{D}}$-module pushforward and [Reference Emerton and Kisin14, 14.3.10, 15.2] shows that the ![]() ${\mathcal{D}}$-module pushforward coincides with the pushforward on unit
${\mathcal{D}}$-module pushforward coincides with the pushforward on unit ![]() $R[F]$-modules). By abuse of notation we denote the image of the natural map
$R[F]$-modules). By abuse of notation we denote the image of the natural map ![]() ${\it\gamma}_{\ast }M\otimes {\it\omega}_{R[t]/R}^{-1}\rightarrow {F^{e}}^{\ast }({\it\gamma}_{\ast }M\otimes {\it\omega}_{R[t]/R}^{-1})$ again by
${\it\gamma}_{\ast }M\otimes {\it\omega}_{R[t]/R}^{-1}\rightarrow {F^{e}}^{\ast }({\it\gamma}_{\ast }M\otimes {\it\omega}_{R[t]/R}^{-1})$ again by ![]() ${\it\gamma}_{\ast }M\otimes {\it\omega}_{R[t]/R}^{-1}$.
${\it\gamma}_{\ast }M\otimes {\it\omega}_{R[t]/R}^{-1}$.
Given a sequence ![]() $i_{l}$ of integers in
$i_{l}$ of integers in ![]() $\{0,\ldots ,p-1\}$ we refer to
$\{0,\ldots ,p-1\}$ we refer to ![]() $\sum _{l=0}^{e-1}i_{l}p^{l}$ as the base-
$\sum _{l=0}^{e-1}i_{l}p^{l}$ as the base-![]() $p$ expansion of
$p$ expansion of ![]() $(i_{1},\ldots ,i_{e})$. Varying
$(i_{1},\ldots ,i_{e})$. Varying ![]() $e$ we call the number
$e$ we call the number ![]() $\lim _{e\rightarrow \infty }\sum _{l=0}^{e-1}i_{l}p^{l}/p^{e}$the
$\lim _{e\rightarrow \infty }\sum _{l=0}^{e-1}i_{l}p^{l}/p^{e}$the ![]() $p$-weighted limit of the base-
$p$-weighted limit of the base-![]() $p$ expansion if it exists.
$p$ expansion if it exists.
With this notation Stadnik defines a ![]() $b$-function (for the pair
$b$-function (for the pair ![]() $({\it\gamma}_{\ast }M\otimes {\it\omega}_{R[t]/R}^{-1},{\it\gamma}_{+}{\mathcal{M}})$) as any polynomial
$({\it\gamma}_{\ast }M\otimes {\it\omega}_{R[t]/R}^{-1},{\it\gamma}_{+}{\mathcal{M}})$) as any polynomial ![]() $b(s)\in \mathbb{C}[s]$ with roots in
$b(s)\in \mathbb{C}[s]$ with roots in ![]() $(0,1]$ that satisfies the following property:
$(0,1]$ that satisfies the following property:
If ![]() ${\it\lambda}$ is a root of
${\it\lambda}$ is a root of ![]() $b(1-s)$ then there exists an integer
$b(1-s)$ then there exists an integer ![]() $n$ such that for all
$n$ such that for all ![]() $e\geqslant 0$ the set
$e\geqslant 0$ the set
contains the base ![]() $p$-expansions of the eigenvalues of the
$p$-expansions of the eigenvalues of the ![]() ${\it\theta}_{p^{l}},l=0,\ldots ,e-1$, on the quotient
${\it\theta}_{p^{l}},l=0,\ldots ,e-1$, on the quotient
The set of ![]() $b$-functions forms an ideal in
$b$-functions forms an ideal in ![]() $\mathbb{C}[s]$ and we denote its monic generator by
$\mathbb{C}[s]$ and we denote its monic generator by ![]() $\tilde{b}_{M,f}(s)$.
$\tilde{b}_{M,f}(s)$.
The main result of [Reference Stadnik26] is that ![]() $\tilde{b}_{M,f}(s)$ is a nonzero polynomial with rational roots. We reprove this here using Theorem 5.4 under the additional assumption that
$\tilde{b}_{M,f}(s)$ is a nonzero polynomial with rational roots. We reprove this here using Theorem 5.4 under the additional assumption that ![]() $M\otimes {\it\omega}_{R}$ is
$M\otimes {\it\omega}_{R}$ is ![]() $F$-regular and that
$F$-regular and that ![]() $f$ is not a zero divisor on
$f$ is not a zero divisor on ![]() $M$.
$M$.
Remark 6.1. Note that ![]() ${\rm\Omega}_{R[t]/R}$ is free of rank
${\rm\Omega}_{R[t]/R}$ is free of rank ![]() $1$ and
$1$ and ![]() $dt=d(t-f)$. By definition
$dt=d(t-f)$. By definition ![]() $\partial _{t}$ is the differential operator in
$\partial _{t}$ is the differential operator in ![]() $\text{Hom}_{R}({\rm\Omega}_{R[t]/R},R)=R\oplus Der_{R[t]/R}$ given by the dual of
$\text{Hom}_{R}({\rm\Omega}_{R[t]/R},R)=R\oplus Der_{R[t]/R}$ given by the dual of ![]() $dt$. In particular, we have
$dt$. In particular, we have ![]() $\partial _{t}=\partial _{t-f}$. Hence, applying the automorphism
$\partial _{t}=\partial _{t-f}$. Hence, applying the automorphism ![]() $t\mapsto t+f$ we are precisely in the setting where our hypersurface equation is given by
$t\mapsto t+f$ we are precisely in the setting where our hypersurface equation is given by ![]() $t=0$ and the Euler operators are given by
$t=0$ and the Euler operators are given by ![]() ${\it\theta}_{e}=t^{p^{e}}\partial _{t}^{[p^{e}]}$, where we use the inclusion
${\it\theta}_{e}=t^{p^{e}}\partial _{t}^{[p^{e}]}$, where we use the inclusion ![]() ${\mathcal{D}}_{R[t]/R}\subseteq {\mathcal{D}}_{R[t]}$. The latter is the setting in which Stadnik works.
${\mathcal{D}}_{R[t]/R}\subseteq {\mathcal{D}}_{R[t]}$. The latter is the setting in which Stadnik works.
Also note that Stadnik considers the quotient
but since ![]() $[t,{\it\theta}_{i}]={\it\theta}_{i-1}$ and
$[t,{\it\theta}_{i}]={\it\theta}_{i-1}$ and ![]() $t({\it\gamma}_{\ast }M\otimes {\it\omega}_{R[t]/R}^{-1})={\it\gamma}_{\ast }fM\otimes {\it\omega}_{R[t]/R}^{-1}$ this quotient coincides with the one we consider.
$t({\it\gamma}_{\ast }M\otimes {\it\omega}_{R[t]/R}^{-1})={\it\gamma}_{\ast }fM\otimes {\it\omega}_{R[t]/R}^{-1}$ this quotient coincides with the one we consider.
The equivalence of our notion and that of Stadnik is obtained from the equivalence of left and right ![]() ${\mathcal{D}}_{S}^{e}$-modules which we recall in a special setting. For an
${\mathcal{D}}_{S}^{e}$-modules which we recall in a special setting. For an ![]() $S$-module
$S$-module ![]() $M$ the
$M$ the ![]() $e\text{th}$ Frobenius pull backFootnote 5
$e\text{th}$ Frobenius pull backFootnote 5 ![]() ${F^{e}}^{\ast }M=F_{\ast }^{e}R\otimes _{R}M$ is a left
${F^{e}}^{\ast }M=F_{\ast }^{e}R\otimes _{R}M$ is a left ![]() ${\mathcal{D}}_{S}^{e}$-module via the action of
${\mathcal{D}}_{S}^{e}$-module via the action of ![]() ${\mathcal{D}}_{S}^{e}$ on
${\mathcal{D}}_{S}^{e}$ on ![]() $F_{\ast }^{e}S$. Tensoring with
$F_{\ast }^{e}S$. Tensoring with ![]() ${\it\omega}_{S}$ one obtains an isomorphism
${\it\omega}_{S}$ one obtains an isomorphism ![]() ${\it\omega}_{S}\otimes {F^{e}}^{\ast }M\cong {F^{e}}^{!}({\it\omega}_{S}\otimes M)=\text{Hom}_{S}(F_{\ast }^{e}S,{\it\omega}_{S}\otimes M)$ and the latter naturally carries the structure of a right
${\it\omega}_{S}\otimes {F^{e}}^{\ast }M\cong {F^{e}}^{!}({\it\omega}_{S}\otimes M)=\text{Hom}_{S}(F_{\ast }^{e}S,{\it\omega}_{S}\otimes M)$ and the latter naturally carries the structure of a right ![]() ${\mathcal{D}}_{S}^{e}$-module via the action on
${\mathcal{D}}_{S}^{e}$-module via the action on ![]() $F_{\ast }^{e}S$. Since
$F_{\ast }^{e}S$. Since ![]() ${\it\omega}_{S}$ is invertible this induces an equivalence of categories between left and right
${\it\omega}_{S}$ is invertible this induces an equivalence of categories between left and right ![]() ${\mathcal{D}}_{S}^{e}$-modules.
${\mathcal{D}}_{S}^{e}$-modules.
Given a smooth ring ![]() $S$ over a perfect field
$S$ over a perfect field ![]() $k$ we can choose a set of local coordinates
$k$ we can choose a set of local coordinates ![]() $x_{1},\ldots ,x_{n}$. For
$x_{1},\ldots ,x_{n}$. For ![]() $i\in \mathbb{N}^{n}$ write
$i\in \mathbb{N}^{n}$ write ![]() $\partial _{i}^{[m_{i}]}=\partial _{x_{i_{1}}}^{[m_{1}]}\cdots \partial _{x_{i_{n}}}^{[m_{n}]}$. Now given any differential operator
$\partial _{i}^{[m_{i}]}=\partial _{x_{i_{1}}}^{[m_{1}]}\cdots \partial _{x_{i_{n}}}^{[m_{n}]}$. Now given any differential operator ![]() $P$ we can write it locally as
$P$ we can write it locally as
where almost all ![]() $i$ are zero. Then we denote the adjoint operator
$i$ are zero. Then we denote the adjoint operator
by ![]() $P^{t}$. Finally, note that one has
$P^{t}$. Finally, note that one has ![]() $(PQ)^{t}=Q^{t}P^{t}$.
$(PQ)^{t}=Q^{t}P^{t}$.
Proposition 6.2. Let ![]() $S=R[t]$ for
$S=R[t]$ for ![]() $R$ smooth over a perfect field
$R$ smooth over a perfect field ![]() $k$ and
$k$ and ![]() $M$ an
$M$ an ![]() $S$-module. Then for a set of local coordinates
$S$-module. Then for a set of local coordinates ![]() $t,x_{1},\ldots ,x_{n}$ the right
$t,x_{1},\ldots ,x_{n}$ the right ![]() ${\mathcal{D}}_{S}^{e}$-module structure on
${\mathcal{D}}_{S}^{e}$-module structure on ![]() ${\it\omega}_{S}\otimes {F^{e}}^{\ast }M$ is locally given by
${\it\omega}_{S}\otimes {F^{e}}^{\ast }M$ is locally given by
and the isomorphism ![]() ${\it\omega}_{S}\otimes {F^{e}}^{\ast }M\rightarrow {F^{e}}^{!}({\it\omega}_{S}\otimes M)$ is
${\it\omega}_{S}\otimes {F^{e}}^{\ast }M\rightarrow {F^{e}}^{!}({\it\omega}_{S}\otimes M)$ is ![]() ${\mathcal{D}}_{S}^{e}$-linear. In particular, for
${\mathcal{D}}_{S}^{e}$-linear. In particular, for ![]() $1\otimes v\otimes m\in {\it\omega}_{S/R}\otimes _{R}{\it\omega}_{R}\otimes {F^{e}}^{\ast }M$ one has
$1\otimes v\otimes m\in {\it\omega}_{S/R}\otimes _{R}{\it\omega}_{R}\otimes {F^{e}}^{\ast }M$ one has ![]() $(1\otimes v\otimes m)\cdot {\it\theta}_{p^{l}}=(1\otimes v\otimes -{\it\vartheta}_{p^{l}}m)$ for any
$(1\otimes v\otimes m)\cdot {\it\theta}_{p^{l}}=(1\otimes v\otimes -{\it\vartheta}_{p^{l}}m)$ for any ![]() $0\leqslant l\leqslant e-1$.
$0\leqslant l\leqslant e-1$.
Proof. First of all, we reduce to the case ![]() $M=S$. The
$M=S$. The ![]() ${\mathcal{D}}_{S}^{e}$-module structure on
${\mathcal{D}}_{S}^{e}$-module structure on ![]() ${F^{e}}^{\ast }M=F_{\ast }^{e}S\otimes _{S}M$ and on
${F^{e}}^{\ast }M=F_{\ast }^{e}S\otimes _{S}M$ and on ![]() ${F^{e}}^{!}({\it\omega}_{S}\otimes M)=\text{Hom}_{S}(F_{\ast }^{e}S,{\it\omega}_{S}\otimes M)$ is given by the action of
${F^{e}}^{!}({\it\omega}_{S}\otimes M)=\text{Hom}_{S}(F_{\ast }^{e}S,{\it\omega}_{S}\otimes M)$ is given by the action of ![]() ${\mathcal{D}}_{S}^{e}$ on
${\mathcal{D}}_{S}^{e}$ on ![]() $F_{\ast }^{e}S$. Moreover, the isomorphism
$F_{\ast }^{e}S$. Moreover, the isomorphism ![]() ${\it\omega}_{S}\otimes {F^{e}}^{\ast }M\rightarrow {F^{e}}^{!}({\it\omega}_{S}\otimes M)$ factors as the composition of the canonical isomorphisms
${\it\omega}_{S}\otimes {F^{e}}^{\ast }M\rightarrow {F^{e}}^{!}({\it\omega}_{S}\otimes M)$ factors as the composition of the canonical isomorphisms
![]()
where ![]() ${\rm\Sigma}:{\it\omega}_{S}\otimes {F^{e}}^{\ast }S\rightarrow {F^{e}}^{!}{\it\omega}_{S}$ denotes the isomorphism
${\rm\Sigma}:{\it\omega}_{S}\otimes {F^{e}}^{\ast }S\rightarrow {F^{e}}^{!}{\it\omega}_{S}$ denotes the isomorphism ![]() $ds\otimes f\mapsto C^{e}(ds)\cdot f=[x\mapsto {\it\kappa}^{e}(xfds)]$.
$ds\otimes f\mapsto C^{e}(ds)\cdot f=[x\mapsto {\it\kappa}^{e}(xfds)]$.
Now the claim follows from [Reference Berthelot3, Proposition 1.1.7(i), Corollary 1.2.6] with ![]() ${\mathcal{M}}={\it\omega}_{S}$ and
${\mathcal{M}}={\it\omega}_{S}$ and ![]() ${\mathcal{E}}=F_{\ast }^{e}S$: Since
${\mathcal{E}}=F_{\ast }^{e}S$: Since ![]() $k$ is perfect we have
$k$ is perfect we have ![]() ${\mathcal{D}}_{S/k}^{e}={\mathcal{D}}_{S}^{e}$. By [Reference Berthelot2, Proposition 2.2.7] the image of
${\mathcal{D}}_{S/k}^{e}={\mathcal{D}}_{S}^{e}$. By [Reference Berthelot2, Proposition 2.2.7] the image of ![]() ${\mathcal{D}}_{S}^{(e)}$ in
${\mathcal{D}}_{S}^{(e)}$ in ![]() ${\mathcal{D}}_{S}$ corresponds to
${\mathcal{D}}_{S}$ corresponds to ![]() ${\mathcal{D}}_{S}^{e}$ so that Berthelot’s results also apply to
${\mathcal{D}}_{S}^{e}$ so that Berthelot’s results also apply to ![]() ${\mathcal{D}}_{S}^{e}$-modules.◻
${\mathcal{D}}_{S}^{e}$-modules.◻
Corollary 6.3. Let ![]() $S=R[t]$ for a regular ring
$S=R[t]$ for a regular ring ![]() $R$ essentially of finite type over an
$R$ essentially of finite type over an ![]() $F$-finite field and
$F$-finite field and ![]() $M$ an
$M$ an ![]() $S$-module. Then
$S$-module. Then ![]() ${F^{e}}^{\ast }M$ admits a nontrivial
${F^{e}}^{\ast }M$ admits a nontrivial ![]() $(-i_{1},\ldots ,-i_{e})$-eigenspace for the
$(-i_{1},\ldots ,-i_{e})$-eigenspace for the ![]() $-{\it\vartheta}$ if and only if
$-{\it\vartheta}$ if and only if ![]() ${F^{e}}^{!}(M\otimes {\it\omega}_{S})$ admits a nontrivial
${F^{e}}^{!}(M\otimes {\it\omega}_{S})$ admits a nontrivial ![]() $(i_{1},\ldots ,i_{e})$-eigenspace for the
$(i_{1},\ldots ,i_{e})$-eigenspace for the ![]() ${\it\theta}$.
${\it\theta}$.
Proof. The “only if”-part is immediate from Proposition 6.2. Conversely, ![]() ${F^{e}}^{!}(M\otimes {\it\omega}_{S})\otimes {\it\omega}_{S}^{-1}$ is canonically isomorphic to
${F^{e}}^{!}(M\otimes {\it\omega}_{S})\otimes {\it\omega}_{S}^{-1}$ is canonically isomorphic to ![]() ${F^{e}}^{\ast }M$ and a similar argument applies in this case.◻
${F^{e}}^{\ast }M$ and a similar argument applies in this case.◻
Lemma 6.4. Let ![]() $(M,{\rm\Phi})$ be a root of a unit
$(M,{\rm\Phi})$ be a root of a unit ![]() $R[F]$-module
$R[F]$-module ![]() ${\mathcal{M}}$ and
${\mathcal{M}}$ and ![]() ${\it\gamma}:\text{Spec}\,R\rightarrow \text{Spec}\,S=R[t]$ a closed immersion and
${\it\gamma}:\text{Spec}\,R\rightarrow \text{Spec}\,S=R[t]$ a closed immersion and ![]() $({\it\gamma}_{\ast }M\otimes {\it\omega}_{S/R}^{-1},{\rm\Phi}\otimes \text{id})$ the corresponding root for
$({\it\gamma}_{\ast }M\otimes {\it\omega}_{S/R}^{-1},{\rm\Phi}\otimes \text{id})$ the corresponding root for ![]() ${\it\gamma}_{+}{\mathcal{M}}$.
${\it\gamma}_{+}{\mathcal{M}}$.
Then ![]() $({\it\gamma}_{\ast }({\it\omega}_{R}\otimes M),\tilde{C})$ and
$({\it\gamma}_{\ast }({\it\omega}_{R}\otimes M),\tilde{C})$ and ![]() $({\it\omega}_{R}\otimes M,C)$ are naturally Cartier modules and the map
$({\it\omega}_{R}\otimes M,C)$ are naturally Cartier modules and the map ![]() $\tilde{C}:{\it\gamma}_{\ast }({\it\omega}_{R}\otimes M)\rightarrow F^{!}{\it\gamma}_{\ast }{\it\omega}_{R}\otimes M$ is given by the composition of
$\tilde{C}:{\it\gamma}_{\ast }({\it\omega}_{R}\otimes M)\rightarrow F^{!}{\it\gamma}_{\ast }{\it\omega}_{R}\otimes M$ is given by the composition of ![]() ${\it\gamma}_{\ast }({\it\omega}_{R}\otimes M)\rightarrow {\it\gamma}_{\ast }F^{!}({\it\omega}_{R}\otimes M)\rightarrow F^{!}({\it\gamma}_{\ast }{\it\omega}_{R}\otimes M)$, where the first map is
${\it\gamma}_{\ast }({\it\omega}_{R}\otimes M)\rightarrow {\it\gamma}_{\ast }F^{!}({\it\omega}_{R}\otimes M)\rightarrow F^{!}({\it\gamma}_{\ast }{\it\omega}_{R}\otimes M)$, where the first map is ![]() ${\it\gamma}_{\ast }C$ and the second is the composition of maps described in Proposition 3.3. In particular, if
${\it\gamma}_{\ast }C$ and the second is the composition of maps described in Proposition 3.3. In particular, if ![]() $N$ denotes the image of the natural map
$N$ denotes the image of the natural map ![]() ${\it\gamma}_{\ast }M\otimes {\it\omega}_{R[t]/R}^{-1}\rightarrow {F^{e}}^{\ast }({\it\gamma}_{\ast }M\otimes {\it\omega}_{R[t]/R}^{-1})$ then
${\it\gamma}_{\ast }M\otimes {\it\omega}_{R[t]/R}^{-1}\rightarrow {F^{e}}^{\ast }({\it\gamma}_{\ast }M\otimes {\it\omega}_{R[t]/R}^{-1})$ then ![]() ${\it\omega}_{R[t]}\otimes N$ is the image of the natural map
${\it\omega}_{R[t]}\otimes N$ is the image of the natural map ![]() ${\it\gamma}_{\ast }({\it\omega}_{R}\otimes M)\rightarrow {F^{e}}^{!}({\it\gamma}_{\ast }{\it\omega}_{R}\otimes M)$.
${\it\gamma}_{\ast }({\it\omega}_{R}\otimes M)\rightarrow {F^{e}}^{!}({\it\gamma}_{\ast }{\it\omega}_{R}\otimes M)$.
Proof. We shorten ![]() ${\it\omega}_{R}\otimes M$ to
${\it\omega}_{R}\otimes M$ to ![]() $M^{\prime }$. It is easy to see that the Cartier structure given on
$M^{\prime }$. It is easy to see that the Cartier structure given on ![]() ${\it\gamma}_{\ast }M^{\prime }$ is the one induced from
${\it\gamma}_{\ast }M^{\prime }$ is the one induced from ![]() $M^{\prime }$ by
$M^{\prime }$ by
![]()
Hence, one may reduce the problem to checking that given a Cartier module ![]() $(A,{\it\kappa})$ with adjoint
$(A,{\it\kappa})$ with adjoint ![]() $C$ the adjoint of the structural map of
$C$ the adjoint of the structural map of ![]() ${\it\gamma}_{\ast }A$ is given by the composition of the map described in Proposition 3.3 with
${\it\gamma}_{\ast }A$ is given by the composition of the map described in Proposition 3.3 with ![]() ${\it\gamma}_{\ast }C$. This is an easy computation which will be left to the reader.◻
${\it\gamma}_{\ast }C$. This is an easy computation which will be left to the reader.◻
Lemma 6.5. Let ![]() $R$ be smooth over a perfect field and
$R$ be smooth over a perfect field and ![]() $f\in R$ a hypersurface. Let
$f\in R$ a hypersurface. Let ![]() ${\it\gamma}:\text{Spec}\,R\rightarrow \text{Spec}\,R[t]$ be the graph embedding along
${\it\gamma}:\text{Spec}\,R\rightarrow \text{Spec}\,R[t]$ be the graph embedding along ![]() $f$. Given an
$f$. Given an ![]() $R$-module
$R$-module ![]() $M$ we have
$M$ we have
Proof. According to our established abuse of notation we have to show that for ![]() $m$ in the image of
$m$ in the image of ![]() ${\it\gamma}_{\ast }M\otimes {\it\omega}_{R[t]/R}^{-1}\rightarrow {F^{e}}^{\ast }{\it\gamma}_{\ast }M\otimes {\it\omega}_{R[t]/R}^{-1}$ one has that
${\it\gamma}_{\ast }M\otimes {\it\omega}_{R[t]/R}^{-1}\rightarrow {F^{e}}^{\ast }{\it\gamma}_{\ast }M\otimes {\it\omega}_{R[t]/R}^{-1}$ one has that ![]() ${\it\omega}\otimes P\cdot m$ for any
${\it\omega}\otimes P\cdot m$ for any ![]() $P\in D_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]$ is contained in the
$P\in D_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]$ is contained in the ![]() ${\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]$-module generated by the image of
${\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]$-module generated by the image of ![]() ${\it\gamma}_{\ast }({\it\omega}_{R}\otimes M)\rightarrow {F^{e}}^{!}{\it\gamma}_{\ast }({\it\omega}_{R}\otimes M)$ and vice versa. We may verify this locally and then it follows from Proposition 6.2 and the fact that
${\it\gamma}_{\ast }({\it\omega}_{R}\otimes M)\rightarrow {F^{e}}^{!}{\it\gamma}_{\ast }({\it\omega}_{R}\otimes M)$ and vice versa. We may verify this locally and then it follows from Proposition 6.2 and the fact that ![]() ${\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]$ is closed under taking adjoints. This is clear for
${\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]$ is closed under taking adjoints. This is clear for ![]() ${\mathcal{D}}_{R}^{e}$ and for
${\mathcal{D}}_{R}^{e}$ and for ![]() ${\it\theta}_{p^{i}}$ one has for the transposed operator
${\it\theta}_{p^{i}}$ one has for the transposed operator ![]() $({\it\theta}_{p^{i}})^{t}=-{\it\vartheta}_{p^{i}}=-(1+{\it\theta}_{p^{i}})$ by Lemma 1.1 (i).◻
$({\it\theta}_{p^{i}})^{t}=-{\it\vartheta}_{p^{i}}=-(1+{\it\theta}_{p^{i}})$ by Lemma 1.1 (i).◻
Corollary 6.6. In the situation of Lemma 6.5 we have an isomorphism
Proof. Note that
so that the claim follows from Lemma 6.5 and tensoring the obvious short exact sequence with ![]() ${\it\omega}_{S}$.◻
${\it\omega}_{S}$.◻
Corollary 6.7. The ![]() ${\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]$-module
${\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]$-module
has a nontrivial ![]() ${\it\vartheta}$-eigenspace with eigenvalue
${\it\vartheta}$-eigenspace with eigenvalue ![]() $(-i_{1},\ldots ,-i_{e})$ if and only if the right
$(-i_{1},\ldots ,-i_{e})$ if and only if the right ![]() ${\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]$-module
${\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]$-module
has a nontrivial ![]() ${\it\theta}$-eigenspace with eigenvalue
${\it\theta}$-eigenspace with eigenvalue ![]() $(i_{1},\ldots ,i_{e})$.
$(i_{1},\ldots ,i_{e})$.
Proof. Note that the left module embeds into ![]() ${\mathcal{D}}_{R}^{e}{\it\gamma}_{\ast }M\otimes {\it\omega}_{R[t]/R}^{-1}/{\it\gamma}_{\ast }M\otimes {\it\omega}_{R[t]/R}^{-1}$ and similarly for the right module. Then the claim follows from Corollaries 6.3 and 6.6 ◻
${\mathcal{D}}_{R}^{e}{\it\gamma}_{\ast }M\otimes {\it\omega}_{R[t]/R}^{-1}/{\it\gamma}_{\ast }M\otimes {\it\omega}_{R[t]/R}^{-1}$ and similarly for the right module. Then the claim follows from Corollaries 6.3 and 6.6 ◻
Remark 6.8. One should be able to obtain a similar correspondence between right and left ![]() ${\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]$-modules under the weaker assumption that
${\mathcal{D}}_{R}^{e}[{\it\theta}_{1},\ldots ,{\it\theta}_{p^{e-1}}]$-modules under the weaker assumption that ![]() $R$ is regular, essentially of finite type over an
$R$ is regular, essentially of finite type over an ![]() $F$-finite field. However, in this case one cannot appeal to Berthelot’s results. Since Stadnik works under the assumptions that
$F$-finite field. However, in this case one cannot appeal to Berthelot’s results. Since Stadnik works under the assumptions that ![]() $R$ is smooth over a perfect field we did not pursue this further.
$R$ is smooth over a perfect field we did not pursue this further.
We now have the necessary ingredients to state and prove the main results of this section.
Theorem 6.9. Let ![]() ${\it\gamma}:\text{Spec}\,R\rightarrow \text{Spec}\,R[t]$ be the graph embedding along a hypersurface
${\it\gamma}:\text{Spec}\,R\rightarrow \text{Spec}\,R[t]$ be the graph embedding along a hypersurface ![]() $f$ and let
$f$ and let ![]() $(M,{\rm\Phi})$ be a root of a unit
$(M,{\rm\Phi})$ be a root of a unit ![]() $R[F]$-module
$R[F]$-module ![]() ${\mathcal{M}}$. Assume that the Cartier module
${\mathcal{M}}$. Assume that the Cartier module ![]() $M\otimes {\it\omega}_{R}$ is
$M\otimes {\it\omega}_{R}$ is ![]() $F$-regularFootnote 6 and that
$F$-regularFootnote 6 and that ![]() $f$ is not a zero divisor on
$f$ is not a zero divisor on ![]() $M$. Then if
$M$. Then if ![]() ${\it\mu}_{e}$ denotes the base-
${\it\mu}_{e}$ denotes the base-![]() $p$ expansions of the eigenvalues of the
$p$ expansions of the eigenvalues of the ![]() ${\it\theta}_{p^{l}}$ operating on the left modules
${\it\theta}_{p^{l}}$ operating on the left modules
and ![]() ${\it\lambda}_{e}$ denotes the base-
${\it\lambda}_{e}$ denotes the base-![]() $p$ expansions of the eigenvalues of
$p$ expansions of the eigenvalues of ![]() ${\it\theta}_{p^{l}}$ operating on the right modules
${\it\theta}_{p^{l}}$ operating on the right modules
one has the following relation ![]() ${\it\mu}_{e}+{\it\lambda}_{e}=p^{e}-1$ and
${\it\mu}_{e}+{\it\lambda}_{e}=p^{e}-1$ and
In particular, the ![]() $p$-weighted limit of the
$p$-weighted limit of the ![]() ${\it\mu}_{e}$ exists.
${\it\mu}_{e}$ exists.
Proof. If ![]() ${\it\theta}_{p^{l}}$ operates from the left with eigenvalue
${\it\theta}_{p^{l}}$ operates from the left with eigenvalue ![]() $-i_{l}-1$ then by Corollary 6.7 and the relation
$-i_{l}-1$ then by Corollary 6.7 and the relation ![]() ${\it\theta}_{p^{l}}+1={\it\vartheta}_{p^{l}}$ we have that
${\it\theta}_{p^{l}}+1={\it\vartheta}_{p^{l}}$ we have that ![]() ${\it\theta}_{p^{l}}$ operates via
${\it\theta}_{p^{l}}$ operates via ![]() $i_{l}$ on the right. So we get
$i_{l}$ on the right. So we get ![]() ${\it\mu}_{e}=\sum _{l=0}^{e-1}(p-1-i_{l})p^{l}$ as the base-
${\it\mu}_{e}=\sum _{l=0}^{e-1}(p-1-i_{l})p^{l}$ as the base-![]() $p$ expansion for the operation of the
$p$ expansion for the operation of the ![]() ${\it\theta}_{p^{l}}$ on the left. Similarly, we have
${\it\theta}_{p^{l}}$ on the left. Similarly, we have ![]() ${\it\lambda}_{e}=\sum _{l=0}^{e-1}i_{l}p^{l}$.
${\it\lambda}_{e}=\sum _{l=0}^{e-1}i_{l}p^{l}$.
By Theorem 5.4 the ![]() $p$-weighted limit over the
$p$-weighted limit over the ![]() ${\it\lambda}_{e}$ exists. Moreover,
${\it\lambda}_{e}$ exists. Moreover,
so that the claim follows. ◻
We denote the limit for ![]() $e\rightarrow \infty$ of the polynomials
$e\rightarrow \infty$ of the polynomials ![]() $b_{M,f}^{e}(s)$ introduced in Definition 3.7 by
$b_{M,f}^{e}(s)$ introduced in Definition 3.7 by ![]() $b_{M,f}(s)$. With this notation we can now compare Stadnik’s notion of Bernstein–Sato polynomial to our notion:
$b_{M,f}(s)$. With this notation we can now compare Stadnik’s notion of Bernstein–Sato polynomial to our notion:
Corollary 6.10. Assume the situation of Theorem 6.9. Let ![]() ${\it\lambda}_{1},\ldots ,{\it\lambda}_{m}$ be
${\it\lambda}_{1},\ldots ,{\it\lambda}_{m}$ be ![]() $p$-weighted limits of the base-
$p$-weighted limits of the base-![]() $p$ expansions of the eigenvalues of the
$p$ expansions of the eigenvalues of the ![]() ${\it\theta}_{p^{l}}$ acting on
${\it\theta}_{p^{l}}$ acting on
Then ![]() $\tilde{b}_{M,f}(s)=\prod _{i}(s-{\it\lambda}_{i})$. In particular,
$\tilde{b}_{M,f}(s)=\prod _{i}(s-{\it\lambda}_{i})$. In particular, ![]() $\tilde{b}_{M,f}(s)=b_{M,f}(s)$
$\tilde{b}_{M,f}(s)=b_{M,f}(s)$
Proof. First of all, we use Theorem 6.9 to ensure that the ![]() $p$-weighted limits actually do exist. Recall from the discussion before Theorem 5.4 that for all
$p$-weighted limits actually do exist. Recall from the discussion before Theorem 5.4 that for all ![]() $e\geqslant 1$ the base-
$e\geqslant 1$ the base-![]() $p$ expansions of the eigenvalues of
$p$ expansions of the eigenvalues of ![]() ${\it\theta}$ are given by
${\it\theta}$ are given by ![]() $\lceil {\it\lambda}p^{e}\rceil -1$. This implies that
$\lceil {\it\lambda}p^{e}\rceil -1$. This implies that ![]() $b(s)$ is a Bernstein–Sato polynomial.
$b(s)$ is a Bernstein–Sato polynomial.
In the other direction we have to show that ![]() $b(s)$ is minimal in the sense that we may not omit any of the
$b(s)$ is minimal in the sense that we may not omit any of the ![]() ${\it\lambda}_{i}$. Assume that we have omitted
${\it\lambda}_{i}$. Assume that we have omitted ![]() ${\it\lambda}_{m}$ and for some
${\it\lambda}_{m}$ and for some ![]() $n\geqslant 0$ the set
$n\geqslant 0$ the set ![]() $\{\lceil {\it\lambda}_{m}p^{e}\rceil -a\,|\,0\leqslant a\leqslant p^{n}\}$ is contained in the set
$\{\lceil {\it\lambda}_{m}p^{e}\rceil -a\,|\,0\leqslant a\leqslant p^{n}\}$ is contained in the set ![]() $\{\lceil {\it\lambda}_{i}p^{e}\rceil -a\,|\,0\leqslant a\leqslant p^{n},1\leqslant i\leqslant m-1\}$. In particular, the
$\{\lceil {\it\lambda}_{i}p^{e}\rceil -a\,|\,0\leqslant a\leqslant p^{n},1\leqslant i\leqslant m-1\}$. In particular, the ![]() $\lceil {\it\lambda}_{m}p^{e}\rceil -1$ are all contained in this set. Since all parameters except
$\lceil {\it\lambda}_{m}p^{e}\rceil -1$ are all contained in this set. Since all parameters except ![]() $e$ of this set are finite we may assume that
$e$ of this set are finite we may assume that ![]() $\lceil {\it\lambda}_{m}p^{e}\rceil -1=\lceil {\it\lambda}_{i}p^{e}\rceil -a$ for some fixed
$\lceil {\it\lambda}_{m}p^{e}\rceil -1=\lceil {\it\lambda}_{i}p^{e}\rceil -a$ for some fixed ![]() $a,i$ and infinitely many
$a,i$ and infinitely many ![]() $e$. Dividing by
$e$. Dividing by ![]() $p^{e}$ and passing to the limit
$p^{e}$ and passing to the limit ![]() $e\rightarrow \infty$ yields
$e\rightarrow \infty$ yields ![]() ${\it\lambda}_{i}={\it\lambda}_{m}$ — a contradiction.◻
${\it\lambda}_{i}={\it\lambda}_{m}$ — a contradiction.◻
Acknowledgments
The idea for this paper was conceived while Axel Stäbler was a guest of the University of Michigan. In particular, he would like to thank Mircea Mustaţă and Karen Smith for making this visit possible.