Hostname: page-component-848d4c4894-m9kch Total loading time: 0 Render date: 2024-05-17T10:25:08.656Z Has data issue: false hasContentIssue false
  • English
  • Français

A CONVERSE THEOREM FOR BORCHERDS PRODUCTS ON 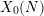$X_{0}(N)$

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  01 March 2019

JAN HENDRIK BRUINIER  and
MARKUS SCHWAGENSCHEIDT
JAN HENDRIK BRUINIER
Affiliation:
Fachbereich Mathematik, Technische Universität Darmstadt, Schlossgartenstraße 7, D–64289 Darmstadt, Germany email bruinier@mathematik.tu-darmstadt.de
MARKUS SCHWAGENSCHEIDT
Affiliation:
Mathematical Institute, University of Cologne, Weyertal 86-90, D–50931 Cologne, Germany email mschwage@math.uni-koeln.de
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that every Fricke-invariant meromorphic modular form for 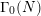$\unicode[STIX]{x1D6E4}_{0}(N)$ whose divisor on 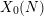$X_{0}(N)$ is defined over 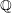$\mathbb{Q}$ and supported on Heegner divisors and the cusps is a generalized Borcherds product associated to a harmonic Maass form of weight 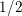$1/2$. Further, we derive a criterion for the finiteness of the multiplier systems of generalized Borcherds products in terms of the vanishing of the central derivatives of 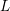$L$-functions of certain weight 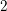$2$ newforms. We also prove similar results for twisted Borcherds products.

MSC classification

Primary: 11F27: Theta series; Weil representation; theta correspondences 11F37: Forms of half-integer weight; nonholomorphic modular forms
Type
Article
Information
Nagoya Mathematical Journal , Volume 240 , December 2020 , pp. 237 - 256
Check for updates
Copyright
© 2019 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Borcherds, R. E., Automorphic forms with singularities on Grassmannians, Invent. Math. 132(3) (1998), 491–562.10.1007/s002220050232Google Scholar
Bruinier, J. H., Borcherds Products on O (2, l) and Chern Classes of Heegner Divisors, Lecture Notes in Mathematics, 1780, Springer, Berlin, 2002.10.1007/b83278Google Scholar
Bruinier, J. H., On the converse theorem for Borcherds products, J. Algebra 397 (2014), 315–342.10.1016/j.jalgebra.2013.08.034Google Scholar
Bruinier, J. H. and Freitag, E., Local Borcherds products, Ann. Inst. Fourier 51 (2001), 1–27.10.5802/aif.1812Google Scholar
Bruinier, J. H. and Funke, J., On two geometric theta lifts, Duke Math. J. 125(1) (2004), 45–90.10.1215/S0012-7094-04-12513-8Google Scholar
Bruinier, J. H. and Funke, J., “On the injectivity of the Kudla–Millson lift and surjectivity of the Borcherds lift”, in Moonshine – The First Quarter Century and Beyond (eds. Lepowski, J., McKay, J. and Tuite, M.) Cambridge University Press, 2010, 12–39.10.1017/CBO9780511730054.004Google Scholar
Bruinier, J. H. and Ono, K., Heegner divisors, L-functions and harmonic weak Maass forms, Ann. of Math. (2) 172(3) (2010), 2135–2181.10.4007/annals.2010.172.2135Google Scholar
Bruinier, J. H. and Schwagenscheidt, M., Algebraic formulas for the coefficients of mock theta functions and Weyl vectors of Borcherds products, J. Algebra 478 (2017), 38–57.10.1016/j.jalgebra.2016.12.034Google Scholar
Eichler, M. and Zagier, D., The Theory of Jacobi Forms, Progress in Mathematics 55, Birkhäuser Boston Inc., Boston, MA, 1985.10.1007/978-1-4684-9162-3Google Scholar
Heim, B. and Murase, A., A characterization of holomorphic Borcherds lifts by symmetries, Int. Math. Res. Not. 21 (2015), 11150–11185.10.1093/imrn/rnv021Google Scholar
McGraw, W. J., The rationality of vector valued modular forms associated with the Weil representation, Math. Ann. 326(1) (2003), 105–122.10.1007/s00208-003-0413-1Google Scholar
Scholl, A. J., Fourier coefficients of Eisenstein series on non-congruence subgroups, Math. Proc. Cambridge Philos. Soc. 99 (1986), 11–17.10.1017/S0305004100063866Google Scholar
Skoruppa, N.-P. and Zagier, D., Jacobi forms and a certain space of modular forms, Invent. Math. 94(1) (1988), 113–146.10.1007/BF01394347Google Scholar
Waldschmidt, M., Nombres Transcendants et Groupes Algébriques, Astérisque, 69–70, Société Mathématique de France, Paris, 1979.Google Scholar
Wüstholz, G., Zum Periodenproblem, Invent. Math. 78(3) (1984), 381–391.10.1007/BF01388443Google Scholar