Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chung, Dong
and
Chung, Tae
1998.
First order differential operators in white noise analysis.
Proceedings of the American Mathematical Society,
Vol. 126,
Issue. 8,
p.
2369.
BARHOUMI, ABDESSATAR
OUERDIANE, HABIB
and
RGUIGUI, HAFEDH
2012.
QWN-EULER OPERATOR AND ASSOCIATED CAUCHY PROBLEM.
Infinite Dimensional Analysis, Quantum Probability and Related Topics,
Vol. 15,
Issue. 01,
p.
1250004.
Barhoumi, Abdessatar
Ammou, Bilel Kacem Ben
and
Rguigui, Hafedh
2015.
Operator theory: quantum white noise approach.
Quantum Studies: Mathematics and Foundations,
Vol. 2,
Issue. 2,
p.
221.
Barhoumi, Abdessatar
and
Rguigui, Hafedh
2016.
QWN-first-order Wick differential operators and an associated transport equation.
Random Operators and Stochastic Equations,
Vol. 24,
Issue. 1,
p.
15.




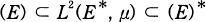 gives a fundamental framework of white noise calculus [2] as distribution theory on Gaussian space. It is proved in Kubo-Takenaka [7] that (
gives a fundamental framework of white noise calculus [2] as distribution theory on Gaussian space. It is proved in Kubo-Takenaka [7] that (