Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-05-25T00:14:23.057Z Has data issue: false hasContentIssue false
  • English
  • Français

EXPLICIT SURJECTIVITY RESULTS FOR DRINFELD MODULES OF RANK 2

Part of: Arithmetic algebraic geometry Algebraic number theory: global fields

Published online by Cambridge University Press:  27 July 2017

IMIN CHEN  and
YOONJIN LEE
IMIN CHEN
Affiliation:
Department of Mathematics, Simon Fraser University, Burnaby, British Columbia, CANADA V5A 1S6 email ichen@math.sfu.ca
YOONJIN LEE
Affiliation:
Department of Mathematics, Ewha Womans University, 52 Ewhayeodae-gil, Seodaemun-gu, Seoul, 03760, South Korea email yoonjinl@ewha.ac.kr
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 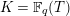$K=\mathbb{F}_{q}(T)$ and 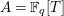$A=\mathbb{F}_{q}[T]$. Suppose that 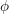$\unicode[STIX]{x1D719}$ is a Drinfeld 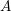$A$-module of rank 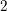$2$ over 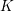$K$ which does not have complex multiplication. We obtain an explicit upper bound (dependent on 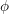$\unicode[STIX]{x1D719}$) on the degree of primes 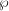${\wp}$ of 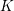$K$ such that the image of the Galois representation on the 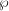${\wp}$-torsion points of 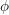$\unicode[STIX]{x1D719}$ is not surjective, in the case of 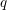$q$ odd. Our results are a Drinfeld module analogue of Serre’s explicit large image results for the Galois representations on 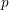$p$-torsion points of elliptic curves (Serre, Propriétés galoisiennes des points d’ordre fini des courbes elliptiques, Invent. Math. 15 (1972), 259–331; Serre, Quelques applications du théorème de densité de Chebotarev, Inst. Hautes Etudes Sci. Publ. Math. 54 (1981), 323–401.) and are unconditional because the generalized Riemann hypothesis for function fields holds. An explicit isogeny theorem for Drinfeld 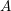$A$-modules of rank 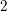$2$ over 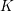$K$ is also proven.

MSC classification

Primary: 11G09: Drinfel'd modules; higher-dimensional motives, etc.
Secondary: 11R58: Arithmetic theory of algebraic function fields
Type
Article
Information
Nagoya Mathematical Journal , Volume 234 , June 2019 , pp. 17 - 45
Copyright
© 2017 Foundation Nagoya Mathematical Journal  

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Imin Chen is supported by an NSERC Discovery Grant and Yoonjin Lee is a corresponding author and supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2009-0093827) and also by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MEST) (NRF-2017R1A2B2004574).

References

Armana, C., Torsion des modules de Drinfeld de rang 2 et formes modulaires de Drinfeld (French) , Algebra Number Theory 6(6) (2012), 1239–1288.10.2140/ant.2012.6.1239Google Scholar
Chen, I. and Lee, Y., Newton polygons of exponential functions attached to Drinfeld modules of rank 2 , Proc. Amer. Math. Soc. 141 (2013), 83–91.10.1090/S0002-9939-2012-11300-0Google Scholar
Chen, I. and Lee, Y., Explicit isogeny theorems for Drinfeld modules , Pac. J. Math. 263(1) (2013), 87–116.10.2140/pjm.2013.263.87Google Scholar
Cojocaru, A. and Hall, C., Uniform results for Serre’s theorem for elliptic curves , Int. Math. Res. Not. 50 (2005), 3065–3080.10.1155/IMRN.2005.3065Google Scholar
David, C., Frobenius distributions of Drinfeld modules of any rank , J. Number Theory 90(2) (2001), 329–340.10.1006/jnth.2000.2664Google Scholar
Drinfeld, V. G., Elliptic modules , Math. USSR Sb. 31 (1977), 159–170.10.1070/SM1977v031n02ABEH002296Google Scholar
Gekeler, E.-U., On finite Drinfeld modules , J. Algebra 141 (1991), 167–182.Google Scholar
Gekeler, E., Frobenius distributions of Drinfeld modules over finite fields , Trans. Amer. Math. Soc. 360(4) (2008), 1695–1721.10.1090/S0002-9947-07-04558-8Google Scholar
Goss, D., Basic Structures of Function Field Arithmetic, Springer, Berlin, 1996.10.1007/978-3-642-61480-4Google Scholar
Goss, D., “ L-series of t-motives and Drinfeld modules ”, in The Arithmetic of Function Fields: Proceedings of the Workshop at Ohio State University 1991 (eds. Goss, D. et al. ) Berlin-New York, 1992, 313–402.10.1515/9783110886153Google Scholar
Gardeyn, F., t-motives and Galois representations, Ph.D Thesis, ETH Zurich, 2001.Google Scholar
Gardeyn, F., Une borne pour l’action de l’inertie sauvage sur la torsion d’un module de Drinfeld , Arch. Math. 79 (2002), 241–251.10.1007/s00013-002-8310-5Google Scholar
Huppert, B., Endliche Gruppen I, Grundlehren der Mathematischen Wissenschaften 134 , Springer, Berlin, 1967.10.1007/978-3-642-64981-3Google Scholar
Kraus, A., Une remarque sur les points de torsion des courbes elliptiques , C. R. Acad. Sci. Paris Sér. I Math. 321(9) (1995), 1143–1146.Google Scholar
Lang, S., Introduction to Modular Forms, Grundlehren der Mathematischen Wissenschaften 222 , Springer, Berlin, 1976, ix+261.Google Scholar
Lombardo, D., Bounds for Serre’s open image theorem for elliptic curves over number fields , Algebra Number Theory 9(10) (2015), 2347–2395.10.2140/ant.2015.9.2347Google Scholar
Mazur, B., Rational isogenies of prime degree , Invent. Math. 44(2) (1978), 129–162.10.1007/BF01390348Google Scholar
Murty, V. K. and Scherk, J., Effective versions of the Chebotarev density theorem for function fields , C. R. Acad. Sci. Paris Sr. I Math. 319(6) (1994), 523–528.Google Scholar
Pál, A., On the torsion of Drinfeld modules of rank two , J. Reine Angew. Math. 640 (2010), 1–45.10.1515/crelle.2010.017Google Scholar
Pink, R., The Mumford–Tate Conjecture for Drinfeld Modules , Publ. Res. Inst. Math. Sci. 33 (1997), 393–425.10.2977/prims/1195145322Google Scholar
Pink, R. and Rütsche, E., Image of the group ring of the Galois representation associated to Drinfeld modules , J. Number Theory 129 (2009), 866–881.10.1016/j.jnt.2008.12.003Google Scholar
Poonen, B., Fractional power series and pairings on Drinfeld modules , J. Amer. Math. Soc. 9(3) (1996), 783–812.10.1090/S0894-0347-96-00203-2Google Scholar
Rosen, M., Number Theory in Function Fields, Springer, 2002.10.1007/978-1-4757-6046-0Google Scholar
Serre, J.-P., Propriétés galoisiennes des points d’ordre fini des courbes elliptiques , Invent. Math. 15 (1972), 259–331.10.1007/BF01405086Google Scholar
Serre, J.-P., Local Fields, Graduate Texts in Mathematics, Springer, New York, 1979.10.1007/978-1-4757-5673-9Google Scholar
Serre, J-P., Quelques applications du théorème de densité de Chebotarev , Inst. Hautes Etudes Sci. Publ. Math. 54 (1981), 323–401.10.1007/BF02698692Google Scholar
Taguchi, Y., “ Ramifications arising from Drinfeld modules ”, in The Arithmetic of Function Fields (Columbus, OH, 1991), Ohio State Univ. Math. Res. Inst. Publ. 2 , de Gruyter, Berlin, 1992, 171–187.Google Scholar
Taguchi, Y., On 𝜙-modules , J. Number Theory 60 (1996), 124–141.10.1006/jnth.1996.0117Google Scholar
Takahashi, T., Good reduction of elliptic modules , J. Math. Soc. Japan 34 (1982), 475–487.10.2969/jmsj/03430475Google Scholar
Thakur, D.S., Function Field Arithmetic, World Scientific Publishing Co., Inc., 2004.10.1142/5535Google Scholar
van der Heiden, G.-J., Weil pairing for Drinfeld modules , Monatsch. Math. 143 (2004), 115–143.10.1007/s00605-004-0261-4Google Scholar