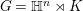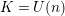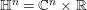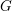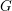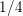1 Introduction
A classical theorem of Hardy proved in 1933 in the case of the real line, says that an integrable function
![]() $f$
and its Fourier transform
$f$
and its Fourier transform
![]() $\hat{f}$
cannot both have arbitrary Gaussian decay unless
$\hat{f}$
cannot both have arbitrary Gaussian decay unless
![]() $f$
is identically zero. More precisely, if both
$f$
is identically zero. More precisely, if both
![]() $f(x)e^{\unicode[STIX]{x1D6FC}\Vert x\Vert ^{2}}$
and
$f(x)e^{\unicode[STIX]{x1D6FC}\Vert x\Vert ^{2}}$
and
![]() $\hat{f}(\unicode[STIX]{x1D709})e^{\unicode[STIX]{x1D6FD}\Vert \unicode[STIX]{x1D709}\Vert ^{2}}$
are in
$\hat{f}(\unicode[STIX]{x1D709})e^{\unicode[STIX]{x1D6FD}\Vert \unicode[STIX]{x1D709}\Vert ^{2}}$
are in
![]() $L^{\infty }(\mathbb{R}^{n})$
for some
$L^{\infty }(\mathbb{R}^{n})$
for some
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}>0$
then the following conclusions hold:
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}>0$
then the following conclusions hold:
-
(1)
 $f=0$
whenever
$f=0$
whenever
 $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}>1/4.$
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}>1/4.$
-
(2) The function
 $f$
is a constant multiple of
$f$
is a constant multiple of
 $e^{-\unicode[STIX]{x1D6FC}\Vert x\Vert ^{2}}$
when
$e^{-\unicode[STIX]{x1D6FC}\Vert x\Vert ^{2}}$
when
 $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=1/4$
.
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=1/4$
. -
(3) When
 $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}<1/4$
, there are infinitely many linearly independent functions satisfying both conditions.
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}<1/4$
, there are infinitely many linearly independent functions satisfying both conditions.
Here the Fourier transform
![]() $\widehat{f}$
is defined by
$\widehat{f}$
is defined by
and
![]() $\Vert x\Vert =\langle x,x\rangle ^{1/2}$
is the Euclidean norm. Actually, the bound
$\Vert x\Vert =\langle x,x\rangle ^{1/2}$
is the Euclidean norm. Actually, the bound
![]() $\frac{1}{4}$
is sharp and the strong Gaussian decay of
$\frac{1}{4}$
is sharp and the strong Gaussian decay of
![]() $f$
and
$f$
and
![]() $\widehat{f}$
is only required with respect to a one-dimensional subgroup of
$\widehat{f}$
is only required with respect to a one-dimensional subgroup of
![]() $\mathbb{R}^{n}$
. For a detailed proof of Hardy’s theorem, see [Reference Hardy7]. Hardy’s theorem initially proved for the Euclidean Fourier transform has been extended to several setups including the Heisenberg group and many other various classes of nonabelian connected Lie groups ([Reference Baklouti and Kaniuth3, Reference Baklouti and Kaniuth4, Reference Eguchi, Koizumi and Kumahara6, Reference Sengupta12–Reference Sitaram and Sundari14, Reference Sundari16, Reference Thangavelu17] and [Reference Thangavelu19]). Specifically, analogues of Hardy’s theorem have been proved for motion groups ([Reference Eguchi, Koizumi and Kumahara6] and [Reference Sundari16]). In case of a Lie group
$\mathbb{R}^{n}$
. For a detailed proof of Hardy’s theorem, see [Reference Hardy7]. Hardy’s theorem initially proved for the Euclidean Fourier transform has been extended to several setups including the Heisenberg group and many other various classes of nonabelian connected Lie groups ([Reference Baklouti and Kaniuth3, Reference Baklouti and Kaniuth4, Reference Eguchi, Koizumi and Kumahara6, Reference Sengupta12–Reference Sitaram and Sundari14, Reference Sundari16, Reference Thangavelu17] and [Reference Thangavelu19]). Specifically, analogues of Hardy’s theorem have been proved for motion groups ([Reference Eguchi, Koizumi and Kumahara6] and [Reference Sundari16]). In case of a Lie group
![]() $G$
, the Euclidean norms on
$G$
, the Euclidean norms on
![]() $\mathbb{R}^{n}$
and on
$\mathbb{R}^{n}$
and on
![]() $\widehat{\mathbb{R}^{n}}$
have to be replaced by certain norm functions on
$\widehat{\mathbb{R}^{n}}$
have to be replaced by certain norm functions on
![]() $G$
and the Hilbert–Schmidt norm of the operator-valued Fourier transform on the unitary dual
$G$
and the Hilbert–Schmidt norm of the operator-valued Fourier transform on the unitary dual
![]() $\widehat{G}$
of
$\widehat{G}$
of
![]() $G$
, respectively depending upon the parameters involved in the problem in question.
$G$
, respectively depending upon the parameters involved in the problem in question.
In this context, we mention that in [Reference Sarkar, Thangavelu, Sarkar and Thangavelu10], Sarkar and Thangavelu gave an analogue of Hardy’s theorem for the Euclidean motion group
![]() $M_{n}:=SO(n)\ltimes \mathbb{R}^{n}$
by means of the heat kernel. Indeed, denoting by
$M_{n}:=SO(n)\ltimes \mathbb{R}^{n}$
by means of the heat kernel. Indeed, denoting by
![]() $\unicode[STIX]{x1D6E5}_{n}$
the standard Laplacian on
$\unicode[STIX]{x1D6E5}_{n}$
the standard Laplacian on
![]() $\mathbb{R}^{n}$
and by
$\mathbb{R}^{n}$
and by
the associated heat kernel, they proved the following result.
Theorem 1.1. Let
![]() $f\in L^{1}(M_{n})$
satisfy the following conditions:
$f\in L^{1}(M_{n})$
satisfy the following conditions:
-
(1)
 $|f(k,x)|\leqslant C(1+\Vert x\Vert )^{N}p_{s}^{n}(x),\;(k,x)\in M_{n}$
.
$|f(k,x)|\leqslant C(1+\Vert x\Vert )^{N}p_{s}^{n}(x),\;(k,x)\in M_{n}$
. -
(2)
 $\Vert \unicode[STIX]{x1D70B}_{r,\unicode[STIX]{x1D70E}}(f)\Vert _{HS}\leqslant C(1+r)^{N}e^{-tr^{2}}\;(r,\unicode[STIX]{x1D70E})\in \mathbb{R}_{+}^{\ast }\times \widehat{SO(n-1)}$
.
$\Vert \unicode[STIX]{x1D70B}_{r,\unicode[STIX]{x1D70E}}(f)\Vert _{HS}\leqslant C(1+r)^{N}e^{-tr^{2}}\;(r,\unicode[STIX]{x1D70E})\in \mathbb{R}_{+}^{\ast }\times \widehat{SO(n-1)}$
.
Then
![]() $f=0$
whenever
$f=0$
whenever
![]() $s<t$
. When
$s<t$
. When
![]() $s=t$
,
$s=t$
,
![]() $f$
can be expressed as a finite linear combination of functions of the form
$f$
can be expressed as a finite linear combination of functions of the form
where
![]() $P_{m,j}$
are solid harmonics of degree
$P_{m,j}$
are solid harmonics of degree
![]() $m$
and
$m$
and
![]() $g_{m,j}$
are certain bounded functions in
$g_{m,j}$
are certain bounded functions in
![]() $L^{2}(SO(n))$
.
$L^{2}(SO(n))$
.
A weaker version of the last theorem for the case
![]() $s<t$
is known from the work of Sundari (cf. [Reference Sundari16]). For arbitrary compact extension
$s<t$
is known from the work of Sundari (cf. [Reference Sundari16]). For arbitrary compact extension
![]() $M_{K}:=K\ltimes \mathbb{R}^{n}$
of
$M_{K}:=K\ltimes \mathbb{R}^{n}$
of
![]() $\mathbb{R}^{n}$
, the following analogue of Hardy’s uncertainty principle was also recently proved (cf. [Reference Azouazi, Baklouti and Elloumi2]).
$\mathbb{R}^{n}$
, the following analogue of Hardy’s uncertainty principle was also recently proved (cf. [Reference Azouazi, Baklouti and Elloumi2]).
Theorem 1.2. Let
![]() $q\in \mathbb{N}$
,
$q\in \mathbb{N}$
,
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
be positive real numbers and let
$\unicode[STIX]{x1D6FD}$
be positive real numbers and let
![]() $f$
be a measurable function on
$f$
be a measurable function on
![]() $M_{K}$
satisfying the following decay conditions:
$M_{K}$
satisfying the following decay conditions:
-
(i)
 $|f(k,x)|\leqslant \unicode[STIX]{x1D711}(k)(1+\Vert x\Vert ^{2})^{q}e^{-\unicode[STIX]{x1D6FC}\Vert x\Vert ^{2}}$
for all
$|f(k,x)|\leqslant \unicode[STIX]{x1D711}(k)(1+\Vert x\Vert ^{2})^{q}e^{-\unicode[STIX]{x1D6FC}\Vert x\Vert ^{2}}$
for all
 $x\in \mathbb{R}^{n}$
and
$x\in \mathbb{R}^{n}$
and
 $k\in K$
, where
$k\in K$
, where
 $\unicode[STIX]{x1D711}\in L^{2}(K)$
,
$\unicode[STIX]{x1D711}\in L^{2}(K)$
, -
(ii)
 $\Vert \unicode[STIX]{x1D70B}_{\ell ,\unicode[STIX]{x1D70E}}(f)\Vert _{HS}\leqslant \unicode[STIX]{x1D713}_{\ell }(\unicode[STIX]{x1D70E})(1+\Vert \ell \Vert ^{2})^{q}e^{-\unicode[STIX]{x1D6FD}\Vert \ell \Vert ^{2}}$
, for all
$\Vert \unicode[STIX]{x1D70B}_{\ell ,\unicode[STIX]{x1D70E}}(f)\Vert _{HS}\leqslant \unicode[STIX]{x1D713}_{\ell }(\unicode[STIX]{x1D70E})(1+\Vert \ell \Vert ^{2})^{q}e^{-\unicode[STIX]{x1D6FD}\Vert \ell \Vert ^{2}}$
, for all
 $\ell \in \mathbb{R}^{n}$
and all
$\ell \in \mathbb{R}^{n}$
and all
 $\unicode[STIX]{x1D70E}\in \widehat{K_{\ell }}$
, with
$\unicode[STIX]{x1D70E}\in \widehat{K_{\ell }}$
, with
 $\Vert \unicode[STIX]{x1D713}_{\ell }\Vert _{l^{2}(\widehat{K_{\ell }})}\leqslant C$
for some positive constant
$\Vert \unicode[STIX]{x1D713}_{\ell }\Vert _{l^{2}(\widehat{K_{\ell }})}\leqslant C$
for some positive constant
 $C$
independent of
$C$
independent of
 $\ell$
.
$\ell$
.
Then the following conclusions hold:
-
(1)
 $f=0$
almost everywhere whenever
$f=0$
almost everywhere whenever
 $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}>1/4$
.
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}>1/4$
. -
(2) If
 $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}<1/4$
, then there are infinitely many linearly independent functions satisfying both conditions (i) and (ii).
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}<1/4$
, then there are infinitely many linearly independent functions satisfying both conditions (i) and (ii). -
(3) When
 $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=1/4$
, the function
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=1/4$
, the function
 $f$
is of the form
$f$
is of the form
 $f(k,x)=\unicode[STIX]{x1D701}(k,x)e^{-\unicode[STIX]{x1D6FC}\Vert x\Vert ^{2}}$
where
$f(k,x)=\unicode[STIX]{x1D701}(k,x)e^{-\unicode[STIX]{x1D6FC}\Vert x\Vert ^{2}}$
where
 $x\mapsto \unicode[STIX]{x1D701}(k,x)$
is polynomial on
$x\mapsto \unicode[STIX]{x1D701}(k,x)$
is polynomial on
 $x$
of degree
$x$
of degree
 ${\leqslant}2q$
and
${\leqslant}2q$
and
 $k\mapsto \unicode[STIX]{x1D701}(k,x)$
is an
$k\mapsto \unicode[STIX]{x1D701}(k,x)$
is an
 $L^{2}$
-function on
$L^{2}$
-function on
 $K$
.
$K$
.
In this paper, our main goal is to prove a suitable analogue of Theorem 1.1 in the context of Heisenberg motion groups. Let
![]() $\mathbb{H}^{n}:=\mathbb{C}^{n}\times \mathbb{R}$
be the Heisenberg group with the group operation defined by
$\mathbb{H}^{n}:=\mathbb{C}^{n}\times \mathbb{R}$
be the Heisenberg group with the group operation defined by
Alternatively, we can consider
![]() $\mathbb{H}^{n}$
as
$\mathbb{H}^{n}$
as
![]() $\mathbb{R}^{n}\times \mathbb{R}^{n}\times \mathbb{R}$
with the group law
$\mathbb{R}^{n}\times \mathbb{R}^{n}\times \mathbb{R}$
with the group law
Let
![]() $K=U(n)$
act on
$K=U(n)$
act on
![]() $\mathbb{H}^{n}$
by the automorphisms
$\mathbb{H}^{n}$
by the automorphisms
and let
![]() $G=\mathbb{H}^{n}\rtimes K$
be the Heisenberg motion group with the group law
$G=\mathbb{H}^{n}\rtimes K$
be the Heisenberg motion group with the group law
We will prove two analogues of Hardy’s uncertainty principle for the Heisenberg motion group. The first one makes use of the heat kernel of the Heisenberg group and that of the associated compact group
![]() $K$
and the second utilizes the Euclidean norms. We will thus prove parallel versions of the uncertainty principle as in Euclidean motion groups (cf. Theorems 1.1 and 2.1) without taking into account the polynomial growth in the conditions of decay.
$K$
and the second utilizes the Euclidean norms. We will thus prove parallel versions of the uncertainty principle as in Euclidean motion groups (cf. Theorems 1.1 and 2.1) without taking into account the polynomial growth in the conditions of decay.
Our second formulation of Hardy’s uncertainty principle (cf. Section 3) comes as a direct consequence of Miyachi’s uncertainty principle. In 1997 Miyachi [Reference Miyachi9] proved the following uncertainty principle which includes both Hardy and Cowling–Price theorems as corollaries.
Theorem 1.3. Let
![]() $f$
be an integrable function on
$f$
be an integrable function on
![]() $\mathbb{R}^{n}$
such that
$\mathbb{R}^{n}$
such that
for some positive number
![]() $\unicode[STIX]{x1D6FC}$
. Further assume that
$\unicode[STIX]{x1D6FC}$
. Further assume that
for some positive numbers
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $c$
. If
$c$
. If
![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=1/4$
, then
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=1/4$
, then
![]() $f$
is a constant multiple of the Gaussian
$f$
is a constant multiple of the Gaussian
![]() $e^{-\unicode[STIX]{x1D6FC}\Vert .\Vert ^{2}}$
.
$e^{-\unicode[STIX]{x1D6FC}\Vert .\Vert ^{2}}$
.
This result leads to the following corollary.
Corollary 1.4. (Cf. [Reference Azouazi, Baklouti and Elloumi1])
Under the same conditions of Theorem 1.3, the function
![]() $f$
vanishes almost everywhere if
$f$
vanishes almost everywhere if
![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}>1/4.$
When
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}>1/4.$
When
![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}<\frac{1}{4}$
, there exist infinitely many linearly independent functions satisfying both conditions.
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}<\frac{1}{4}$
, there exist infinitely many linearly independent functions satisfying both conditions.
The last part of the paper is devoted to formulate and prove an analogue of Miyachi’s theorem for Heisenberg motion groups. As a direct consequence, we also derive an analogue of Cowling–Price uncertainty principle and prove the sharpness of the constant
![]() $1/4$
in both the settings.
$1/4$
in both the settings.
2 A heat kernel version of Hardy’s uncertainty principle for Heisenberg motion groups
Let
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(z,t),\unicode[STIX]{x1D706}\in \mathbb{R}^{\ast }$
be the Schrödinger representation of
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(z,t),\unicode[STIX]{x1D706}\in \mathbb{R}^{\ast }$
be the Schrödinger representation of
![]() $\mathbb{H}^{n}$
realized on
$\mathbb{H}^{n}$
realized on
![]() $L^{2}(\mathbb{R}^{n})$
and defined as:
$L^{2}(\mathbb{R}^{n})$
and defined as:
For each
![]() $k\in K\subset U(n),(x,y,t)\mapsto (k\cdot (x,y),t)$
is an automorphism of
$k\in K\subset U(n),(x,y,t)\mapsto (k\cdot (x,y),t)$
is an automorphism of
![]() $\mathbb{H}^{n}$
because
$\mathbb{H}^{n}$
because
![]() $U(n)$
preserves the symplectic form
$U(n)$
preserves the symplectic form
![]() $xy-yv$
on
$xy-yv$
on
![]() $\mathbb{R}^{2n}$
. If
$\mathbb{R}^{2n}$
. If
![]() $\unicode[STIX]{x1D70C}$
is a representation of
$\unicode[STIX]{x1D70C}$
is a representation of
![]() $\mathbb{H}^{n}$
then using this automorphism we can define another representation
$\mathbb{H}^{n}$
then using this automorphism we can define another representation
![]() $\unicode[STIX]{x1D70C}_{k}$
by
$\unicode[STIX]{x1D70C}_{k}$
by
![]() $\unicode[STIX]{x1D70C}_{k}(x,u,t)=\unicode[STIX]{x1D70C}(k\cdot (x,u),t)$
which coincides with
$\unicode[STIX]{x1D70C}_{k}(x,u,t)=\unicode[STIX]{x1D70C}(k\cdot (x,u),t)$
which coincides with
![]() $\unicode[STIX]{x1D70C}$
at the center. If we take
$\unicode[STIX]{x1D70C}$
at the center. If we take
![]() $\unicode[STIX]{x1D70C}$
to be the Schrödinger representation
$\unicode[STIX]{x1D70C}$
to be the Schrödinger representation
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}$
, then by Stone–von Neumann theorem
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}$
, then by Stone–von Neumann theorem
![]() $\unicode[STIX]{x1D70C}_{k}$
is unitarily equivalent to
$\unicode[STIX]{x1D70C}_{k}$
is unitarily equivalent to
![]() $\unicode[STIX]{x1D70C}$
and there exists a unitary operator
$\unicode[STIX]{x1D70C}$
and there exists a unitary operator
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(k)$
such that:
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(k)$
such that:
The operator-valued function
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}$
, which can be extended to the double cover of
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}$
, which can be extended to the double cover of
![]() $\text{Sp}(n,\mathbb{R})$
, can be chosen so that it becomes a unitary representation of
$\text{Sp}(n,\mathbb{R})$
, can be chosen so that it becomes a unitary representation of
![]() $K$
on
$K$
on
![]() $L^{2}(\mathbb{R}^{n})$
and is called the metaplectic representation. Let
$L^{2}(\mathbb{R}^{n})$
and is called the metaplectic representation. Let
![]() $\unicode[STIX]{x1D70E}\in \widehat{K}$
acting on a Hilbert space
$\unicode[STIX]{x1D70E}\in \widehat{K}$
acting on a Hilbert space
![]() $V_{\unicode[STIX]{x1D70E}}$
. We define for each
$V_{\unicode[STIX]{x1D70E}}$
. We define for each
![]() $\unicode[STIX]{x1D706}\in \mathbb{R}^{\ast }$
and
$\unicode[STIX]{x1D706}\in \mathbb{R}^{\ast }$
and
![]() $\unicode[STIX]{x1D70E}\in \widehat{K}$
, the representation
$\unicode[STIX]{x1D70E}\in \widehat{K}$
, the representation
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}$
on
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}$
on
![]() $L^{2}(\mathbb{R}^{n})\otimes V_{\unicode[STIX]{x1D70E}}$
by
$L^{2}(\mathbb{R}^{n})\otimes V_{\unicode[STIX]{x1D70E}}$
by
Then it is shown that
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}$
are all irreducible unitary representations of
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}$
are all irreducible unitary representations of
![]() $G$
. They are enough to describe the Plancherel measure of
$G$
. They are enough to describe the Plancherel measure of
![]() $G$
(cf. [Reference Sen11]). For an integrable function
$G$
(cf. [Reference Sen11]). For an integrable function
![]() $f$
on
$f$
on
![]() $G$
its Fourier transform
$G$
its Fourier transform
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f)$
is the operator-valued function given by
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f)$
is the operator-valued function given by
where
![]() $dg$
is the Haar measure on
$dg$
is the Haar measure on
![]() $G.$
Observe that
$G.$
Observe that
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f)$
is a bounded linear operator acting on
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f)$
is a bounded linear operator acting on
![]() $L^{2}(\mathbb{R}^{n})\otimes V_{\unicode[STIX]{x1D70E}}.$
$L^{2}(\mathbb{R}^{n})\otimes V_{\unicode[STIX]{x1D70E}}.$
Let
![]() $\mathscr{L}$
be the sublaplacian on
$\mathscr{L}$
be the sublaplacian on
![]() $\mathbb{H}^{n}$
with the associated heat kernel
$\mathbb{H}^{n}$
with the associated heat kernel
![]() $p_{a}(z,t)$
, which is given by:
$p_{a}(z,t)$
, which is given by:
Let
![]() $\unicode[STIX]{x1D6E5}_{K}$
be the Laplacian on
$\unicode[STIX]{x1D6E5}_{K}$
be the Laplacian on
![]() $K$
with the associated heat kernel
$K$
with the associated heat kernel
![]() $q_{a}(k)$
. Let
$q_{a}(k)$
. Let
![]() $h_{a}(z,t,k)=p_{a}\otimes q_{a}(z,t,k)$
be the heat kernel on
$h_{a}(z,t,k)=p_{a}\otimes q_{a}(z,t,k)$
be the heat kernel on
![]() $G=\mathbb{H}^{n}\rtimes K$
associated to
$G=\mathbb{H}^{n}\rtimes K$
associated to
![]() $\mathscr{L}+\unicode[STIX]{x1D6E5}_{K}$
. We prove the following two theorems.
$\mathscr{L}+\unicode[STIX]{x1D6E5}_{K}$
. We prove the following two theorems.
Theorem 2.1. Let
![]() $f$
be a measurable function on
$f$
be a measurable function on
![]() $G$
which satisfies:
$G$
which satisfies:
-
(i)
 $|f(z,t,k)|\leqslant C\;h_{a}(z,t,k).$
$|f(z,t,k)|\leqslant C\;h_{a}(z,t,k).$
-
(ii) For every
 $\unicode[STIX]{x1D706}\in \mathbb{R}^{\ast }\text{and }\unicode[STIX]{x1D70E}\in \widehat{K},$
$\unicode[STIX]{x1D706}\in \mathbb{R}^{\ast }\text{and }\unicode[STIX]{x1D70E}\in \widehat{K},$
 $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f)^{\star }\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f)\leqslant C\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(h_{b})^{\star }\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(h_{b})$
,
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f)^{\star }\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f)\leqslant C\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(h_{b})^{\star }\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(h_{b})$
,
for some positive constant
![]() $C$
. Further assume that
$C$
. Further assume that
![]() $f$
is central in the
$f$
is central in the
![]() $K$
-variable in the sense that
$K$
-variable in the sense that
![]() $f(z,t,k)=f(z,t,uku^{-1})$
for any
$f(z,t,k)=f(z,t,uku^{-1})$
for any
![]() $k,u\in K$
and
$k,u\in K$
and
![]() $(z,t)\in \mathbb{H}^{n}$
. Then
$(z,t)\in \mathbb{H}^{n}$
. Then
![]() $f=0$
whenever
$f=0$
whenever
![]() $a<b$
.
$a<b$
.
The following remarks are in order. In the above theorem we are not able to relax the condition that
![]() $f$
is central in the last variable. We believe the result is true without this assumption though our proof requires it. Uncertainty principles for general functions with no restrictions on
$f$
is central in the last variable. We believe the result is true without this assumption though our proof requires it. Uncertainty principles for general functions with no restrictions on
![]() $K$
-types is still an open problem even in the context of semisimple Lie groups. The only group on which a general version of Hardy’s uncertainty principle has been proved is
$K$
-types is still an open problem even in the context of semisimple Lie groups. The only group on which a general version of Hardy’s uncertainty principle has been proved is
![]() $\text{SU}(1,1)$
, see [Reference Kawazoe and Liu8] and [Reference Thangavelu18].
$\text{SU}(1,1)$
, see [Reference Kawazoe and Liu8] and [Reference Thangavelu18].
We also remark that we do not know what happens when
![]() $a=b$
in the above theorem. The same comment applies to Hardy’s theorem (see [Reference Thangavelu19, Theorem 2.9.2]) on the Heisenberg group also. However, we have the following version which treats the equality case which is the analogue of [Reference Thangavelu19, Theorem 2.9.5].
$a=b$
in the above theorem. The same comment applies to Hardy’s theorem (see [Reference Thangavelu19, Theorem 2.9.2]) on the Heisenberg group also. However, we have the following version which treats the equality case which is the analogue of [Reference Thangavelu19, Theorem 2.9.5].
For an integrable function
![]() $f$
on
$f$
on
![]() $G$
, define the partial Fourier transform
$G$
, define the partial Fourier transform
Theorem 2.2. Let
![]() $f$
be a measurable function on
$f$
be a measurable function on
![]() $G$
which is central in the
$G$
which is central in the
![]() $K$
-variable and satisfies:
$K$
-variable and satisfies:
-
(i)
 $|f^{\unicode[STIX]{x1D706}}(z,k)|\leqslant C\,p_{a}^{\unicode[STIX]{x1D706}}(z)q_{a}(k)\;$
for all
$|f^{\unicode[STIX]{x1D706}}(z,k)|\leqslant C\,p_{a}^{\unicode[STIX]{x1D706}}(z)q_{a}(k)\;$
for all
 $\unicode[STIX]{x1D706}\in \mathbb{R}^{\ast }\;$
$\unicode[STIX]{x1D706}\in \mathbb{R}^{\ast }\;$
-
(ii) For every
 $\unicode[STIX]{x1D706}\in \mathbb{R}^{\ast }\text{and }\unicode[STIX]{x1D70E}\in \widehat{K},$
$\unicode[STIX]{x1D706}\in \mathbb{R}^{\ast }\text{and }\unicode[STIX]{x1D70E}\in \widehat{K},$
 $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f)^{\star }\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f)\leqslant C\,\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(h_{a})^{\star }\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(h_{a})$
,
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f)^{\star }\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f)\leqslant C\,\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(h_{a})^{\star }\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(h_{a})$
,
for some positive constant
![]() $C$
. Then
$C$
. Then
![]() $f(z,t,k)=\unicode[STIX]{x1D70C}_{a}(z,t)\;\unicode[STIX]{x1D711}(k)$
, for some
$f(z,t,k)=\unicode[STIX]{x1D70C}_{a}(z,t)\;\unicode[STIX]{x1D711}(k)$
, for some
![]() $\unicode[STIX]{x1D711}\in L^{2}(K)$
.
$\unicode[STIX]{x1D711}\in L^{2}(K)$
.
The above theorems are proved by reducing them to the following result for Laguerre expansions. We let
stand for Laguerre functions of type
![]() $(n-1)$
on
$(n-1)$
on
![]() $\mathbb{C}^{n}.$
Any radial function
$\mathbb{C}^{n}.$
Any radial function
![]() $f$
on
$f$
on
![]() $\mathbb{C}^{n}$
can be expanded in terms of
$\mathbb{C}^{n}$
can be expanded in terms of
![]() $\unicode[STIX]{x1D711}_{k,\unicode[STIX]{x1D706}}^{n-1}(z)$
. Let
$\unicode[STIX]{x1D711}_{k,\unicode[STIX]{x1D706}}^{n-1}(z)$
. Let
![]() $f(z,k)$
be a radial function on
$f(z,k)$
be a radial function on
![]() $\mathbb{C}^{n}$
taking values in
$\mathbb{C}^{n}$
taking values in
![]() $L^{2}(K)$
. Define
$L^{2}(K)$
. Define
as the Laguerre coefficients of
![]() $f$
. We have the following theorem.
$f$
. We have the following theorem.
Theorem 2.3. Let
![]() $\unicode[STIX]{x1D706}\in \mathbb{R}^{\ast }$
be fixed. Assume that
$\unicode[STIX]{x1D706}\in \mathbb{R}^{\ast }$
be fixed. Assume that
![]() $f\in L^{2}(\mathbb{C}^{n},\;L^{2}(K))$
is a radial function which satisfies:
$f\in L^{2}(\mathbb{C}^{n},\;L^{2}(K))$
is a radial function which satisfies:
-
(i)
 $\left(\int _{K}|f(z,k)|^{2}\,dk\right)^{\frac{1}{2}}\leqslant Cp_{a}^{\unicode[STIX]{x1D706}}(z),$
$\left(\int _{K}|f(z,k)|^{2}\,dk\right)^{\frac{1}{2}}\leqslant Cp_{a}^{\unicode[STIX]{x1D706}}(z),$
-
(ii) For all
 $m$
,
$m$
,
 $\left(\int _{K}|R_{m}^{\unicode[STIX]{x1D706}}(f,k)|^{2}\,dk\right)^{\frac{1}{2}}\;\leqslant C\;((2m+n)|\unicode[STIX]{x1D706}|)^{\frac{n-1}{2}}e^{-(2m+n)|\unicode[STIX]{x1D706}|b}$
$\left(\int _{K}|R_{m}^{\unicode[STIX]{x1D706}}(f,k)|^{2}\,dk\right)^{\frac{1}{2}}\;\leqslant C\;((2m+n)|\unicode[STIX]{x1D706}|)^{\frac{n-1}{2}}e^{-(2m+n)|\unicode[STIX]{x1D706}|b}$
for some positive constant
![]() $C$
. Then
$C$
. Then
![]() $f=0$
whenever
$f=0$
whenever
![]() $a<b$
and
$a<b$
and
![]() $f(z,k)=c\,p_{a}^{\unicode[STIX]{x1D706}}(z)\unicode[STIX]{x1D711}(k)$
for some
$f(z,k)=c\,p_{a}^{\unicode[STIX]{x1D706}}(z)\unicode[STIX]{x1D711}(k)$
for some
![]() $\unicode[STIX]{x1D711}\in L^{2}(K)$
when
$\unicode[STIX]{x1D711}\in L^{2}(K)$
when
![]() $a=b$
.
$a=b$
.
We do not prove the above theorem but remark that the proof is similar to that of Hardy’s theorem for the Heisenberg group [Reference Thangavelu19, Theorem 2.9.2]. In fact, Hardy’s theorem is proved by reducing it to the above. See the proofs of [Reference Thangavelu19, Theorems 2.9.4 and 2.9.5].
In proving Theorems 2.1 and 2.2, we make use of certain results such as Peter–Weyl theorem from the representation theory of compact Lie groups. For the convenience of the reader we collect the relevant results referring the reader to [Reference Sugiura15] for details. Given a compact Lie group
![]() $K$
let
$K$
let
![]() $\widehat{K}$
stand for its unitary dual consisting of equivalence classes of irreducible unitary representations. If
$\widehat{K}$
stand for its unitary dual consisting of equivalence classes of irreducible unitary representations. If
![]() $\unicode[STIX]{x1D70E}$
is one such representation realized on a
$\unicode[STIX]{x1D70E}$
is one such representation realized on a
![]() $d_{\unicode[STIX]{x1D70E}}$
dimensional Hilbert space
$d_{\unicode[STIX]{x1D70E}}$
dimensional Hilbert space
![]() $H_{\unicode[STIX]{x1D70E}}$
with an orthonormal basis
$H_{\unicode[STIX]{x1D70E}}$
with an orthonormal basis
![]() $v_{j},j=1,2,\ldots ,d_{\unicode[STIX]{x1D70E}}$
we denote the matrix coefficients
$v_{j},j=1,2,\ldots ,d_{\unicode[STIX]{x1D70E}}$
we denote the matrix coefficients
![]() $(\unicode[STIX]{x1D70E}(k)v_{j},v_{i})$
by
$(\unicode[STIX]{x1D70E}(k)v_{j},v_{i})$
by
![]() $\unicode[STIX]{x1D70E}_{ij}(k).$
Then Peter–Weyl theorem asserts that the functions
$\unicode[STIX]{x1D70E}_{ij}(k).$
Then Peter–Weyl theorem asserts that the functions
![]() $\{\sqrt{d_{\unicode[STIX]{x1D70E}}}\unicode[STIX]{x1D70E}_{ij}:1\leqslant i,j\leqslant d_{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D70E}\in \widehat{K}\}$
is an orthonormal basis for
$\{\sqrt{d_{\unicode[STIX]{x1D70E}}}\unicode[STIX]{x1D70E}_{ij}:1\leqslant i,j\leqslant d_{\unicode[STIX]{x1D70E}},\unicode[STIX]{x1D70E}\in \widehat{K}\}$
is an orthonormal basis for
![]() $L^{2}(K).$
Thus one has the expansion
$L^{2}(K).$
Thus one has the expansion
and the Plancherel formula holds:
By introducing the character
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D70E}}(k)$
as the trace of
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D70E}}(k)$
as the trace of
![]() $\unicode[STIX]{x1D70E}(k)$
the Peter–Weyl expansion can also be written as
$\unicode[STIX]{x1D70E}(k)$
the Peter–Weyl expansion can also be written as
We will make use of these results in the case of
![]() $K=U(n).$
$K=U(n).$
Proof of Theorem 2.1.
The proof is long and is given in several steps. We start the proof with the following calculation of
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(h_{a})$
. Let
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(h_{a})$
. Let
![]() $\{v_{1},v_{2},\ldots ,v_{d(\unicode[STIX]{x1D70E})}\}$
be an orthonormal basis for
$\{v_{1},v_{2},\ldots ,v_{d(\unicode[STIX]{x1D70E})}\}$
be an orthonormal basis for
![]() $V_{\unicode[STIX]{x1D70E}}$
. Let
$V_{\unicode[STIX]{x1D70E}}$
. Let
![]() $(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})_{\unicode[STIX]{x1D6FC}\in \mathbb{N}^{n}}$
stand for the Hermite basis for
$(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})_{\unicode[STIX]{x1D6FC}\in \mathbb{N}^{n}}$
stand for the Hermite basis for
![]() $L^{2}(\mathbb{R}^{n})$
. We have the following:
$L^{2}(\mathbb{R}^{n})$
. We have the following:
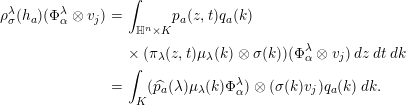 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(h_{a})(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\otimes v_{j}) & = & \displaystyle \int _{\mathbb{H}^{n}\times K}p_{a}(z,t)q_{a}(k)\nonumber\\ \displaystyle & & \displaystyle \times \,(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(z,t)\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(k)\otimes \unicode[STIX]{x1D70E}(k))(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\otimes v_{j})\,dz\,dt\,dk\nonumber\\ \displaystyle & = & \displaystyle \int _{K}(\widehat{p_{a}}(\unicode[STIX]{x1D706})\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(k)\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})\otimes (\unicode[STIX]{x1D70E}(k)v_{j})q_{a}(k)\,dk.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(h_{a})(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\otimes v_{j}) & = & \displaystyle \int _{\mathbb{H}^{n}\times K}p_{a}(z,t)q_{a}(k)\nonumber\\ \displaystyle & & \displaystyle \times \,(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(z,t)\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(k)\otimes \unicode[STIX]{x1D70E}(k))(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\otimes v_{j})\,dz\,dt\,dk\nonumber\\ \displaystyle & = & \displaystyle \int _{K}(\widehat{p_{a}}(\unicode[STIX]{x1D706})\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(k)\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})\otimes (\unicode[STIX]{x1D70E}(k)v_{j})q_{a}(k)\,dk.\end{eqnarray}$$
Here
![]() $\widehat{p_{a}}(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(p_{a})$
is the Fourier transform of the heat kernel
$\widehat{p_{a}}(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(p_{a})$
is the Fourier transform of the heat kernel
![]() $p_{a}$
and it is well known that
$p_{a}$
and it is well known that
![]() $\widehat{p_{a}}(\unicode[STIX]{x1D706})=e^{-aH(\unicode[STIX]{x1D706})}$
is the Hermite semigroup generated by the Hermite operator
$\widehat{p_{a}}(\unicode[STIX]{x1D706})=e^{-aH(\unicode[STIX]{x1D706})}$
is the Hermite semigroup generated by the Hermite operator
![]() $H(\unicode[STIX]{x1D706})=(-\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D706}^{2}~|x|^{2}),$
see [Reference Thangavelu19, Section 2.8]. If
$H(\unicode[STIX]{x1D706})=(-\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D706}^{2}~|x|^{2}),$
see [Reference Thangavelu19, Section 2.8]. If
![]() $|\unicode[STIX]{x1D6FC}|=N$
, then the space
$|\unicode[STIX]{x1D6FC}|=N$
, then the space
![]() $E_{N}^{\unicode[STIX]{x1D706}}$
spanned by
$E_{N}^{\unicode[STIX]{x1D706}}$
spanned by
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}$
,
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}$
,
![]() $|\unicode[STIX]{x1D6FD}|=N$
is invariant under
$|\unicode[STIX]{x1D6FD}|=N$
is invariant under
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(k)$
. Thus there exist some functions
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(k)$
. Thus there exist some functions
![]() $c_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)$
on
$c_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)$
on
![]() $K$
such that
$K$
such that
As
![]() $\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(k)$
is unitary, we have
$\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(k)$
is unitary, we have
We also know that the matrix coefficients
![]() $(\unicode[STIX]{x1D70E}(k)v_{j},v_{i})$
form an orthogonal system in
$(\unicode[STIX]{x1D70E}(k)v_{j},v_{i})$
form an orthogonal system in
![]() $L^{2}(K)$
. We can write
$L^{2}(K)$
. We can write
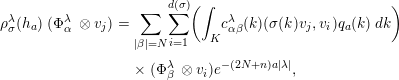 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(h_{a})\;(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\;\otimes v_{j}) & = & \displaystyle \mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=N}\mathop{\sum }_{i=1}^{d(\unicode[STIX]{x1D70E})}\biggl(\int _{K}c_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)(\unicode[STIX]{x1D70E}(k)v_{j},v_{i})q_{a}(k)\,dk\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\;\otimes v_{i})e^{-(2N+n)a|\unicode[STIX]{x1D706}|},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(h_{a})\;(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\;\otimes v_{j}) & = & \displaystyle \mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=N}\mathop{\sum }_{i=1}^{d(\unicode[STIX]{x1D70E})}\biggl(\int _{K}c_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)(\unicode[STIX]{x1D70E}(k)v_{j},v_{i})q_{a}(k)\,dk\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\;\otimes v_{i})e^{-(2N+n)a|\unicode[STIX]{x1D706}|},\nonumber\end{eqnarray}$$
where we have used the relation
which follows from the fact that
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}$
are eigenfunctions of
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}$
are eigenfunctions of
![]() $H(\unicode[STIX]{x1D706})$
with eigenvalue
$H(\unicode[STIX]{x1D706})$
with eigenvalue
![]() $(2|\unicode[STIX]{x1D6FD}|+n)|\unicode[STIX]{x1D706}|,$
see [Reference Thangavelu19, Section 2.3]. Thus,
$(2|\unicode[STIX]{x1D6FD}|+n)|\unicode[STIX]{x1D706}|,$
see [Reference Thangavelu19, Section 2.3]. Thus,
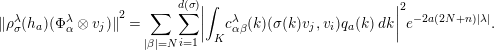 $$\begin{eqnarray}{\Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(h_{a})(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\otimes v_{j})\Vert }^{2}=\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=N}\mathop{\sum }_{i=1}^{d(\unicode[STIX]{x1D70E})}\biggl|\int _{K}c_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)(\unicode[STIX]{x1D70E}(k)v_{j},v_{i})q_{a}(k)\,dk\biggr|^{2}e^{-2a(2N+n)|\unicode[STIX]{x1D706}|}.\end{eqnarray}$$
$$\begin{eqnarray}{\Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(h_{a})(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\otimes v_{j})\Vert }^{2}=\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=N}\mathop{\sum }_{i=1}^{d(\unicode[STIX]{x1D70E})}\biggl|\int _{K}c_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)(\unicode[STIX]{x1D70E}(k)v_{j},v_{i})q_{a}(k)\,dk\biggr|^{2}e^{-2a(2N+n)|\unicode[STIX]{x1D706}|}.\end{eqnarray}$$
Summing over all
![]() $j=1,2,\ldots ,d(\unicode[STIX]{x1D70E})$
and then over all
$j=1,2,\ldots ,d(\unicode[STIX]{x1D70E})$
and then over all
![]() $\unicode[STIX]{x1D70E}\in \widehat{K}$
and using Peter–Weyl theorem we get
$\unicode[STIX]{x1D70E}\in \widehat{K}$
and using Peter–Weyl theorem we get
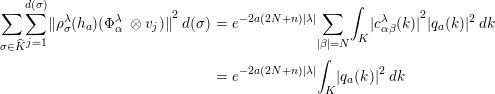 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D70E}\in \widehat{K}}\mathop{\sum }_{j=1}^{d(\unicode[STIX]{x1D70E})}{\Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(h_{a})(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\;\otimes v_{j})\Vert }^{2}\,d(\unicode[STIX]{x1D70E}) & = & \displaystyle e^{-2a(2N+n)|\unicode[STIX]{x1D706}|}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=N}\int _{K}{|c_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)|}^{2}|q_{a}(k)|^{2}\,dk\nonumber\\ \displaystyle & = & \displaystyle e^{-2a(2N+n)|\unicode[STIX]{x1D706}|}\int _{K}|q_{a}(k)|^{2}\,dk\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D70E}\in \widehat{K}}\mathop{\sum }_{j=1}^{d(\unicode[STIX]{x1D70E})}{\Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(h_{a})(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\;\otimes v_{j})\Vert }^{2}\,d(\unicode[STIX]{x1D70E}) & = & \displaystyle e^{-2a(2N+n)|\unicode[STIX]{x1D706}|}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=N}\int _{K}{|c_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)|}^{2}|q_{a}(k)|^{2}\,dk\nonumber\\ \displaystyle & = & \displaystyle e^{-2a(2N+n)|\unicode[STIX]{x1D706}|}\int _{K}|q_{a}(k)|^{2}\,dk\nonumber\end{eqnarray}$$
in view of (2.5). Hence we note that
The hypothesis
![]() ${\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f)}^{\star }\;\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f)\;\leqslant \;C\;{\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(h_{a})}^{\star }\;\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(h_{a})$
leads to:
${\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f)}^{\star }\;\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f)\;\leqslant \;C\;{\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(h_{a})}^{\star }\;\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(h_{a})$
leads to:
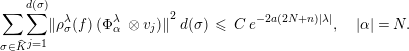 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D70E}\in \widehat{K}}\mathop{\sum }_{j=1}^{d(\unicode[STIX]{x1D70E})}{\Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f)\;(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\;\otimes v_{j})\Vert }^{2}\,d(\unicode[STIX]{x1D70E})\;\leqslant \;C\;e^{-2a(2N+n)|\unicode[STIX]{x1D706}|},\quad |\unicode[STIX]{x1D6FC}|=N.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D70E}\in \widehat{K}}\mathop{\sum }_{j=1}^{d(\unicode[STIX]{x1D70E})}{\Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f)\;(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\;\otimes v_{j})\Vert }^{2}\,d(\unicode[STIX]{x1D70E})\;\leqslant \;C\;e^{-2a(2N+n)|\unicode[STIX]{x1D706}|},\quad |\unicode[STIX]{x1D6FC}|=N.\end{eqnarray}$$
Let
![]() $M=\;U(n-1)$
considered as a subgroup of
$M=\;U(n-1)$
considered as a subgroup of
![]() $U(n)=K$
and let
$U(n)=K$
and let
![]() $\widehat{K_{M}}$
stand for the set of all class one representations in
$\widehat{K_{M}}$
stand for the set of all class one representations in
![]() $\widehat{K}$
. By Peter–Weyl theorem, we have
$\widehat{K}$
. By Peter–Weyl theorem, we have
It can be shown that the integral is nonzero only when
![]() $\unicode[STIX]{x1D6FF}\in \widehat{K_{M}}$
. Hence evaluating at
$\unicode[STIX]{x1D6FF}\in \widehat{K_{M}}$
. Hence evaluating at
![]() $u^{\prime }=e$
, we get:
$u^{\prime }=e$
, we get:
Define
![]() $f_{\unicode[STIX]{x1D6FF}}(z,t,k)=\int _{K}f(u^{-1}z,t,k)\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FF}}(u)\,du,$
so that
$f_{\unicode[STIX]{x1D6FF}}(z,t,k)=\int _{K}f(u^{-1}z,t,k)\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FF}}(u)\,du,$
so that
Note that
![]() $f_{\unicode[STIX]{x1D6FF}}$
satisfies hypothesis (i) of Theorems 2.1 and 2.2. We will show that they also satisfy hypothesis (ii) whenever
$f_{\unicode[STIX]{x1D6FF}}$
satisfies hypothesis (i) of Theorems 2.1 and 2.2. We will show that they also satisfy hypothesis (ii) whenever
![]() $f$
satisfies the same. Hence Theorems 2.1 and 2.2 will be proved once we prove them for
$f$
satisfies the same. Hence Theorems 2.1 and 2.2 will be proved once we prove them for
![]() $f_{\unicode[STIX]{x1D6FF}}$
for each
$f_{\unicode[STIX]{x1D6FF}}$
for each
![]() $\unicode[STIX]{x1D6FF}\in \widehat{K_{M}}$
.
$\unicode[STIX]{x1D6FF}\in \widehat{K_{M}}$
.
Proposition 2.4. Let
![]() $f(z,t,k)$
be central in the
$f(z,t,k)$
be central in the
![]() $K$
-variable. Then the condition
$K$
-variable. Then the condition
holds whenever
holds.
Proof. Recall that for
![]() $\unicode[STIX]{x1D6FF}\in \widehat{K_{M}},$
$\unicode[STIX]{x1D6FF}\in \widehat{K_{M}},$
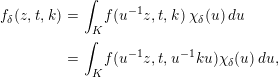 $$\begin{eqnarray}\displaystyle f_{\unicode[STIX]{x1D6FF}}(z,t,k) & = & \displaystyle \int _{K}f(u^{-1}z,t,k)\;\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FF}}(u)\,du\nonumber\\ \displaystyle & = & \displaystyle \int _{K}f(u^{-1}z,t,u^{-1}ku)\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FF}}(u)\,du,\nonumber\\ \displaystyle & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{\unicode[STIX]{x1D6FF}}(z,t,k) & = & \displaystyle \int _{K}f(u^{-1}z,t,k)\;\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FF}}(u)\,du\nonumber\\ \displaystyle & = & \displaystyle \int _{K}f(u^{-1}z,t,u^{-1}ku)\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FF}}(u)\,du,\nonumber\\ \displaystyle & & \displaystyle \nonumber\end{eqnarray}$$
and
We now compute:
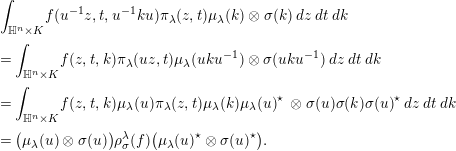 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbb{H}^{n}\times K}f(u^{-1}z,t,u^{-1}ku)\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(z,t)\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(k)\otimes \unicode[STIX]{x1D70E}(k)\,dz\,dt\,dk\nonumber\\ \displaystyle & & \displaystyle =\int _{\mathbb{H}^{n}\times K}f(z,t,k)\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(uz,t)\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(uku^{-1})\otimes \unicode[STIX]{x1D70E}(uku^{-1})\,dz\,dt\,dk\nonumber\\ \displaystyle & & \displaystyle =\int _{\mathbb{H}^{n}\times K}f(z,t,k)\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(u)\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(z,t)\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(k){\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(u)}^{\star }\;\otimes \unicode[STIX]{x1D70E}(u)\unicode[STIX]{x1D70E}(k)\unicode[STIX]{x1D70E}(u)^{\star }\,dz\,dt\,dk\nonumber\\ \displaystyle & & \displaystyle =\big(\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(u)\otimes \unicode[STIX]{x1D70E}(u)\big)\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f)\big({\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(u)}^{\star }\otimes \unicode[STIX]{x1D70E}(u)^{\star }\big).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\mathbb{H}^{n}\times K}f(u^{-1}z,t,u^{-1}ku)\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(z,t)\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(k)\otimes \unicode[STIX]{x1D70E}(k)\,dz\,dt\,dk\nonumber\\ \displaystyle & & \displaystyle =\int _{\mathbb{H}^{n}\times K}f(z,t,k)\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(uz,t)\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(uku^{-1})\otimes \unicode[STIX]{x1D70E}(uku^{-1})\,dz\,dt\,dk\nonumber\\ \displaystyle & & \displaystyle =\int _{\mathbb{H}^{n}\times K}f(z,t,k)\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(u)\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(z,t)\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(k){\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(u)}^{\star }\;\otimes \unicode[STIX]{x1D70E}(u)\unicode[STIX]{x1D70E}(k)\unicode[STIX]{x1D70E}(u)^{\star }\,dz\,dt\,dk\nonumber\\ \displaystyle & & \displaystyle =\big(\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(u)\otimes \unicode[STIX]{x1D70E}(u)\big)\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f)\big({\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(u)}^{\star }\otimes \unicode[STIX]{x1D70E}(u)^{\star }\big).\nonumber\end{eqnarray}$$
Thus:
Therefore, we get
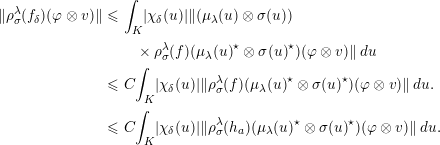 $$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f_{\unicode[STIX]{x1D6FF}})(\unicode[STIX]{x1D711}\otimes v)\Vert & {\leqslant} & \displaystyle \int _{K}|\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FF}}(u)|\Vert (\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(u)\otimes \unicode[STIX]{x1D70E}(u))\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f)({\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(u)}^{\star }\otimes \unicode[STIX]{x1D70E}(u)^{\star })(\unicode[STIX]{x1D711}\otimes v)\Vert \,du\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C\int _{K}|\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FF}}(u)|\Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f)({\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(u)}^{\star }\otimes \unicode[STIX]{x1D70E}(u)^{\star })(\unicode[STIX]{x1D711}\otimes v)\Vert \,du.\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C\int _{K}|\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FF}}(u)|\Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(h_{a})({\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(u)}^{\star }\otimes \unicode[STIX]{x1D70E}(u)^{\star })(\unicode[STIX]{x1D711}\otimes v)\Vert \,du.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f_{\unicode[STIX]{x1D6FF}})(\unicode[STIX]{x1D711}\otimes v)\Vert & {\leqslant} & \displaystyle \int _{K}|\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FF}}(u)|\Vert (\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(u)\otimes \unicode[STIX]{x1D70E}(u))\nonumber\\ \displaystyle & & \displaystyle \quad \times \,\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f)({\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(u)}^{\star }\otimes \unicode[STIX]{x1D70E}(u)^{\star })(\unicode[STIX]{x1D711}\otimes v)\Vert \,du\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C\int _{K}|\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FF}}(u)|\Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f)({\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(u)}^{\star }\otimes \unicode[STIX]{x1D70E}(u)^{\star })(\unicode[STIX]{x1D711}\otimes v)\Vert \,du.\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C\int _{K}|\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FF}}(u)|\Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(h_{a})({\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(u)}^{\star }\otimes \unicode[STIX]{x1D70E}(u)^{\star })(\unicode[STIX]{x1D711}\otimes v)\Vert \,du.\nonumber\end{eqnarray}$$
Since
![]() $h_{a}(z,t,k)$
is central in
$h_{a}(z,t,k)$
is central in
![]() $K$
and radial in
$K$
and radial in
![]() $z$
, we see that:
$z$
, we see that:
Consequently,
This completes the proof of Proposition 2.4.◻
From the above proposition it is clear that
![]() $f_{\unicode[STIX]{x1D6FF}}$
satisfies the same hypotheses as
$f_{\unicode[STIX]{x1D6FF}}$
satisfies the same hypotheses as
![]() $f$
. Our strategy is to show that under the hypothesis of Theorem 2.1,
$f$
. Our strategy is to show that under the hypothesis of Theorem 2.1,
![]() $f_{\unicode[STIX]{x1D6FF}}=0$
for each
$f_{\unicode[STIX]{x1D6FF}}=0$
for each
![]() $\unicode[STIX]{x1D6FF}$
which will immediately imply that
$\unicode[STIX]{x1D6FF}$
which will immediately imply that
![]() $f=0.$
$f=0.$
Corollary 2.5. Under the hypothesis (ii) of Theorems 2.1 and 2.2 we have:
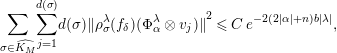 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D70E}\in \widehat{K_{M}}}\mathop{\sum }_{j=1}^{d(\unicode[STIX]{x1D70E})}d(\unicode[STIX]{x1D70E}){\Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f_{\unicode[STIX]{x1D6FF}})(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\otimes v_{j})\Vert }^{2}\leqslant C\;e^{-2(2|\unicode[STIX]{x1D6FC}|+n)b|\unicode[STIX]{x1D706}|},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D70E}\in \widehat{K_{M}}}\mathop{\sum }_{j=1}^{d(\unicode[STIX]{x1D70E})}d(\unicode[STIX]{x1D70E}){\Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f_{\unicode[STIX]{x1D6FF}})(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\otimes v_{j})\Vert }^{2}\leqslant C\;e^{-2(2|\unicode[STIX]{x1D6FC}|+n)b|\unicode[STIX]{x1D706}|},\end{eqnarray}$$
for some positive constant
![]() $C$
provided that
$C$
provided that
![]() $f$
is central in the
$f$
is central in the
![]() $K$
-variable.
$K$
-variable.
Proof. The corollary is proved by repeating the argument leading to (2.7) by replacing
![]() $f$
with
$f$
with
![]() $f_{\unicode[STIX]{x1D6FF}}.$
◻
$f_{\unicode[STIX]{x1D6FF}}.$
◻
For each
![]() $p$
and
$p$
and
![]() $q\in \mathbb{N}$
, there exists an irreducible unitary class-1 representation
$q\in \mathbb{N}$
, there exists an irreducible unitary class-1 representation
![]() $\unicode[STIX]{x1D6FF}_{p,q}$
of
$\unicode[STIX]{x1D6FF}_{p,q}$
of
![]() $K$
realized on
$K$
realized on
![]() $\mathscr{H}_{p,q}$
, the space of all bigraded spherical harmonics of bidegree
$\mathscr{H}_{p,q}$
, the space of all bigraded spherical harmonics of bidegree
![]() $(p,q)$
. Moreover, each
$(p,q)$
. Moreover, each
![]() $\unicode[STIX]{x1D6FF}\in \widehat{K_{M}}$
is unitarily equivalent to one and only one of
$\unicode[STIX]{x1D6FF}\in \widehat{K_{M}}$
is unitarily equivalent to one and only one of
![]() $\unicode[STIX]{x1D6FF}_{p,q}$
. When
$\unicode[STIX]{x1D6FF}_{p,q}$
. When
![]() $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}_{p,q}$
, we can expand
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D6FF}_{p,q}$
, we can expand
![]() $f_{\unicode[STIX]{x1D6FF}}$
in terms of solid harmonics:
$f_{\unicode[STIX]{x1D6FF}}$
in terms of solid harmonics:
where
![]() $d(p,q)=\dim \mathscr{H}_{p,q},\;g_{l}(z,t,k)$
are radial in
$d(p,q)=\dim \mathscr{H}_{p,q},\;g_{l}(z,t,k)$
are radial in
![]() $z$
and
$z$
and
![]() $P_{l}$
are solid harmonics whose restrictions to
$P_{l}$
are solid harmonics whose restrictions to
![]() $S^{2n-1}$
form an orthonormal basis for
$S^{2n-1}$
form an orthonormal basis for
![]() $\mathscr{H}_{p,q}$
.
$\mathscr{H}_{p,q}$
.
In what follows we make use of several results from the theory of Weyl transform and Weyl correspondence. For all the results and unexplained terminologies used we refer the reader to Sections 2.6 and 2.7 of the book [Reference Thangavelu19]. First we make use of the Hecke–Bochner formula [Reference Thangavelu19, Theorem 2.6.2] for the Weyl transform:
where
![]() $G(P_{l})$
is the Weyl correspondence associated to
$G(P_{l})$
is the Weyl correspondence associated to
![]() $P_{l}$
and (assuming
$P_{l}$
and (assuming
![]() $\unicode[STIX]{x1D706}>0$
)
$\unicode[STIX]{x1D706}>0$
)
where
![]() $N=n+p+q$
and
$N=n+p+q$
and
Also,
![]() $P_{m}(\unicode[STIX]{x1D706})$
stands for the spectral projections associated to the Hermite operator
$P_{m}(\unicode[STIX]{x1D706})$
stands for the spectral projections associated to the Hermite operator
![]() $H(\unicode[STIX]{x1D706})=(-\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D706}^{2}|x|^{2}).$
Thus we have
$H(\unicode[STIX]{x1D706})=(-\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D706}^{2}|x|^{2}).$
Thus we have
Fix
![]() $\unicode[STIX]{x1D6FC}$
with
$\unicode[STIX]{x1D6FC}$
with
![]() $|\unicode[STIX]{x1D6FC}|=m+p$
and choose an orthonormal basis
$|\unicode[STIX]{x1D6FC}|=m+p$
and choose an orthonormal basis
![]() $\{v_{i}:\;i=1,2,\ldots ,d(\unicode[STIX]{x1D70E})\}$
for
$\{v_{i}:\;i=1,2,\ldots ,d(\unicode[STIX]{x1D70E})\}$
for
![]() $V_{\unicode[STIX]{x1D70E}}$
. Then
$V_{\unicode[STIX]{x1D70E}}$
. Then
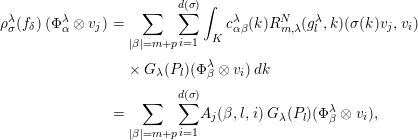 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f_{\unicode[STIX]{x1D6FF}})\;(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\otimes v_{j}) & = & \displaystyle \mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=m+p}\mathop{\sum }_{i=1}^{d(\unicode[STIX]{x1D70E})}\int _{K}c_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)R_{m,\unicode[STIX]{x1D706}}^{N}(g_{l}^{\unicode[STIX]{x1D706}},k)(\unicode[STIX]{x1D70E}(k)v_{j},v_{i})\nonumber\\ \displaystyle & & \displaystyle \times \,G_{\unicode[STIX]{x1D706}}(P_{l})(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\otimes v_{i})\,dk\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=m+p}\mathop{\sum }_{i=1}^{d(\unicode[STIX]{x1D70E})}A_{j}(\unicode[STIX]{x1D6FD},l,i)\;G_{\unicode[STIX]{x1D706}}(P_{l})(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\otimes v_{i}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f_{\unicode[STIX]{x1D6FF}})\;(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\otimes v_{j}) & = & \displaystyle \mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=m+p}\mathop{\sum }_{i=1}^{d(\unicode[STIX]{x1D70E})}\int _{K}c_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)R_{m,\unicode[STIX]{x1D706}}^{N}(g_{l}^{\unicode[STIX]{x1D706}},k)(\unicode[STIX]{x1D70E}(k)v_{j},v_{i})\nonumber\\ \displaystyle & & \displaystyle \times \,G_{\unicode[STIX]{x1D706}}(P_{l})(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\otimes v_{i})\,dk\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=m+p}\mathop{\sum }_{i=1}^{d(\unicode[STIX]{x1D70E})}A_{j}(\unicode[STIX]{x1D6FD},l,i)\;G_{\unicode[STIX]{x1D706}}(P_{l})(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\otimes v_{i}),\nonumber\end{eqnarray}$$
where
We will calculate:
We make the observation that:
This can be easily verified using results (see [Reference Thangavelu19, equation (2.6.22)]):
and
Therefore,
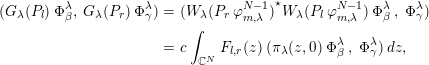 $$\begin{eqnarray}\displaystyle (G_{\unicode[STIX]{x1D706}}(P_{l})\;\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}},\;G_{\unicode[STIX]{x1D706}}(P_{r})\;\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D706}}) & = & \displaystyle ({W_{\unicode[STIX]{x1D706}}(P_{r}\;\unicode[STIX]{x1D711}_{m,\unicode[STIX]{x1D706}}^{N-1})}^{\star }W_{\unicode[STIX]{x1D706}}(P_{l}\;\unicode[STIX]{x1D711}_{m,\unicode[STIX]{x1D706}}^{N-1})\;\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\;,\;\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D706}})\nonumber\\ \displaystyle & = & \displaystyle c\;\int _{\mathbb{C}^{N}}\;F_{l,r}(z)\;(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(z,0)\;\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\;,\;\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D706}})\,dz,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (G_{\unicode[STIX]{x1D706}}(P_{l})\;\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}},\;G_{\unicode[STIX]{x1D706}}(P_{r})\;\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D706}}) & = & \displaystyle ({W_{\unicode[STIX]{x1D706}}(P_{r}\;\unicode[STIX]{x1D711}_{m,\unicode[STIX]{x1D706}}^{N-1})}^{\star }W_{\unicode[STIX]{x1D706}}(P_{l}\;\unicode[STIX]{x1D711}_{m,\unicode[STIX]{x1D706}}^{N-1})\;\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\;,\;\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D706}})\nonumber\\ \displaystyle & = & \displaystyle c\;\int _{\mathbb{C}^{N}}\;F_{l,r}(z)\;(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(z,0)\;\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\;,\;\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D706}})\,dz,\nonumber\end{eqnarray}$$
where
Using the homogeneity of
![]() $P_{l}$
and
$P_{l}$
and
![]() $P_{r}$
, we see that
$P_{r}$
, we see that
![]() $F_{l,r}(z)$
is polyradial, that is, radial in each
$F_{l,r}(z)$
is polyradial, that is, radial in each
![]() $z_{j}$
separately. But
$z_{j}$
separately. But
![]() $(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(z,0)\;\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\;,\;\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D706}})$
is homogeneous of type
$(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(z,0)\;\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\;,\;\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D706}})$
is homogeneous of type
![]() $(\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D6FD})$
and hence the integral is zero if
$(\unicode[STIX]{x1D6FE}-\unicode[STIX]{x1D6FD})$
and hence the integral is zero if
![]() $\unicode[STIX]{x1D6FD}\neq \unicode[STIX]{x1D6FE}$
.
$\unicode[STIX]{x1D6FD}\neq \unicode[STIX]{x1D6FE}$
.
In view of the above observation, we get:
Consider now the sum
![]() $S=\sum _{\unicode[STIX]{x1D70E}}\,d(\unicode[STIX]{x1D70E})\;\sum _{i,j=1}^{d(\unicode[STIX]{x1D70E})}\;A_{j}(\unicode[STIX]{x1D6FD},l,i)\;\overline{A_{j}(\unicode[STIX]{x1D6FD},r,i)}$
. By Peter–Weyl theorem, we see that
$S=\sum _{\unicode[STIX]{x1D70E}}\,d(\unicode[STIX]{x1D70E})\;\sum _{i,j=1}^{d(\unicode[STIX]{x1D70E})}\;A_{j}(\unicode[STIX]{x1D6FD},l,i)\;\overline{A_{j}(\unicode[STIX]{x1D6FD},r,i)}$
. By Peter–Weyl theorem, we see that
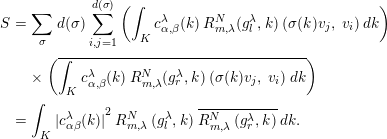 $$\begin{eqnarray}\displaystyle S & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D70E}}\,d(\unicode[STIX]{x1D70E})\;\mathop{\sum }_{i,j=1}^{d(\unicode[STIX]{x1D70E})}\;\bigg(\int _{K}\;c_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)\;R_{m,\unicode[STIX]{x1D706}}^{N}(g_{l}^{\unicode[STIX]{x1D706}},k)\;(\unicode[STIX]{x1D70E}(k)v_{j},\;v_{i})\,dk\bigg)\nonumber\\ \displaystyle & & \displaystyle \times \,\bigg(\overline{\int _{K}\;c_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)\;R_{m,\unicode[STIX]{x1D706}}^{N}(g_{r}^{\unicode[STIX]{x1D706}},k)\;(\unicode[STIX]{x1D70E}(k)v_{j},\;v_{i})\,dk}\bigg)\nonumber\\ \displaystyle & = & \displaystyle \int _{K}\;{|c_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)|}^{2}\;R_{m,\unicode[STIX]{x1D706}}^{N}\;(g_{l}^{\unicode[STIX]{x1D706}},k)\;\overline{R_{m,\unicode[STIX]{x1D706}}^{N}\;(g_{r}^{\unicode[STIX]{x1D706}},k)}\,dk.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D70E}}\,d(\unicode[STIX]{x1D70E})\;\mathop{\sum }_{i,j=1}^{d(\unicode[STIX]{x1D70E})}\;\bigg(\int _{K}\;c_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)\;R_{m,\unicode[STIX]{x1D706}}^{N}(g_{l}^{\unicode[STIX]{x1D706}},k)\;(\unicode[STIX]{x1D70E}(k)v_{j},\;v_{i})\,dk\bigg)\nonumber\\ \displaystyle & & \displaystyle \times \,\bigg(\overline{\int _{K}\;c_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)\;R_{m,\unicode[STIX]{x1D706}}^{N}(g_{r}^{\unicode[STIX]{x1D706}},k)\;(\unicode[STIX]{x1D70E}(k)v_{j},\;v_{i})\,dk}\bigg)\nonumber\\ \displaystyle & = & \displaystyle \int _{K}\;{|c_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)|}^{2}\;R_{m,\unicode[STIX]{x1D706}}^{N}\;(g_{l}^{\unicode[STIX]{x1D706}},k)\;\overline{R_{m,\unicode[STIX]{x1D706}}^{N}\;(g_{r}^{\unicode[STIX]{x1D706}},k)}\,dk.\nonumber\end{eqnarray}$$
Therefore,
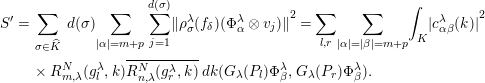 $$\begin{eqnarray}\displaystyle S^{\prime } & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D70E}\in \widehat{K}}\,d(\unicode[STIX]{x1D70E})\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=m+p}\;\mathop{\sum }_{j=1}^{d(\unicode[STIX]{x1D70E})}{\Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f_{\unicode[STIX]{x1D6FF}})(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\otimes v_{j})\Vert }^{2}=\mathop{\sum }_{l,r}\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=|\unicode[STIX]{x1D6FD}|=m+p}\int _{K}{|c_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)|}^{2}\nonumber\\ \displaystyle & & \displaystyle \times \,R_{m,\unicode[STIX]{x1D706}}^{N}(g_{l}^{\unicode[STIX]{x1D706}},k)\overline{R_{n,\unicode[STIX]{x1D706}}^{N}(g_{r}^{\unicode[STIX]{x1D706}},k)}\,dk(G_{\unicode[STIX]{x1D706}}(P_{l})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}},G_{\unicode[STIX]{x1D706}}(P_{r})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S^{\prime } & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D70E}\in \widehat{K}}\,d(\unicode[STIX]{x1D70E})\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=m+p}\;\mathop{\sum }_{j=1}^{d(\unicode[STIX]{x1D70E})}{\Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f_{\unicode[STIX]{x1D6FF}})(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\otimes v_{j})\Vert }^{2}=\mathop{\sum }_{l,r}\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=|\unicode[STIX]{x1D6FD}|=m+p}\int _{K}{|c_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)|}^{2}\nonumber\\ \displaystyle & & \displaystyle \times \,R_{m,\unicode[STIX]{x1D706}}^{N}(g_{l}^{\unicode[STIX]{x1D706}},k)\overline{R_{n,\unicode[STIX]{x1D706}}^{N}(g_{r}^{\unicode[STIX]{x1D706}},k)}\,dk(G_{\unicode[STIX]{x1D706}}(P_{l})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}},G_{\unicode[STIX]{x1D706}}(P_{r})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}).\nonumber\end{eqnarray}$$
Since
![]() $\sum _{|\unicode[STIX]{x1D6FC}|=m+p}{|c_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)|}^{2}=1$
, we get
$\sum _{|\unicode[STIX]{x1D6FC}|=m+p}{|c_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)|}^{2}=1$
, we get
But the later sum is
![]() $(P_{l},P_{r})_{L^{2}(S^{n-1})}$
which equals zero for
$(P_{l},P_{r})_{L^{2}(S^{n-1})}$
which equals zero for
![]() $l\neq r$
. Hence:
$l\neq r$
. Hence:
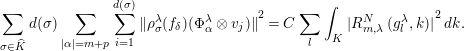 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D70E}\in \widehat{K}}\,d(\unicode[STIX]{x1D70E})\;\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=m+p}\;\mathop{\sum }_{i=1}^{d(\unicode[STIX]{x1D70E})}\;{\Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f_{\unicode[STIX]{x1D6FF}})(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\otimes v_{j})\Vert }^{2}=C\;\mathop{\sum }_{l}\;\int _{K}\;{|R_{m,\unicode[STIX]{x1D706}}^{N}\;(g_{l}^{\unicode[STIX]{x1D706}},k)|}^{2}\,dk.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D70E}\in \widehat{K}}\,d(\unicode[STIX]{x1D70E})\;\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=m+p}\;\mathop{\sum }_{i=1}^{d(\unicode[STIX]{x1D70E})}\;{\Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(f_{\unicode[STIX]{x1D6FF}})(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\otimes v_{j})\Vert }^{2}=C\;\mathop{\sum }_{l}\;\int _{K}\;{|R_{m,\unicode[STIX]{x1D706}}^{N}\;(g_{l}^{\unicode[STIX]{x1D706}},k)|}^{2}\,dk.\end{eqnarray}$$
In view of Corollary 2.5, we see that
![]() $\int _{K}\;{|R_{m,\unicode[STIX]{x1D706}}^{N}\;(g_{l}^{\unicode[STIX]{x1D706}},k)|}^{2}\,dk\leqslant Ce^{-(2m+n)2b|\unicode[STIX]{x1D706}|}$
for any
$\int _{K}\;{|R_{m,\unicode[STIX]{x1D706}}^{N}\;(g_{l}^{\unicode[STIX]{x1D706}},k)|}^{2}\,dk\leqslant Ce^{-(2m+n)2b|\unicode[STIX]{x1D706}|}$
for any
![]() $l$
.
$l$
.
By appealing to Theorem 2.3, we can prove Theorems 2.1 and 2.2.
3 Miyachi Theorem on Heisenberg motion groups
Our attention is focused in this section on an analogue of Miyachi’s Theorem for the Heisenberg motion group
![]() $G=\mathbb{H}^{n}\rtimes K$
. Given
$G=\mathbb{H}^{n}\rtimes K$
. Given
![]() $f\in L^{2}(G)$
, consider the group Fourier transform:
$f\in L^{2}(G)$
, consider the group Fourier transform:
 $$\begin{eqnarray}\displaystyle \hat{f}(\unicode[STIX]{x1D706},\unicode[STIX]{x1D70E}) & = & \displaystyle \int _{K}\int _{\mathbb{R}}\int _{\mathbb{C}}f(z,t,k)\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(z,t,k)\,dz\,dt\,dk\nonumber\\ \displaystyle & = & \displaystyle \int _{K}\int _{\mathbb{C}^{n}}f^{\unicode[STIX]{x1D706}}(z,k)(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(z,0)\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(k))\otimes \unicode[STIX]{x1D70E}(k)\,dz\,dk,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hat{f}(\unicode[STIX]{x1D706},\unicode[STIX]{x1D70E}) & = & \displaystyle \int _{K}\int _{\mathbb{R}}\int _{\mathbb{C}}f(z,t,k)\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D706}}(z,t,k)\,dz\,dt\,dk\nonumber\\ \displaystyle & = & \displaystyle \int _{K}\int _{\mathbb{C}^{n}}f^{\unicode[STIX]{x1D706}}(z,k)(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(z,0)\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(k))\otimes \unicode[STIX]{x1D70E}(k)\,dz\,dk,\nonumber\end{eqnarray}$$
where the partial Fourier transform
![]() $f^{\unicode[STIX]{x1D706}}(z,k)$
is as in formula (2.2). Then for
$f^{\unicode[STIX]{x1D706}}(z,k)$
is as in formula (2.2). Then for
![]() $f\in (L^{1}\cap L^{2})(G)$
, one gets as in [Reference Sen11, page 30] that
$f\in (L^{1}\cap L^{2})(G)$
, one gets as in [Reference Sen11, page 30] that
and the Plancherel formula for the group
![]() $G$
reads:
$G$
reads:
where
![]() $d(\unicode[STIX]{x1D70E})$
stands for the dimension of the space
$d(\unicode[STIX]{x1D70E})$
stands for the dimension of the space
![]() $V_{\unicode[STIX]{x1D70E}}$
of the representation
$V_{\unicode[STIX]{x1D70E}}$
of the representation
![]() $\unicode[STIX]{x1D70E}$
as in the second section. We also introduce the Euclidean norm on
$\unicode[STIX]{x1D70E}$
as in the second section. We also introduce the Euclidean norm on
![]() $\mathbb{H}^{n}$
as
$\mathbb{H}^{n}$
as
Our first result in this section is the following theorem.
Theorem 3.1. Let
![]() $f$
be a square integrable function on
$f$
be a square integrable function on
![]() $G$
which satisfies:
$G$
which satisfies:
-
(i)
 $e^{a\Vert x\Vert ^{2}}f(x,k)\in L^{1}(G)+L^{\infty }(G)$
.
$e^{a\Vert x\Vert ^{2}}f(x,k)\in L^{1}(G)+L^{\infty }(G)$
. -
(ii)
 $\int _{\mathbb{R}}\log ^{+}((\sum _{\unicode[STIX]{x1D6FF}\in \widehat{K}}\,d(\unicode[STIX]{x1D6FF})|\unicode[STIX]{x1D706}|^{n}e^{2b\unicode[STIX]{x1D706}^{2}}\Vert \widehat{f}(\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FF})\Vert _{HS}^{2})/(c))\,d\unicode[STIX]{x1D706}<\infty$
for some positive constant
$\int _{\mathbb{R}}\log ^{+}((\sum _{\unicode[STIX]{x1D6FF}\in \widehat{K}}\,d(\unicode[STIX]{x1D6FF})|\unicode[STIX]{x1D706}|^{n}e^{2b\unicode[STIX]{x1D706}^{2}}\Vert \widehat{f}(\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FF})\Vert _{HS}^{2})/(c))\,d\unicode[STIX]{x1D706}<\infty$
for some positive constant
 $c$
. Then
$c$
. Then-
(1) If
 $ab>\frac{1}{4}$
,
$ab>\frac{1}{4}$
,
 $\;f=0$
almost everywhere on
$\;f=0$
almost everywhere on
 $G$
.
$G$
. -
(2) If
 $ab=\frac{1}{4}$
,
$ab=\frac{1}{4}$
,
 $f(z,t,k)=e^{-at^{2}}f(z,0,k)$
for any
$f(z,t,k)=e^{-at^{2}}f(z,0,k)$
for any
 $(z,t,k)\in \mathbb{C}^{n}\times \mathbb{R}\times K$
.
$(z,t,k)\in \mathbb{C}^{n}\times \mathbb{R}\times K$
. -
(3) If
 $ab<\frac{1}{4}$
, there exist an infinite number of linearly independent functions meeting hypotheses
$ab<\frac{1}{4}$
, there exist an infinite number of linearly independent functions meeting hypotheses
 $(i)$
and
$(i)$
and
 $(ii)$
.
$(ii)$
.
-
Proof. Let
![]() $\unicode[STIX]{x1D711}$
be a Schwartz function on
$\unicode[STIX]{x1D711}$
be a Schwartz function on
![]() $\mathbb{C}^{n}\times K$
and
$\mathbb{C}^{n}\times K$
and
![]() $F$
the function defined on
$F$
the function defined on
![]() $\mathbb{R}$
by
$\mathbb{R}$
by
Then for
![]() $\unicode[STIX]{x1D706}\in \mathbb{R}$
,
$\unicode[STIX]{x1D706}\in \mathbb{R}$
,
and therefore
for some positive constant
![]() $C$
. On the other hand, we get by virtue of formula (3.1) that:
$C$
. On the other hand, we get by virtue of formula (3.1) that:
As such, for some constant
![]() $c>0$
, we get:
$c>0$
, we get:
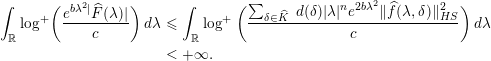 $$\begin{eqnarray}\displaystyle \int _{\mathbb{R}}\log ^{+}\biggl(\frac{e^{b\unicode[STIX]{x1D706}^{2}|}\widehat{F}(\unicode[STIX]{x1D706})|}{c}\biggr)\,d\unicode[STIX]{x1D706} & {\leqslant} & \displaystyle \int _{\mathbb{R}}\log ^{+}\bigg(\frac{\mathop{\sum }_{\unicode[STIX]{x1D6FF}\in \widehat{K}}\,d(\unicode[STIX]{x1D6FF})|\unicode[STIX]{x1D706}|^{n}e^{2b\unicode[STIX]{x1D706}^{2}}\Vert \widehat{f}(\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FF})\Vert _{HS}^{2}}{c}\bigg)\,d\unicode[STIX]{x1D706}\nonumber\\ \displaystyle & {<} & \displaystyle +\infty .\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{\mathbb{R}}\log ^{+}\biggl(\frac{e^{b\unicode[STIX]{x1D706}^{2}|}\widehat{F}(\unicode[STIX]{x1D706})|}{c}\biggr)\,d\unicode[STIX]{x1D706} & {\leqslant} & \displaystyle \int _{\mathbb{R}}\log ^{+}\bigg(\frac{\mathop{\sum }_{\unicode[STIX]{x1D6FF}\in \widehat{K}}\,d(\unicode[STIX]{x1D6FF})|\unicode[STIX]{x1D706}|^{n}e^{2b\unicode[STIX]{x1D706}^{2}}\Vert \widehat{f}(\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FF})\Vert _{HS}^{2}}{c}\bigg)\,d\unicode[STIX]{x1D706}\nonumber\\ \displaystyle & {<} & \displaystyle +\infty .\nonumber\end{eqnarray}$$
On the other hand, clearly
![]() $F\in L^{\infty }(\mathbb{R})+L^{1}(\mathbb{R})$
. So by Theorem 1.3, if
$F\in L^{\infty }(\mathbb{R})+L^{1}(\mathbb{R})$
. So by Theorem 1.3, if
![]() $ab>\frac{1}{4}$
,
$ab>\frac{1}{4}$
,
![]() $F=0$
almost everywhere and so is
$F=0$
almost everywhere and so is
![]() $f$
as
$f$
as
![]() $\unicode[STIX]{x1D711}$
is taken arbitrary on
$\unicode[STIX]{x1D711}$
is taken arbitrary on
![]() $\mathbb{C}^{n}\times K$
.
$\mathbb{C}^{n}\times K$
.
When
![]() $ab=\frac{1}{4}$
, taking a well chosen Hilbert basis of
$ab=\frac{1}{4}$
, taking a well chosen Hilbert basis of
![]() $L^{2}(\mathbb{C}^{n}\times K)$
consisting of Schwartz functions, we get the second assertion.
$L^{2}(\mathbb{C}^{n}\times K)$
consisting of Schwartz functions, we get the second assertion.
We now look at the third case where
![]() $ab<\frac{1}{4}$
. Let
$ab<\frac{1}{4}$
. Let
![]() $f$
be a function of
$f$
be a function of
![]() $L^{2}(G)$
of the from
$L^{2}(G)$
of the from
![]() $f=f_{1}\otimes f_{2}$
, where
$f=f_{1}\otimes f_{2}$
, where
![]() $f_{1}$
is defined on
$f_{1}$
is defined on
![]() $\mathbb{H}^{n}$
and
$\mathbb{H}^{n}$
and
![]() $f_{2}$
on
$f_{2}$
on
![]() $K$
. Let as earlier
$K$
. Let as earlier
![]() $(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})_{\unicode[STIX]{x1D6FC}\in \mathbb{N}^{n}}$
be the Hermite basis for
$(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}})_{\unicode[STIX]{x1D6FC}\in \mathbb{N}^{n}}$
be the Hermite basis for
![]() $L^{2}(\mathbb{R}^{n})$
and let
$L^{2}(\mathbb{R}^{n})$
and let
![]() $c_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)$
be the functions defined on
$c_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)$
be the functions defined on
![]() $K$
by the relation
$K$
by the relation
Then for
![]() $(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\otimes v_{i})_{\unicode[STIX]{x1D6FC}\in \mathbb{N}^{n},~i=1,\ldots ,d(\unicode[STIX]{x1D70E})}$
as before, we get
$(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\otimes v_{i})_{\unicode[STIX]{x1D6FC}\in \mathbb{N}^{n},~i=1,\ldots ,d(\unicode[STIX]{x1D70E})}$
as before, we get
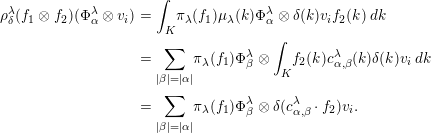 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FF}}^{\unicode[STIX]{x1D706}}(f_{1}\otimes f_{2})(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\otimes v_{i}) & = & \displaystyle \int _{K}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(f_{1})\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(k)\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\otimes \unicode[STIX]{x1D6FF}(k)v_{i}f_{2}(k)\,dk\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(f_{1})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\otimes \int _{K}f_{2}(k)c_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)\unicode[STIX]{x1D6FF}(k)v_{i}\,dk\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(f_{1})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\otimes \unicode[STIX]{x1D6FF}(c_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\cdot f_{2})v_{i}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FF}}^{\unicode[STIX]{x1D706}}(f_{1}\otimes f_{2})(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\otimes v_{i}) & = & \displaystyle \int _{K}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(f_{1})\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D706}}(k)\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\otimes \unicode[STIX]{x1D6FF}(k)v_{i}f_{2}(k)\,dk\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(f_{1})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\otimes \int _{K}f_{2}(k)c_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)\unicode[STIX]{x1D6FF}(k)v_{i}\,dk\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(f_{1})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\otimes \unicode[STIX]{x1D6FF}(c_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\cdot f_{2})v_{i}.\nonumber\end{eqnarray}$$
By the Cauchy–Schwartz inequality
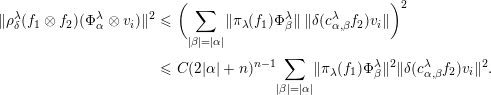 $$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FF}}^{\unicode[STIX]{x1D706}}(f_{1}\otimes f_{2})(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\otimes v_{i})\Vert ^{2} & {\leqslant} & \displaystyle \biggl(\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(f_{1})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\Vert \,\Vert \unicode[STIX]{x1D6FF}(c_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}f_{2})v_{i}\Vert \biggr)^{2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C(2|\unicode[STIX]{x1D6FC}|+n)^{n-1}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(f_{1})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\Vert ^{2}\Vert \unicode[STIX]{x1D6FF}(c_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}f_{2})v_{i}\Vert ^{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FF}}^{\unicode[STIX]{x1D706}}(f_{1}\otimes f_{2})(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\otimes v_{i})\Vert ^{2} & {\leqslant} & \displaystyle \biggl(\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(f_{1})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\Vert \,\Vert \unicode[STIX]{x1D6FF}(c_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}f_{2})v_{i}\Vert \biggr)^{2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C(2|\unicode[STIX]{x1D6FC}|+n)^{n-1}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(f_{1})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\Vert ^{2}\Vert \unicode[STIX]{x1D6FF}(c_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}f_{2})v_{i}\Vert ^{2}.\nonumber\end{eqnarray}$$
On the other hand, for
![]() $A=\sum _{\unicode[STIX]{x1D6FF}\in \widehat{K}}~d(\unicode[STIX]{x1D6FF})\sum _{i=1}^{d(\unicode[STIX]{x1D6FF})}\,\Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FF}}^{\unicode[STIX]{x1D706}}(f_{1}\otimes f_{2})(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\otimes v_{i})\Vert ^{2}$
, we have
$A=\sum _{\unicode[STIX]{x1D6FF}\in \widehat{K}}~d(\unicode[STIX]{x1D6FF})\sum _{i=1}^{d(\unicode[STIX]{x1D6FF})}\,\Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FF}}^{\unicode[STIX]{x1D706}}(f_{1}\otimes f_{2})(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FC}}^{\unicode[STIX]{x1D706}}\otimes v_{i})\Vert ^{2}$
, we have
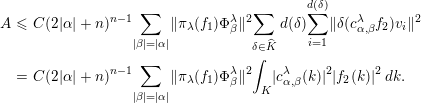 $$\begin{eqnarray}\displaystyle A & {\leqslant} & \displaystyle C(2|\unicode[STIX]{x1D6FC}|+n)^{n-1}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(f_{1})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\Vert ^{2}\mathop{\sum }_{\unicode[STIX]{x1D6FF}\in \widehat{K}}\,d(\unicode[STIX]{x1D6FF})\mathop{\sum }_{i=1}^{d(\unicode[STIX]{x1D6FF})}\Vert \unicode[STIX]{x1D6FF}(c_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}f_{2})v_{i}\Vert ^{2}\nonumber\\ \displaystyle & = & \displaystyle C(2|\unicode[STIX]{x1D6FC}|+n)^{n-1}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(f_{1})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\Vert ^{2}\int _{K}|c_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)|^{2}|f_{2}(k)|^{2}\,dk.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A & {\leqslant} & \displaystyle C(2|\unicode[STIX]{x1D6FC}|+n)^{n-1}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(f_{1})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\Vert ^{2}\mathop{\sum }_{\unicode[STIX]{x1D6FF}\in \widehat{K}}\,d(\unicode[STIX]{x1D6FF})\mathop{\sum }_{i=1}^{d(\unicode[STIX]{x1D6FF})}\Vert \unicode[STIX]{x1D6FF}(c_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}f_{2})v_{i}\Vert ^{2}\nonumber\\ \displaystyle & = & \displaystyle C(2|\unicode[STIX]{x1D6FC}|+n)^{n-1}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(f_{1})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\Vert ^{2}\int _{K}|c_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)|^{2}|f_{2}(k)|^{2}\,dk.\nonumber\end{eqnarray}$$
Hence for
![]() $B=\sum _{\unicode[STIX]{x1D6FF}\in \widehat{K}}~d(\unicode[STIX]{x1D6FF})\Vert \widehat{f}(\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FF})\Vert _{HS}^{2}$
, one gets:
$B=\sum _{\unicode[STIX]{x1D6FF}\in \widehat{K}}~d(\unicode[STIX]{x1D6FF})\Vert \widehat{f}(\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FF})\Vert _{HS}^{2}$
, one gets:
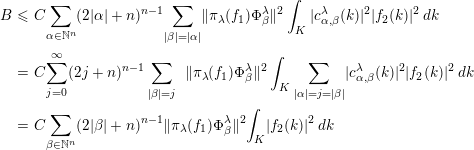 $$\begin{eqnarray}\displaystyle B & {\leqslant} & \displaystyle C\mathop{\sum }_{\unicode[STIX]{x1D6FC}\in \mathbb{N}^{n}}(2|\unicode[STIX]{x1D6FC}|+n)^{n-1}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(f_{1})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\Vert ^{2}\int _{K}|c_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)|^{2}|f_{2}(k)|^{2}\,dk\nonumber\\ \displaystyle & = & \displaystyle C\mathop{\sum }_{j=0}^{\infty }(2j+n)^{n-1}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=j}~\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(f_{1})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\Vert ^{2}\int _{K}\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=j=|\unicode[STIX]{x1D6FD}|}|c_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)|^{2}|f_{2}(k)|^{2}\,dk\nonumber\\ \displaystyle & = & \displaystyle C\mathop{\sum }_{\unicode[STIX]{x1D6FD}\in \mathbb{N}^{n}}(2|\unicode[STIX]{x1D6FD}|+n)^{n-1}\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(f_{1})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\Vert ^{2}\int _{K}|f_{2}(k)|^{2}\,dk\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B & {\leqslant} & \displaystyle C\mathop{\sum }_{\unicode[STIX]{x1D6FC}\in \mathbb{N}^{n}}(2|\unicode[STIX]{x1D6FC}|+n)^{n-1}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=|\unicode[STIX]{x1D6FC}|}\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(f_{1})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\Vert ^{2}\int _{K}|c_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)|^{2}|f_{2}(k)|^{2}\,dk\nonumber\\ \displaystyle & = & \displaystyle C\mathop{\sum }_{j=0}^{\infty }(2j+n)^{n-1}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=j}~\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(f_{1})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\Vert ^{2}\int _{K}\mathop{\sum }_{|\unicode[STIX]{x1D6FC}|=j=|\unicode[STIX]{x1D6FD}|}|c_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}(k)|^{2}|f_{2}(k)|^{2}\,dk\nonumber\\ \displaystyle & = & \displaystyle C\mathop{\sum }_{\unicode[STIX]{x1D6FD}\in \mathbb{N}^{n}}(2|\unicode[STIX]{x1D6FD}|+n)^{n-1}\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(f_{1})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\Vert ^{2}\int _{K}|f_{2}(k)|^{2}\,dk\nonumber\end{eqnarray}$$
in view of equality (2.5). Since
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(\mathscr{L}f_{1})=\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(f_{1})H(\unicode[STIX]{x1D706})$
and
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(\mathscr{L}f_{1})=\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(f_{1})H(\unicode[STIX]{x1D706})$
and
![]() $H(\unicode[STIX]{x1D706})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}=(2|\unicode[STIX]{x1D6FD}|+n)|\unicode[STIX]{x1D706}|\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}$
as explained earlier we see that
$H(\unicode[STIX]{x1D706})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}=(2|\unicode[STIX]{x1D6FD}|+n)|\unicode[STIX]{x1D706}|\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}$
as explained earlier we see that
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FF}\in \widehat{K}}d(\unicode[STIX]{x1D6FF})\Vert \widehat{f}(\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FF})\Vert _{HS}^{2} & {\leqslant} & \displaystyle C|\unicode[STIX]{x1D706}|^{-n+1}\mathop{\sum }_{\unicode[STIX]{x1D6FD}\in \mathbb{N}^{n}}\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(\mathscr{L}^{\frac{n-1}{2}}f_{1})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\Vert _{2}^{2}\,\Vert f_{2}\Vert _{2}^{2}\nonumber\\ \displaystyle & = & \displaystyle C|\unicode[STIX]{x1D706}|^{-n+1}\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(\mathscr{L}^{\frac{n-1}{2}}f_{1})\Vert _{HS}^{2}\Vert f_{2}\Vert _{2}^{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FF}\in \widehat{K}}d(\unicode[STIX]{x1D6FF})\Vert \widehat{f}(\unicode[STIX]{x1D706},\unicode[STIX]{x1D6FF})\Vert _{HS}^{2} & {\leqslant} & \displaystyle C|\unicode[STIX]{x1D706}|^{-n+1}\mathop{\sum }_{\unicode[STIX]{x1D6FD}\in \mathbb{N}^{n}}\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(\mathscr{L}^{\frac{n-1}{2}}f_{1})\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D706}}\Vert _{2}^{2}\,\Vert f_{2}\Vert _{2}^{2}\nonumber\\ \displaystyle & = & \displaystyle C|\unicode[STIX]{x1D706}|^{-n+1}\Vert \unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D706}}(\mathscr{L}^{\frac{n-1}{2}}f_{1})\Vert _{HS}^{2}\Vert f_{2}\Vert _{2}^{2}.\nonumber\end{eqnarray}$$
Consequently,
It is possible to choose functions
![]() $f_{1}\in L^{1}\cap L^{2}(\mathbb{H}^{n})$
such that
$f_{1}\in L^{1}\cap L^{2}(\mathbb{H}^{n})$
such that
So, for well chosen functions
![]() $f\in L^{2}(K)$
we can arrange
$f\in L^{2}(K)$
we can arrange
This achieves the proof of (iii).◻
As a direct consequence of Theorem 3.1, we get the following theorem.
Theorem 3.2. (Hardy’s theorem for Heisenberg motion groups.)
Let
![]() $f$
be a measurable function on
$f$
be a measurable function on
![]() $G$
such that:
$G$
such that:
-
(i)
 $|f(z,t,k)|\leqslant Ce^{-a\Vert (z,t)\Vert ^{2}}$
for all
$|f(z,t,k)|\leqslant Ce^{-a\Vert (z,t)\Vert ^{2}}$
for all
 $(z,t,k)\in G.$
$(z,t,k)\in G.$
-
(ii)
 $|\unicode[STIX]{x1D706}|^{\frac{n}{2}}\Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FF}}^{\unicode[STIX]{x1D706}}(f)\Vert _{HS}\leqslant C_{\unicode[STIX]{x1D6FF}}e^{-b\unicode[STIX]{x1D706}}$
$|\unicode[STIX]{x1D706}|^{\frac{n}{2}}\Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FF}}^{\unicode[STIX]{x1D706}}(f)\Vert _{HS}\leqslant C_{\unicode[STIX]{x1D6FF}}e^{-b\unicode[STIX]{x1D706}}$
for some
![]() $C>0$
and
$C>0$
and
![]() $C_{\unicode[STIX]{x1D6FF}}>0$
such that
$C_{\unicode[STIX]{x1D6FF}}>0$
such that
![]() $\sum _{\unicode[STIX]{x1D6FF}\in \widehat{K}}\,d(\unicode[STIX]{x1D6FF})C_{\unicode[STIX]{x1D6FF}}^{2}<+\infty$
. Then we have:
$\sum _{\unicode[STIX]{x1D6FF}\in \widehat{K}}\,d(\unicode[STIX]{x1D6FF})C_{\unicode[STIX]{x1D6FF}}^{2}<+\infty$
. Then we have:
-
(1) If
 $ab>\frac{1}{4}$
,
$ab>\frac{1}{4}$
,
 $\;f=0$
almost everywhere on
$\;f=0$
almost everywhere on
 $G$
.
$G$
. -
(2) If
 $ab=\frac{1}{4}$
,
$ab=\frac{1}{4}$
,
 $f(z,t,k)=e^{-at^{2}}f(z,0,k)$
for any
$f(z,t,k)=e^{-at^{2}}f(z,0,k)$
for any
 $(z,t,k)\in \mathbb{C}^{n}\times \mathbb{R}\times K$
.
$(z,t,k)\in \mathbb{C}^{n}\times \mathbb{R}\times K$
. -
(3) If
 $ab<\frac{1}{4}$
, there exist an infinite number of linearly independent functions meeting hypotheses
$ab<\frac{1}{4}$
, there exist an infinite number of linearly independent functions meeting hypotheses
 $(i)$
and
$(i)$
and
 $(ii)$
.
$(ii)$
.
As a further generalization, our next objective in this paper is to prove the following analogue of Cowling–Price theorem for Heisenberg motion groups. We have the following theorem.
Theorem 3.3. (An analogue of Cowling–Price theorem for Heisenberg motion groups.)
Let
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
be positive real numbers,
$\unicode[STIX]{x1D6FD}$
be positive real numbers,
![]() $1\leqslant p,q\leqslant \infty$
such that
$1\leqslant p,q\leqslant \infty$
such that
![]() $\min (p,q)$
is finite, and let
$\min (p,q)$
is finite, and let
![]() $f$
be a square integrable function on
$f$
be a square integrable function on
![]() $G$
satisfying the following decay conditions:
$G$
satisfying the following decay conditions:
-
(i)
 $e^{\unicode[STIX]{x1D6FC}\Vert \cdot \Vert ^{2}}f\in L^{p}(G)$
.
$e^{\unicode[STIX]{x1D6FC}\Vert \cdot \Vert ^{2}}f\in L^{p}(G)$
. -
(ii)
 $e^{2\unicode[STIX]{x1D6FD}|\unicode[STIX]{x1D706}|^{2}}|\unicode[STIX]{x1D706}|^{n}\sum _{\unicode[STIX]{x1D70E}\in \widehat{K}}\,d(\unicode[STIX]{x1D70E})\Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FF}}^{\unicode[STIX]{x1D706}}(f)\Vert _{HS}^{2}\in L^{q}(\mathbb{R})$
.
$e^{2\unicode[STIX]{x1D6FD}|\unicode[STIX]{x1D706}|^{2}}|\unicode[STIX]{x1D706}|^{n}\sum _{\unicode[STIX]{x1D70E}\in \widehat{K}}\,d(\unicode[STIX]{x1D70E})\Vert \unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FF}}^{\unicode[STIX]{x1D706}}(f)\Vert _{HS}^{2}\in L^{q}(\mathbb{R})$
.
Then the following conclusions hold:
-
(1)
 $f=0$
almost everywhere whenever
$f=0$
almost everywhere whenever
 $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\geqslant 1/4$
.
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}\geqslant 1/4$
. -
(2) If
 $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}<1/4$
, then there are infinitely many linearly independent functions satisfying both conditions (i) and (ii).
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}<1/4$
, then there are infinitely many linearly independent functions satisfying both conditions (i) and (ii).
Proof. Let
![]() $f$
be a function meeting the hypotheses of the theorem. Then, first we obtain that
$f$
be a function meeting the hypotheses of the theorem. Then, first we obtain that
![]() $f$
verifies the condition
$f$
verifies the condition
![]() $(i)$
of Theorem 3.1 since
$(i)$
of Theorem 3.1 since
![]() $L^{p}\subset L^{1}+L^{\infty }$
. Furthermore, based on the inequality,
$L^{p}\subset L^{1}+L^{\infty }$
. Furthermore, based on the inequality,
![]() $Log^{+}(x)\leqslant x$
for
$Log^{+}(x)\leqslant x$
for
![]() $x\in \mathbb{R}_{+}$
, we can see that
$x\in \mathbb{R}_{+}$
, we can see that
![]() $f$
verifies the second condition of Theorem 3.1. Hence
$f$
verifies the second condition of Theorem 3.1. Hence
![]() $f=0$
almost everywhere whenever
$f=0$
almost everywhere whenever
![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}>1/4$
. Second, if
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}>1/4$
. Second, if
![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=1/4$
then
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}=1/4$
then
![]() $f(z,t,k)=\unicode[STIX]{x1D706}(k,z)e^{-\unicode[STIX]{x1D6FC}t^{2}}$
for some function
$f(z,t,k)=\unicode[STIX]{x1D706}(k,z)e^{-\unicode[STIX]{x1D6FC}t^{2}}$
for some function
![]() $\unicode[STIX]{x1D706}\in L^{2}(K\times \mathbb{C}^{n})$
. But then
$\unicode[STIX]{x1D706}\in L^{2}(K\times \mathbb{C}^{n})$
. But then
![]() $e^{\unicode[STIX]{x1D6FC}\Vert \cdot \Vert ^{2}}f$
is independent of the variable
$e^{\unicode[STIX]{x1D6FC}\Vert \cdot \Vert ^{2}}f$
is independent of the variable
![]() $t$
and hence the condition
$t$
and hence the condition
![]() $e^{\unicode[STIX]{x1D6FC}\Vert \cdot \Vert ^{2}}f\in L^{p}(G)$
forces
$e^{\unicode[STIX]{x1D6FC}\Vert \cdot \Vert ^{2}}f\in L^{p}(G)$
forces
![]() $\unicode[STIX]{x1D706}(k,z)$
to be zero for almost every
$\unicode[STIX]{x1D706}(k,z)$
to be zero for almost every
![]() $k\in K$
and
$k\in K$
and
![]() $z\in \mathbb{C}^{n}$
. Finally for
$z\in \mathbb{C}^{n}$
. Finally for
![]() $\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}<1/4$
, restricting to the setting of Heisenberg groups, we know that there exists an infinite family of linearly independent functions
$\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}<1/4$
, restricting to the setting of Heisenberg groups, we know that there exists an infinite family of linearly independent functions
![]() $f_{\unicode[STIX]{x1D700}},\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D700}<1/\unicode[STIX]{x1D6FD}$
with the property:
$f_{\unicode[STIX]{x1D700}},\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D700}<1/\unicode[STIX]{x1D6FD}$
with the property:
some positive constant
![]() $C_{\unicode[STIX]{x1D700}}$
. Hence inequality (3.2) enables us to achieve the proof.◻
$C_{\unicode[STIX]{x1D700}}$
. Hence inequality (3.2) enables us to achieve the proof.◻
Acknowledgments
The authors are deeply indebted to the referees for their many valuable comments and suggestions on an earlier version of the paper.