Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-13T19:28:50.263Z Has data issue: false hasContentIssue false
  • English
  • Français

Integral geometry under cut loci in compact symmetric spaces

Published online by Cambridge University Press:  22 January 2016

Hiroyuki Tasaki
Hiroyuki Tasaki*
Affiliation:
Institute of Mathematics University of Tsukuba, Tsukuba, Ibaraki 305, Japan e-mail: tasaki@math.tsukuba.ac.jp
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The theory of integral geometry has mainly treated identities between integral invariants of submanifolds in Riemannian homogeneous spaces like as 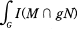dμg(g) where M and N are submanifolds in a Riemannian homogeneous spaces of a Lie group G and I(M ∩ gN) is an integral invariant of M ∩ gN. For example Poincaré’s formula is one of typical identities in integral geometry, which is as follows. We denote by M(R2) the identity component of the group of isometries of the plane R2 with a suitable invariant measure μM(R2).

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 137 , March 1995 , pp. 33 - 53
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1995

References

[ 1 ] Berger, M., Du côté de chez Pu, Ann. scient. Éc. Norm. Sup., 5 (1972), 1–44.Google Scholar
[ 2 ] Brothers, J. E., Integral geometry in homogeneous spaces, Trans. A. M. S., 124 (1966), 480–517.Google Scholar
[ 3 ] Chern, S. S., On integral geometry in Klein spaces, Ann. Math., 43 (1942), 178–189.Google Scholar
[ 4 ] Harvey, R. and Lawson, H. B. Jr., Calibrated geometries, Acta Math., 148 (1982), 47–157.Google Scholar
[ 5 ] Helgason, S., Totally geodesic spheres in compact symmetric spaces, Math. Ann., 165 (1966), 309–317.Google Scholar
[ 6 ] Helgason, S., Differential geometry, Lie groups, and symmetric spaces, Academic Press, New York, 1978.Google Scholar
[ 7 ] Howard, R., Classical integral geometry in Riemannian homogeneous spaces, Contemporary Math., 63 (1987), 179–204.Google Scholar
[ 8 ] Kobayashi, S., On conjugate and cut loci, in Studies in global geometry and analysis, (S. S. Chern, ed.), MAA 1967, 96–122.Google Scholar
[ 9 ] Kurita, M., An extension of Poincaré formula in integral geometry, Nagoya Math. J., 2 (1950), 55–61.Google Scholar
[10] Vân, Lê Hôong, Application of integral geometry to minimal surfaces, Int. J. Math., 4 (1993), 89–111.Google Scholar
[11] Vân, Lê Hôong, Curvature estimate for the volume growth of globally minimal submanifolds, Math. Ann., 296 (1993), 103–118.Google Scholar
[12] Ohnita, Y., On stability of minimal submanifolds in compact symmetric spaces, Composite Math., 64 (1987), 157–189.Google Scholar
[13] Sakai, T., On the cut loci of compact symmetric spaces, Hokkaido Math. J., 6 (1977), 136–161.Google Scholar
[14] Sakai, T., On the structure of cut loci in compact Riemannian symmetric spaces, Math. Ann., 235(1978), 129–148.Google Scholar
[15] Santaló, L. A., Integral geometry and geometric probability, Addison-Wesley, London, 1976.Google Scholar
[16] Takeuchi, M., On conjugate loci and cut loci of compact symmetric spaces I, Tsukuba J. Math., 2 (1978), 35–68.Google Scholar
[17] Takeuchi, M., Basic transformations of symmetric R -spaces, Osaka J. Math., 25 (1988), 259–297.Google Scholar
[18] Tasaki, H., Certain minimal or homologically volume minimizing submanifolds in compact symmetric spaces, Tsukuba J. Math., 9 (1985), 117–131.Google Scholar
[19] Tasaki, H., The cut locus and the diastasis of a Hermitian symmetric space of compact type, Osaka J. Math., 22 (1985), 863–870.Google Scholar
[20] Wong, Y. C., Differential geometry of Grassmann manifolds, Proc. Nat. Acad. Sci. U. S. A., 57 (1967), 589–594.Google Scholar
[21] Wong, Y. C., Conjugate loci in Grassmann manifolds, Bull. A. M. S., 74 (1968), 240–245.Google Scholar