Hostname: page-component-848d4c4894-2pzkn Total loading time: 0 Render date: 2024-05-24T14:44:39.929Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Theorem of Schwarz Type for Quasiconformal Mappings in Space

Published online by Cambridge University Press:  22 January 2016

Kazuo Ikoma
Kazuo Ikoma*
Affiliation:
Department of Mathematics, Yamagata University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A space ring R is defined as a domain whose complement in the Moebius space consists of two components. The modulus of R can be defined in variously different but essentially equivalent ways (see e.g. Gehring [3] and Krivov [5]), which is denoted by mod R. Following Gehring [2], we refer to a homeomorphism y(x) of a space domain D as a k-quasiconformal mapping, if the modulus condition

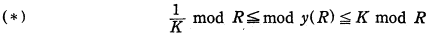
is satisfied for all bounded rings R with their closure 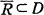, where y(R) denotes the image of R by y = y(x). Then, it is evident that the inverse of a k-quasi-conformal mapping is itself k-quasiconformal and that a k1-quasiconformal mapping followed by a k2-quasiconformal one is k1k2-quasiconformal. It is also well known that the restriction of a Moebius transformation to a space domain is equivalent to a 1-quasiconformal mapping of its domain.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 29 , March 1967 , pp. 19 - 30
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1967

References

[1] Gehring, F. W., Symmetrization of rings in space, Trans. Amer. Math. Soc., 101 (1961), 499–516.Google Scholar
[2] Gehring, F. W., Rings and quasiconformal mappings in space, ibid., 103 (1962), 353–393.Google Scholar
[3] Gehring, F. W., Extremal length definitions for the comformal capacity of rings in space, Mich. Math. J., 9 (1962), 137–150.CrossRefGoogle Scholar
[4] Ikoma, K., On the distortion and correspondence under quasiconformal mappings in space, Nagoya Math. J., 25 (1965), 175–203.CrossRefGoogle Scholar
[5] Krivov, V. V., Some properties of moduli in space, Dokl. Acad. Nauk SSSR 154 (1964), 510–513 (Soviet Math. Dokl. 5 (1964), 113–117).Google Scholar
[6] Väisälä, J., On quasiconformal mappings in space, Ann. Acad. Sci. Fenn., A. I. 298 (1961), 1–36.Google Scholar