Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Peter, Manfred
2003.
Dirichlet series and automorphic functions associated to a quadratic form.
Nagoya Mathematical Journal,
Vol. 171,
Issue. ,
p.
1.
Kable, Anthony
2006.
Symmetry in the functional equation of a local zeta distribution.
Tohoku Mathematical Journal,
Vol. 58,
Issue. 4,
Mizuno, Yoshinori
2012.
Dirichlet series associated with square of class numbers of binary quadratic forms.
Mathematische Zeitschrift,
Vol. 272,
Issue. 3-4,
p.
1115.
Matz, Jasmin
2016.
Families of Automorphic Forms and the Trace Formula.
p.
351.




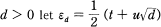 where
where 