Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jurek, Zbigniew J.
1992.
Probability in Banach Spaces, 8:.
p.
137.
Jurek, Zbigniew J
and
Schreiber, Bertram M
1992.
Fourier transforms of measures from the classes Uβ′ −2 < β ≤ −1.
Journal of Multivariate Analysis,
Vol. 41,
Issue. 2,
p.
194.
Maejima, Makoto
and
Ueda, Yohei
2010.
Compositions of mappings of infinitely divisible distributions with applications to finding the limits of some nested subclasses.
Electronic Communications in Probability,
Vol. 15,
Issue. none,
Maejima, Makoto
and
Ueda, Yohei
2010.
α-selfdecomposable distributions and related Ornstein–Uhlenbeck type processes.
Stochastic Processes and their Applications,
Vol. 120,
Issue. 12,
p.
2363.
Maejima, Makoto
and
Ueda, Yohei
2010.
A note on a bivariate gamma distribution.
Statistics & Probability Letters,
Vol. 80,
Issue. 23-24,
p.
1991.
MAEJIMA, Makoto
and
UEDA, Yohei
2011.
Nested Subclasses of the Class of $\alpha$-selfdecomposable Distributions.
Tokyo Journal of Mathematics,
Vol. 34,
Issue. 2,
Jurek, Zbigniew J.
2011.
The random integral representation conjecture: a quarter of a century later.
Lithuanian Mathematical Journal,
Vol. 51,
Issue. 3,
p.
362.
James, Lancelot F.
and
Zhang, Zhiyuan
2011.
Quantile clocks.
The Annals of Applied Probability,
Vol. 21,
Issue. 5,
Maejima, Makoto
and
Ueda, Yohei
2013.
Examples of -selfdecomposable distributions.
Statistics & Probability Letters,
Vol. 83,
Issue. 1,
p.
286.
Sato, Ken-iti
2013.
Inversions of Infinitely Divisible Distributions and Conjugates of Stochastic Integral Mappings.
Journal of Theoretical Probability,
Vol. 26,
Issue. 4,
p.
901.
Jurek, Zbigniew J.
2014.
A random integral calculus on generalized s-selfdecomposable probability measures.
Sankhya A,
Vol. 76,
Issue. 1,
p.
1.
Maejima, Makoto
2015.
Lévy Matters V.
Vol. 2149,
Issue. ,
p.
1.
Rocha-Arteaga, Alfonso
and
Sato, Ken-iti
2019.
Topics in Infinitely Divisible Distributions and Lévy Processes, Revised Edition.
p.
27.




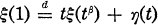 for each 0 <
for each 0 < 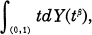 where
where 