Es sei f eine meromorphe nichtkonstante Funktion im Kreise |z|, < 1. Die Theorie des Verhaltens von f auf dem Rande des Kreises wird von zwei bekannten Sätzen beherrscht: der Satz von Riesz-Lusin-Priwaloff-Frostman-Nevanlinna, auf Grund dessen eine Menge aus |z| = 1, für die die Winkelgrenzwerte von f in einer Menge der Kapazität Null liegen, vom Lebesgueschen Masse Null ist und der Satz von Fatou-Nevanlinna, welcher besagt, dass, falls die Funktion f beschränktartig ist, dann hat sie fast überall auf |z| = 1 Winkelgrenzwerte. In vorliegender Arbeit werden diese zwei Sätze auf folgende Weise verallgemeinert. An Stelle des Kreises |z| < 1 betrachten wir eine beliebige Riemannsche Fläche R mit Greenscher Funktion, und an Stelle der meromorphen Funktion f nehmen wir eine nichtkonstante analytische Abbildung von R in einer Riemannschen Fläche R′(R′ offen oder kompakt, mit oder ohne Greenscher Funktion). Es sei Δ, bzw. Δ′, der ideale Rand von R, bzw. R′, im Sinne von Martin [11]; wir werden im Abschnitt IV eine Teilmenge 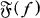der Menge Δ und eine Abbildung 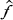von 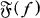(f) in R′ ∪ Δ′ definieren. Die Verallgemeinerung des Satzes von Fatou-Nevanlinna besteht in der Behauptung, dass, falls f eine Lindelöfsche Abbildung ist [6], so ist Δ-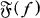(f) von harmonischen Masse Null und die des Satzes von Riesz-Lusin-Priwaloff-Frostman-Nevanlinna darin, dass, wenn 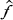(A) eine polare Menge auf R′∪Δ′ ist, so ist die Menge A ⊂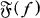(f) vom harmonischen Masse Null.