Hostname: page-component-848d4c4894-hfldf Total loading time: 0 Render date: 2024-05-19T05:24:07.263Z Has data issue: false hasContentIssue false
  • English
  • Français

Baire's category in existence problems for non-convex lower semicontinuous evolution differential inclusions

Part of: Existence theories General theory in ordinary differential equations Differential equations in abstract spaces

Published online by Cambridge University Press:  15 June 2011

F.S. De Blasi  and
G. Pianigiani
F.S. De Blasi
Affiliation:
Dipartimento di Matematica, Università di Roma ‘Tor Vergata’, Via della Ricerca Scientifica 1, 00133 Roma, Italy (deblasi@mat.uniroma2.it)
G. Pianigiani
Affiliation:
Dipartimento di Matematica per le Decisioni, Università di Firenze, Via Lombroso 6/17, 50134 Firenze, Italy (giulio.pianigiani@unifi.it)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The existence of mild solutions to the non-convex Cauchy problem

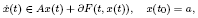
is investigated. Here A is the infinitesimal generator of a C0-semigroup in a reflexive and separable Banach space 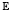, F is a Pompeiu–Hausdorff lower semicontinuous multifunction whose values are closed convex and bounded sets with non-empty interior contained in 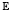, and ∂F(t, x(t)) denotes the boundary of F(t, x(t)). Our approach is based on the Baire category method, with appropriate modifications which are actually necessary because, under our assumptions, the underlying metric space that naturally enters in the Baire method, i.e. the solution set of the convexified Cauchy problem (CF), can fail to be a complete metric space.

Keywords

Baire methodBanach spacesinfinitesimal generatorC0-semigroupnon-convex evolution inclusionsPompeiu–Hausdorff lower semicontinuity

MSC classification

Secondary: 34G25: Evolution inclusions 34A60: Differential inclusions 49J27: Problems in abstract spaces
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 54 , Issue 3 , October 2011 , pp. 645 - 667
Copyright
Copyright © Edinburgh Mathematical Society 2011

References

1.Aubin, J. P. and Cellina, A., Differential inclusions (Springer, 1984).CrossRefGoogle Scholar
2.Bressan, A., Differential inclusions with non-closed non-convex right-hand side, J. Diff. Eqns 3 (1990), 633–638.Google Scholar
3.Bressan, A., Cellina, A. and Colombo, G., Upper semicontinuous differential inclusions without convexity, Proc. Am. Math. Soc. 111 (1989), 771–775.CrossRefGoogle Scholar
4.Bressan, A. and Colombo, G., Generalized Baire category and differential inclusions in Banach spaces, J. Diff. Eqns 76 (1988), 135–158.CrossRefGoogle Scholar
5.Cellina, A., On the differential inclusion ẋ ∈ [−1, 1], Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Natur. 69 (1980), 1–6.Google Scholar
6.Cellina, A., A view on differential inclusions, Rend. Sem. Mat. Univ. Polit. Torino 63 (2005), 197–209.Google Scholar
7.De Blasi, F. S., Characterization of certain classes of semicontinuous multifunctions by continuous approximations, J. Math. Analysis Applic. 106 (1985), 1–18.CrossRefGoogle Scholar
8.De Blasi, F. S. and Pianigiani, G., A Baire category approach to the existence of solutions of multivalued differential equations in Banach spaces, Funkcial. Ekvac. 25 (1982), 153–162.Google Scholar
9.De Blasi, F. S. and Pianigiani, G., Remarks on Hausdorff continuous multifunctions and selections, Commun. Math. Univ. Carol. 24 (1983), 553–561.Google Scholar
10.De Blasi, F. S. and Pianigiani, G., Differential inclusions in Banach spaces, J. Diff. Eqns 66 (1987), 208–229.CrossRefGoogle Scholar
11.De Blasi, F. S. and Pianigiani, G., Non-convex-valued differential inclusions in Banach spaces, J. Math. Analysis Applic. 157 (1991), 469–494.CrossRefGoogle Scholar
12.De Blasi, F. S. and Pianigiani, G., Baire category and the bang-bang property for evolution differential inclusions of contractive type, J. Math. Analysis Applic. 367 (2010), 550–567.CrossRefGoogle Scholar
13.De Blasi, F. S., Pianigiani, G. and Staicu, V., Topological properties of non-convex differential inclusions of evolution type, Nonlin. Analysis 24 (1995), 711–720.CrossRefGoogle Scholar
14.Donchev, T., Farkhi, E. and Mordukhovich, B. S., Discrete approximations, relaxation, and optimization of one-sided Lipschitzian differential inclusions in Hilbert spaces, J. Diff. Eqns 243 (2007), 301–328.CrossRefGoogle Scholar
15.Godunov, A. N., Peano's Theorem in Banach spaces, Funct. Analysis Applic. 9 (1975), 53–55.CrossRefGoogle Scholar
16.Gromov, M., Partial differential relations (Springer, 1986).CrossRefGoogle Scholar
17.Hu, S. and Papageorgiou, N. S., Handbook of multivalued analysis, Volumes I and II (Kluwer, Dordrecht, 1998).Google Scholar
18.Mordukhovich, B. S., Variational analysis and generalized differentiation, Volumes I and II (Springer, 2006).CrossRefGoogle Scholar
19.Müller, S. and Sverák, V., Unexpected solutions of first and second order partial differential equations, in Proceedings of the International Congress of Mathematicians, Documenta Mathematica Book Series, Extra Volume II, pp. 671–702 (Deutsche Mathematiker-Vereinigung, Bielefeld, 1998).Google Scholar
20.Müller, S. and Sychev, M. A., Optimal existence theorems for nonhomogeneous differential inclusions, J. Funct. Analysis 181 (2001), 447–475.CrossRefGoogle Scholar
21.Papageorgiou, N. S., On the properties of the solution set of non-convex evolution inclusions of the differential type, Commun. Math. Univ. Carol. 34 (1993), 673–687.Google Scholar
22.Papageorgiou, N. S., On the bang-bang principle for nonlinear evolution inclusions, Aequ. Math. 45 (1993), 267–280.CrossRefGoogle Scholar
23.Papageorgiou, N. S., On parametric evolution inclusions of the subdifferential type with applications to optimal control problems, Trans. Am. Math. Soc. 347 (1995), 203–231.CrossRefGoogle Scholar
24.Pazy, A., Semigroup of linear operators and applications to partial differential equations (Springer, 1983).CrossRefGoogle Scholar
25.Pianigiani, G., Differential inclusions: the Baire category method, in Methods of nonconvex analysis (ed. Cellina, A.), Lecture Notes in Mathematics, Volume 1446, pp. 104–136 (Springer, 1990).CrossRefGoogle Scholar
26.Sychev, M. A., A few remarks on differential inclusions, Proc. R. Soc. Edinb. A136 (2006), 649–668.CrossRefGoogle Scholar
27.Taylor, A. E., General theory of functions and integration (Blaisdell, Waltham, MA, 1965).Google Scholar
28.Tolstonogov, A. A., Extremal selections of multivalued mappings and the bang-bang principle for evolution inclusions, Sov. Math. Dokl. 43 (1991), 589–593.Google Scholar
29.Tolstonogov, A. A., Extreme continuous selectors of multivalued maps and their applications, J. Diff. Eqns 122 (1995), 161–180.CrossRefGoogle Scholar
30.Tolstonogov, A. A., Differential inclusions in a Banach space (Kluwer, Dordrecht, 2000).CrossRefGoogle Scholar