Hostname: page-component-848d4c4894-m9kch Total loading time: 0 Render date: 2024-06-12T04:15:54.311Z Has data issue: false hasContentIssue false
  • English
  • Français

The Circle Transfer and Cobordism Categories

Part of: Homology and cohomology theories Fiber spaces and bundles

Published online by Cambridge University Press:  11 January 2019

Jeffrey Giansiracusa
Jeffrey Giansiracusa*
Affiliation:
Department of Mathematics Swansea University, Singleton Park, Swansea SA2 8PP, UK (j.h.giansiracusa@swansea.ac.uk)
Get access Rights & Permissions [Opens in a new window]

Abstract

The circle transfer 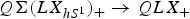$Q\Sigma (LX_{hS^1})_+ \to QLX_+$ has appeared in several contexts in topology. In this note, we observe that this map admits a geometric re-interpretation as a morphism of cobordism categories of 0-manifolds and 1-cobordisms. Let 𝒞1(X) denote the one-dimensional cobordism category and let Circ(X) ⊂ 𝒞1(X) denote the subcategory whose objects are disjoint unions of unparametrized circles. Multiplication in S1 induces a functor Circ(X) → Circ(LX), and the composition of this functor with the inclusion of Circ(LX) into 𝒞1(LX) is homotopic to the circle transfer. As a corollary, we describe the inclusion of the subcategory of cylinders into the two-dimensional cobordism category 𝒞2(X) and find that it is null-homotopic when X is a point.

Keywords

cobordismcircle transferfree loop spacePontrjagin-Thomequivariant homotopy

MSC classification

Primary: 55R12: Transfer
Secondary: 55N22: Bordism and cobordism theories, formal group laws
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 62 , Issue 3 , August 2019 , pp. 719 - 731
Copyright
Copyright © Edinburgh Mathematical Society 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Baker, A., On the detection of some elements in the image of the double transfer using K(2)-theory, Math. Z. 197(3) (1988), 439–454.Google Scholar
2.Baker, A., Carlisle, D., Gray, B., Hilditch, S., Ray, N. and Wood, R., On the iterated complex transfer, Math. Z. 199(2) (1988), 191–207.Google Scholar
3.Bökstedt, M., Hsiang, W. C. and Madsen, I., The cyclotomic trace and algebraic K-theory of spaces, Invent. Math. 111(3) (1993), 465–539.Google Scholar
4.Galatius, S., Madsen, I., Tillmann, U. and Weiss, M., The homotopy type of the cobordism category, Acta Math. 202(2) (2009), 195–239.Google Scholar
5.Gramain, A., Le type d'homotopie du groupe des difféomorphismes d'une surface compacte, Ann. Sci. Éc. Norm. Supér. (4) 6 (1973), 53–66.Google Scholar
6.Imaoka, M., μ-elements in S 1-transfer images, Osaka J. Math. 28(4) (1991), 975–984.Google Scholar
7.Lewis, L. G. Jr., May, J. P., Steinberger, M. and McClure, J. E., Equivariant stable homotopy theory, Lecture Notes in Mathematics, Volume 1213 (Springer-Verlag, Berlin, 1986).Google Scholar
8.Madsen, I. and Schlichtkrull, C., The circle transfer and K-theory, in Geometry and topology: Aarhus, Contemporary Mathematics, Volume 258, pp. 307–328 (American Mathematical Society, Providence, RI, 2000).Google Scholar
9.Madsen, I. and Tillmann, U., The stable mapping class group and $Q({\open C}P_ + ^\infty)$, Invent. Math. 145(3) (2001), 509–544.Google Scholar
10.Miller, H., Universal Bernoulli numbers and the S 1-transfer, in Current trends in algebraic topology, part 2: London, Ontario, CMS Conference Proceedings, Volume 2, pp. 437–449 (American Mathematical Society, Providence, RI, 1982).Google Scholar
11.Mukai, J., The S 1-transfer map and homotopy groups of suspended complex projective spaces, Math. J. Okayama Univ. 24(2) (1982), 179–200.Google Scholar
12.Mukai, J., The element $\overline \kappa $, is not in the image of the S 1-transfer, Math. J. Okayama Univ. 36 (1994), 133–143.Google Scholar
13.Rognes, J., The smooth Whitehead spectrum of a point at odd regular primes, Geom. Topol. 7 (2003), 155–184.Google Scholar