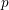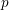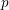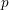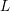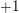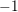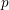1 Introduction
The main results of this paper are the general formula for the
![]() $p$
-adic heights of Heegner points of Theorem B below, and its version in anticyclotomic families (contained in Theorem C). They are preceded by a flexible construction of the relevant
$p$
-adic heights of Heegner points of Theorem B below, and its version in anticyclotomic families (contained in Theorem C). They are preceded by a flexible construction of the relevant
![]() $p$
-adic
$p$
-adic
![]() $L$
-function (Theorem A), and complemented by a version of the Waldspurger formula in anticyclotomic families (presented in Theorem C as well). In Theorem D, we give an application to a version of the
$L$
-function (Theorem A), and complemented by a version of the Waldspurger formula in anticyclotomic families (presented in Theorem C as well). In Theorem D, we give an application to a version of the
![]() $p$
-adic Birch and Swinnerton-Dyer conjecture in anticyclotomic families. In Theorem E, we state a result on the generic non-vanishing of
$p$
-adic Birch and Swinnerton-Dyer conjecture in anticyclotomic families. In Theorem E, we state a result on the generic non-vanishing of
![]() $p$
-adic heights on CM abelian varieties, as a special case of a theorem to appear in joint work with Burungale.
$p$
-adic heights on CM abelian varieties, as a special case of a theorem to appear in joint work with Burungale.
Our theorems are key ingredients of a new Gross–Zagier formula for exceptional zeros [Reference DisegniDis16], and of a universal
![]() $p$
-adic Gross–Zagier formula specialising to analogues of Theorem B in all weights. These will be given in separate works. Here we would just like to mention that all of them, as well as Theorem E, make essential use of the new generality of the present work.
$p$
-adic Gross–Zagier formula specialising to analogues of Theorem B in all weights. These will be given in separate works. Here we would just like to mention that all of them, as well as Theorem E, make essential use of the new generality of the present work.
The rest of this introductory section contains the statements of our results, followed by an outline of their proofs. To avoid interrupting the flow of exposition, the discussion of previous and related works (notably by Perrin-Riou and Howard) has mostly been concentrated in § 1.6.
1.1 Heegner points and multiplicity one
Let
![]() $A$
be a simple abelian variety of
$A$
be a simple abelian variety of
![]() $\mathbf{GL}_{2}$
-type over a totally real field
$\mathbf{GL}_{2}$
-type over a totally real field
![]() $F$
; recall that this means that
$F$
; recall that this means that
 $M:=\operatorname{End}^{0}(A)$
is a field of dimension equal to the dimension of
$M:=\operatorname{End}^{0}(A)$
is a field of dimension equal to the dimension of
![]() $A$
. One knows how to systematically construct points on
$A$
. One knows how to systematically construct points on
![]() $A$
when
$A$
when
![]() $A$
admits parametrisations by Shimura curves in the following sense. Let
$A$
admits parametrisations by Shimura curves in the following sense. Let
![]() $\mathbf{B}$
be a quaternion algebra over the adèle ring
$\mathbf{B}$
be a quaternion algebra over the adèle ring
 $\mathbf{A}=\mathbf{A}_{F}$
of
$\mathbf{A}=\mathbf{A}_{F}$
of
![]() $F$
, and assume that
$F$
, and assume that
![]() $\mathbf{B}$
is incoherent, i.e. that its ramification set
$\mathbf{B}$
is incoherent, i.e. that its ramification set
![]() $\unicode[STIX]{x1D6F4}_{\mathbf{B}}$
has odd cardinality. We further assume that
$\unicode[STIX]{x1D6F4}_{\mathbf{B}}$
has odd cardinality. We further assume that
![]() $\unicode[STIX]{x1D6F4}_{\mathbf{B}}$
contains all the archimedean places of
$\unicode[STIX]{x1D6F4}_{\mathbf{B}}$
contains all the archimedean places of
![]() $F$
. Under these conditions there is a tower of Shimura curves
$F$
. Under these conditions there is a tower of Shimura curves
![]() $\{X_{U}\}$
over
$\{X_{U}\}$
over
![]() $F$
indexed by the open compact subgroups
$F$
indexed by the open compact subgroups
 $U\subset \mathbf{B}^{\infty \times }$
; let
$U\subset \mathbf{B}^{\infty \times }$
; let
 $X=X(\mathbf{B}):=\mathop{\varprojlim }\nolimits_{U}X_{U}$
. For each
$X=X(\mathbf{B}):=\mathop{\varprojlim }\nolimits_{U}X_{U}$
. For each
![]() $U$
, there is a canonical Hodge class
$U$
, there is a canonical Hodge class
 $\unicode[STIX]{x1D709}_{U}\in \operatorname{Pic}(X_{U})_{\mathbf{Q}}$
having degree
$\unicode[STIX]{x1D709}_{U}\in \operatorname{Pic}(X_{U})_{\mathbf{Q}}$
having degree
![]() $1$
in each connected component, inducing a compatible family
$1$
in each connected component, inducing a compatible family
 $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D709}}=(\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D709},U})_{U}$
of quasi-embeddingsFootnote
1
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D709}}=(\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D709},U})_{U}$
of quasi-embeddingsFootnote
1
 $\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D709},U}:X_{U}{\hookrightarrow}J_{U}:=\operatorname{Alb}X_{U}$
. We write
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D709},U}:X_{U}{\hookrightarrow}J_{U}:=\operatorname{Alb}X_{U}$
. We write
 $J:=\varprojlim J_{U}$
. The
$J:=\varprojlim J_{U}$
. The
![]() $M$
-vector space
$M$
-vector space
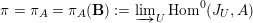 $$\begin{eqnarray}\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{A}=\unicode[STIX]{x1D70B}_{A}(\mathbf{B}):=\mathop{\varinjlim }\nolimits_{U}\operatorname{Hom}^{0}(J_{U},A)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{A}=\unicode[STIX]{x1D70B}_{A}(\mathbf{B}):=\mathop{\varinjlim }\nolimits_{U}\operatorname{Hom}^{0}(J_{U},A)\end{eqnarray}$$
is either zero or a smooth irreducible admissible representation of
![]() $\mathbf{B}^{\infty \times }$
. It comes with a natural stable lattice
$\mathbf{B}^{\infty \times }$
. It comes with a natural stable lattice
![]() $\unicode[STIX]{x1D70B}_{\mathbf{Z}}\subset \unicode[STIX]{x1D70B}$
, and its central character
$\unicode[STIX]{x1D70B}_{\mathbf{Z}}\subset \unicode[STIX]{x1D70B}$
, and its central character
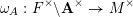 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{A}:F^{\times }\backslash \mathbf{A}^{\times }\rightarrow M^{\times }\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{A}:F^{\times }\backslash \mathbf{A}^{\times }\rightarrow M^{\times }\end{eqnarray}$$
corresponds, up to twist by the cyclotomic character, to the determinant of the Tate module under the class field theory isomorphism. When
![]() $\unicode[STIX]{x1D70B}_{A}$
is non-zero,
$\unicode[STIX]{x1D70B}_{A}$
is non-zero,
![]() $A$
is said to be parametrised by
$A$
is said to be parametrised by
![]() $X(\mathbf{B})$
. Under the conditions we are going to impose on
$X(\mathbf{B})$
. Under the conditions we are going to impose on
![]() $A$
, the existence of such a parametrisation, for a suitable choice of
$A$
, the existence of such a parametrisation, for a suitable choice of
![]() $\mathbf{B}$
(see below), is equivalent to the modularity conjecture. Recall that the latter asserts the existence of a unique
$\mathbf{B}$
(see below), is equivalent to the modularity conjecture. Recall that the latter asserts the existence of a unique
![]() $M$
-rational (Definition 1.2.1 below) automorphic representation
$M$
-rational (Definition 1.2.1 below) automorphic representation
![]() $\unicode[STIX]{x1D70E}_{A}$
of weight
$\unicode[STIX]{x1D70E}_{A}$
of weight
![]() $2$
such that there is an equality of
$2$
such that there is an equality of
![]() $L$
-functions
$L$
-functions
 $L(A,s+1/2)=L(s,\unicode[STIX]{x1D70E}_{A})$
. The conjecture is known to be true for ‘almost all’ elliptic curves
$L(A,s+1/2)=L(s,\unicode[STIX]{x1D70E}_{A})$
. The conjecture is known to be true for ‘almost all’ elliptic curves
![]() $A$
(see [Reference Le HungLeH14]), and when
$A$
(see [Reference Le HungLeH14]), and when
![]() $A_{\overline{F}}$
has complex multiplication.
$A_{\overline{F}}$
has complex multiplication.
Heegner points. Let
![]() $A$
be parametrised by
$A$
be parametrised by
![]() $X(\mathbf{B})$
and let
$X(\mathbf{B})$
and let
![]() $E$
be a CM extension of
$E$
be a CM extension of
![]() $F$
admitting an
$F$
admitting an
![]() $\mathbf{A}^{\infty }$
-embedding
$\mathbf{A}^{\infty }$
-embedding
 $E_{\mathbf{A}^{\infty }}{\hookrightarrow}\mathbf{B}^{\infty }$
, which we fix; we denote by
$E_{\mathbf{A}^{\infty }}{\hookrightarrow}\mathbf{B}^{\infty }$
, which we fix; we denote by
![]() $\unicode[STIX]{x1D702}$
the associated quadratic character and by
$\unicode[STIX]{x1D702}$
the associated quadratic character and by
![]() $D_{E}$
its absolute discriminant. Then
$D_{E}$
its absolute discriminant. Then
![]() $E^{\times }$
acts on
$E^{\times }$
acts on
![]() $X$
and by the theory of complex multiplication each closed point of the subscheme
$X$
and by the theory of complex multiplication each closed point of the subscheme
![]() $X^{E^{\times }}$
is defined over
$X^{E^{\times }}$
is defined over
![]() $E^{\text{ab}}$
, the maximal abelian extension of
$E^{\text{ab}}$
, the maximal abelian extension of
![]() $E$
. We fix one such CM point
$E$
. We fix one such CM point
![]() $P$
. Let
$P$
. Let
![]() $L(\unicode[STIX]{x1D712})$
be a field extension of
$L(\unicode[STIX]{x1D712})$
be a field extension of
![]() $M$
and let
$M$
and let
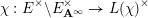 $$\begin{eqnarray}\unicode[STIX]{x1D712}:E^{\times }\backslash E_{\boldsymbol{ A}^{\infty }}^{\times }\rightarrow L(\unicode[STIX]{x1D712})^{\times }\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}:E^{\times }\backslash E_{\boldsymbol{ A}^{\infty }}^{\times }\rightarrow L(\unicode[STIX]{x1D712})^{\times }\end{eqnarray}$$
be a finite-order Hecke character such that
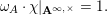 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{A}\cdot \unicode[STIX]{x1D712}|_{\mathbf{A}^{\infty ,\times }}=1.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{A}\cdot \unicode[STIX]{x1D712}|_{\mathbf{A}^{\infty ,\times }}=1.\end{eqnarray}$$
We can view
![]() $\unicode[STIX]{x1D712}$
as a character of
$\unicode[STIX]{x1D712}$
as a character of
 $\mathscr{G}_{E}:=\operatorname{Gal}(\overline{E}/E)$
via the reciprocity map of class field theory (normalised, in this work, by sending uniformisers to geometric Frobenii). For each
$\mathscr{G}_{E}:=\operatorname{Gal}(\overline{E}/E)$
via the reciprocity map of class field theory (normalised, in this work, by sending uniformisers to geometric Frobenii). For each
![]() $f\in \unicode[STIX]{x1D70B}_{A}$
, we then have a Heegner point
$f\in \unicode[STIX]{x1D70B}_{A}$
, we then have a Heegner point
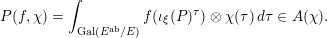 $$\begin{eqnarray}P(f,\unicode[STIX]{x1D712})=\int _{\operatorname{ Gal}(E^{\text{ab}}/E)}f(\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D709}}(P)^{\unicode[STIX]{x1D70F}})\otimes \unicode[STIX]{x1D712}(\unicode[STIX]{x1D70F})\,d\unicode[STIX]{x1D70F}\in A(\unicode[STIX]{x1D712}).\end{eqnarray}$$
$$\begin{eqnarray}P(f,\unicode[STIX]{x1D712})=\int _{\operatorname{ Gal}(E^{\text{ab}}/E)}f(\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D709}}(P)^{\unicode[STIX]{x1D70F}})\otimes \unicode[STIX]{x1D712}(\unicode[STIX]{x1D70F})\,d\unicode[STIX]{x1D70F}\in A(\unicode[STIX]{x1D712}).\end{eqnarray}$$
Here the integration uses the Haar measure of total volume
![]() $1$
, and
$1$
, and
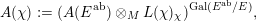 $$\begin{eqnarray}A(\unicode[STIX]{x1D712}):=(A(E^{\text{ab}})\otimes _{M}L(\unicode[STIX]{x1D712})_{\unicode[STIX]{x1D712}})^{\operatorname{Gal}(E^{\text{ab}}/E)},\end{eqnarray}$$
$$\begin{eqnarray}A(\unicode[STIX]{x1D712}):=(A(E^{\text{ab}})\otimes _{M}L(\unicode[STIX]{x1D712})_{\unicode[STIX]{x1D712}})^{\operatorname{Gal}(E^{\text{ab}}/E)},\end{eqnarray}$$
where
![]() $L(\unicode[STIX]{x1D712})_{\unicode[STIX]{x1D712}}$
denotes the one-dimensional Galois module
$L(\unicode[STIX]{x1D712})_{\unicode[STIX]{x1D712}}$
denotes the one-dimensional Galois module
![]() $L(\unicode[STIX]{x1D712})$
with action given by
$L(\unicode[STIX]{x1D712})$
with action given by
![]() $\unicode[STIX]{x1D712}$
. The functional
$\unicode[STIX]{x1D712}$
. The functional
 $f\mapsto P(f,\unicode[STIX]{x1D712})$
defines an element of
$f\mapsto P(f,\unicode[STIX]{x1D712})$
defines an element of
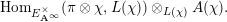 $$\begin{eqnarray}\operatorname{Hom}_{E_{\mathbf{A}^{\infty }}^{\times }}(\unicode[STIX]{x1D70B}\otimes \unicode[STIX]{x1D712},L(\unicode[STIX]{x1D712}))\otimes _{L(\unicode[STIX]{x1D712})}A(\unicode[STIX]{x1D712}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{E_{\mathbf{A}^{\infty }}^{\times }}(\unicode[STIX]{x1D70B}\otimes \unicode[STIX]{x1D712},L(\unicode[STIX]{x1D712}))\otimes _{L(\unicode[STIX]{x1D712})}A(\unicode[STIX]{x1D712}).\end{eqnarray}$$
A foundational local result of Tunnell and Saito [Reference TunnellTun83, Reference SaitoSai93] asserts that, for any irreducible representation
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $\mathbf{B}^{\times }$
, the
$\mathbf{B}^{\times }$
, the
![]() $L(\unicode[STIX]{x1D712})$
-dimension of
$L(\unicode[STIX]{x1D712})$
-dimension of
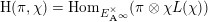 $$\begin{eqnarray}\text{H}(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D712})=\operatorname{Hom}_{E_{\mathbf{A}^{\infty }}^{\times }}(\unicode[STIX]{x1D70B}\otimes \unicode[STIX]{x1D712}L(\unicode[STIX]{x1D712}))\end{eqnarray}$$
$$\begin{eqnarray}\text{H}(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D712})=\operatorname{Hom}_{E_{\mathbf{A}^{\infty }}^{\times }}(\unicode[STIX]{x1D70B}\otimes \unicode[STIX]{x1D712}L(\unicode[STIX]{x1D712}))\end{eqnarray}$$
is either zero or one. It is one exactly when, for all places
![]() $v$
of
$v$
of
![]() $F$
, the local condition
$F$
, the local condition
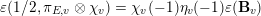 $$\begin{eqnarray}\unicode[STIX]{x1D700}(1/2,\unicode[STIX]{x1D70B}_{E,v}\otimes \unicode[STIX]{x1D712}_{v})=\unicode[STIX]{x1D712}_{v}(-1)\unicode[STIX]{x1D702}_{v}(-1)\unicode[STIX]{x1D700}(\mathbf{B}_{v})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D700}(1/2,\unicode[STIX]{x1D70B}_{E,v}\otimes \unicode[STIX]{x1D712}_{v})=\unicode[STIX]{x1D712}_{v}(-1)\unicode[STIX]{x1D702}_{v}(-1)\unicode[STIX]{x1D700}(\mathbf{B}_{v})\end{eqnarray}$$
holds, where
![]() $\unicode[STIX]{x1D70B}_{E}$
is the base-change of
$\unicode[STIX]{x1D70B}_{E}$
is the base-change of
![]() $\unicode[STIX]{x1D70B}$
to
$\unicode[STIX]{x1D70B}$
to
![]() $E$
,
$E$
,
 $\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{E/F}$
is the quadratic character of
$\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{E/F}$
is the quadratic character of
![]() $\mathbf{A}^{\times }$
associated to
$\mathbf{A}^{\times }$
associated to
![]() $E$
, and
$E$
, and
 $\unicode[STIX]{x1D700}(\mathbf{B}_{v})=+1$
if
$\unicode[STIX]{x1D700}(\mathbf{B}_{v})=+1$
if
![]() $\mathbf{B}_{v}$
is split and
$\mathbf{B}_{v}$
is split and
![]() $-1$
if
$-1$
if
![]() $\mathbf{B}_{v}$
is ramified. In this case, denoting by
$\mathbf{B}_{v}$
is ramified. In this case, denoting by
![]() $\unicode[STIX]{x1D70B}^{\vee }$
the
$\unicode[STIX]{x1D70B}^{\vee }$
the
![]() $M$
-contragredient representation, there is an explicit generator
$M$
-contragredient representation, there is an explicit generator
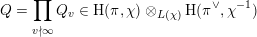 $$\begin{eqnarray}Q=\mathop{\prod }_{v\nmid \infty }Q_{v}\in \text{H}(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D712})\otimes _{L(\unicode[STIX]{x1D712})}\text{H}(\unicode[STIX]{x1D70B}^{\vee },\unicode[STIX]{x1D712}^{-1})\end{eqnarray}$$
$$\begin{eqnarray}Q=\mathop{\prod }_{v\nmid \infty }Q_{v}\in \text{H}(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D712})\otimes _{L(\unicode[STIX]{x1D712})}\text{H}(\unicode[STIX]{x1D70B}^{\vee },\unicode[STIX]{x1D712}^{-1})\end{eqnarray}$$
defined by integration of local matrix coefficients
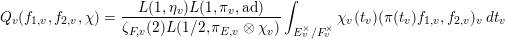 $$\begin{eqnarray}Q_{v}(f_{1,v},f_{2,v},\unicode[STIX]{x1D712})=\frac{L(1,\unicode[STIX]{x1D702}_{v})L(1,\unicode[STIX]{x1D70B}_{v},\operatorname{ad})}{\unicode[STIX]{x1D701}_{F,v}(2)L(1/2,\unicode[STIX]{x1D70B}_{E,v}\otimes \unicode[STIX]{x1D712}_{v})}\int _{E_{v}^{\times }/F_{v}^{\times }}\unicode[STIX]{x1D712}_{v}(t_{v})(\unicode[STIX]{x1D70B}(t_{v})f_{1,v},f_{2,v})_{v}\,dt_{v}\end{eqnarray}$$
$$\begin{eqnarray}Q_{v}(f_{1,v},f_{2,v},\unicode[STIX]{x1D712})=\frac{L(1,\unicode[STIX]{x1D702}_{v})L(1,\unicode[STIX]{x1D70B}_{v},\operatorname{ad})}{\unicode[STIX]{x1D701}_{F,v}(2)L(1/2,\unicode[STIX]{x1D70B}_{E,v}\otimes \unicode[STIX]{x1D712}_{v})}\int _{E_{v}^{\times }/F_{v}^{\times }}\unicode[STIX]{x1D712}_{v}(t_{v})(\unicode[STIX]{x1D70B}(t_{v})f_{1,v},f_{2,v})_{v}\,dt_{v}\end{eqnarray}$$
for a decomposition
 $(\cdot ,\cdot )=\bigotimes _{v}(\cdot ,\cdot )_{v}$
of the pairing
$(\cdot ,\cdot )=\bigotimes _{v}(\cdot ,\cdot )_{v}$
of the pairing
 $\unicode[STIX]{x1D70B}\otimes _{M}\unicode[STIX]{x1D70B}^{\vee }\rightarrow M$
, and Haar measures
$\unicode[STIX]{x1D70B}\otimes _{M}\unicode[STIX]{x1D70B}^{\vee }\rightarrow M$
, and Haar measures
![]() $dt_{v}$
assigning to
$dt_{v}$
assigning to
 $\mathscr{O}_{E,v}^{\times }/\mathscr{O}_{F_{v}}^{\times }$
the volume
$\mathscr{O}_{E,v}^{\times }/\mathscr{O}_{F_{v}}^{\times }$
the volume
![]() $1$
if
$1$
if
![]() $v$
is unramified in
$v$
is unramified in
![]() $E$
and
$E$
and
![]() $2$
if
$2$
if
![]() $v$
ramifies in
$v$
ramifies in
![]() $E$
. The normalisation is such that given
$E$
. The normalisation is such that given
![]() $f_{1}$
,
$f_{1}$
,
![]() $f_{2}$
, all but finitely many terms in the product are equal to
$f_{2}$
, all but finitely many terms in the product are equal to
![]() $1$
. The pairings
$1$
. The pairings
![]() $Q_{v}$
in fact depend on the choice of decomposition, which in general needs an extension of scalars; the global pairing is defined over
$Q_{v}$
in fact depend on the choice of decomposition, which in general needs an extension of scalars; the global pairing is defined over
![]() $M$
and independent of choices.
$M$
and independent of choices.
Note that the local root numbers are unchanged if one replaces
![]() $\unicode[STIX]{x1D70B}$
by its Jacquet–Langlands transfer to another quaternion algebra, and that when
$\unicode[STIX]{x1D70B}$
by its Jacquet–Langlands transfer to another quaternion algebra, and that when
![]() $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{A}$
they equal the local root numbers
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{A}$
they equal the local root numbers
 $\unicode[STIX]{x1D700}(A_{E,v},\unicode[STIX]{x1D712}_{v})$
of the motive
$\unicode[STIX]{x1D700}(A_{E,v},\unicode[STIX]{x1D712}_{v})$
of the motive
 $H_{1}(A\times _{\operatorname{Spec}F}\operatorname{Spec}E)\otimes _{M}\unicode[STIX]{x1D712}$
[Reference GrossGro91]. In this way one can view the local conditions
$H_{1}(A\times _{\operatorname{Spec}F}\operatorname{Spec}E)\otimes _{M}\unicode[STIX]{x1D712}$
[Reference GrossGro91]. In this way one can view the local conditions
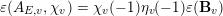 $$\begin{eqnarray}\unicode[STIX]{x1D700}(A_{E,v},\unicode[STIX]{x1D712}_{v})=\unicode[STIX]{x1D712}_{v}(-1)\unicode[STIX]{x1D702}_{v}(-1)\unicode[STIX]{x1D700}(\mathbf{B}_{v})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D700}(A_{E,v},\unicode[STIX]{x1D712}_{v})=\unicode[STIX]{x1D712}_{v}(-1)\unicode[STIX]{x1D702}_{v}(-1)\unicode[STIX]{x1D700}(\mathbf{B}_{v})\end{eqnarray}$$
as determining a unique totally definite quaternion algebra
 $\mathbf{B}\supset E_{\mathbf{A}}$
over
$\mathbf{B}\supset E_{\mathbf{A}}$
over
![]() $\mathbf{A}$
, which is incoherent precisely when the global root number
$\mathbf{A}$
, which is incoherent precisely when the global root number
 $\unicode[STIX]{x1D700}(A_{E},\unicode[STIX]{x1D712})=-1$
. In this case,
$\unicode[STIX]{x1D700}(A_{E},\unicode[STIX]{x1D712})=-1$
. In this case,
![]() $A$
is parametrised by
$A$
is parametrised by
![]() $X(\mathbf{B})$
in the sense described above if and only if
$X(\mathbf{B})$
in the sense described above if and only if
![]() $A$
is modular in the sense that the Galois representation afforded by its Tate module is attached to a cuspidal automorphic representation of
$A$
is modular in the sense that the Galois representation afforded by its Tate module is attached to a cuspidal automorphic representation of
 $\mathbf{GL}_{2}(\mathbf{A}_{F})$
of parallel weight
$\mathbf{GL}_{2}(\mathbf{A}_{F})$
of parallel weight
![]() $2$
. We assume this to be the case.
$2$
. We assume this to be the case.
Gross–Zagier formulas. There is a natural identification
 $\unicode[STIX]{x1D70B}^{\vee }=\unicode[STIX]{x1D70B}_{A^{\vee }}$
, where
$\unicode[STIX]{x1D70B}^{\vee }=\unicode[STIX]{x1D70B}_{A^{\vee }}$
, where
![]() $A^{\vee }$
is the dual abelian variety (explicitly, this is induced by the perfect
$A^{\vee }$
is the dual abelian variety (explicitly, this is induced by the perfect
 $M=\operatorname{End}^{0}(A)$
-valued pairing
$M=\operatorname{End}^{0}(A)$
-valued pairing
 $f_{1,U}\otimes f_{2,U}\mapsto \operatorname{vol}(X_{U})^{-1}f_{1,U}\circ f_{2}^{\vee }$
using the canonical autoduality of
$f_{1,U}\otimes f_{2,U}\mapsto \operatorname{vol}(X_{U})^{-1}f_{1,U}\circ f_{2}^{\vee }$
using the canonical autoduality of
![]() $J_{U}$
for any sufficiently small
$J_{U}$
for any sufficiently small
![]() $U$
; the normalising factor
$U$
; the normalising factor
 $\operatorname{vol}(X_{U})\in \mathbf{Q}^{\times }$
is the hyperbolic volume of
$\operatorname{vol}(X_{U})\in \mathbf{Q}^{\times }$
is the hyperbolic volume of
 $X_{U}(\mathbf{C}_{\unicode[STIX]{x1D70F}})$
for any
$X_{U}(\mathbf{C}_{\unicode[STIX]{x1D70F}})$
for any
 $\unicode[STIX]{x1D70F}:F{\hookrightarrow}\mathbf{C}$
; see [Reference Yuan, Zhang and ZhangYZZ12, §1.2.2]). Similarly to the above, we have a Heegner point functional
$\unicode[STIX]{x1D70F}:F{\hookrightarrow}\mathbf{C}$
; see [Reference Yuan, Zhang and ZhangYZZ12, §1.2.2]). Similarly to the above, we have a Heegner point functional
 $P^{\vee }(\cdot ,\unicode[STIX]{x1D712}^{-1})\in \text{H}(\unicode[STIX]{x1D70B}^{\vee },\unicode[STIX]{x1D712}^{-1})\otimes _{L}A^{\vee }(\unicode[STIX]{x1D712}^{-1})$
. Then the multiplicity-one result of Tunnell and Saito implies that for each bilinear pairing
$P^{\vee }(\cdot ,\unicode[STIX]{x1D712}^{-1})\in \text{H}(\unicode[STIX]{x1D70B}^{\vee },\unicode[STIX]{x1D712}^{-1})\otimes _{L}A^{\vee }(\unicode[STIX]{x1D712}^{-1})$
. Then the multiplicity-one result of Tunnell and Saito implies that for each bilinear pairing
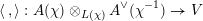 $$\begin{eqnarray}\langle \,,\rangle :A(\unicode[STIX]{x1D712})\otimes _{L(\unicode[STIX]{x1D712})}A^{\vee }(\unicode[STIX]{x1D712}^{-1})\rightarrow V\end{eqnarray}$$
$$\begin{eqnarray}\langle \,,\rangle :A(\unicode[STIX]{x1D712})\otimes _{L(\unicode[STIX]{x1D712})}A^{\vee }(\unicode[STIX]{x1D712}^{-1})\rightarrow V\end{eqnarray}$$
with values in an
![]() $L(\unicode[STIX]{x1D712})$
-vector space
$L(\unicode[STIX]{x1D712})$
-vector space
![]() $V$
, there is an element
$V$
, there is an element
![]() $\mathscr{L}\in V$
such that
$\mathscr{L}\in V$
such that
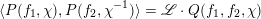 $$\begin{eqnarray}\langle P(f_{1},\unicode[STIX]{x1D712}),P(f_{2},\unicode[STIX]{x1D712}^{-1})\rangle =\mathscr{L}\cdot Q(f_{1},f_{2},\unicode[STIX]{x1D712})\end{eqnarray}$$
$$\begin{eqnarray}\langle P(f_{1},\unicode[STIX]{x1D712}),P(f_{2},\unicode[STIX]{x1D712}^{-1})\rangle =\mathscr{L}\cdot Q(f_{1},f_{2},\unicode[STIX]{x1D712})\end{eqnarray}$$
for all
![]() $f_{1}\in \unicode[STIX]{x1D70B}$
,
$f_{1}\in \unicode[STIX]{x1D70B}$
,
 $f_{2}\in \unicode[STIX]{x1D70B}^{\vee }$
.
$f_{2}\in \unicode[STIX]{x1D70B}^{\vee }$
.
In this framework, we may call the ‘Gross–Zagier formula’ a formula for
![]() $\mathscr{L}$
in terms of
$\mathscr{L}$
in terms of
![]() $L$
-functions. When
$L$
-functions. When
![]() $\langle \,,\rangle$
is the Néron–Tate height pairing valued in
$\langle \,,\rangle$
is the Néron–Tate height pairing valued in
 $\mathbf{C}\stackrel{\unicode[STIX]{x1D704}}{{\hookleftarrow}}M$
for an archimedean place
$\mathbf{C}\stackrel{\unicode[STIX]{x1D704}}{{\hookleftarrow}}M$
for an archimedean place
![]() $\unicode[STIX]{x1D704}$
, the generalisation by Yuan–Zhang–Zhang [Reference Yuan, Zhang and ZhangYZZ12] of the classical Gross–Zagier formula [Reference Gross and ZagierGZ86, Reference ZhangZha01a, Reference ZhangZha01b, Reference ZhangZha04] yields
$\unicode[STIX]{x1D704}$
, the generalisation by Yuan–Zhang–Zhang [Reference Yuan, Zhang and ZhangYZZ12] of the classical Gross–Zagier formula [Reference Gross and ZagierGZ86, Reference ZhangZha01a, Reference ZhangZha01b, Reference ZhangZha04] yields
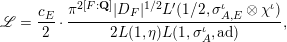 $$\begin{eqnarray}\mathscr{L}=\frac{c_{E}}{2}\cdot \frac{\unicode[STIX]{x1D70B}^{2[F:\mathbf{Q}]}|D_{F}|^{1/2}L^{\prime }(1/2,\unicode[STIX]{x1D70E}_{A,E}^{\unicode[STIX]{x1D704}}\otimes \unicode[STIX]{x1D712}^{\unicode[STIX]{x1D704}})}{2L(1,\unicode[STIX]{x1D702})L(1,\unicode[STIX]{x1D70E}_{A}^{\unicode[STIX]{x1D704}},\operatorname{ad})},\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{L}=\frac{c_{E}}{2}\cdot \frac{\unicode[STIX]{x1D70B}^{2[F:\mathbf{Q}]}|D_{F}|^{1/2}L^{\prime }(1/2,\unicode[STIX]{x1D70E}_{A,E}^{\unicode[STIX]{x1D704}}\otimes \unicode[STIX]{x1D712}^{\unicode[STIX]{x1D704}})}{2L(1,\unicode[STIX]{x1D702})L(1,\unicode[STIX]{x1D70E}_{A}^{\unicode[STIX]{x1D704}},\operatorname{ad})},\end{eqnarray}$$
where
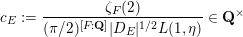 $$\begin{eqnarray}c_{E}:=\frac{\unicode[STIX]{x1D701}_{F}(2)}{(\unicode[STIX]{x1D70B}/2)^{[F:\mathbf{Q}]}|D_{E}|^{1/2}L(1,\unicode[STIX]{x1D702})}\in \mathbf{Q}^{\times }\end{eqnarray}$$
$$\begin{eqnarray}c_{E}:=\frac{\unicode[STIX]{x1D701}_{F}(2)}{(\unicode[STIX]{x1D70B}/2)^{[F:\mathbf{Q}]}|D_{E}|^{1/2}L(1,\unicode[STIX]{x1D702})}\in \mathbf{Q}^{\times }\end{eqnarray}$$
and, in the present Introduction,
![]() $L$
-functions are as usual Euler products over all the finite places.Footnote
2
(However in the main body of the paper we will embrace the convention of [Reference Yuan, Zhang and ZhangYZZ12] of including the archimedean factors.) The most important factor is the central derivative of the
$L$
-functions are as usual Euler products over all the finite places.Footnote
2
(However in the main body of the paper we will embrace the convention of [Reference Yuan, Zhang and ZhangYZZ12] of including the archimedean factors.) The most important factor is the central derivative of the
![]() $L$
-function
$L$
-function
 $L(s,\unicode[STIX]{x1D70E}_{A,E}^{\unicode[STIX]{x1D704}}\otimes \unicode[STIX]{x1D712})$
.
$L(s,\unicode[STIX]{x1D70E}_{A,E}^{\unicode[STIX]{x1D704}}\otimes \unicode[STIX]{x1D712})$
.
When
![]() $\langle \,,\rangle$
is the product of the
$\langle \,,\rangle$
is the product of the
![]() $v$
-adic logarithms on
$v$
-adic logarithms on
![]() $A(F_{v})$
and
$A(F_{v})$
and
![]() $A^{\vee }(F_{v})$
, for a prime
$A^{\vee }(F_{v})$
, for a prime
![]() $v$
of
$v$
of
![]() $F$
which splits in
$F$
which splits in
![]() $E$
, the
$E$
, the
![]() $v$
-adic Waldspurger formula of Liu–Zhang–Zhang [Reference Liu, Zhang and ZhangLZZ15] (generalising [Reference Bertolini, Darmon and PrasannaBDP13]) identifies
$v$
-adic Waldspurger formula of Liu–Zhang–Zhang [Reference Liu, Zhang and ZhangLZZ15] (generalising [Reference Bertolini, Darmon and PrasannaBDP13]) identifies
![]() $\mathscr{L}$
with the special value of a
$\mathscr{L}$
with the special value of a
![]() $v$
-adic Rankin–Selberg
$v$
-adic Rankin–Selberg
![]() $L$
-function obtained by interpolating the values
$L$
-function obtained by interpolating the values
 $L(1/2,\unicode[STIX]{x1D70E}_{A,E}\otimes \unicode[STIX]{x1D712}^{\prime \prime })$
at anticyclotomic Hecke characters
$L(1/2,\unicode[STIX]{x1D70E}_{A,E}\otimes \unicode[STIX]{x1D712}^{\prime \prime })$
at anticyclotomic Hecke characters
![]() $\unicode[STIX]{x1D712}^{\prime \prime }$
of
$\unicode[STIX]{x1D712}^{\prime \prime }$
of
![]() $E$
of higher weight at
$E$
of higher weight at
![]() $v$
(in particular, the central value for the given character
$v$
(in particular, the central value for the given character
![]() $\unicode[STIX]{x1D712}$
lies outside the range of interpolation).
$\unicode[STIX]{x1D712}$
lies outside the range of interpolation).
The object of this paper is a formula for
![]() $\mathscr{L}$
when
$\mathscr{L}$
when
![]() $\langle \,,\rangle$
is a
$\langle \,,\rangle$
is a
![]() $p$
-adic height pairing. In this case
$p$
-adic height pairing. In this case
![]() $\mathscr{L}$
is given by the central derivative of a
$\mathscr{L}$
is given by the central derivative of a
![]() $p$
-adic Rankin–Selberg
$p$
-adic Rankin–Selberg
![]() $L$
-function obtained by interpolation of
$L$
-function obtained by interpolation of
 $L(1/2,\unicode[STIX]{x1D70E}_{A,E},\unicode[STIX]{x1D712}^{\prime })$
at finite-order Hecke characters of
$L(1/2,\unicode[STIX]{x1D70E}_{A,E},\unicode[STIX]{x1D712}^{\prime })$
at finite-order Hecke characters of
![]() $E$
, precisely up to the factor
$E$
, precisely up to the factor
![]() $c_{E}/2$
of (1.1.3). We describe in more detail the objects involved.
$c_{E}/2$
of (1.1.3). We describe in more detail the objects involved.
1.2 The
 $p$
-adic
$p$
-adic
 $L$
-function
$L$
-function
We construct the relevant
![]() $p$
-adic
$p$
-adic
![]() $L$
-function as a function on a space of
$L$
-function as a function on a space of
![]() $p$
-adic characters (which can be regarded as an abelian eigenvariety), characterised by an interpolation property at locally constant characters. It further depends on a choice of local models at
$p$
-adic characters (which can be regarded as an abelian eigenvariety), characterised by an interpolation property at locally constant characters. It further depends on a choice of local models at
![]() $p$
(in the present case, additive characters); this point is relevant for the study of fields of rationality and does not seem to have received much attention in the literature on
$p$
(in the present case, additive characters); this point is relevant for the study of fields of rationality and does not seem to have received much attention in the literature on
![]() $p$
-adic
$p$
-adic
![]() $L$
-functions.
$L$
-functions.
Definition 1.2.1. An
![]() $M$
-rational
Footnote
3
cuspidal automorphic representation of
$M$
-rational
Footnote
3
cuspidal automorphic representation of
![]() $\mathbf{GL}_{2}$
of weight
$\mathbf{GL}_{2}$
of weight
![]() $2$
is a representation
$2$
is a representation
![]() $\unicode[STIX]{x1D70E}^{\infty }$
of
$\unicode[STIX]{x1D70E}^{\infty }$
of
 $\mathbf{GL}_{2}(\mathbf{A}^{\infty })$
on a rational vector space
$\mathbf{GL}_{2}(\mathbf{A}^{\infty })$
on a rational vector space
![]() $V_{\unicode[STIX]{x1D70E}^{\infty }}$
with
$V_{\unicode[STIX]{x1D70E}^{\infty }}$
with
 $\operatorname{End}_{\mathbf{GL}_{2}(\mathbf{A}^{\infty })}\unicode[STIX]{x1D70E}^{\infty }=M$
(then
$\operatorname{End}_{\mathbf{GL}_{2}(\mathbf{A}^{\infty })}\unicode[STIX]{x1D70E}^{\infty }=M$
(then
![]() $V_{\unicode[STIX]{x1D70E}^{\infty }}$
acquires the structure of an
$V_{\unicode[STIX]{x1D70E}^{\infty }}$
acquires the structure of an
![]() $M$
-vector space), such that
$M$
-vector space), such that
 $\unicode[STIX]{x1D70E}^{\infty }\otimes _{\mathbf{Q}}\unicode[STIX]{x1D70E}_{\infty }^{(2)}=\bigoplus _{\unicode[STIX]{x1D704}:M{\hookrightarrow}\mathbf{C}}\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D704}}$
is a direct sum of irreducible cuspidal automorphic representations; here
$\unicode[STIX]{x1D70E}^{\infty }\otimes _{\mathbf{Q}}\unicode[STIX]{x1D70E}_{\infty }^{(2)}=\bigoplus _{\unicode[STIX]{x1D704}:M{\hookrightarrow}\mathbf{C}}\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D704}}$
is a direct sum of irreducible cuspidal automorphic representations; here
![]() $\unicode[STIX]{x1D70E}_{\infty }^{(2)}$
, a complex representation of
$\unicode[STIX]{x1D70E}_{\infty }^{(2)}$
, a complex representation of
 $\mathbf{GL}_{2}(F_{\infty })\cong \mathbf{GL}_{2}(\mathbf{R})^{[F:\mathbf{Q}]}$
, is the product of a discrete series of parallel weight
$\mathbf{GL}_{2}(F_{\infty })\cong \mathbf{GL}_{2}(\mathbf{R})^{[F:\mathbf{Q}]}$
, is the product of a discrete series of parallel weight
![]() $2$
and a trivial central character.
$2$
and a trivial central character.
We fix from now on a rational prime
![]() $p$
.
$p$
.
Definition 1.2.2. Let
![]() $F_{v}$
and
$F_{v}$
and
![]() $L$
be finite extensions of
$L$
be finite extensions of
![]() $\mathbf{Q}_{p}$
, let
$\mathbf{Q}_{p}$
, let
![]() $\unicode[STIX]{x1D70E}_{v}$
be a smooth irreducible representation of
$\unicode[STIX]{x1D70E}_{v}$
be a smooth irreducible representation of
 $\mathbf{GL}_{2}(F_{v})$
on an
$\mathbf{GL}_{2}(F_{v})$
on an
![]() $L$
-vector space, and let
$L$
-vector space, and let
 $\unicode[STIX]{x1D6FC}_{v}:F_{v}^{\times }\rightarrow \mathscr{O}_{L}^{\times }$
be a smooth character valued in the units of
$\unicode[STIX]{x1D6FC}_{v}:F_{v}^{\times }\rightarrow \mathscr{O}_{L}^{\times }$
be a smooth character valued in the units of
![]() $L$
. We say that
$L$
. We say that
![]() $\unicode[STIX]{x1D70E}_{v}$
is nearly ordinary for weight
$\unicode[STIX]{x1D70E}_{v}$
is nearly ordinary for weight
![]() $2$
with unit character
$2$
with unit character
![]() $\unicode[STIX]{x1D6FC}_{v}$
if
$\unicode[STIX]{x1D6FC}_{v}$
if
![]() $\unicode[STIX]{x1D70E}_{v}$
is an infinite-dimensional subrepresentation of the un-normalised principal series
$\unicode[STIX]{x1D70E}_{v}$
is an infinite-dimensional subrepresentation of the un-normalised principal series
 $\operatorname{Ind}(|\cdot |_{v}\unicode[STIX]{x1D6FC}_{v},\unicode[STIX]{x1D6FD}_{v})$
for some other character
$\operatorname{Ind}(|\cdot |_{v}\unicode[STIX]{x1D6FC}_{v},\unicode[STIX]{x1D6FD}_{v})$
for some other character
 $\unicode[STIX]{x1D6FD}_{v}:F_{v}^{\times }\rightarrow L^{\times }$
. (Concretely,
$\unicode[STIX]{x1D6FD}_{v}:F_{v}^{\times }\rightarrow L^{\times }$
. (Concretely,
![]() $\unicode[STIX]{x1D70E}_{v}$
is then either an irreducible principal series or special of the form
$\unicode[STIX]{x1D70E}_{v}$
is then either an irreducible principal series or special of the form
 $\operatorname{St}(\unicode[STIX]{x1D6FC}_{v}):=\operatorname{St}\otimes (\unicode[STIX]{x1D6FC}_{v}\circ \det )$
, where
$\operatorname{St}(\unicode[STIX]{x1D6FC}_{v}):=\operatorname{St}\otimes (\unicode[STIX]{x1D6FC}_{v}\circ \det )$
, where
![]() $\operatorname{St}$
is the Steinberg representation.)
$\operatorname{St}$
is the Steinberg representation.)
If
![]() $M$
is a number field,
$M$
is a number field,
![]() $\mathfrak{p}$
is a prime of
$\mathfrak{p}$
is a prime of
![]() $M$
above
$M$
above
![]() $p$
, and
$p$
, and
![]() $\unicode[STIX]{x1D70E}_{v}$
is a representation of
$\unicode[STIX]{x1D70E}_{v}$
is a representation of
 $\mathbf{GL}_{2}(F_{v})$
on an
$\mathbf{GL}_{2}(F_{v})$
on an
![]() $M$
-vector space, we say that
$M$
-vector space, we say that
![]() $\unicode[STIX]{x1D70E}_{v}$
is nearly
$\unicode[STIX]{x1D70E}_{v}$
is nearly
![]() $\mathfrak{p}$
-ordinary for weight
$\mathfrak{p}$
-ordinary for weight
![]() $2$
if there is a finite extension
$2$
if there is a finite extension
![]() $L$
of
$L$
of
![]() $M_{\mathfrak{p}}$
such that
$M_{\mathfrak{p}}$
such that
 $\unicode[STIX]{x1D70E}_{v}\otimes _{M}L$
is nearly
$\unicode[STIX]{x1D70E}_{v}\otimes _{M}L$
is nearly
![]() $\mathfrak{p}$
-ordinary for weight
$\mathfrak{p}$
-ordinary for weight
![]() $2$
.
$2$
.
In the rest of this paper we omit the clause ‘for weight
![]() $2$
’.Footnote
4
$2$
’.Footnote
4
Fix an
![]() $M$
-rational cuspidal automorphic representation
$M$
-rational cuspidal automorphic representation
![]() $\unicode[STIX]{x1D70E}^{\infty }$
of
$\unicode[STIX]{x1D70E}^{\infty }$
of
 $\mathbf{GL}_{2}(\mathbf{A}^{\infty })$
of weight
$\mathbf{GL}_{2}(\mathbf{A}^{\infty })$
of weight
![]() $2$
; if there is no risk of confusion we will lighten the notation and write
$2$
; if there is no risk of confusion we will lighten the notation and write
![]() $\unicode[STIX]{x1D70E}$
instead of
$\unicode[STIX]{x1D70E}$
instead of
![]() $\unicode[STIX]{x1D70E}^{\infty }$
. Let
$\unicode[STIX]{x1D70E}^{\infty }$
. Let
 $\unicode[STIX]{x1D714}:F^{\times }\backslash \mathbf{A}^{\times }\rightarrow M^{\times }$
be the central character of
$\unicode[STIX]{x1D714}:F^{\times }\backslash \mathbf{A}^{\times }\rightarrow M^{\times }$
be the central character of
![]() $\unicode[STIX]{x1D70E}$
, which is necessarily of finite order.
$\unicode[STIX]{x1D70E}$
, which is necessarily of finite order.
Fix moreover a prime
![]() $\mathfrak{p}$
of
$\mathfrak{p}$
of
![]() $M$
above
$M$
above
![]() $p$
and assume that for all
$p$
and assume that for all
![]() $v|p$
the local components
$v|p$
the local components
![]() $\unicode[STIX]{x1D70E}_{v}$
of
$\unicode[STIX]{x1D70E}_{v}$
of
![]() $\unicode[STIX]{x1D70E}$
are nearly
$\unicode[STIX]{x1D70E}$
are nearly
![]() $\mathfrak{p}$
-ordinary with respective characters
$\mathfrak{p}$
-ordinary with respective characters
![]() $\unicode[STIX]{x1D6FC}_{v}$
; we write
$\unicode[STIX]{x1D6FC}_{v}$
; we write
![]() $\unicode[STIX]{x1D6FC}$
to denote the collection
$\unicode[STIX]{x1D6FC}$
to denote the collection
![]() $(\unicode[STIX]{x1D6FC}_{v})_{v|p}$
. We replace
$(\unicode[STIX]{x1D6FC}_{v})_{v|p}$
. We replace
![]() $L$
by its subfield
$L$
by its subfield
![]() $M_{\mathfrak{p}}(\unicode[STIX]{x1D6FC})$
generated by the values of all the
$M_{\mathfrak{p}}(\unicode[STIX]{x1D6FC})$
generated by the values of all the
![]() $\unicode[STIX]{x1D6FC}_{v}$
, and we similarly let
$\unicode[STIX]{x1D6FC}_{v}$
, and we similarly let
 $M(\unicode[STIX]{x1D6FC})\subset L$
be the finite extension of
$M(\unicode[STIX]{x1D6FC})\subset L$
be the finite extension of
![]() $M$
generated by the values of all the
$M$
generated by the values of all the
![]() $\unicode[STIX]{x1D6FC}_{v}$
.
$\unicode[STIX]{x1D6FC}_{v}$
.
Spaces of
![]() $p$
-adic and locally constant characters. Fix throughout this work an arbitrary compact open subgroup
$p$
-adic and locally constant characters. Fix throughout this work an arbitrary compact open subgroup
 $V^{p}\subset \widehat{\mathscr{O}}_{E}^{p,\times }:=\prod _{w\nmid p}\mathscr{O}_{E,w}^{\times }$
. Let
$V^{p}\subset \widehat{\mathscr{O}}_{E}^{p,\times }:=\prod _{w\nmid p}\mathscr{O}_{E,w}^{\times }$
. Let
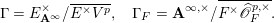 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}=E_{\mathbf{A}^{\infty }}^{\times }/\overline{E^{\times }V^{p}},\quad \unicode[STIX]{x1D6E4}_{F}=\mathbf{A}^{\infty ,\times }/\overline{F^{\times }\widehat{\mathscr{O}}_{F}^{p,\times }}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}=E_{\mathbf{A}^{\infty }}^{\times }/\overline{E^{\times }V^{p}},\quad \unicode[STIX]{x1D6E4}_{F}=\mathbf{A}^{\infty ,\times }/\overline{F^{\times }\widehat{\mathscr{O}}_{F}^{p,\times }}.\end{eqnarray}$$
Then we have rigid spaces
 $\mathscr{Y}^{\prime }=\mathscr{Y}_{\unicode[STIX]{x1D714}}^{\prime }(V^{p})$
,
$\mathscr{Y}^{\prime }=\mathscr{Y}_{\unicode[STIX]{x1D714}}^{\prime }(V^{p})$
,
 $\mathscr{Y}=\mathscr{Y}_{\unicode[STIX]{x1D714}}(V^{p})$
,
$\mathscr{Y}=\mathscr{Y}_{\unicode[STIX]{x1D714}}(V^{p})$
,
![]() $\mathscr{Y}_{F}$
of respective dimensions
$\mathscr{Y}_{F}$
of respective dimensions
 $[F:\mathbf{Q}]+1+\unicode[STIX]{x1D6FF}$
,
$[F:\mathbf{Q}]+1+\unicode[STIX]{x1D6FF}$
,
![]() $[F:\mathbf{Q}]$
,
$[F:\mathbf{Q}]$
,
![]() $1+\unicode[STIX]{x1D6FF}$
(where
$1+\unicode[STIX]{x1D6FF}$
(where
![]() $\unicode[STIX]{x1D6FF}\geqslant 0$
is the Leopoldt defect of
$\unicode[STIX]{x1D6FF}\geqslant 0$
is the Leopoldt defect of
![]() $F$
, conjectured to be zero) representing the functors on
$F$
, conjectured to be zero) representing the functors on
![]() $L$
-affinoid algebras
$L$
-affinoid algebras
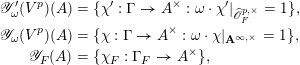 $$\begin{eqnarray}\displaystyle \mathscr{Y}_{\unicode[STIX]{x1D714}}^{\prime }(V^{p})(A) & = & \displaystyle \{\unicode[STIX]{x1D712}^{\prime }:\unicode[STIX]{x1D6E4}\rightarrow A^{\times }:\unicode[STIX]{x1D714}\cdot \unicode[STIX]{x1D712}^{\prime }|_{\widehat{\mathscr{O}}_{F}^{p,\times }}=1\},\nonumber\\ \displaystyle \mathscr{Y}_{\unicode[STIX]{x1D714}}(V^{p})(A) & = & \displaystyle \{\unicode[STIX]{x1D712}:\unicode[STIX]{x1D6E4}\rightarrow A^{\times }:\unicode[STIX]{x1D714}\cdot \unicode[STIX]{x1D712}|_{\mathbf{A}^{\infty ,\times }}=1\},\nonumber\\ \displaystyle \mathscr{Y}_{F}(A) & = & \displaystyle \{\unicode[STIX]{x1D712}_{F}:\unicode[STIX]{x1D6E4}_{F}\rightarrow A^{\times }\},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{Y}_{\unicode[STIX]{x1D714}}^{\prime }(V^{p})(A) & = & \displaystyle \{\unicode[STIX]{x1D712}^{\prime }:\unicode[STIX]{x1D6E4}\rightarrow A^{\times }:\unicode[STIX]{x1D714}\cdot \unicode[STIX]{x1D712}^{\prime }|_{\widehat{\mathscr{O}}_{F}^{p,\times }}=1\},\nonumber\\ \displaystyle \mathscr{Y}_{\unicode[STIX]{x1D714}}(V^{p})(A) & = & \displaystyle \{\unicode[STIX]{x1D712}:\unicode[STIX]{x1D6E4}\rightarrow A^{\times }:\unicode[STIX]{x1D714}\cdot \unicode[STIX]{x1D712}|_{\mathbf{A}^{\infty ,\times }}=1\},\nonumber\\ \displaystyle \mathscr{Y}_{F}(A) & = & \displaystyle \{\unicode[STIX]{x1D712}_{F}:\unicode[STIX]{x1D6E4}_{F}\rightarrow A^{\times }\},\nonumber\end{eqnarray}$$
where the sets on the right-hand sides are intended to consist of continuous homomorphisms. The inclusion
 $\mathscr{Y}\subset \mathscr{Y}^{\prime }$
sits in the Cartesian diagram
$\mathscr{Y}\subset \mathscr{Y}^{\prime }$
sits in the Cartesian diagram
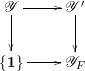
where the vertical maps are given by
 $\unicode[STIX]{x1D712}^{\prime }\mapsto \unicode[STIX]{x1D712}_{F}=\unicode[STIX]{x1D714}\cdot \unicode[STIX]{x1D712}^{\prime }|_{\mathbf{A}^{\infty ,\times }}$
. When
$\unicode[STIX]{x1D712}^{\prime }\mapsto \unicode[STIX]{x1D712}_{F}=\unicode[STIX]{x1D714}\cdot \unicode[STIX]{x1D712}^{\prime }|_{\mathbf{A}^{\infty ,\times }}$
. When
![]() $\unicode[STIX]{x1D714}=\mathbf{1}$
,
$\unicode[STIX]{x1D714}=\mathbf{1}$
,
![]() $\mathscr{Y}_{\mathbf{1}}$
is a group object (the ‘Cartier dual’ of
$\mathscr{Y}_{\mathbf{1}}$
is a group object (the ‘Cartier dual’ of
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}$
); in general,
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{F}$
); in general,
![]() $\mathscr{Y}_{\unicode[STIX]{x1D714}}$
is a principal homogeneous space for
$\mathscr{Y}_{\unicode[STIX]{x1D714}}$
is a principal homogeneous space for
![]() $\mathscr{Y}_{\mathbf{1}}$
under the action
$\mathscr{Y}_{\mathbf{1}}$
under the action
 $\unicode[STIX]{x1D712}_{0}\cdot \unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{0}\unicode[STIX]{x1D712}$
.
$\unicode[STIX]{x1D712}_{0}\cdot \unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{0}\unicode[STIX]{x1D712}$
.
Let
![]() $\boldsymbol{\unicode[STIX]{x1D707}}_{\mathbf{Q}}$
denote the ind-scheme over
$\boldsymbol{\unicode[STIX]{x1D707}}_{\mathbf{Q}}$
denote the ind-scheme over
![]() $\mathbf{Q}$
of all roots of unity and
$\mathbf{Q}$
of all roots of unity and
![]() $\boldsymbol{\unicode[STIX]{x1D707}}_{M}$
its base-change to
$\boldsymbol{\unicode[STIX]{x1D707}}_{M}$
its base-change to
![]() $M$
. Then there are ind-schemes
$M$
. Then there are ind-schemes
![]() $\mathscr{Y}^{\prime \,\text{l.c.}}$
,
$\mathscr{Y}^{\prime \,\text{l.c.}}$
,
![]() $\mathscr{Y}^{\text{l.c.}}$
,
$\mathscr{Y}^{\text{l.c.}}$
,
![]() $\mathscr{Y}_{F}^{\text{l.c.}}$
, ind-finite over
$\mathscr{Y}_{F}^{\text{l.c.}}$
, ind-finite over
![]() $M$
, representing the functors on
$M$
, representing the functors on
![]() $M$
-algebras
$M$
-algebras
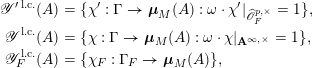 $$\begin{eqnarray}\displaystyle \mathscr{Y}^{\prime \,\text{l.c.}}(A) & = & \displaystyle \{\unicode[STIX]{x1D712}^{\prime }:\unicode[STIX]{x1D6E4}\rightarrow \boldsymbol{\unicode[STIX]{x1D707}}_{M}(A):\unicode[STIX]{x1D714}\cdot \unicode[STIX]{x1D712}^{\prime }|_{\widehat{\mathscr{O}}_{F}^{p,\times }}=1\},\nonumber\\ \displaystyle \mathscr{Y}^{\text{l.c.}}(A) & = & \displaystyle \{\unicode[STIX]{x1D712}:\unicode[STIX]{x1D6E4}\rightarrow \boldsymbol{\unicode[STIX]{x1D707}}_{M}(A):\unicode[STIX]{x1D714}\cdot \unicode[STIX]{x1D712}|_{\mathbf{A}^{\infty ,\times }}=1\},\nonumber\\ \displaystyle \mathscr{Y}_{F}^{\text{l.c.}}(A) & = & \displaystyle \{\unicode[STIX]{x1D712}_{F}:\unicode[STIX]{x1D6E4}_{F}\rightarrow \boldsymbol{\unicode[STIX]{x1D707}}_{M}(A)\},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{Y}^{\prime \,\text{l.c.}}(A) & = & \displaystyle \{\unicode[STIX]{x1D712}^{\prime }:\unicode[STIX]{x1D6E4}\rightarrow \boldsymbol{\unicode[STIX]{x1D707}}_{M}(A):\unicode[STIX]{x1D714}\cdot \unicode[STIX]{x1D712}^{\prime }|_{\widehat{\mathscr{O}}_{F}^{p,\times }}=1\},\nonumber\\ \displaystyle \mathscr{Y}^{\text{l.c.}}(A) & = & \displaystyle \{\unicode[STIX]{x1D712}:\unicode[STIX]{x1D6E4}\rightarrow \boldsymbol{\unicode[STIX]{x1D707}}_{M}(A):\unicode[STIX]{x1D714}\cdot \unicode[STIX]{x1D712}|_{\mathbf{A}^{\infty ,\times }}=1\},\nonumber\\ \displaystyle \mathscr{Y}_{F}^{\text{l.c.}}(A) & = & \displaystyle \{\unicode[STIX]{x1D712}_{F}:\unicode[STIX]{x1D6E4}_{F}\rightarrow \boldsymbol{\unicode[STIX]{x1D707}}_{M}(A)\},\nonumber\end{eqnarray}$$
where the sets on the right-hand sides are intended to consist of locally constant (equivalently, finite-order) characters.
Definition 1.2.3. Let
![]() $\mathscr{Y}^{?}$
be one of the above rigid spaces and
$\mathscr{Y}^{?}$
be one of the above rigid spaces and
 $\mathscr{Y}^{?,\text{l.c.},\text{an}}\subset \mathscr{Y}^{?}$
be the (ind-)rigid space which is the analytification of
$\mathscr{Y}^{?,\text{l.c.},\text{an}}\subset \mathscr{Y}^{?}$
be the (ind-)rigid space which is the analytification of
 $\mathscr{Y}_{L}^{?,\text{l.c.}}:=\mathscr{Y}^{?,\text{l.c.}}\times _{\operatorname{Spec}M}\operatorname{Spec}L$
. For any finite extension
$\mathscr{Y}_{L}^{?,\text{l.c.}}:=\mathscr{Y}^{?,\text{l.c.}}\times _{\operatorname{Spec}M}\operatorname{Spec}L$
. For any finite extension
![]() $M^{\prime }$
of
$M^{\prime }$
of
![]() $M$
contained in
$M$
contained in
![]() $L$
, there is a natural map of locally
$L$
, there is a natural map of locally
![]() $M^{\prime }$
-ringed spaces
$M^{\prime }$
-ringed spaces
 $j_{M^{\prime }}:\mathscr{Y}^{?,\text{l.c.},\text{an}}\rightarrow \mathscr{Y}_{M^{\prime }}^{?,\text{l.c.}}$
. Let
$j_{M^{\prime }}:\mathscr{Y}^{?,\text{l.c.},\text{an}}\rightarrow \mathscr{Y}_{M^{\prime }}^{?,\text{l.c.}}$
. Let
![]() $M^{\prime }$
be a finite extension of
$M^{\prime }$
be a finite extension of
![]() $M$
contained in
$M$
contained in
![]() $L$
. We say that a section
$L$
. We say that a section
![]() $G$
of the structure sheaf of
$G$
of the structure sheaf of
![]() $\mathscr{Y}^{?}$
is algebraic on
$\mathscr{Y}^{?}$
is algebraic on
![]() $\mathscr{Y}_{M^{\prime }}^{?,\text{l.c.}}$
if its restriction to
$\mathscr{Y}_{M^{\prime }}^{?,\text{l.c.}}$
if its restriction to
 $\mathscr{Y}^{?,\text{l.c.},\text{an}}$
equals
$\mathscr{Y}^{?,\text{l.c.},\text{an}}$
equals
![]() $j_{M^{\prime }}^{\sharp }G^{\prime }$
for a (necessarily unique) section
$j_{M^{\prime }}^{\sharp }G^{\prime }$
for a (necessarily unique) section
![]() $G^{\prime }$
of the structure sheaf of
$G^{\prime }$
of the structure sheaf of
![]() $\mathscr{Y}_{M^{\prime }}^{?,\text{l.c.}}$
.Footnote
5
$\mathscr{Y}_{M^{\prime }}^{?,\text{l.c.}}$
.Footnote
5
In the situation of the definition, we will abusively still denote by
![]() $G$
the function
$G$
the function
![]() $G^{\prime }$
on
$G^{\prime }$
on
![]() $\mathscr{Y}_{M^{\prime }}^{?,\text{l.c.}}$
.
$\mathscr{Y}_{M^{\prime }}^{?,\text{l.c.}}$
.
Local additive character. Let
![]() $v$
be a non-archimedean place of
$v$
be a non-archimedean place of
![]() $F$
,
$F$
,
 $p_{v}\subset \mathscr{O}_{F,v}$
the maximal ideal, and
$p_{v}\subset \mathscr{O}_{F,v}$
the maximal ideal, and
 $d_{v}\subset \mathscr{O}_{F,v}$
the different. We define the space of additive characters of
$d_{v}\subset \mathscr{O}_{F,v}$
the different. We define the space of additive characters of
![]() $F_{v}$
of level
$F_{v}$
of level
![]() $0$
to be
$0$
to be
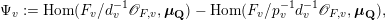 $$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{v}:=\operatorname{Hom}(F_{v}/d_{v}^{-1}\mathscr{O}_{F,v},\boldsymbol{\unicode[STIX]{x1D707}}_{\mathbf{Q}})-\operatorname{Hom}(F_{v}/p_{v}^{-1}d_{v}^{-1}\mathscr{O}_{F,v},\boldsymbol{\unicode[STIX]{x1D707}}_{\mathbf{Q}}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{v}:=\operatorname{Hom}(F_{v}/d_{v}^{-1}\mathscr{O}_{F,v},\boldsymbol{\unicode[STIX]{x1D707}}_{\mathbf{Q}})-\operatorname{Hom}(F_{v}/p_{v}^{-1}d_{v}^{-1}\mathscr{O}_{F,v},\boldsymbol{\unicode[STIX]{x1D707}}_{\mathbf{Q}}),\end{eqnarray}$$
where we regard
 $\operatorname{Hom}(F_{v}/p_{v}^{n}\mathscr{O}_{F,v},\boldsymbol{\unicode[STIX]{x1D707}}_{\mathbf{Q}})$
as a profinite group scheme over
$\operatorname{Hom}(F_{v}/p_{v}^{n}\mathscr{O}_{F,v},\boldsymbol{\unicode[STIX]{x1D707}}_{\mathbf{Q}})$
as a profinite group scheme over
![]() $\mathbf{Q}$
.Footnote
6
The scheme
$\mathbf{Q}$
.Footnote
6
The scheme
![]() $\unicode[STIX]{x1D6F9}_{v}$
is a torsor for the action of
$\unicode[STIX]{x1D6F9}_{v}$
is a torsor for the action of
![]() $\mathscr{O}_{F,v}^{\times }$
(viewed as a constant profinite group scheme over
$\mathscr{O}_{F,v}^{\times }$
(viewed as a constant profinite group scheme over
![]() $\mathbf{Q}$
) by
$\mathbf{Q}$
) by
 $a.\unicode[STIX]{x1D713}(x):=\unicode[STIX]{x1D713}(ax)$
.
$a.\unicode[STIX]{x1D713}(x):=\unicode[STIX]{x1D713}(ax)$
.
If
 $\unicode[STIX]{x1D714}_{v}^{\prime }:\mathscr{O}_{F,v}^{\times }\rightarrow \mathscr{O}(\mathscr{X})^{\times }$
is a continuous character for a scheme or rigid space
$\unicode[STIX]{x1D714}_{v}^{\prime }:\mathscr{O}_{F,v}^{\times }\rightarrow \mathscr{O}(\mathscr{X})^{\times }$
is a continuous character for a scheme or rigid space
![]() $\mathscr{X}$
, we denote by
$\mathscr{X}$
, we denote by
 $\mathscr{O}_{\mathscr{X}\times \unicode[STIX]{x1D6F9}_{v}}(\unicode[STIX]{x1D714}_{v}^{\prime })\subset \mathscr{O}_{\mathscr{X}\times \unicode[STIX]{x1D6F9}_{v}}$
the subsheaf of functions
$\mathscr{O}_{\mathscr{X}\times \unicode[STIX]{x1D6F9}_{v}}(\unicode[STIX]{x1D714}_{v}^{\prime })\subset \mathscr{O}_{\mathscr{X}\times \unicode[STIX]{x1D6F9}_{v}}$
the subsheaf of functions
![]() $G$
satisfying
$G$
satisfying
 $G(x,a.\unicode[STIX]{x1D713})=\unicode[STIX]{x1D714}_{v}^{\prime }(a)(x)G(x,\unicode[STIX]{x1D713})$
for
$G(x,a.\unicode[STIX]{x1D713})=\unicode[STIX]{x1D714}_{v}^{\prime }(a)(x)G(x,\unicode[STIX]{x1D713})$
for
 $a\in \mathscr{O}_{F,v}^{\times }$
. By the defining property, we can identify
$a\in \mathscr{O}_{F,v}^{\times }$
. By the defining property, we can identify
 $\mathscr{O}_{\mathscr{X}\times \unicode[STIX]{x1D6F9}_{v}}(\unicode[STIX]{x1D714}_{v}^{\prime })$
with
$\mathscr{O}_{\mathscr{X}\times \unicode[STIX]{x1D6F9}_{v}}(\unicode[STIX]{x1D714}_{v}^{\prime })$
with
 $\text{p}_{\mathscr{X}\ast }\mathscr{O}_{\mathscr{X}\times \unicode[STIX]{x1D6F9}_{v}}(\unicode[STIX]{x1D714}_{v}^{\prime })$
(where
$\text{p}_{\mathscr{X}\ast }\mathscr{O}_{\mathscr{X}\times \unicode[STIX]{x1D6F9}_{v}}(\unicode[STIX]{x1D714}_{v}^{\prime })$
(where
 $\text{p}_{\mathscr{X}}:\mathscr{X}\times \unicode[STIX]{x1D6F9}_{v}\rightarrow \mathscr{X}$
is the projection), a locally free rank-
$\text{p}_{\mathscr{X}}:\mathscr{X}\times \unicode[STIX]{x1D6F9}_{v}\rightarrow \mathscr{X}$
is the projection), a locally free rank-
![]() $1$
$1$
![]() $\mathscr{O}_{\mathscr{X}}$
-module with action by
$\mathscr{O}_{\mathscr{X}}$
-module with action by
 $\mathscr{G}_{\mathbf{Q}}:=\operatorname{Gal}(\overline{\mathbf{Q}}/\mathbf{Q})$
. Finally, we denote
$\mathscr{G}_{\mathbf{Q}}:=\operatorname{Gal}(\overline{\mathbf{Q}}/\mathbf{Q})$
. Finally, we denote
 $\unicode[STIX]{x1D6F9}_{p}:=\prod _{v|p}\unicode[STIX]{x1D6F9}_{v}$
and, if
$\unicode[STIX]{x1D6F9}_{p}:=\prod _{v|p}\unicode[STIX]{x1D6F9}_{v}$
and, if
 $\unicode[STIX]{x1D714}_{p}^{\prime }=\prod _{v|p}\unicode[STIX]{x1D714}_{v}^{\prime }:\mathscr{O}_{F,p}^{\times }\rightarrow \mathscr{O}(\mathscr{X})^{\times }$
,
$\unicode[STIX]{x1D714}_{p}^{\prime }=\prod _{v|p}\unicode[STIX]{x1D714}_{v}^{\prime }:\mathscr{O}_{F,p}^{\times }\rightarrow \mathscr{O}(\mathscr{X})^{\times }$
,
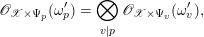 $$\begin{eqnarray}\mathscr{O}_{\mathscr{X}\times \unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D714}_{p}^{\prime })=\bigotimes _{v|p}\mathscr{O}_{\mathscr{X}\times \unicode[STIX]{x1D6F9}_{v}}(\unicode[STIX]{x1D714}_{v}^{\prime }),\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{O}_{\mathscr{X}\times \unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D714}_{p}^{\prime })=\bigotimes _{v|p}\mathscr{O}_{\mathscr{X}\times \unicode[STIX]{x1D6F9}_{v}}(\unicode[STIX]{x1D714}_{v}^{\prime }),\end{eqnarray}$$
where the tensor product is in the category of
![]() $\mathscr{O}_{\mathscr{X}}$
-modules. Its space of global sections over
$\mathscr{O}_{\mathscr{X}}$
-modules. Its space of global sections over
![]() $\mathscr{X}$
will be denoted by
$\mathscr{X}$
will be denoted by
 $\mathscr{O}_{\mathscr{X}\times \unicode[STIX]{x1D6F9}_{p}}(\mathscr{X}\times \unicode[STIX]{x1D6F9}_{p},\unicode[STIX]{x1D714}_{p}^{\prime })$
or simply
$\mathscr{O}_{\mathscr{X}\times \unicode[STIX]{x1D6F9}_{p}}(\mathscr{X}\times \unicode[STIX]{x1D6F9}_{p},\unicode[STIX]{x1D714}_{p}^{\prime })$
or simply
 $\mathscr{O}_{\mathscr{X}\times \unicode[STIX]{x1D6F9}_{p}}(\mathscr{X},\unicode[STIX]{x1D714}_{p}^{\prime })$
.
$\mathscr{O}_{\mathscr{X}\times \unicode[STIX]{x1D6F9}_{p}}(\mathscr{X},\unicode[STIX]{x1D714}_{p}^{\prime })$
.
These sheaves will appear in the next theorem with
 $\unicode[STIX]{x1D714}_{v}^{\prime }=\unicode[STIX]{x1D714}_{v}\unicode[STIX]{x1D712}_{F,\text{univ},v}^{-1}:\mathscr{O}_{F,v}^{\times }\rightarrow \mathscr{O}(\mathscr{Y}^{\prime })^{\times }$
, where
$\unicode[STIX]{x1D714}_{v}^{\prime }=\unicode[STIX]{x1D714}_{v}\unicode[STIX]{x1D712}_{F,\text{univ},v}^{-1}:\mathscr{O}_{F,v}^{\times }\rightarrow \mathscr{O}(\mathscr{Y}^{\prime })^{\times }$
, where
![]() $\unicode[STIX]{x1D714}_{v}$
is the central character of
$\unicode[STIX]{x1D714}_{v}$
is the central character of
![]() $\unicode[STIX]{x1D70E}_{v}$
and
$\unicode[STIX]{x1D70E}_{v}$
and
 $\unicode[STIX]{x1D712}_{F,\text{univ},v}:\mathscr{O}_{F,v}^{\times }\rightarrow \mathscr{O}(\mathscr{Y}_{F})^{\times }\rightarrow \mathscr{O}(\mathscr{Y}^{\prime })^{\times }$
comes from the restriction of the universal
$\unicode[STIX]{x1D712}_{F,\text{univ},v}:\mathscr{O}_{F,v}^{\times }\rightarrow \mathscr{O}(\mathscr{Y}_{F})^{\times }\rightarrow \mathscr{O}(\mathscr{Y}^{\prime })^{\times }$
comes from the restriction of the universal
 $\mathscr{O}(\mathscr{Y}_{F})^{\times }$
-valued character of
$\mathscr{O}(\mathscr{Y}_{F})^{\times }$
-valued character of
![]() $\unicode[STIX]{x1D6E4}_{F}$
. As
$\unicode[STIX]{x1D6E4}_{F}$
. As
![]() $\unicode[STIX]{x1D6F9}_{p}$
is a scheme over
$\unicode[STIX]{x1D6F9}_{p}$
is a scheme over
![]() $\mathbf{Q}$
and
$\mathbf{Q}$
and
![]() $\unicode[STIX]{x1D712}_{F,\text{univ}}$
is obviously algebraic on
$\unicode[STIX]{x1D712}_{F,\text{univ}}$
is obviously algebraic on
![]() $\mathscr{Y}_{F}^{\text{l.c.}}$
, the notion of Definition 1.2.3 extends to define
$\mathscr{Y}_{F}^{\text{l.c.}}$
, the notion of Definition 1.2.3 extends to define
![]() $\mathscr{Y}_{M^{\prime }}^{\prime \,\text{l.c.}}$
-algebraicity of sections of
$\mathscr{Y}_{M^{\prime }}^{\prime \,\text{l.c.}}$
-algebraicity of sections of
 $\mathscr{O}_{\mathscr{Y}^{\prime }\times \unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D714}_{v}^{\prime })$
(and we use the terminology ‘algebraic on
$\mathscr{O}_{\mathscr{Y}^{\prime }\times \unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D714}_{v}^{\prime })$
(and we use the terminology ‘algebraic on
 $\mathscr{Y}_{M^{\prime }}^{\prime \,\text{l.c.}}\times \unicode[STIX]{x1D6F9}_{p}(\unicode[STIX]{x1D714}_{v}^{\prime })$
’).
$\mathscr{Y}_{M^{\prime }}^{\prime \,\text{l.c.}}\times \unicode[STIX]{x1D6F9}_{p}(\unicode[STIX]{x1D714}_{v}^{\prime })$
’).
As a last preliminary, we introduce notation for bounded functions: if
![]() $\mathscr{X}$
is a rigid space, then
$\mathscr{X}$
is a rigid space, then
 $\mathscr{O}_{\mathscr{X}}(\mathscr{X})^{\text{b}}\subset \mathscr{O}_{\mathscr{X}}(\mathscr{X})$
is the space of global sections
$\mathscr{O}_{\mathscr{X}}(\mathscr{X})^{\text{b}}\subset \mathscr{O}_{\mathscr{X}}(\mathscr{X})$
is the space of global sections
![]() $G$
such that
$G$
such that
 $\sup _{x\in \mathscr{X}}|G(x)|$
is finite; similarly, in the above situation, we let
$\sup _{x\in \mathscr{X}}|G(x)|$
is finite; similarly, in the above situation, we let
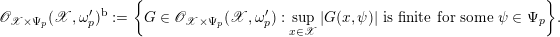 $$\begin{eqnarray}\mathscr{O}_{\mathscr{X}\times \unicode[STIX]{x1D6F9}_{p}}(\mathscr{X},\unicode[STIX]{x1D714}_{p}^{\prime })^{\text{b}}:=\biggl\{G\in \mathscr{O}_{\mathscr{ X}\times \unicode[STIX]{x1D6F9}_{p}}(\mathscr{X},\unicode[STIX]{x1D714}_{p}^{\prime }):\sup _{x\in \mathscr{X}}|G(x,\unicode[STIX]{x1D713})|~\text{is finite for some }\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}_{p}\biggr\}.\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{O}_{\mathscr{X}\times \unicode[STIX]{x1D6F9}_{p}}(\mathscr{X},\unicode[STIX]{x1D714}_{p}^{\prime })^{\text{b}}:=\biggl\{G\in \mathscr{O}_{\mathscr{ X}\times \unicode[STIX]{x1D6F9}_{p}}(\mathscr{X},\unicode[STIX]{x1D714}_{p}^{\prime }):\sup _{x\in \mathscr{X}}|G(x,\unicode[STIX]{x1D713})|~\text{is finite for some }\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}_{p}\biggr\}.\end{eqnarray}$$
As
![]() $\unicode[STIX]{x1D714}_{p}^{\prime }$
is continuous,
$\unicode[STIX]{x1D714}_{p}^{\prime }$
is continuous,
![]() $\unicode[STIX]{x1D714}_{p}^{\prime }(a)$
is bounded in
$\unicode[STIX]{x1D714}_{p}^{\prime }(a)$
is bounded in
 $a\in \mathscr{O}_{F,p}^{\times }$
: we could then equivalently replace ‘is finite for some
$a\in \mathscr{O}_{F,p}^{\times }$
: we could then equivalently replace ‘is finite for some
![]() $\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}_{p}$
’ with ‘is uniformly bounded for all
$\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}_{p}$
’ with ‘is uniformly bounded for all
![]() $\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}_{p}$
’.
$\unicode[STIX]{x1D713}\in \unicode[STIX]{x1D6F9}_{p}$
’.
Theorem A. There is a bounded analytic function
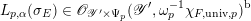 $$\begin{eqnarray}L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})\in \mathscr{O}_{\mathscr{Y}^{\prime }\times \unicode[STIX]{x1D6F9}_{p}}(\mathscr{Y}^{\prime },\unicode[STIX]{x1D714}_{p}^{-1}\unicode[STIX]{x1D712}_{F,\text{univ},p})^{\text{b}}\end{eqnarray}$$
$$\begin{eqnarray}L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})\in \mathscr{O}_{\mathscr{Y}^{\prime }\times \unicode[STIX]{x1D6F9}_{p}}(\mathscr{Y}^{\prime },\unicode[STIX]{x1D714}_{p}^{-1}\unicode[STIX]{x1D712}_{F,\text{univ},p})^{\text{b}}\end{eqnarray}$$
uniquely determined by the following property:
 $L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})$
is algebraic on
$L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})$
is algebraic on
 $\mathscr{Y}_{M(\unicode[STIX]{x1D6FC})}^{\prime \,\text{l.c.}}\times \unicode[STIX]{x1D6F9}_{p}$
and, for each
$\mathscr{Y}_{M(\unicode[STIX]{x1D6FC})}^{\prime \,\text{l.c.}}\times \unicode[STIX]{x1D6F9}_{p}$
and, for each
![]() $\mathbf{C}$
-valued geometric point
$\mathbf{C}$
-valued geometric point
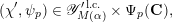 $$\begin{eqnarray}(\unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D713}_{p})\in \mathscr{Y}_{M(\unicode[STIX]{x1D6FC})}^{\prime \,\text{l.c.}}\times \unicode[STIX]{x1D6F9}_{p}(\mathbf{C}),\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D713}_{p})\in \mathscr{Y}_{M(\unicode[STIX]{x1D6FC})}^{\prime \,\text{l.c.}}\times \unicode[STIX]{x1D6F9}_{p}(\mathbf{C}),\end{eqnarray}$$
letting
 $\unicode[STIX]{x1D704}:M(\unicode[STIX]{x1D6FC}){\hookrightarrow}\mathbf{C}$
be the embedding induced by the composition
$\unicode[STIX]{x1D704}:M(\unicode[STIX]{x1D6FC}){\hookrightarrow}\mathbf{C}$
be the embedding induced by the composition
 $\operatorname{Spec}\mathbf{C}\stackrel{\unicode[STIX]{x1D712}^{\prime }}{\rightarrow }\mathscr{Y}_{M(\unicode[STIX]{x1D6FC})}^{\prime \,\text{l.c.}}\rightarrow \operatorname{Spec}M(\unicode[STIX]{x1D6FC})$
, we have
$\operatorname{Spec}\mathbf{C}\stackrel{\unicode[STIX]{x1D712}^{\prime }}{\rightarrow }\mathscr{Y}_{M(\unicode[STIX]{x1D6FC})}^{\prime \,\text{l.c.}}\rightarrow \operatorname{Spec}M(\unicode[STIX]{x1D6FC})$
, we have
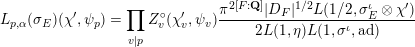 $$\begin{eqnarray}L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})(\unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D713}_{p})=\mathop{\prod }_{v|p}Z_{v}^{\circ }(\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v})\frac{\unicode[STIX]{x1D70B}^{2[F:\mathbf{Q}]}|D_{F}|^{1/2}L(1/2,\unicode[STIX]{x1D70E}_{E}^{\unicode[STIX]{x1D704}}\otimes \unicode[STIX]{x1D712}^{\prime })}{2L(1,\unicode[STIX]{x1D702})L(1,\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D704}},\operatorname{ad})}\end{eqnarray}$$
$$\begin{eqnarray}L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})(\unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D713}_{p})=\mathop{\prod }_{v|p}Z_{v}^{\circ }(\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v})\frac{\unicode[STIX]{x1D70B}^{2[F:\mathbf{Q}]}|D_{F}|^{1/2}L(1/2,\unicode[STIX]{x1D70E}_{E}^{\unicode[STIX]{x1D704}}\otimes \unicode[STIX]{x1D712}^{\prime })}{2L(1,\unicode[STIX]{x1D702})L(1,\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D704}},\operatorname{ad})}\end{eqnarray}$$
in
![]() $\mathbf{C}$
. The interpolation factor is explicitly
$\mathbf{C}$
. The interpolation factor is explicitly
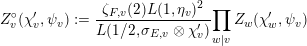 $$\begin{eqnarray}Z_{v}^{\circ }(\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v}):=\frac{\unicode[STIX]{x1D701}_{F,v}(2)L(1,\unicode[STIX]{x1D702}_{v})^{2}}{L(1/2,\unicode[STIX]{x1D70E}_{E,v}\otimes \unicode[STIX]{x1D712}_{v}^{\prime })}\mathop{\prod }_{w|v}Z_{w}(\unicode[STIX]{x1D712}_{w}^{\prime },\unicode[STIX]{x1D713}_{v})\end{eqnarray}$$
$$\begin{eqnarray}Z_{v}^{\circ }(\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v}):=\frac{\unicode[STIX]{x1D701}_{F,v}(2)L(1,\unicode[STIX]{x1D702}_{v})^{2}}{L(1/2,\unicode[STIX]{x1D70E}_{E,v}\otimes \unicode[STIX]{x1D712}_{v}^{\prime })}\mathop{\prod }_{w|v}Z_{w}(\unicode[STIX]{x1D712}_{w}^{\prime },\unicode[STIX]{x1D713}_{v})\end{eqnarray}$$
with
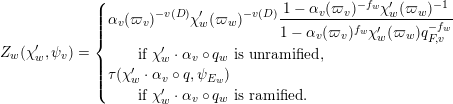 $$\begin{eqnarray}Z_{w}(\unicode[STIX]{x1D712}_{w}^{\prime },\unicode[STIX]{x1D713}_{v})=\left\{\begin{array}{@{}l@{}}\displaystyle \unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})^{-v(D)}\unicode[STIX]{x1D712}_{w}^{\prime }(\unicode[STIX]{x1D71B}_{w})^{-v(D)}\frac{1-\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})^{-f_{w}}\unicode[STIX]{x1D712}_{w}^{\prime }(\unicode[STIX]{x1D71B}_{w})^{-1}}{1-\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})^{f_{w}}\unicode[STIX]{x1D712}_{w}^{\prime }(\unicode[STIX]{x1D71B}_{w})q_{F,v}^{-f_{w}}}\quad \\ \qquad \text{if }\unicode[STIX]{x1D712}_{w}^{\prime }\cdot \unicode[STIX]{x1D6FC}_{v}\circ q_{w}\text{ is unramified},\quad \\ \unicode[STIX]{x1D70F}(\unicode[STIX]{x1D712}_{w}^{\prime }\cdot \unicode[STIX]{x1D6FC}_{v}\circ q,\unicode[STIX]{x1D713}_{E_{w}})\quad \\ \qquad \text{if }\unicode[STIX]{x1D712}_{w}^{\prime }\cdot \unicode[STIX]{x1D6FC}_{v}\circ q_{w}\text{ is ramified}.\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}Z_{w}(\unicode[STIX]{x1D712}_{w}^{\prime },\unicode[STIX]{x1D713}_{v})=\left\{\begin{array}{@{}l@{}}\displaystyle \unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})^{-v(D)}\unicode[STIX]{x1D712}_{w}^{\prime }(\unicode[STIX]{x1D71B}_{w})^{-v(D)}\frac{1-\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})^{-f_{w}}\unicode[STIX]{x1D712}_{w}^{\prime }(\unicode[STIX]{x1D71B}_{w})^{-1}}{1-\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})^{f_{w}}\unicode[STIX]{x1D712}_{w}^{\prime }(\unicode[STIX]{x1D71B}_{w})q_{F,v}^{-f_{w}}}\quad \\ \qquad \text{if }\unicode[STIX]{x1D712}_{w}^{\prime }\cdot \unicode[STIX]{x1D6FC}_{v}\circ q_{w}\text{ is unramified},\quad \\ \unicode[STIX]{x1D70F}(\unicode[STIX]{x1D712}_{w}^{\prime }\cdot \unicode[STIX]{x1D6FC}_{v}\circ q,\unicode[STIX]{x1D713}_{E_{w}})\quad \\ \qquad \text{if }\unicode[STIX]{x1D712}_{w}^{\prime }\cdot \unicode[STIX]{x1D6FC}_{v}\circ q_{w}\text{ is ramified}.\quad \end{array}\right.\end{eqnarray}$$
Here
![]() $d$
,
$d$
,
 $D\in \mathbf{A}^{\infty ,\times }$
are generators of the different of
$D\in \mathbf{A}^{\infty ,\times }$
are generators of the different of
![]() $F$
and the relative discriminant of
$F$
and the relative discriminant of
![]() $E/F$
, respectively,
$E/F$
, respectively,
![]() $q_{w}$
is the relative norm of
$q_{w}$
is the relative norm of
![]() $E/F$
,
$E/F$
,
![]() $f_{w}$
is the inertia degree of
$f_{w}$
is the inertia degree of
![]() $w|v$
, and
$w|v$
, and
![]() $q_{F,v}$
is the cardinality of the residue field at
$q_{F,v}$
is the cardinality of the residue field at
![]() $v$
; finally, for any character
$v$
; finally, for any character
![]() $\widetilde{\unicode[STIX]{x1D712}}_{w}^{\prime }$
of
$\widetilde{\unicode[STIX]{x1D712}}_{w}^{\prime }$
of
![]() $E_{w}^{\times }$
of conductor
$E_{w}^{\times }$
of conductor
![]() $\mathfrak{f}$
,
$\mathfrak{f}$
,
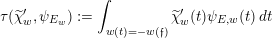 $$\begin{eqnarray}\unicode[STIX]{x1D70F}(\widetilde{\unicode[STIX]{x1D712}}_{w}^{\prime },\unicode[STIX]{x1D713}_{E_{w}}):=\int _{w(t)=-w(\mathfrak{f})}\widetilde{\unicode[STIX]{x1D712}}_{w}^{\prime }(t)\unicode[STIX]{x1D713}_{E,w}(t)\,dt\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}(\widetilde{\unicode[STIX]{x1D712}}_{w}^{\prime },\unicode[STIX]{x1D713}_{E_{w}}):=\int _{w(t)=-w(\mathfrak{f})}\widetilde{\unicode[STIX]{x1D712}}_{w}^{\prime }(t)\unicode[STIX]{x1D713}_{E,w}(t)\,dt\end{eqnarray}$$
with
![]() $dt$
the additive Haar measure on
$dt$
the additive Haar measure on
![]() $E_{w}$
giving
$E_{w}$
giving
 $\operatorname{vol}(\mathscr{O}_{E_{w}},dt)=1$
, and
$\operatorname{vol}(\mathscr{O}_{E_{w}},dt)=1$
, and
 $\unicode[STIX]{x1D713}_{E,w}=\unicode[STIX]{x1D713}_{F,v}\circ \operatorname{Tr}_{E_{w}/F_{v}}$
.
$\unicode[STIX]{x1D713}_{E,w}=\unicode[STIX]{x1D713}_{F,v}\circ \operatorname{Tr}_{E_{w}/F_{v}}$
.
Remark 1.2.4. It follows from the description of Lemma A.1.1 that the interpolation factors
![]() $Z_{v}^{\circ }$
,
$Z_{v}^{\circ }$
,
![]() $Z_{w}$
are sections of
$Z_{w}$
are sections of
 $\mathscr{O}_{\mathscr{ Y}_{v}^{\prime \,\text{l.c.}}\times \unicode[STIX]{x1D6F9}_{v}}(\unicode[STIX]{x1D714}_{v}\unicode[STIX]{x1D712}_{F,\text{univ},v}^{-1}),$
where
$\mathscr{O}_{\mathscr{ Y}_{v}^{\prime \,\text{l.c.}}\times \unicode[STIX]{x1D6F9}_{v}}(\unicode[STIX]{x1D714}_{v}\unicode[STIX]{x1D712}_{F,\text{univ},v}^{-1}),$
where
![]() $\mathscr{Y}_{v}^{\prime \,\text{l.c.}}$
is the ind-finite reduced ind-scheme over
$\mathscr{Y}_{v}^{\prime \,\text{l.c.}}$
is the ind-finite reduced ind-scheme over
![]() $M(\unicode[STIX]{x1D6FC})$
representing
$M(\unicode[STIX]{x1D6FC})$
representing
![]() $\boldsymbol{\unicode[STIX]{x1D707}}_{M(\unicode[STIX]{x1D6FC})}$
-valued characters of
$\boldsymbol{\unicode[STIX]{x1D707}}_{M(\unicode[STIX]{x1D6FC})}$
-valued characters of
![]() $E_{v}^{\times }$
. (Later, we will also similarly denote by
$E_{v}^{\times }$
. (Later, we will also similarly denote by
 $\mathscr{Y}_{v}^{\text{l.c.}}\subset \mathscr{Y}_{v}^{\prime \,\text{l.c.}}$
the subscheme of characters satisfying
$\mathscr{Y}_{v}^{\text{l.c.}}\subset \mathscr{Y}_{v}^{\prime \,\text{l.c.}}$
the subscheme of characters satisfying
 $\unicode[STIX]{x1D712}_{v}|_{F_{v}^{\times }}=\unicode[STIX]{x1D714}_{v}^{-1}$
.)
$\unicode[STIX]{x1D712}_{v}|_{F_{v}^{\times }}=\unicode[STIX]{x1D714}_{v}^{-1}$
.)
In fact, we only construct
 $L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})$
as a bounded section of
$L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})$
as a bounded section of
 $\mathscr{O}_{\mathscr{Y}^{\prime }\times \unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D714}_{p}^{-1}\unicode[STIX]{x1D712}_{F,\text{univ},p})(D)$
, where
$\mathscr{O}_{\mathscr{Y}^{\prime }\times \unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D714}_{p}^{-1}\unicode[STIX]{x1D712}_{F,\text{univ},p})(D)$
, where
![]() $D$
is a divisor on
$D$
is a divisor on
![]() $\mathscr{Y}^{\prime }$
supported away from
$\mathscr{Y}^{\prime }$
supported away from
![]() $\mathscr{Y}$
(i.e. for any polynomial function
$\mathscr{Y}$
(i.e. for any polynomial function
![]() $G$
on
$G$
on
![]() $\mathscr{Y}^{\prime }$
with divisor of zeroes
$\mathscr{Y}^{\prime }$
with divisor of zeroes
![]() ${\geqslant}D$
, the function
${\geqslant}D$
, the function
 $G\cdot L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})$
is a bounded global section of
$G\cdot L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})$
is a bounded global section of
 $\mathscr{O}_{\mathscr{Y}^{\prime }\times \unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D714}_{p}^{-1}\unicode[STIX]{x1D712}_{F,\text{univ},p})$
);Footnote
7
see Theorem 3.7.1 together with Proposition A.2.2 for the precise statement. This is sufficient for our purposes and to determine
$\mathscr{O}_{\mathscr{Y}^{\prime }\times \unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D714}_{p}^{-1}\unicode[STIX]{x1D712}_{F,\text{univ},p})$
);Footnote
7
see Theorem 3.7.1 together with Proposition A.2.2 for the precise statement. This is sufficient for our purposes and to determine
 $L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})$
uniquely. One can then deduce that it is possible to take
$L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})$
uniquely. One can then deduce that it is possible to take
![]() $D=0$
by comparing our
$D=0$
by comparing our
![]() $p$
-adic
$p$
-adic
![]() $L$
-function to some other construction where this difficulty does not arise. One such construction has been announced by David Hansen.
$L$
-function to some other construction where this difficulty does not arise. One such construction has been announced by David Hansen.
1.3
 $p$
-adic Gross–Zagier formula
$p$
-adic Gross–Zagier formula
Let us go back to the situation in which
![]() $A$
is a modular abelian variety of
$A$
is a modular abelian variety of
![]() $\mathbf{GL}_{2}$
-type, associated with an automorphic representation
$\mathbf{GL}_{2}$
-type, associated with an automorphic representation
![]() $\unicode[STIX]{x1D70E}_{A}$
of
$\unicode[STIX]{x1D70E}_{A}$
of
 $\operatorname{Res}_{F/\mathbf{Q}}\mathbf{GL}_{2}$
of character
$\operatorname{Res}_{F/\mathbf{Q}}\mathbf{GL}_{2}$
of character
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{A}$
.
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{A}$
.
![]() $p$
-adic heights. Several authors (notably Mazur–Tate, Schneider, Zarhin, Nekovář) have defined
$p$
-adic heights. Several authors (notably Mazur–Tate, Schneider, Zarhin, Nekovář) have defined
![]() $p$
-adic height pairings on
$p$
-adic height pairings on
 $A(\overline{F})\times A^{\vee }(\overline{F})$
for an abelian variety
$A(\overline{F})\times A^{\vee }(\overline{F})$
for an abelian variety
![]() $A$
. These pairings are analogous to the classical Néron–Tate height pairings: in particular, they admit a decomposition into a sum of local symbols indexed by the (finite) places of
$A$
. These pairings are analogous to the classical Néron–Tate height pairings: in particular, they admit a decomposition into a sum of local symbols indexed by the (finite) places of
![]() $F$
; for
$F$
; for
![]() $v\nmid p$
such symbols can be calculated from intersections of zero-cycles and degree-zero divisors on the local integral models of
$v\nmid p$
such symbols can be calculated from intersections of zero-cycles and degree-zero divisors on the local integral models of
![]() $A$
.
$A$
.
In the general context of Nekovář [Reference NekovářNek93], adopted in this paper and recalled in § 4.1, height pairings can be defined for any geometric Galois representation
![]() $V$
over a
$V$
over a
![]() $p$
-adic field; we are interested in the case
$p$
-adic field; we are interested in the case
 $V=V_{\mathfrak{p}}A\otimes _{M_{\mathfrak{p}}}L$
, where
$V=V_{\mathfrak{p}}A\otimes _{M_{\mathfrak{p}}}L$
, where
 $M=\operatorname{End}^{0}A$
and
$M=\operatorname{End}^{0}A$
and
![]() $L$
is a finite extension of a
$L$
is a finite extension of a
![]() $p$
-adic completion
$p$
-adic completion
![]() $M_{\mathfrak{p}}$
of
$M_{\mathfrak{p}}$
of
![]() $M$
. Different from the Néron–Tate heights,
$M$
. Different from the Néron–Tate heights,
![]() $p$
-adic heights are associated with the auxiliary choice of splittings of the Hodge filtration on
$p$
-adic heights are associated with the auxiliary choice of splittings of the Hodge filtration on
 $\mathbf{D}_{\text{dR}}(V|_{\mathscr{G}_{F_{v}}})$
for the primes
$\mathbf{D}_{\text{dR}}(V|_{\mathscr{G}_{F_{v}}})$
for the primes
![]() $v|p$
; in our case,
$v|p$
; in our case,
 $\mathbf{D}_{\text{dR}}(V|_{\mathscr{G}_{F_{v}}})=H_{\text{dR}}^{1}(A^{\vee }/F_{v})\otimes _{M_{\mathfrak{p}}}L$
. When
$\mathbf{D}_{\text{dR}}(V|_{\mathscr{G}_{F_{v}}})=H_{\text{dR}}^{1}(A^{\vee }/F_{v})\otimes _{M_{\mathfrak{p}}}L$
. When
![]() $V|_{\mathscr{G}_{F_{v}}}$
is potentially ordinary, meaning that it is reducible in the category of de Rham representations (see more precisely Definition 4.1.1),Footnote
8
there is a canonical such choice. If
$V|_{\mathscr{G}_{F_{v}}}$
is potentially ordinary, meaning that it is reducible in the category of de Rham representations (see more precisely Definition 4.1.1),Footnote
8
there is a canonical such choice. If
![]() $A$
is modular corresponding to an
$A$
is modular corresponding to an
![]() $M$
-rational cuspidal automorphic representation
$M$
-rational cuspidal automorphic representation
![]() $\unicode[STIX]{x1D70E}_{A}^{\infty }$
, it follows from [Reference CarayolCar86, Théorème A], together with [Reference NekovářNek06, (proof of) Proposition 12.11.5(iv)], that the restriction of
$\unicode[STIX]{x1D70E}_{A}^{\infty }$
, it follows from [Reference CarayolCar86, Théorème A], together with [Reference NekovářNek06, (proof of) Proposition 12.11.5(iv)], that the restriction of
 $V=V_{\mathfrak{p}}A\otimes L$
to
$V=V_{\mathfrak{p}}A\otimes L$
to
![]() $\mathscr{G}_{F_{v}}$
is potentially ordinary if and only if
$\mathscr{G}_{F_{v}}$
is potentially ordinary if and only if
 $\unicode[STIX]{x1D70E}_{A,v}\otimes L$
is nearly
$\unicode[STIX]{x1D70E}_{A,v}\otimes L$
is nearly
![]() $\mathfrak{p}$
-ordinary.
$\mathfrak{p}$
-ordinary.
We assume this to be the case for all
![]() $v|p$
. One then has a canonical
$v|p$
. One then has a canonical
![]() $p$
-adic height pairing
$p$
-adic height pairing
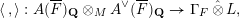 $$\begin{eqnarray}\langle \,,\rangle :A(\overline{F})_{\mathbf{Q}}\otimes _{M}A^{\vee }(\overline{F})_{\boldsymbol{ Q}}\rightarrow \unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L,\end{eqnarray}$$
$$\begin{eqnarray}\langle \,,\rangle :A(\overline{F})_{\mathbf{Q}}\otimes _{M}A^{\vee }(\overline{F})_{\boldsymbol{ Q}}\rightarrow \unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L,\end{eqnarray}$$
whose precise definition will be recalled at the end of § 4.1. Its equivariance properties under the action of
 $\mathscr{G}_{F}=\operatorname{Gal}(\overline{F}/F)$
allow us to deduce from it pairings
$\mathscr{G}_{F}=\operatorname{Gal}(\overline{F}/F)$
allow us to deduce from it pairings
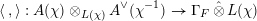 $$\begin{eqnarray}\langle \,,\rangle :A(\unicode[STIX]{x1D712})\otimes _{L(\unicode[STIX]{x1D712})}A^{\vee }(\unicode[STIX]{x1D712}^{-1})\rightarrow \unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L(\unicode[STIX]{x1D712})\end{eqnarray}$$
$$\begin{eqnarray}\langle \,,\rangle :A(\unicode[STIX]{x1D712})\otimes _{L(\unicode[STIX]{x1D712})}A^{\vee }(\unicode[STIX]{x1D712}^{-1})\rightarrow \unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L(\unicode[STIX]{x1D712})\end{eqnarray}$$
for any character
 $\unicode[STIX]{x1D712}\in \mathscr{Y}_{L}^{\text{l.c.}}$
.
$\unicode[STIX]{x1D712}\in \mathscr{Y}_{L}^{\text{l.c.}}$
.
Remark 1.3.1. Suppose that
 $\ell :\unicode[STIX]{x1D6E4}_{F}\rightarrow L(\unicode[STIX]{x1D712})$
is any continuous homomorphism such that, for all
$\ell :\unicode[STIX]{x1D6E4}_{F}\rightarrow L(\unicode[STIX]{x1D712})$
is any continuous homomorphism such that, for all
![]() $v|p$
,
$v|p$
,
 $\ell _{v}|_{\mathscr{O}_{F,v}^{\times }}\neq 0$
; we then call
$\ell _{v}|_{\mathscr{O}_{F,v}^{\times }}\neq 0$
; we then call
![]() $\ell$
a ramified logarithm. Then it is conjectured, but not known in general, that the pairings deduced from (1.3.2) by composition with
$\ell$
a ramified logarithm. Then it is conjectured, but not known in general, that the pairings deduced from (1.3.2) by composition with
![]() $\ell$
are non-degenerate. See Theorem E for a new result in this direction.
$\ell$
are non-degenerate. See Theorem E for a new result in this direction.
Remark 1.3.2. If
![]() $\unicode[STIX]{x1D712}$
is not exceptional in the sense of the next definition, then (1.3.2) is known to coincide with the norm-adapted height pairings à la Schneider [Reference SchneiderSch82, Reference NekovářNek93], by [Reference NekovářNek93], and with the Mazur–Tate [Reference Mazur and TateMT83] height pairings, by [Reference Iovita and WernerIW03].
$\unicode[STIX]{x1D712}$
is not exceptional in the sense of the next definition, then (1.3.2) is known to coincide with the norm-adapted height pairings à la Schneider [Reference SchneiderSch82, Reference NekovářNek93], by [Reference NekovářNek93], and with the Mazur–Tate [Reference Mazur and TateMT83] height pairings, by [Reference Iovita and WernerIW03].
Definition 1.3.3. A locally constant character
![]() $\unicode[STIX]{x1D712}_{w}$
of
$\unicode[STIX]{x1D712}_{w}$
of
![]() $E_{w}^{\times }$
is said to be not exceptional if
$E_{w}^{\times }$
is said to be not exceptional if
 $Z_{w}(\unicode[STIX]{x1D712}_{w})\neq 0$
.Footnote
9
A character
$Z_{w}(\unicode[STIX]{x1D712}_{w})\neq 0$
.Footnote
9
A character
 $\unicode[STIX]{x1D712}\in \mathscr{Y}_{M(\unicode[STIX]{x1D6FC})}^{\text{l.c.}}$
is said to be not exceptional if for all
$\unicode[STIX]{x1D712}\in \mathscr{Y}_{M(\unicode[STIX]{x1D6FC})}^{\text{l.c.}}$
is said to be not exceptional if for all
![]() $w|p$
,
$w|p$
,
![]() $\unicode[STIX]{x1D712}_{w}$
is not exceptional.
$\unicode[STIX]{x1D712}_{w}$
is not exceptional.
The formula. Let
 $\mathscr{Y}=\mathscr{Y}_{\unicode[STIX]{x1D714}}\subset \mathscr{Y}^{\prime }=\mathscr{Y}_{\unicode[STIX]{x1D714}}^{\prime }$
be the rigid spaces defined above. Denote by
$\mathscr{Y}=\mathscr{Y}_{\unicode[STIX]{x1D714}}\subset \mathscr{Y}^{\prime }=\mathscr{Y}_{\unicode[STIX]{x1D714}}^{\prime }$
be the rigid spaces defined above. Denote by
 $\mathscr{I}_{\mathscr{Y}}\subset \mathscr{O}_{\mathscr{Y}^{\prime }}$
the ideal sheaf of
$\mathscr{I}_{\mathscr{Y}}\subset \mathscr{O}_{\mathscr{Y}^{\prime }}$
the ideal sheaf of
![]() $\mathscr{Y}$
and by
$\mathscr{Y}$
and by
 $\mathscr{N}_{\mathscr{Y}/\mathscr{Y}^{\prime }}^{\ast }=(\mathscr{I}_{\mathscr{Y}}/\mathscr{I}_{\mathscr{Y}}^{2})|_{\mathscr{Y}}$
the conormal sheaf. By (1.2.1), it is canonically trivial:
$\mathscr{N}_{\mathscr{Y}/\mathscr{Y}^{\prime }}^{\ast }=(\mathscr{I}_{\mathscr{Y}}/\mathscr{I}_{\mathscr{Y}}^{2})|_{\mathscr{Y}}$
the conormal sheaf. By (1.2.1), it is canonically trivial:
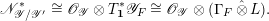 $$\begin{eqnarray}\mathscr{N}_{\mathscr{Y}/\mathscr{Y}^{\prime }}^{\ast }\cong \mathscr{O}_{\mathscr{ Y}}\otimes T_{\mathbf{1}}^{\ast }\mathscr{Y}_{F}\cong \mathscr{O}_{\mathscr{Y}}\otimes (\unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L).\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{N}_{\mathscr{Y}/\mathscr{Y}^{\prime }}^{\ast }\cong \mathscr{O}_{\mathscr{ Y}}\otimes T_{\mathbf{1}}^{\ast }\mathscr{Y}_{F}\cong \mathscr{O}_{\mathscr{Y}}\otimes (\unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L).\end{eqnarray}$$
For a section
![]() $G$
of
$G$
of
![]() $\mathscr{I}_{\mathscr{Y}}$
, denote by
$\mathscr{I}_{\mathscr{Y}}$
, denote by
 $\text{d}_{F}G\in \mathscr{N}_{\mathscr{Y}/\mathscr{Y}^{\prime }}^{\ast }$
its image; it can be thought of as the differential in the
$\text{d}_{F}G\in \mathscr{N}_{\mathscr{Y}/\mathscr{Y}^{\prime }}^{\ast }$
its image; it can be thought of as the differential in the
![]() $1+\unicode[STIX]{x1D6FF}$
cyclotomic variable(s).
$1+\unicode[STIX]{x1D6FF}$
cyclotomic variable(s).
Let
 $\unicode[STIX]{x1D712}\in \mathscr{Y}^{\text{l.c.},\text{an}}$
be a character such that
$\unicode[STIX]{x1D712}\in \mathscr{Y}^{\text{l.c.},\text{an}}$
be a character such that
 $\unicode[STIX]{x1D700}(A_{E},\unicode[STIX]{x1D712})=-1$
; denote by
$\unicode[STIX]{x1D700}(A_{E},\unicode[STIX]{x1D712})=-1$
; denote by
![]() $L(\unicode[STIX]{x1D712})$
its residue field. By the interpolation property, the complex functional equation, and the constancy of local root numbers, the
$L(\unicode[STIX]{x1D712})$
its residue field. By the interpolation property, the complex functional equation, and the constancy of local root numbers, the
![]() $p$
-adic
$p$
-adic
![]() $L$
-function
$L$
-function
 $L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{A,E})$
is a section of
$L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{A,E})$
is a section of
![]() $\mathscr{I}_{\mathscr{Y}}$
in the connected component of
$\mathscr{I}_{\mathscr{Y}}$
in the connected component of
![]() $\unicode[STIX]{x1D712}\in \mathscr{Y}^{\prime }$
(see Lemma 10.2.2). Let
$\unicode[STIX]{x1D712}\in \mathscr{Y}^{\prime }$
(see Lemma 10.2.2). Let
![]() $\mathbf{B}$
be the incoherent quaternion algebra determined by (1.1.1) and let
$\mathbf{B}$
be the incoherent quaternion algebra determined by (1.1.1) and let
 $\unicode[STIX]{x1D70B}_{A}=\unicode[STIX]{x1D70B}_{A}(\mathbf{B})$
,
$\unicode[STIX]{x1D70B}_{A}=\unicode[STIX]{x1D70B}_{A}(\mathbf{B})$
,
 $\unicode[STIX]{x1D70B}_{A^{\vee }}=\unicode[STIX]{x1D70B}_{A^{\vee }}(\mathbf{B})$
.
$\unicode[STIX]{x1D70B}_{A^{\vee }}=\unicode[STIX]{x1D70B}_{A^{\vee }}(\mathbf{B})$
.
Theorem B. Suppose that:
-
– for all
 $v|p$
,
$v|p$
,
 $A/F_{v}$
has potentially
$A/F_{v}$
has potentially
 $\mathfrak{p}$
-ordinary good or semistable reduction;
$\mathfrak{p}$
-ordinary good or semistable reduction; -
– for all
 $v|p$
,
$v|p$
,
 $E_{v}/F_{v}$
is split;
$E_{v}/F_{v}$
is split; -
– the sign
 $\unicode[STIX]{x1D700}(A_{E},\unicode[STIX]{x1D712})=-1$
and
$\unicode[STIX]{x1D700}(A_{E},\unicode[STIX]{x1D712})=-1$
and
 $\unicode[STIX]{x1D712}$
is not exceptional (Definition 1.3.3).
$\unicode[STIX]{x1D712}$
is not exceptional (Definition 1.3.3).
Then for all
 $f_{1}\in \unicode[STIX]{x1D70B}_{A}$
,
$f_{1}\in \unicode[STIX]{x1D70B}_{A}$
,
 $f_{2}\in \unicode[STIX]{x1D70B}_{A^{\vee }}$
, we have
$f_{2}\in \unicode[STIX]{x1D70B}_{A^{\vee }}$
, we have
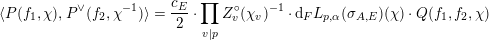 $$\begin{eqnarray}\langle P(f_{1},\unicode[STIX]{x1D712}),P^{\vee }(f_{2},\unicode[STIX]{x1D712}^{-1})\rangle =\frac{c_{E}}{2}\cdot \mathop{\prod }_{v|p}Z_{v}^{\circ }(\unicode[STIX]{x1D712}_{v})^{-1}\cdot \text{d}_{F}L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{A,E})(\unicode[STIX]{x1D712})\cdot Q(f_{1},f_{2},\unicode[STIX]{x1D712})\end{eqnarray}$$
$$\begin{eqnarray}\langle P(f_{1},\unicode[STIX]{x1D712}),P^{\vee }(f_{2},\unicode[STIX]{x1D712}^{-1})\rangle =\frac{c_{E}}{2}\cdot \mathop{\prod }_{v|p}Z_{v}^{\circ }(\unicode[STIX]{x1D712}_{v})^{-1}\cdot \text{d}_{F}L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{A,E})(\unicode[STIX]{x1D712})\cdot Q(f_{1},f_{2},\unicode[STIX]{x1D712})\end{eqnarray}$$
in
 $\mathscr{N}_{\mathscr{Y}/\mathscr{Y}^{\prime }}^{\ast }\text{}_{|\unicode[STIX]{x1D712}}\cong \unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L(\unicode[STIX]{x1D712})$
. Here
$\mathscr{N}_{\mathscr{Y}/\mathscr{Y}^{\prime }}^{\ast }\text{}_{|\unicode[STIX]{x1D712}}\cong \unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L(\unicode[STIX]{x1D712})$
. Here
![]() $c_{E}$
is as in (1.1.4).
$c_{E}$
is as in (1.1.4).
In the right-hand side, we have considered Remark 1.2.4 and used the canonical isomorphism
 $\mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D714}_{p}^{-1})\otimes _{M}\mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D714}_{p})=M$
.
$\mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D714}_{p}^{-1})\otimes _{M}\mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D714}_{p})=M$
.
1.4 Anticyclotomic theory
Consider the setup of § 1.2. Recall that in the case
 $\unicode[STIX]{x1D700}(1/2,\unicode[STIX]{x1D70E}_{E},\unicode[STIX]{x1D712})=+1$
, the definite quaternion algebra
$\unicode[STIX]{x1D700}(1/2,\unicode[STIX]{x1D70E}_{E},\unicode[STIX]{x1D712})=+1$
, the definite quaternion algebra
![]() $\mathbf{B}$
defined by (1.1.1) is coherent, i.e. it arises as
$\mathbf{B}$
defined by (1.1.1) is coherent, i.e. it arises as
 $\mathbf{B}=B\otimes _{F}\mathbf{A}_{F}$
for a quaternion algebra
$\mathbf{B}=B\otimes _{F}\mathbf{A}_{F}$
for a quaternion algebra
![]() $B$
over
$B$
over
![]() $F$
; we may assume that the embedding
$F$
; we may assume that the embedding
 $E_{\mathbf{A}}{\hookrightarrow}\mathbf{B}$
arises from an embedding
$E_{\mathbf{A}}{\hookrightarrow}\mathbf{B}$
arises from an embedding
 $i:E{\hookrightarrow}B$
. Let
$i:E{\hookrightarrow}B$
. Let
![]() $\unicode[STIX]{x1D70B}$
be the automorphic representation of
$\unicode[STIX]{x1D70B}$
be the automorphic representation of
![]() $\mathbf{B}^{\times }$
attached to
$\mathbf{B}^{\times }$
attached to
![]() $\unicode[STIX]{x1D70E}$
by the Jacquet–Langlands correspondence; it is realised in the space of locally constant functions
$\unicode[STIX]{x1D70E}$
by the Jacquet–Langlands correspondence; it is realised in the space of locally constant functions
 $B^{\times }\backslash \mathbf{B}^{\times }\rightarrow M$
, and this gives a stable lattice
$B^{\times }\backslash \mathbf{B}^{\times }\rightarrow M$
, and this gives a stable lattice
 $\unicode[STIX]{x1D70B}_{\mathscr{O}_{M}}\subset \unicode[STIX]{x1D70B}$
. Then, given a character
$\unicode[STIX]{x1D70B}_{\mathscr{O}_{M}}\subset \unicode[STIX]{x1D70B}$
. Then, given a character
 $\unicode[STIX]{x1D712}\in \mathscr{Y}^{\text{l.c.}}$
, the formalism of § 1.1 applies to the period functional
$\unicode[STIX]{x1D712}\in \mathscr{Y}^{\text{l.c.}}$
, the formalism of § 1.1 applies to the period functional
 $p\in \text{H}(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D712})$
defined by
$p\in \text{H}(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D712})$
defined by
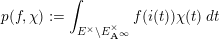 $$\begin{eqnarray}p(f,\unicode[STIX]{x1D712}):=\int _{E^{\times }\backslash E_{\mathbf{A}^{\infty }}^{\times }}f(i(t))\unicode[STIX]{x1D712}(t)\,dt\end{eqnarray}$$
$$\begin{eqnarray}p(f,\unicode[STIX]{x1D712}):=\int _{E^{\times }\backslash E_{\mathbf{A}^{\infty }}^{\times }}f(i(t))\unicode[STIX]{x1D712}(t)\,dt\end{eqnarray}$$
and to its dual
 $p^{\vee }(\cdot ,\unicode[STIX]{x1D712}^{-1})\in \text{H}(\unicode[STIX]{x1D70B}^{\vee },\unicode[STIX]{x1D712}^{-1})$
. Here
$p^{\vee }(\cdot ,\unicode[STIX]{x1D712}^{-1})\in \text{H}(\unicode[STIX]{x1D70B}^{\vee },\unicode[STIX]{x1D712}^{-1})$
. Here
![]() $dt$
is the Haar measure of total volume
$dt$
is the Haar measure of total volume
![]() $1$
.
$1$
.
The formula expressing the decomposition of their product was proved by Waldspurger (see [Reference WaldspurgerWal85] or [Reference Yuan, Zhang and ZhangYZZ12]): for all finite-order characters
 $\unicode[STIX]{x1D712}:E^{\times }\backslash E_{\mathbf{A}}^{\times }\rightarrow M(\unicode[STIX]{x1D712})^{\times }$
valued in some extension
$\unicode[STIX]{x1D712}:E^{\times }\backslash E_{\mathbf{A}}^{\times }\rightarrow M(\unicode[STIX]{x1D712})^{\times }$
valued in some extension
 $M(\unicode[STIX]{x1D712})\supset M$
, and for all
$M(\unicode[STIX]{x1D712})\supset M$
, and for all
![]() $f_{1}\in \unicode[STIX]{x1D70B}$
,
$f_{1}\in \unicode[STIX]{x1D70B}$
,
 $f_{2}\in \unicode[STIX]{x1D70B}^{\vee }$
, we have
$f_{2}\in \unicode[STIX]{x1D70B}^{\vee }$
, we have
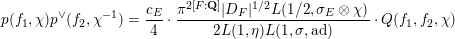 $$\begin{eqnarray}p(f_{1},\unicode[STIX]{x1D712})p^{\vee }(f_{2},\unicode[STIX]{x1D712}^{-1})=\frac{c_{E}}{4}\cdot \frac{\unicode[STIX]{x1D70B}^{2[F:\mathbf{Q}]}|D_{F}|^{1/2}L(1/2,\unicode[STIX]{x1D70E}_{E}\otimes \unicode[STIX]{x1D712})}{2L(1,\unicode[STIX]{x1D702})L(1,\unicode[STIX]{x1D70E},\operatorname{ad})}\cdot Q(f_{1},f_{2},\unicode[STIX]{x1D712})\end{eqnarray}$$
$$\begin{eqnarray}p(f_{1},\unicode[STIX]{x1D712})p^{\vee }(f_{2},\unicode[STIX]{x1D712}^{-1})=\frac{c_{E}}{4}\cdot \frac{\unicode[STIX]{x1D70B}^{2[F:\mathbf{Q}]}|D_{F}|^{1/2}L(1/2,\unicode[STIX]{x1D70E}_{E}\otimes \unicode[STIX]{x1D712})}{2L(1,\unicode[STIX]{x1D702})L(1,\unicode[STIX]{x1D70E},\operatorname{ad})}\cdot Q(f_{1},f_{2},\unicode[STIX]{x1D712})\end{eqnarray}$$
in
![]() $M(\unicode[STIX]{x1D712})$
. Notice that here we could trivially modify the right-hand side to replace the complex
$M(\unicode[STIX]{x1D712})$
. Notice that here we could trivially modify the right-hand side to replace the complex
![]() $L$
-function with the
$L$
-function with the
![]() $p$
-adic
$p$
-adic
![]() $L$
-function, thanks to the interpolation property defining the latter.
$L$
-function, thanks to the interpolation property defining the latter.
The
![]() $L$
-function terms of both the Waldspurger and the
$L$
-function terms of both the Waldspurger and the
![]() $p$
-adic Gross–Zagier formulas thus admit an interpolation as analytic functions (or sections of a sheaf) on
$p$
-adic Gross–Zagier formulas thus admit an interpolation as analytic functions (or sections of a sheaf) on
![]() $\mathscr{Y}_{\unicode[STIX]{x1D714}}$
. We can show that the other terms do as well.
$\mathscr{Y}_{\unicode[STIX]{x1D714}}$
. We can show that the other terms do as well.
Let
![]() $\unicode[STIX]{x1D70B}$
be the
$\unicode[STIX]{x1D70B}$
be the
![]() $M$
-rational representation of the (coherent or incoherent) quaternion algebra
$M$
-rational representation of the (coherent or incoherent) quaternion algebra
 $\mathbf{B}^{\times }\supset E_{\mathbf{A}}^{\times }$
considered above, with central character
$\mathbf{B}^{\times }\supset E_{\mathbf{A}}^{\times }$
considered above, with central character
![]() $\unicode[STIX]{x1D714}$
. It will be convenient to denote
$\unicode[STIX]{x1D714}$
. It will be convenient to denote
![]() $\unicode[STIX]{x1D70B}^{+}=\unicode[STIX]{x1D70B}$
,
$\unicode[STIX]{x1D70B}^{+}=\unicode[STIX]{x1D70B}$
,
 $\unicode[STIX]{x1D70B}^{-}=\unicode[STIX]{x1D70B}^{\vee }$
,
$\unicode[STIX]{x1D70B}^{-}=\unicode[STIX]{x1D70B}^{\vee }$
,
![]() $p^{+}=p$
,
$p^{+}=p$
,
 $p^{-}=p^{\vee }$
,
$p^{-}=p^{\vee }$
,
 $\mathscr{Y}_{\pm }=\mathscr{Y}_{\unicode[STIX]{x1D714}^{\pm 1}}$
, and, in the incoherent case,
$\mathscr{Y}_{\pm }=\mathscr{Y}_{\unicode[STIX]{x1D714}^{\pm 1}}$
, and, in the incoherent case,
 $A^{+}=A$
,
$A^{+}=A$
,
 $A^{-}=A^{\vee }$
,
$A^{-}=A^{\vee }$
,
 $P^{+}=P$
,
$P^{+}=P$
,
 $P^{-}=P^{\vee }$
,
$P^{-}=P^{\vee }$
,
![]() $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{A}$
.
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{A}$
.
We have a natural isomorphism
 $\mathscr{Y}_{+}\cong \mathscr{Y}_{-}$
given by inversion. If
$\mathscr{Y}_{+}\cong \mathscr{Y}_{-}$
given by inversion. If
![]() $\mathscr{F}$
is a sheaf on
$\mathscr{F}$
is a sheaf on
![]() $\mathscr{Y}_{-}$
, we denote by
$\mathscr{Y}_{-}$
, we denote by
![]() $\mathscr{F}^{\unicode[STIX]{x1D704}}$
its pullback to a sheaf on
$\mathscr{F}^{\unicode[STIX]{x1D704}}$
its pullback to a sheaf on
![]() $\mathscr{Y}_{+}$
; the same notation is used to transfer sections of such sheaves.
$\mathscr{Y}_{+}$
; the same notation is used to transfer sections of such sheaves.
Big Selmer groups and heights. Let
 $\unicode[STIX]{x1D712}_{\text{univ}}^{\pm }:\unicode[STIX]{x1D6E4}\rightarrow (\mathscr{O}(\mathscr{Y}_{\pm })^{\text{b}})^{\times }$
be the tautological character such that
$\unicode[STIX]{x1D712}_{\text{univ}}^{\pm }:\unicode[STIX]{x1D6E4}\rightarrow (\mathscr{O}(\mathscr{Y}_{\pm })^{\text{b}})^{\times }$
be the tautological character such that
 $\unicode[STIX]{x1D712}_{\text{univ}}^{\pm }(t)(\unicode[STIX]{x1D712})=\unicode[STIX]{x1D712}(t)^{\pm 1}$
for all
$\unicode[STIX]{x1D712}_{\text{univ}}^{\pm }(t)(\unicode[STIX]{x1D712})=\unicode[STIX]{x1D712}(t)^{\pm 1}$
for all
![]() $\unicode[STIX]{x1D712}\in \mathscr{Y}_{\pm }$
, and define an
$\unicode[STIX]{x1D712}\in \mathscr{Y}_{\pm }$
, and define an
 $\mathscr{O}(\mathscr{Y}_{\pm })^{\text{b}}$
-module
$\mathscr{O}(\mathscr{Y}_{\pm })^{\text{b}}$
-module
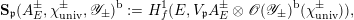 $$\begin{eqnarray}\mathbf{S}_{\mathfrak{p}}(A_{E}^{\pm },\unicode[STIX]{x1D712}_{\text{univ}}^{\pm },\mathscr{Y}_{\pm })^{\text{b}}:=H_{f}^{1}(E,V_{\mathfrak{ p}}A_{E}^{\pm }\otimes \mathscr{O}(\mathscr{Y}_{\pm })^{\text{b}}(\unicode[STIX]{x1D712}_{\text{univ}}^{\pm })),\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{S}_{\mathfrak{p}}(A_{E}^{\pm },\unicode[STIX]{x1D712}_{\text{univ}}^{\pm },\mathscr{Y}_{\pm })^{\text{b}}:=H_{f}^{1}(E,V_{\mathfrak{ p}}A_{E}^{\pm }\otimes \mathscr{O}(\mathscr{Y}_{\pm })^{\text{b}}(\unicode[STIX]{x1D712}_{\text{univ}}^{\pm })),\end{eqnarray}$$
where
 $\mathscr{O}(\mathscr{Y}_{\pm })^{\text{b}}(\unicode[STIX]{x1D712}_{\text{univ}}^{\pm })$
denotes the module of bounded global sections
$\mathscr{O}(\mathscr{Y}_{\pm })^{\text{b}}(\unicode[STIX]{x1D712}_{\text{univ}}^{\pm })$
denotes the module of bounded global sections
 $\mathscr{O}(\mathscr{Y}_{\pm })^{\text{b}}$
with
$\mathscr{O}(\mathscr{Y}_{\pm })^{\text{b}}$
with
![]() $\mathscr{G}_{E}$
-action by
$\mathscr{G}_{E}$
-action by
![]() $\unicode[STIX]{x1D712}_{\text{univ}}^{\pm }$
. Here, for a topological
$\unicode[STIX]{x1D712}_{\text{univ}}^{\pm }$
. Here, for a topological
![]() $\mathbf{Q}_{p}[\mathscr{G}_{E}]$
-module
$\mathbf{Q}_{p}[\mathscr{G}_{E}]$
-module
![]() $V$
which is potentially ordinary at all
$V$
which is potentially ordinary at all
![]() $w|p$
in the sense of Definition 4.1.1 below, with exact sequences
$w|p$
in the sense of Definition 4.1.1 below, with exact sequences
 $0\rightarrow V_{w}^{+}\rightarrow V_{w}\rightarrow V_{w}^{-}\rightarrow 0$
, the (Greenberg) Selmer group
$0\rightarrow V_{w}^{+}\rightarrow V_{w}\rightarrow V_{w}^{-}\rightarrow 0$
, the (Greenberg) Selmer group
 $H_{f}^{1}(E,V)\subset H^{1}(E,V):=H^{1}(\mathscr{G}_{E},V)$
is the group of those continuous cohomology classes
$H_{f}^{1}(E,V)\subset H^{1}(E,V):=H^{1}(\mathscr{G}_{E},V)$
is the group of those continuous cohomology classes
![]() $c$
which are unramified away from
$c$
which are unramified away from
![]() $p$
and such that, for every
$p$
and such that, for every
![]() $w|p$
, the restriction of
$w|p$
, the restriction of
![]() $c$
to a decomposition group at a
$c$
to a decomposition group at a
![]() $w$
is in the kernel of
$w$
is in the kernel of
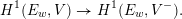 $$\begin{eqnarray}H^{1}(E_{w},V)\rightarrow H^{1}(E_{w},V^{-}).\end{eqnarray}$$
$$\begin{eqnarray}H^{1}(E_{w},V)\rightarrow H^{1}(E_{w},V^{-}).\end{eqnarray}$$
(In the case at hand,
 $V_{w}^{-}=V_{\mathfrak{p}}A_{E}^{\pm }|_{\mathscr{G}_{E,w}}^{-}$
is the maximal potentially unramified quotient of
$V_{w}^{-}=V_{\mathfrak{p}}A_{E}^{\pm }|_{\mathscr{G}_{E,w}}^{-}$
is the maximal potentially unramified quotient of
 $V_{\mathfrak{p}}A_{E}^{\pm }|_{\mathscr{G}_{E,w}}$
; cf. § 4.1.) For every non-exceptional
$V_{\mathfrak{p}}A_{E}^{\pm }|_{\mathscr{G}_{E,w}}$
; cf. § 4.1.) For every non-exceptional
 $\unicode[STIX]{x1D712}^{\pm }\in \mathscr{Y}_{\pm }^{\text{l.c.}}$
, the specialisation
$\unicode[STIX]{x1D712}^{\pm }\in \mathscr{Y}_{\pm }^{\text{l.c.}}$
, the specialisation
 $\mathbf{S}_{\mathfrak{p}}(A_{E}^{\pm },\unicode[STIX]{x1D712}_{\text{univ}}^{\pm },\mathscr{Y}_{\pm })^{\text{b}}\otimes L(\unicode[STIX]{x1D712})$
is isomorphic to the target of the Kummer map
$\mathbf{S}_{\mathfrak{p}}(A_{E}^{\pm },\unicode[STIX]{x1D712}_{\text{univ}}^{\pm },\mathscr{Y}_{\pm })^{\text{b}}\otimes L(\unicode[STIX]{x1D712})$
is isomorphic to the target of the Kummer map
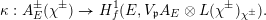 $$\begin{eqnarray}\unicode[STIX]{x1D705}:A_{E}^{\pm }(\unicode[STIX]{x1D712}^{\pm })\rightarrow H_{f}^{1}(E,V_{\mathfrak{ p}}A_{E}\otimes L(\unicode[STIX]{x1D712}^{\pm })_{\unicode[STIX]{x1D712}^{\pm }}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D705}:A_{E}^{\pm }(\unicode[STIX]{x1D712}^{\pm })\rightarrow H_{f}^{1}(E,V_{\mathfrak{ p}}A_{E}\otimes L(\unicode[STIX]{x1D712}^{\pm })_{\unicode[STIX]{x1D712}^{\pm }}).\end{eqnarray}$$
The work of Nekovář [Reference NekovářNek06] explains the exceptional specialisations and provides a height pairing on the big Selmer groups. The key underlying object is the Selmer complex
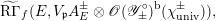 $$\begin{eqnarray}\widetilde{\text{R}\unicode[STIX]{x1D6E4}}_{f}(E,V_{\mathfrak{p}}A_{E}^{\pm }\otimes \mathscr{O}(\mathscr{Y}_{\pm }^{\circ })^{\text{b}}(\unicode[STIX]{x1D712}_{\text{univ}}^{\pm })),\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\text{R}\unicode[STIX]{x1D6E4}}_{f}(E,V_{\mathfrak{p}}A_{E}^{\pm }\otimes \mathscr{O}(\mathscr{Y}_{\pm }^{\circ })^{\text{b}}(\unicode[STIX]{x1D712}_{\text{univ}}^{\pm })),\end{eqnarray}$$
an object in the derived category of
 $\mathscr{O}(\mathscr{Y}_{\pm })^{\text{b}}$
-modules defined as in [Reference NekovářNek06, §0.8] taking
$\mathscr{O}(\mathscr{Y}_{\pm })^{\text{b}}$
-modules defined as in [Reference NekovářNek06, §0.8] taking
 $T=V_{\mathfrak{p}}A_{E}^{\pm }\otimes \mathscr{O}(\mathscr{Y}_{\pm }^{\circ })^{\text{b}}(\unicode[STIX]{x1D712}_{\text{univ}}^{\pm })$
and
$T=V_{\mathfrak{p}}A_{E}^{\pm }\otimes \mathscr{O}(\mathscr{Y}_{\pm }^{\circ })^{\text{b}}(\unicode[STIX]{x1D712}_{\text{univ}}^{\pm })$
and
 $U_{w}^{+}=V_{\mathfrak{p}}A_{E}^{\pm }|_{\mathscr{G}_{E_{w}}}^{+}\otimes \mathscr{O}(\mathscr{Y}_{\pm }^{\circ })^{\text{b}}(\unicode[STIX]{x1D712}_{\text{univ}}^{\pm })$
in the notation of [Reference NekovářNek06]. Its first cohomology group
$U_{w}^{+}=V_{\mathfrak{p}}A_{E}^{\pm }|_{\mathscr{G}_{E_{w}}}^{+}\otimes \mathscr{O}(\mathscr{Y}_{\pm }^{\circ })^{\text{b}}(\unicode[STIX]{x1D712}_{\text{univ}}^{\pm })$
in the notation of [Reference NekovářNek06]. Its first cohomology group
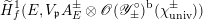 $$\begin{eqnarray}\widetilde{H}_{f}^{1}(E,V_{\mathfrak{ p}}A_{E}^{\pm }\otimes \mathscr{O}(\mathscr{Y}_{\pm }^{\circ })^{\text{b}}(\unicode[STIX]{x1D712}_{\text{univ}}^{\pm }))\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{H}_{f}^{1}(E,V_{\mathfrak{ p}}A_{E}^{\pm }\otimes \mathscr{O}(\mathscr{Y}_{\pm }^{\circ })^{\text{b}}(\unicode[STIX]{x1D712}_{\text{univ}}^{\pm }))\end{eqnarray}$$
satisfies the following property. For every
![]() $L$
-algebra quotient
$L$
-algebra quotient
![]() $R$
of
$R$
of
 $\mathscr{O}(\mathscr{Y}_{+}^{\circ })^{\text{b}}$
, letting
$\mathscr{O}(\mathscr{Y}_{+}^{\circ })^{\text{b}}$
, letting
 $\unicode[STIX]{x1D712}_{R}^{\pm }:\unicode[STIX]{x1D6E4}\rightarrow R^{\times }$
be the character deduced from
$\unicode[STIX]{x1D712}_{R}^{\pm }:\unicode[STIX]{x1D6E4}\rightarrow R^{\times }$
be the character deduced from
![]() $\unicode[STIX]{x1D712}_{\text{univ}}^{\pm }$
, there is an exact sequence [Reference NekovářNek06, (0.8.0.1)]
$\unicode[STIX]{x1D712}_{\text{univ}}^{\pm }$
, there is an exact sequence [Reference NekovářNek06, (0.8.0.1)]
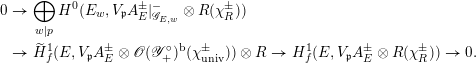 $$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle \displaystyle \underset{w|p}{\bigoplus }\,H^{0}(E_{w},V_{\mathfrak{p}}A_{E}^{\pm }|_{\mathscr{G}_{E,w}}^{-}\otimes R(\unicode[STIX]{x1D712}_{R}^{\pm }))\nonumber\\ \displaystyle & \rightarrow & \displaystyle \widetilde{H}_{f}^{1}(E,V_{\mathfrak{p}}A_{E}^{\pm }\otimes \mathscr{O}(\mathscr{Y}_{+}^{\circ })^{\text{b}}(\unicode[STIX]{x1D712}_{\text{univ}}^{\pm }))\otimes R\rightarrow H_{f}^{1}(E,V_{\mathfrak{p}}A_{E}^{\pm }\otimes R(\unicode[STIX]{x1D712}_{R}^{\pm }))\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle \displaystyle \underset{w|p}{\bigoplus }\,H^{0}(E_{w},V_{\mathfrak{p}}A_{E}^{\pm }|_{\mathscr{G}_{E,w}}^{-}\otimes R(\unicode[STIX]{x1D712}_{R}^{\pm }))\nonumber\\ \displaystyle & \rightarrow & \displaystyle \widetilde{H}_{f}^{1}(E,V_{\mathfrak{p}}A_{E}^{\pm }\otimes \mathscr{O}(\mathscr{Y}_{+}^{\circ })^{\text{b}}(\unicode[STIX]{x1D712}_{\text{univ}}^{\pm }))\otimes R\rightarrow H_{f}^{1}(E,V_{\mathfrak{p}}A_{E}^{\pm }\otimes R(\unicode[STIX]{x1D712}_{R}^{\pm }))\rightarrow 0.\end{eqnarray}$$
When
 $R=\mathscr{O}(\mathscr{Y}_{\pm })^{\text{b}}$
itself, each group
$R=\mathscr{O}(\mathscr{Y}_{\pm })^{\text{b}}$
itself, each group
 $H^{0}(E_{w},V_{\mathfrak{p}}A_{E}^{\pm }|_{\mathscr{G}_{E,w}}^{-}\otimes \mathscr{O}(\mathscr{Y}_{\pm })^{\text{b}}(\unicode[STIX]{x1D712}_{\text{univ}}^{\pm }))$
vanishes as
$H^{0}(E_{w},V_{\mathfrak{p}}A_{E}^{\pm }|_{\mathscr{G}_{E,w}}^{-}\otimes \mathscr{O}(\mathscr{Y}_{\pm })^{\text{b}}(\unicode[STIX]{x1D712}_{\text{univ}}^{\pm }))$
vanishes as
![]() $\unicode[STIX]{x1D712}_{\text{univ},w}$
is infinitely ramified; hence,
$\unicode[STIX]{x1D712}_{\text{univ},w}$
is infinitely ramified; hence,
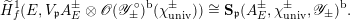 $$\begin{eqnarray}\widetilde{H}_{f}^{1}(E,V_{\mathfrak{ p}}A_{E}^{\pm }\otimes \mathscr{O}(\mathscr{Y}_{\pm }^{\circ })^{\text{b}}(\unicode[STIX]{x1D712}_{\text{univ}}^{\pm }))\cong \mathbf{S}_{\mathfrak{ p}}(A_{E}^{\pm },\unicode[STIX]{x1D712}_{\text{univ}}^{\pm },\mathscr{Y}_{\pm })^{\text{b}}.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{H}_{f}^{1}(E,V_{\mathfrak{ p}}A_{E}^{\pm }\otimes \mathscr{O}(\mathscr{Y}_{\pm }^{\circ })^{\text{b}}(\unicode[STIX]{x1D712}_{\text{univ}}^{\pm }))\cong \mathbf{S}_{\mathfrak{ p}}(A_{E}^{\pm },\unicode[STIX]{x1D712}_{\text{univ}}^{\pm },\mathscr{Y}_{\pm })^{\text{b}}.\end{eqnarray}$$
When
 $R=L(\unicode[STIX]{x1D712})$
with
$R=L(\unicode[STIX]{x1D712})$
with
 $\unicode[STIX]{x1D712}\in \mathscr{Y}^{\text{l.c.}}$
, the group
$\unicode[STIX]{x1D712}\in \mathscr{Y}^{\text{l.c.}}$
, the group
 $H^{0}(E_{w},V_{\mathfrak{p}}A_{E}^{\pm }|_{\mathscr{G}_{E,w}}^{-}\otimes L(\unicode[STIX]{x1D712}^{\pm })_{\unicode[STIX]{x1D712}^{\pm }})$
vanishes unless
$H^{0}(E_{w},V_{\mathfrak{p}}A_{E}^{\pm }|_{\mathscr{G}_{E,w}}^{-}\otimes L(\unicode[STIX]{x1D712}^{\pm })_{\unicode[STIX]{x1D712}^{\pm }})$
vanishes unless
 $\unicode[STIX]{x1D712}_{w}\cdot \unicode[STIX]{x1D6FC}_{v}\circ q_{w}=\mathbf{1}$
on
$\unicode[STIX]{x1D712}_{w}\cdot \unicode[STIX]{x1D6FC}_{v}\circ q_{w}=\mathbf{1}$
on
![]() $E_{w}^{\times }$
, that is, unless
$E_{w}^{\times }$
, that is, unless
![]() $\unicode[STIX]{x1D712}_{w}$
is exceptional.
$\unicode[STIX]{x1D712}_{w}$
is exceptional.
Finally, by [Reference NekovářNek06, ch. 11], there is a big height pairing
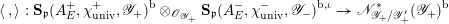 $$\begin{eqnarray}\langle \,,\rangle :\mathbf{S}_{\mathfrak{p}}(A_{E}^{+},\unicode[STIX]{x1D712}_{\text{univ}}^{+},\mathscr{Y}_{+})^{\text{b}}\otimes _{\mathscr{ O}_{\mathcal{Y}_{+}}}\mathbf{S}_{\mathfrak{p}}(A_{E}^{-},\unicode[STIX]{x1D712}_{\text{univ}}^{-},\mathscr{Y}_{-})^{\text{b},\unicode[STIX]{x1D704}}\rightarrow \mathscr{N}_{\mathscr{ Y}_{+}/\mathscr{Y}_{+}^{\prime }}^{\ast }(\mathscr{Y}_{+})^{\text{b}}\end{eqnarray}$$
$$\begin{eqnarray}\langle \,,\rangle :\mathbf{S}_{\mathfrak{p}}(A_{E}^{+},\unicode[STIX]{x1D712}_{\text{univ}}^{+},\mathscr{Y}_{+})^{\text{b}}\otimes _{\mathscr{ O}_{\mathcal{Y}_{+}}}\mathbf{S}_{\mathfrak{p}}(A_{E}^{-},\unicode[STIX]{x1D712}_{\text{univ}}^{-},\mathscr{Y}_{-})^{\text{b},\unicode[STIX]{x1D704}}\rightarrow \mathscr{N}_{\mathscr{ Y}_{+}/\mathscr{Y}_{+}^{\prime }}^{\ast }(\mathscr{Y}_{+})^{\text{b}}\end{eqnarray}$$
interpolating the height pairings on
 $H_{f}^{1}(E,V_{\mathfrak{p}}A\otimes L(\unicode[STIX]{x1D712}^{\pm })_{\unicode[STIX]{x1D712}^{\pm }})$
for non-exceptional
$H_{f}^{1}(E,V_{\mathfrak{p}}A\otimes L(\unicode[STIX]{x1D712}^{\pm })_{\unicode[STIX]{x1D712}^{\pm }})$
for non-exceptional
 $\unicode[STIX]{x1D712}\in \mathscr{Y}^{\text{l.c.}}$
(and more generally certain ‘extended’ pairings on
$\unicode[STIX]{x1D712}\in \mathscr{Y}^{\text{l.c.}}$
(and more generally certain ‘extended’ pairings on
 $\widetilde{H}_{f}^{1}(E,V_{\mathfrak{p}}A\otimes L(\unicode[STIX]{x1D712}^{\pm })_{\unicode[STIX]{x1D712}^{\pm }})$
for all
$\widetilde{H}_{f}^{1}(E,V_{\mathfrak{p}}A\otimes L(\unicode[STIX]{x1D712}^{\pm })_{\unicode[STIX]{x1D712}^{\pm }})$
for all
 $\unicode[STIX]{x1D712}\in \mathscr{Y}^{\text{l.c.}}$
; these will play no role here).
$\unicode[STIX]{x1D712}\in \mathscr{Y}^{\text{l.c.}}$
; these will play no role here).
Heegner–theta elements and anticyclotomic formulas. Keep the assumptions that for all
![]() $v|p$
,
$v|p$
,
![]() $E_{v}/F_{v}$
is split and
$E_{v}/F_{v}$
is split and
 $\unicode[STIX]{x1D70B}_{v}\cong \unicode[STIX]{x1D70E}_{v}$
is
$\unicode[STIX]{x1D70B}_{v}\cong \unicode[STIX]{x1D70E}_{v}$
is
![]() $\mathfrak{p}$
-nearly ordinary with unit character
$\mathfrak{p}$
-nearly ordinary with unit character
![]() $\unicode[STIX]{x1D6FC}_{v}$
. Then, after tensoring with
$\unicode[STIX]{x1D6FC}_{v}$
. Then, after tensoring with
 $\mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D6F9}_{p})$
(in order to use Kirillov models at
$\mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D6F9}_{p})$
(in order to use Kirillov models at
![]() $p$
), we will have a decomposition
$p$
), we will have a decomposition
 $\unicode[STIX]{x1D70B}^{\pm }\cong \unicode[STIX]{x1D70B}^{\pm ,p}\otimes \unicode[STIX]{x1D70B}_{p}^{\pm }$
, which is an isometry with respect to pairings
$\unicode[STIX]{x1D70B}^{\pm }\cong \unicode[STIX]{x1D70B}^{\pm ,p}\otimes \unicode[STIX]{x1D70B}_{p}^{\pm }$
, which is an isometry with respect to pairings
![]() $(\,,\,)^{p}$
,
$(\,,\,)^{p}$
,
![]() $(\,,\,)_{p}$
on each of the factors. By (1.1.2), for each
$(\,,\,)_{p}$
on each of the factors. By (1.1.2), for each
 $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}^{p}\unicode[STIX]{x1D712}_{p}\in \mathscr{Y}_{M}^{\text{l.c.}}$
we can then define a toric period
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}^{p}\unicode[STIX]{x1D712}_{p}\in \mathscr{Y}_{M}^{\text{l.c.}}$
we can then define a toric period
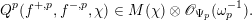 $$\begin{eqnarray}Q^{p}(f^{+,p},f^{-,p},\unicode[STIX]{x1D712})\in M(\unicode[STIX]{x1D712})\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D714}_{p}^{-1}).\end{eqnarray}$$
$$\begin{eqnarray}Q^{p}(f^{+,p},f^{-,p},\unicode[STIX]{x1D712})\in M(\unicode[STIX]{x1D712})\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D714}_{p}^{-1}).\end{eqnarray}$$
Given
 $f^{\pm ,p}\in \unicode[STIX]{x1D70B}^{\pm ,p}$
, we will construct an explicit pair of elements
$f^{\pm ,p}\in \unicode[STIX]{x1D70B}^{\pm ,p}$
, we will construct an explicit pair of elements
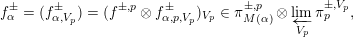 $$\begin{eqnarray}f_{\unicode[STIX]{x1D6FC}}^{\pm }=(f_{\unicode[STIX]{x1D6FC},V_{p}}^{\pm })=(f^{\pm ,p}\otimes f_{\unicode[STIX]{x1D6FC},p,V_{p}}^{\pm })_{V_{p}}\in \unicode[STIX]{x1D70B}_{M(\unicode[STIX]{x1D6FC})}^{\pm ,p}\otimes \underset{V_{p}}{\varprojlim }\,\unicode[STIX]{x1D70B}_{p}^{\pm ,V_{p}},\end{eqnarray}$$
$$\begin{eqnarray}f_{\unicode[STIX]{x1D6FC}}^{\pm }=(f_{\unicode[STIX]{x1D6FC},V_{p}}^{\pm })=(f^{\pm ,p}\otimes f_{\unicode[STIX]{x1D6FC},p,V_{p}}^{\pm })_{V_{p}}\in \unicode[STIX]{x1D70B}_{M(\unicode[STIX]{x1D6FC})}^{\pm ,p}\otimes \underset{V_{p}}{\varprojlim }\,\unicode[STIX]{x1D70B}_{p}^{\pm ,V_{p}},\end{eqnarray}$$
where the inverse system is indexed by compact open subgroups
 $V_{p}\subset E_{p}^{\times }\subset \mathbf{B}_{p}^{\times }$
containing
$V_{p}\subset E_{p}^{\times }\subset \mathbf{B}_{p}^{\times }$
containing
 $\operatorname{Ker}(\unicode[STIX]{x1D714}_{p})$
, with transition maps being given by averages under their
$\operatorname{Ker}(\unicode[STIX]{x1D714}_{p})$
, with transition maps being given by averages under their
![]() $\unicode[STIX]{x1D70B}_{p}^{\pm }$
-action, and
$\unicode[STIX]{x1D70B}_{p}^{\pm }$
-action, and
![]() $f_{\unicode[STIX]{x1D6FC},p,V_{p}}^{\pm }$
are suitable elements of
$f_{\unicode[STIX]{x1D6FC},p,V_{p}}^{\pm }$
are suitable elements of
![]() $\unicode[STIX]{x1D70B}_{p}^{\pm ,V_{p}}$
. We compute in Lemma 10.1.2 that we have
$\unicode[STIX]{x1D70B}_{p}^{\pm ,V_{p}}$
. We compute in Lemma 10.1.2 that we have
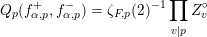 $$\begin{eqnarray}Q_{p}(f_{\unicode[STIX]{x1D6FC},p}^{+},f_{\unicode[STIX]{x1D6FC},p}^{-})=\unicode[STIX]{x1D701}_{F,p}(2)^{-1}\mathop{\prod }_{v|p}Z_{v}^{\circ }\end{eqnarray}$$
$$\begin{eqnarray}Q_{p}(f_{\unicode[STIX]{x1D6FC},p}^{+},f_{\unicode[STIX]{x1D6FC},p}^{-})=\unicode[STIX]{x1D701}_{F,p}(2)^{-1}\mathop{\prod }_{v|p}Z_{v}^{\circ }\end{eqnarray}$$
as sections of
 $\bigotimes _{v|p}\mathscr{O}_{\mathscr{ Y}_{v}^{\text{l.c.}}\times \unicode[STIX]{x1D6F9}_{v}}(\unicode[STIX]{x1D714}_{v})$
, where the left-hand side in the above expression is computed, for each
$\bigotimes _{v|p}\mathscr{O}_{\mathscr{ Y}_{v}^{\text{l.c.}}\times \unicode[STIX]{x1D6F9}_{v}}(\unicode[STIX]{x1D714}_{v})$
, where the left-hand side in the above expression is computed, for each
 $\unicode[STIX]{x1D712}_{p}\in \prod _{v|p}\mathscr{Y}_{v}^{\text{l.c.}}$
, as the limit of
$\unicode[STIX]{x1D712}_{p}\in \prod _{v|p}\mathscr{Y}_{v}^{\text{l.c.}}$
, as the limit of
 $Q_{p}(f_{\unicode[STIX]{x1D6FC},p,V_{p}}^{+},f_{\unicode[STIX]{x1D6FC},p,V_{p}}^{-})$
as
$Q_{p}(f_{\unicode[STIX]{x1D6FC},p,V_{p}}^{+},f_{\unicode[STIX]{x1D6FC},p,V_{p}}^{-})$
as
 $V_{p}\rightarrow \operatorname{Ker}(\unicode[STIX]{x1D714}_{p})$
.
$V_{p}\rightarrow \operatorname{Ker}(\unicode[STIX]{x1D714}_{p})$
.
For the following theorem, note that all the local signs in (1.1.1) extend to locally constant functions of
![]() $\mathscr{Y}_{+}$
(this is a simple special case of [Reference Pottharst and XiaoPX14, Proposition 3.3.4]); the quaternion algebra over
$\mathscr{Y}_{+}$
(this is a simple special case of [Reference Pottharst and XiaoPX14, Proposition 3.3.4]); the quaternion algebra over
![]() $\mathbf{A}$
determined by (1.1.1) is then also constant along the connected components of
$\mathbf{A}$
determined by (1.1.1) is then also constant along the connected components of
![]() $\mathscr{Y}_{+}$
. We will say that a connected component
$\mathscr{Y}_{+}$
. We will say that a connected component
 $\mathscr{Y}_{+}^{\circ }\subset \mathscr{Y}_{+}$
is of type
$\mathscr{Y}_{+}^{\circ }\subset \mathscr{Y}_{+}$
is of type
 $\unicode[STIX]{x1D700}\in \{\pm 1\}$
if
$\unicode[STIX]{x1D700}\in \{\pm 1\}$
if
 $\unicode[STIX]{x1D700}(1/2,\unicode[STIX]{x1D70E}_{E},\unicode[STIX]{x1D712})=\unicode[STIX]{x1D700}$
along
$\unicode[STIX]{x1D700}(1/2,\unicode[STIX]{x1D70E}_{E},\unicode[STIX]{x1D712})=\unicode[STIX]{x1D700}$
along
![]() $\mathscr{Y}^{\circ }$
.
$\mathscr{Y}^{\circ }$
.
Theorem C. Let
 $\mathscr{Y}_{+}^{\circ }\subset \mathscr{Y}_{+}$
be a connected component of type
$\mathscr{Y}_{+}^{\circ }\subset \mathscr{Y}_{+}$
be a connected component of type
![]() $\unicode[STIX]{x1D700}$
, let
$\unicode[STIX]{x1D700}$
, let
![]() $\mathbf{B}$
be the quaternion algebra determined by (1.1.1), and let
$\mathbf{B}$
be the quaternion algebra determined by (1.1.1), and let
![]() $\unicode[STIX]{x1D70B}^{\pm }$
be the representations of
$\unicode[STIX]{x1D70B}^{\pm }$
be the representations of
![]() $\mathbf{B}^{\times }$
constructed above. Finally, let
$\mathbf{B}^{\times }$
constructed above. Finally, let
 $\mathscr{Y}_{-}^{\circ }\subset \mathscr{Y}_{-}$
be the image of
$\mathscr{Y}_{-}^{\circ }\subset \mathscr{Y}_{-}$
be the image of
![]() $\mathscr{Y}_{+}^{\circ }$
under the inversion map.
$\mathscr{Y}_{+}^{\circ }$
under the inversion map.
-
(1) (Heegner–theta elements.) For each
 $f^{\pm ,p}\in \unicode[STIX]{x1D70B}^{\pm ,p}$
, there are elements uniquely determined by the property that, for any compact open subgroup
$f^{\pm ,p}\in \unicode[STIX]{x1D70B}^{\pm ,p}$
, there are elements uniquely determined by the property that, for any compact open subgroup $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6FC}}^{\pm }(f^{\pm ,p}) & \in & \displaystyle \mathscr{O}_{\mathscr{Y}_{+}}(\mathscr{Y}_{\pm }^{\circ })^{\text{b}}\quad \text{if }\unicode[STIX]{x1D700}=+1,\nonumber\\ \displaystyle \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{\pm }(f^{\pm ,p}) & \in & \displaystyle \mathbf{S}_{\mathfrak{p}}(A_{E}^{\pm },\unicode[STIX]{x1D712}_{\text{univ}}^{\pm },\mathscr{Y}_{\pm }^{\circ })^{\text{b}}\quad \text{if }\unicode[STIX]{x1D700}=-1\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6FC}}^{\pm }(f^{\pm ,p}) & \in & \displaystyle \mathscr{O}_{\mathscr{Y}_{+}}(\mathscr{Y}_{\pm }^{\circ })^{\text{b}}\quad \text{if }\unicode[STIX]{x1D700}=+1,\nonumber\\ \displaystyle \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{\pm }(f^{\pm ,p}) & \in & \displaystyle \mathbf{S}_{\mathfrak{p}}(A_{E}^{\pm },\unicode[STIX]{x1D712}_{\text{univ}}^{\pm },\mathscr{Y}_{\pm }^{\circ })^{\text{b}}\quad \text{if }\unicode[STIX]{x1D700}=-1\nonumber\end{eqnarray}$$
 $V_{p}\subset E_{p}^{\times }$
and any
$V_{p}\subset E_{p}^{\times }$
and any
 $V_{p}$
-invariant character
$V_{p}$
-invariant character
 $\unicode[STIX]{x1D712}^{\pm }\in \mathscr{Y}_{\pm }^{\circ }$
, we have where
$\unicode[STIX]{x1D712}^{\pm }\in \mathscr{Y}_{\pm }^{\circ }$
, we have where $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6FC}}^{\pm }(f^{\pm ,p})(\unicode[STIX]{x1D712}^{\pm }) & = & \displaystyle p(f_{\unicode[STIX]{x1D6FC},V_{p}}^{\pm },\unicode[STIX]{x1D712}^{\pm }),\nonumber\\ \displaystyle \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{\pm }(f^{\pm ,p})(\unicode[STIX]{x1D712}^{\pm }) & = & \displaystyle \unicode[STIX]{x1D705}(P(f_{\unicode[STIX]{x1D6FC},V_{p}}^{\pm },\unicode[STIX]{x1D712}^{\pm })),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6FC}}^{\pm }(f^{\pm ,p})(\unicode[STIX]{x1D712}^{\pm }) & = & \displaystyle p(f_{\unicode[STIX]{x1D6FC},V_{p}}^{\pm },\unicode[STIX]{x1D712}^{\pm }),\nonumber\\ \displaystyle \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{\pm }(f^{\pm ,p})(\unicode[STIX]{x1D712}^{\pm }) & = & \displaystyle \unicode[STIX]{x1D705}(P(f_{\unicode[STIX]{x1D6FC},V_{p}}^{\pm },\unicode[STIX]{x1D712}^{\pm })),\nonumber\end{eqnarray}$$
 $f_{\unicode[STIX]{x1D6FC}}^{\pm }$
is the element (1.4.8),
$f_{\unicode[STIX]{x1D6FC}}^{\pm }$
is the element (1.4.8),
 $p(\cdot )$
is the period integral (1.4.1), and
$p(\cdot )$
is the period integral (1.4.1), and
 $\unicode[STIX]{x1D705}$
is the Kummer map (1.4.3).
$\unicode[STIX]{x1D705}$
is the Kummer map (1.4.3).
-
(2) There is an element
uniquely determined by the property that, for all $$\begin{eqnarray}\mathscr{Q}=\unicode[STIX]{x1D701}_{F,p}(2)^{-1}\mathop{\prod }_{v\nmid p}\mathscr{Q}_{v}\in \operatorname{Hom}_{\mathscr{ O}(\mathscr{Y}_{+}^{\circ })^{\text{b}}[E_{\mathbf{A}^{p\infty }}^{\times }]}(\unicode[STIX]{x1D70B}^{+,p}\otimes \unicode[STIX]{x1D70B}^{-,p}\otimes \mathscr{O}(\mathscr{Y}_{+}^{\circ })^{\text{b}},\mathscr{O}(\mathscr{Y}_{+}^{\circ })^{\text{b}}\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D714}_{p}^{-1}))\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{Q}=\unicode[STIX]{x1D701}_{F,p}(2)^{-1}\mathop{\prod }_{v\nmid p}\mathscr{Q}_{v}\in \operatorname{Hom}_{\mathscr{ O}(\mathscr{Y}_{+}^{\circ })^{\text{b}}[E_{\mathbf{A}^{p\infty }}^{\times }]}(\unicode[STIX]{x1D70B}^{+,p}\otimes \unicode[STIX]{x1D70B}^{-,p}\otimes \mathscr{O}(\mathscr{Y}_{+}^{\circ })^{\text{b}},\mathscr{O}(\mathscr{Y}_{+}^{\circ })^{\text{b}}\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D714}_{p}^{-1}))\end{eqnarray}$$
 $f^{\pm ,p}\in \unicode[STIX]{x1D70B}^{\pm ,p}$
and all
$f^{\pm ,p}\in \unicode[STIX]{x1D70B}^{\pm ,p}$
and all
 $\unicode[STIX]{x1D712}\in \mathscr{Y}_{+}^{\circ \,\text{l.c.}}$
, we have
$\unicode[STIX]{x1D712}\in \mathscr{Y}_{+}^{\circ \,\text{l.c.}}$
, we have  $$\begin{eqnarray}\mathscr{Q}(f^{+,p},f^{-,p})(\unicode[STIX]{x1D712})=\unicode[STIX]{x1D701}_{F,p}(2)^{-1}\cdot Q^{p}(f^{+,p},f^{-,p},\unicode[STIX]{x1D712}^{p}).\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{Q}(f^{+,p},f^{-,p})(\unicode[STIX]{x1D712})=\unicode[STIX]{x1D701}_{F,p}(2)^{-1}\cdot Q^{p}(f^{+,p},f^{-,p},\unicode[STIX]{x1D712}^{p}).\end{eqnarray}$$
-
(3) (Anticyclotomic Waldspurger formula.) If
 $\unicode[STIX]{x1D700}=+1$
, we have in
$\unicode[STIX]{x1D700}=+1$
, we have in $$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6FC}}^{+}(f^{+,p})\cdot \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6FC}}^{-}(f^{-,p})^{\unicode[STIX]{x1D704}}=\frac{c_{E}}{4}\cdot L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})\cdot \mathscr{Q}(f^{+,p},f^{-,p})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6FC}}^{+}(f^{+,p})\cdot \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6FC}}^{-}(f^{-,p})^{\unicode[STIX]{x1D704}}=\frac{c_{E}}{4}\cdot L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})\cdot \mathscr{Q}(f^{+,p},f^{-,p})\end{eqnarray}$$
 $\mathscr{O}(\mathscr{Y}_{+}^{\circ })^{\text{b}}$
.
$\mathscr{O}(\mathscr{Y}_{+}^{\circ })^{\text{b}}$
.
-
(4) (Anticyclotomic Gross–Zagier formula.) If
 $\unicode[STIX]{x1D700}=-1$
and
$\unicode[STIX]{x1D700}=-1$
and
 $A$
has potentially
$A$
has potentially
 $\mathfrak{p}$
-ordinary reduction at all
$\mathfrak{p}$
-ordinary reduction at all
 $v|p$
, we have in
$v|p$
, we have in $$\begin{eqnarray}\langle \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f^{+,p}),\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-}(f^{-,p})^{\unicode[STIX]{x1D704}}\rangle =\frac{c_{E}}{2}\cdot \text{d}_{F}L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})\cdot \mathscr{Q}(f^{+,p},f^{-,p})\end{eqnarray}$$
$$\begin{eqnarray}\langle \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f^{+,p}),\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-}(f^{-,p})^{\unicode[STIX]{x1D704}}\rangle =\frac{c_{E}}{2}\cdot \text{d}_{F}L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})\cdot \mathscr{Q}(f^{+,p},f^{-,p})\end{eqnarray}$$
 $\mathscr{N}_{\mathscr{Y}_{+}/\mathscr{Y}_{+}^{\prime }}^{\ast }(\mathscr{Y}_{+}^{\circ })^{\text{b}}$
.
$\mathscr{N}_{\mathscr{Y}_{+}/\mathscr{Y}_{+}^{\prime }}^{\ast }(\mathscr{Y}_{+}^{\circ })^{\text{b}}$
.
In parts (3) and (4), we have used the canonical isomorphism
 $\mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D714}_{p})\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D714}_{p}^{-1})\cong M$
. The height pairing of part (4) is (1.4.6).
$\mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D714}_{p})\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D714}_{p}^{-1})\cong M$
. The height pairing of part (4) is (1.4.6).
Remark 1.4.1. Theorem C
(4) specialises to
![]() $0=0$
at any exceptional character
$0=0$
at any exceptional character
 $\unicode[STIX]{x1D712}\in \mathscr{Y}^{\text{l.c.}}$
, and in fact by the archimedean Gross–Zagier formula of [Reference Yuan, Zhang and ZhangYZZ12] it follows that the ‘pair of points’
$\unicode[STIX]{x1D712}\in \mathscr{Y}^{\text{l.c.}}$
, and in fact by the archimedean Gross–Zagier formula of [Reference Yuan, Zhang and ZhangYZZ12] it follows that the ‘pair of points’
 $\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f^{+,p})\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-}(f^{-,p})^{\unicode[STIX]{x1D704}}$
itself vanishes there. The leading term of
$\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f^{+,p})\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-}(f^{-,p})^{\unicode[STIX]{x1D704}}$
itself vanishes there. The leading term of
![]() $L_{p,\unicode[STIX]{x1D6FC}}$
at exceptional characters is studied in [Reference DisegniDis16].
$L_{p,\unicode[STIX]{x1D6FC}}$
at exceptional characters is studied in [Reference DisegniDis16].
1.5 Applications
Theorem B has by now standard applications to the
![]() $p$
-adic and the classical Birch and Swinnerton-Dyer conjectures; the interested reader will have no difficulty in obtaining them as in [Reference Perrin-RiouPer87, Reference DisegniDis15]. We obtain in particular one
$p$
-adic and the classical Birch and Swinnerton-Dyer conjectures; the interested reader will have no difficulty in obtaining them as in [Reference Perrin-RiouPer87, Reference DisegniDis15]. We obtain in particular one
![]() $p$
-divisibility in the classical Birch and Swinnerton-Dyer conjecture for a
$p$
-divisibility in the classical Birch and Swinnerton-Dyer conjecture for a
![]() $p$
-ordinary CM elliptic curve
$p$
-ordinary CM elliptic curve
![]() $A$
over a totally real field as in [Reference DisegniDis15, Theorem D] without the spurious assumptions of [Reference DisegniDis15] on the behaviour of
$A$
over a totally real field as in [Reference DisegniDis15, Theorem D] without the spurious assumptions of [Reference DisegniDis15] on the behaviour of
![]() $p$
in
$p$
in
![]() $F$
. In the rest of this subsection, we describe two other applications.
$F$
. In the rest of this subsection, we describe two other applications.
On the
![]() $p$
-adic Birch and Swinnerton-Dyer conjecture in anticyclotomic families. The next theorem, which can be thought of as a case of the
$p$
-adic Birch and Swinnerton-Dyer conjecture in anticyclotomic families. The next theorem, which can be thought of as a case of the
![]() $p$
-adic Birch and Swinnerton-Dyer conjecture in anticyclotomic families, combines Theorem C
(4) with work of Fouquet [Reference FouquetFou13] to generalise a result of Howard [Reference HowardHow05] towards a conjecture of Perrin-Riou [Reference Perrin-RiouPer87]. We first introduce some notation: let
$p$
-adic Birch and Swinnerton-Dyer conjecture in anticyclotomic families, combines Theorem C
(4) with work of Fouquet [Reference FouquetFou13] to generalise a result of Howard [Reference HowardHow05] towards a conjecture of Perrin-Riou [Reference Perrin-RiouPer87]. We first introduce some notation: let
 $\unicode[STIX]{x1D6EC}:=\mathscr{O}(\mathscr{Y}_{+}^{\circ })^{\text{b}}$
, and let the anticyclotomic height regulator
$\unicode[STIX]{x1D6EC}:=\mathscr{O}(\mathscr{Y}_{+}^{\circ })^{\text{b}}$
, and let the anticyclotomic height regulator
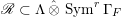 $$\begin{eqnarray}\mathscr{R}\subset \unicode[STIX]{x1D6EC}\,\hat{\otimes }\,\operatorname{Sym}^{r}\unicode[STIX]{x1D6E4}_{F}\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{R}\subset \unicode[STIX]{x1D6EC}\,\hat{\otimes }\,\operatorname{Sym}^{r}\unicode[STIX]{x1D6E4}_{F}\end{eqnarray}$$
be the discriminant of (1.4.6) on the
![]() $\unicode[STIX]{x1D6EC}$
-module
$\unicode[STIX]{x1D6EC}$
-module
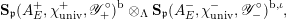 $$\begin{eqnarray}\mathbf{S}_{\mathfrak{p}}(A_{E}^{+},\unicode[STIX]{x1D712}_{\text{univ}}^{+},\mathscr{Y}_{+}^{\circ })^{\text{b}}\otimes _{\unicode[STIX]{x1D6EC}}\mathbf{S}_{\mathfrak{ p}}(A_{E}^{-},\unicode[STIX]{x1D712}_{\text{univ}}^{-},\mathscr{Y}_{-}^{\circ })^{\text{b},\unicode[STIX]{x1D704}},\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{S}_{\mathfrak{p}}(A_{E}^{+},\unicode[STIX]{x1D712}_{\text{univ}}^{+},\mathscr{Y}_{+}^{\circ })^{\text{b}}\otimes _{\unicode[STIX]{x1D6EC}}\mathbf{S}_{\mathfrak{ p}}(A_{E}^{-},\unicode[STIX]{x1D712}_{\text{univ}}^{-},\mathscr{Y}_{-}^{\circ })^{\text{b},\unicode[STIX]{x1D704}},\end{eqnarray}$$
where the integer
![]() $r$
in (1.5.1) is the generic rank of the finite-type
$r$
in (1.5.1) is the generic rank of the finite-type
![]() $\unicode[STIX]{x1D6EC}$
-module
$\unicode[STIX]{x1D6EC}$
-module
 $\mathbf{S}_{\mathfrak{p}}(A_{E}^{+},\unicode[STIX]{x1D712}_{\text{univ}}^{+},\mathscr{Y}_{+}^{\circ })^{\text{b}}$
. Recall that this module is the first cohomology of the Selmer complex
$\mathbf{S}_{\mathfrak{p}}(A_{E}^{+},\unicode[STIX]{x1D712}_{\text{univ}}^{+},\mathscr{Y}_{+}^{\circ })^{\text{b}}$
. Recall that this module is the first cohomology of the Selmer complex
 $\widetilde{\text{R}\unicode[STIX]{x1D6E4}}_{f}(E,V_{\mathfrak{p}}A^{+}\otimes \mathscr{O}(\mathscr{Y}_{+}^{\circ })^{\text{b}}(\unicode[STIX]{x1D712}_{\text{univ}}^{+}))$
of (1.4.4). Let
$\widetilde{\text{R}\unicode[STIX]{x1D6E4}}_{f}(E,V_{\mathfrak{p}}A^{+}\otimes \mathscr{O}(\mathscr{Y}_{+}^{\circ })^{\text{b}}(\unicode[STIX]{x1D712}_{\text{univ}}^{+}))$
of (1.4.4). Let
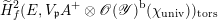 $$\begin{eqnarray}\widetilde{H}_{f}^{2}(E,V_{\mathfrak{ p}}A^{+}\otimes \mathscr{O}(\mathscr{Y})^{\text{b}}(\unicode[STIX]{x1D712}_{\text{univ}}))_{\text{tors}}\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{H}_{f}^{2}(E,V_{\mathfrak{ p}}A^{+}\otimes \mathscr{O}(\mathscr{Y})^{\text{b}}(\unicode[STIX]{x1D712}_{\text{univ}}))_{\text{tors}}\end{eqnarray}$$
be the torsion part of the second cohomology group. Its characteristic ideal in
![]() $\unicode[STIX]{x1D6EC}$
can roughly be thought of as interpolating the
$\unicode[STIX]{x1D6EC}$
can roughly be thought of as interpolating the
![]() $p$
-parts of the rational terms (order of the Tate–Shafarevich group, Tamagawa numbers) appearing on the algebraic side of the Birch and Swinnerton-Dyer conjecture for
$p$
-parts of the rational terms (order of the Tate–Shafarevich group, Tamagawa numbers) appearing on the algebraic side of the Birch and Swinnerton-Dyer conjecture for
![]() $A(\unicode[STIX]{x1D712})$
.
$A(\unicode[STIX]{x1D712})$
.
Theorem D. In the situation of Theorem C (4), assume furthermore that:
-
–
 $p\geqslant 5$
;
$p\geqslant 5$
; -
–
 $V_{\mathfrak{p}}A$
is potentially crystalline as a
$V_{\mathfrak{p}}A$
is potentially crystalline as a
 $\mathscr{G}_{F_{v}}$
-representation for all
$\mathscr{G}_{F_{v}}$
-representation for all
 $v|p$
;
$v|p$
; -
– the character
 $\unicode[STIX]{x1D714}$
is trivial and
$\unicode[STIX]{x1D714}$
is trivial and
 $\mathscr{Y}^{\circ }$
is the connected component of
$\mathscr{Y}^{\circ }$
is the connected component of
 $\mathbf{1}\in \mathscr{Y}$
;
$\mathbf{1}\in \mathscr{Y}$
; -
– the residual representation
 $\overline{\unicode[STIX]{x1D70C}}:\mathscr{G}_{F}\rightarrow \operatorname{Aut}_{\mathbf{F}_{\mathfrak{p}}}(T_{\mathfrak{p}}A\otimes \mathbf{F}_{\mathfrak{p}})$
is irreducible (where
$\overline{\unicode[STIX]{x1D70C}}:\mathscr{G}_{F}\rightarrow \operatorname{Aut}_{\mathbf{F}_{\mathfrak{p}}}(T_{\mathfrak{p}}A\otimes \mathbf{F}_{\mathfrak{p}})$
is irreducible (where
 $\mathbf{F}_{\mathfrak{p}}$
is the residue field of
$\mathbf{F}_{\mathfrak{p}}$
is the residue field of
 $M_{\mathfrak{p}}$
), and it remains irreducible when restricted to the Galois group of the Hilbert class field of
$M_{\mathfrak{p}}$
), and it remains irreducible when restricted to the Galois group of the Hilbert class field of
 $E$
;
$E$
; -
– for all
 $v|p$
, the image of
$v|p$
, the image of
 $\unicode[STIX]{x1D70C}|_{\mathscr{G}_{F,v}}$
is not scalar.
$\unicode[STIX]{x1D70C}|_{\mathscr{G}_{F,v}}$
is not scalar.
Then
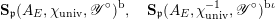 $$\begin{eqnarray}\mathbf{S}_{\mathfrak{p}}(A_{E},\unicode[STIX]{x1D712}_{\text{univ}},\mathscr{Y}^{\circ })^{\text{b}},\quad \mathbf{S}_{\mathfrak{p}}(A_{E},\unicode[STIX]{x1D712}_{\text{univ}}^{-1},\mathscr{Y}^{\circ })^{\text{b}\unicode[STIX]{x1D704}}\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{S}_{\mathfrak{p}}(A_{E},\unicode[STIX]{x1D712}_{\text{univ}},\mathscr{Y}^{\circ })^{\text{b}},\quad \mathbf{S}_{\mathfrak{p}}(A_{E},\unicode[STIX]{x1D712}_{\text{univ}}^{-1},\mathscr{Y}^{\circ })^{\text{b}\unicode[STIX]{x1D704}}\end{eqnarray}$$
both have generic rank
![]() $1$
over
$1$
over
![]() $\unicode[STIX]{x1D6EC}$
, a non-torsion element of their tensor product over
$\unicode[STIX]{x1D6EC}$
, a non-torsion element of their tensor product over
![]() $\unicode[STIX]{x1D6EC}$
is given by any
$\unicode[STIX]{x1D6EC}$
is given by any
 $\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f^{+,p})\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-}(f^{-,p})^{\unicode[STIX]{x1D704}}$
such that
$\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f^{+,p})\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-}(f^{-,p})^{\unicode[STIX]{x1D704}}$
such that
 $\mathscr{Q}(f^{+,p},f^{-,p})\neq 0$
, and
$\mathscr{Q}(f^{+,p},f^{-,p})\neq 0$
, and
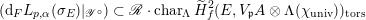 $$\begin{eqnarray}(\text{d}_{F}L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})|_{\mathscr{Y}^{\circ }})\subset \mathscr{R}\cdot \operatorname{char}_{\unicode[STIX]{x1D6EC}}\widetilde{H}_{f}^{2}(E,V_{\mathfrak{ p}}A\otimes \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D712}_{\text{univ}}))_{\text{tors}}\end{eqnarray}$$
$$\begin{eqnarray}(\text{d}_{F}L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})|_{\mathscr{Y}^{\circ }})\subset \mathscr{R}\cdot \operatorname{char}_{\unicode[STIX]{x1D6EC}}\widetilde{H}_{f}^{2}(E,V_{\mathfrak{ p}}A\otimes \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D712}_{\text{univ}}))_{\text{tors}}\end{eqnarray}$$
as
![]() $\unicode[STIX]{x1D6EC}$
-submodules of
$\unicode[STIX]{x1D6EC}$
-submodules of
![]() $\unicode[STIX]{x1D6EC}\,\hat{\otimes }\,\unicode[STIX]{x1D6E4}_{F}$
.
$\unicode[STIX]{x1D6EC}\,\hat{\otimes }\,\unicode[STIX]{x1D6E4}_{F}$
.
The ‘potentially crystalline’ assumption for
![]() $V_{\mathfrak{p}}A$
, which is satisfied if
$V_{\mathfrak{p}}A$
, which is satisfied if
![]() $A$
has potentially good reduction at all
$A$
has potentially good reduction at all
![]() $v|p$
, is imposed in order for
$v|p$
, is imposed in order for
 $V_{\mathfrak{p}}A\otimes \mathscr{O}(\mathscr{Y}^{\circ })^{\text{b}}$
to be ‘non-exceptional’ in the sense of [Reference FouquetFou13] (which is more restrictive than ours); the assumption on
$V_{\mathfrak{p}}A\otimes \mathscr{O}(\mathscr{Y}^{\circ })^{\text{b}}$
to be ‘non-exceptional’ in the sense of [Reference FouquetFou13] (which is more restrictive than ours); the assumption on
![]() $\unicode[STIX]{x1D714}$
allows us to invoke the results of [Reference Cornut and VatsalCV05, Reference Aflalo and NekovářAN10] on the non-vanishing of anticyclotomic Heegner points, and to write
$\unicode[STIX]{x1D714}$
allows us to invoke the results of [Reference Cornut and VatsalCV05, Reference Aflalo and NekovářAN10] on the non-vanishing of anticyclotomic Heegner points, and to write
 $A=A^{+}=A^{-}$
,
$A=A^{+}=A^{-}$
,
 $\mathscr{Y}=\mathscr{Y}_{+}=\mathscr{Y}_{-}=\mathscr{Y}_{\mathbf{1}}$
. See [Reference FouquetFou13, Theorem B(ii)] for the exact assumptions needed, which are slightly weaker.
$\mathscr{Y}=\mathscr{Y}_{+}=\mathscr{Y}_{-}=\mathscr{Y}_{\mathbf{1}}$
. See [Reference FouquetFou13, Theorem B(ii)] for the exact assumptions needed, which are slightly weaker.
The proof of Theorem D will be given in § 10.3.
Remark 1.5.1. When
![]() $F=\mathbf{Q}$
, the converse divisibility to (1.5.2) was recently proved by Wan [Reference WanWan14] under some assumptions.
$F=\mathbf{Q}$
, the converse divisibility to (1.5.2) was recently proved by Wan [Reference WanWan14] under some assumptions.
Generic non-vanishing of
![]() $p$
-adic heights on CM abelian varieties. The non-vanishing of (cyclotomic)
$p$
-adic heights on CM abelian varieties. The non-vanishing of (cyclotomic)
![]() $p$
-adic heights is in general, as we have mentioned, a deep conjecture (or a ‘strong suspicion’) of Schneider [Reference SchneiderSch85]. The following result provides some new evidence towards it. It is a corollary of Theorem C
(4) together with the non-vanishing results for Katz
$p$
-adic heights is in general, as we have mentioned, a deep conjecture (or a ‘strong suspicion’) of Schneider [Reference SchneiderSch85]. The following result provides some new evidence towards it. It is a corollary of Theorem C
(4) together with the non-vanishing results for Katz
![]() $p$
-adic
$p$
-adic
![]() $L$
-functions of Hida [Reference HidaHid10], Hsieh [Reference HsiehHsi14], and Burungale [Reference BurungaleBur15] (via a factorisation of the
$L$
-functions of Hida [Reference HidaHid10], Hsieh [Reference HsiehHsi14], and Burungale [Reference BurungaleBur15] (via a factorisation of the
![]() $p$
-adic
$p$
-adic
![]() $L$
-function). The result is a special case of a finer one to appear in forthcoming joint work with Burungale. For CM elliptic curves over
$L$
-function). The result is a special case of a finer one to appear in forthcoming joint work with Burungale. For CM elliptic curves over
![]() $\mathbf{Q}$
, it was known as a consequence of different non-vanishing results of Bertrand [Reference BertrandBer83] and Rohrlich [Reference RohrlichRoh84] (see [Reference Agboola and HowardAH06, Appendix A, by K. Rubin]).
$\mathbf{Q}$
, it was known as a consequence of different non-vanishing results of Bertrand [Reference BertrandBer83] and Rohrlich [Reference RohrlichRoh84] (see [Reference Agboola and HowardAH06, Appendix A, by K. Rubin]).
Theorem E. In the situation of Theorem C
(4), suppose that
![]() $A_{E}$
has complex multiplicationFootnote
10
and that
$A_{E}$
has complex multiplicationFootnote
10
and that
 $p\nmid 2D_{F}h_{E}^{-}$
, where
$p\nmid 2D_{F}h_{E}^{-}$
, where
 $h_{E}^{-}=h_{E}/h_{F}$
is the relative class number. Let
$h_{E}^{-}=h_{E}/h_{F}$
is the relative class number. Let
![]() $\langle \,,\rangle _{\text{cyc}}$
be the pairing deduced from (1.4.6) by the map
$\langle \,,\rangle _{\text{cyc}}$
be the pairing deduced from (1.4.6) by the map
 $\mathscr{N}_{\mathscr{Y}/\mathscr{Y}^{\prime }}(\mathscr{Y}^{\circ })^{\text{b}}\cong \mathscr{O}(\mathscr{Y}^{\circ })^{\text{b}}\,\hat{\otimes }\,\unicode[STIX]{x1D6E4}_{F}\rightarrow \mathscr{O}(\mathscr{Y}^{\circ })^{\text{b}}\,\hat{\otimes }\,\unicode[STIX]{x1D6E4}_{\text{cyc}}$
, where
$\mathscr{N}_{\mathscr{Y}/\mathscr{Y}^{\prime }}(\mathscr{Y}^{\circ })^{\text{b}}\cong \mathscr{O}(\mathscr{Y}^{\circ })^{\text{b}}\,\hat{\otimes }\,\unicode[STIX]{x1D6E4}_{F}\rightarrow \mathscr{O}(\mathscr{Y}^{\circ })^{\text{b}}\,\hat{\otimes }\,\unicode[STIX]{x1D6E4}_{\text{cyc}}$
, where
 $\unicode[STIX]{x1D6E4}_{\text{cyc}}=\unicode[STIX]{x1D6E4}_{\mathbf{Q}}$
viewed as a quotient of
$\unicode[STIX]{x1D6E4}_{\text{cyc}}=\unicode[STIX]{x1D6E4}_{\mathbf{Q}}$
viewed as a quotient of
![]() $\unicode[STIX]{x1D6E4}_{F}$
via the adèlic norm map.
$\unicode[STIX]{x1D6E4}_{F}$
via the adèlic norm map.
Then, for any
![]() $f^{\pm ,p}$
such that
$f^{\pm ,p}$
such that
 $\mathscr{Q}(f^{+,p},f^{-,p})\neq 0$
in
$\mathscr{Q}(f^{+,p},f^{-,p})\neq 0$
in
 $\mathscr{O}(\mathscr{Y}^{\circ })^{\text{b}}$
, we have
$\mathscr{O}(\mathscr{Y}^{\circ })^{\text{b}}$
, we have
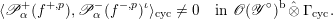 $$\begin{eqnarray}\langle \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f^{+,p}),\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-}(f^{-,p})^{\unicode[STIX]{x1D704}}\rangle _{\text{cyc}}\neq 0\quad \text{in }\mathscr{O}(\mathscr{Y}^{\circ })^{\text{b}}\,\hat{\otimes }\,\unicode[STIX]{x1D6E4}_{\text{cyc}}.\end{eqnarray}$$
$$\begin{eqnarray}\langle \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f^{+,p}),\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-}(f^{-,p})^{\unicode[STIX]{x1D704}}\rangle _{\text{cyc}}\neq 0\quad \text{in }\mathscr{O}(\mathscr{Y}^{\circ })^{\text{b}}\,\hat{\otimes }\,\unicode[STIX]{x1D6E4}_{\text{cyc}}.\end{eqnarray}$$
1.6 History and related work
We briefly discuss previous work towards our main theorems, and some related works. We will loosely term the ‘classical context’ the following specialisation of the setting of our main results:
![]() $A$
is an elliptic curve over
$A$
is an elliptic curve over
![]() $\mathbf{Q}$
with conductor
$\mathbf{Q}$
with conductor
![]() $N$
and good ordinary reduction at
$N$
and good ordinary reduction at
![]() $p$
;
$p$
;
![]() $p$
is odd; the quadratic imaginary field
$p$
is odd; the quadratic imaginary field
![]() $E$
has discriminant coprime to
$E$
has discriminant coprime to
![]() $N$
and it satisfies the Heegner condition: all primes dividing
$N$
and it satisfies the Heegner condition: all primes dividing
![]() $N$
split in
$N$
split in
![]() $E$
(this implies that
$E$
(this implies that
![]() $\mathbf{B}^{\infty }$
is split); the parametrisation
$\mathbf{B}^{\infty }$
is split); the parametrisation
 $f:J\rightarrow A$
factors through the Jacobian of the modular curve
$f:J\rightarrow A$
factors through the Jacobian of the modular curve
![]() $X_{0}(N)$
; the character
$X_{0}(N)$
; the character
![]() $\unicode[STIX]{x1D712}$
is unramified everywhere, or unramified away from
$\unicode[STIX]{x1D712}$
is unramified everywhere, or unramified away from
![]() $p$
.
$p$
.
Ancestors. In the classical context, Theorems A and B were proved by Perrin-Riou [Reference Perrin-RiouPer87]; intermediate steps towards the present generality were taken in [Reference DisegniDis15, Reference MaMa16]. When
![]() $E/F$
is split above
$E/F$
is split above
![]() $p$
, Theorem A can essentially be deduced from a general theorem of Hida [Reference HidaHid91] (cf. [Reference WanWan15, §7.3]), except for the location of the possible poles. Theorems C
(4) and D in the classical context are due to Howard [Reference HowardHow05] (in fact, Theorems B and C
(4) were first envisioned by Mazur [Reference MazurMaz83] in that context, whereas Perrin-Riou [Reference Perrin-RiouPer87] had conjectured the equality in (1.5.2)). Theorem C
(3) is hardly new and has many antecedents in the literature: see e.g. [Reference Van OrderVan12] and references therein.
$p$
, Theorem A can essentially be deduced from a general theorem of Hida [Reference HidaHid91] (cf. [Reference WanWan15, §7.3]), except for the location of the possible poles. Theorems C
(4) and D in the classical context are due to Howard [Reference HowardHow05] (in fact, Theorems B and C
(4) were first envisioned by Mazur [Reference MazurMaz83] in that context, whereas Perrin-Riou [Reference Perrin-RiouPer87] had conjectured the equality in (1.5.2)). Theorem C
(3) is hardly new and has many antecedents in the literature: see e.g. [Reference Van OrderVan12] and references therein.
Relatives. Some analogues of Theorem B were proven in situations which differ from the classical context in directions which are orthogonal to those of the present work: Nekovář [Reference NekovářNek95] and Shnidman [Reference ShnidmanShn16] dealt with the case of higher weights; Kobayashi [Reference KobayashiKob13] dealt with the case of elliptic curves with supersingular reduction.
Friends. We have already mentioned two other fully general Gross–Zagier formulas in the sense of § 1.1, namely the original archimedean one of [Reference Yuan, Zhang and ZhangYZZ12] generalising [Reference Gross and ZagierGZ86], and a different
![]() $p$
-adic formula proved in [Reference Liu, Zhang and ZhangLZZ15] generalising [Reference Bertolini, Darmon and PrasannaBDP13]. The panorama of existing formulas of this type is complemented by a handful of results, mostly in the classical context, valid in the presence of an exceptional zero (the case excluded in Theorem B). We refer the reader to [Reference DisegniDis16], where we prove a new such formula for
$p$
-adic formula proved in [Reference Liu, Zhang and ZhangLZZ15] generalising [Reference Bertolini, Darmon and PrasannaBDP13]. The panorama of existing formulas of this type is complemented by a handful of results, mostly in the classical context, valid in the presence of an exceptional zero (the case excluded in Theorem B). We refer the reader to [Reference DisegniDis16], where we prove a new such formula for
![]() $p$
-adic heights and review other ones due to Bertolini–Darmon. It is to be expected that all of those results should be generalisable to the framework of § 1.1.
$p$
-adic heights and review other ones due to Bertolini–Darmon. It is to be expected that all of those results should be generalisable to the framework of § 1.1.
Children. Finally, explicit versions of any Gross–Zagier formula in the framework of § 1.1 can be obtained by the explicit computation of the local integrals
![]() $Q_{v}$
. This is carried out in [Reference Cai, Shu and TianCST14], where it is applied to the cases of the archimedean Gross–Zagier formula and of the Waldspurger formula; the application to an explicit version of Theorem B can be obtained in exactly the same manner. An explicit version of the anticyclotomic formulas of Theorem C can also be obtained as a consequence: see [Reference DisegniDis16] for a special case.
$Q_{v}$
. This is carried out in [Reference Cai, Shu and TianCST14], where it is applied to the cases of the archimedean Gross–Zagier formula and of the Waldspurger formula; the application to an explicit version of Theorem B can be obtained in exactly the same manner. An explicit version of the anticyclotomic formulas of Theorem C can also be obtained as a consequence: see [Reference DisegniDis16] for a special case.
1.7 Outline of proofs and organisation of the paper
Let us briefly explain the main arguments and at the same time the organisation of the paper.
For the sake of simplicity, the notation used in this introductory discussion slightly differs from that of the body text, and we ignore powers of
![]() $\unicode[STIX]{x1D70B}$
, square roots of discriminants, and choices of additive character.
$\unicode[STIX]{x1D70B}$
, square roots of discriminants, and choices of additive character.
Construction of the
![]() $p$
-adic
$p$
-adic
![]() $L$
-function (§ 3). It is crucial for us to have a flexible construction which does not depend on choices of newforms. The starting point is Waldspurger’s [Reference WaldspurgerWal85] Rankin–Selberg integral
$L$
-function (§ 3). It is crucial for us to have a flexible construction which does not depend on choices of newforms. The starting point is Waldspurger’s [Reference WaldspurgerWal85] Rankin–Selberg integral
 $$\begin{eqnarray}\frac{(\unicode[STIX]{x1D711},I(\unicode[STIX]{x1D719},\unicode[STIX]{x1D712}^{\prime }))_{\text{Pet}}}{2L(1,\unicode[STIX]{x1D70E},\text{ad})/\unicode[STIX]{x1D701}_{F}(2)}=\frac{L(1/2,\unicode[STIX]{x1D70E}_{E}\otimes \unicode[STIX]{x1D712}^{\prime })}{L(1,\unicode[STIX]{x1D702})}\mathop{\prod }_{v}R_{v}^{\natural }(\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime }),\end{eqnarray}$$
$$\begin{eqnarray}\frac{(\unicode[STIX]{x1D711},I(\unicode[STIX]{x1D719},\unicode[STIX]{x1D712}^{\prime }))_{\text{Pet}}}{2L(1,\unicode[STIX]{x1D70E},\text{ad})/\unicode[STIX]{x1D701}_{F}(2)}=\frac{L(1/2,\unicode[STIX]{x1D70E}_{E}\otimes \unicode[STIX]{x1D712}^{\prime })}{L(1,\unicode[STIX]{x1D702})}\mathop{\prod }_{v}R_{v}^{\natural }(\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime }),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D70E}$
,
$\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D70E}$
,
![]() $I(\unicode[STIX]{x1D719},\unicode[STIX]{x1D712}^{\prime })$
is a mixed theta-Eisenstein series depending on a choice of an adèlic Schwartz function
$I(\unicode[STIX]{x1D719},\unicode[STIX]{x1D712}^{\prime })$
is a mixed theta-Eisenstein series depending on a choice of an adèlic Schwartz function
![]() $\unicode[STIX]{x1D719}$
, and
$\unicode[STIX]{x1D719}$
, and
 $R_{v}^{\natural }(\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}^{\prime })$
are normalised local integrals (almost all of which are equal to
$R_{v}^{\natural }(\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}^{\prime })$
are normalised local integrals (almost all of which are equal to
![]() $1$
). Then, after dividing both sides by the period
$1$
). Then, after dividing both sides by the period
 $2L(1,\unicode[STIX]{x1D70E},\text{ad})$
, we can:
$2L(1,\unicode[STIX]{x1D70E},\text{ad})$
, we can:
-
– interpolate the kernel
 $\unicode[STIX]{x1D712}^{\prime }\mapsto I(0,\unicode[STIX]{x1D719},\unicode[STIX]{x1D712}^{\prime })$
to a
$\unicode[STIX]{x1D712}^{\prime }\mapsto I(0,\unicode[STIX]{x1D719},\unicode[STIX]{x1D712}^{\prime })$
to a
 $\mathscr{Y}^{\prime }$
-family
$\mathscr{Y}^{\prime }$
-family
 $\mathscr{I}(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712}^{\prime })$
of
$\mathscr{I}(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712}^{\prime })$
of
 $p$
-adic modular forms for any choice of the components
$p$
-adic modular forms for any choice of the components
 $\unicode[STIX]{x1D719}^{p\infty }$
, and a well-chosen
$\unicode[STIX]{x1D719}^{p\infty }$
, and a well-chosen
 $\unicode[STIX]{x1D719}_{p\infty }$
(we will set
$\unicode[STIX]{x1D719}_{p\infty }$
(we will set
 $\unicode[STIX]{x1D719}_{v}(x,u)$
to be ‘standard’ at
$\unicode[STIX]{x1D719}_{v}(x,u)$
to be ‘standard’ at
 $v|\infty$
, and close to a delta function in
$v|\infty$
, and close to a delta function in
 $x$
at
$x$
at
 $v|p$
);
$v|p$
); -
– interpolate the functional ‘Petersson product with
 $\unicode[STIX]{x1D711}$
’ to a functional
$\unicode[STIX]{x1D711}$
’ to a functional
 $\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
on
$\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
on
 $p$
-adic modular forms, for any
$p$
-adic modular forms, for any
 $\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D70E}$
which is a ‘
$\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D70E}$
which is a ‘
 $\text{U}_{v}$
-eigenvector of eigenvalue
$\text{U}_{v}$
-eigenvector of eigenvalue
 $\unicode[STIX]{x1D6FC}_{v}$
’ at the places
$\unicode[STIX]{x1D6FC}_{v}$
’ at the places
 $v|p$
, and is antiholomorphic at infinity;
$v|p$
, and is antiholomorphic at infinity; -
– interpolate the normalised local integrals
 $\unicode[STIX]{x1D712}^{\prime }\mapsto R_{v}^{\natural }(\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime })$
to functions
$\unicode[STIX]{x1D712}^{\prime }\mapsto R_{v}^{\natural }(\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime })$
to functions
 $\mathscr{R}_{v}^{\natural }(\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D719}_{v})$
for all
$\mathscr{R}_{v}^{\natural }(\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D719}_{v})$
for all
 $v\nmid p\infty$
and any
$v\nmid p\infty$
and any
 $\unicode[STIX]{x1D711}_{v}$
,
$\unicode[STIX]{x1D711}_{v}$
,
 $\unicode[STIX]{x1D719}_{v}$
.
$\unicode[STIX]{x1D719}_{v}$
.
To conclude, we cover
![]() $\mathscr{Y}^{\prime }$
by finitely many open subsets
$\mathscr{Y}^{\prime }$
by finitely many open subsets
![]() $\mathscr{U}_{i}$
; for each
$\mathscr{U}_{i}$
; for each
![]() $i$
, we choose appropriate
$i$
, we choose appropriate
![]() $\unicode[STIX]{x1D711}^{p}$
,
$\unicode[STIX]{x1D711}^{p}$
,
![]() $\unicode[STIX]{x1D719}^{p}$
and we defineFootnote
11
$\unicode[STIX]{x1D719}^{p}$
and we defineFootnote
11
 $$\begin{eqnarray}L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})|_{\mathscr{U}_{i}}=\frac{\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\mathscr{I}(\unicode[STIX]{x1D711}^{p\infty }))}{\mathop{\prod }_{v\nmid p\infty }\mathscr{R}_{v}^{\natural }(\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D719}_{v})}.\end{eqnarray}$$
$$\begin{eqnarray}L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})|_{\mathscr{U}_{i}}=\frac{\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\mathscr{I}(\unicode[STIX]{x1D711}^{p\infty }))}{\mathop{\prod }_{v\nmid p\infty }\mathscr{R}_{v}^{\natural }(\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D719}_{v})}.\end{eqnarray}$$
The explicit computation of the local integrals at
![]() $p$
(in the Appendix) and at infinity yields the interpolation factor.
$p$
(in the Appendix) and at infinity yields the interpolation factor.
Proof of the Gross–Zagier formula and its anticyclotomic version. We outline the main arguments of our proof, with an emphasis on the reduction steps.
Multiplicity one. We borrow or adapt many ideas (and calculations) from [Reference Yuan, Zhang and ZhangYZZ12], in particular the systematic use of the multiplicity-one principle of § 1.1. As both sides of the formula are functionals in the same one-dimensional vector space, it is enough to prove the result for one pair
![]() $f_{1}$
,
$f_{1}$
,
![]() $f_{2}$
with
$f_{2}$
with
 $Q(f_{1},f_{2},\unicode[STIX]{x1D712})\neq 0$
; finding such
$Q(f_{1},f_{2},\unicode[STIX]{x1D712})\neq 0$
; finding such
![]() $f_{1}\otimes f_{2}$
is a local problem. It is equivalent to choosing functions
$f_{1}\otimes f_{2}$
is a local problem. It is equivalent to choosing functions
 $\unicode[STIX]{x1D711}_{v}\otimes \unicode[STIX]{x1D719}_{v}^{\prime }=\unicode[STIX]{x1D703}^{-1}(f_{1}\otimes f_{2})$
as just above, by the Shimizu lift
$\unicode[STIX]{x1D711}_{v}\otimes \unicode[STIX]{x1D719}_{v}^{\prime }=\unicode[STIX]{x1D703}^{-1}(f_{1}\otimes f_{2})$
as just above, by the Shimizu lift
![]() $\unicode[STIX]{x1D703}$
realising the Jacquet–Langlands correspondence (§ 5.1). For
$\unicode[STIX]{x1D703}$
realising the Jacquet–Langlands correspondence (§ 5.1). For
![]() $v|p$
, we thus have an explicit choice of such, corresponding to the one made above.Footnote
12
For
$v|p$
, we thus have an explicit choice of such, corresponding to the one made above.Footnote
12
For
![]() $v\nmid p$
, we can introduce several restrictions on
$v\nmid p$
, we can introduce several restrictions on
![]() $(\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D719}_{v})$
as in [Reference Yuan, Zhang and ZhangYZZ12], with the effect of simplifying many calculations of local heights (§ 6).
$(\unicode[STIX]{x1D711}_{v},\unicode[STIX]{x1D719}_{v})$
as in [Reference Yuan, Zhang and ZhangYZZ12], with the effect of simplifying many calculations of local heights (§ 6).
Arithmetic theta lifting and kernel identity (§ 5). In [Reference Yuan, Zhang and ZhangYZZ12], the authors introduce an arithmetic–geometric analogue of the Shimizu lift, by means of which they are able to write also the Heegner-points side of their formula as a Petersson product with
![]() $\unicode[STIX]{x1D711}$
of a certain geometric kernel. We can adapt without difficulty their results to reduce our formula to the assertionFootnote
13
that
$\unicode[STIX]{x1D711}$
of a certain geometric kernel. We can adapt without difficulty their results to reduce our formula to the assertionFootnote
13
that
 $$\begin{eqnarray}\text{d}_{F}\mathscr{I}(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712})-2L_{(p)}(1,\unicode[STIX]{x1D702})\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})\end{eqnarray}$$
$$\begin{eqnarray}\text{d}_{F}\mathscr{I}(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712})-2L_{(p)}(1,\unicode[STIX]{x1D702})\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})\end{eqnarray}$$
is killed by the
![]() $p$
-adic Petersson product
$p$
-adic Petersson product
![]() $\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
. Here
$\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
. Here
 $\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})$
is a modular form depending on
$\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})$
is a modular form depending on
![]() $\unicode[STIX]{x1D719}$
encoding the height pairings of CM points on Shimura curves and their Hecke translates; it generalises the classical generating series
$\unicode[STIX]{x1D719}$
encoding the height pairings of CM points on Shimura curves and their Hecke translates; it generalises the classical generating series
 $\sum _{m}\langle \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D709}}(P)[\unicode[STIX]{x1D712}],T(m)\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D709}}(P)\rangle \mathbf{q}^{m}$
.
$\sum _{m}\langle \unicode[STIX]{x1D704}_{\unicode[STIX]{x1D709}}(P)[\unicode[STIX]{x1D712}],T(m)\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D709}}(P)\rangle \mathbf{q}^{m}$
.
Decomposition and comparison (§§ 7–8). Both terms in the kernel identity are sums of local terms indexed by the finite places of
![]() $F$
. For
$F$
. For
![]() $v\nmid p$
, we compute both sides and show that the difference essentially coincides with the one computed in [Reference Yuan, Zhang and ZhangYZZ12]: it is either zero or, at bad places, a modular form orthogonal to all forms in
$v\nmid p$
, we compute both sides and show that the difference essentially coincides with the one computed in [Reference Yuan, Zhang and ZhangYZZ12]: it is either zero or, at bad places, a modular form orthogonal to all forms in
![]() $\unicode[STIX]{x1D70E}$
. In fact, we can show this only for a certain restricted set of
$\unicode[STIX]{x1D70E}$
. In fact, we can show this only for a certain restricted set of
![]() $q$
-expansion coefficients; as the global kernels are
$q$
-expansion coefficients; as the global kernels are
![]() $p$
-adic modular forms, this will suffice by a simple approximation argument (Lemma 2.1.2).
$p$
-adic modular forms, this will suffice by a simple approximation argument (Lemma 2.1.2).
![]() $p$
-adic Arakelov theory or analytic continuation. The argument just sketched relies on calculations of arithmetic intersections of CM points; this in general does not suffice, as we need to consider the contribution of the Hodge classes in the generating series too. It will turn out that such contribution vanishes; two approaches can be followed to show this. The first one, in analogy with [Reference ZhangZha01a, Reference Yuan, Zhang and ZhangYZZ12] and already used in a simpler context in [Reference DisegniDis15], is to make use of Besser’s
$p$
-adic Arakelov theory or analytic continuation. The argument just sketched relies on calculations of arithmetic intersections of CM points; this in general does not suffice, as we need to consider the contribution of the Hodge classes in the generating series too. It will turn out that such contribution vanishes; two approaches can be followed to show this. The first one, in analogy with [Reference ZhangZha01a, Reference Yuan, Zhang and ZhangYZZ12] and already used in a simpler context in [Reference DisegniDis15], is to make use of Besser’s
![]() $p$
-adic Arakelov theoryFootnote
14
[Reference BesserBes05] in order to separate such contribution.
$p$
-adic Arakelov theoryFootnote
14
[Reference BesserBes05] in order to separate such contribution.
We will follow an alternative approach (see Proposition 10.2.3), which exploits the generality of our context and the existence of extra variables in the
![]() $p$
-adic world. Once having constructed the Heegner–theta element
$p$
-adic world. Once having constructed the Heegner–theta element
![]() $\mathscr{P}^{\pm }$
, the anticyclotomic formula of Theorem C
(4) is essentially a corollary of Theorem B for all finite-order characters
$\mathscr{P}^{\pm }$
, the anticyclotomic formula of Theorem C
(4) is essentially a corollary of Theorem B for all finite-order characters
![]() $\unicode[STIX]{x1D712}$
: we only need to check the compatibility
$\unicode[STIX]{x1D712}$
: we only need to check the compatibility
 $Q_{v}(f_{\unicode[STIX]{x1D6FC},v}^{+},f_{\unicode[STIX]{x1D6FC},v}^{-},\unicode[STIX]{x1D712})=\unicode[STIX]{x1D701}_{F,v}(2)^{-1}\cdot Z_{v}(\unicode[STIX]{x1D712}_{v})$
for all
$Q_{v}(f_{\unicode[STIX]{x1D6FC},v}^{+},f_{\unicode[STIX]{x1D6FC},v}^{-},\unicode[STIX]{x1D712})=\unicode[STIX]{x1D701}_{F,v}(2)^{-1}\cdot Z_{v}(\unicode[STIX]{x1D712}_{v})$
for all
![]() $v|p$
by explicit computation. Conversely, thanks to the multiplicity-one result, it is also true that Theorem B for any
$v|p$
by explicit computation. Conversely, thanks to the multiplicity-one result, it is also true that Theorem B for any
![]() $\unicode[STIX]{x1D712}$
is obtained as a corollary of Theorem C
(4) by specialisation. We make use of both of these observations: we first prove Theorem B for all but finitely many finite-order characters
$\unicode[STIX]{x1D712}$
is obtained as a corollary of Theorem C
(4) by specialisation. We make use of both of these observations: we first prove Theorem B for all but finitely many finite-order characters
![]() $\unicode[STIX]{x1D712}$
; this suffices to deduce Theorem C
(4) by an analytic continuation argument, which finally yields Theorem B for the remaining characters
$\unicode[STIX]{x1D712}$
; this suffices to deduce Theorem C
(4) by an analytic continuation argument, which finally yields Theorem B for the remaining characters
![]() $\unicode[STIX]{x1D712}$
as well. The initially excluded characters are those (such as the trivial character when it is contemplated) for which the contribution of the Hodge classes is not already annihilated by
$\unicode[STIX]{x1D712}$
as well. The initially excluded characters are those (such as the trivial character when it is contemplated) for which the contribution of the Hodge classes is not already annihilated by
![]() $\unicode[STIX]{x1D712}$
-averaging; for all other characters the Arakelov-theoretic arguments just mentioned are then unnecessary.
$\unicode[STIX]{x1D712}$
-averaging; for all other characters the Arakelov-theoretic arguments just mentioned are then unnecessary.
Annihilation of
![]() $p$
-adic heights (§ 9). We are left to deal with the contribution of the places
$p$
-adic heights (§ 9). We are left to deal with the contribution of the places
![]() $v|p$
. We can show quite easily that this is zero for the analytic kernel. As in the original work of Perrin-Riou [Reference Perrin-RiouPer87], the vanishing of the contribution of the geometric kernel is the heart of the argument. We establish it via an elaboration of a method of Nekovář [Reference NekovářNek95] and Shnidman [Reference ShnidmanShn16]. The key new ingredient in adapting it to our semistable case is a simple integrality criterion for local heights in terms of intersections, introduced in § 4.3, after a review of the theory of heights.
$v|p$
. We can show quite easily that this is zero for the analytic kernel. As in the original work of Perrin-Riou [Reference Perrin-RiouPer87], the vanishing of the contribution of the geometric kernel is the heart of the argument. We establish it via an elaboration of a method of Nekovář [Reference NekovářNek95] and Shnidman [Reference ShnidmanShn16]. The key new ingredient in adapting it to our semistable case is a simple integrality criterion for local heights in terms of intersections, introduced in § 4.3, after a review of the theory of heights.
Local toric period. Finally, in the Appendix we compute the local toric period
 $Q(\unicode[STIX]{x1D703}(\unicode[STIX]{x1D711}_{v}\otimes \unicode[STIX]{x1D719}_{v}^{\prime }),\unicode[STIX]{x1D712}_{v})$
for
$Q(\unicode[STIX]{x1D703}(\unicode[STIX]{x1D711}_{v}\otimes \unicode[STIX]{x1D719}_{v}^{\prime }),\unicode[STIX]{x1D712}_{v})$
for
![]() $v|p$
and compare it to the interpolation factor of the
$v|p$
and compare it to the interpolation factor of the
![]() $p$
-adic
$p$
-adic
![]() $L$
-function. Both are highly ramified local integrals, and they turn out to differ by the multiplicative constant
$L$
-function. Both are highly ramified local integrals, and they turn out to differ by the multiplicative constant
 $L(1,\unicode[STIX]{x1D702}_{v})$
; this completes the comparison between the kernel identity and Theorem B.
$L(1,\unicode[STIX]{x1D702}_{v})$
; this completes the comparison between the kernel identity and Theorem B.
1.8 Notation
We largely follow the notation and conventions of [Reference Yuan, Zhang and ZhangYZZ12, §1.6].
![]() $L$
-functions. In the rest of the paper (and unlike in the Introduction, where we adhere to the more standard convention), all complex
$L$
-functions. In the rest of the paper (and unlike in the Introduction, where we adhere to the more standard convention), all complex
![]() $L$
- and zeta functions are complete including the
$L$
- and zeta functions are complete including the
![]() $\unicode[STIX]{x1D6E4}$
-factors at the infinite places. (This is to facilitate referring to the results and calculations of [Reference Yuan, Zhang and ZhangYZZ12], where this convention is adopted.)
$\unicode[STIX]{x1D6E4}$
-factors at the infinite places. (This is to facilitate referring to the results and calculations of [Reference Yuan, Zhang and ZhangYZZ12], where this convention is adopted.)
Fields and adèles. The fields
![]() $E$
and
$E$
and
![]() $F$
will be as fixed in the Introduction unless otherwise noted. The adèle ring of
$F$
will be as fixed in the Introduction unless otherwise noted. The adèle ring of
![]() $F$
will be denoted
$F$
will be denoted
![]() $\mathbf{A}_{F}$
or simply
$\mathbf{A}_{F}$
or simply
![]() $\mathbf{A}$
; it contains the ring
$\mathbf{A}$
; it contains the ring
![]() $\mathbf{A}^{\infty }$
of finite adèles. We let
$\mathbf{A}^{\infty }$
of finite adèles. We let
![]() $D_{F}$
and
$D_{F}$
and
![]() $D_{E}$
be the absolute discriminants of
$D_{E}$
be the absolute discriminants of
![]() $F$
and
$F$
and
![]() $E$
, respectively. We also choose an idèle
$E$
, respectively. We also choose an idèle
 $d\in \mathbf{A}^{\infty ,\times }$
generating the different of
$d\in \mathbf{A}^{\infty ,\times }$
generating the different of
![]() $F/\mathbf{Q}$
, and an idèle
$F/\mathbf{Q}$
, and an idèle
 $D\in \mathbf{A}^{\infty ,\times }$
generating the relative discriminant of
$D\in \mathbf{A}^{\infty ,\times }$
generating the relative discriminant of
![]() $E/F$
.
$E/F$
.
We use standard notation to restrict adèlic objects (groups,
![]() $L$
-functions, and so on) away from a finite set of places
$L$
-functions, and so on) away from a finite set of places
![]() $S$
, e.g.
$S$
, e.g.
 $\mathbf{A}^{S}:=\prod _{v\notin S}^{\prime }F_{v}$
, whereas
$\mathbf{A}^{S}:=\prod _{v\notin S}^{\prime }F_{v}$
, whereas
 $F_{S}:=\prod _{v\in S}F_{v}$
. When
$F_{S}:=\prod _{v\in S}F_{v}$
. When
![]() $S$
is the set of places above
$S$
is the set of places above
![]() $p$
(respectively
$p$
(respectively
![]() $\infty$
), we use this notation with ‘
$\infty$
), we use this notation with ‘
![]() $S$
’ replaced by ‘
$S$
’ replaced by ‘
![]() $p$
’ (respectively ‘
$p$
’ (respectively ‘
![]() $\infty$
’).
$\infty$
’).
We denote by
 $F_{\infty }^{+}\subset F_{\infty }$
the group of
$F_{\infty }^{+}\subset F_{\infty }$
the group of
![]() $(x_{\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}|\infty }$
with
$(x_{\unicode[STIX]{x1D70F}})_{\unicode[STIX]{x1D70F}|\infty }$
with
![]() $x_{\unicode[STIX]{x1D70F}}>0$
for all
$x_{\unicode[STIX]{x1D70F}}>0$
for all
![]() $\unicode[STIX]{x1D70F}$
, and we let
$\unicode[STIX]{x1D70F}$
, and we let
 $\mathbf{A}_{+}^{\times }:=\mathbf{A}^{\infty ,\times }F_{\infty }^{+}$
,
$\mathbf{A}_{+}^{\times }:=\mathbf{A}^{\infty ,\times }F_{\infty }^{+}$
,
 $F_{+}^{\times }:=F^{\times }\cap F_{\infty }^{+}$
.
$F_{+}^{\times }:=F^{\times }\cap F_{\infty }^{+}$
.
For a non-archimedean prime
![]() $v$
of a number field
$v$
of a number field
![]() $F$
, we denote by
$F$
, we denote by
![]() $q_{F,v}$
the cardinality of the residue field and by
$q_{F,v}$
the cardinality of the residue field and by
![]() $\unicode[STIX]{x1D71B}_{v}$
a uniformiser.
$\unicode[STIX]{x1D71B}_{v}$
a uniformiser.
Subgroups of
![]() $\mathbf{GL}_{2}$
. We consider
$\mathbf{GL}_{2}$
. We consider
![]() $\mathbf{GL}_{2}$
as an algebraic group over
$\mathbf{GL}_{2}$
as an algebraic group over
![]() $F$
. We denote by
$F$
. We denote by
![]() $P$
, respectively
$P$
, respectively
![]() $P^{1}$
, the subgroup of
$P^{1}$
, the subgroup of
![]() $\mathbf{GL}_{2}$
, respectively
$\mathbf{GL}_{2}$
, respectively
![]() $\mathbf{SL}_{2}$
, consisting of upper-triangular matrices; by
$\mathbf{SL}_{2}$
, consisting of upper-triangular matrices; by
 $A\subset P\subset \mathbf{GL}_{2}$
the diagonal torus; and by
$A\subset P\subset \mathbf{GL}_{2}$
the diagonal torus; and by
 $N\subset P\subset \mathbf{GL}_{2}$
the unipotent radical of
$N\subset P\subset \mathbf{GL}_{2}$
the unipotent radical of
![]() $P$
. We let
$P$
. We let
 $n(x):=(\!\begin{smallmatrix}1 & x\\ & 1\end{smallmatrix}\!)$
and
$n(x):=(\!\begin{smallmatrix}1 & x\\ & 1\end{smallmatrix}\!)$
and
 $$\begin{eqnarray}w:=\left(\begin{array}{@{}cc@{}} & 1\\ -1 & \end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}w:=\left(\begin{array}{@{}cc@{}} & 1\\ -1 & \end{array}\right).\end{eqnarray}$$
Quadratic torus. We let
 $T:=\operatorname{Res}_{E/F}\mathbf{G}_{m}$
; the embedding
$T:=\operatorname{Res}_{E/F}\mathbf{G}_{m}$
; the embedding
 $T(\mathbf{A}^{\infty })\subset \mathbf{B}^{\times }$
is fixed. We let
$T(\mathbf{A}^{\infty })\subset \mathbf{B}^{\times }$
is fixed. We let
 $Z:=\mathbf{G}_{m,F}$
, and view it both as a subgroup of
$Z:=\mathbf{G}_{m,F}$
, and view it both as a subgroup of
![]() $T$
and as the centre of
$T$
and as the centre of
![]() $\mathbf{GL}_{2}$
.
$\mathbf{GL}_{2}$
.
Automorphic quotients. If
![]() $G$
is a reductive group over the totally real field
$G$
is a reductive group over the totally real field
![]() $F$
, we denote
$F$
, we denote
 $$\begin{eqnarray}[G]:=G(F)\backslash G(\mathbf{A})/Z(\mathbf{A}).\end{eqnarray}$$
$$\begin{eqnarray}[G]:=G(F)\backslash G(\mathbf{A})/Z(\mathbf{A}).\end{eqnarray}$$
Measures. We choose local and global Haar measures as in [Reference Yuan, Zhang and ZhangYZZ12]. In particular, we have
 $$\begin{eqnarray}\operatorname{vol}(\mathbf{GL}_{2}(\mathscr{O}_{F,v}))=|d|_{v}^{2}\unicode[STIX]{x1D701}_{F,v}(2)^{-1}\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{vol}(\mathbf{GL}_{2}(\mathscr{O}_{F,v}))=|d|_{v}^{2}\unicode[STIX]{x1D701}_{F,v}(2)^{-1}\end{eqnarray}$$
for all non-archimedean
![]() $v$
.
$v$
.
We denote by
![]() $dt$
the local and global measures on
$dt$
the local and global measures on
![]() $T/Z$
of [Reference Yuan, Zhang and ZhangYZZ12], which give
$T/Z$
of [Reference Yuan, Zhang and ZhangYZZ12], which give
 $\operatorname{vol}([T],dt)=2L(1,\unicode[STIX]{x1D702})$
. The global measure
$\operatorname{vol}([T],dt)=2L(1,\unicode[STIX]{x1D702})$
. The global measure
 $$\begin{eqnarray}d^{\circ }t:=|D_{F}|^{1/2}|D_{E/F}|^{1/2}\,dt\end{eqnarray}$$
$$\begin{eqnarray}d^{\circ }t:=|D_{F}|^{1/2}|D_{E/F}|^{1/2}\,dt\end{eqnarray}$$
gives
 $\operatorname{vol}([T],d^{\circ }t)\in \mathbf{Q}^{\times }$
.
$\operatorname{vol}([T],d^{\circ }t)\in \mathbf{Q}^{\times }$
.
Regularised averages and integration. We borrow some notation from [Reference Yuan, Zhang and ZhangYZZ12, §1.6.7]. If
![]() $G$
is a topological group with a left Haar measure
$G$
is a topological group with a left Haar measure
![]() $dg$
with finite volume, we define
$dg$
with finite volume, we define
 $$\begin{eqnarray}\unicode[STIX]{x2A0D}_{G}f\,dg:=\frac{1}{\operatorname{vol}(G)}\int _{G}f(g)\,dg.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2A0D}_{G}f\,dg:=\frac{1}{\operatorname{vol}(G)}\int _{G}f(g)\,dg.\end{eqnarray}$$
(This reduces to the usual average when
![]() $G$
is a finite group.)
$G$
is a finite group.)
If
![]() $F$
is a totally real field and
$F$
is a totally real field and
![]() $f$
is a function on
$f$
is a function on
 $F^{\times }\backslash \mathbf{A}^{\times }$
invariant under
$F^{\times }\backslash \mathbf{A}^{\times }$
invariant under
![]() $F_{\infty }^{\times }$
, we denote
$F_{\infty }^{\times }$
, we denote
 $$\begin{eqnarray}\unicode[STIX]{x2A0D}_{\mathbf{A}^{\times }}f(z)\,dz:=\unicode[STIX]{x2A0D}_{F^{\times }\backslash \mathbf{A}^{\times }/F_{\unicode[STIX]{x1D70F}}^{\times }}f(z)\,dz,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2A0D}_{\mathbf{A}^{\times }}f(z)\,dz:=\unicode[STIX]{x2A0D}_{F^{\times }\backslash \mathbf{A}^{\times }/F_{\unicode[STIX]{x1D70F}}^{\times }}f(z)\,dz,\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D70F}$
is any archimedean place of
$\unicode[STIX]{x1D70F}$
is any archimedean place of
![]() $F$
. If
$F$
. If
![]() $f$
is further invariant under a compact open subgroup
$f$
is further invariant under a compact open subgroup
![]() $U$
, this reduces to the average over
$U$
, this reduces to the average over
 $F^{\times }\backslash \mathbf{A}^{\times }/F_{\infty }^{\times }U$
.
$F^{\times }\backslash \mathbf{A}^{\times }/F_{\infty }^{\times }U$
.
Finally, let
![]() $G$
be a reductive group over
$G$
be a reductive group over
![]() $F$
with an embedding of
$F$
with an embedding of
![]() $\mathbf{G}_{m/F}$
into the centre
$\mathbf{G}_{m/F}$
into the centre
![]() $G$
, and assume that
$G$
, and assume that
![]() $dg$
is a left Haar measure giving finite volume to
$dg$
is a left Haar measure giving finite volume to
 $[G]=G(F)\backslash G(\mathbf{A})/Z(\mathbf{A})$
. Let
$[G]=G(F)\backslash G(\mathbf{A})/Z(\mathbf{A})$
. Let
![]() $f$
be a function on
$f$
be a function on
 $G(F)\backslash G(\mathbf{A})/Z(F_{\infty })$
; then we define
$G(F)\backslash G(\mathbf{A})/Z(F_{\infty })$
; then we define
 $$\begin{eqnarray}\int _{[G]}^{\ast }f(g)\,dg:=\int _{[G]}\unicode[STIX]{x2A0D}_{Z(\mathbf{A})}f(zg)\,dz\,dg\end{eqnarray}$$
$$\begin{eqnarray}\int _{[G]}^{\ast }f(g)\,dg:=\int _{[G]}\unicode[STIX]{x2A0D}_{Z(\mathbf{A})}f(zg)\,dz\,dg\end{eqnarray}$$
and
 $$\begin{eqnarray}\unicode[STIX]{x2A0D}_{[G]}f(g)\,dg:=\frac{1}{\operatorname{vol}([G])}\int _{[G]}\unicode[STIX]{x2A0D}_{Z(\mathbf{A})}f(zg)\,dz\,dg.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2A0D}_{[G]}f(g)\,dg:=\frac{1}{\operatorname{vol}([G])}\int _{[G]}\unicode[STIX]{x2A0D}_{Z(\mathbf{A})}f(zg)\,dz\,dg.\end{eqnarray}$$
Note in particular that for functions which factor through a compact quotient of
 $G(F)\backslash G(A)$
and are locally constant there, the regularised integration reduces to a finite sum and, when using
$G(F)\backslash G(A)$
and are locally constant there, the regularised integration reduces to a finite sum and, when using
![]() $\mathbf{Q}$
-valued measures such as the measure
$\mathbf{Q}$
-valued measures such as the measure
![]() $d^{\circ }t$
on
$d^{\circ }t$
on
![]() $T$
, it makes sense for functions taking
$T$
, it makes sense for functions taking
![]() $p$
-adic values as well.
$p$
-adic values as well.
Multi-indices. If
![]() $S$
is a set and
$S$
is a set and
![]() $r\in \mathbf{Z}^{S}$
,
$r\in \mathbf{Z}^{S}$
,
![]() $p\in G^{S}$
for some group
$p\in G^{S}$
for some group
![]() $G$
, we often write
$G$
, we often write
 $p^{r}:=\prod _{v\in S}p_{v}^{r_{v}}$
. This will typically be applied in the following situation:
$p^{r}:=\prod _{v\in S}p_{v}^{r_{v}}$
. This will typically be applied in the following situation:
![]() $S=S_{p}$
is the set of places of
$S=S_{p}$
is the set of places of
![]() $F$
above
$F$
above
![]() $p$
,
$p$
,
![]() $G$
is the (semi)group of ideals of
$G$
is the (semi)group of ideals of
![]() $\mathscr{O}_{F}$
, and
$\mathscr{O}_{F}$
, and
![]() $p_{v}$
is the ideal corresponding to
$p_{v}$
is the ideal corresponding to
![]() $v$
.
$v$
.
Functions of
![]() $p$
-adic characters. When
$p$
-adic characters. When
![]() $\mathscr{Y}^{?}$
is one of the rigid spaces introduced above and
$\mathscr{Y}^{?}$
is one of the rigid spaces introduced above and
 $G(A)\in \mathscr{O}(\mathscr{Y}^{?})$
is a function on
$G(A)\in \mathscr{O}(\mathscr{Y}^{?})$
is a function on
![]() $\mathscr{Y}^{?}$
depending on other ‘parameters’
$\mathscr{Y}^{?}$
depending on other ‘parameters’
![]() $A$
(e.g. a
$A$
(e.g. a
![]() $p$
-adic
$p$
-adic
![]() $L$
-function), we write
$L$
-function), we write
 $G(A;\unicode[STIX]{x1D712})$
for the evaluation
$G(A;\unicode[STIX]{x1D712})$
for the evaluation
 $G(A)(\unicode[STIX]{x1D712})$
.
$G(A)(\unicode[STIX]{x1D712})$
.
2
 $p$
-adic modular forms
$p$
-adic modular forms
2.1 Modular forms and their
 $q$
-expansions
$q$
-expansions
Let
 $K\subset \mathbf{GL}_{2}(\widehat{\mathscr{O}}_{F})$
be an open compact subgroup. Recall that a Hilbert automorphic form of level
$K\subset \mathbf{GL}_{2}(\widehat{\mathscr{O}}_{F})$
be an open compact subgroup. Recall that a Hilbert automorphic form of level
![]() $K$
is a smooth function of moderate growth
$K$
is a smooth function of moderate growth
 $$\begin{eqnarray}\unicode[STIX]{x1D711}:\mathbf{GL}_{2}(F)\backslash \mathbf{GL}_{2}(\mathbf{A})/K\rightarrow \mathbf{C}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}:\mathbf{GL}_{2}(F)\backslash \mathbf{GL}_{2}(\mathbf{A})/K\rightarrow \mathbf{C}.\end{eqnarray}$$
Let
 $k\in \mathbf{Z}^{\operatorname{Hom}(F,\mathbf{R})}$
. Then an automorphic form is said to be of weight
$k\in \mathbf{Z}^{\operatorname{Hom}(F,\mathbf{R})}$
. Then an automorphic form is said to be of weight
![]() $k$
if it satisfies
$k$
if it satisfies
 $$\begin{eqnarray}\unicode[STIX]{x1D711}(gr_{\unicode[STIX]{x1D703}})=\unicode[STIX]{x1D711}(g)\unicode[STIX]{x1D713}_{\infty }(k\cdot \unicode[STIX]{x1D703})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}(gr_{\unicode[STIX]{x1D703}})=\unicode[STIX]{x1D711}(g)\unicode[STIX]{x1D713}_{\infty }(k\cdot \unicode[STIX]{x1D703})\end{eqnarray}$$
for all
 $r_{\unicode[STIX]{x1D703}}=((\!\begin{smallmatrix}\cos 2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D703}_{v} & \sin 2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D703}_{v}\\ -\sin 2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D703}_{v} & \cos 2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D703}_{v}\end{smallmatrix}\!))_{v|\infty }\in \mathbf{SO}_{2}(F_{\infty })$
. It is said to be holomorphic of weight
$r_{\unicode[STIX]{x1D703}}=((\!\begin{smallmatrix}\cos 2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D703}_{v} & \sin 2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D703}_{v}\\ -\sin 2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D703}_{v} & \cos 2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D703}_{v}\end{smallmatrix}\!))_{v|\infty }\in \mathbf{SO}_{2}(F_{\infty })$
. It is said to be holomorphic of weight
![]() $k$
if for all
$k$
if for all
 $g\in \mathbf{GL}_{2}(\mathbf{A}^{\infty })$
, the function of
$g\in \mathbf{GL}_{2}(\mathbf{A}^{\infty })$
, the function of
 $z_{\infty }=(x_{v}+iy_{v})_{v|\infty }\in \mathfrak{h}^{\operatorname{Hom}(F,\mathbf{R})}$
,
$z_{\infty }=(x_{v}+iy_{v})_{v|\infty }\in \mathfrak{h}^{\operatorname{Hom}(F,\mathbf{R})}$
,
 $$\begin{eqnarray}z_{\infty }\mapsto |y_{\infty }|_{\infty }^{-k/2}\unicode[STIX]{x1D711}\left(g(\!\begin{smallmatrix}y_{\infty } & x_{\infty }\\ & 1\end{smallmatrix}\!)\right),\end{eqnarray}$$
$$\begin{eqnarray}z_{\infty }\mapsto |y_{\infty }|_{\infty }^{-k/2}\unicode[STIX]{x1D711}\left(g(\!\begin{smallmatrix}y_{\infty } & x_{\infty }\\ & 1\end{smallmatrix}\!)\right),\end{eqnarray}$$
is holomorphic. Holomorphic Hilbert automorphic forms will be simply called modular forms.
Let
 $\unicode[STIX]{x1D714}:F^{\times }\backslash \mathbf{A}^{\times }\rightarrow \mathbf{C}^{\times }$
be a finite-order character. Then
$\unicode[STIX]{x1D714}:F^{\times }\backslash \mathbf{A}^{\times }\rightarrow \mathbf{C}^{\times }$
be a finite-order character. Then
![]() $\unicode[STIX]{x1D711}$
is said to be of character
$\unicode[STIX]{x1D711}$
is said to be of character
![]() $\unicode[STIX]{x1D714}$
if it satisfies
$\unicode[STIX]{x1D714}$
if it satisfies
 $\unicode[STIX]{x1D711}(zg)=\unicode[STIX]{x1D714}(z)\unicode[STIX]{x1D711}(g)$
for all
$\unicode[STIX]{x1D711}(zg)=\unicode[STIX]{x1D714}(z)\unicode[STIX]{x1D711}(g)$
for all
 $z\in Z(\mathbf{A})\cong \mathbf{A}^{\times }$
. We denote by
$z\in Z(\mathbf{A})\cong \mathbf{A}^{\times }$
. We denote by
 $M_{k}(K,\mathbf{C})$
the space of modular forms of level
$M_{k}(K,\mathbf{C})$
the space of modular forms of level
![]() $K$
and weight
$K$
and weight
![]() $k$
, and by
$k$
, and by
 $S_{k}(K,\mathbf{C})$
its subspace of cuspforms. We further denote by
$S_{k}(K,\mathbf{C})$
its subspace of cuspforms. We further denote by
 $M_{k}(K,\unicode[STIX]{x1D714},\mathbf{C})$
,
$M_{k}(K,\unicode[STIX]{x1D714},\mathbf{C})$
,
 $S_{k}(K,\unicode[STIX]{x1D714},\mathbf{C})$
the subspaces of forms of character
$S_{k}(K,\unicode[STIX]{x1D714},\mathbf{C})$
the subspaces of forms of character
![]() $\unicode[STIX]{x1D714}$
. We identify a scalar weight
$\unicode[STIX]{x1D714}$
. We identify a scalar weight
 $k\in \mathbf{Z}_{{\geqslant}0}$
with the corresponding parallel weight
$k\in \mathbf{Z}_{{\geqslant}0}$
with the corresponding parallel weight
 $(k,\ldots ,k)\in \mathbf{Z}_{{\geqslant}0}^{\operatorname{Hom}(F,\mathbf{R})}$
.
$(k,\ldots ,k)\in \mathbf{Z}_{{\geqslant}0}^{\operatorname{Hom}(F,\mathbf{R})}$
.
For
![]() $v$
a finite place of
$v$
a finite place of
![]() $F$
and
$F$
and
![]() $N$
an ideal of
$N$
an ideal of
![]() $\mathscr{O}_{F,v}$
, we define subgroups of
$\mathscr{O}_{F,v}$
, we define subgroups of
 $\mathbf{GL}_{2}(\mathscr{O}_{F,v})$
by
$\mathbf{GL}_{2}(\mathscr{O}_{F,v})$
by
 $$\begin{eqnarray}\displaystyle K_{0}(N)_{v} & = & \displaystyle \left\{\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\,\biggm\vert\,c\equiv 0~\text{mod}~N\right\},\nonumber\\ \displaystyle K_{1}(N)_{v} & = & \displaystyle \left\{\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\,\biggm\vert\,c,d-1\equiv 0~\text{mod}~N\right\},\nonumber\\ \displaystyle K^{1}(N)_{v} & = & \displaystyle \left\{\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\,\biggm\vert\,c,a-1\equiv 0~\text{mod}~N\right\},\nonumber\\ \displaystyle K_{1}^{1}(N)_{v} & = & \displaystyle \left\{\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\,\biggm\vert\,c,a-1,d-1\equiv 0~\text{mod}~N\right\},\nonumber\\ \displaystyle K(N)_{v} & = & \displaystyle \left\{\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\,\biggm\vert\,b,c,a-1,d-1\equiv 0~\text{mod}~N\right\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{0}(N)_{v} & = & \displaystyle \left\{\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\,\biggm\vert\,c\equiv 0~\text{mod}~N\right\},\nonumber\\ \displaystyle K_{1}(N)_{v} & = & \displaystyle \left\{\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\,\biggm\vert\,c,d-1\equiv 0~\text{mod}~N\right\},\nonumber\\ \displaystyle K^{1}(N)_{v} & = & \displaystyle \left\{\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\,\biggm\vert\,c,a-1\equiv 0~\text{mod}~N\right\},\nonumber\\ \displaystyle K_{1}^{1}(N)_{v} & = & \displaystyle \left\{\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\,\biggm\vert\,c,a-1,d-1\equiv 0~\text{mod}~N\right\},\nonumber\\ \displaystyle K(N)_{v} & = & \displaystyle \left\{\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\,\biggm\vert\,b,c,a-1,d-1\equiv 0~\text{mod}~N\right\}.\nonumber\end{eqnarray}$$
If
![]() $N$
is an ideal of
$N$
is an ideal of
![]() $\mathscr{O}_{F}$
and
$\mathscr{O}_{F}$
and
 $\ast \in \{\text{}_{0},\text{}_{1},\text{}^{1},\text{}_{1}^{1},\emptyset \}$
, we define subgroups
$\ast \in \{\text{}_{0},\text{}_{1},\text{}^{1},\text{}_{1}^{1},\emptyset \}$
, we define subgroups
![]() $K\ast (N)$
of
$K\ast (N)$
of
 $\mathbf{GL}_{2}(\widehat{\mathscr{O}}_{F})$
by
$\mathbf{GL}_{2}(\widehat{\mathscr{O}}_{F})$
by
 $K\ast (N)=\prod _{v}K\ast (N)_{v}$
. If
$K\ast (N)=\prod _{v}K\ast (N)_{v}$
. If
![]() $p$
is a rational prime and
$p$
is a rational prime and
 $r\in \mathbf{Z}_{{\geqslant}0}^{\{v|p\}}$
, we further define
$r\in \mathbf{Z}_{{\geqslant}0}^{\{v|p\}}$
, we further define
 $K\ast (p^{r})_{p}=\prod _{v}K\ast (\unicode[STIX]{x1D71B}_{v}^{r_{v}})_{v}\subset \mathbf{GL}_{2}(\mathscr{O}_{F,p})$
.
$K\ast (p^{r})_{p}=\prod _{v}K\ast (\unicode[STIX]{x1D71B}_{v}^{r_{v}})_{v}\subset \mathbf{GL}_{2}(\mathscr{O}_{F,p})$
.
Fix a non-trivial character
 $\unicode[STIX]{x1D713}:\mathbf{A}/F\rightarrow \mathbf{C}^{\times }$
. Any automorphic form
$\unicode[STIX]{x1D713}:\mathbf{A}/F\rightarrow \mathbf{C}^{\times }$
. Any automorphic form
![]() $\unicode[STIX]{x1D711}$
admits a Fourier–Whittaker expansion
$\unicode[STIX]{x1D711}$
admits a Fourier–Whittaker expansion
 $\unicode[STIX]{x1D711}(g)=\sum _{a\in F}W_{a}(g)$
, where
$\unicode[STIX]{x1D711}(g)=\sum _{a\in F}W_{a}(g)$
, where
 $W_{a}(g)=W_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713},a}(g)$
satisfies
$W_{a}(g)=W_{\unicode[STIX]{x1D711},\unicode[STIX]{x1D713},a}(g)$
satisfies
 $W_{a}(n(x)g)=\,\unicode[STIX]{x1D713}(ax)W_{a}(g)$
for all
$W_{a}(n(x)g)=\,\unicode[STIX]{x1D713}(ax)W_{a}(g)$
for all
![]() $x\in \mathbf{A}$
. If
$x\in \mathbf{A}$
. If
![]() $\unicode[STIX]{x1D711}$
is holomorphic of weight
$\unicode[STIX]{x1D711}$
is holomorphic of weight
![]() $k$
, we can further write
$k$
, we can further write
 $W_{a}(g)=W_{a^{\infty }}(g^{\infty })W_{a,\infty }(g_{\infty })$
with
$W_{a}(g)=W_{a^{\infty }}(g^{\infty })W_{a,\infty }(g_{\infty })$
with
 $W_{a,\infty }(g)=\prod _{v|\infty }W_{a,v}(g)$
, where
$W_{a,\infty }(g)=\prod _{v|\infty }W_{a,v}(g)$
, where
 $W_{a,v}=W_{a,v}^{(k_{v})}$
is the standard holomorphic Whittaker function of weight
$W_{a,v}=W_{a,v}^{(k_{v})}$
is the standard holomorphic Whittaker function of weight
![]() $k$
given by (suppressing the subscripts and using the Iwasawa decomposition)
$k$
given by (suppressing the subscripts and using the Iwasawa decomposition)
 $$\begin{eqnarray}W_{a}^{(k)}((\!\begin{smallmatrix}z & \\ & z\end{smallmatrix}\!)(\!\begin{smallmatrix}y & x\\ & 1\end{smallmatrix}\!)r_{\unicode[STIX]{x1D703}})=\left\{\begin{array}{@{}ll@{}}|y|^{k/2}\unicode[STIX]{x1D713}(a(x+iy))\unicode[STIX]{x1D713}(k\unicode[STIX]{x1D703})\mathbf{1}_{\mathbf{R}_{+}}(ay)\quad & \text{if}~a\neq 0,\\ |y|^{k/2}\unicode[STIX]{x1D713}(k\unicode[STIX]{x1D703})\mathbf{1}_{\mathbf{R}_{+}}(y)\quad & \text{if}~a=0.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}W_{a}^{(k)}((\!\begin{smallmatrix}z & \\ & z\end{smallmatrix}\!)(\!\begin{smallmatrix}y & x\\ & 1\end{smallmatrix}\!)r_{\unicode[STIX]{x1D703}})=\left\{\begin{array}{@{}ll@{}}|y|^{k/2}\unicode[STIX]{x1D713}(a(x+iy))\unicode[STIX]{x1D713}(k\unicode[STIX]{x1D703})\mathbf{1}_{\mathbf{R}_{+}}(ay)\quad & \text{if}~a\neq 0,\\ |y|^{k/2}\unicode[STIX]{x1D713}(k\unicode[STIX]{x1D703})\mathbf{1}_{\mathbf{R}_{+}}(y)\quad & \text{if}~a=0.\end{array}\right.\end{eqnarray}$$
(Similarly, we have a description in terms of the standard antiholomorphic Whittaker function
 $$\begin{eqnarray}W_{a}^{(-k)}((\!\begin{smallmatrix}z & \\ & z\end{smallmatrix}\!)(\!\begin{smallmatrix}y & x\\ & 1\end{smallmatrix}\!)r_{\unicode[STIX]{x1D703}})=\left\{\begin{array}{@{}ll@{}}|y|^{k/2}\unicode[STIX]{x1D713}(a(x+iy))\unicode[STIX]{x1D713}(-k\unicode[STIX]{x1D703})\mathbf{1}_{\mathbf{R}_{+}}(-ay)\quad & \text{if}~a\neq 0,\\ |y|^{k/2}\unicode[STIX]{x1D713}(-k\unicode[STIX]{x1D703})\mathbf{1}_{\mathbf{R}_{+}}(-y)\quad & \text{if}~a=0,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}W_{a}^{(-k)}((\!\begin{smallmatrix}z & \\ & z\end{smallmatrix}\!)(\!\begin{smallmatrix}y & x\\ & 1\end{smallmatrix}\!)r_{\unicode[STIX]{x1D703}})=\left\{\begin{array}{@{}ll@{}}|y|^{k/2}\unicode[STIX]{x1D713}(a(x+iy))\unicode[STIX]{x1D713}(-k\unicode[STIX]{x1D703})\mathbf{1}_{\mathbf{R}_{+}}(-ay)\quad & \text{if}~a\neq 0,\\ |y|^{k/2}\unicode[STIX]{x1D713}(-k\unicode[STIX]{x1D703})\mathbf{1}_{\mathbf{R}_{+}}(-y)\quad & \text{if}~a=0,\end{array}\right.\end{eqnarray}$$
for antiholomorphic forms of weight
![]() $-k<0$
.)
$-k<0$
.)
In this case we have an expansion
 $$\begin{eqnarray}\unicode[STIX]{x1D711}\left(\left(\begin{array}{@{}cc@{}}y & x\\ & 1\end{array}\right)\right)=|y|_{\infty }^{k/2}\mathop{\sum }_{a\in F_{{\geqslant}0}}W_{a}^{\infty }((\!\begin{smallmatrix}y^{\infty } & \\ & 1\end{smallmatrix}\!))\unicode[STIX]{x1D713}_{\infty }(iay_{\infty })\unicode[STIX]{x1D713}(ax)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}\left(\left(\begin{array}{@{}cc@{}}y & x\\ & 1\end{array}\right)\right)=|y|_{\infty }^{k/2}\mathop{\sum }_{a\in F_{{\geqslant}0}}W_{a}^{\infty }((\!\begin{smallmatrix}y^{\infty } & \\ & 1\end{smallmatrix}\!))\unicode[STIX]{x1D713}_{\infty }(iay_{\infty })\unicode[STIX]{x1D713}(ax)\end{eqnarray}$$
for all
 $y\in \mathbf{A}_{+}^{\times },x\in \mathbf{A}$
; here
$y\in \mathbf{A}_{+}^{\times },x\in \mathbf{A}$
; here
![]() $F_{{\geqslant}0}$
denotes the set of
$F_{{\geqslant}0}$
denotes the set of
![]() $a\in F$
satisfying
$a\in F$
satisfying
 $\unicode[STIX]{x1D70F}(a)\geqslant 0$
for all
$\unicode[STIX]{x1D70F}(a)\geqslant 0$
for all
 $\unicode[STIX]{x1D70F}:F{\hookrightarrow}\mathbf{R}$
.
$\unicode[STIX]{x1D70F}:F{\hookrightarrow}\mathbf{R}$
.
For a field
![]() $L$
, let the space of formal
$L$
, let the space of formal
![]() $q$
-expansions
$q$
-expansions
 $C^{\infty }(\mathbf{A}^{\infty ,\times },L)\unicode[STIX]{x27E6}\mathbf{q}^{F_{{\geqslant}0}}\unicode[STIX]{x27E7}^{\circ }$
be the set of those formal sums
$C^{\infty }(\mathbf{A}^{\infty ,\times },L)\unicode[STIX]{x27E6}\mathbf{q}^{F_{{\geqslant}0}}\unicode[STIX]{x27E7}^{\circ }$
be the set of those formal sums
 $W=\sum _{a\in F_{{\geqslant}0}}W_{a}\mathbf{q}^{a}$
with coefficients
$W=\sum _{a\in F_{{\geqslant}0}}W_{a}\mathbf{q}^{a}$
with coefficients
 $W_{a}\in C^{\infty }(\mathbf{A}^{\infty ,\times },L)$
such that, for some compact subset
$W_{a}\in C^{\infty }(\mathbf{A}^{\infty ,\times },L)$
such that, for some compact subset
 $A_{W}\subset \mathbf{A}^{\infty }$
, we have
$A_{W}\subset \mathbf{A}^{\infty }$
, we have
 $W_{a}(y)=0$
unless
$W_{a}(y)=0$
unless
 $ay\in A_{W}$
.
$ay\in A_{W}$
.
Let
![]() $\unicode[STIX]{x1D711}$
be a holomorphic automorphic form. The expression
$\unicode[STIX]{x1D711}$
be a holomorphic automorphic form. The expression
 $$\begin{eqnarray}\text{}^{\mathbf{q}}\unicode[STIX]{x1D711}(y):=\mathop{\sum }_{a\in F}W_{\unicode[STIX]{x1D711},a}^{\infty }((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!))\,\mathbf{q}^{a},\quad y\in \mathbf{A}^{\infty ,\times }\end{eqnarray}$$
$$\begin{eqnarray}\text{}^{\mathbf{q}}\unicode[STIX]{x1D711}(y):=\mathop{\sum }_{a\in F}W_{\unicode[STIX]{x1D711},a}^{\infty }((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!))\,\mathbf{q}^{a},\quad y\in \mathbf{A}^{\infty ,\times }\end{eqnarray}$$
belongs to
 $C^{\infty }(\mathbf{A}^{\infty ,\times },\mathbf{C})\unicode[STIX]{x27E6}\mathbf{q}^{F_{{\geqslant}0}}\unicode[STIX]{x27E7}^{\circ }$
and it is called the formal
$C^{\infty }(\mathbf{A}^{\infty ,\times },\mathbf{C})\unicode[STIX]{x27E6}\mathbf{q}^{F_{{\geqslant}0}}\unicode[STIX]{x27E7}^{\circ }$
and it is called the formal
![]() $q$
-expansion of
$q$
-expansion of
![]() $\unicode[STIX]{x1D711}$
. The space of formal
$\unicode[STIX]{x1D711}$
. The space of formal
![]() $q$
-expansions is an algebra in the obvious way, compatibly with the algebra structure on automorphic forms.
$q$
-expansions is an algebra in the obvious way, compatibly with the algebra structure on automorphic forms.
Proposition 2.1.1 (
 $q$
-expansion principle).
$q$
-expansion principle).
Let
 $K\subset \mathbf{GL}_{2}(\widehat{\mathscr{O}}_{F})$
be an open compact subgroup and let
$K\subset \mathbf{GL}_{2}(\widehat{\mathscr{O}}_{F})$
be an open compact subgroup and let
 $k\in \mathbf{Z}_{{\geqslant}0}^{\operatorname{Hom}(F,\mathbf{R})}$
. The
$k\in \mathbf{Z}_{{\geqslant}0}^{\operatorname{Hom}(F,\mathbf{R})}$
. The
![]() $q$
-expansion map defined by (2.1.3)
$q$
-expansion map defined by (2.1.3)
 $$\begin{eqnarray}\displaystyle M_{k}(K,\mathbf{C}) & \rightarrow & \displaystyle C^{\infty }(\mathbf{A}^{\infty ,\times },\mathbf{C})\unicode[STIX]{x27E6}\mathbf{q}^{F_{{\geqslant}0}}\unicode[STIX]{x27E7}^{\circ }\nonumber\\ \displaystyle \unicode[STIX]{x1D711} & \mapsto & \displaystyle \text{}^{\mathbf{q}}\unicode[STIX]{x1D711}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{k}(K,\mathbf{C}) & \rightarrow & \displaystyle C^{\infty }(\mathbf{A}^{\infty ,\times },\mathbf{C})\unicode[STIX]{x27E6}\mathbf{q}^{F_{{\geqslant}0}}\unicode[STIX]{x27E7}^{\circ }\nonumber\\ \displaystyle \unicode[STIX]{x1D711} & \mapsto & \displaystyle \text{}^{\mathbf{q}}\unicode[STIX]{x1D711}\nonumber\end{eqnarray}$$
is injective.
We say that a formal
![]() $q$
-expansion is modular if it belongs to the image of the
$q$
-expansion is modular if it belongs to the image of the
![]() $q$
-expansion map.
$q$
-expansion map.
Proof. This is (a weak form) of the
![]() $q$
-expansion principle of [Reference RapoportRap78, Théorème 6.7(i)]. In fact, our modular forms
$q$
-expansion principle of [Reference RapoportRap78, Théorème 6.7(i)]. In fact, our modular forms
![]() $\unicode[STIX]{x1D711}$
are identified with tuples
$\unicode[STIX]{x1D711}$
are identified with tuples
 $(\unicode[STIX]{x1D711}_{c})_{c\in \text{Cl}(F)^{+}}$
of Hilbert modular forms in the sense of [Reference RapoportRap78]. Then the non-vanishing of
$(\unicode[STIX]{x1D711}_{c})_{c\in \text{Cl}(F)^{+}}$
of Hilbert modular forms in the sense of [Reference RapoportRap78]. Then the non-vanishing of
![]() $^{\mathbf{q}}\unicode[STIX]{x1D711}$
for
$^{\mathbf{q}}\unicode[STIX]{x1D711}$
for
![]() $\unicode[STIX]{x1D711}\neq 0$
is obtained by applying the result of [Reference RapoportRap78] to each
$\unicode[STIX]{x1D711}\neq 0$
is obtained by applying the result of [Reference RapoportRap78] to each
![]() $\unicode[STIX]{x1D711}_{c}$
. See [Reference RapoportRap78, Lemme 6.12] for the comparison between various notions of Hilbert modular forms used there.◻
$\unicode[STIX]{x1D711}_{c}$
. See [Reference RapoportRap78, Lemme 6.12] for the comparison between various notions of Hilbert modular forms used there.◻
The spaces of formal
![]() $q$
-expansions introduced so far will often be convenient for us in terms of notation, but they are redundant: if
$q$
-expansions introduced so far will often be convenient for us in terms of notation, but they are redundant: if
 $k\in \mathbf{Z}_{{\geqslant}0}$
,
$k\in \mathbf{Z}_{{\geqslant}0}$
,
 $\unicode[STIX]{x1D711}\in M_{k}(K,\mathbf{C})$
, we have
$\unicode[STIX]{x1D711}\in M_{k}(K,\mathbf{C})$
, we have
 $W_{a}((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!))=W_{1}((\!\begin{smallmatrix}ay & \\ & 1\end{smallmatrix}\!))$
for all
$W_{a}((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!))=W_{1}((\!\begin{smallmatrix}ay & \\ & 1\end{smallmatrix}\!))$
for all
![]() $a\in F^{\times }$
,
$a\in F^{\times }$
,
![]() $y\in \mathbf{A}_{+}^{\times }$
. Moreover, if
$y\in \mathbf{A}_{+}^{\times }$
. Moreover, if
 $K\subset K(N)$
, then
$K\subset K(N)$
, then
 $|y^{\infty }|^{-k/2}W_{0}((\!\begin{smallmatrix}y^{\infty } & \\ & 1\end{smallmatrix}\!))$
and
$|y^{\infty }|^{-k/2}W_{0}((\!\begin{smallmatrix}y^{\infty } & \\ & 1\end{smallmatrix}\!))$
and
 $|y^{\infty }|^{-k/2}W_{1}^{\infty }((\!\begin{smallmatrix}y^{\infty } & \\ & 1\end{smallmatrix}\!))$
are further invariant under the action of
$|y^{\infty }|^{-k/2}W_{1}^{\infty }((\!\begin{smallmatrix}y^{\infty } & \\ & 1\end{smallmatrix}\!))$
are further invariant under the action of
 $U_{F}(N)=\{u\in \widehat{\mathscr{O}}_{F}^{\times }\mid u\equiv 1~\text{mod}~N\}$
by multiplication on
$U_{F}(N)=\{u\in \widehat{\mathscr{O}}_{F}^{\times }\mid u\equiv 1~\text{mod}~N\}$
by multiplication on
![]() $y$
(see [Reference HidaHid91, Theorem 1.1]). We term reducible of weight
$y$
(see [Reference HidaHid91, Theorem 1.1]). We term reducible of weight
![]() $k$
those formal
$k$
those formal
![]() $q$
-expansions satisfying these conditions for some
$q$
-expansions satisfying these conditions for some
![]() $N$
.
$N$
.
Define the space of reduced
![]() $q$
-expansions (of level
$q$
-expansions (of level
![]() $N$
) with values in a ring
$N$
) with values in a ring
![]() $A$
to be
$A$
to be
 $$\begin{eqnarray}M^{\prime }(K(N),L):=C(\mathbf{A}^{\infty ,\times }/F_{+}^{\times }U_{F}(N),L)\times L^{\mathbf{A}^{\infty ,\times }/U_{F}(N)};\end{eqnarray}$$
$$\begin{eqnarray}M^{\prime }(K(N),L):=C(\mathbf{A}^{\infty ,\times }/F_{+}^{\times }U_{F}(N),L)\times L^{\mathbf{A}^{\infty ,\times }/U_{F}(N)};\end{eqnarray}$$
if
![]() $K$
is any compact open subgroup, we define
$K$
is any compact open subgroup, we define
 $M^{\prime }(K,L):=M^{\prime }(K(N),L)$
for the largest subgroup
$M^{\prime }(K,L):=M^{\prime }(K(N),L)$
for the largest subgroup
 $K(N)\subset K$
. Let
$K(N)\subset K$
. Let
 $M^{\prime }(L):=\bigcup _{N}M^{\prime }(K(N),L)$
and
$M^{\prime }(L):=\bigcup _{N}M^{\prime }(K(N),L)$
and
 $M^{\prime }(K^{p},L):=\bigcup _{r}M^{\prime }(K^{p}K_{p}(p^{r}),L)$
.
$M^{\prime }(K^{p},L):=\bigcup _{r}M^{\prime }(K^{p}K_{p}(p^{r}),L)$
.
Given a reducible
![]() $q$
-expansion
$q$
-expansion
![]() $W$
of weight
$W$
of weight
![]() $k$
, we can then define the associated reduced
$k$
, we can then define the associated reduced
![]() $q$
-expansion
$q$
-expansion
 $(W_{0}^{\natural }(y),(W_{a}^{\natural })_{a\in \mathbf{A}^{\infty \times }})\in M^{\prime }(L)$
by
$(W_{0}^{\natural }(y),(W_{a}^{\natural })_{a\in \mathbf{A}^{\infty \times }})\in M^{\prime }(L)$
by
 $$\begin{eqnarray}W_{0}^{\natural }(y):=|y|^{-k/2}W_{0}^{\infty }((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!)),\quad W_{a}^{\natural }:=|a|^{-k/2}W_{1}^{\infty }((\!\begin{smallmatrix}a & \\ & 1\end{smallmatrix}\!)).\end{eqnarray}$$
$$\begin{eqnarray}W_{0}^{\natural }(y):=|y|^{-k/2}W_{0}^{\infty }((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!)),\quad W_{a}^{\natural }:=|a|^{-k/2}W_{1}^{\infty }((\!\begin{smallmatrix}a & \\ & 1\end{smallmatrix}\!)).\end{eqnarray}$$
If
![]() $A\subset \mathbf{C}$
is a subring, we denote by
$A\subset \mathbf{C}$
is a subring, we denote by
 $M_{k}(K,A)\subset M_{k}(K,\mathbf{C})$
,
$M_{k}(K,A)\subset M_{k}(K,\mathbf{C})$
,
 $S_{k}(K,A)\subset S_{k}(K,\mathbf{C})$
the subspaces of forms with reduced
$S_{k}(K,A)\subset S_{k}(K,\mathbf{C})$
the subspaces of forms with reduced
![]() $q$
-expansion coefficients in
$q$
-expansion coefficients in
![]() $A$
. If
$A$
. If
![]() $A$
is any
$A$
is any
![]() $\mathbf{Q}$
-algebra, we let
$\mathbf{Q}$
-algebra, we let
 $M_{k}(K,A)=M_{k}(K,\mathbf{Q})\otimes A$
,
$M_{k}(K,A)=M_{k}(K,\mathbf{Q})\otimes A$
,
 $S_{k}(K,A)=S_{k}(K,\mathbf{Q})\otimes A$
. Then it makes sense to talk about the
$S_{k}(K,A)=S_{k}(K,\mathbf{Q})\otimes A$
. Then it makes sense to talk about the
![]() $q$
-expansion of an element of those spaces.
$q$
-expansion of an element of those spaces.
If
![]() $\unicode[STIX]{x1D711}$
is a modular form, we still denote by
$\unicode[STIX]{x1D711}$
is a modular form, we still denote by
![]() $\text{}^{\mathbf{q}}\unicode[STIX]{x1D711}$
its reduced
$\text{}^{\mathbf{q}}\unicode[STIX]{x1D711}$
its reduced
![]() $q$
-expansion; in cases where the distinction is significant, the precise meaning of the expression
$q$
-expansion; in cases where the distinction is significant, the precise meaning of the expression
![]() $\text{}^{\mathbf{q}}\unicode[STIX]{x1D711}$
will be clear from its context.
$\text{}^{\mathbf{q}}\unicode[STIX]{x1D711}$
will be clear from its context.
![]() $p$
-adic modular forms. Let
$p$
-adic modular forms. Let
 $N\subset \mathscr{O}_{F}$
be a non-zero ideal prime to
$N\subset \mathscr{O}_{F}$
be a non-zero ideal prime to
![]() $p$
,
$p$
,
 $U_{F}(Np^{\infty })=\bigcap _{r\geqslant 0}U_{F}(Np^{r})$
. We endow the quotient
$U_{F}(Np^{\infty })=\bigcap _{r\geqslant 0}U_{F}(Np^{r})$
. We endow the quotient
 $\mathbf{A}^{\infty ,\times }/F_{+}^{\times }U_{F}(Np^{\infty })$
with the profinite topology. Let
$\mathbf{A}^{\infty ,\times }/F_{+}^{\times }U_{F}(Np^{\infty })$
with the profinite topology. Let
![]() $L$
be a complete Banach ring with norm
$L$
be a complete Banach ring with norm
![]() $|\cdot |$
. We define the space of
$|\cdot |$
. We define the space of
![]() $p$
-adic reduced
$p$
-adic reduced
![]() $q$
-expansions with values in
$q$
-expansions with values in
![]() $L$
to be
$L$
to be
 $$\begin{eqnarray}M^{\prime }(K^{p}(N),L):=C(\mathbf{A}^{\infty ,\times }/F_{+}^{\times }U_{F}(Np^{\infty }),L)\times L^{\mathbf{A}^{\infty ,\times }/U_{F}(Np^{\infty })}.\end{eqnarray}$$
$$\begin{eqnarray}M^{\prime }(K^{p}(N),L):=C(\mathbf{A}^{\infty ,\times }/F_{+}^{\times }U_{F}(Np^{\infty }),L)\times L^{\mathbf{A}^{\infty ,\times }/U_{F}(Np^{\infty })}.\end{eqnarray}$$
If
 $K^{p}\,\subset \,\mathbf{GL}_{2}(\mathbf{A}^{p\infty })$
is a compact open subgroup in general, we define
$K^{p}\,\subset \,\mathbf{GL}_{2}(\mathbf{A}^{p\infty })$
is a compact open subgroup in general, we define
 $\mathbf{M}^{\prime }(K^{p},L)\,:=\,\mathbf{M}^{\prime }(K^{p}(N),L)$
for the largest subgroup
$\mathbf{M}^{\prime }(K^{p},L)\,:=\,\mathbf{M}^{\prime }(K^{p}(N),L)$
for the largest subgroup
 $K^{p}(N)\subset K^{p}$
.
$K^{p}(N)\subset K^{p}$
.
Define a ‘norm’ (possibly taking the value
![]() $\infty$
)
$\infty$
)
![]() $\Vert \cdot \Vert$
on
$\Vert \cdot \Vert$
on
 $M^{\prime }(K^{p}(N),L)$
by
$M^{\prime }(K^{p}(N),L)$
by
 $$\begin{eqnarray}\Vert (W_{0}^{\natural },(W_{a}^{\natural })_{a\in \mathbf{A}^{\infty ,\times }/U_{F}(Np^{\infty })})\Vert :=\sup _{(y,a)}\{|W_{0}^{\natural }(y)|,|W_{a}^{\natural }|\}.\end{eqnarray}$$
$$\begin{eqnarray}\Vert (W_{0}^{\natural },(W_{a}^{\natural })_{a\in \mathbf{A}^{\infty ,\times }/U_{F}(Np^{\infty })})\Vert :=\sup _{(y,a)}\{|W_{0}^{\natural }(y)|,|W_{a}^{\natural }|\}.\end{eqnarray}$$
It induces a ‘norm’ on the (isomorphic) space of reducible
![]() $q$
-expansions with values in
$q$
-expansions with values in
![]() $L$
. Let
$L$
. Let
 $M^{\prime }(K^{p},L)^{\circ }\subset M^{\prime }(K^{p},L)$
be the set of elements on which
$M^{\prime }(K^{p},L)^{\circ }\subset M^{\prime }(K^{p},L)$
be the set of elements on which
![]() $\Vert ~\Vert$
is finite. We define the Banach space of
$\Vert ~\Vert$
is finite. We define the Banach space of
![]() $p$
-adic reduced
$p$
-adic reduced
![]() $q$
-expansions
$q$
-expansions
 $$\begin{eqnarray}\mathbf{M}^{\prime }(K^{p},L)\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{M}^{\prime }(K^{p},L)\end{eqnarray}$$
to be the completion of
 $M^{\prime }(K^{p},L)^{\circ }$
with respect to the norm
$M^{\prime }(K^{p},L)^{\circ }$
with respect to the norm
![]() $\Vert \cdot \Vert$
. We denote by
$\Vert \cdot \Vert$
. We denote by
 $\mathbf{S}^{\prime }(L)\subset \mathbf{M}^{\prime }(L)$
the space of reduced
$\mathbf{S}^{\prime }(L)\subset \mathbf{M}^{\prime }(L)$
the space of reduced
![]() $q$
-expansions with vanishing constant coefficients; when there is no risk of confusion we shall omit
$q$
-expansions with vanishing constant coefficients; when there is no risk of confusion we shall omit
![]() $L$
from the notation.
$L$
from the notation.
Suppose that
![]() $L$
is a field extension of
$L$
is a field extension of
![]() $\mathbf{Q}_{p}$
. The space of
$\mathbf{Q}_{p}$
. The space of
![]() $p$
-adic modular forms of tame level
$p$
-adic modular forms of tame level
 $K^{p}\subset \mathbf{GL}_{2}(\widehat{\mathscr{O}}_{F}^{p})$
with coefficients in
$K^{p}\subset \mathbf{GL}_{2}(\widehat{\mathscr{O}}_{F}^{p})$
with coefficients in
![]() $L$
, denoted by
$L$
, denoted by
 $\mathbf{M}(K^{p},L)$
, is defined to be the closure in
$\mathbf{M}(K^{p},L)$
, is defined to be the closure in
 $\mathbf{M}^{\prime }(K^{p},L)$
of the subspace generated by the reduced
$\mathbf{M}^{\prime }(K^{p},L)$
of the subspace generated by the reduced
![]() $q$
-expansions of elements of
$q$
-expansions of elements of
 $M_{2}(K^{p}K^{1}(p^{\infty })_{p},L)=\bigcup _{r\geqslant 0}M_{2}(K^{p}K^{1}(p^{r})_{p},L)$
. Tame levels and coefficient rings will be omitted from the notation when they are understood from context. We denote by
$M_{2}(K^{p}K^{1}(p^{\infty })_{p},L)=\bigcup _{r\geqslant 0}M_{2}(K^{p}K^{1}(p^{r})_{p},L)$
. Tame levels and coefficient rings will be omitted from the notation when they are understood from context. We denote by
 $\mathbf{S}:=\mathbf{M}\cap \mathbf{S}^{\prime }$
the space of
$\mathbf{S}:=\mathbf{M}\cap \mathbf{S}^{\prime }$
the space of
![]() $p$
-adic modular cuspforms.
$p$
-adic modular cuspforms.
Approximation. The
![]() $q$
-expansion principle of Proposition 2.1.1 is complemented by the following (obvious) result to provide a
$q$
-expansion principle of Proposition 2.1.1 is complemented by the following (obvious) result to provide a
![]() $p$
-adic replacement for the approximation argument in [Reference Yuan, Zhang and ZhangYZZ12].
$p$
-adic replacement for the approximation argument in [Reference Yuan, Zhang and ZhangYZZ12].
Lemma 2.1.2 (Approximation).
Let
![]() $S$
be a finite set of finite places of
$S$
be a finite set of finite places of
![]() $F$
, not containing any place
$F$
, not containing any place
![]() $v$
above
$v$
above
![]() $p$
. Let
$p$
. Let
![]() $\unicode[STIX]{x1D711}$
be a
$\unicode[STIX]{x1D711}$
be a
![]() $p$
-adic modular cuspform all of whose reduced
$p$
-adic modular cuspform all of whose reduced
![]() $q$
-expansion coefficients
$q$
-expansion coefficients
![]() $W_{a,\unicode[STIX]{x1D711}}^{\natural }$
are zero for all
$W_{a,\unicode[STIX]{x1D711}}^{\natural }$
are zero for all
 $a\in F^{\times }\mathbf{A}^{S\infty ,\times }$
. Then
$a\in F^{\times }\mathbf{A}^{S\infty ,\times }$
. Then
![]() $\unicode[STIX]{x1D711}=0.$
$\unicode[STIX]{x1D711}=0.$
Proof. The form
![]() $\unicode[STIX]{x1D711}$
has some tame level
$\unicode[STIX]{x1D711}$
has some tame level
![]() $K^{p}$
; then its coefficients are invariant under the action of some compact open
$K^{p}$
; then its coefficients are invariant under the action of some compact open
 $U_{F}^{p}\subset \mathbf{A}^{\infty ,\times }$
on the indices
$U_{F}^{p}\subset \mathbf{A}^{\infty ,\times }$
on the indices
![]() $a$
. Since
$a$
. Since
 $F^{\times }\mathbf{A}^{S\infty ,\times }U_{F}^{p}=\mathbf{A}^{\infty ,\times }$
, the lemma follows.◻
$F^{\times }\mathbf{A}^{S\infty ,\times }U_{F}^{p}=\mathbf{A}^{\infty ,\times }$
, the lemma follows.◻
Let
![]() $\overline{\mathbf{S}}^{\prime }$
be the quotient of
$\overline{\mathbf{S}}^{\prime }$
be the quotient of
![]() $\mathbf{S}^{\prime }$
by the subspace of reduced
$\mathbf{S}^{\prime }$
by the subspace of reduced
![]() $q$
-expansions which are zero at all
$q$
-expansions which are zero at all
 $a\in F^{\times }\mathbf{A}^{S\infty ,\times }$
, and let
$a\in F^{\times }\mathbf{A}^{S\infty ,\times }$
, and let
![]() $\overline{\mathbf{S}}$
be the image of
$\overline{\mathbf{S}}$
be the image of
![]() $\mathbf{S}$
in
$\mathbf{S}$
in
![]() $\overline{\mathbf{S}}^{\prime }$
(these notions depend on the set
$\overline{\mathbf{S}}^{\prime }$
(these notions depend on the set
![]() $S$
, which in our uses will be clear from the context). Then the lemma says that in
$S$
, which in our uses will be clear from the context). Then the lemma says that in
 $$\begin{eqnarray}\mathbf{S}\rightarrow \overline{\mathbf{S}}{\hookrightarrow}\overline{\mathbf{S}}^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{S}\rightarrow \overline{\mathbf{S}}{\hookrightarrow}\overline{\mathbf{S}}^{\prime },\end{eqnarray}$$
the first map is an isomorphism and the composition is an injection. We use the notation
 $\overline{\mathbf{S}}_{S}(K^{p}),\overline{\mathbf{S}}_{S}^{\prime }(K^{p})$
if we want to specify the set of places
$\overline{\mathbf{S}}_{S}(K^{p}),\overline{\mathbf{S}}_{S}^{\prime }(K^{p})$
if we want to specify the set of places
![]() $S$
and the tame level
$S$
and the tame level
![]() $K^{p}$
.
$K^{p}$
.
Families. Let
![]() $\mathscr{Y}^{?}$
be one of the rigid spaces defined in the Introduction, and
$\mathscr{Y}^{?}$
be one of the rigid spaces defined in the Introduction, and
 $K^{p}\subset \mathbf{GL}_{2}(\mathbf{A}^{p\infty })$
be a compact open subgroup.
$K^{p}\subset \mathbf{GL}_{2}(\mathbf{A}^{p\infty })$
be a compact open subgroup.
Definition 2.1.3. A
![]() $\mathscr{Y}^{?}$
-family of
$\mathscr{Y}^{?}$
-family of
![]() $q$
-expansions of modular forms of tame level
$q$
-expansions of modular forms of tame level
![]() $K^{p}$
is a reduced
$K^{p}$
is a reduced
![]() $q$
-expansion
$q$
-expansion
![]() $\text{}\underline{\unicode[STIX]{x1D711}}$
with values in
$\text{}\underline{\unicode[STIX]{x1D711}}$
with values in
![]() $\mathscr{O}(\mathscr{Y}^{?})$
, whose coefficients are algebraic on
$\mathscr{O}(\mathscr{Y}^{?})$
, whose coefficients are algebraic on
![]() $\mathscr{Y}^{?\text{l.c.}}$
, and such that for every point
$\mathscr{Y}^{?\text{l.c.}}$
, and such that for every point
 $\unicode[STIX]{x1D712}\in \mathscr{Y}^{?\text{l.c.}}$
,
$\unicode[STIX]{x1D712}\in \mathscr{Y}^{?\text{l.c.}}$
,
![]() $\text{}\underline{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D712})$
is the reduced
$\text{}\underline{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D712})$
is the reduced
![]() $q$
-expansion of a classical modular form
$q$
-expansion of a classical modular form
![]() $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D712})$
of level
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D712})$
of level
 $K^{p}K^{1}(p^{\infty })_{p}$
with coefficients in
$K^{p}K^{1}(p^{\infty })_{p}$
with coefficients in
![]() $M(\unicode[STIX]{x1D712})$
. We say that
$M(\unicode[STIX]{x1D712})$
. We say that
![]() $\text{}\underline{\unicode[STIX]{x1D711}}$
is bounded if it is bounded for the norm (2.1.4).
$\text{}\underline{\unicode[STIX]{x1D711}}$
is bounded if it is bounded for the norm (2.1.4).
Twisted modular forms. It will be convenient to consider the following relaxation of the notion of modular forms.
Definition 2.1.4. A twisted Hilbert automorphic form of weight
 $k\in \mathbf{Z}_{{\geqslant}0}^{\operatorname{Hom}(F,\mathbf{R})}$
and level
$k\in \mathbf{Z}_{{\geqslant}0}^{\operatorname{Hom}(F,\mathbf{R})}$
and level
 $K\subset \mathbf{GL}_{2}(\widehat{\mathscr{O}}_{F})$
is a smooth function
$K\subset \mathbf{GL}_{2}(\widehat{\mathscr{O}}_{F})$
is a smooth function
 $$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D711}}:\mathbf{GL}_{2}(\mathbf{A})/K\times \mathbf{A}^{\times }\rightarrow \mathbf{C}\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D711}}:\mathbf{GL}_{2}(\mathbf{A})/K\times \mathbf{A}^{\times }\rightarrow \mathbf{C}\end{eqnarray}$$
satisfying:
-
– for all
 $\unicode[STIX]{x1D6FE}\in \mathbf{GL}_{2}(F)$
,
$\unicode[STIX]{x1D6FE}\in \mathbf{GL}_{2}(F)$
,
 $r_{\unicode[STIX]{x1D703}}\in \mathbf{SO}_{2}(F_{\infty })$
,
$r_{\unicode[STIX]{x1D703}}\in \mathbf{SO}_{2}(F_{\infty })$
,  $$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D6FE}gr_{\unicode[STIX]{x1D703}},u)=\widetilde{\unicode[STIX]{x1D711}}(g,\det (\unicode[STIX]{x1D6FE})^{-1}u)\unicode[STIX]{x1D713}_{\infty }(k\cdot \unicode[STIX]{x1D703});\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D6FE}gr_{\unicode[STIX]{x1D703}},u)=\widetilde{\unicode[STIX]{x1D711}}(g,\det (\unicode[STIX]{x1D6FE})^{-1}u)\unicode[STIX]{x1D713}_{\infty }(k\cdot \unicode[STIX]{x1D703});\end{eqnarray}$$
-
–
 $\widetilde{\unicode[STIX]{x1D711}}$
is of moderate growth in the variable
$\widetilde{\unicode[STIX]{x1D711}}$
is of moderate growth in the variable
 $g\in \mathbf{GL}_{2}(\mathbf{A})$
and, for all
$g\in \mathbf{GL}_{2}(\mathbf{A})$
and, for all
 $g\in \mathbf{GL}_{2}(\mathbf{A})$
,
$g\in \mathbf{GL}_{2}(\mathbf{A})$
,
 $u=u_{\infty }u^{\infty }\mapsto \widetilde{\unicode[STIX]{x1D711}}(g,u)$
is the product of a function of the variable
$u=u_{\infty }u^{\infty }\mapsto \widetilde{\unicode[STIX]{x1D711}}(g,u)$
is the product of a function of the variable
 $u^{\infty }$
and of the function
$u^{\infty }$
and of the function
 $\mathbf{1}_{F_{\infty }^{+}}(u_{\infty })$
of the variable
$\mathbf{1}_{F_{\infty }^{+}}(u_{\infty })$
of the variable
 $u_{\infty }$
;
$u_{\infty }$
; -
– there exists a compact open subgroup
 $U_{F}\subset \mathbf{A}^{\infty ,\times }$
such that for all
$U_{F}\subset \mathbf{A}^{\infty ,\times }$
such that for all
 $g$
,
$g$
,
 $\widetilde{\unicode[STIX]{x1D711}}(g,\cdot )$
is invariant under
$\widetilde{\unicode[STIX]{x1D711}}(g,\cdot )$
is invariant under
 $U_{F}$
;
$U_{F}$
; -
– for each
 $g\in \mathbf{GL}_{2}(\mathbf{A})$
, there is an open compact subset
$g\in \mathbf{GL}_{2}(\mathbf{A})$
, there is an open compact subset
 $K_{g}\subset \mathbf{A}^{\infty ,\times }$
such that
$K_{g}\subset \mathbf{A}^{\infty ,\times }$
such that
 $\widetilde{\unicode[STIX]{x1D711}}(g,\cdot )$
is supported in
$\widetilde{\unicode[STIX]{x1D711}}(g,\cdot )$
is supported in
 $K_{g}F_{\infty }^{+}$
.
$K_{g}F_{\infty }^{+}$
.
Let
 $\unicode[STIX]{x1D714}:F^{\times }\backslash \mathbf{A}^{\times }\rightarrow \mathbf{C}^{\times }$
be a finite-order character. We say that a twisted automorphic form
$\unicode[STIX]{x1D714}:F^{\times }\backslash \mathbf{A}^{\times }\rightarrow \mathbf{C}^{\times }$
be a finite-order character. We say that a twisted automorphic form
![]() $\widetilde{\unicode[STIX]{x1D711}}$
has central character
$\widetilde{\unicode[STIX]{x1D711}}$
has central character
![]() $\unicode[STIX]{x1D714}$
if it satisfies
$\unicode[STIX]{x1D714}$
if it satisfies
 $$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D711}}(zg,u)=\unicode[STIX]{x1D714}(z)\widetilde{\unicode[STIX]{x1D711}}(g,z^{-2}u)\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D711}}(zg,u)=\unicode[STIX]{x1D714}(z)\widetilde{\unicode[STIX]{x1D711}}(g,z^{-2}u)\end{eqnarray}$$
for all
 $z\in Z(\mathbf{A})\cong \mathbf{A}^{\times }$
. We say that it is holomorphic (of weight
$z\in Z(\mathbf{A})\cong \mathbf{A}^{\times }$
. We say that it is holomorphic (of weight
![]() $k$
) or simply a twisted modular form if
$k$
) or simply a twisted modular form if
 $z_{\infty }\mapsto |y_{\infty }|_{\infty }^{-k/2}\widetilde{\unicode[STIX]{x1D711}}(g(\!\begin{smallmatrix}y_{\infty } & x_{\infty }\\ & 1\end{smallmatrix}\!),u)$
is holomorphic in
$z_{\infty }\mapsto |y_{\infty }|_{\infty }^{-k/2}\widetilde{\unicode[STIX]{x1D711}}(g(\!\begin{smallmatrix}y_{\infty } & x_{\infty }\\ & 1\end{smallmatrix}\!),u)$
is holomorphic in
 $z_{\infty }=(x_{v}+iy_{v})_{v|\infty }\in \mathfrak{h}^{\operatorname{Hom}(F,\mathbf{R})}$
for all
$z_{\infty }=(x_{v}+iy_{v})_{v|\infty }\in \mathfrak{h}^{\operatorname{Hom}(F,\mathbf{R})}$
for all
![]() $u\in \mathbf{A}^{\times }$
.
$u\in \mathbf{A}^{\times }$
.
We let
 $M_{k}^{\text{tw}}(K,\mathbf{C})$
denote the space of twisted modular forms of weight
$M_{k}^{\text{tw}}(K,\mathbf{C})$
denote the space of twisted modular forms of weight
![]() $k$
and
$k$
and
 $M_{k}^{\text{tw}}(K,\unicode[STIX]{x1D714},\mathbf{C})$
its subspace of forms with central character
$M_{k}^{\text{tw}}(K,\unicode[STIX]{x1D714},\mathbf{C})$
its subspace of forms with central character
![]() $\unicode[STIX]{x1D714}$
. We omit the
$\unicode[STIX]{x1D714}$
. We omit the
![]() $K$
from the notation if we do not wish to specify the level.
$K$
from the notation if we do not wish to specify the level.
If
![]() $\widetilde{\unicode[STIX]{x1D711}}$
is a twisted modular form, then, for each
$\widetilde{\unicode[STIX]{x1D711}}$
is a twisted modular form, then, for each
![]() $g,u$
, the function
$g,u$
, the function
 $x\mapsto \unicode[STIX]{x1D711}(n(x)g,u)$
descends to
$x\mapsto \unicode[STIX]{x1D711}(n(x)g,u)$
descends to
![]() $F\backslash \mathbf{A}$
and therefore it admits a Fourier–Whittaker expansion in the usual way. To the restriction of
$F\backslash \mathbf{A}$
and therefore it admits a Fourier–Whittaker expansion in the usual way. To the restriction of
![]() $\widetilde{\unicode[STIX]{x1D711}}$
to
$\widetilde{\unicode[STIX]{x1D711}}$
to
 $\mathbf{GL}_{2}(\mathbf{A})\times F^{\times }$
we then attach a twisted formal
$\mathbf{GL}_{2}(\mathbf{A})\times F^{\times }$
we then attach a twisted formal
![]() $q$
-expansion
$q$
-expansion
 $$\begin{eqnarray}\mathop{\sum }_{a\in F}|y|_{\infty }^{k/2}W_{a}^{\infty }((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!),u)\,\mathbf{q}^{a}~\in C^{\infty }(\mathbf{A}^{\infty ,\times }\times F^{\times },\mathbf{C})\unicode[STIX]{x27E6}\mathbf{q}^{F_{{\geqslant}0}}\unicode[STIX]{x27E7}^{\circ }\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{a\in F}|y|_{\infty }^{k/2}W_{a}^{\infty }((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!),u)\,\mathbf{q}^{a}~\in C^{\infty }(\mathbf{A}^{\infty ,\times }\times F^{\times },\mathbf{C})\unicode[STIX]{x27E6}\mathbf{q}^{F_{{\geqslant}0}}\unicode[STIX]{x27E7}^{\circ }\end{eqnarray}$$
such that
 $$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D711}}\left(\left(\begin{array}{@{}cc@{}}y & x\\ & 1\end{array}\right),u\right)=|y|_{\infty }^{k/2}\mathop{\sum }_{a\in F_{{\geqslant}0}}W_{a}^{\infty }((\!\begin{smallmatrix}y^{\infty } & \\ & 1\end{smallmatrix}\!),u)\unicode[STIX]{x1D713}_{\infty }(iay_{\infty })\unicode[STIX]{x1D713}(ax)\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D711}}\left(\left(\begin{array}{@{}cc@{}}y & x\\ & 1\end{array}\right),u\right)=|y|_{\infty }^{k/2}\mathop{\sum }_{a\in F_{{\geqslant}0}}W_{a}^{\infty }((\!\begin{smallmatrix}y^{\infty } & \\ & 1\end{smallmatrix}\!),u)\unicode[STIX]{x1D713}_{\infty }(iay_{\infty })\unicode[STIX]{x1D713}(ax)\end{eqnarray}$$
for all
 $y\in \mathbf{A}_{+}^{\times },x\in \mathbf{A},u\in F^{\times }$
. Here the space
$y\in \mathbf{A}_{+}^{\times },x\in \mathbf{A},u\in F^{\times }$
. Here the space
 $C^{\infty }(\mathbf{A}^{\infty ,\times }\times F^{\times },\mathbf{C})\unicode[STIX]{x27E6}\mathbf{q}^{F_{{\geqslant}0}}\unicode[STIX]{x27E7}^{\circ }$
consists of
$C^{\infty }(\mathbf{A}^{\infty ,\times }\times F^{\times },\mathbf{C})\unicode[STIX]{x27E6}\mathbf{q}^{F_{{\geqslant}0}}\unicode[STIX]{x27E7}^{\circ }$
consists of
![]() $q$
-expansions
$q$
-expansions
![]() $W$
whose coefficients
$W$
whose coefficients
 $W_{a}(y,u)$
vanish for
$W_{a}(y,u)$
vanish for
![]() $ay$
outside of some compact open subset
$ay$
outside of some compact open subset
 $A_{W}\subset \mathbf{A}^{\infty }$
.
$A_{W}\subset \mathbf{A}^{\infty }$
.
Let
![]() $\widetilde{\unicode[STIX]{x1D711}}$
be a twisted modular form, let
$\widetilde{\unicode[STIX]{x1D711}}$
be a twisted modular form, let
 $U_{F}\subset \mathbf{A}^{\infty ,\times }$
be a compact open subgroup satisfying the condition of the previous definition, and let
$U_{F}\subset \mathbf{A}^{\infty ,\times }$
be a compact open subgroup satisfying the condition of the previous definition, and let
 $\unicode[STIX]{x1D707}_{U_{F}}=F^{\times }\cap U_{F}$
. Then the sum
$\unicode[STIX]{x1D707}_{U_{F}}=F^{\times }\cap U_{F}$
. Then the sum
 $$\begin{eqnarray}\unicode[STIX]{x1D711}(g):=\mathop{\sum }_{u\in \unicode[STIX]{x1D707}_{U_{F}}^{2}\backslash F^{\times }}\widetilde{\unicode[STIX]{x1D711}}(g,u)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}(g):=\mathop{\sum }_{u\in \unicode[STIX]{x1D707}_{U_{F}}^{2}\backslash F^{\times }}\widetilde{\unicode[STIX]{x1D711}}(g,u)\end{eqnarray}$$
is finite for each
![]() $g$
(if
$g$
(if
 $K_{g}\subset \mathbf{A}^{\infty ,\times }$
is a compact subset such that
$K_{g}\subset \mathbf{A}^{\infty ,\times }$
is a compact subset such that
![]() $K_{g}F_{\infty }^{\times }$
contains the support of
$K_{g}F_{\infty }^{\times }$
contains the support of
![]() $\widetilde{\unicode[STIX]{x1D711}}(g,\cdot )$
, the sum is supported on
$\widetilde{\unicode[STIX]{x1D711}}(g,\cdot )$
, the sum is supported on
 $\unicode[STIX]{x1D707}_{U_{F}}^{2}\backslash (F^{\times }\cap K_{g})$
, which is commensurable with the finite group
$\unicode[STIX]{x1D707}_{U_{F}}^{2}\backslash (F^{\times }\cap K_{g})$
, which is commensurable with the finite group
 $\unicode[STIX]{x1D707}_{U_{F}}^{2}\backslash \mathscr{O}_{F}^{\times }$
). It defines a modular form in the usual sense, with formal
$\unicode[STIX]{x1D707}_{U_{F}}^{2}\backslash \mathscr{O}_{F}^{\times }$
). It defines a modular form in the usual sense, with formal
![]() $q$
-expansion
$q$
-expansion
 $$\begin{eqnarray}\text{}^{\mathbf{q}}\unicode[STIX]{x1D711}(y)=\mathop{\sum }_{u\in \unicode[STIX]{x1D707}_{U_{F}}^{2}\backslash F^{\times }}\text{}^{\mathbf{q}}\widetilde{\unicode[STIX]{x1D711}}(y,u).\end{eqnarray}$$
$$\begin{eqnarray}\text{}^{\mathbf{q}}\unicode[STIX]{x1D711}(y)=\mathop{\sum }_{u\in \unicode[STIX]{x1D707}_{U_{F}}^{2}\backslash F^{\times }}\text{}^{\mathbf{q}}\widetilde{\unicode[STIX]{x1D711}}(y,u).\end{eqnarray}$$
One can, similarly to the above, define a norm on the space of twisted formal
![]() $q$
-expansion coefficients of a fixed parallel weight
$q$
-expansion coefficients of a fixed parallel weight
![]() $k$
with values in a Banach ring
$k$
with values in a Banach ring
![]() $L$
, namely
$L$
, namely
 $\Vert W\Vert :=\sup _{(a,y^{\infty },u)}|y^{\infty }|^{-k/2}|W_{a}^{\infty }(y,u)|$
. The
$\Vert W\Vert :=\sup _{(a,y^{\infty },u)}|y^{\infty }|^{-k/2}|W_{a}^{\infty }(y,u)|$
. The
![]() $p$
-adic completion
$p$
-adic completion
 $\mathbf{M}_{k}^{\text{tw}}(K^{p},L)$
of the subspace of
$\mathbf{M}_{k}^{\text{tw}}(K^{p},L)$
of the subspace of
![]() $q$
-expansions of twisted modular forms (of some tame level
$q$
-expansions of twisted modular forms (of some tame level
![]() $K^{p}$
) is called the space of
$K^{p}$
) is called the space of
![]() $p$
-adic twisted modular forms (of tame level
$p$
-adic twisted modular forms (of tame level
![]() $K^{p}$
). Finally, there is a notion of a
$K^{p}$
). Finally, there is a notion of a
![]() $\mathscr{Y}^{?}$
-family of
$\mathscr{Y}^{?}$
-family of
![]() $q$
-expansions of twisted modular forms.
$q$
-expansions of twisted modular forms.
2.2 Hecke algebra and operators
 $\text{U}_{v}$
$\text{U}_{v}$
Let
![]() $L$
be a field and let
$L$
be a field and let
 $$\begin{eqnarray}\mathscr{H}(L)=C_{c}^{\infty }(\mathbf{GL}_{2}(\mathbf{A}^{\infty }),L)\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{H}(L)=C_{c}^{\infty }(\mathbf{GL}_{2}(\mathbf{A}^{\infty }),L)\end{eqnarray}$$
be the Hecke algebra of smooth compactly supported functions with the convolution operation (denoted by
![]() $\ast$
) and, for any finite set of non-archimedean places
$\ast$
) and, for any finite set of non-archimedean places
![]() $S$
, let
$S$
, let
 $\mathscr{H}^{S}(L)=C_{c}^{\infty }(\mathbf{GL}_{2}(\mathbf{A}^{S\infty }),L)$
,
$\mathscr{H}^{S}(L)=C_{c}^{\infty }(\mathbf{GL}_{2}(\mathbf{A}^{S\infty }),L)$
,
 $\mathscr{H}_{S}(L)=C_{c}^{\infty }(\mathbf{GL}_{2}(F_{S}),L)$
. When
$\mathscr{H}_{S}(L)=C_{c}^{\infty }(\mathbf{GL}_{2}(F_{S}),L)$
. When
![]() $L=\mathbf{Q}$
it will be omitted from the notation.
$L=\mathbf{Q}$
it will be omitted from the notation.
The group
 $\mathbf{GL}_{2}(\mathbf{A}^{\infty })$
has a natural left action on automorphic forms by right multiplication. This action is extended to elements
$\mathbf{GL}_{2}(\mathbf{A}^{\infty })$
has a natural left action on automorphic forms by right multiplication. This action is extended to elements
 $f\in \mathscr{H}\otimes \mathbf{C}$
by
$f\in \mathscr{H}\otimes \mathbf{C}$
by
 $$\begin{eqnarray}T(f)\unicode[STIX]{x1D711}(g)=\int _{\mathbf{GL}_{2}(\mathbf{A}^{\infty })}f(h)\unicode[STIX]{x1D711}(gh)\,dh,\end{eqnarray}$$
$$\begin{eqnarray}T(f)\unicode[STIX]{x1D711}(g)=\int _{\mathbf{GL}_{2}(\mathbf{A}^{\infty })}f(h)\unicode[STIX]{x1D711}(gh)\,dh,\end{eqnarray}$$
where
 $dh=\prod dh_{v}$
with
$dh=\prod dh_{v}$
with
![]() $dh_{v}$
the Haar measure on
$dh_{v}$
the Haar measure on
 $\mathbf{GL}_{2}(F_{v})$
assigning volume
$\mathbf{GL}_{2}(F_{v})$
assigning volume
![]() $1$
to
$1$
to
 $\mathbf{GL}_{2}(\mathscr{O}_{F,v})$
. If
$\mathbf{GL}_{2}(\mathscr{O}_{F,v})$
. If
 $K\subset \mathbf{GL}_{2}(\mathbf{A}^{\infty })$
is a compact open subgroup, we define
$K\subset \mathbf{GL}_{2}(\mathbf{A}^{\infty })$
is a compact open subgroup, we define
 $e_{K}=T(\operatorname{vol}(K)^{-1}\mathbf{1}_{K})\in \mathscr{H}$
. It acts as a projector on
$e_{K}=T(\operatorname{vol}(K)^{-1}\mathbf{1}_{K})\in \mathscr{H}$
. It acts as a projector on
![]() $K$
-invariant forms. If
$K$
-invariant forms. If
 $g\in \mathbf{GL}_{2}(\mathbf{A}^{\infty })$
and
$g\in \mathbf{GL}_{2}(\mathbf{A}^{\infty })$
and
![]() $K$
,
$K$
,
 $K^{\prime }\subset \mathbf{GL}_{2}(\widehat{\mathscr{O}}_{F})$
are open compact subgroups, we define the operator
$K^{\prime }\subset \mathbf{GL}_{2}(\widehat{\mathscr{O}}_{F})$
are open compact subgroups, we define the operator
 $[KgK^{\prime }]:=T(\mathbf{1}_{KgK^{\prime }})$
.
$[KgK^{\prime }]:=T(\mathbf{1}_{KgK^{\prime }})$
.
By the strong multiplicity-one theorem, for each level
![]() $K$
, each
$K$
, each
![]() $M$
-rational automorphic representation
$M$
-rational automorphic representation
![]() $\unicode[STIX]{x1D70E}$
which is a discrete series of weight
$\unicode[STIX]{x1D70E}$
which is a discrete series of weight
![]() $2$
at all infinite places, and each finite set of non-archimedean places
$2$
at all infinite places, and each finite set of non-archimedean places
![]() $S$
such that
$S$
such that
![]() $K$
is maximal away from
$K$
is maximal away from
![]() $S$
, there are spherical (that is,
$S$
, there are spherical (that is,
![]() $K(1)^{S}$
-bi-invariant) elements
$K(1)^{S}$
-bi-invariant) elements
 $T(\unicode[STIX]{x1D70E})\in \mathscr{H}^{S}(M)$
whose action on
$T(\unicode[STIX]{x1D70E})\in \mathscr{H}^{S}(M)$
whose action on
 $M_{2}(K,M)$
is given by the idempotent projection
$M_{2}(K,M)$
is given by the idempotent projection
![]() $e_{\unicode[STIX]{x1D70E}}$
onto
$e_{\unicode[STIX]{x1D70E}}$
onto
 $\unicode[STIX]{x1D70E}^{K}\subset M_{2}(K,M)$
.
$\unicode[STIX]{x1D70E}^{K}\subset M_{2}(K,M)$
.
On the space
 $\mathbf{M}(K^{p},L)$
of
$\mathbf{M}(K^{p},L)$
of
![]() $p$
-adic modular forms, with
$p$
-adic modular forms, with
 $K^{p}\supset K(N)^{p}$
, there is a continuous action of
$K^{p}\supset K(N)^{p}$
, there is a continuous action of
 $Z(Np^{\infty }):=\mathbf{A}^{\infty ,\times }/\overline{F^{\times }U_{F}(Np^{\infty })}$
, extending the central action
$Z(Np^{\infty }):=\mathbf{A}^{\infty ,\times }/\overline{F^{\times }U_{F}(Np^{\infty })}$
, extending the central action
 $z.\unicode[STIX]{x1D711}(g)=\unicode[STIX]{x1D711}(gz)$
on modular forms. For a continuous character
$z.\unicode[STIX]{x1D711}(g)=\unicode[STIX]{x1D711}(gz)$
on modular forms. For a continuous character
 $\unicode[STIX]{x1D714}:Z(Np^{\infty })\rightarrow L^{\times }$
, we denote by
$\unicode[STIX]{x1D714}:Z(Np^{\infty })\rightarrow L^{\times }$
, we denote by
 $\mathbf{M}(K^{p},\unicode[STIX]{x1D714},L)$
the set of
$\mathbf{M}(K^{p},\unicode[STIX]{x1D714},L)$
the set of
![]() $p$
-adic modular forms
$p$
-adic modular forms
![]() $\unicode[STIX]{x1D711}$
satisfying
$\unicode[STIX]{x1D711}$
satisfying
 $z.\unicode[STIX]{x1D711}=\unicode[STIX]{x1D714}(z)\unicode[STIX]{x1D711}$
, and by
$z.\unicode[STIX]{x1D711}=\unicode[STIX]{x1D714}(z)\unicode[STIX]{x1D711}$
, and by
 $\mathbf{S}(K^{p},\unicode[STIX]{x1D714},L)$
its subspace of cuspidal forms. If
$\mathbf{S}(K^{p},\unicode[STIX]{x1D714},L)$
its subspace of cuspidal forms. If
![]() $\unicode[STIX]{x1D714}$
is the restriction of a finite-order character of
$\unicode[STIX]{x1D714}$
is the restriction of a finite-order character of
 $Z(\mathbf{A}^{\infty })/U_{F}(Np^{\infty })$
, then we have
$Z(\mathbf{A}^{\infty })/U_{F}(Np^{\infty })$
, then we have
 $M_{2}(K^{p}K(p^{\infty })_{p},\unicode[STIX]{x1D714},L)\subset \mathbf{M}(K^{p},\unicode[STIX]{x1D714},L)$
.
$M_{2}(K^{p}K(p^{\infty })_{p},\unicode[STIX]{x1D714},L)\subset \mathbf{M}(K^{p},\unicode[STIX]{x1D714},L)$
.
The action of
 $\mathscr{H}^{Sp}=C_{c}^{\infty }(\mathbf{GL}_{2}(\mathbf{A}^{Sp\infty }),\mathbf{Q})$
extends continuously to the space
$\mathscr{H}^{Sp}=C_{c}^{\infty }(\mathbf{GL}_{2}(\mathbf{A}^{Sp\infty }),\mathbf{Q})$
extends continuously to the space
 $\mathbf{S}(K^{p},\unicode[STIX]{x1D714},L)$
if
$\mathbf{S}(K^{p},\unicode[STIX]{x1D714},L)$
if
![]() $K^{p}$
is maximal away from
$K^{p}$
is maximal away from
![]() $S$
; explicitly, if
$S$
; explicitly, if
![]() $\unicode[STIX]{x1D711}$
is the
$\unicode[STIX]{x1D711}$
is the
![]() $q$
-expansion with reduced coefficients
$q$
-expansion with reduced coefficients
![]() $W_{a,\unicode[STIX]{x1D711}}^{\natural }$
and
$W_{a,\unicode[STIX]{x1D711}}^{\natural }$
and
 $h(x)=\mathbf{1}_{K(1)^{Np}(\!\begin{smallmatrix}\unicode[STIX]{x1D71B}_{v} & \\ & 1\end{smallmatrix}\!)K(1)^{Np}}$
, we have
$h(x)=\mathbf{1}_{K(1)^{Np}(\!\begin{smallmatrix}\unicode[STIX]{x1D71B}_{v} & \\ & 1\end{smallmatrix}\!)K(1)^{Np}}$
, we have
 $$\begin{eqnarray}W_{a,T(h)\unicode[STIX]{x1D711}}^{\natural }=W_{a\unicode[STIX]{x1D71B}_{v},\unicode[STIX]{x1D711}}^{\natural }+\unicode[STIX]{x1D714}^{-1}(\unicode[STIX]{x1D71B}_{v})W_{a/\unicode[STIX]{x1D71B}_{v},\unicode[STIX]{x1D711}}^{\natural }.\end{eqnarray}$$
$$\begin{eqnarray}W_{a,T(h)\unicode[STIX]{x1D711}}^{\natural }=W_{a\unicode[STIX]{x1D71B}_{v},\unicode[STIX]{x1D711}}^{\natural }+\unicode[STIX]{x1D714}^{-1}(\unicode[STIX]{x1D71B}_{v})W_{a/\unicode[STIX]{x1D71B}_{v},\unicode[STIX]{x1D711}}^{\natural }.\end{eqnarray}$$
Moreover, if
![]() $S^{\prime }$
is another set of finite places not containing those above
$S^{\prime }$
is another set of finite places not containing those above
![]() $p$
and
$p$
and
 $S^{\prime \prime }=S\cup S^{\prime }$
, the action of
$S^{\prime \prime }=S\cup S^{\prime }$
, the action of
![]() $\mathscr{H}^{S^{\prime \prime }p}$
extends in the same way to the space
$\mathscr{H}^{S^{\prime \prime }p}$
extends in the same way to the space
 $\overline{\mathbf{S}}^{\prime }=\overline{\mathbf{S}}_{S^{\prime }}^{\prime }(K^{p})$
defined after Lemma 2.1.2.
$\overline{\mathbf{S}}^{\prime }=\overline{\mathbf{S}}_{S^{\prime }}^{\prime }(K^{p})$
defined after Lemma 2.1.2.
Operators
![]() $\text{U}_{v}$
. Let
$\text{U}_{v}$
. Let
![]() $v$
be a finite place of
$v$
be a finite place of
![]() $F$
,
$F$
,
 $\unicode[STIX]{x1D71B}_{v}\in F_{v}$
a uniformiser, and
$\unicode[STIX]{x1D71B}_{v}\in F_{v}$
a uniformiser, and
 $K^{v}\subset \mathbf{GL}_{2}(\widehat{\mathscr{O}}_{F}^{v})$
a compact open subgroup. For each
$K^{v}\subset \mathbf{GL}_{2}(\widehat{\mathscr{O}}_{F}^{v})$
a compact open subgroup. For each
![]() $r\geqslant 1$
, we define Hecke operators
$r\geqslant 1$
, we define Hecke operators
 $$\begin{eqnarray}\displaystyle \text{U}_{v,r}^{\ast } & = & \displaystyle [K^{v}K_{1}^{1}(\unicode[STIX]{x1D71B}_{v}^{r})_{v}(\!\begin{smallmatrix}\unicode[STIX]{x1D71B}_{v} & \\ & 1\end{smallmatrix}\!)K^{v}K_{1}^{1}(\unicode[STIX]{x1D71B}_{v}^{r})_{v}],\nonumber\\ \displaystyle \text{U}_{v,\ast ,r} & = & \displaystyle [K^{v}K_{1}^{1}(\unicode[STIX]{x1D71B}_{v}^{r})_{v}(\!\begin{smallmatrix}1 & \\ & \unicode[STIX]{x1D71B}_{v}^{-1}\end{smallmatrix}\!)K^{v}K_{1}^{1}(\unicode[STIX]{x1D71B}_{v}^{r})_{v}].\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{U}_{v,r}^{\ast } & = & \displaystyle [K^{v}K_{1}^{1}(\unicode[STIX]{x1D71B}_{v}^{r})_{v}(\!\begin{smallmatrix}\unicode[STIX]{x1D71B}_{v} & \\ & 1\end{smallmatrix}\!)K^{v}K_{1}^{1}(\unicode[STIX]{x1D71B}_{v}^{r})_{v}],\nonumber\\ \displaystyle \text{U}_{v,\ast ,r} & = & \displaystyle [K^{v}K_{1}^{1}(\unicode[STIX]{x1D71B}_{v}^{r})_{v}(\!\begin{smallmatrix}1 & \\ & \unicode[STIX]{x1D71B}_{v}^{-1}\end{smallmatrix}\!)K^{v}K_{1}^{1}(\unicode[STIX]{x1D71B}_{v}^{r})_{v}].\nonumber\end{eqnarray}$$
They depend on the choice of uniformisers
![]() $\unicode[STIX]{x1D71B}_{v}$
, although a sufficiently high (depending on
$\unicode[STIX]{x1D71B}_{v}$
, although a sufficiently high (depending on
![]() $r$
) integer power of them does not. They are compatible with changing
$r$
) integer power of them does not. They are compatible with changing
![]() $r$
in the sense that
$r$
in the sense that
 $\text{U}_{v,\ast ,r}e_{K^{1}(\unicode[STIX]{x1D71B}_{v}^{r^{\prime }})_{v}}=\text{U}_{v,\ast r^{\prime }}$
for
$\text{U}_{v,\ast ,r}e_{K^{1}(\unicode[STIX]{x1D71B}_{v}^{r^{\prime }})_{v}}=\text{U}_{v,\ast r^{\prime }}$
for
![]() $r^{\prime }\leqslant r$
and similarly for
$r^{\prime }\leqslant r$
and similarly for
![]() $\text{U}_{v,r}^{\ast }$
; we will hence omit the
$\text{U}_{v,r}^{\ast }$
; we will hence omit the
![]() $r$
from the notation. If
$r$
from the notation. If
 $\unicode[STIX]{x1D711}\in S_{2}(K^{p}K^{1}(p^{r})_{p},\unicode[STIX]{x1D714})$
has reduced
$\unicode[STIX]{x1D711}\in S_{2}(K^{p}K^{1}(p^{r})_{p},\unicode[STIX]{x1D714})$
has reduced
![]() $q$
-expansion coefficients
$q$
-expansion coefficients
![]() $W_{\unicode[STIX]{x1D711},a}^{\natural }$
for
$W_{\unicode[STIX]{x1D711},a}^{\natural }$
for
 $a\in \mathbf{A}^{\infty ,\times }$
, then
$a\in \mathbf{A}^{\infty ,\times }$
, then
![]() $\text{U}_{v,\ast }\unicode[STIX]{x1D711}$
has reduced
$\text{U}_{v,\ast }\unicode[STIX]{x1D711}$
has reduced
![]() $q$
-expansion coefficients
$q$
-expansion coefficients
 $W_{\text{U}_{v,\ast }\unicode[STIX]{x1D711},a}^{\natural }=\unicode[STIX]{x1D714}^{-1}(\unicode[STIX]{x1D71B}_{v})W_{\unicode[STIX]{x1D711},a\unicode[STIX]{x1D714}_{v}}^{\natural }$
. By this formula we can extend
$W_{\text{U}_{v,\ast }\unicode[STIX]{x1D711},a}^{\natural }=\unicode[STIX]{x1D714}^{-1}(\unicode[STIX]{x1D71B}_{v})W_{\unicode[STIX]{x1D711},a\unicode[STIX]{x1D714}_{v}}^{\natural }$
. By this formula we can extend
![]() $\text{U}_{v,\ast }$
to a continuous operator on
$\text{U}_{v,\ast }$
to a continuous operator on
![]() $p$
-adic reduced
$p$
-adic reduced
![]() $q$
-expansions, and in particular on
$q$
-expansions, and in particular on
![]() $p$
-adic modular forms.
$p$
-adic modular forms.
Atkin–Lehner operators. Let
![]() $v$
be a finite place and fix the same uniformiser
$v$
be a finite place and fix the same uniformiser
![]() $\unicode[STIX]{x1D71B}_{v}$
as in the previous paragraph. Then we define elements
$\unicode[STIX]{x1D71B}_{v}$
as in the previous paragraph. Then we define elements
 $$\begin{eqnarray}w_{r,v}:=\left(\begin{array}{@{}cc@{}} & 1\\ -\unicode[STIX]{x1D71B}_{v}^{r} & \end{array}\right)\in \mathbf{GL}_{2}(F_{v})\subset \mathbf{GL}_{2}(\mathbf{A})\end{eqnarray}$$
$$\begin{eqnarray}w_{r,v}:=\left(\begin{array}{@{}cc@{}} & 1\\ -\unicode[STIX]{x1D71B}_{v}^{r} & \end{array}\right)\in \mathbf{GL}_{2}(F_{v})\subset \mathbf{GL}_{2}(\mathbf{A})\end{eqnarray}$$
for
![]() $r\geqslant 0$
, and denote by the same names the operators they induce on automorphic forms by right multiplication. We have
$r\geqslant 0$
, and denote by the same names the operators they induce on automorphic forms by right multiplication. We have
 $w_{r,v}^{-1}K_{1}^{1}(\unicode[STIX]{x1D71B}^{s})_{v}w_{r,v}=K_{1}^{1}(\unicode[STIX]{x1D71B}_{v}^{s})_{v}$
.
$w_{r,v}^{-1}K_{1}^{1}(\unicode[STIX]{x1D71B}^{s})_{v}w_{r,v}=K_{1}^{1}(\unicode[STIX]{x1D71B}_{v}^{s})_{v}$
.
If
 $r=(r_{v})_{v|p}$
, we define
$r=(r_{v})_{v|p}$
, we define
 $w_{r}=(w_{r_{v},v})_{v|p}\in \mathbf{GL}_{2}(F_{p})=\prod _{v|p}\mathbf{GL}_{2}(F_{v})$
, and similarly
$w_{r}=(w_{r_{v},v})_{v|p}\in \mathbf{GL}_{2}(F_{p})=\prod _{v|p}\mathbf{GL}_{2}(F_{v})$
, and similarly
![]() $w_{r}^{-1}$
.
$w_{r}^{-1}$
.
2.3 Universal Kirillov and Whittaker models
Let
![]() $F_{v}$
be a non-archimedean local field, and recall the space
$F_{v}$
be a non-archimedean local field, and recall the space
![]() $\unicode[STIX]{x1D6F9}_{v}$
of abstract additive characters of level
$\unicode[STIX]{x1D6F9}_{v}$
of abstract additive characters of level
![]() $0$
of
$0$
of
![]() $F_{v}$
defined in § 1.2. Let
$F_{v}$
defined in § 1.2. Let
 $\unicode[STIX]{x1D713}_{\text{univ},v}:F_{v}\rightarrow \mathscr{O}(\unicode[STIX]{x1D6F9}_{v})^{\times }$
be the tautological character, which we identify with an action of the unipotent subgroup
$\unicode[STIX]{x1D713}_{\text{univ},v}:F_{v}\rightarrow \mathscr{O}(\unicode[STIX]{x1D6F9}_{v})^{\times }$
be the tautological character, which we identify with an action of the unipotent subgroup
 $N=N(F_{v})\cong F_{v}\subset \mathbf{GL}_{2}(F_{v})$
on the sheaf
$N=N(F_{v})\cong F_{v}\subset \mathbf{GL}_{2}(F_{v})$
on the sheaf
![]() $\mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}$
. Let
$\mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}$
. Let
![]() $\unicode[STIX]{x1D70E}_{v}$
be an infinite-dimensional representation of
$\unicode[STIX]{x1D70E}_{v}$
be an infinite-dimensional representation of
 $\mathbf{GL}_{2}(F_{v})$
on a vector space over a number field
$\mathbf{GL}_{2}(F_{v})$
on a vector space over a number field
![]() $M$
. A Whittaker model over
$M$
. A Whittaker model over
 $M\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}$
for
$M\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}$
for
 $\unicode[STIX]{x1D70E}_{v}\otimes _{\mathbf{Q}}\mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}$
is a non-trivial
$\unicode[STIX]{x1D70E}_{v}\otimes _{\mathbf{Q}}\mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}$
is a non-trivial
 $\mathbf{GL}_{2}(F_{v})$
-equivariant map
$\mathbf{GL}_{2}(F_{v})$
-equivariant map
 $\unicode[STIX]{x1D70E}_{v}\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}\rightarrow M\otimes \operatorname{Ind}_{N}^{\mathbf{GL}_{2}(F_{v})}\unicode[STIX]{x1D713}_{\text{univ},v}$
of free sheaves over
$\unicode[STIX]{x1D70E}_{v}\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}\rightarrow M\otimes \operatorname{Ind}_{N}^{\mathbf{GL}_{2}(F_{v})}\unicode[STIX]{x1D713}_{\text{univ},v}$
of free sheaves over
 $M\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}$
. We will often identify this map with its image.
$M\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}$
. We will often identify this map with its image.
Let
 $P_{0}\subset \mathbf{GL}_{2}(F_{v})$
be the mirabolic group of matrices
$P_{0}\subset \mathbf{GL}_{2}(F_{v})$
be the mirabolic group of matrices
![]() $(\!\begin{smallmatrix}a & b\\ & 1\end{smallmatrix}\!)$
. A Kirillov model over
$(\!\begin{smallmatrix}a & b\\ & 1\end{smallmatrix}\!)$
. A Kirillov model over
 $M\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}$
for
$M\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}$
for
 $\unicode[STIX]{x1D70E}_{v}\otimes _{\mathbf{Q}}\mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}$
is a non-trivial
$\unicode[STIX]{x1D70E}_{v}\otimes _{\mathbf{Q}}\mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}$
is a non-trivial
![]() $P_{0}$
-equivariant map
$P_{0}$
-equivariant map
 $\unicode[STIX]{x1D70E}_{v}\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}\rightarrow M\otimes \operatorname{Ind}_{N}^{P_{0}}\unicode[STIX]{x1D713}_{\text{univ},v}$
. We will often identify this map with its image and the image with a subsheaf of
$\unicode[STIX]{x1D70E}_{v}\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}\rightarrow M\otimes \operatorname{Ind}_{N}^{P_{0}}\unicode[STIX]{x1D713}_{\text{univ},v}$
. We will often identify this map with its image and the image with a subsheaf of
 $C^{\infty }(F_{v}^{\times },M)\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}$
by restricting functions from
$C^{\infty }(F_{v}^{\times },M)\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}$
by restricting functions from
![]() $P_{0}$
to
$P_{0}$
to
 $\{(\!\begin{smallmatrix}a & \\ & 1\end{smallmatrix}\!)~|~a\in F_{v}^{\times }\}\cong F_{v}^{\times }$
.
$\{(\!\begin{smallmatrix}a & \\ & 1\end{smallmatrix}\!)~|~a\in F_{v}^{\times }\}\cong F_{v}^{\times }$
.
Lemma 2.3.1. Let
![]() $\unicode[STIX]{x1D70E}_{v}$
be an irreducible admissible infinite-dimensional representation of
$\unicode[STIX]{x1D70E}_{v}$
be an irreducible admissible infinite-dimensional representation of
 $\mathbf{GL}_{2}(F_{v})$
on a rational vector space,
$\mathbf{GL}_{2}(F_{v})$
on a rational vector space,
 $M=\operatorname{End}(\unicode[STIX]{x1D70E}_{v})$
. Then
$M=\operatorname{End}(\unicode[STIX]{x1D70E}_{v})$
. Then
 $\unicode[STIX]{x1D70E}_{v}\otimes _{\mathbf{Q}}\mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}$
admits a Whittaker model
$\unicode[STIX]{x1D70E}_{v}\otimes _{\mathbf{Q}}\mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}$
admits a Whittaker model
 $\mathscr{W}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})$
(respectively, a Kirillov model
$\mathscr{W}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})$
(respectively, a Kirillov model
 $\mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})$
) over
$\mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})$
) over
 $M\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}$
, unique up to
$M\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}$
, unique up to
 $(M\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}})^{\times }$
, whose specialisation at every closed point
$(M\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}})^{\times }$
, whose specialisation at every closed point
 $\unicode[STIX]{x1D713}_{v}\in \unicode[STIX]{x1D6F9}_{v}$
is the unique Whittaker model
$\unicode[STIX]{x1D713}_{v}\in \unicode[STIX]{x1D6F9}_{v}$
is the unique Whittaker model
 $\mathscr{W}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{v})$
(respectively, the unique Kirillov model
$\mathscr{W}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{v})$
(respectively, the unique Kirillov model
 $\mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{v})$
) of
$\mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{v})$
) of
 $\unicode[STIX]{x1D70E}_{v}\otimes \mathbf{Q}(\unicode[STIX]{x1D713}_{v})$
.
$\unicode[STIX]{x1D70E}_{v}\otimes \mathbf{Q}(\unicode[STIX]{x1D713}_{v})$
.
If we view
 $\mathscr{W}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})$
(respectively,
$\mathscr{W}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})$
(respectively,
 $\mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})$
) as a subsheaf of
$\mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})$
) as a subsheaf of
 $C^{\infty }(\mathbf{GL}_{2}(F_{v}),M)\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}$
(respectively, as a subsheaf of
$C^{\infty }(\mathbf{GL}_{2}(F_{v}),M)\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}$
(respectively, as a subsheaf of
 $C^{\infty }(F_{v}^{\times },M)\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}$
), then the restriction map
$C^{\infty }(F_{v}^{\times },M)\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}$
), then the restriction map
 $W\mapsto f$
,
$W\mapsto f$
,
 $f(y):=W((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!))$
, induces an isomorphism
$f(y):=W((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!))$
, induces an isomorphism
 $\mathscr{W}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})\rightarrow \mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})$
.
$\mathscr{W}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})\rightarrow \mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})$
.
We call
 $\mathscr{W}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})$
(respectively,
$\mathscr{W}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})$
(respectively,
 $\mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})$
) the universal Whittaker model (respectively, the universal Kirillov model) for
$\mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})$
) the universal Whittaker model (respectively, the universal Kirillov model) for
![]() $\unicode[STIX]{x1D70E}_{v}$
. The universal Kirillov model admits a natural
$\unicode[STIX]{x1D70E}_{v}$
. The universal Kirillov model admits a natural
![]() $M$
-structure, that is, an
$M$
-structure, that is, an
![]() $M$
-vector spaceFootnote
15
$M$
-vector spaceFootnote
15
 $$\begin{eqnarray}\mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})_{M}\subset C^{\infty }(F_{v}^{\times },M)\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})_{M}\subset C^{\infty }(F_{v}^{\times },M)\end{eqnarray}$$
such that
 $\mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})_{M}\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}=\mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})$
.
$\mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})_{M}\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}=\mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})$
.
Proof. The proof of existence and uniqueness of Whittaker models given e.g. in [Reference BumpBum97, §4.4] carries over to our context after replacing
![]() $\mathbf{C}$
by
$\mathbf{C}$
by
 $M\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}$
and the fixed
$M\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}$
and the fixed
![]() $\mathbf{C}^{\times }$
-valued character
$\mathbf{C}^{\times }$
-valued character
![]() $\unicode[STIX]{x1D713}_{v}$
of [Reference BumpBum97] with
$\unicode[STIX]{x1D713}_{v}$
of [Reference BumpBum97] with
![]() $\unicode[STIX]{x1D713}_{\text{univ},v}$
. The analogous result for Kirillov models, together with the isomorphism
$\unicode[STIX]{x1D713}_{\text{univ},v}$
. The analogous result for Kirillov models, together with the isomorphism
 $\mathscr{W}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})\rightarrow \mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})$
, follows formally from Frobenius reciprocity as in [Reference Bushnell and HenniartBH06, Corollary 36.2]. We prove the assertion on the
$\mathscr{W}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})\rightarrow \mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})$
, follows formally from Frobenius reciprocity as in [Reference Bushnell and HenniartBH06, Corollary 36.2]. We prove the assertion on the
![]() $M$
-structure for
$M$
-structure for
 $\mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})$
, after dropping subscripts
$\mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})$
, after dropping subscripts
![]() $v$
.
$v$
.
As in the classical case, the space of Schwartz functions
 $\mathscr{S}(F^{\times },M)\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}}$
is an irreducible
$\mathscr{S}(F^{\times },M)\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}}$
is an irreducible
![]() $P_{0}$
-representation (see [Reference Bushnell and HenniartBH06, Corollary 8.2]) and hence contained in
$P_{0}$
-representation (see [Reference Bushnell and HenniartBH06, Corollary 8.2]) and hence contained in
 $\mathscr{K}:=\mathscr{K}(\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D704}},\unicode[STIX]{x1D713}_{\text{univ}})\subset C^{\infty }(F^{\times },M)\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}}$
. Moreover,
$\mathscr{K}:=\mathscr{K}(\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D704}},\unicode[STIX]{x1D713}_{\text{univ}})\subset C^{\infty }(F^{\times },M)\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}}$
. Moreover,
 $\overline{\mathscr{K}}:=\mathscr{K}/\mathscr{S}(F^{\times },M)\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}}$
is a free sheaf over
$\overline{\mathscr{K}}:=\mathscr{K}/\mathscr{S}(F^{\times },M)\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}}$
is a free sheaf over
 $M\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}}$
of rank
$M\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}}$
of rank
![]() $d\leqslant 2$
depending on the type of
$d\leqslant 2$
depending on the type of
![]() $\unicode[STIX]{x1D70E}_{}$
(as can be checked on the points of
$\unicode[STIX]{x1D70E}_{}$
(as can be checked on the points of
![]() $\unicode[STIX]{x1D6F9}$
by the classical theory). Since the space
$\unicode[STIX]{x1D6F9}$
by the classical theory). Since the space
 $\mathscr{S}(F^{\times },M)\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}}$
has the obvious
$\mathscr{S}(F^{\times },M)\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}}$
has the obvious
![]() $M$
-structure
$M$
-structure
 $\mathscr{S}(F^{\times },M)$
, it suffices to describe
$\mathscr{S}(F^{\times },M)$
, it suffices to describe
![]() $d$
generators for
$d$
generators for
![]() $\overline{\mathscr{K}}$
represented by functions in
$\overline{\mathscr{K}}$
represented by functions in
 $C^{\infty }(F^{\times },M)$
.
$C^{\infty }(F^{\times },M)$
.
If
![]() $\unicode[STIX]{x1D70E}$
is supercuspidal, then
$\unicode[STIX]{x1D70E}$
is supercuspidal, then
![]() $d=0$
and there is nothing to prove. If
$d=0$
and there is nothing to prove. If
 $\unicode[STIX]{x1D70E}=\operatorname{St}(\unicode[STIX]{x1D707}|\cdot |^{-1})$
is special with
$\unicode[STIX]{x1D70E}=\operatorname{St}(\unicode[STIX]{x1D707}|\cdot |^{-1})$
is special with
![]() $M^{\times }$
-valued central character
$M^{\times }$
-valued central character
 $\unicode[STIX]{x1D707}^{2}|\cdot |^{-2}$
, then
$\unicode[STIX]{x1D707}^{2}|\cdot |^{-2}$
, then
![]() $d=1$
and a generator for
$d=1$
and a generator for
![]() $\overline{\mathscr{K}}$
is
$\overline{\mathscr{K}}$
is
 $f_{\unicode[STIX]{x1D707}}(y):=\unicode[STIX]{x1D707}(y)\mathbf{1}_{\mathscr{O}_{F}-\{0\}}(y)$
. If
$f_{\unicode[STIX]{x1D707}}(y):=\unicode[STIX]{x1D707}(y)\mathbf{1}_{\mathscr{O}_{F}-\{0\}}(y)$
. If
![]() $\unicode[STIX]{x1D70E}$
is an irreducible principal series
$\unicode[STIX]{x1D70E}$
is an irreducible principal series
 $\operatorname{Ind}(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}|\cdot |^{-1})$
(plain un-normalised induction) with
$\operatorname{Ind}(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}|\cdot |^{-1})$
(plain un-normalised induction) with
![]() $M^{\times }$
-valued characters
$M^{\times }$
-valued characters
![]() $\unicode[STIX]{x1D707}_{1}$
,
$\unicode[STIX]{x1D707}_{1}$
,
![]() $\unicode[STIX]{x1D707}_{2}$
, then
$\unicode[STIX]{x1D707}_{2}$
, then
![]() $d=2$
; if
$d=2$
; if
 $\unicode[STIX]{x1D707}_{1}\neq \unicode[STIX]{x1D707}_{2}$
, a pair of generators for
$\unicode[STIX]{x1D707}_{1}\neq \unicode[STIX]{x1D707}_{2}$
, a pair of generators for
![]() $\overline{\mathscr{K}}$
is
$\overline{\mathscr{K}}$
is
 $\{f_{\unicode[STIX]{x1D707}_{1}},f_{\unicode[STIX]{x1D707}_{2}}\}$
. If
$\{f_{\unicode[STIX]{x1D707}_{1}},f_{\unicode[STIX]{x1D707}_{2}}\}$
. If
 $\unicode[STIX]{x1D707}_{1}=\unicode[STIX]{x1D707}_{2}=\unicode[STIX]{x1D707}$
, a pair of generators is
$\unicode[STIX]{x1D707}_{1}=\unicode[STIX]{x1D707}_{2}=\unicode[STIX]{x1D707}$
, a pair of generators is
 $\{f_{\unicode[STIX]{x1D707}},f_{\unicode[STIX]{x1D707}}^{\prime }\}$
with
$\{f_{\unicode[STIX]{x1D707}},f_{\unicode[STIX]{x1D707}}^{\prime }\}$
with
 $f_{\unicode[STIX]{x1D707}}^{\prime }(y):=v(y)\unicode[STIX]{x1D707}(y)\mathbf{1}_{\mathscr{O}_{F}-\{0\}}(y).$
◻
$f_{\unicode[STIX]{x1D707}}^{\prime }(y):=v(y)\unicode[STIX]{x1D707}(y)\mathbf{1}_{\mathscr{O}_{F}-\{0\}}(y).$
◻
We will often slightly abusively identify Whittaker and Kirillov models by
 $W\mapsto f$
,
$W\mapsto f$
,
 $f(y)=W((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!))$
.
$f(y)=W((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!))$
.
If
![]() $\unicode[STIX]{x1D70E}^{\infty }$
is an
$\unicode[STIX]{x1D70E}^{\infty }$
is an
![]() $M$
-rational automorphic representation of weight
$M$
-rational automorphic representation of weight
![]() $2$
, then after choosing any embedding
$2$
, then after choosing any embedding
 $\unicode[STIX]{x1D704}:M{\hookrightarrow}\mathbf{C}$
and any non-trivial character
$\unicode[STIX]{x1D704}:M{\hookrightarrow}\mathbf{C}$
and any non-trivial character
 $\unicode[STIX]{x1D713}:\mathbf{A}/F\rightarrow \mathbf{C}^{\times }$
, the
$\unicode[STIX]{x1D713}:\mathbf{A}/F\rightarrow \mathbf{C}^{\times }$
, the
![]() $q$
-expansion coefficients of any
$q$
-expansion coefficients of any
![]() $\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D70E}^{\infty }$
can be identified with the product of the local Kirillov restrictions
$\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D70E}^{\infty }$
can be identified with the product of the local Kirillov restrictions
![]() $f_{v}$
of the Whittaker function
$f_{v}$
of the Whittaker function
 $W=W_{v}$
of
$W=W_{v}$
of
![]() $\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D704}}$
(when
$\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D704}}$
(when
![]() $W$
is indeed factorisable). Equivalently, the
$W$
is indeed factorisable). Equivalently, the
![]() $f_{v}$
belong to the
$f_{v}$
belong to the
![]() $M$
-rational subspaces and are therefore independent of the choice of additive character.
$M$
-rational subspaces and are therefore independent of the choice of additive character.
Lemma 2.3.2. In the situation of the previous lemma, there is a pairing
 $$\begin{eqnarray}(\,,\,)_{v}:\mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})\otimes _{M}\mathscr{K}(\unicode[STIX]{x1D70E}_{v}^{\vee },\unicode[STIX]{x1D713}_{\text{univ},v}^{-1})\rightarrow M\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}\end{eqnarray}$$
$$\begin{eqnarray}(\,,\,)_{v}:\mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})\otimes _{M}\mathscr{K}(\unicode[STIX]{x1D70E}_{v}^{\vee },\unicode[STIX]{x1D713}_{\text{univ},v}^{-1})\rightarrow M\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}\end{eqnarray}$$
such that for any
![]() $f_{1}$
,
$f_{1}$
,
![]() $f_{2}$
in the
$f_{2}$
in the
![]() $M$
-rational subspaces
$M$
-rational subspaces
 $\mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})_{M}$
, respectively,
$\mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})_{M}$
, respectively,
 $\mathscr{K}(\unicode[STIX]{x1D70E}_{v}^{\vee },\unicode[STIX]{x1D713}_{\text{univ},v}^{-1})_{M}$
, the pairing
$\mathscr{K}(\unicode[STIX]{x1D70E}_{v}^{\vee },\unicode[STIX]{x1D713}_{\text{univ},v}^{-1})_{M}$
, the pairing
 $(f_{1},f_{2})_{v}\in M$
, and for any
$(f_{1},f_{2})_{v}\in M$
, and for any
 $\unicode[STIX]{x1D704}:M{\hookrightarrow}\mathbf{C}$
, we have
$\unicode[STIX]{x1D704}:M{\hookrightarrow}\mathbf{C}$
, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D704}(f_{1},f_{2})_{v}=\frac{\unicode[STIX]{x1D701}_{F,v}(2)}{L(1,\unicode[STIX]{x1D70E}_{v}^{\unicode[STIX]{x1D704}}\times \unicode[STIX]{x1D70E}_{v}^{\unicode[STIX]{x1D704}\vee })}\int _{F_{v}^{\times }}\unicode[STIX]{x1D704}f_{1}(y)\unicode[STIX]{x1D704}f_{2}(y)\,\frac{d^{\times }y}{|d|_{v}^{1/2}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}(f_{1},f_{2})_{v}=\frac{\unicode[STIX]{x1D701}_{F,v}(2)}{L(1,\unicode[STIX]{x1D70E}_{v}^{\unicode[STIX]{x1D704}}\times \unicode[STIX]{x1D70E}_{v}^{\unicode[STIX]{x1D704}\vee })}\int _{F_{v}^{\times }}\unicode[STIX]{x1D704}f_{1}(y)\unicode[STIX]{x1D704}f_{2}(y)\,\frac{d^{\times }y}{|d|_{v}^{1/2}}.\end{eqnarray}$$
The right-hand side is understood in the sense of analytic continuation to
![]() $s=0$
for the function of
$s=0$
for the function of
![]() $s$
defined, for
$s$
defined, for
![]() $\Re (s)$
sufficiently large, by the normalised convergent integral
$\Re (s)$
sufficiently large, by the normalised convergent integral
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D701}_{F,v}(2)}{L(1+s,\unicode[STIX]{x1D70E}_{v}^{\unicode[STIX]{x1D704}}\times \unicode[STIX]{x1D70E}_{v}^{\unicode[STIX]{x1D704}\vee })}\int _{F^{\times }}\unicode[STIX]{x1D704}f_{1}(y)\unicode[STIX]{x1D704}f_{2}(y)|y|^{s}\,\frac{d^{\times }y}{|d|_{v}^{1/2}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D701}_{F,v}(2)}{L(1+s,\unicode[STIX]{x1D70E}_{v}^{\unicode[STIX]{x1D704}}\times \unicode[STIX]{x1D70E}_{v}^{\unicode[STIX]{x1D704}\vee })}\int _{F^{\times }}\unicode[STIX]{x1D704}f_{1}(y)\unicode[STIX]{x1D704}f_{2}(y)|y|^{s}\,\frac{d^{\times }y}{|d|_{v}^{1/2}}.\end{eqnarray}$$
The normalisation is such that the pairing equals
![]() $1$
when
$1$
when
![]() $\unicode[STIX]{x1D70E}_{v}$
is an unramified principal series and the
$\unicode[STIX]{x1D70E}_{v}$
is an unramified principal series and the
![]() $f_{i}$
are normalised new vectors.
$f_{i}$
are normalised new vectors.
Proof. We use the notation of the proof of Lemma 2.3.1, dropping all subscripts
![]() $v$
. We simply need to show that the given expression belongs to
$v$
. We simply need to show that the given expression belongs to
![]() $\unicode[STIX]{x1D704}M$
if
$\unicode[STIX]{x1D704}M$
if
![]() $f_{1}$
,
$f_{1}$
,
![]() $f_{2}$
belong to the
$f_{2}$
belong to the
![]() $M$
-rational subspace of
$M$
-rational subspace of
![]() $\mathscr{K}$
and that any pole of the integral
$\mathscr{K}$
and that any pole of the integral
 $I_{s}(f_{1},f_{2}):=\int _{F^{\times }}\unicode[STIX]{x1D704}f_{1}(y)\unicode[STIX]{x1D704}f_{2}(y)|y|^{s}\,(d^{\times }y/|d|^{1/2})$
is cancelled by a pole of
$I_{s}(f_{1},f_{2}):=\int _{F^{\times }}\unicode[STIX]{x1D704}f_{1}(y)\unicode[STIX]{x1D704}f_{2}(y)|y|^{s}\,(d^{\times }y/|d|^{1/2})$
is cancelled by a pole of
 $L(1+s,\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D704}}\times \unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D704}\vee })$
. If either of
$L(1+s,\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D704}}\times \unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D704}\vee })$
. If either of
 $f_{i}\in \mathscr{S}(F^{\times },M)$
, the integral is just a finite sum of elements in
$f_{i}\in \mathscr{S}(F^{\times },M)$
, the integral is just a finite sum of elements in
![]() $\unicode[STIX]{x1D704}M$
. Then we only need to compute the integral when
$\unicode[STIX]{x1D704}M$
. Then we only need to compute the integral when
![]() $f_{1}$
,
$f_{1}$
,
![]() $f_{2}$
are among the
$f_{2}$
are among the
![]() $M$
-rational generators of
$M$
-rational generators of
![]() $\overline{\mathscr{K}}$
, which is a standard calculation.
$\overline{\mathscr{K}}$
, which is a standard calculation.
In our application there will be no poles by the Weil conjectures, so we limit ourselves to proving the statement in the case where
 $\unicode[STIX]{x1D70E}=\operatorname{Ind}(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}|\cdot |^{-1})$
is a principal series with
$\unicode[STIX]{x1D70E}=\operatorname{Ind}(\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}|\cdot |^{-1})$
is a principal series with
 $\unicode[STIX]{x1D707}_{1}\neq \unicode[STIX]{x1D707}_{2}$
. (The other cases are similar; cf. also the proof of Proposition 3.6.1.) Then
$\unicode[STIX]{x1D707}_{1}\neq \unicode[STIX]{x1D707}_{2}$
. (The other cases are similar; cf. also the proof of Proposition 3.6.1.) Then
 $\unicode[STIX]{x1D70E}^{\vee }=\operatorname{Ind}(\unicode[STIX]{x1D707}_{1}^{\prime },\unicode[STIX]{x1D707}_{2}^{\prime }|\cdot |^{-1})$
with
$\unicode[STIX]{x1D70E}^{\vee }=\operatorname{Ind}(\unicode[STIX]{x1D707}_{1}^{\prime },\unicode[STIX]{x1D707}_{2}^{\prime }|\cdot |^{-1})$
with
 $\unicode[STIX]{x1D707}_{1}^{\prime }=\unicode[STIX]{x1D707}_{1}^{-1}|\cdot |$
,
$\unicode[STIX]{x1D707}_{1}^{\prime }=\unicode[STIX]{x1D707}_{1}^{-1}|\cdot |$
,
 $\unicode[STIX]{x1D707}_{2}^{\prime }=\unicode[STIX]{x1D707}_{2}^{-1}|\cdot |$
, and (dropping also the
$\unicode[STIX]{x1D707}_{2}^{\prime }=\unicode[STIX]{x1D707}_{2}^{-1}|\cdot |$
, and (dropping also the
![]() $\unicode[STIX]{x1D704}$
from the notation)
$\unicode[STIX]{x1D704}$
from the notation)
 $L(1+s,\unicode[STIX]{x1D70E}\times \unicode[STIX]{x1D70E}^{\vee })=(1-q_{F}^{-1-s})^{-2}(1-\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D707}_{2}^{\prime }(v)q_{F}^{-s})^{-1}(1-\unicode[STIX]{x1D707}_{1}^{\prime }\unicode[STIX]{x1D707}_{2}(v)q_{F}^{-s})^{-1}$
, where
$L(1+s,\unicode[STIX]{x1D70E}\times \unicode[STIX]{x1D70E}^{\vee })=(1-q_{F}^{-1-s})^{-2}(1-\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D707}_{2}^{\prime }(v)q_{F}^{-s})^{-1}(1-\unicode[STIX]{x1D707}_{1}^{\prime }\unicode[STIX]{x1D707}_{2}(v)q_{F}^{-s})^{-1}$
, where
 $\unicode[STIX]{x1D707}(v):=\unicode[STIX]{x1D707}(\unicode[STIX]{x1D71B}_{v})$
if
$\unicode[STIX]{x1D707}(v):=\unicode[STIX]{x1D707}(\unicode[STIX]{x1D71B}_{v})$
if
![]() $\unicode[STIX]{x1D707}$
is an unramified character and
$\unicode[STIX]{x1D707}$
is an unramified character and
 $\unicode[STIX]{x1D707}(v):=0$
otherwise.
$\unicode[STIX]{x1D707}(v):=0$
otherwise.
Assume that
 $f_{1}=f_{\unicode[STIX]{x1D707}_{1}}$
(the case
$f_{1}=f_{\unicode[STIX]{x1D707}_{1}}$
(the case
 $f_{1}=f_{\unicode[STIX]{x1D707}_{2}}$
is similar). If
$f_{1}=f_{\unicode[STIX]{x1D707}_{2}}$
is similar). If
 $f_{2}=f_{\unicode[STIX]{x1D707}_{1}^{\prime }}$
, then
$f_{2}=f_{\unicode[STIX]{x1D707}_{1}^{\prime }}$
, then
 $I_{s}(f_{1},f_{2})=(1-q_{F}^{-1-s})^{-1}$
has no pole at
$I_{s}(f_{1},f_{2})=(1-q_{F}^{-1-s})^{-1}$
has no pole at
![]() $s=0$
. If
$s=0$
. If
 $f_{2}=f_{\unicode[STIX]{x1D707}_{2}^{\prime }}$
, then
$f_{2}=f_{\unicode[STIX]{x1D707}_{2}^{\prime }}$
, then
 $I_{s}(f_{1},f_{2})=(1-\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D707}_{2}^{\prime }(v)q_{F}^{-s})^{-1}$
, whose inverse is a factor of
$I_{s}(f_{1},f_{2})=(1-\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D707}_{2}^{\prime }(v)q_{F}^{-s})^{-1}$
, whose inverse is a factor of
 $L(1+s,\unicode[STIX]{x1D70E}_{v}\times \unicode[STIX]{x1D70E}_{v}^{\vee })^{-1}$
in
$L(1+s,\unicode[STIX]{x1D70E}_{v}\times \unicode[STIX]{x1D70E}_{v}^{\vee })^{-1}$
in
![]() $M[q_{F}^{-s}]$
.◻
$M[q_{F}^{-s}]$
.◻
2.4
 $p$
-critical forms and the
$p$
-critical forms and the
 $p$
-adic Petersson product
$p$
-adic Petersson product
As in [Reference DisegniDis15], we introduce the following notion.
Definition 2.4.1. Let
 $W=(0,(W_{a}))\in \mathbf{S}^{\prime }(L)$
be a reduced
$W=(0,(W_{a}))\in \mathbf{S}^{\prime }(L)$
be a reduced
![]() $q$
-expansion without constant term, with values in a
$q$
-expansion without constant term, with values in a
![]() $p$
-adic field
$p$
-adic field
![]() $L$
, and let
$L$
, and let
![]() $v|p$
. We say that
$v|p$
. We say that
![]() $W$
is
$W$
is
![]() $v$
-critical if for some integer
$v$
-critical if for some integer
![]() $r$
, the following condition is satisfied: there is
$r$
, the following condition is satisfied: there is
![]() $c\in \mathbf{Z}$
such that, for each
$c\in \mathbf{Z}$
such that, for each
 $a\in \mathbf{A}^{\infty ,\times }$
with
$a\in \mathbf{A}^{\infty ,\times }$
with
 $v(a)=r$
and
$v(a)=r$
and
![]() $s\in \mathbf{N}$
,
$s\in \mathbf{N}$
,
 $$\begin{eqnarray}W_{a\unicode[STIX]{x1D71B}_{v}^{s}}\in q_{F,v}^{s-c}\mathscr{O}_{L}.\end{eqnarray}$$
$$\begin{eqnarray}W_{a\unicode[STIX]{x1D71B}_{v}^{s}}\in q_{F,v}^{s-c}\mathscr{O}_{L}.\end{eqnarray}$$
We say that
![]() $W$
is
$W$
is
![]() $p$
-critical if it is a sum of
$p$
-critical if it is a sum of
![]() $v$
-critical
$v$
-critical
![]() $q$
-expansions for
$q$
-expansions for
![]() $v|p$
.
$v|p$
.
For each
![]() $v|p$
, we define ordinary projectors
$v|p$
, we define ordinary projectors
![]() $e_{v}$
and
$e_{v}$
and
![]() $e$
on
$e$
on
 $\mathbf{M}(K^{p},\unicode[STIX]{x1D714},L)$
by
$\mathbf{M}(K^{p},\unicode[STIX]{x1D714},L)$
by
 $$\begin{eqnarray}e_{v}(\unicode[STIX]{x1D711}^{\prime })=\lim _{n\rightarrow \infty }\text{U}_{v,\ast }^{n!}\unicode[STIX]{x1D711}^{\prime },\quad e:=\mathop{\prod }_{v}e_{v}.\end{eqnarray}$$
$$\begin{eqnarray}e_{v}(\unicode[STIX]{x1D711}^{\prime })=\lim _{n\rightarrow \infty }\text{U}_{v,\ast }^{n!}\unicode[STIX]{x1D711}^{\prime },\quad e:=\mathop{\prod }_{v}e_{v}.\end{eqnarray}$$
They are independent of the choice of uniformisers. The image of
![]() $e_{v}$
is contained in
$e_{v}$
is contained in
 $M_{2}(K^{p}K_{1}^{1}(p^{\infty }),\unicode[STIX]{x1D714},L).$
It is clear that
$M_{2}(K^{p}K_{1}^{1}(p^{\infty }),\unicode[STIX]{x1D714},L).$
It is clear that
![]() $v$
-critical forms belong to the kernel of
$v$
-critical forms belong to the kernel of
![]() $e_{v}$
.
$e_{v}$
.
![]() $p$
-adic Petersson product. Let
$p$
-adic Petersson product. Let
![]() $M$
be a number field, and let
$M$
be a number field, and let
![]() $\unicode[STIX]{x1D70E}^{\infty }$
be an
$\unicode[STIX]{x1D70E}^{\infty }$
be an
![]() $M$
-rational cuspidal automorphic representation of
$M$
-rational cuspidal automorphic representation of
![]() $\mathbf{GL}_{2}$
of weight
$\mathbf{GL}_{2}$
of weight
![]() $2$
as in Definition 1.2.1, with central character
$2$
as in Definition 1.2.1, with central character
 $\unicode[STIX]{x1D714}:F^{\times }\backslash \mathbf{A}\rightarrow M^{\times }$
.
$\unicode[STIX]{x1D714}:F^{\times }\backslash \mathbf{A}\rightarrow M^{\times }$
.
Following Hida, we will define a
![]() $p$
-adic analogue of the Petersson inner product with a form
$p$
-adic analogue of the Petersson inner product with a form
![]() $\unicode[STIX]{x1D711}$
in
$\unicode[STIX]{x1D711}$
in
![]() $\unicode[STIX]{x1D70E}^{\infty }$
when
$\unicode[STIX]{x1D70E}^{\infty }$
when
![]() $\unicode[STIX]{x1D70E}_{p}$
is
$\unicode[STIX]{x1D70E}_{p}$
is
![]() $\mathfrak{p}$
-ordinary for a prime
$\mathfrak{p}$
-ordinary for a prime
![]() $\mathfrak{p}|p$
of
$\mathfrak{p}|p$
of
![]() $M$
. First we define an algebraic version of the Petersson product, which requires no ordinariness assumption. If
$M$
. First we define an algebraic version of the Petersson product, which requires no ordinariness assumption. If
 $\unicode[STIX]{x1D704}:M{\hookrightarrow}\mathbf{C}$
, let
$\unicode[STIX]{x1D704}:M{\hookrightarrow}\mathbf{C}$
, let
 $\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D704}}:=\unicode[STIX]{x1D704}\unicode[STIX]{x1D711}\otimes \unicode[STIX]{x1D711}_{\infty }\in \unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D704}}$
be the automorphic form whose Whittaker function at infinity is antiholomorphic of smallest
$\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D704}}:=\unicode[STIX]{x1D704}\unicode[STIX]{x1D711}\otimes \unicode[STIX]{x1D711}_{\infty }\in \unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D704}}$
be the automorphic form whose Whittaker function at infinity is antiholomorphic of smallest
![]() $K_{\infty }$
-type.
$K_{\infty }$
-type.
Lemma 2.4.2. There is a unique pairing
 $$\begin{eqnarray}(\,,\,)_{\unicode[STIX]{x1D70E}^{\infty }}:\unicode[STIX]{x1D70E}^{\infty }\otimes _{M}M_{2}(\unicode[STIX]{x1D714}^{-1},M)\rightarrow M\end{eqnarray}$$
$$\begin{eqnarray}(\,,\,)_{\unicode[STIX]{x1D70E}^{\infty }}:\unicode[STIX]{x1D70E}^{\infty }\otimes _{M}M_{2}(\unicode[STIX]{x1D714}^{-1},M)\rightarrow M\end{eqnarray}$$
such that for any
 $\unicode[STIX]{x1D711}_{1}\in \unicode[STIX]{x1D70E}^{\infty }$
,
$\unicode[STIX]{x1D711}_{1}\in \unicode[STIX]{x1D70E}^{\infty }$
,
 $\unicode[STIX]{x1D711}_{2}\in M_{2}(\unicode[STIX]{x1D714}^{-1},M)$
, and
$\unicode[STIX]{x1D711}_{2}\in M_{2}(\unicode[STIX]{x1D714}^{-1},M)$
, and
 $\unicode[STIX]{x1D704}:M{\hookrightarrow}\mathbf{C}$
, we have
$\unicode[STIX]{x1D704}:M{\hookrightarrow}\mathbf{C}$
, we have
 $$\begin{eqnarray}(\unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{2})_{\unicode[STIX]{x1D70E}}=\frac{|D_{F}|^{1/2}\unicode[STIX]{x1D701}_{F}(2)}{L(1,\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D704}},\operatorname{ad})}(\unicode[STIX]{x1D711}_{1}^{\unicode[STIX]{x1D704}},\unicode[STIX]{x1D704}\unicode[STIX]{x1D711}_{2}),\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{2})_{\unicode[STIX]{x1D70E}}=\frac{|D_{F}|^{1/2}\unicode[STIX]{x1D701}_{F}(2)}{L(1,\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D704}},\operatorname{ad})}(\unicode[STIX]{x1D711}_{1}^{\unicode[STIX]{x1D704}},\unicode[STIX]{x1D704}\unicode[STIX]{x1D711}_{2}),\end{eqnarray}$$
where
 $$\begin{eqnarray}(\unicode[STIX]{x1D711}_{1}^{\prime },\unicode[STIX]{x1D711}_{2}^{\prime }):=\int _{\boldsymbol{ GL}_{2}(F)Z(\mathbf{A})\backslash \mathbf{GL}_{2}(\mathbf{A})}\unicode[STIX]{x1D711}_{1}^{\prime }(g)\unicode[STIX]{x1D711}_{2}^{\prime }(g)\,dg\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D711}_{1}^{\prime },\unicode[STIX]{x1D711}_{2}^{\prime }):=\int _{\boldsymbol{ GL}_{2}(F)Z(\mathbf{A})\backslash \mathbf{GL}_{2}(\mathbf{A})}\unicode[STIX]{x1D711}_{1}^{\prime }(g)\unicode[STIX]{x1D711}_{2}^{\prime }(g)\,dg\end{eqnarray}$$
is the usual Petersson product on complex automorphic forms with respect to the Tamagawa measure
![]() $dg$
.
$dg$
.
Proof. Note first that if such a pairing exists, it annihilates forms on the right-hand side which are orthogonal (under the complex Petersson product in any embedding) to forms in
![]() $\unicode[STIX]{x1D70E}$
. Then we just need to use a well-known formula for the adjoint
$\unicode[STIX]{x1D70E}$
. Then we just need to use a well-known formula for the adjoint
![]() $L$
-value in terms of Petersson product; we quote it in the version given in [Reference Tian, Yuan and ZhangTYZ14, p. 55]: for an antiholomorphic form
$L$
-value in terms of Petersson product; we quote it in the version given in [Reference Tian, Yuan and ZhangTYZ14, p. 55]: for an antiholomorphic form
![]() $\unicode[STIX]{x1D711}_{1}^{\prime }$
in the space of
$\unicode[STIX]{x1D711}_{1}^{\prime }$
in the space of
![]() $\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D704}}$
and a holomorphic form
$\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D704}}$
and a holomorphic form
![]() $\unicode[STIX]{x1D711}_{2}^{\prime }$
in the space of
$\unicode[STIX]{x1D711}_{2}^{\prime }$
in the space of
![]() $\unicode[STIX]{x1D70E}^{\vee ,\unicode[STIX]{x1D704}}$
, both rational over
$\unicode[STIX]{x1D70E}^{\vee ,\unicode[STIX]{x1D704}}$
, both rational over
![]() $\unicode[STIX]{x1D704}M$
, with factorisable Whittaker functions
$\unicode[STIX]{x1D704}M$
, with factorisable Whittaker functions
![]() $W_{i}^{\unicode[STIX]{x1D704}}$
, we have
$W_{i}^{\unicode[STIX]{x1D704}}$
, we have
 $$\begin{eqnarray}\frac{|D_{F}|^{1/2}\unicode[STIX]{x1D701}_{F}(2)(\unicode[STIX]{x1D711}_{1}^{\prime },\unicode[STIX]{x1D711}_{2}^{\prime })}{2L(1,\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D704}},\text{ad})}=\mathop{\prod }_{v}(W_{1,v}^{\unicode[STIX]{x1D704}},W_{2,v}^{\unicode[STIX]{x1D704}})_{v}\end{eqnarray}$$
$$\begin{eqnarray}\frac{|D_{F}|^{1/2}\unicode[STIX]{x1D701}_{F}(2)(\unicode[STIX]{x1D711}_{1}^{\prime },\unicode[STIX]{x1D711}_{2}^{\prime })}{2L(1,\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D704}},\text{ad})}=\mathop{\prod }_{v}(W_{1,v}^{\unicode[STIX]{x1D704}},W_{2,v}^{\unicode[STIX]{x1D704}})_{v}\end{eqnarray}$$
where for all
![]() $v$
the local pairings are given by the right-hand side of (2.3.1) and do not depend on the choice of additive characters. Each local factor in the product is rational over
$v$
the local pairings are given by the right-hand side of (2.3.1) and do not depend on the choice of additive characters. Each local factor in the product is rational over
![]() $\unicode[STIX]{x1D704}M$
and almost all of them are equal to
$\unicode[STIX]{x1D704}M$
and almost all of them are equal to
![]() $1$
.◻
$1$
.◻
Remark 2.4.3. If
 $\unicode[STIX]{x1D711}_{2}\in M_{2}(M)$
does not have central character
$\unicode[STIX]{x1D711}_{2}\in M_{2}(M)$
does not have central character
![]() $\unicode[STIX]{x1D714}^{-1}$
, we can still define
$\unicode[STIX]{x1D714}^{-1}$
, we can still define
 $(\unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{2})_{\unicode[STIX]{x1D70E}^{\infty }}:=(\unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{2,\unicode[STIX]{x1D714}^{-1}})_{\unicode[STIX]{x1D70E}^{\infty }}$
, where
$(\unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{2})_{\unicode[STIX]{x1D70E}^{\infty }}:=(\unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{2,\unicode[STIX]{x1D714}^{-1}})_{\unicode[STIX]{x1D70E}^{\infty }}$
, where
 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{2,\unicode[STIX]{x1D714}^{-1}}(g):=\unicode[STIX]{x2A0D}_{Z(F)\backslash Z(\mathbf{A})}\unicode[STIX]{x1D711}_{2}(zg)\unicode[STIX]{x1D714}(z)\,dz.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{2,\unicode[STIX]{x1D714}^{-1}}(g):=\unicode[STIX]{x2A0D}_{Z(F)\backslash Z(\mathbf{A})}\unicode[STIX]{x1D711}_{2}(zg)\unicode[STIX]{x1D714}(z)\,dz.\end{eqnarray}$$
Now fix a prime
![]() $\mathfrak{p}|p$
of
$\mathfrak{p}|p$
of
![]() $M$
and a finite extension
$M$
and a finite extension
![]() $L$
of
$L$
of
![]() $M_{\mathfrak{p}}$
, and assume that for all
$M_{\mathfrak{p}}$
, and assume that for all
![]() $v|p$
,
$v|p$
,
![]() $\unicode[STIX]{x1D70E}_{v}\otimes L$
is nearly
$\unicode[STIX]{x1D70E}_{v}\otimes L$
is nearly
![]() $\mathfrak{p}$
-ordinary with unit character
$\mathfrak{p}$
-ordinary with unit character
 $\unicode[STIX]{x1D6FC}_{v}:F_{v}^{\times }\rightarrow \mathscr{O}_{L}^{\times }$
in the sense of Definition 1.2.2. Fix a Whittaker functional
$\unicode[STIX]{x1D6FC}_{v}:F_{v}^{\times }\rightarrow \mathscr{O}_{L}^{\times }$
in the sense of Definition 1.2.2. Fix a Whittaker functional
 $\mathscr{W}_{p}=\prod _{v}\mathscr{W}_{v}$
at
$\mathscr{W}_{p}=\prod _{v}\mathscr{W}_{v}$
at
![]() $p$
and let
$p$
and let
 $\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D70E}^{\infty }\otimes _{M}M(\unicode[STIX]{x1D6FC})$
be a form in the space of
$\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D70E}^{\infty }\otimes _{M}M(\unicode[STIX]{x1D6FC})$
be a form in the space of
![]() $\unicode[STIX]{x1D70E}^{\infty }$
whose image under
$\unicode[STIX]{x1D70E}^{\infty }$
whose image under
![]() $\mathscr{W}_{v}$
is the function (viewed in the
$\mathscr{W}_{v}$
is the function (viewed in the
![]() $M(\unicode[STIX]{x1D6FC})$
-rational part of any Kirillov model)
$M(\unicode[STIX]{x1D6FC})$
-rational part of any Kirillov model)
 $$\begin{eqnarray}W_{v}(y)=\mathbf{1}_{\mathscr{O}_{F}-\{0\}}(y)|y|\unicode[STIX]{x1D6FC}_{v}(y).\end{eqnarray}$$
$$\begin{eqnarray}W_{v}(y)=\mathbf{1}_{\mathscr{O}_{F}-\{0\}}(y)|y|\unicode[STIX]{x1D6FC}_{v}(y).\end{eqnarray}$$
Note that
![]() $W_{v}$
, viewed in a Kirillov model associated to an additive character of level
$W_{v}$
, viewed in a Kirillov model associated to an additive character of level
![]() $0$
, satisfies
$0$
, satisfies
 $\text{U}_{v}^{\ast }W_{v}=\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})W_{v}$
.
$\text{U}_{v}^{\ast }W_{v}=\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})W_{v}$
.
In the next proposition, we use the notation
 $\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{r}:=\prod _{v|p}\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})^{r_{v}}$
.
$\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{r}:=\prod _{v|p}\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})^{r_{v}}$
.
Proposition 2.4.4. There exists a unique bounded linear functional
 $$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}:\mathbf{M}(K^{p},\unicode[STIX]{x1D714}^{-1},L)\rightarrow L\end{eqnarray}$$
$$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}:\mathbf{M}(K^{p},\unicode[STIX]{x1D714}^{-1},L)\rightarrow L\end{eqnarray}$$
satisfying the following.
-
(1) Let
 $r=(r_{v})_{v|p}\in \mathbf{Z}_{{\geqslant}1}^{\{v|p\}}$
. The restriction of
$r=(r_{v})_{v|p}\in \mathbf{Z}_{{\geqslant}1}^{\{v|p\}}$
. The restriction of
 $\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
to
$\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
to
 $M_{2}(K^{p}K^{1}(p^{r})_{p},M(\unicode[STIX]{x1D6FC}))$
is given by (2.4.3)for any choice of uniformisers
$M_{2}(K^{p}K^{1}(p^{r})_{p},M(\unicode[STIX]{x1D6FC}))$
is given by (2.4.3)for any choice of uniformisers $$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D711}^{\prime })=\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}(w_{r}\unicode[STIX]{x1D711},\unicode[STIX]{x1D711}^{\prime })_{\unicode[STIX]{x1D70E}^{\infty }}=\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}(\unicode[STIX]{x1D711},w_{r}^{-1}\unicode[STIX]{x1D711}^{\prime })_{\unicode[STIX]{x1D70E}^{\infty }}\in M(\unicode[STIX]{x1D6FC})\end{eqnarray}$$
$$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D711}^{\prime })=\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}(w_{r}\unicode[STIX]{x1D711},\unicode[STIX]{x1D711}^{\prime })_{\unicode[STIX]{x1D70E}^{\infty }}=\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}(\unicode[STIX]{x1D711},w_{r}^{-1}\unicode[STIX]{x1D711}^{\prime })_{\unicode[STIX]{x1D70E}^{\infty }}\in M(\unicode[STIX]{x1D6FC})\end{eqnarray}$$
 $\unicode[STIX]{x1D71B}_{v}$
in the definitions of
$\unicode[STIX]{x1D71B}_{v}$
in the definitions of
 $\text{U}_{v,\ast }$
,
$\text{U}_{v,\ast }$
,
 $\text{U}_{v}^{\ast }$
,
$\text{U}_{v}^{\ast }$
,
 $w_{r}$
.
$w_{r}$
.
-
(2) We have
for all $$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\text{U}_{v,\ast }\unicode[STIX]{x1D711}^{\prime })=\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D711}^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\text{U}_{v,\ast }\unicode[STIX]{x1D711}^{\prime })=\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D711}^{\prime })\end{eqnarray}$$
 $v|p$
and all
$v|p$
and all
 $\unicode[STIX]{x1D711}^{\prime }$
.
$\unicode[STIX]{x1D711}^{\prime }$
.
-
(3)
 $\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
vanishes on
$\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
vanishes on
 $p$
-critical forms.
$p$
-critical forms. -
(4) Let
 $T(\unicode[STIX]{x1D70E}^{\vee })\in \mathscr{H}^{S}(M)$
(where
$T(\unicode[STIX]{x1D70E}^{\vee })\in \mathscr{H}^{S}(M)$
(where
 $S$
is any sufficiently large set of finite places containing those dividing
$S$
is any sufficiently large set of finite places containing those dividing
 $p$
) be any element whose image
$p$
) be any element whose image
 $T(\unicode[STIX]{x1D70E})^{\unicode[STIX]{x1D704}}\in \mathscr{H}^{S}(M)\otimes _{M,\unicode[STIX]{x1D704}}\mathbf{C}$
acts on
$T(\unicode[STIX]{x1D70E})^{\unicode[STIX]{x1D704}}\in \mathscr{H}^{S}(M)\otimes _{M,\unicode[STIX]{x1D704}}\mathbf{C}$
acts on
 $S_{2}(K^{p}K^{1}(p^{r})_{p},\mathbf{C})$
as the idempotent projector onto
$S_{2}(K^{p}K^{1}(p^{r})_{p},\mathbf{C})$
as the idempotent projector onto
 $(\unicode[STIX]{x1D70E}^{\vee ,\unicode[STIX]{x1D704}})^{K^{p}K^{1}(p^{r})_{p}}$
for any
$(\unicode[STIX]{x1D70E}^{\vee ,\unicode[STIX]{x1D704}})^{K^{p}K^{1}(p^{r})_{p}}$
for any
 $\unicode[STIX]{x1D704}:M{\hookrightarrow}\mathbf{C}$
and
$\unicode[STIX]{x1D704}:M{\hookrightarrow}\mathbf{C}$
and
 $r\geqslant 1$
. Let
$r\geqslant 1$
. Let
 $T_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })$
be the image of
$T_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })$
be the image of
 $T(\unicode[STIX]{x1D70E}^{\vee })$
in
$T(\unicode[STIX]{x1D70E}^{\vee })$
in
 $\mathscr{H}^{S}(M)\otimes _{M,\unicode[STIX]{x1D704}_{\mathfrak{p}}}L$
. Then
$\mathscr{H}^{S}(M)\otimes _{M,\unicode[STIX]{x1D704}_{\mathfrak{p}}}L$
. Then  $$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}\circ T_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })=\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}.\end{eqnarray}$$
$$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}\circ T_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })=\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}.\end{eqnarray}$$
Proof. By property (2), for each
![]() $v$
we must have
$v$
we must have
 $$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(e_{v}\unicode[STIX]{x1D711}^{\prime })=\lim _{n\rightarrow \infty }\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\text{U}_{v,\ast }^{n!}\unicode[STIX]{x1D711}^{\prime })=\lim _{n\rightarrow \infty }\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})^{n!}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D711}^{\prime })=\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D711}^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(e_{v}\unicode[STIX]{x1D711}^{\prime })=\lim _{n\rightarrow \infty }\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\text{U}_{v,\ast }^{n!}\unicode[STIX]{x1D711}^{\prime })=\lim _{n\rightarrow \infty }\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})^{n!}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D711}^{\prime })=\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D711}^{\prime })\end{eqnarray}$$
as
![]() $\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})$
is a
$\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})$
is a
![]() $p$
-adic unit; note that this expression does not depend on the choice of uniformisers. It follows that
$p$
-adic unit; note that this expression does not depend on the choice of uniformisers. It follows that
![]() $\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
must factor through the ordinary projection
$\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
must factor through the ordinary projection
 $$\begin{eqnarray}e:\mathbf{M}(K^{p},\unicode[STIX]{x1D714}^{-1},L)\rightarrow M_{2}(K^{p}K^{1}(p^{\infty })_{p},\unicode[STIX]{x1D714}^{-1},L),\end{eqnarray}$$
$$\begin{eqnarray}e:\mathbf{M}(K^{p},\unicode[STIX]{x1D714}^{-1},L)\rightarrow M_{2}(K^{p}K^{1}(p^{\infty })_{p},\unicode[STIX]{x1D714}^{-1},L),\end{eqnarray}$$
which implies property (3). On the image of
![]() $e$
,
$e$
,
![]() $\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
must be defined defined by (2.4.3), which makes uniqueness and property (4) clear.
$\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
must be defined defined by (2.4.3), which makes uniqueness and property (4) clear.
It remains to show the existence (that is, that (2.4.3) is compatible with changing
![]() $r$
) and that the first equality in (2.4.3) holds for all
$r$
) and that the first equality in (2.4.3) holds for all
![]() $r$
for the functional
$r$
for the functional
![]() $\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
just defined (the second one is trivial). For the latter, we have
$\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
just defined (the second one is trivial). For the latter, we have
 $$\begin{eqnarray}\displaystyle (w_{r}\unicode[STIX]{x1D711},\text{U}_{v,\ast }\unicode[STIX]{x1D711}^{\prime }) & = & \displaystyle (w_{r}\unicode[STIX]{x1D711},K^{1}(\unicode[STIX]{x1D71B}_{v}^{r_{v}})_{v}(\!\begin{smallmatrix}1 & \\ & \unicode[STIX]{x1D71B}_{v}^{-1}\end{smallmatrix}\!)\unicode[STIX]{x1D711}^{\prime })=((\!\begin{smallmatrix}1 & \\ & \unicode[STIX]{x1D71B}_{v}\end{smallmatrix}\!)K^{1}(\unicode[STIX]{x1D71B}_{v}^{r_{v}})_{v}w_{r}\unicode[STIX]{x1D711},\unicode[STIX]{x1D711}^{\prime })\nonumber\\ \displaystyle & = & \displaystyle (w_{r}K_{1}(\unicode[STIX]{x1D71B}_{v}^{r_{v}})_{v}(\!\begin{smallmatrix}\unicode[STIX]{x1D71B}_{v} & \\ & 1\end{smallmatrix}\!)\unicode[STIX]{x1D711},\unicode[STIX]{x1D711}^{\prime })=(w_{r}\text{U}_{v}^{\ast }\unicode[STIX]{x1D711},\unicode[STIX]{x1D711}^{\prime })=\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})(w_{r}\unicode[STIX]{x1D711},\unicode[STIX]{x1D711}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (w_{r}\unicode[STIX]{x1D711},\text{U}_{v,\ast }\unicode[STIX]{x1D711}^{\prime }) & = & \displaystyle (w_{r}\unicode[STIX]{x1D711},K^{1}(\unicode[STIX]{x1D71B}_{v}^{r_{v}})_{v}(\!\begin{smallmatrix}1 & \\ & \unicode[STIX]{x1D71B}_{v}^{-1}\end{smallmatrix}\!)\unicode[STIX]{x1D711}^{\prime })=((\!\begin{smallmatrix}1 & \\ & \unicode[STIX]{x1D71B}_{v}\end{smallmatrix}\!)K^{1}(\unicode[STIX]{x1D71B}_{v}^{r_{v}})_{v}w_{r}\unicode[STIX]{x1D711},\unicode[STIX]{x1D711}^{\prime })\nonumber\\ \displaystyle & = & \displaystyle (w_{r}K_{1}(\unicode[STIX]{x1D71B}_{v}^{r_{v}})_{v}(\!\begin{smallmatrix}\unicode[STIX]{x1D71B}_{v} & \\ & 1\end{smallmatrix}\!)\unicode[STIX]{x1D711},\unicode[STIX]{x1D711}^{\prime })=(w_{r}\text{U}_{v}^{\ast }\unicode[STIX]{x1D711},\unicode[STIX]{x1D711}^{\prime })=\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})(w_{r}\unicode[STIX]{x1D711},\unicode[STIX]{x1D711}^{\prime }).\end{eqnarray}$$
The compatibility with change of
![]() $r$
can be seen by a similar calculation.◻
$r$
can be seen by a similar calculation.◻
We still use the notation
![]() $\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
for the linear form deduced from
$\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
for the linear form deduced from
![]() $\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
by extending scalars to some
$\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
by extending scalars to some
![]() $L$
-algebra. The analogous remark will apply to
$L$
-algebra. The analogous remark will apply to
![]() $(\,,\,)_{\unicode[STIX]{x1D70E}_{\infty }}$
.
$(\,,\,)_{\unicode[STIX]{x1D70E}_{\infty }}$
.
3 The
 $p$
-adic
$p$
-adic
 $L$
-function
$L$
-function
3.1 Weil representation
We start by recalling from [Reference WaldspurgerWal85, Reference Yuan, Zhang and ZhangYZZ12] the definition of the Weil representation for groups of similitudes.
Local case. Let
 $V=(V,q)$
be a quadratic space of even dimension over a local field
$V=(V,q)$
be a quadratic space of even dimension over a local field
![]() $F$
of characteristic not 2. Fix a non-trivial additive character
$F$
of characteristic not 2. Fix a non-trivial additive character
![]() $\unicode[STIX]{x1D713}$
of
$\unicode[STIX]{x1D713}$
of
![]() $F$
. For simplicity, we assume that
$F$
. For simplicity, we assume that
![]() $V$
has even dimension. For
$V$
has even dimension. For
![]() $u\in F^{\times }$
, we denote by
$u\in F^{\times }$
, we denote by
![]() $V_{u}$
the quadratic space
$V_{u}$
the quadratic space
![]() $(V,uq)$
. We let
$(V,uq)$
. We let
 $\mathbf{GL}_{2}(F)\times \mathbf{GO}(V)$
act on the usual space of Schwartz functionsFootnote
16
$\mathbf{GL}_{2}(F)\times \mathbf{GO}(V)$
act on the usual space of Schwartz functionsFootnote
16
 $\mathscr{S}(V\times F^{\times })$
as follows (here
$\mathscr{S}(V\times F^{\times })$
as follows (here
 $\unicode[STIX]{x1D708}:\mathbf{GO}(V)\rightarrow \mathbf{G}_{m}$
denotes the similitude character):
$\unicode[STIX]{x1D708}:\mathbf{GO}(V)\rightarrow \mathbf{G}_{m}$
denotes the similitude character):
-
–
 $r(h)\unicode[STIX]{x1D719}(x,u)=\unicode[STIX]{x1D719}(h^{-1}x,\unicode[STIX]{x1D708}(h)u)$
for
$r(h)\unicode[STIX]{x1D719}(x,u)=\unicode[STIX]{x1D719}(h^{-1}x,\unicode[STIX]{x1D708}(h)u)$
for
 $h\in \mathbf{GO}(V)$
;
$h\in \mathbf{GO}(V)$
; -
–
 $r(n(b))\unicode[STIX]{x1D719}(x,u)=\unicode[STIX]{x1D713}(buq(x))\unicode[STIX]{x1D719}(x,u)$
for
$r(n(b))\unicode[STIX]{x1D719}(x,u)=\unicode[STIX]{x1D713}(buq(x))\unicode[STIX]{x1D719}(x,u)$
for
 $n(b)\in N(F)\subset \mathbf{GL}_{2}(F)$
;
$n(b)\in N(F)\subset \mathbf{GL}_{2}(F)$
; -
–
 $r((\!\begin{smallmatrix}a & \\ & d\end{smallmatrix}\!))\unicode[STIX]{x1D719}(x,u)=\unicode[STIX]{x1D712}_{V_{u}}(a)|a/d|^{\dim V/4}\unicode[STIX]{x1D719}(at,d^{-1}a^{-1}u)$
;
$r((\!\begin{smallmatrix}a & \\ & d\end{smallmatrix}\!))\unicode[STIX]{x1D719}(x,u)=\unicode[STIX]{x1D712}_{V_{u}}(a)|a/d|^{\dim V/4}\unicode[STIX]{x1D719}(at,d^{-1}a^{-1}u)$
; -
–
 $r(w)\unicode[STIX]{x1D719}(x,u)=\unicode[STIX]{x1D6FE}(V_{u})\hat{\unicode[STIX]{x1D719}}(x,u)$
for
$r(w)\unicode[STIX]{x1D719}(x,u)=\unicode[STIX]{x1D6FE}(V_{u})\hat{\unicode[STIX]{x1D719}}(x,u)$
for
 $w=(\!\begin{smallmatrix} & 1\\ -1 & \end{smallmatrix}\!)$
.
$w=(\!\begin{smallmatrix} & 1\\ -1 & \end{smallmatrix}\!)$
.
Here
 $\unicode[STIX]{x1D712}_{V}=\unicode[STIX]{x1D712}_{(V,q)}$
is the quadratic character attached to
$\unicode[STIX]{x1D712}_{V}=\unicode[STIX]{x1D712}_{(V,q)}$
is the quadratic character attached to
![]() $V$
,
$V$
,
![]() $\unicode[STIX]{x1D6FE}(V,q)$
is a fourth root of unity, and
$\unicode[STIX]{x1D6FE}(V,q)$
is a fourth root of unity, and
![]() $\hat{\unicode[STIX]{x1D719}}$
denotes the Fourier transform in the first variable with respect to the self-dual measure for the character
$\hat{\unicode[STIX]{x1D719}}$
denotes the Fourier transform in the first variable with respect to the self-dual measure for the character
 $\unicode[STIX]{x1D713}_{u}(x)=\unicode[STIX]{x1D713}(ux)$
. We will need to note the following facts (see e.g. [Reference Jacquet and LanglandsJL70]):
$\unicode[STIX]{x1D713}_{u}(x)=\unicode[STIX]{x1D713}(ux)$
. We will need to note the following facts (see e.g. [Reference Jacquet and LanglandsJL70]):
![]() $\unicode[STIX]{x1D712}_{V}$
is trivial if
$\unicode[STIX]{x1D712}_{V}$
is trivial if
![]() $V$
is a quaternion algebra over
$V$
is a quaternion algebra over
![]() $F$
or
$F$
or
 $V=F\oplus F$
, and
$V=F\oplus F$
, and
![]() $\unicode[STIX]{x1D712}_{V}=\unicode[STIX]{x1D702}$
if
$\unicode[STIX]{x1D712}_{V}=\unicode[STIX]{x1D702}$
if
![]() $V$
is a separable quadratic extension
$V$
is a separable quadratic extension
![]() $E$
of
$E$
of
![]() $F$
with associated character
$F$
with associated character
![]() $\unicode[STIX]{x1D702}$
; and
$\unicode[STIX]{x1D702}$
; and
 $\unicode[STIX]{x1D6FE}(V)=+1$
if
$\unicode[STIX]{x1D6FE}(V)=+1$
if
![]() $V$
is the space of
$V$
is the space of
![]() $2\times 2$
matrices or
$2\times 2$
matrices or
 $V=F\oplus F$
,
$V=F\oplus F$
,
 $\unicode[STIX]{x1D6FE}(V)=-1$
if
$\unicode[STIX]{x1D6FE}(V)=-1$
if
![]() $V$
is a non-split quaternion algebra.
$V$
is a non-split quaternion algebra.
We state here a lemma which will be useful later.
Lemma 3.1.1. Let
![]() $F$
be a non-archimedean local field and
$F$
be a non-archimedean local field and
 $\unicode[STIX]{x1D719}\in \mathscr{S}(V\times F^{\times })$
a Schwartz function with support contained in
$\unicode[STIX]{x1D719}\in \mathscr{S}(V\times F^{\times })$
a Schwartz function with support contained in
 $$\begin{eqnarray}\{(x,u)\in V\times F^{\times }:uq(x)\in \mathscr{O}_{F}\}.\end{eqnarray}$$
$$\begin{eqnarray}\{(x,u)\in V\times F^{\times }:uq(x)\in \mathscr{O}_{F}\}.\end{eqnarray}$$
Suppose that the character
![]() $\unicode[STIX]{x1D713}$
used to construct the Weil representation has level
$\unicode[STIX]{x1D713}$
used to construct the Weil representation has level
![]() $0$
. Then
$0$
. Then
![]() $\unicode[STIX]{x1D719}$
is invariant under
$\unicode[STIX]{x1D719}$
is invariant under
 $K_{1}^{1}(\unicode[STIX]{x1D71B}^{r})\subset \mathbf{GL}_{2}(\mathscr{O}_{F})$
for sufficiently large
$K_{1}^{1}(\unicode[STIX]{x1D71B}^{r})\subset \mathbf{GL}_{2}(\mathscr{O}_{F})$
for sufficiently large
![]() $r$
. If moreover
$r$
. If moreover
![]() $\unicode[STIX]{x1D719}(x,u)$
depends only on
$\unicode[STIX]{x1D719}(x,u)$
depends only on
![]() $x$
and on the valuation
$x$
and on the valuation
![]() $v(u)$
, then
$v(u)$
, then
![]() $\unicode[STIX]{x1D719}$
is invariant under
$\unicode[STIX]{x1D719}$
is invariant under
 $K^{1}(\unicode[STIX]{x1D71B}^{r})$
.
$K^{1}(\unicode[STIX]{x1D71B}^{r})$
.
Proof. By continuity of the Weil representation, for the first assertion it suffices to show the invariance under
![]() $N(\mathscr{O}_{F})$
. This follows from the observation that under our assumption, in the formula
$N(\mathscr{O}_{F})$
. This follows from the observation that under our assumption, in the formula
 $$\begin{eqnarray}r(n(b))\unicode[STIX]{x1D719}(x,u)=\unicode[STIX]{x1D713}(ubq(x))\unicode[STIX]{x1D719}(x,u),\end{eqnarray}$$
$$\begin{eqnarray}r(n(b))\unicode[STIX]{x1D719}(x,u)=\unicode[STIX]{x1D713}(ubq(x))\unicode[STIX]{x1D719}(x,u),\end{eqnarray}$$
the multiplier
 $\unicode[STIX]{x1D713}(ubq(x))=1$
whenever
$\unicode[STIX]{x1D713}(ubq(x))=1$
whenever
![]() $(x,u)$
is in the support of
$(x,u)$
is in the support of
![]() $\unicode[STIX]{x1D719}$
. The second assertion is then equivalent to the invariance of
$\unicode[STIX]{x1D719}$
. The second assertion is then equivalent to the invariance of
![]() $\unicode[STIX]{x1D719}$
under the subgroup
$\unicode[STIX]{x1D719}$
under the subgroup
 $(\!\begin{smallmatrix}1 & \\ & \mathscr{O}_{F}^{\times }\end{smallmatrix}\!)\subset \mathbf{GL}_{2}(\mathscr{O}_{F})$
, which is clear.◻
$(\!\begin{smallmatrix}1 & \\ & \mathscr{O}_{F}^{\times }\end{smallmatrix}\!)\subset \mathbf{GL}_{2}(\mathscr{O}_{F})$
, which is clear.◻
Fock model and reduced Fock model. Assume that
![]() $F=\mathbf{R}$
and
$F=\mathbf{R}$
and
![]() $V$
is positive definite. Then we will prefer to consider a modified version of the previous setting. Let the Fock model
$V$
is positive definite. Then we will prefer to consider a modified version of the previous setting. Let the Fock model
 $\mathscr{S}(V\times \mathbf{R}^{\times },\mathbf{C})$
be the space of functions spanned by those of the form
$\mathscr{S}(V\times \mathbf{R}^{\times },\mathbf{C})$
be the space of functions spanned by those of the form
 $$\begin{eqnarray}H(u)P(x)e^{-2\unicode[STIX]{x1D70B}|u|q(x)},\end{eqnarray}$$
$$\begin{eqnarray}H(u)P(x)e^{-2\unicode[STIX]{x1D70B}|u|q(x)},\end{eqnarray}$$
where
![]() $H$
is a compactly supported smooth function on
$H$
is a compactly supported smooth function on
![]() $\mathbf{R}^{\times }$
and
$\mathbf{R}^{\times }$
and
![]() $P$
is a complex polynomial function on
$P$
is a complex polynomial function on
![]() $V$
. This space is not stable under the action of
$V$
. This space is not stable under the action of
 $\mathbf{GL}_{2}(\mathbf{R})$
, but it is so under the restriction of the induced
$\mathbf{GL}_{2}(\mathbf{R})$
, but it is so under the restriction of the induced
 $(\mathfrak{gl}_{2,\mathbf{R}},\mathbf{O}_{2}(\mathbf{R}))$
-action on the usual Schwartz space (see [Reference Yuan, Zhang and ZhangYZZ12, §2.1.2]).
$(\mathfrak{gl}_{2,\mathbf{R}},\mathbf{O}_{2}(\mathbf{R}))$
-action on the usual Schwartz space (see [Reference Yuan, Zhang and ZhangYZZ12, §2.1.2]).
We will also need to consider the reduced Fock space
 $\overline{\mathscr{S}}(V\times \mathbf{R}^{\times })$
spanned by functions of the form
$\overline{\mathscr{S}}(V\times \mathbf{R}^{\times })$
spanned by functions of the form
 $$\begin{eqnarray}\unicode[STIX]{x1D719}(x,u)=(P_{1}(uq(x))+\text{sgn}(u)P_{2}(uq(x)))e^{-2\unicode[STIX]{x1D70B}|u|q(x)},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}(x,u)=(P_{1}(uq(x))+\text{sgn}(u)P_{2}(uq(x)))e^{-2\unicode[STIX]{x1D70B}|u|q(x)},\end{eqnarray}$$
where
![]() $P_{1}$
,
$P_{1}$
,
![]() $P_{2}$
are polynomial functions with rational coefficients. It contains the standard Schwartz function
$P_{2}$
are polynomial functions with rational coefficients. It contains the standard Schwartz function
 $$\begin{eqnarray}\unicode[STIX]{x1D719}(x,u)=\mathbf{1}_{\mathbf{R}_{+}}(u)e^{-2\unicode[STIX]{x1D70B}|u|q(x)},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}(x,u)=\mathbf{1}_{\mathbf{R}_{+}}(u)e^{-2\unicode[STIX]{x1D70B}|u|q(x)},\end{eqnarray}$$
which for
![]() $x\neq 0$
satisfies
$x\neq 0$
satisfies
 $$\begin{eqnarray}r(g)\unicode[STIX]{x1D719}(x,u)=W_{uq(x)}^{(d)}(g)\end{eqnarray}$$
$$\begin{eqnarray}r(g)\unicode[STIX]{x1D719}(x,u)=W_{uq(x)}^{(d)}(g)\end{eqnarray}$$
if
![]() $V$
has dimension
$V$
has dimension
![]() $2d$
and
$2d$
and
![]() $W^{(d)}$
is the standard holomorphic Whittaker function (2.1.1) (see [Reference Yuan, Zhang and ZhangYZZ12, §4.1.1]).
$W^{(d)}$
is the standard holomorphic Whittaker function (2.1.1) (see [Reference Yuan, Zhang and ZhangYZZ12, §4.1.1]).
By [Reference Yuan, Zhang and ZhangYZZ12, §§4.4.1 and 3.4.1], there is a surjective quotient map
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}rcl@{}}\mathscr{S}(V\times \mathbf{R}^{\times },\mathbf{C})\ & \rightarrow \ & \overline{\mathscr{S}}(V\times \mathbf{R}^{\times })\otimes _{\mathbf{Q}}\mathbf{C}\\ \unicode[STIX]{x1D6F7}\ & \mapsto \ & \unicode[STIX]{x1D719}(x,u)=\overline{\unicode[STIX]{x1D6F7}}(x,u)=\displaystyle \int _{\mathbf{R}^{\times }}\unicode[STIX]{x2A0D}_{\mathbf{O}(V)}r(ch)\unicode[STIX]{x1D6F7}(x,u)\,dh\,dc.\end{array} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}rcl@{}}\mathscr{S}(V\times \mathbf{R}^{\times },\mathbf{C})\ & \rightarrow \ & \overline{\mathscr{S}}(V\times \mathbf{R}^{\times })\otimes _{\mathbf{Q}}\mathbf{C}\\ \unicode[STIX]{x1D6F7}\ & \mapsto \ & \unicode[STIX]{x1D719}(x,u)=\overline{\unicode[STIX]{x1D6F7}}(x,u)=\displaystyle \int _{\mathbf{R}^{\times }}\unicode[STIX]{x2A0D}_{\mathbf{O}(V)}r(ch)\unicode[STIX]{x1D6F7}(x,u)\,dh\,dc.\end{array} & & \displaystyle\end{eqnarray}$$
We let
 $\mathscr{S}(V\times \mathbf{R}^{\times })\subset \mathscr{S}(V\times \mathbf{R}^{\times },\mathbf{C})$
be the preimage of
$\mathscr{S}(V\times \mathbf{R}^{\times })\subset \mathscr{S}(V\times \mathbf{R}^{\times },\mathbf{C})$
be the preimage of
 $\overline{\mathscr{S}}(V\times \mathbf{R}^{\times })$
. For the sake of uniformity, when
$\overline{\mathscr{S}}(V\times \mathbf{R}^{\times })$
. For the sake of uniformity, when
![]() $F$
is non-archimedean we set
$F$
is non-archimedean we set
 $\overline{\mathscr{S}}(V\times F^{\times }):=\mathscr{S}(V\times F^{\times })$
.
$\overline{\mathscr{S}}(V\times F^{\times }):=\mathscr{S}(V\times F^{\times })$
.
Global case. Let
![]() $(\mathbf{V},q)$
be an even-dimensional quadratic space over the adèles
$(\mathbf{V},q)$
be an even-dimensional quadratic space over the adèles
 $\mathbf{A}=\mathbf{A}_{F}$
of a totally real number field
$\mathbf{A}=\mathbf{A}_{F}$
of a totally real number field
![]() $F$
, and suppose that
$F$
, and suppose that
![]() $\mathbf{V}_{\infty }$
is positive definite; we say that
$\mathbf{V}_{\infty }$
is positive definite; we say that
![]() $\mathbf{V}$
is coherent if it has a model over
$\mathbf{V}$
is coherent if it has a model over
![]() $F$
and incoherent otherwise. Given an
$F$
and incoherent otherwise. Given an
![]() $\widehat{\mathscr{O}}_{F}$
-lattice
$\widehat{\mathscr{O}}_{F}$
-lattice
![]() $\mathscr{V}\subset \mathbf{V}$
, we define the space
$\mathscr{V}\subset \mathbf{V}$
, we define the space
 $\mathscr{S}(\mathbf{V}\times \mathbf{A}^{\times })$
as the restricted tensor product of the corresponding local spaces, with respect to the spherical elements
$\mathscr{S}(\mathbf{V}\times \mathbf{A}^{\times })$
as the restricted tensor product of the corresponding local spaces, with respect to the spherical elements
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{v}(x,u)=\mathbf{1}_{\mathscr{V}_{v}}(x)\mathbf{1}_{\unicode[STIX]{x1D71B}_{v}^{n_{v}}}(u),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{v}(x,u)=\mathbf{1}_{\mathscr{V}_{v}}(x)\mathbf{1}_{\unicode[STIX]{x1D71B}_{v}^{n_{v}}}(u),\end{eqnarray}$$
if
![]() $\unicode[STIX]{x1D713}_{v}$
has level
$\unicode[STIX]{x1D713}_{v}$
has level
![]() $n_{v}$
. We call such
$n_{v}$
. We call such
![]() $\unicode[STIX]{x1D719}_{v}$
the standard Schwartz function at a non-archimedean place
$\unicode[STIX]{x1D719}_{v}$
the standard Schwartz function at a non-archimedean place
![]() $v$
. We define similarly the reduced space
$v$
. We define similarly the reduced space
 $\overline{\mathscr{S}}(\mathbf{V}\times \mathbf{A}^{\times })$
, which admits a quotient map
$\overline{\mathscr{S}}(\mathbf{V}\times \mathbf{A}^{\times })$
, which admits a quotient map
 $$\begin{eqnarray}\mathscr{S}(\mathbf{V}\times \mathbf{A}^{\times })\rightarrow \overline{\mathscr{S}}(\mathbf{V}\times \mathbf{A}^{\times })\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{S}(\mathbf{V}\times \mathbf{A}^{\times })\rightarrow \overline{\mathscr{S}}(\mathbf{V}\times \mathbf{A}^{\times })\end{eqnarray}$$
defined by the product of the maps (3.1.2) at the infinite places and of the identity at the finite places. The Weil representation of
 $\mathbf{GL}_{2}(\mathbf{A}^{\infty })\times \mathbf{GO}(\mathbf{V}^{\infty })\times (\mathfrak{gl}_{2,F_{\infty }},\mathbf{O}(\mathbf{V}_{\infty }))$
is the restricted tensor product of the local representations.
$\mathbf{GL}_{2}(\mathbf{A}^{\infty })\times \mathbf{GO}(\mathbf{V}^{\infty })\times (\mathfrak{gl}_{2,F_{\infty }},\mathbf{O}(\mathbf{V}_{\infty }))$
is the restricted tensor product of the local representations.
3.2 Eisenstein series
Let
![]() $\mathbf{V}_{2}$
be a two-dimensional quadratic space over
$\mathbf{V}_{2}$
be a two-dimensional quadratic space over
![]() $\mathbf{A}_{F}$
, totally definite at the archimedean places. Consider the Eisenstein series
$\mathbf{A}_{F}$
, totally definite at the archimedean places. Consider the Eisenstein series
 $$\begin{eqnarray}E_{r}(g,u,\unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F})=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in P^{1}(F)\backslash \text{SL}_{2}(F)}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{F},r}(\unicode[STIX]{x1D6FE}gw_{r})r(\unicode[STIX]{x1D6FE}g)\unicode[STIX]{x1D719}_{2}(0,u),\end{eqnarray}$$
$$\begin{eqnarray}E_{r}(g,u,\unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F})=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in P^{1}(F)\backslash \text{SL}_{2}(F)}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{F},r}(\unicode[STIX]{x1D6FE}gw_{r})r(\unicode[STIX]{x1D6FE}g)\unicode[STIX]{x1D719}_{2}(0,u),\end{eqnarray}$$
where
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{F},r}(g)=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D712}_{F}(d)^{-1}\quad & \text{if}~g=(\!\begin{smallmatrix}a & b\\ & d\end{smallmatrix}\!)k~\text{with}~k\in K_{1}^{1}(p^{r}),\\ 0\quad & \text{if}~g\notin PK_{0}(p^{r})\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{F},r}(g)=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D712}_{F}(d)^{-1}\quad & \text{if}~g=(\!\begin{smallmatrix}a & b\\ & d\end{smallmatrix}\!)k~\text{with}~k\in K_{1}^{1}(p^{r}),\\ 0\quad & \text{if}~g\notin PK_{0}(p^{r})\end{array}\right.\end{eqnarray}$$
and
 $\unicode[STIX]{x1D719}_{2}\in \overline{\mathscr{S}}(\mathbf{V}_{2}\times \mathbf{A}^{\times })$
. (The defining sum is in fact not absolutely convergent, so it must be interpreted in the sense of analytic continuation at
$\unicode[STIX]{x1D719}_{2}\in \overline{\mathscr{S}}(\mathbf{V}_{2}\times \mathbf{A}^{\times })$
. (The defining sum is in fact not absolutely convergent, so it must be interpreted in the sense of analytic continuation at
![]() $s=0$
from the series obtained by replacing
$s=0$
from the series obtained by replacing
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{F,r}}$
with
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{F,r}}$
with
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{F,r}}\unicode[STIX]{x1D6FF}_{s}$
, where
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{F,r}}\unicode[STIX]{x1D6FF}_{s}$
, where
 $\unicode[STIX]{x1D6FF}_{s}(g)=|a/d|^{s}$
if
$\unicode[STIX]{x1D6FF}_{s}(g)=|a/d|^{s}$
if
 $g=(\!\begin{smallmatrix}a & b\\ & d\end{smallmatrix}\!)k$
,
$g=(\!\begin{smallmatrix}a & b\\ & d\end{smallmatrix}\!)k$
,
 $k\in K_{0}(1)$
.) It belongs to the space
$k\in K_{0}(1)$
.) It belongs to the space
 $M_{1}^{\text{tw}}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D712}_{F}^{-1},\mathbf{C})$
of twisted modular forms of parallel weight
$M_{1}^{\text{tw}}(\unicode[STIX]{x1D702}\unicode[STIX]{x1D712}_{F}^{-1},\mathbf{C})$
of twisted modular forms of parallel weight
![]() $1$
and central character
$1$
and central character
![]() $\unicode[STIX]{x1D702}\unicode[STIX]{x1D712}_{F}^{-1}$
.
$\unicode[STIX]{x1D702}\unicode[STIX]{x1D712}_{F}^{-1}$
.
After a suitable modification, we study its Fourier–Whittaker expansion and show that it interpolates to a
![]() $\mathscr{Y}_{F}$
-family of
$\mathscr{Y}_{F}$
-family of
![]() $q$
-expansions of twisted modular forms.
$q$
-expansions of twisted modular forms.
Proposition 3.2.1. We have
 $$\begin{eqnarray}L^{(p)}(1,\unicode[STIX]{x1D702}\unicode[STIX]{x1D712}_{F})E_{r}((\!\begin{smallmatrix}y & x\\ & 1\end{smallmatrix}\!),u,\unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F})=\mathop{\sum }_{a\in F}W_{a,r}((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!),u,\unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F})\unicode[STIX]{x1D713}(ax),\end{eqnarray}$$
$$\begin{eqnarray}L^{(p)}(1,\unicode[STIX]{x1D702}\unicode[STIX]{x1D712}_{F})E_{r}((\!\begin{smallmatrix}y & x\\ & 1\end{smallmatrix}\!),u,\unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F})=\mathop{\sum }_{a\in F}W_{a,r}((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!),u,\unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F})\unicode[STIX]{x1D713}(ax),\end{eqnarray}$$
where
 $$\begin{eqnarray}W_{a,r}(g,u,\unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F})=\mathop{\prod }_{v}W_{a,r,v}(g,u,\unicode[STIX]{x1D719}_{2,v},\unicode[STIX]{x1D712}_{F,v}),\end{eqnarray}$$
$$\begin{eqnarray}W_{a,r}(g,u,\unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F})=\mathop{\prod }_{v}W_{a,r,v}(g,u,\unicode[STIX]{x1D719}_{2,v},\unicode[STIX]{x1D712}_{F,v}),\end{eqnarray}$$
with, for each
![]() $v$
and
$v$
and
![]() $a\in F_{v}$
,
$a\in F_{v}$
,
 $$\begin{eqnarray}W_{a,r,v}(g,u,\unicode[STIX]{x1D719}_{2,v},\unicode[STIX]{x1D712}_{F,v})=L^{(p)}(1,\unicode[STIX]{x1D702}_{v}\unicode[STIX]{x1D712}_{F,v})\int _{F_{v}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{F},v,r}(wn(b)gw_{r})r(wn(b)g)\unicode[STIX]{x1D719}_{2,v}(0,u)\unicode[STIX]{x1D713}_{v}(-ab)\,db.\end{eqnarray}$$
$$\begin{eqnarray}W_{a,r,v}(g,u,\unicode[STIX]{x1D719}_{2,v},\unicode[STIX]{x1D712}_{F,v})=L^{(p)}(1,\unicode[STIX]{x1D702}_{v}\unicode[STIX]{x1D712}_{F,v})\int _{F_{v}}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{F},v,r}(wn(b)gw_{r})r(wn(b)g)\unicode[STIX]{x1D719}_{2,v}(0,u)\unicode[STIX]{x1D713}_{v}(-ab)\,db.\end{eqnarray}$$
Here
 $L^{(p)}(s,\unicode[STIX]{x1D709}_{v}):=L(s,\unicode[STIX]{x1D709}_{v})$
if
$L^{(p)}(s,\unicode[STIX]{x1D709}_{v}):=L(s,\unicode[STIX]{x1D709}_{v})$
if
![]() $v\nmid p$
and
$v\nmid p$
and
 $L^{(p)}(s,\unicode[STIX]{x1D709}_{v}):=1$
if
$L^{(p)}(s,\unicode[STIX]{x1D709}_{v}):=1$
if
![]() $v|p$
, and we use the convention that
$v|p$
, and we use the convention that
![]() $r_{v}=0$
if
$r_{v}=0$
if
![]() $v\nmid p$
.
$v\nmid p$
.
Proof. The standard expansion of Eisenstein series reads
 $$\begin{eqnarray}E_{r}(gw_{r},u,\unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F})=\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{F},r}(gw_{r})r(g)\unicode[STIX]{x1D719}_{2}(0,u)+\mathop{\sum }_{a\in F}W_{a,r}^{\ast }(g,u,\unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F})\unicode[STIX]{x1D713}(ax),\end{eqnarray}$$
$$\begin{eqnarray}E_{r}(gw_{r},u,\unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F})=\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{F},r}(gw_{r})r(g)\unicode[STIX]{x1D719}_{2}(0,u)+\mathop{\sum }_{a\in F}W_{a,r}^{\ast }(g,u,\unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F})\unicode[STIX]{x1D713}(ax),\end{eqnarray}$$
where
 $W_{a,r}^{\ast }=L^{(p)}(1,\unicode[STIX]{x1D702}\unicode[STIX]{x1D712}_{F})^{-1}W_{a,r}$
; but it is easy to check that
$W_{a,r}^{\ast }=L^{(p)}(1,\unicode[STIX]{x1D702}\unicode[STIX]{x1D712}_{F})^{-1}W_{a,r}$
; but it is easy to check that
 $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{F,r}}((\!\begin{smallmatrix}y & x\\ & 1\end{smallmatrix}\!)w_{r})=0$
.◻
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{F,r}}((\!\begin{smallmatrix}y & x\\ & 1\end{smallmatrix}\!)w_{r})=0$
.◻
We choose convenient normalisations for the local Whittaker functions: let
 $\unicode[STIX]{x1D6FE}_{u,v}=\unicode[STIX]{x1D6FE}(\mathbf{V}_{2,v},uq)$
be the Weil index and, for
$\unicode[STIX]{x1D6FE}_{u,v}=\unicode[STIX]{x1D6FE}(\mathbf{V}_{2,v},uq)$
be the Weil index and, for
![]() $a\in F_{v}^{\times }$
, set
$a\in F_{v}^{\times }$
, set
 $$\begin{eqnarray}W_{a,r,v}^{\circ }(g,u,\unicode[STIX]{x1D719}_{2,v},\unicode[STIX]{x1D712}_{F,v}):=\unicode[STIX]{x1D6FE}_{u,v}^{-1}W_{a,r,v}(g,u,\unicode[STIX]{x1D719}_{2,v},\unicode[STIX]{x1D712}_{F,v}).\end{eqnarray}$$
$$\begin{eqnarray}W_{a,r,v}^{\circ }(g,u,\unicode[STIX]{x1D719}_{2,v},\unicode[STIX]{x1D712}_{F,v}):=\unicode[STIX]{x1D6FE}_{u,v}^{-1}W_{a,r,v}(g,u,\unicode[STIX]{x1D719}_{2,v},\unicode[STIX]{x1D712}_{F,v}).\end{eqnarray}$$
For the constant term, set
 $$\begin{eqnarray}W_{0,r,v}^{\circ }(g,u,\unicode[STIX]{x1D719}_{2,v},\unicode[STIX]{x1D712}_{F,v}):=\frac{\unicode[STIX]{x1D6FE}_{u,v}^{-1}}{L^{(p)}(0,\unicode[STIX]{x1D702}_{v}\unicode[STIX]{x1D712}_{F,v})}W_{0,r,v}(g,u,\unicode[STIX]{x1D719}_{2,v},\unicode[STIX]{x1D712}_{F,v}).\end{eqnarray}$$
$$\begin{eqnarray}W_{0,r,v}^{\circ }(g,u,\unicode[STIX]{x1D719}_{2,v},\unicode[STIX]{x1D712}_{F,v}):=\frac{\unicode[STIX]{x1D6FE}_{u,v}^{-1}}{L^{(p)}(0,\unicode[STIX]{x1D702}_{v}\unicode[STIX]{x1D712}_{F,v})}W_{0,r,v}(g,u,\unicode[STIX]{x1D719}_{2,v},\unicode[STIX]{x1D712}_{F,v}).\end{eqnarray}$$
Then for the global Whittaker functions we have
 $$\begin{eqnarray}W_{a,r}(g,u,\unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F})=-\unicode[STIX]{x1D700}(\mathbf{V}_{2})\mathop{\prod }_{v}W_{a,r,v}^{\circ }(g,u,\unicode[STIX]{x1D719}_{2,v}\unicode[STIX]{x1D712}_{F,v})\end{eqnarray}$$
$$\begin{eqnarray}W_{a,r}(g,u,\unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F})=-\unicode[STIX]{x1D700}(\mathbf{V}_{2})\mathop{\prod }_{v}W_{a,r,v}^{\circ }(g,u,\unicode[STIX]{x1D719}_{2,v}\unicode[STIX]{x1D712}_{F,v})\end{eqnarray}$$
if
![]() $a\in F^{\times }$
, where
$a\in F^{\times }$
, where
 $\unicode[STIX]{x1D700}(\mathbf{V}_{2})=\prod _{v}\unicode[STIX]{x1D6FE}_{u,v}$
equals
$\unicode[STIX]{x1D700}(\mathbf{V}_{2})=\prod _{v}\unicode[STIX]{x1D6FE}_{u,v}$
equals
![]() $-1$
if
$-1$
if
![]() $\mathbf{V}_{2}$
is coherent or
$\mathbf{V}_{2}$
is coherent or
![]() $+1$
if
$+1$
if
![]() $\mathbf{V}_{2}$
is incoherent; and
$\mathbf{V}_{2}$
is incoherent; and
 $$\begin{eqnarray}W_{0,r}(g,u,\unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F})=-\unicode[STIX]{x1D700}(\mathbf{V}_{2})L^{(p)}(0,\unicode[STIX]{x1D702}\unicode[STIX]{x1D712}_{F})\mathop{\prod }_{v}W_{0,r,v}^{\circ }(g,u,\unicode[STIX]{x1D719}_{2,v},\unicode[STIX]{x1D712}_{F,v}).\end{eqnarray}$$
$$\begin{eqnarray}W_{0,r}(g,u,\unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F})=-\unicode[STIX]{x1D700}(\mathbf{V}_{2})L^{(p)}(0,\unicode[STIX]{x1D702}\unicode[STIX]{x1D712}_{F})\mathop{\prod }_{v}W_{0,r,v}^{\circ }(g,u,\unicode[STIX]{x1D719}_{2,v},\unicode[STIX]{x1D712}_{F,v}).\end{eqnarray}$$
We sometimes drop
![]() $\unicode[STIX]{x1D719}_{2}$
from the notation in what follows.
$\unicode[STIX]{x1D719}_{2}$
from the notation in what follows.
Lemma 3.2.2. For each finite place
![]() $v$
and
$v$
and
![]() $y\in F_{v}^{\times }$
,
$y\in F_{v}^{\times }$
,
![]() $x\in F_{v}$
,
$x\in F_{v}$
,
![]() $u\in F_{v}^{\times }$
, we have
$u\in F_{v}^{\times }$
, we have
 $$\begin{eqnarray}W_{a,v}((\!\begin{smallmatrix}y & x\\ & 1\end{smallmatrix}\!),u)=\unicode[STIX]{x1D713}_{v}(ax)\unicode[STIX]{x1D712}_{F}(y)^{-1}|y|^{1/2}W_{ay,v}(1,y^{-1}u).\end{eqnarray}$$
$$\begin{eqnarray}W_{a,v}((\!\begin{smallmatrix}y & x\\ & 1\end{smallmatrix}\!),u)=\unicode[STIX]{x1D713}_{v}(ax)\unicode[STIX]{x1D712}_{F}(y)^{-1}|y|^{1/2}W_{ay,v}(1,y^{-1}u).\end{eqnarray}$$
The proof is an easy calculation.
Proposition 3.2.3. The local Whittaker functions satisfy the following.
-
(1) If
 $v\nmid p\infty$
, then
$v\nmid p\infty$
, then
 $W_{a,v,r}^{\circ }=W_{a,v}^{\circ }$
does not depend on
$W_{a,v,r}^{\circ }=W_{a,v}^{\circ }$
does not depend on
 $r$
and, for all
$r$
and, for all
 $a\in F_{v}$
, where
$a\in F_{v}$
, where $$\begin{eqnarray}W_{a,v}^{\circ }(1,u,\unicode[STIX]{x1D712}_{F})=|d_{v}|^{1/2}L(1,\unicode[STIX]{x1D702}_{v}\unicode[STIX]{x1D712}_{F,v})(1-\unicode[STIX]{x1D712}_{F,v}(\unicode[STIX]{x1D71B}_{v}))\mathop{\sum }_{n=0}^{\infty }\unicode[STIX]{x1D712}_{F,v}(\unicode[STIX]{x1D71B}_{v})^{n}q_{F,v}^{n}\int _{D_{n}(a)}\unicode[STIX]{x1D719}_{2,v}(x_{2},u)\,d_{u}x_{2},\end{eqnarray}$$
$$\begin{eqnarray}W_{a,v}^{\circ }(1,u,\unicode[STIX]{x1D712}_{F})=|d_{v}|^{1/2}L(1,\unicode[STIX]{x1D702}_{v}\unicode[STIX]{x1D712}_{F,v})(1-\unicode[STIX]{x1D712}_{F,v}(\unicode[STIX]{x1D71B}_{v}))\mathop{\sum }_{n=0}^{\infty }\unicode[STIX]{x1D712}_{F,v}(\unicode[STIX]{x1D71B}_{v})^{n}q_{F,v}^{n}\int _{D_{n}(a)}\unicode[STIX]{x1D719}_{2,v}(x_{2},u)\,d_{u}x_{2},\end{eqnarray}$$
 $d_{u}x_{2}$
is the self-dual measure on
$d_{u}x_{2}$
is the self-dual measure on
 $(\mathbf{V}_{2,v},uq)$
and (When the sum is infinite, it is to be understood in the sense of analytic continuation from characters
$(\mathbf{V}_{2,v},uq)$
and (When the sum is infinite, it is to be understood in the sense of analytic continuation from characters $$\begin{eqnarray}D_{n}(a)=\{x_{2}\in \mathbf{V}_{2,v}\mid uq(x_{2})\in a+p_{v}^{n}d_{v}^{-1}\}.\end{eqnarray}$$
$$\begin{eqnarray}D_{n}(a)=\{x_{2}\in \mathbf{V}_{2,v}\mid uq(x_{2})\in a+p_{v}^{n}d_{v}^{-1}\}.\end{eqnarray}$$
 $\unicode[STIX]{x1D712}_{F}|\cdot |^{s}$
with
$\unicode[STIX]{x1D712}_{F}|\cdot |^{s}$
with
 $s>0$
; cf. the proof of Lemma 3.3.1 below.)
$s>0$
; cf. the proof of Lemma 3.3.1 below.)
-
(2) If
 $v|p$
and
$v|p$
and
 $\unicode[STIX]{x1D719}_{2,v}$
is the standard Schwartz function, then
$\unicode[STIX]{x1D719}_{2,v}$
is the standard Schwartz function, then  $$\begin{eqnarray}W_{a,r,v}^{\circ }(1,u,\unicode[STIX]{x1D712}_{F})=\left\{\begin{array}{@{}ll@{}}|d_{v}|^{3/2}|D_{v}|^{1/2}\unicode[STIX]{x1D712}_{F,v}(-1)\quad & \text{if}~v(a)\geqslant -v(d_{v})\text{ and }v(u)=-v(d_{v}),\\ 0\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}W_{a,r,v}^{\circ }(1,u,\unicode[STIX]{x1D712}_{F})=\left\{\begin{array}{@{}ll@{}}|d_{v}|^{3/2}|D_{v}|^{1/2}\unicode[STIX]{x1D712}_{F,v}(-1)\quad & \text{if}~v(a)\geqslant -v(d_{v})\text{ and }v(u)=-v(d_{v}),\\ 0\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
-
(3) If
 $v|\infty$
and
$v|\infty$
and
 $\unicode[STIX]{x1D719}_{2,v}$
is the standard Schwartz function, then
$\unicode[STIX]{x1D719}_{2,v}$
is the standard Schwartz function, then  $$\begin{eqnarray}W_{a,v}(1,u)=\left\{\begin{array}{@{}ll@{}}2e^{-2\unicode[STIX]{x1D70B}a}\quad & \text{if }ua>0,\\ 1\quad & \text{if }a=0,\\ 0\quad & \text{if }ua<0.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}W_{a,v}(1,u)=\left\{\begin{array}{@{}ll@{}}2e^{-2\unicode[STIX]{x1D70B}a}\quad & \text{if }ua>0,\\ 1\quad & \text{if }a=0,\\ 0\quad & \text{if }ua<0.\end{array}\right.\end{eqnarray}$$
Proof. Part (1) is proved similarly to [Reference Yuan, Zhang and ZhangYZZ12, Proposition 6.10(1)], whose Whittaker function
 $W_{a,v}^{\circ }(s,1,u)$
equals our
$W_{a,v}^{\circ }(s,1,u)$
equals our
 $L(1,\unicode[STIX]{x1D702}_{v}|\cdot |_{v}^{s})^{-1}W_{a,v}^{\circ }(1,u,|\cdot |_{v}^{s})$
. The proof of Part 2 is similar to that of [Reference DisegniDis15, Proposition 3.2.1, places
$L(1,\unicode[STIX]{x1D702}_{v}|\cdot |_{v}^{s})^{-1}W_{a,v}^{\circ }(1,u,|\cdot |_{v}^{s})$
. The proof of Part 2 is similar to that of [Reference DisegniDis15, Proposition 3.2.1, places
![]() $|M/\unicode[STIX]{x1D6FF}$
]. Part (3) is also well known; see e.g. [Reference Yuan, Zhang and ZhangYZZ12, Proposition 2.11], whose normalisation differs from ours by a factor of
$|M/\unicode[STIX]{x1D6FF}$
]. Part (3) is also well known; see e.g. [Reference Yuan, Zhang and ZhangYZZ12, Proposition 2.11], whose normalisation differs from ours by a factor of
 $\unicode[STIX]{x1D6FE}_{v}L(1,\unicode[STIX]{x1D702}_{v})^{-1}=\unicode[STIX]{x1D70B}i$
.◻
$\unicode[STIX]{x1D6FE}_{v}L(1,\unicode[STIX]{x1D702}_{v})^{-1}=\unicode[STIX]{x1D70B}i$
.◻
Lemma 3.2.4. Let
![]() $a\in F$
. For all finite places
$a\in F$
. For all finite places
![]() $v$
,
$v$
,
 $|d|_{v}^{-3/2}|D_{v}|^{-1/2}W_{a,v}^{\circ }(1,u,\unicode[STIX]{x1D712}_{F})\in \mathbf{Q}[\unicode[STIX]{x1D712}_{F},\unicode[STIX]{x1D719}_{v}]$
and, for almost all
$|d|_{v}^{-3/2}|D_{v}|^{-1/2}W_{a,v}^{\circ }(1,u,\unicode[STIX]{x1D712}_{F})\in \mathbf{Q}[\unicode[STIX]{x1D712}_{F},\unicode[STIX]{x1D719}_{v}]$
and, for almost all
![]() $v$
, we have
$v$
, we have
 $$\begin{eqnarray}|d|_{v}^{-3/2}|D_{v}|^{-1/2}W_{a,v}^{\circ }(1,u,\unicode[STIX]{x1D712}_{F})=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }v(a)\geqslant -v(d_{v})\text{ and }v(u)=-v(d_{v}),\\ 0\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}|d|_{v}^{-3/2}|D_{v}|^{-1/2}W_{a,v}^{\circ }(1,u,\unicode[STIX]{x1D712}_{F})=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }v(a)\geqslant -v(d_{v})\text{ and }v(u)=-v(d_{v}),\\ 0\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
3.3 Eisenstein family
Recall from § 1.2 the profinite groups
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
![]() $\unicode[STIX]{x1D6E4}_{F}$
and the associated rigid spaces
$\unicode[STIX]{x1D6E4}_{F}$
and the associated rigid spaces
![]() $\mathscr{Y}^{\prime }$
,
$\mathscr{Y}^{\prime }$
,
![]() $\mathscr{Y}$
,
$\mathscr{Y}$
,
![]() $\mathscr{Y}_{F}$
(only the latter is relevant for this subsection). For each finite place
$\mathscr{Y}_{F}$
(only the latter is relevant for this subsection). For each finite place
![]() $v\nmid p$
of
$v\nmid p$
of
![]() $F$
, there are local versions
$F$
, there are local versions
 $$\begin{eqnarray}\mathscr{Y}_{v}^{\prime },\quad \mathscr{Y}_{v},\quad \mathscr{Y}_{F,v},\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{Y}_{v}^{\prime },\quad \mathscr{Y}_{v},\quad \mathscr{Y}_{F,v},\end{eqnarray}$$
which are schemes over
![]() $M$
representing the corresponding spaces of
$M$
representing the corresponding spaces of
![]() $\mathbf{G}_{m,M}$
-valued homomorphisms with domain
$\mathbf{G}_{m,M}$
-valued homomorphisms with domain
 $E_{v}^{\times }/(V^{p}\cap E_{v}^{\times })$
(for
$E_{v}^{\times }/(V^{p}\cap E_{v}^{\times })$
(for
![]() $\mathscr{Y}_{v}^{\prime }$
,
$\mathscr{Y}_{v}^{\prime }$
,
![]() $\mathscr{Y}_{v}$
, where
$\mathscr{Y}_{v}$
, where
 $V^{p}\subset E_{\mathbf{A}^{p\infty }}^{\times }$
is the subgroup fixed in the Introduction) or
$V^{p}\subset E_{\mathbf{A}^{p\infty }}^{\times }$
is the subgroup fixed in the Introduction) or
![]() $F_{v}^{\times }$
(for
$F_{v}^{\times }$
(for
![]() $\mathscr{Y}_{F,v}$
).Footnote
17
Letting
$\mathscr{Y}_{F,v}$
).Footnote
17
Letting
![]() $\bigotimes ^{\prime }$
denote the restricted tensor product with respect to the constant function
$\bigotimes ^{\prime }$
denote the restricted tensor product with respect to the constant function
![]() $1$
, and the symbol
$1$
, and the symbol
![]() $\mathscr{Y}^{?}$
stand for any of the symbols
$\mathscr{Y}^{?}$
stand for any of the symbols
![]() $\mathscr{Y}^{\prime }$
,
$\mathscr{Y}^{\prime }$
,
![]() $\mathscr{Y}$
,
$\mathscr{Y}$
,
![]() $\mathscr{Y}_{F}$
, we let
$\mathscr{Y}_{F}$
, we let
 $$\begin{eqnarray}\mathscr{O}_{\mathscr{Y}^{?}}(\mathscr{Y}^{?})^{\text{f}}\subset \mathscr{O}_{\mathscr{ Y}^{?}}(\mathscr{Y}^{?})^{\text{b}}\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{O}_{\mathscr{Y}^{?}}(\mathscr{Y}^{?})^{\text{f}}\subset \mathscr{O}_{\mathscr{ Y}^{?}}(\mathscr{Y}^{?})^{\text{b}}\end{eqnarray}$$
denote the image of
 $\bigotimes _{v\nmid p}^{\prime }\mathscr{O}(\mathscr{Y}_{v}^{?})\otimes _{M}L\rightarrow \mathscr{O}_{\mathscr{Y}^{?}}(\mathscr{Y}^{?})$
.
$\bigotimes _{v\nmid p}^{\prime }\mathscr{O}(\mathscr{Y}_{v}^{?})\otimes _{M}L\rightarrow \mathscr{O}_{\mathscr{Y}^{?}}(\mathscr{Y}^{?})$
.
Lemma 3.3.1. For each
![]() $a\in F$
,
$a\in F$
,
 $y\in \mathbf{A}^{\infty ,\times }$
, and rational Schwartz function
$y\in \mathbf{A}^{\infty ,\times }$
, and rational Schwartz function
![]() $\unicode[STIX]{x1D719}_{2}^{p\infty }$
, there are:
$\unicode[STIX]{x1D719}_{2}^{p\infty }$
, there are:
-
(1) for each
 $v\nmid p\infty$
:
$v\nmid p\infty$
:-
(a) a Schwartz function
 $\unicode[STIX]{x1D719}_{2,v}(\cdot )\in \mathscr{S}(V_{2,v},\mathscr{O}(\mathscr{Y}_{F,v}))$
such that
$\unicode[STIX]{x1D719}_{2,v}(\cdot )\in \mathscr{S}(V_{2,v},\mathscr{O}(\mathscr{Y}_{F,v}))$
such that
 $\unicode[STIX]{x1D719}_{2,v}(\mathbf{1})=\unicode[STIX]{x1D719}_{2,v}$
and
$\unicode[STIX]{x1D719}_{2,v}(\mathbf{1})=\unicode[STIX]{x1D719}_{2,v}$
and
 $\unicode[STIX]{x1D719}_{2,v}(\cdot )$
is identically equal to
$\unicode[STIX]{x1D719}_{2,v}(\cdot )$
is identically equal to
 $\unicode[STIX]{x1D719}_{2,v}$
if
$\unicode[STIX]{x1D719}_{2,v}$
if
 $\unicode[STIX]{x1D719}_{2,v}$
is standard;
$\unicode[STIX]{x1D719}_{2,v}$
is standard; -
(b) a function
satisfying $$\begin{eqnarray}W_{a,v}^{\circ }(y_{v},u,\unicode[STIX]{x1D719}_{2,v})\in \mathscr{O}_{\mathscr{Y}_{F,v}}(\mathscr{Y}_{F,v})\end{eqnarray}$$
for all
$$\begin{eqnarray}W_{a,v}^{\circ }(y_{v},u,\unicode[STIX]{x1D719}_{2,v})\in \mathscr{O}_{\mathscr{Y}_{F,v}}(\mathscr{Y}_{F,v})\end{eqnarray}$$
for all $$\begin{eqnarray}\mathscr{W}_{a,v}^{\circ }(y_{v},u,\unicode[STIX]{x1D719}_{2,v};\unicode[STIX]{x1D712}_{F})=|d_{v}|^{-3/2}|D_{v}|^{-1/2}W_{a,r,v}^{\circ }((\!\begin{smallmatrix}y_{v} & \\ & 1\end{smallmatrix}\!),u,\unicode[STIX]{x1D719}_{2,v}(\unicode[STIX]{x1D712}_{F,v}),\unicode[STIX]{x1D712}_{F,v})\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{W}_{a,v}^{\circ }(y_{v},u,\unicode[STIX]{x1D719}_{2,v};\unicode[STIX]{x1D712}_{F})=|d_{v}|^{-3/2}|D_{v}|^{-1/2}W_{a,r,v}^{\circ }((\!\begin{smallmatrix}y_{v} & \\ & 1\end{smallmatrix}\!),u,\unicode[STIX]{x1D719}_{2,v}(\unicode[STIX]{x1D712}_{F,v}),\unicode[STIX]{x1D712}_{F,v})\end{eqnarray}$$
 $\unicode[STIX]{x1D712}_{F,v}\in \mathscr{Y}_{F,v}(\mathbf{C})$
;
$\unicode[STIX]{x1D712}_{F,v}\in \mathscr{Y}_{F,v}(\mathbf{C})$
;
-
-
(2) a global function
which is algebraic on $$\begin{eqnarray}\mathscr{W}_{a}(y,u,\unicode[STIX]{x1D719}_{2}^{p\infty })\in \mathscr{O}_{\mathscr{ Y}_{F}}(\mathscr{Y}_{F})^{\text{b}},\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{W}_{a}(y,u,\unicode[STIX]{x1D719}_{2}^{p\infty })\in \mathscr{O}_{\mathscr{ Y}_{F}}(\mathscr{Y}_{F})^{\text{b}},\end{eqnarray}$$
 $\mathscr{Y}_{F}^{\text{l.c.}}$
and satisfies for each
$\mathscr{Y}_{F}^{\text{l.c.}}$
and satisfies for each $$\begin{eqnarray}\mathscr{W}_{a}(y,u,\unicode[STIX]{x1D719}_{2}^{p\infty };\unicode[STIX]{x1D712}_{F})=|D_{F}|^{1/2}|D_{E}|^{1/2}W_{a,r}^{\infty }((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!),u,\unicode[STIX]{x1D719}_{2}(\unicode[STIX]{x1D712}_{F}),\unicode[STIX]{x1D712}_{F})\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{W}_{a}(y,u,\unicode[STIX]{x1D719}_{2}^{p\infty };\unicode[STIX]{x1D712}_{F})=|D_{F}|^{1/2}|D_{E}|^{1/2}W_{a,r}^{\infty }((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!),u,\unicode[STIX]{x1D719}_{2}(\unicode[STIX]{x1D712}_{F}),\unicode[STIX]{x1D712}_{F})\end{eqnarray}$$
 $\unicode[STIX]{x1D712}_{F}\in \mathscr{Y}_{F}^{\text{l.c.}}(\mathbf{C})$
; here
$\unicode[STIX]{x1D712}_{F}\in \mathscr{Y}_{F}^{\text{l.c.}}(\mathbf{C})$
; here
 $\unicode[STIX]{x1D719}_{2}(\unicode[STIX]{x1D712}_{F})=\prod _{v\nmid p\infty }\unicode[STIX]{x1D719}_{2,v}(\unicode[STIX]{x1D712}_{F,v})_{2}\unicode[STIX]{x1D719}_{2,p\infty }$
with
$\unicode[STIX]{x1D719}_{2}(\unicode[STIX]{x1D712}_{F})=\prod _{v\nmid p\infty }\unicode[STIX]{x1D719}_{2,v}(\unicode[STIX]{x1D712}_{F,v})_{2}\unicode[STIX]{x1D719}_{2,p\infty }$
with
 $\unicode[STIX]{x1D719}_{2,v}$
the standard Schwartz function for each
$\unicode[STIX]{x1D719}_{2,v}$
the standard Schwartz function for each
 $v|p\infty$
. The function
$v|p\infty$
. The function
 $|y|^{-1/2}\mathscr{W}_{a}(y,u,\unicode[STIX]{x1D719}_{2}^{p\infty })$
is bounded solely in terms of
$|y|^{-1/2}\mathscr{W}_{a}(y,u,\unicode[STIX]{x1D719}_{2}^{p\infty })$
is bounded solely in terms of
 $\max |\unicode[STIX]{x1D719}_{2}^{p\infty }|$
and, if
$\max |\unicode[STIX]{x1D719}_{2}^{p\infty }|$
and, if
 $a\neq 0$
, then
$a\neq 0$
, then
 $\mathscr{W}_{a}\in \mathscr{O}(\mathscr{Y}_{F})^{\text{f}}$
.
$\mathscr{W}_{a}\in \mathscr{O}(\mathscr{Y}_{F})^{\text{f}}$
.
Proof. If
![]() $a\neq 0$
, by Lemma 3.2.4 and Proposition 3.2.3
(2), we can deduce the existence of the global function in part (2) from the local result of part (1). If
$a\neq 0$
, by Lemma 3.2.4 and Proposition 3.2.3
(2), we can deduce the existence of the global function in part (2) from the local result of part (1). If
![]() $a=0$
, then by (3.2.2) the same is true thanks to the well-known existence [Reference Deligne and RibetDR80] of a bounded analytic function on
$a=0$
, then by (3.2.2) the same is true thanks to the well-known existence [Reference Deligne and RibetDR80] of a bounded analytic function on
![]() $\mathscr{Y}_{F}$
interpolating
$\mathscr{Y}_{F}$
interpolating
 $\unicode[STIX]{x1D712}_{F}\mapsto L^{(p)}(0,\unicode[STIX]{x1D702}\unicode[STIX]{x1D712}_{F})$
.
$\unicode[STIX]{x1D712}_{F}\mapsto L^{(p)}(0,\unicode[STIX]{x1D702}\unicode[STIX]{x1D712}_{F})$
.
It thus suffices to prove part (1), and moreover we may restrict to
![]() $y=1$
in view of Lemma 3.2.2. We can uniquely write
$y=1$
in view of Lemma 3.2.2. We can uniquely write
 $\unicode[STIX]{x1D719}_{2,v}=c\unicode[STIX]{x1D719}_{2,v}^{\circ }+\unicode[STIX]{x1D719}_{2,v}^{\prime }$
, where
$\unicode[STIX]{x1D719}_{2,v}=c\unicode[STIX]{x1D719}_{2,v}^{\circ }+\unicode[STIX]{x1D719}_{2,v}^{\prime }$
, where
![]() $\unicode[STIX]{x1D719}_{2,v}^{\circ }$
is the standard Schwartz function and
$\unicode[STIX]{x1D719}_{2,v}^{\circ }$
is the standard Schwartz function and
 $c=\unicode[STIX]{x1D719}_{2,v}(0)$
. Then we set
$c=\unicode[STIX]{x1D719}_{2,v}(0)$
. Then we set
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{2,v}(\unicode[STIX]{x1D712}_{F,v}):=c\unicode[STIX]{x1D719}_{2,v}^{\circ }+\frac{L(1,\unicode[STIX]{x1D702}_{v})}{L(1,\unicode[STIX]{x1D702}_{v}\unicode[STIX]{x1D712}_{F,v})}\unicode[STIX]{x1D719}_{2,v}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{2,v}(\unicode[STIX]{x1D712}_{F,v}):=c\unicode[STIX]{x1D719}_{2,v}^{\circ }+\frac{L(1,\unicode[STIX]{x1D702}_{v})}{L(1,\unicode[STIX]{x1D702}_{v}\unicode[STIX]{x1D712}_{F,v})}\unicode[STIX]{x1D719}_{2,v}^{\prime }.\end{eqnarray}$$
We need to show that, upon substituting it in the expression for the local Whittaker functions given in Proposition 3.2.3
(1), we obtain a Laurent polynomial in
 $\unicode[STIX]{x1D712}_{F,v}(\unicode[STIX]{x1D71B}_{v})$
(which gives the canonical coordinate on
$\unicode[STIX]{x1D712}_{F,v}(\unicode[STIX]{x1D71B}_{v})$
(which gives the canonical coordinate on
 $\mathscr{Y}_{F,v}\cong \mathbf{G}_{m,M}$
). By linearity and Lemma 3.2.4, it suffices to show this for the summand
$\mathscr{Y}_{F,v}\cong \mathbf{G}_{m,M}$
). By linearity and Lemma 3.2.4, it suffices to show this for the summand
 $(L(1,\unicode[STIX]{x1D702}_{v})/L(1,\unicode[STIX]{x1D702}_{v}\unicode[STIX]{x1D712}_{F,v}))\unicode[STIX]{x1D719}_{2,v}^{\prime }$
, whose coefficient is designed to cancel the factor
$(L(1,\unicode[STIX]{x1D702}_{v})/L(1,\unicode[STIX]{x1D702}_{v}\unicode[STIX]{x1D712}_{F,v}))\unicode[STIX]{x1D719}_{2,v}^{\prime }$
, whose coefficient is designed to cancel the factor
 $L(1,\unicode[STIX]{x1D702}_{v},\unicode[STIX]{x1D712}_{v})$
appearing in that expression. The only source of possible poles is the infinite sum. For
$L(1,\unicode[STIX]{x1D702}_{v},\unicode[STIX]{x1D712}_{v})$
appearing in that expression. The only source of possible poles is the infinite sum. For
![]() $n$
sufficiently large, if
$n$
sufficiently large, if
![]() $a$
is not in the image of
$a$
is not in the image of
![]() $uq$
, then
$uq$
, then
![]() $D_{n}(a)$
is empty and therefore the sum is actually finite. On the other hand if
$D_{n}(a)$
is empty and therefore the sum is actually finite. On the other hand if
 $a=uq(x_{a})$
, then for
$a=uq(x_{a})$
, then for
![]() $n$
large the function
$n$
large the function
![]() $\unicode[STIX]{x1D719}_{2,v}$
is constant and equal to
$\unicode[STIX]{x1D719}_{2,v}$
is constant and equal to
 $\unicode[STIX]{x1D719}_{2,v}(x_{a})$
on
$\unicode[STIX]{x1D719}_{2,v}(x_{a})$
on
![]() $D_{n}(a)$
; it follows that
$D_{n}(a)$
; it follows that
 $$\begin{eqnarray}\int _{D_{n}(a)}\unicode[STIX]{x1D719}_{2,v}(x_{2},u)\,d_{u}x_{2}=c^{\prime }q_{F,v}^{-n}\end{eqnarray}$$
$$\begin{eqnarray}\int _{D_{n}(a)}\unicode[STIX]{x1D719}_{2,v}(x_{2},u)\,d_{u}x_{2}=c^{\prime }q_{F,v}^{-n}\end{eqnarray}$$
for some constant
![]() $c^{\prime }$
independent of
$c^{\prime }$
independent of
![]() $n$
and
$n$
and
![]() $\unicode[STIX]{x1D712}_{F,v}$
. Then the tail of the sum is
$\unicode[STIX]{x1D712}_{F,v}$
. Then the tail of the sum is
 $$\begin{eqnarray}\mathop{\sum }_{n\geqslant n_{0}}c^{\prime }\unicode[STIX]{x1D712}_{F,v}(\unicode[STIX]{x1D71B}_{v})^{n}=c^{\prime }\frac{\unicode[STIX]{x1D712}_{F,v}(\unicode[STIX]{x1D71B}_{v})^{n_{0}}}{1-\unicode[STIX]{x1D712}_{F,v}(\unicode[STIX]{x1D71B})};\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{n\geqslant n_{0}}c^{\prime }\unicode[STIX]{x1D712}_{F,v}(\unicode[STIX]{x1D71B}_{v})^{n}=c^{\prime }\frac{\unicode[STIX]{x1D712}_{F,v}(\unicode[STIX]{x1D71B}_{v})^{n_{0}}}{1-\unicode[STIX]{x1D712}_{F,v}(\unicode[STIX]{x1D71B})};\end{eqnarray}$$
its product with the factor
 $1-\unicode[STIX]{x1D712}_{F,v}(\unicode[STIX]{x1D71B}_{v})$
appearing in front of it is then also a polynomial in
$1-\unicode[STIX]{x1D712}_{F,v}(\unicode[STIX]{x1D71B}_{v})$
appearing in front of it is then also a polynomial in
 $\unicode[STIX]{x1D712}_{F,v}(\unicode[STIX]{x1D71B}_{v})$
.
$\unicode[STIX]{x1D712}_{F,v}(\unicode[STIX]{x1D71B}_{v})$
.
Finally, the last two statements of part (2) follow by the construction and Lemma 3.2.2. ◻
Proposition 3.3.2. There is a bounded
![]() $\mathscr{Y}_{F}$
-family of
$\mathscr{Y}_{F}$
-family of
![]() $q$
-expansions of twisted modular forms of parallel weight
$q$
-expansions of twisted modular forms of parallel weight
![]() $1$
$1$
 $$\begin{eqnarray}\mathscr{E}(u,\unicode[STIX]{x1D719}_{2}^{p\infty })\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{E}(u,\unicode[STIX]{x1D719}_{2}^{p\infty })\end{eqnarray}$$
such that for any
 $\unicode[STIX]{x1D712}_{F}\in \mathscr{Y}_{F}^{\text{l.c.}}(\mathbf{C})$
and any
$\unicode[STIX]{x1D712}_{F}\in \mathscr{Y}_{F}^{\text{l.c.}}(\mathbf{C})$
and any
 $r=(r_{v})_{v|p}$
satisfying
$r=(r_{v})_{v|p}$
satisfying
 $c(\unicode[STIX]{x1D712}_{F})|p^{r}$
, we have
$c(\unicode[STIX]{x1D712}_{F})|p^{r}$
, we have
 $$\begin{eqnarray}\mathscr{E}(u,\unicode[STIX]{x1D719}_{2}^{p\infty };\unicode[STIX]{x1D712}_{F})=|D_{F}|\frac{L^{(p)}(1,\unicode[STIX]{x1D702}\unicode[STIX]{x1D712}_{F})}{L^{(p)}(1,\unicode[STIX]{x1D702})}\,\text{}^{\mathbf{q}}E_{r}(u,\unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F}),\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{E}(u,\unicode[STIX]{x1D719}_{2}^{p\infty };\unicode[STIX]{x1D712}_{F})=|D_{F}|\frac{L^{(p)}(1,\unicode[STIX]{x1D702}\unicode[STIX]{x1D712}_{F})}{L^{(p)}(1,\unicode[STIX]{x1D702})}\,\text{}^{\mathbf{q}}E_{r}(u,\unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F}),\end{eqnarray}$$
where
 $\unicode[STIX]{x1D719}_{2}=\unicode[STIX]{x1D719}_{2}^{p\infty }(\unicode[STIX]{x1D712}_{F})\unicode[STIX]{x1D719}_{2,p\infty }$
with
$\unicode[STIX]{x1D719}_{2}=\unicode[STIX]{x1D719}_{2}^{p\infty }(\unicode[STIX]{x1D712}_{F})\unicode[STIX]{x1D719}_{2,p\infty }$
with
![]() $\unicode[STIX]{x1D719}_{2,v}$
the standard Schwartz function for
$\unicode[STIX]{x1D719}_{2,v}$
the standard Schwartz function for
![]() $v|p\infty$
.
$v|p\infty$
.
3.4 Analytic kernel
We first construct certain bounded
![]() $\mathscr{Y}^{?}$
-families of
$\mathscr{Y}^{?}$
-families of
![]() $q$
-expansions of modular forms for
$q$
-expansions of modular forms for
 $\mathscr{Y}^{?}=\mathscr{Y}_{F}$
or
$\mathscr{Y}^{?}=\mathscr{Y}_{F}$
or
![]() $\mathscr{Y}^{\prime }$
. In general, if
$\mathscr{Y}^{\prime }$
. In general, if
![]() $\mathscr{Y}^{?}$
is the space of
$\mathscr{Y}^{?}$
is the space of
![]() $p$
-adic characters of a profinite group
$p$
-adic characters of a profinite group
![]() $\unicode[STIX]{x1D6E4}^{?}$
, then it is equivalent to giving a compatible system, for each extension
$\unicode[STIX]{x1D6E4}^{?}$
, then it is equivalent to giving a compatible system, for each extension
![]() $L^{\prime }$
of
$L^{\prime }$
of
![]() $L$
, of bounded functionals
$L$
, of bounded functionals
 $\mathscr{C}(\unicode[STIX]{x1D6E4}^{?},L^{\prime })\rightarrow \mathbf{M}(K^{p},L^{\prime })$
, where the source is the space of
$\mathscr{C}(\unicode[STIX]{x1D6E4}^{?},L^{\prime })\rightarrow \mathbf{M}(K^{p},L^{\prime })$
, where the source is the space of
![]() $L^{\prime }$
-valued continuous functions on
$L^{\prime }$
-valued continuous functions on
![]() $\unicode[STIX]{x1D6E4}^{?}$
. This can be applied to the case of
$\unicode[STIX]{x1D6E4}^{?}$
. This can be applied to the case of
![]() $\mathscr{Y}_{F}$
(with
$\mathscr{Y}_{F}$
(with
![]() $\unicode[STIX]{x1D6E4}_{F}$
), and to the case of
$\unicode[STIX]{x1D6E4}_{F}$
), and to the case of
![]() $\mathscr{Y}^{\prime }$
with the variation that
$\mathscr{Y}^{\prime }$
with the variation that
![]() $\mathscr{Y}^{\prime }$
-families correspond to bounded functionals on the space
$\mathscr{Y}^{\prime }$
-families correspond to bounded functionals on the space
 $\mathscr{C}(\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D714},L^{\prime })$
of functions
$\mathscr{C}(\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D714},L^{\prime })$
of functions
![]() $f$
on
$f$
on
![]() $\unicode[STIX]{x1D6E4}$
satisfying
$\unicode[STIX]{x1D6E4}$
satisfying
 $f(zt)=\unicode[STIX]{x1D714}^{-1}(z)f(t)$
for all
$f(zt)=\unicode[STIX]{x1D714}^{-1}(z)f(t)$
for all
 $z\in \mathbf{A}^{\infty ,\times }$
.
$z\in \mathbf{A}^{\infty ,\times }$
.
Let
![]() $\mathbf{B}$
be a (coherent or incoherent) totally definite quaternion algebra over
$\mathbf{B}$
be a (coherent or incoherent) totally definite quaternion algebra over
 $\mathbf{A}=\mathbf{A}_{F}$
and let
$\mathbf{A}=\mathbf{A}_{F}$
and let
![]() $E$
be a totally imaginary quadratic extension of
$E$
be a totally imaginary quadratic extension of
![]() $F$
with an embedding
$F$
with an embedding
 $E_{\mathbf{A}}{\hookrightarrow}\mathbf{B}$
which we fix. Let
$E_{\mathbf{A}}{\hookrightarrow}\mathbf{B}$
which we fix. Let
![]() $\mathbf{V}$
be the orthogonal space
$\mathbf{V}$
be the orthogonal space
![]() $\mathbf{B}$
with reduced norm
$\mathbf{B}$
with reduced norm
![]() $q$
. We have an orthogonal decomposition
$q$
. We have an orthogonal decomposition
 $$\begin{eqnarray}\mathbf{V}=\mathbf{V}_{1}\oplus \mathbf{V}_{2},\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{V}=\mathbf{V}_{1}\oplus \mathbf{V}_{2},\end{eqnarray}$$
where
 $$\begin{eqnarray}\mathbf{V}_{1}=E_{\mathbf{A}},\quad \mathbf{V}_{2}=E_{\mathbf{A}}\mathfrak{j},\quad \mathfrak{j}\notin E_{\mathbf{A}},\quad \mathfrak{j}^{2}\in \mathbf{A}^{\times }.\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{V}_{1}=E_{\mathbf{A}},\quad \mathbf{V}_{2}=E_{\mathbf{A}}\mathfrak{j},\quad \mathfrak{j}\notin E_{\mathbf{A}},\quad \mathfrak{j}^{2}\in \mathbf{A}^{\times }.\end{eqnarray}$$
The restriction of
![]() $q$
to
$q$
to
![]() $\mathbf{V}_{1}$
is the adelisation of the norm of
$\mathbf{V}_{1}$
is the adelisation of the norm of
![]() $E/F$
.
$E/F$
.
We have an embedding (cf. [Reference Yuan, Zhang and ZhangYZZ12, p. 36])
 $$\begin{eqnarray}\mathbf{A}^{\times }\backslash \mathbf{B}^{\times }\times \mathbf{B}^{\times }{\hookrightarrow}\mathbf{GO}(\mathbf{V}),\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{A}^{\times }\backslash \mathbf{B}^{\times }\times \mathbf{B}^{\times }{\hookrightarrow}\mathbf{GO}(\mathbf{V}),\end{eqnarray}$$
where
 $\mathbf{B}^{\times }\times \mathbf{B}^{\times }$
acts on
$\mathbf{B}^{\times }\times \mathbf{B}^{\times }$
acts on
![]() $\mathbf{V}$
by
$\mathbf{V}$
by
 $(h_{1},h_{2})x=h_{1}xh_{2}^{-1}$
.
$(h_{1},h_{2})x=h_{1}xh_{2}^{-1}$
.
Let
 $\unicode[STIX]{x1D719}^{p\infty }\in \mathscr{S}(\mathbf{V}^{p\infty }\times \mathbf{A}^{p\infty ,\times })$
be a Schwartz function and let
$\unicode[STIX]{x1D719}^{p\infty }\in \mathscr{S}(\mathbf{V}^{p\infty }\times \mathbf{A}^{p\infty ,\times })$
be a Schwartz function and let
 $U^{p}\subset \mathbf{B}^{\infty \times }$
be a compact open subgroup fixing
$U^{p}\subset \mathbf{B}^{\infty \times }$
be a compact open subgroup fixing
![]() $\unicode[STIX]{x1D719}^{p\infty }$
. For
$\unicode[STIX]{x1D719}^{p\infty }$
. For
 $\unicode[STIX]{x1D719}_{1}\in \mathscr{S}(\mathbf{V}_{1}\times \mathbf{A}^{\times })$
a Schwartz function such that
$\unicode[STIX]{x1D719}_{1}\in \mathscr{S}(\mathbf{V}_{1}\times \mathbf{A}^{\times })$
a Schwartz function such that
![]() $\unicode[STIX]{x1D719}_{1,\infty }$
is standard, let
$\unicode[STIX]{x1D719}_{1,\infty }$
is standard, let
 $\unicode[STIX]{x1D703}(u,\unicode[STIX]{x1D719}_{1})$
be the twisted modular form
$\unicode[STIX]{x1D703}(u,\unicode[STIX]{x1D719}_{1})$
be the twisted modular form
 $$\begin{eqnarray}\unicode[STIX]{x1D703}(g,u,\unicode[STIX]{x1D719}_{1}):=\mathop{\sum }_{x_{1}\in E}r(g)\unicode[STIX]{x1D719}_{1}(x_{1},u).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}(g,u,\unicode[STIX]{x1D719}_{1}):=\mathop{\sum }_{x_{1}\in E}r(g)\unicode[STIX]{x1D719}_{1}(x_{1},u).\end{eqnarray}$$
We define the modular form
 $$\begin{eqnarray}I_{F,r}(\unicode[STIX]{x1D719}_{1}\otimes \unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F})=\frac{c_{U^{p}}}{|D_{F}|^{1/2}}\cdot \frac{L^{(p)}(1,\unicode[STIX]{x1D702}\unicode[STIX]{x1D712}_{F})}{L^{(p)}(1,\unicode[STIX]{x1D702})}\mathop{\sum }_{u\in \unicode[STIX]{x1D707}_{U^{p}}^{2}\backslash F^{\times }}\unicode[STIX]{x1D703}(u,\unicode[STIX]{x1D719}_{1})E_{r}(u,\unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F})\end{eqnarray}$$
$$\begin{eqnarray}I_{F,r}(\unicode[STIX]{x1D719}_{1}\otimes \unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F})=\frac{c_{U^{p}}}{|D_{F}|^{1/2}}\cdot \frac{L^{(p)}(1,\unicode[STIX]{x1D702}\unicode[STIX]{x1D712}_{F})}{L^{(p)}(1,\unicode[STIX]{x1D702})}\mathop{\sum }_{u\in \unicode[STIX]{x1D707}_{U^{p}}^{2}\backslash F^{\times }}\unicode[STIX]{x1D703}(u,\unicode[STIX]{x1D719}_{1})E_{r}(u,\unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F})\end{eqnarray}$$
for sufficiently large
 $r=(r_{v})_{v|p}$
, and the
$r=(r_{v})_{v|p}$
, and the
![]() $\mathscr{Y}_{F}$
-family of
$\mathscr{Y}_{F}$
-family of
![]() $q$
-expansions of weight-
$q$
-expansions of weight-
![]() $2$
modular forms
$2$
modular forms
 $$\begin{eqnarray}\mathscr{I}_{F}(\unicode[STIX]{x1D719}_{1}^{\infty }\otimes \unicode[STIX]{x1D719}_{2}^{p\infty };\unicode[STIX]{x1D712}_{F})=c_{U^{p}}\mathop{\sum }_{u\in \unicode[STIX]{x1D707}_{U^{p}}^{2}\backslash F^{\times }}\text{}^{\mathbf{q}}\unicode[STIX]{x1D703}(u,\unicode[STIX]{x1D719}_{1})\mathscr{E}(u,\unicode[STIX]{x1D719}_{2}^{p\infty };\unicode[STIX]{x1D712}_{F}),\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{I}_{F}(\unicode[STIX]{x1D719}_{1}^{\infty }\otimes \unicode[STIX]{x1D719}_{2}^{p\infty };\unicode[STIX]{x1D712}_{F})=c_{U^{p}}\mathop{\sum }_{u\in \unicode[STIX]{x1D707}_{U^{p}}^{2}\backslash F^{\times }}\text{}^{\mathbf{q}}\unicode[STIX]{x1D703}(u,\unicode[STIX]{x1D719}_{1})\mathscr{E}(u,\unicode[STIX]{x1D719}_{2}^{p\infty };\unicode[STIX]{x1D712}_{F}),\end{eqnarray}$$
where, letting
 $\unicode[STIX]{x1D707}_{U^{p}}=F^{\times }\cap U^{p}\mathscr{O}_{\mathbf{B},p}^{\times }$
, we set
$\unicode[STIX]{x1D707}_{U^{p}}=F^{\times }\cap U^{p}\mathscr{O}_{\mathbf{B},p}^{\times }$
, we set
 $$\begin{eqnarray}c_{U^{p}}:=\frac{2^{[F:\mathbf{Q}]-1}h_{F}}{[\mathscr{O}_{F}^{\times }:\unicode[STIX]{x1D707}_{U^{p}}^{2}]}\end{eqnarray}$$
$$\begin{eqnarray}c_{U^{p}}:=\frac{2^{[F:\mathbf{Q}]-1}h_{F}}{[\mathscr{O}_{F}^{\times }:\unicode[STIX]{x1D707}_{U^{p}}^{2}]}\end{eqnarray}$$
and
 $\unicode[STIX]{x1D719}(x_{1},x_{2},u)=\unicode[STIX]{x1D719}_{1}(x_{1},u)\unicode[STIX]{x1D719}_{2}(x_{2},u)$
with
$\unicode[STIX]{x1D719}(x_{1},x_{2},u)=\unicode[STIX]{x1D719}_{1}(x_{1},u)\unicode[STIX]{x1D719}_{2}(x_{2},u)$
with
 $\unicode[STIX]{x1D719}_{i}=\unicode[STIX]{x1D719}_{i}^{p\infty }\unicode[STIX]{x1D719}_{i,p\infty }$
for
$\unicode[STIX]{x1D719}_{i}=\unicode[STIX]{x1D719}_{i}^{p\infty }\unicode[STIX]{x1D719}_{i,p\infty }$
for
![]() $\unicode[STIX]{x1D719}_{i,v}$
the standard Schwartz function if
$\unicode[STIX]{x1D719}_{i,v}$
the standard Schwartz function if
![]() $v|\infty$
or
$v|\infty$
or
![]() $i=2$
and
$i=2$
and
![]() $v|p$
. The definition is independent of the choice of
$v|p$
. The definition is independent of the choice of
![]() $U^{p}$
(cf. [Reference Yuan, Zhang and ZhangYZZ12, (5.1.3)]).
$U^{p}$
(cf. [Reference Yuan, Zhang and ZhangYZZ12, (5.1.3)]).
The action of the subgroup
 $T(\mathbf{A})\times T(\mathbf{A})\subset \mathbf{B}^{\times }\times \mathbf{B}^{\times }$
on
$T(\mathbf{A})\times T(\mathbf{A})\subset \mathbf{B}^{\times }\times \mathbf{B}^{\times }$
on
 $\mathscr{S}(\mathbf{V}\times \mathbf{A}^{\times })=\mathscr{S}(\mathbf{V}_{1}\times \mathbf{A}^{\times })\otimes \mathscr{S}(\mathbf{V}_{2}\times \mathbf{A}^{\times })$
preserves this tensor product decomposition and thus it can be written as
$\mathscr{S}(\mathbf{V}\times \mathbf{A}^{\times })=\mathscr{S}(\mathbf{V}_{1}\times \mathbf{A}^{\times })\otimes \mathscr{S}(\mathbf{V}_{2}\times \mathbf{A}^{\times })$
preserves this tensor product decomposition and thus it can be written as
 $r=r_{1}\otimes r_{2}$
for the actions
$r=r_{1}\otimes r_{2}$
for the actions
![]() $r_{1}$
,
$r_{1}$
,
![]() $r_{2}$
on each of the two factors. We obtain an action of
$r_{2}$
on each of the two factors. We obtain an action of
 $T(\mathbf{A}^{\infty })\times T(\mathbf{A}^{\infty })$
on the forms
$T(\mathbf{A}^{\infty })\times T(\mathbf{A}^{\infty })$
on the forms
![]() $I_{F,r}$
and the families
$I_{F,r}$
and the families
![]() $\mathscr{I}_{F}$
with orbits
$\mathscr{I}_{F}$
with orbits
 $$\begin{eqnarray}\displaystyle I_{F,r}((t_{1},t_{2}),\unicode[STIX]{x1D719}_{1}\otimes \unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F}) & := & \displaystyle \frac{c_{U^{p}}}{|D_{F}|^{1/2}}\frac{L^{(p)}(1,\unicode[STIX]{x1D702}\unicode[STIX]{x1D712}_{F})}{L^{(p)}(1,\unicode[STIX]{x1D702})}\mathop{\sum }_{u\in \unicode[STIX]{x1D707}_{U^{p}}^{2}\backslash F^{\times }}\unicode[STIX]{x1D703}(u,r_{1}(t_{1},t_{2}),\unicode[STIX]{x1D719}_{1})E_{r}(u,\unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F}^{\unicode[STIX]{x1D704}}),\nonumber\\ \displaystyle \mathscr{I}_{F}((t_{1},t_{2}),\unicode[STIX]{x1D719}_{1}^{\infty }\otimes \unicode[STIX]{x1D719}_{2}^{p\infty };\unicode[STIX]{x1D712}_{F}) & := & \displaystyle c_{U^{p}}\mathop{\sum }_{u\in \unicode[STIX]{x1D707}_{U^{p}}^{2}\backslash F^{\times }}\text{}^{\mathbf{q}}\unicode[STIX]{x1D703}(q(t)u,r_{1}(t_{1},t_{2})\unicode[STIX]{x1D719}_{1})\mathscr{E}(q(t)u,\unicode[STIX]{x1D719}_{2}^{p\infty };\unicode[STIX]{x1D712}_{F}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{F,r}((t_{1},t_{2}),\unicode[STIX]{x1D719}_{1}\otimes \unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F}) & := & \displaystyle \frac{c_{U^{p}}}{|D_{F}|^{1/2}}\frac{L^{(p)}(1,\unicode[STIX]{x1D702}\unicode[STIX]{x1D712}_{F})}{L^{(p)}(1,\unicode[STIX]{x1D702})}\mathop{\sum }_{u\in \unicode[STIX]{x1D707}_{U^{p}}^{2}\backslash F^{\times }}\unicode[STIX]{x1D703}(u,r_{1}(t_{1},t_{2}),\unicode[STIX]{x1D719}_{1})E_{r}(u,\unicode[STIX]{x1D719}_{2},\unicode[STIX]{x1D712}_{F}^{\unicode[STIX]{x1D704}}),\nonumber\\ \displaystyle \mathscr{I}_{F}((t_{1},t_{2}),\unicode[STIX]{x1D719}_{1}^{\infty }\otimes \unicode[STIX]{x1D719}_{2}^{p\infty };\unicode[STIX]{x1D712}_{F}) & := & \displaystyle c_{U^{p}}\mathop{\sum }_{u\in \unicode[STIX]{x1D707}_{U^{p}}^{2}\backslash F^{\times }}\text{}^{\mathbf{q}}\unicode[STIX]{x1D703}(q(t)u,r_{1}(t_{1},t_{2})\unicode[STIX]{x1D719}_{1})\mathscr{E}(q(t)u,\unicode[STIX]{x1D719}_{2}^{p\infty };\unicode[STIX]{x1D712}_{F}).\nonumber\end{eqnarray}$$
It is a bounded action in the sense that the orbit
 $\{\mathscr{I}_{F}((t_{1},t_{2}),\unicode[STIX]{x1D719}_{1}^{\infty }\otimes \unicode[STIX]{x1D719}_{2}^{p\infty })\mid t_{1},t_{2}\in T(\mathbf{A}^{\infty })\}$
is a bounded subset of the space of
$\{\mathscr{I}_{F}((t_{1},t_{2}),\unicode[STIX]{x1D719}_{1}^{\infty }\otimes \unicode[STIX]{x1D719}_{2}^{p\infty })\mid t_{1},t_{2}\in T(\mathbf{A}^{\infty })\}$
is a bounded subset of the space of
![]() $\mathscr{Y}_{F}$
-families of
$\mathscr{Y}_{F}$
-families of
![]() $q$
-expansions, as both
$q$
-expansions, as both
![]() $\mathscr{E}$
and
$\mathscr{E}$
and
![]() $\text{}^{\mathbf{q}}\unicode[STIX]{x1D703}$
are bounded in terms of
$\text{}^{\mathbf{q}}\unicode[STIX]{x1D703}$
are bounded in terms of
 $\max |\unicode[STIX]{x1D719}^{p\infty }|$
.
$\max |\unicode[STIX]{x1D719}^{p\infty }|$
.
Define, for the fixed finite-order character
 $\unicode[STIX]{x1D714}:F^{\times }\backslash \mathbf{A}^{\times }\rightarrow M^{\times }$
,
$\unicode[STIX]{x1D714}:F^{\times }\backslash \mathbf{A}^{\times }\rightarrow M^{\times }$
,
 $$\begin{eqnarray}\mathscr{I}_{F,\unicode[STIX]{x1D714}^{-1}}((t_{1},t_{2}),\unicode[STIX]{x1D719}_{1}^{\infty }\otimes \unicode[STIX]{x1D719}_{2}^{p\infty };\unicode[STIX]{x1D712}_{F}):=\unicode[STIX]{x2A0D}_{\mathbf{A}^{\times }}\unicode[STIX]{x1D714}^{-1}(z)\unicode[STIX]{x1D712}_{F}(z)\mathscr{I}_{F}((zt_{1},t_{2}),\unicode[STIX]{x1D719}_{1}^{\infty }\otimes \unicode[STIX]{x1D719}_{2}^{p\infty };\unicode[STIX]{x1D712}_{F})\,dz,\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{I}_{F,\unicode[STIX]{x1D714}^{-1}}((t_{1},t_{2}),\unicode[STIX]{x1D719}_{1}^{\infty }\otimes \unicode[STIX]{x1D719}_{2}^{p\infty };\unicode[STIX]{x1D712}_{F}):=\unicode[STIX]{x2A0D}_{\mathbf{A}^{\times }}\unicode[STIX]{x1D714}^{-1}(z)\unicode[STIX]{x1D712}_{F}(z)\mathscr{I}_{F}((zt_{1},t_{2}),\unicode[STIX]{x1D719}_{1}^{\infty }\otimes \unicode[STIX]{x1D719}_{2}^{p\infty };\unicode[STIX]{x1D712}_{F})\,dz,\end{eqnarray}$$
a bounded
![]() $\mathscr{Y}_{F}$
-family of
$\mathscr{Y}_{F}$
-family of
![]() $q$
-expansions of forms of central character
$q$
-expansions of forms of central character
![]() $\unicode[STIX]{x1D714}^{-1}$
, corresponding to a bounded functional on
$\unicode[STIX]{x1D714}^{-1}$
, corresponding to a bounded functional on
 $\mathscr{C}(\unicode[STIX]{x1D6E4}_{F},L)$
valued in
$\mathscr{C}(\unicode[STIX]{x1D6E4}_{F},L)$
valued in
 $\mathbf{M}(K^{p},\unicode[STIX]{x1D714}^{-1},L)$
for a suitable
$\mathbf{M}(K^{p},\unicode[STIX]{x1D714}^{-1},L)$
for a suitable
![]() $K^{p}$
.
$K^{p}$
.
We further obtain a bounded functional
![]() $\mathscr{I}$
on
$\mathscr{I}$
on
 $\mathscr{C}(\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D714},L)$
, valued in
$\mathscr{C}(\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D714},L)$
, valued in
 $\mathbf{M}(K^{p},\unicode[STIX]{x1D714}^{-1},L)$
, which is defined on the set (generating a dense subalgebra) of finite-order characters
$\mathbf{M}(K^{p},\unicode[STIX]{x1D714}^{-1},L)$
, which is defined on the set (generating a dense subalgebra) of finite-order characters
 $\unicode[STIX]{x1D712}^{\prime }\in \mathscr{C}(\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D714},L)$
by
$\unicode[STIX]{x1D712}^{\prime }\in \mathscr{C}(\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D714},L)$
by
 $$\begin{eqnarray}\mathscr{I}(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712}^{\prime }):=\int _{[T]}\unicode[STIX]{x1D712}^{\prime }(t)\mathscr{I}_{F,\unicode[STIX]{x1D714}^{-1}}((t,1),\unicode[STIX]{x1D719}_{1}^{p}\unicode[STIX]{x1D719}_{1,p}\otimes \unicode[STIX]{x1D719}_{2}^{p};\unicode[STIX]{x1D714}\cdot \unicode[STIX]{x1D712}^{\prime }|_{\boldsymbol{ A}^{\times }})\,d^{\circ }t\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{I}(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712}^{\prime }):=\int _{[T]}\unicode[STIX]{x1D712}^{\prime }(t)\mathscr{I}_{F,\unicode[STIX]{x1D714}^{-1}}((t,1),\unicode[STIX]{x1D719}_{1}^{p}\unicode[STIX]{x1D719}_{1,p}\otimes \unicode[STIX]{x1D719}_{2}^{p};\unicode[STIX]{x1D714}\cdot \unicode[STIX]{x1D712}^{\prime }|_{\boldsymbol{ A}^{\times }})\,d^{\circ }t\end{eqnarray}$$
if
 $\unicode[STIX]{x1D719}^{p\infty }=\unicode[STIX]{x1D719}_{1}^{p\infty }\otimes \unicode[STIX]{x1D719}_{2}^{p\infty }$
. Here
$\unicode[STIX]{x1D719}^{p\infty }=\unicode[STIX]{x1D719}_{1}^{p\infty }\otimes \unicode[STIX]{x1D719}_{2}^{p\infty }$
. Here
 $\unicode[STIX]{x1D719}_{1}^{\infty }=\unicode[STIX]{x1D719}_{1}^{p\infty }\unicode[STIX]{x1D719}_{1,p}$
with
$\unicode[STIX]{x1D719}_{1}^{\infty }=\unicode[STIX]{x1D719}_{1}^{p\infty }\unicode[STIX]{x1D719}_{1,p}$
with
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{1,v}(x_{1},u)=\unicode[STIX]{x1D6FF}_{1,U_{T,v}}(x_{1})\mathbf{1}_{\mathscr{O}_{F,v}^{\times }}(u)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{1,v}(x_{1},u)=\unicode[STIX]{x1D6FF}_{1,U_{T,v}}(x_{1})\mathbf{1}_{\mathscr{O}_{F,v}^{\times }}(u)\end{eqnarray}$$
if
![]() $v|p$
, where
$v|p$
, where
 $U_{T,p}\subset \mathscr{O}_{E,p}^{\times }$
is a compact open subgroup small enough that
$U_{T,p}\subset \mathscr{O}_{E,p}^{\times }$
is a compact open subgroup small enough that
 $\unicode[STIX]{x1D712}_{p}^{\prime }|_{U_{T,p}}=1$
and
$\unicode[STIX]{x1D712}_{p}^{\prime }|_{U_{T,p}}=1$
and
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{1,U_{T,v}}(x_{1})=\frac{\operatorname{vol}(\mathscr{O}_{E,v},dx)}{\operatorname{vol}(U_{T,v},dx)}\mathbf{1}_{U_{v}\cap \mathscr{O}_{E}}(x_{1}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{1,U_{T,v}}(x_{1})=\frac{\operatorname{vol}(\mathscr{O}_{E,v},dx)}{\operatorname{vol}(U_{T,v},dx)}\mathbf{1}_{U_{v}\cap \mathscr{O}_{E}}(x_{1}).\end{eqnarray}$$
(The notation is meant to suggest a Dirac delta at
![]() $1$
in the variable
$1$
in the variable
![]() $x_{1}$
, to which this is the finest
$x_{1}$
, to which this is the finest
 $U_{v}\times U_{v}$
-invariant approximation. Both volumes are taken with respect to a Haar measure on
$U_{v}\times U_{v}$
-invariant approximation. Both volumes are taken with respect to a Haar measure on
![]() $E_{v}$
.)
$E_{v}$
.)
By construction, the induced rigid analytic function on
 $\mathscr{Y}^{\prime }=\mathscr{Y}_{\unicode[STIX]{x1D714}}^{\prime }$
, still denoted by
$\mathscr{Y}^{\prime }=\mathscr{Y}_{\unicode[STIX]{x1D714}}^{\prime }$
, still denoted by
![]() $\mathscr{I}$
, satisfies the following.
$\mathscr{I}$
, satisfies the following.
Proposition 3.4.1. There is a bounded
![]() $\mathscr{Y}^{\prime }$
-family of
$\mathscr{Y}^{\prime }$
-family of
![]() $q$
-expansions of modular forms
$q$
-expansions of modular forms
 $\mathscr{I}(\unicode[STIX]{x1D719}^{p\infty })$
such that for each
$\mathscr{I}(\unicode[STIX]{x1D719}^{p\infty })$
such that for each
 $\unicode[STIX]{x1D712}^{\prime }\in \mathscr{Y}^{\prime \,\text{l.c.}}(\mathbf{C})$
, we have
$\unicode[STIX]{x1D712}^{\prime }\in \mathscr{Y}^{\prime \,\text{l.c.}}(\mathbf{C})$
, we have
 $$\begin{eqnarray}\mathscr{I}(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712}^{\prime })=|D_{E}|^{1/2}|D_{F}|\,\text{}^{\mathbf{q}}I_{r}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D712}^{\prime }\text{}^{\unicode[STIX]{x1D704}}),\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{I}(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712}^{\prime })=|D_{E}|^{1/2}|D_{F}|\,\text{}^{\mathbf{q}}I_{r}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D712}^{\prime }\text{}^{\unicode[STIX]{x1D704}}),\end{eqnarray}$$
where
 $$\begin{eqnarray}I_{r}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D712}^{\prime }):=\int _{[T]}^{\ast }\unicode[STIX]{x1D712}^{\prime }(t)I_{F,r}((t,1),\unicode[STIX]{x1D719},\unicode[STIX]{x1D712}_{F})\,dt\end{eqnarray}$$
$$\begin{eqnarray}I_{r}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D712}^{\prime }):=\int _{[T]}^{\ast }\unicode[STIX]{x1D712}^{\prime }(t)I_{F,r}((t,1),\unicode[STIX]{x1D719},\unicode[STIX]{x1D712}_{F})\,dt\end{eqnarray}$$
with
![]() $I_{F,r}(\unicode[STIX]{x1D719})$
as in (3.4.1), with
$I_{F,r}(\unicode[STIX]{x1D719})$
as in (3.4.1), with
![]() $\unicode[STIX]{x1D719}_{p\infty }$
chosen as above.
$\unicode[STIX]{x1D719}_{p\infty }$
chosen as above.
3.5 Waldspurger’s Rankin–Selberg integral
Let
 $\unicode[STIX]{x1D712}^{\prime }\in \mathscr{Y}_{M(\unicode[STIX]{x1D6FC})}^{\prime \,\text{l.c.}}(\mathbf{C})$
be a character and
$\unicode[STIX]{x1D712}^{\prime }\in \mathscr{Y}_{M(\unicode[STIX]{x1D6FC})}^{\prime \,\text{l.c.}}(\mathbf{C})$
be a character and
 $\unicode[STIX]{x1D704}:M(\unicode[STIX]{x1D6FC}){\hookrightarrow}\mathbf{C}$
be the induced embedding. Let
$\unicode[STIX]{x1D704}:M(\unicode[STIX]{x1D6FC}){\hookrightarrow}\mathbf{C}$
be the induced embedding. Let
 $\unicode[STIX]{x1D713}:\mathbf{A}/F\rightarrow \mathbf{C}^{\times }$
be an additive character and let
$\unicode[STIX]{x1D713}:\mathbf{A}/F\rightarrow \mathbf{C}^{\times }$
be an additive character and let
![]() $r=r_{\unicode[STIX]{x1D713}}$
be the associated Weil representation.
$r=r_{\unicode[STIX]{x1D713}}$
be the associated Weil representation.
Proposition 3.5.1. Let
![]() $\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D704}}$
be a form with factorisable Whittaker function, and let
$\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D704}}$
be a form with factorisable Whittaker function, and let
 $\unicode[STIX]{x1D719}=\bigotimes _{v}\unicode[STIX]{x1D719}_{v}\in \overline{\mathscr{S}}(\mathbf{V}\times \mathbf{A}^{\times })$
. For sufficiently large
$\unicode[STIX]{x1D719}=\bigotimes _{v}\unicode[STIX]{x1D719}_{v}\in \overline{\mathscr{S}}(\mathbf{V}\times \mathbf{A}^{\times })$
. For sufficiently large
 $r=(r_{v})_{v|p}$
, we have
$r=(r_{v})_{v|p}$
, we have
 $$\begin{eqnarray}\mathop{\prod }_{v|p}\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B}_{v})^{-r_{v}}\cdot (\unicode[STIX]{x1D711},w_{r}^{-1}I_{r}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D712}^{\prime }))=\mathop{\prod }_{v}R_{r,v}^{\circ }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v}),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{v|p}\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B}_{v})^{-r_{v}}\cdot (\unicode[STIX]{x1D711},w_{r}^{-1}I_{r}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D712}^{\prime }))=\mathop{\prod }_{v}R_{r,v}^{\circ }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v}),\end{eqnarray}$$
where
 $$\begin{eqnarray}R_{r,v}^{\circ }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v})=\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})^{-r_{v}}\frac{L^{(p)}(1,\unicode[STIX]{x1D702}_{v}\unicode[STIX]{x1D712}_{F,v})}{L^{(p)}(1,\unicode[STIX]{x1D702}_{v})}R_{r,v}\end{eqnarray}$$
$$\begin{eqnarray}R_{r,v}^{\circ }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v})=\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})^{-r_{v}}\frac{L^{(p)}(1,\unicode[STIX]{x1D702}_{v}\unicode[STIX]{x1D712}_{F,v})}{L^{(p)}(1,\unicode[STIX]{x1D702}_{v})}R_{r,v}\end{eqnarray}$$
with
 $$\begin{eqnarray}R_{r,v}=\int _{Z(F_{v})N(F_{v})\backslash \mathbf{GL}_{2}(F_{v})}W_{-1,v}(g)\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{F,r,v}}(g)\int _{T(F_{v})}\unicode[STIX]{x1D712}_{v}^{\prime }(t)r(gw_{r}^{-1})\unicode[STIX]{x1D6F7}_{v}(t^{-1},q(t))\,dt\,dg.\end{eqnarray}$$
$$\begin{eqnarray}R_{r,v}=\int _{Z(F_{v})N(F_{v})\backslash \mathbf{GL}_{2}(F_{v})}W_{-1,v}(g)\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{F,r,v}}(g)\int _{T(F_{v})}\unicode[STIX]{x1D712}_{v}^{\prime }(t)r(gw_{r}^{-1})\unicode[STIX]{x1D6F7}_{v}(t^{-1},q(t))\,dt\,dg.\end{eqnarray}$$
Here
 $\unicode[STIX]{x1D6F7}_{v}=\unicode[STIX]{x1D719}_{v}$
if
$\unicode[STIX]{x1D6F7}_{v}=\unicode[STIX]{x1D719}_{v}$
if
![]() $v$
is non-archimedean and
$v$
is non-archimedean and
![]() $\unicode[STIX]{x1D6F7}_{v}$
is a preimage of
$\unicode[STIX]{x1D6F7}_{v}$
is a preimage of
![]() $\unicode[STIX]{x1D719}_{v}$
under (3.1.3) if
$\unicode[STIX]{x1D719}_{v}$
under (3.1.3) if
![]() $v$
is archimedean,
$v$
is archimedean,
![]() $W_{-1,v}$
is the local Whittaker function of
$W_{-1,v}$
is the local Whittaker function of
![]() $\unicode[STIX]{x1D711}$
for the character
$\unicode[STIX]{x1D711}$
for the character
![]() $\overline{\unicode[STIX]{x1D713}}_{v}$
, and we use the convention that
$\overline{\unicode[STIX]{x1D713}}_{v}$
, and we use the convention that
![]() $r_{v}=0$
,
$r_{v}=0$
,
 $w_{r,v}=1$
,
$w_{r,v}=1$
,
 $\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})^{-r_{v}}=1$
if
$\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})^{-r_{v}}=1$
if
![]() $v\nmid p$
.
$v\nmid p$
.
Note that the integral
![]() $R_{r,v}$
does not depend on
$R_{r,v}$
does not depend on
![]() $r\geqslant \text{}\underline{1}$
unless
$r\geqslant \text{}\underline{1}$
unless
![]() $v|p$
and it does not depend on
$v|p$
and it does not depend on
![]() $\unicode[STIX]{x1D712}^{\prime }$
if
$\unicode[STIX]{x1D712}^{\prime }$
if
![]() $v|\infty$
; we will accordingly simplify the notation in these cases.
$v|\infty$
; we will accordingly simplify the notation in these cases.
Proof. This is shown similarly to [Reference Yuan, Zhang and ZhangYZZ12, Proposition 2.5]; see [Reference Yuan, Zhang and ZhangYZZ12, (5.1.3)] for the equality between the kernel functions denoted there by
 $I(s,\unicode[STIX]{x1D712},\unicode[STIX]{x1D719})$
(similar to our
$I(s,\unicode[STIX]{x1D712},\unicode[STIX]{x1D719})$
(similar to our
 $c_{U^{p}}^{-1}I_{r}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D712}^{\prime })$
) and
$c_{U^{p}}^{-1}I_{r}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D712}^{\prime })$
) and
 $I(s,\unicode[STIX]{x1D712},\unicode[STIX]{x1D6F7})$
(which intervenes in the analogue in [Reference Yuan, Zhang and ZhangYZZ12] of the left-hand side of (3.5.1)).◻
$I(s,\unicode[STIX]{x1D712},\unicode[STIX]{x1D6F7})$
(which intervenes in the analogue in [Reference Yuan, Zhang and ZhangYZZ12] of the left-hand side of (3.5.1)).◻
We will sometimes lighten a bit the notation for
![]() $R_{v}^{\circ }$
by omitting
$R_{v}^{\circ }$
by omitting
![]() $\unicode[STIX]{x1D713}_{v}$
from it.
$\unicode[STIX]{x1D713}_{v}$
from it.
Lemma 3.5.2. When everything is unramified, we have
 $$\begin{eqnarray}R_{v}^{\circ }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime })=\frac{L(1/2,\unicode[STIX]{x1D70E}_{E,v}\otimes \unicode[STIX]{x1D712}_{v}^{\prime })}{\unicode[STIX]{x1D701}_{F,v}(2)L(1,\unicode[STIX]{x1D702}_{v})}.\end{eqnarray}$$
$$\begin{eqnarray}R_{v}^{\circ }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime })=\frac{L(1/2,\unicode[STIX]{x1D70E}_{E,v}\otimes \unicode[STIX]{x1D712}_{v}^{\prime })}{\unicode[STIX]{x1D701}_{F,v}(2)L(1,\unicode[STIX]{x1D702}_{v})}.\end{eqnarray}$$
Proof. With a slightly different setup,Footnote 18 Waldspurger [Reference WaldspurgerWal85, Lemmes 2 and 3] showed that
 $$\begin{eqnarray}R_{v}(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime })=\frac{L(1/2,\unicode[STIX]{x1D70E}_{E,v}\otimes \unicode[STIX]{x1D712}_{v}^{\prime })}{\unicode[STIX]{x1D701}_{F,v}(2)L(1,\unicode[STIX]{x1D702}_{v}\unicode[STIX]{x1D712}_{F,v})}\end{eqnarray}$$
$$\begin{eqnarray}R_{v}(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime })=\frac{L(1/2,\unicode[STIX]{x1D70E}_{E,v}\otimes \unicode[STIX]{x1D712}_{v}^{\prime })}{\unicode[STIX]{x1D701}_{F,v}(2)L(1,\unicode[STIX]{x1D702}_{v}\unicode[STIX]{x1D712}_{F,v})}\end{eqnarray}$$
when
 $\unicode[STIX]{x1D712}_{F,v}=|\cdot |^{s}$
, but his calculation goes through for any unramified character
$\unicode[STIX]{x1D712}_{F,v}=|\cdot |^{s}$
, but his calculation goes through for any unramified character
![]() $\unicode[STIX]{x1D712}_{F,v}$
.◻
$\unicode[STIX]{x1D712}_{F,v}$
.◻
Define
 $$\begin{eqnarray}R_{r,v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v}\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v}):=|d_{v}|^{-2}|D_{v}|^{-1/2}\frac{\unicode[STIX]{x1D701}_{F,v}(2)L(1,\unicode[STIX]{x1D702}_{v})}{L(1/2,\unicode[STIX]{x1D70E}_{E,v}\otimes \unicode[STIX]{x1D712}_{v}^{\prime })}R_{r,v}^{\circ }(W_{v},\unicode[STIX]{x1D719}_{v}\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v}).\end{eqnarray}$$
$$\begin{eqnarray}R_{r,v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v}\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v}):=|d_{v}|^{-2}|D_{v}|^{-1/2}\frac{\unicode[STIX]{x1D701}_{F,v}(2)L(1,\unicode[STIX]{x1D702}_{v})}{L(1/2,\unicode[STIX]{x1D70E}_{E,v}\otimes \unicode[STIX]{x1D712}_{v}^{\prime })}R_{r,v}^{\circ }(W_{v},\unicode[STIX]{x1D719}_{v}\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v}).\end{eqnarray}$$
Then the previous lemma combined with Proposition 3.5.1 gives the following result.
Proposition 3.5.3. We have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D704}\unicode[STIX]{x1D6FC}^{-r}(\unicode[STIX]{x1D711},w_{r}^{-1}I(\unicode[STIX]{x1D719},\unicode[STIX]{x1D712}^{\prime }))\nonumber\\ \displaystyle & & \displaystyle \quad =|D_{F}|^{-1}|D_{E}|^{-1/2}\frac{L^{(\infty )}(1/2,\unicode[STIX]{x1D70E}_{E}\otimes \unicode[STIX]{x1D712}^{\prime })}{\unicode[STIX]{x1D701}_{F}^{(\infty )}(2)L^{(\infty )}(1,\unicode[STIX]{x1D702})}\mathop{\prod }_{v\nmid \infty }R_{r,v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime })\mathop{\prod }_{v|\infty }R_{v}^{\circ }(W_{v},\unicode[STIX]{x1D6F7}_{v},\unicode[STIX]{x1D712}_{v}^{\prime }),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D704}\unicode[STIX]{x1D6FC}^{-r}(\unicode[STIX]{x1D711},w_{r}^{-1}I(\unicode[STIX]{x1D719},\unicode[STIX]{x1D712}^{\prime }))\nonumber\\ \displaystyle & & \displaystyle \quad =|D_{F}|^{-1}|D_{E}|^{-1/2}\frac{L^{(\infty )}(1/2,\unicode[STIX]{x1D70E}_{E}\otimes \unicode[STIX]{x1D712}^{\prime })}{\unicode[STIX]{x1D701}_{F}^{(\infty )}(2)L^{(\infty )}(1,\unicode[STIX]{x1D702})}\mathop{\prod }_{v\nmid \infty }R_{r,v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime })\mathop{\prod }_{v|\infty }R_{v}^{\circ }(W_{v},\unicode[STIX]{x1D6F7}_{v},\unicode[STIX]{x1D712}_{v}^{\prime }),\nonumber\end{eqnarray}$$
where all but finitely many of the factors in the infinite product are equal to
![]() $1$
.
$1$
.
Archimedean zeta integral. We compute the local integral
![]() $R_{v}$
when
$R_{v}$
when
![]() $v|\infty$
.
$v|\infty$
.
Lemma 3.5.4. If
![]() $v|\infty$
,
$v|\infty$
,
![]() $\unicode[STIX]{x1D719}_{v}$
is standard, and
$\unicode[STIX]{x1D719}_{v}$
is standard, and
![]() $W_{-1,v}$
is the standard antiholomorphic Whittaker function of weight
$W_{-1,v}$
is the standard antiholomorphic Whittaker function of weight
![]() $2$
of (2.1.2), then
$2$
of (2.1.2), then
 $$\begin{eqnarray}R_{v}^{\circ }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime })=R_{v}(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime })=1/2.\end{eqnarray}$$
$$\begin{eqnarray}R_{v}^{\circ }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime })=R_{v}(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime })=1/2.\end{eqnarray}$$
Proof. By the Iwasawa decomposition, we can uniquely write any
 $g\in \mathbf{GL}_{2}(\mathbf{R})$
as
$g\in \mathbf{GL}_{2}(\mathbf{R})$
as
 $$\begin{eqnarray}g=\left(\begin{array}{@{}cc@{}}1 & x\\ & 1\end{array}\right)\left(\begin{array}{@{}cc@{}}z & \\ & z\end{array}\right)\left(\begin{array}{@{}cc@{}}y & \\ & 1\end{array}\right)\left(\begin{array}{@{}cc@{}}\cos \unicode[STIX]{x1D703} & \sin \unicode[STIX]{x1D703}\\ -\sin \unicode[STIX]{x1D703} & \cos \unicode[STIX]{x1D703}\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}g=\left(\begin{array}{@{}cc@{}}1 & x\\ & 1\end{array}\right)\left(\begin{array}{@{}cc@{}}z & \\ & z\end{array}\right)\left(\begin{array}{@{}cc@{}}y & \\ & 1\end{array}\right)\left(\begin{array}{@{}cc@{}}\cos \unicode[STIX]{x1D703} & \sin \unicode[STIX]{x1D703}\\ -\sin \unicode[STIX]{x1D703} & \cos \unicode[STIX]{x1D703}\end{array}\right)\end{eqnarray}$$
with
![]() $x\in \mathbf{R}$
,
$x\in \mathbf{R}$
,
![]() $z\in \mathbf{R}^{\times }$
,
$z\in \mathbf{R}^{\times }$
,
![]() $y\in \mathbf{R}^{\times }$
,
$y\in \mathbf{R}^{\times }$
,
 $\unicode[STIX]{x1D703}\in [0,2\unicode[STIX]{x1D70B})$
; the local Tamagawa measure is then
$\unicode[STIX]{x1D703}\in [0,2\unicode[STIX]{x1D70B})$
; the local Tamagawa measure is then
 $dg=dx\,d^{\times }z\,(d^{\times }y/|y|)\,(d\unicode[STIX]{x1D703}/2)$
. The integral in
$dg=dx\,d^{\times }z\,(d^{\times }y/|y|)\,(d\unicode[STIX]{x1D703}/2)$
. The integral in
 $Z(\mathbf{R})\subset T(\mathbf{R})$
realises the map
$Z(\mathbf{R})\subset T(\mathbf{R})$
realises the map
![]() $\unicode[STIX]{x1D6F7}\rightarrow \unicode[STIX]{x1D719}$
; and it is easy to verify that
$\unicode[STIX]{x1D6F7}\rightarrow \unicode[STIX]{x1D719}$
; and it is easy to verify that
 $r(g)\unicode[STIX]{x1D719}(1,1)$
is the standard holomorphic Whittaker function of weight
$r(g)\unicode[STIX]{x1D719}(1,1)$
is the standard holomorphic Whittaker function of weight
![]() $2$
.
$2$
.
We then have, dropping subscripts
![]() $v$
,
$v$
,
 $$\begin{eqnarray}\displaystyle R_{v}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D719}) & = & \displaystyle \int _{T(\mathbf{R})/Z(\mathbf{R})}\int _{0}^{2\unicode[STIX]{x1D70B}}\int _{\mathbf{R}^{\times }}(|y|e^{-2\unicode[STIX]{x1D70B}y})^{2}\,\frac{d^{\times }y}{|y|}\,\frac{d\unicode[STIX]{x1D703}}{2}\,dt\nonumber\\ \displaystyle & = & \displaystyle 2\cdot (4\unicode[STIX]{x1D70B})^{-1}\unicode[STIX]{x1D70B}=1/2,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R_{v}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D719}) & = & \displaystyle \int _{T(\mathbf{R})/Z(\mathbf{R})}\int _{0}^{2\unicode[STIX]{x1D70B}}\int _{\mathbf{R}^{\times }}(|y|e^{-2\unicode[STIX]{x1D70B}y})^{2}\,\frac{d^{\times }y}{|y|}\,\frac{d\unicode[STIX]{x1D703}}{2}\,dt\nonumber\\ \displaystyle & = & \displaystyle 2\cdot (4\unicode[STIX]{x1D70B})^{-1}\unicode[STIX]{x1D70B}=1/2,\nonumber\end{eqnarray}$$
where
![]() $(4\unicode[STIX]{x1D70B})^{-1}$
comes from a change of variable,
$(4\unicode[STIX]{x1D70B})^{-1}$
comes from a change of variable,
 $2=\operatorname{vol}(T(\mathbf{R})/Z(\mathbf{R}))$
, and
$2=\operatorname{vol}(T(\mathbf{R})/Z(\mathbf{R}))$
, and
![]() $\unicode[STIX]{x1D70B}$
comes from the integration in
$\unicode[STIX]{x1D70B}$
comes from the integration in
![]() $d\unicode[STIX]{x1D703}$
.◻
$d\unicode[STIX]{x1D703}$
.◻
3.6 Interpolation of local zeta integrals
When
![]() $v\nmid p$
, the normalised local zeta integrals admit an interpolation as well. Recall from § 1.2 that
$v\nmid p$
, the normalised local zeta integrals admit an interpolation as well. Recall from § 1.2 that
![]() $\unicode[STIX]{x1D6F9}_{v}$
denotes the scheme of all local additive characters of level
$\unicode[STIX]{x1D6F9}_{v}$
denotes the scheme of all local additive characters of level
![]() $0$
.
$0$
.
Proposition 3.6.1. Let
![]() $v\nmid p$
be a finite place, and let
$v\nmid p$
be a finite place, and let
 $\mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})$
be the universal Kirillov model of
$\mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})$
be the universal Kirillov model of
![]() $\unicode[STIX]{x1D70E}_{v}$
. Then, for any
$\unicode[STIX]{x1D70E}_{v}$
. Then, for any
 $\unicode[STIX]{x1D719}_{v}\in \mathscr{S}(V_{v}\times F_{v}^{\times })$
,
$\unicode[STIX]{x1D719}_{v}\in \mathscr{S}(V_{v}\times F_{v}^{\times })$
,
 $W_{v}\in \mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})$
, there exists a function
$W_{v}\in \mathscr{K}(\unicode[STIX]{x1D70E}_{v},\unicode[STIX]{x1D713}_{\text{univ},v})$
, there exists a function
 $$\begin{eqnarray}\mathscr{R}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v})\in L(1,\unicode[STIX]{x1D702}_{v}\unicode[STIX]{x1D712}_{F,v})\mathscr{O}_{\mathscr{Y}_{v}^{\prime }\times \unicode[STIX]{x1D6F9}_{v}}(\mathscr{Y}_{v}^{\prime },\unicode[STIX]{x1D714}_{v}\unicode[STIX]{x1D712}_{F,v,\text{univ}}^{-1})\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{R}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v})\in L(1,\unicode[STIX]{x1D702}_{v}\unicode[STIX]{x1D712}_{F,v})\mathscr{O}_{\mathscr{Y}_{v}^{\prime }\times \unicode[STIX]{x1D6F9}_{v}}(\mathscr{Y}_{v}^{\prime },\unicode[STIX]{x1D714}_{v}\unicode[STIX]{x1D712}_{F,v,\text{univ}}^{-1})\end{eqnarray}$$
such that for all
 $\unicode[STIX]{x1D712}_{v}^{\prime }\in \mathscr{Y}_{v}^{\prime }(\mathbf{C})$
,
$\unicode[STIX]{x1D712}_{v}^{\prime }\in \mathscr{Y}_{v}^{\prime }(\mathbf{C})$
,
 $\unicode[STIX]{x1D713}_{v}\in \unicode[STIX]{x1D6F9}_{v}(\mathbf{C})$
, we have
$\unicode[STIX]{x1D713}_{v}\in \unicode[STIX]{x1D6F9}_{v}(\mathbf{C})$
, we have
 $$\begin{eqnarray}\mathscr{R}_{v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v};\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v})=R_{v}^{\natural }(W_{v}^{\unicode[STIX]{x1D704}},\unicode[STIX]{x1D719}_{v}(\unicode[STIX]{x1D712}_{v}^{\prime }),\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v}),\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{R}_{v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v};\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v})=R_{v}^{\natural }(W_{v}^{\unicode[STIX]{x1D704}},\unicode[STIX]{x1D719}_{v}(\unicode[STIX]{x1D712}_{v}^{\prime }),\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v}),\end{eqnarray}$$
where
 $\unicode[STIX]{x1D719}_{v}(\unicode[STIX]{x1D712}_{v}^{\prime })=\unicode[STIX]{x1D719}_{1,v}\unicode[STIX]{x1D719}_{2,v}(\unicode[STIX]{x1D712}_{F,v})$
with
$\unicode[STIX]{x1D719}_{v}(\unicode[STIX]{x1D712}_{v}^{\prime })=\unicode[STIX]{x1D719}_{1,v}\unicode[STIX]{x1D719}_{2,v}(\unicode[STIX]{x1D712}_{F,v})$
with
 $\unicode[STIX]{x1D719}_{2,v}(\unicode[STIX]{x1D712}_{F,v})$
is as in (3.3.2).
$\unicode[STIX]{x1D719}_{2,v}(\unicode[STIX]{x1D712}_{F,v})$
is as in (3.3.2).
In the statement, we consider
 $L(1,\unicode[STIX]{x1D702}_{v}\unicode[STIX]{x1D712}_{F,v})^{-1}$
as an element of
$L(1,\unicode[STIX]{x1D702}_{v}\unicode[STIX]{x1D712}_{F,v})^{-1}$
as an element of
![]() $\mathscr{O}(\mathscr{Y}_{v}^{\prime })$
(coming by pullback from
$\mathscr{O}(\mathscr{Y}_{v}^{\prime })$
(coming by pullback from
![]() $\mathscr{Y}_{F,v}$
). Note that it equals the non-zero constant
$\mathscr{Y}_{F,v}$
). Note that it equals the non-zero constant
 $L(1,\unicode[STIX]{x1D702}_{v})^{-1}$
along
$L(1,\unicode[STIX]{x1D702}_{v})^{-1}$
along
 $\mathscr{Y}_{v}\subset \mathscr{Y}_{v}^{\prime }$
.
$\mathscr{Y}_{v}\subset \mathscr{Y}_{v}^{\prime }$
.
Proof. Note that the assertion on the subsheaf of
![]() $\mathscr{O}_{\mathscr{Y}_{v}\times \unicode[STIX]{x1D6F9}_{v}}$
of which
$\mathscr{O}_{\mathscr{Y}_{v}\times \unicode[STIX]{x1D6F9}_{v}}$
of which
![]() $\mathscr{R}_{v}^{\natural }$
is a section simply encodes the dependence of
$\mathscr{R}_{v}^{\natural }$
is a section simply encodes the dependence of
![]() $R_{v}^{\natural }$
on the additive character, which is easy to ascertain by a change of variables. By the definitions, it suffices to show that
$R_{v}^{\natural }$
on the additive character, which is easy to ascertain by a change of variables. By the definitions, it suffices to show that
 $$\begin{eqnarray}L(1/2,\unicode[STIX]{x1D70E}_{E,v}\otimes \unicode[STIX]{x1D712}_{v}^{\prime })^{-1}R_{v}(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}L(1/2,\unicode[STIX]{x1D70E}_{E,v}\otimes \unicode[STIX]{x1D712}_{v}^{\prime })^{-1}R_{v}(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime })\end{eqnarray}$$
extends to a regular function on
![]() $\mathscr{Y}_{v}^{\prime }$
. We will more precisely show that
$\mathscr{Y}_{v}^{\prime }$
. We will more precisely show that
 $L(1/2,\unicode[STIX]{x1D70E}_{E,v}\otimes \unicode[STIX]{x1D712}_{v}^{\prime })^{-1}$
is a product of various factors all of which extend to regular functions on
$L(1/2,\unicode[STIX]{x1D70E}_{E,v}\otimes \unicode[STIX]{x1D712}_{v}^{\prime })^{-1}$
is a product of various factors all of which extend to regular functions on
![]() $\mathscr{Y}_{v}^{\prime }$
, and that the product of some of those factors and
$\mathscr{Y}_{v}^{\prime }$
, and that the product of some of those factors and
 $R_{v}(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime })$
also extends to a regular function on
$R_{v}(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime })$
also extends to a regular function on
![]() $\mathscr{Y}_{v}^{\prime }$
. Concretely, if
$\mathscr{Y}_{v}^{\prime }$
. Concretely, if
 $A\subset E_{v}^{\times }/(E_{v}^{\times }\cap V^{p})$
is any finite set, then the evaluations
$A\subset E_{v}^{\times }/(E_{v}^{\times }\cap V^{p})$
is any finite set, then the evaluations
 $\unicode[STIX]{x1D712}_{v}^{\prime }\mapsto (\unicode[STIX]{x1D712}_{v}^{\prime }(a))_{a\in A}$
define a morphism
$\unicode[STIX]{x1D712}_{v}^{\prime }\mapsto (\unicode[STIX]{x1D712}_{v}^{\prime }(a))_{a\in A}$
define a morphism
 $\operatorname{ev}_{A}:\mathscr{Y}_{v}^{\prime }\rightarrow \mathbf{G}_{m,M}^{A}$
,Footnote
19
so that finite sums of evaluations of characters are regular functions on
$\operatorname{ev}_{A}:\mathscr{Y}_{v}^{\prime }\rightarrow \mathbf{G}_{m,M}^{A}$
,Footnote
19
so that finite sums of evaluations of characters are regular functions on
![]() $\mathscr{Y}_{v}^{\prime }$
obtained by pullback along
$\mathscr{Y}_{v}^{\prime }$
obtained by pullback along
![]() $\operatorname{ev}_{A}$
.
$\operatorname{ev}_{A}$
.
Interpolation of
![]() $R_{v}$
. Within the expression for
$R_{v}$
. Within the expression for
![]() $R_{v}$
, we can use the Iwasawa decomposition and note that integration over
$R_{v}$
, we can use the Iwasawa decomposition and note that integration over
 $K=\mathbf{GL}_{2}(\mathscr{O}_{F,v})$
yields a finite sum of integrals of the form (dropping subscripts
$K=\mathbf{GL}_{2}(\mathscr{O}_{F,v})$
yields a finite sum of integrals of the form (dropping subscripts
![]() $v$
)Footnote
20
$v$
)Footnote
20
 $$\begin{eqnarray}\int _{F^{\times }}f^{\prime }(y)\int _{T(F)}\unicode[STIX]{x1D712}^{\prime }(t)\unicode[STIX]{x1D719}^{\prime }(yt^{-1},y^{-1}q(t))\,dt\,dy\end{eqnarray}$$
$$\begin{eqnarray}\int _{F^{\times }}f^{\prime }(y)\int _{T(F)}\unicode[STIX]{x1D712}^{\prime }(t)\unicode[STIX]{x1D719}^{\prime }(yt^{-1},y^{-1}q(t))\,dt\,dy\end{eqnarray}$$
for some Schwartz functions
![]() $\unicode[STIX]{x1D719}^{\prime }$
and elements
$\unicode[STIX]{x1D719}^{\prime }$
and elements
![]() $f^{\prime }$
of the Kirillov model of
$f^{\prime }$
of the Kirillov model of
![]() $\unicode[STIX]{x1D70E}$
: namely, the translates of
$\unicode[STIX]{x1D70E}$
: namely, the translates of
![]() $W_{-1}$
and of
$W_{-1}$
and of
![]() $\unicode[STIX]{x1D719}_{v}$
by the action of
$\unicode[STIX]{x1D719}_{v}$
by the action of
![]() $K$
. (More precisely, taking into account the dependence on
$K$
. (More precisely, taking into account the dependence on
![]() $\unicode[STIX]{x1D712}^{\prime }$
of
$\unicode[STIX]{x1D712}^{\prime }$
of
![]() $\unicode[STIX]{x1D719}$
, also products of the above integrals and of
$\unicode[STIX]{x1D719}$
, also products of the above integrals and of
 $L(1,\unicode[STIX]{x1D702}\unicode[STIX]{x1D712}_{F,v})^{-1}$
can occur; the factor
$L(1,\unicode[STIX]{x1D702}\unicode[STIX]{x1D712}_{F,v})^{-1}$
can occur; the factor
 $L(1,\unicode[STIX]{x1D702}\unicode[STIX]{x1D712}_{F,v})^{-1}$
clearly interpolates to a regular function on
$L(1,\unicode[STIX]{x1D702}\unicode[STIX]{x1D712}_{F,v})^{-1}$
clearly interpolates to a regular function on
![]() $\mathscr{Y}_{v}^{\prime }$
.)
$\mathscr{Y}_{v}^{\prime }$
.)
It is easy to see that the integral reduces to a finite sum if either
![]() $W$
is compactly supported or
$W$
is compactly supported or
![]() $\unicode[STIX]{x1D719}_{1}^{\prime }(\cdot ,u)$
is supported away from
$\unicode[STIX]{x1D719}_{1}^{\prime }(\cdot ,u)$
is supported away from
![]() $0\in E$
. It thus suffices to study the case where
$0\in E$
. It thus suffices to study the case where
 $\unicode[STIX]{x1D719}_{1}^{\prime }(x_{1},u)=\mathbf{1}_{\mathscr{O}_{E}}(x_{1})\unicode[STIX]{x1D719}_{F}^{\prime }(u)$
, and
$\unicode[STIX]{x1D719}_{1}^{\prime }(x_{1},u)=\mathbf{1}_{\mathscr{O}_{E}}(x_{1})\unicode[STIX]{x1D719}_{F}^{\prime }(u)$
, and
![]() $f^{\prime }$
belongs to the basis of the quotient space
$f^{\prime }$
belongs to the basis of the quotient space
![]() $\overline{\mathscr{K}}$
introduced in the proof of Lemma 2.3.1. Moreover, up to simple manipulations, we may assume that
$\overline{\mathscr{K}}$
introduced in the proof of Lemma 2.3.1. Moreover, up to simple manipulations, we may assume that
![]() $\unicode[STIX]{x1D719}_{F}(u)$
is close to a delta function supported at
$\unicode[STIX]{x1D719}_{F}(u)$
is close to a delta function supported at
![]() $u=1$
. We distinguish three different cases.
$u=1$
. We distinguish three different cases.
![]() $\unicode[STIX]{x1D70E}_{v}$
is supercuspidal. In this case
$\unicode[STIX]{x1D70E}_{v}$
is supercuspidal. In this case
![]() $\overline{\mathscr{K}}=0$
and there is nothing to prove.
$\overline{\mathscr{K}}=0$
and there is nothing to prove.
![]() $\unicode[STIX]{x1D70E}_{v}$
is a special representation
$\unicode[STIX]{x1D70E}_{v}$
is a special representation
 $\operatorname{St}(\unicode[STIX]{x1D707}|\cdot |^{-1})$
. In this case
$\operatorname{St}(\unicode[STIX]{x1D707}|\cdot |^{-1})$
. In this case
![]() $\overline{\mathscr{K}}$
is spanned by
$\overline{\mathscr{K}}$
is spanned by
 $f_{\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D707}\cdot \mathbf{1}_{\mathscr{O}_{F}-\{0\}}$
. We find that the integral is essentiallyFootnote
21
$f_{\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D707}\cdot \mathbf{1}_{\mathscr{O}_{F}-\{0\}}$
. We find that the integral is essentiallyFootnote
21
![]() $0$
if there is a place
$0$
if there is a place
![]() $w$
of
$w$
of
![]() $E$
above
$E$
above
![]() $v$
such that, for
$v$
such that, for
 $\unicode[STIX]{x1D712}_{w}^{\prime }:=\unicode[STIX]{x1D712}_{v}^{\prime }|_{E_{w}^{\times }}$
, the character
$\unicode[STIX]{x1D712}_{w}^{\prime }:=\unicode[STIX]{x1D712}_{v}^{\prime }|_{E_{w}^{\times }}$
, the character
 $\unicode[STIX]{x1D712}_{w}^{\prime }\cdot \unicode[STIX]{x1D707}\circ q$
of
$\unicode[STIX]{x1D712}_{w}^{\prime }\cdot \unicode[STIX]{x1D707}\circ q$
of
![]() $E_{w}^{\times }$
is ramified; and it essentially equals
$E_{w}^{\times }$
is ramified; and it essentially equals
 $$\begin{eqnarray}\mathop{\prod }_{w|v}(1-\unicode[STIX]{x1D712}_{w}^{\prime }(\unicode[STIX]{x1D71B}_{w})\unicode[STIX]{x1D707}(q(\unicode[STIX]{x1D71B}_{w}))q_{E,w}^{-1})^{-1}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{w|v}(1-\unicode[STIX]{x1D712}_{w}^{\prime }(\unicode[STIX]{x1D71B}_{w})\unicode[STIX]{x1D707}(q(\unicode[STIX]{x1D71B}_{w}))q_{E,w}^{-1})^{-1}\end{eqnarray}$$
otherwise.Footnote
22
In the latter case,
 $L(1/2,\unicode[STIX]{x1D70E}_{E,v}\otimes \unicode[STIX]{x1D712}_{w}^{\prime })$
is also equal to (3.6.2). We conclude that (3.6.1) extends to a regular function on
$L(1/2,\unicode[STIX]{x1D70E}_{E,v}\otimes \unicode[STIX]{x1D712}_{w}^{\prime })$
is also equal to (3.6.2). We conclude that (3.6.1) extends to a regular function on
![]() $\mathscr{Y}_{v}^{\prime }$
.
$\mathscr{Y}_{v}^{\prime }$
.
![]() $\unicode[STIX]{x1D70E}_{v}$
is an irreducible principal series
$\unicode[STIX]{x1D70E}_{v}$
is an irreducible principal series
 $\operatorname{Ind}(\unicode[STIX]{x1D707},\unicode[STIX]{x1D707}^{\prime }|\cdot |^{-1})$
.Footnote
23
The space
$\operatorname{Ind}(\unicode[STIX]{x1D707},\unicode[STIX]{x1D707}^{\prime }|\cdot |^{-1})$
.Footnote
23
The space
![]() $\overline{\mathscr{K}}$
has dimension
$\overline{\mathscr{K}}$
has dimension
![]() $2$
and
$2$
and
![]() $f_{\unicode[STIX]{x1D707}}$
as above provides a non-zero element. Again the corresponding integral yields either
$f_{\unicode[STIX]{x1D707}}$
as above provides a non-zero element. Again the corresponding integral yields either
![]() $0$
or (3.6.2), the latter happening precisely when (3.6.2) is a factor of
$0$
or (3.6.2), the latter happening precisely when (3.6.2) is a factor of
 $L(1/2,\unicode[STIX]{x1D70E}_{E}\otimes \unicode[STIX]{x1D712})$
. If
$L(1/2,\unicode[STIX]{x1D70E}_{E}\otimes \unicode[STIX]{x1D712})$
. If
![]() $\unicode[STIX]{x1D707}^{\prime }\neq \unicode[STIX]{x1D707}$
, then a second basis element is
$\unicode[STIX]{x1D707}^{\prime }\neq \unicode[STIX]{x1D707}$
, then a second basis element is
![]() $f_{\unicode[STIX]{x1D707}^{\prime }}$
, for which the same discussion applies. If
$f_{\unicode[STIX]{x1D707}^{\prime }}$
, for which the same discussion applies. If
![]() $\unicode[STIX]{x1D707}^{\prime }=\unicode[STIX]{x1D707}$
, then a second basis element is
$\unicode[STIX]{x1D707}^{\prime }=\unicode[STIX]{x1D707}$
, then a second basis element is
 $f_{\unicode[STIX]{x1D707}}^{\prime }(y):=v(y)\unicode[STIX]{x1D707}(y)\mathbf{1}_{\mathscr{O}_{F}-\{0\}}(y)$
. The integral is essentially
$f_{\unicode[STIX]{x1D707}}^{\prime }(y):=v(y)\unicode[STIX]{x1D707}(y)\mathbf{1}_{\mathscr{O}_{F}-\{0\}}(y)$
. The integral is essentially
![]() $0$
if some
$0$
if some
 $\unicode[STIX]{x1D712}_{w}^{\prime }\cdot \unicode[STIX]{x1D707}\circ q$
is ramified, and
$\unicode[STIX]{x1D712}_{w}^{\prime }\cdot \unicode[STIX]{x1D707}\circ q$
is ramified, and
 $$\begin{eqnarray}\mathop{\prod }_{w|v}(1-\unicode[STIX]{x1D712}_{w}^{\prime }(\unicode[STIX]{x1D71B}_{w})\unicode[STIX]{x1D707}(q(\unicode[STIX]{x1D71B}_{w}))q_{E,w}^{-1})^{-2}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{w|v}(1-\unicode[STIX]{x1D712}_{w}^{\prime }(\unicode[STIX]{x1D71B}_{w})\unicode[STIX]{x1D707}(q(\unicode[STIX]{x1D71B}_{w}))q_{E,w}^{-1})^{-2}\end{eqnarray}$$
otherwise. In the latter case,
 $L(1/2,\unicode[STIX]{x1D70E}_{E,v}\otimes \unicode[STIX]{x1D712}_{w}^{\prime })$
equals (3.6.3) as well.
$L(1/2,\unicode[STIX]{x1D70E}_{E,v}\otimes \unicode[STIX]{x1D712}_{w}^{\prime })$
equals (3.6.3) as well.
Interpolation of
 $L(1/2,\unicode[STIX]{x1D70E}_{E,v}\otimes \unicode[STIX]{x1D712}_{v}^{\prime })^{-1}$
. Depending only on
$L(1/2,\unicode[STIX]{x1D70E}_{E,v}\otimes \unicode[STIX]{x1D712}_{v}^{\prime })^{-1}$
. Depending only on
![]() $\unicode[STIX]{x1D70E}_{v}$
, as recalled above, for each place
$\unicode[STIX]{x1D70E}_{v}$
, as recalled above, for each place
![]() $w|v$
of
$w|v$
of
![]() $E$
, there exist at most two characters
$E$
, there exist at most two characters
![]() $\unicode[STIX]{x1D708}_{w,i_{w}}$
of
$\unicode[STIX]{x1D708}_{w,i_{w}}$
of
![]() $E_{w}^{\times }$
such that for all
$E_{w}^{\times }$
such that for all
 $\unicode[STIX]{x1D712}_{v}^{\prime }\in \mathscr{Y}_{v}^{\prime }(\mathbf{C})$
, we can write
$\unicode[STIX]{x1D712}_{v}^{\prime }\in \mathscr{Y}_{v}^{\prime }(\mathbf{C})$
, we can write
 $L(1/2,\unicode[STIX]{x1D70E}_{E,v}\otimes \unicode[STIX]{x1D712}_{v}^{\prime })^{-1}=\prod _{w,i_{w}}^{\prime }(1-\unicode[STIX]{x1D708}_{w}\unicode[STIX]{x1D712}_{w}^{\prime }(\unicode[STIX]{x1D71B}_{w}))$
, where the product
$L(1/2,\unicode[STIX]{x1D70E}_{E,v}\otimes \unicode[STIX]{x1D712}_{v}^{\prime })^{-1}=\prod _{w,i_{w}}^{\prime }(1-\unicode[STIX]{x1D708}_{w}\unicode[STIX]{x1D712}_{w}^{\prime }(\unicode[STIX]{x1D71B}_{w}))$
, where the product
![]() $\prod ^{\prime }$
extends over those pairs
$\prod ^{\prime }$
extends over those pairs
![]() $(w,i_{w})$
such that
$(w,i_{w})$
such that
 $\unicode[STIX]{x1D708}_{w,i_{w}}\unicode[STIX]{x1D712}_{w}^{\prime }$
is unramified. We can replace the partial product by a genuine product and each of the factors by
$\unicode[STIX]{x1D708}_{w,i_{w}}\unicode[STIX]{x1D712}_{w}^{\prime }$
is unramified. We can replace the partial product by a genuine product and each of the factors by
 $$\begin{eqnarray}\displaystyle & 1-\biggl(\underset{x\in \mathscr{O}_{E,w}^{\times }/(V^{p}\cap E_{w}^{\times })}{\sum ^{\prime }}\unicode[STIX]{x1D708}_{w,i_{w}}(x)\unicode[STIX]{x1D712}_{w}^{\prime }(x)\biggr)\cdot \unicode[STIX]{x1D708}_{w,i_{w}}\unicode[STIX]{x1D712}_{w}^{\prime }(\unicode[STIX]{x1D71B}_{w}), & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & 1-\biggl(\underset{x\in \mathscr{O}_{E,w}^{\times }/(V^{p}\cap E_{w}^{\times })}{\sum ^{\prime }}\unicode[STIX]{x1D708}_{w,i_{w}}(x)\unicode[STIX]{x1D712}_{w}^{\prime }(x)\biggr)\cdot \unicode[STIX]{x1D708}_{w,i_{w}}\unicode[STIX]{x1D712}_{w}^{\prime }(\unicode[STIX]{x1D71B}_{w}), & \displaystyle \nonumber\end{eqnarray}$$
where
![]() $\sum ^{\prime }$
denotes average. This expression is the value at
$\sum ^{\prime }$
denotes average. This expression is the value at
![]() $\unicode[STIX]{x1D712}_{v}^{\prime }$
of an element of
$\unicode[STIX]{x1D712}_{v}^{\prime }$
of an element of
![]() $\mathscr{O}(\mathscr{Y}_{v}^{\prime })$
, as desired. ◻
$\mathscr{O}(\mathscr{Y}_{v}^{\prime })$
, as desired. ◻
3.7 Definition and interpolation property
Let
 $\mathscr{M}_{\mathscr{Y}^{\prime }-\mathscr{Y}}$
be the multiplicative part of
$\mathscr{M}_{\mathscr{Y}^{\prime }-\mathscr{Y}}$
be the multiplicative part of
![]() $\mathscr{O}(\mathscr{Y}^{\prime })^{\text{f}}$
consisting of functions whose restriction to
$\mathscr{O}(\mathscr{Y}^{\prime })^{\text{f}}$
consisting of functions whose restriction to
![]() $\mathscr{Y}$
is invertible. (Recall that
$\mathscr{Y}$
is invertible. (Recall that
 $\mathscr{O}(\mathscr{Y}^{\prime })^{\text{f}}\subset \mathscr{O}(\mathscr{Y}^{\prime })^{\text{b}}$
is the image of
$\mathscr{O}(\mathscr{Y}^{\prime })^{\text{f}}\subset \mathscr{O}(\mathscr{Y}^{\prime })^{\text{b}}$
is the image of
 $\bigotimes _{v\nmid p\infty }\mathscr{O}(\mathscr{Y}_{v}^{\prime })$
.)
$\bigotimes _{v\nmid p\infty }\mathscr{O}(\mathscr{Y}_{v}^{\prime })$
.)
Theorem 3.7.1. There exists a unique function
 $$\begin{eqnarray}L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})~\in \mathscr{O}_{\mathscr{Y}^{\prime }\times \unicode[STIX]{x1D6F9}_{p}}(\mathscr{Y}^{\prime },\unicode[STIX]{x1D714}_{p}\unicode[STIX]{x1D712}_{F,\text{univ},p}^{-1})^{\text{b}}[\mathscr{M}_{\mathscr{ Y}^{\prime }-\mathscr{Y}}^{-1}]\end{eqnarray}$$
$$\begin{eqnarray}L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})~\in \mathscr{O}_{\mathscr{Y}^{\prime }\times \unicode[STIX]{x1D6F9}_{p}}(\mathscr{Y}^{\prime },\unicode[STIX]{x1D714}_{p}\unicode[STIX]{x1D712}_{F,\text{univ},p}^{-1})^{\text{b}}[\mathscr{M}_{\mathscr{ Y}^{\prime }-\mathscr{Y}}^{-1}]\end{eqnarray}$$
which is algebraic on
 $\mathscr{Y}_{M(\unicode[STIX]{x1D6FC})}^{\prime \,\text{l.c.}}\times \unicode[STIX]{x1D6F9}_{p}$
and satisfies
$\mathscr{Y}_{M(\unicode[STIX]{x1D6FC})}^{\prime \,\text{l.c.}}\times \unicode[STIX]{x1D6F9}_{p}$
and satisfies
 $$\begin{eqnarray}L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})(\unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D713}_{p})=\frac{\unicode[STIX]{x1D70B}^{2[F:\mathbf{Q}]}|D_{F}|^{1/2}L^{(\infty )}(1/2,\unicode[STIX]{x1D70E}_{E}^{\unicode[STIX]{x1D704}},\unicode[STIX]{x1D712}^{\prime }\text{}^{\unicode[STIX]{x1D704}})}{2L^{(\infty )}(1,\unicode[STIX]{x1D702})L^{(\infty )}(1,\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D704}},\operatorname{ad})}\mathop{\prod }_{v|p}Z_{v}^{\circ }(\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v})\end{eqnarray}$$
$$\begin{eqnarray}L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})(\unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D713}_{p})=\frac{\unicode[STIX]{x1D70B}^{2[F:\mathbf{Q}]}|D_{F}|^{1/2}L^{(\infty )}(1/2,\unicode[STIX]{x1D70E}_{E}^{\unicode[STIX]{x1D704}},\unicode[STIX]{x1D712}^{\prime }\text{}^{\unicode[STIX]{x1D704}})}{2L^{(\infty )}(1,\unicode[STIX]{x1D702})L^{(\infty )}(1,\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D704}},\operatorname{ad})}\mathop{\prod }_{v|p}Z_{v}^{\circ }(\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v})\end{eqnarray}$$
for every
 $\unicode[STIX]{x1D712}^{\prime }\in \mathscr{Y}_{M(\unicode[STIX]{x1D6FC})}^{\prime }(\mathbf{C})$
inducing an embedding
$\unicode[STIX]{x1D712}^{\prime }\in \mathscr{Y}_{M(\unicode[STIX]{x1D6FC})}^{\prime }(\mathbf{C})$
inducing an embedding
 $\unicode[STIX]{x1D704}:M(\unicode[STIX]{x1D6FC}){\hookrightarrow}\mathbf{C}$
. Here
$\unicode[STIX]{x1D704}:M(\unicode[STIX]{x1D6FC}){\hookrightarrow}\mathbf{C}$
. Here
![]() $Z_{v}^{\circ }$
is as in Theorem A.
$Z_{v}^{\circ }$
is as in Theorem A.
Let
 $\mathscr{Y}^{\prime \circ }\subset \mathscr{Y}^{\prime }$
be any connected component,
$\mathscr{Y}^{\prime \circ }\subset \mathscr{Y}^{\prime }$
be any connected component,
 $\mathscr{Y}^{\circ }:=\mathscr{Y}\cap \mathscr{Y}^{\prime \circ }$
the corresponding connected component of
$\mathscr{Y}^{\circ }:=\mathscr{Y}\cap \mathscr{Y}^{\prime \circ }$
the corresponding connected component of
![]() $\mathscr{Y}$
, and let
$\mathscr{Y}$
, and let
![]() $\mathbf{B}$
be the quaternion algebra over
$\mathbf{B}$
be the quaternion algebra over
![]() $\mathbf{A}^{\infty }$
determined by (1.1.1) for any (equivalently, all) points
$\mathbf{A}^{\infty }$
determined by (1.1.1) for any (equivalently, all) points
![]() $\unicode[STIX]{x1D712}\in \mathscr{Y}^{\circ }$
. For any
$\unicode[STIX]{x1D712}\in \mathscr{Y}^{\circ }$
. For any
 $\unicode[STIX]{x1D711}^{p\infty }\in \unicode[STIX]{x1D70E}^{p\infty }$
and
$\unicode[STIX]{x1D711}^{p\infty }\in \unicode[STIX]{x1D70E}^{p\infty }$
and
 $\unicode[STIX]{x1D719}^{p\infty }\in \mathscr{S}(\mathbf{V}^{p\infty }\times \mathbf{A}^{p\infty ,\times })$
, we have
$\unicode[STIX]{x1D719}^{p\infty }\in \mathscr{S}(\mathbf{V}^{p\infty }\times \mathbf{A}^{p\infty ,\times })$
, we have
 $$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\mathscr{I}(\unicode[STIX]{x1D719}^{p\infty }))|_{\mathscr{ Y}^{\prime \circ }}=L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})|_{\mathscr{Y}^{\prime \circ }\times \unicode[STIX]{x1D6F9}_{p}}\mathop{\prod }_{v\nmid p\infty }\mathscr{R}_{v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v})|_{\mathscr{Y}^{\prime \circ }\times \unicode[STIX]{x1D6F9}_{p}}\end{eqnarray}$$
$$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\mathscr{I}(\unicode[STIX]{x1D719}^{p\infty }))|_{\mathscr{ Y}^{\prime \circ }}=L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})|_{\mathscr{Y}^{\prime \circ }\times \unicode[STIX]{x1D6F9}_{p}}\mathop{\prod }_{v\nmid p\infty }\mathscr{R}_{v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v})|_{\mathscr{Y}^{\prime \circ }\times \unicode[STIX]{x1D6F9}_{p}}\end{eqnarray}$$
in
 $\mathscr{O}_{\mathscr{Y}^{\prime }}(\mathscr{Y}^{\prime \circ })^{\text{b}}$
, where both
$\mathscr{O}_{\mathscr{Y}^{\prime }}(\mathscr{Y}^{\prime \circ })^{\text{b}}$
, where both
![]() $\mathscr{I}$
and
$\mathscr{I}$
and
![]() $\mathscr{R}^{\natural }$
are constructed using
$\mathscr{R}^{\natural }$
are constructed using
![]() $\mathbf{V}$
. On the right-hand side, the product
$\mathbf{V}$
. On the right-hand side, the product
 $\prod _{v\nmid p}\mathscr{R}_{v}^{\natural }$
makes sense over
$\prod _{v\nmid p}\mathscr{R}_{v}^{\natural }$
makes sense over
 $\mathscr{Y}^{\prime \circ }\times \unicode[STIX]{x1D6F9}_{p}$
by the decomposition
$\mathscr{Y}^{\prime \circ }\times \unicode[STIX]{x1D6F9}_{p}$
by the decomposition
 $\unicode[STIX]{x1D70E}\cong \mathscr{K}(\unicode[STIX]{x1D70E}^{p},\unicode[STIX]{x1D6F9}_{p})\otimes \mathscr{K}(\unicode[STIX]{x1D70E}_{p},\unicode[STIX]{x1D6F9}_{p})$
induced by the Whittaker functional fixed in the definition of
$\unicode[STIX]{x1D70E}\cong \mathscr{K}(\unicode[STIX]{x1D70E}^{p},\unicode[STIX]{x1D6F9}_{p})\otimes \mathscr{K}(\unicode[STIX]{x1D70E}_{p},\unicode[STIX]{x1D6F9}_{p})$
induced by the Whittaker functional fixed in the definition of
![]() $\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
.Footnote
24
$\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
.Footnote
24
Proof. The definition can be given locally by taking quotients in (3.7.1) for any given
 $(W^{p\infty },\unicode[STIX]{x1D719}^{p\infty })$
. Note that on the right-hand side of (3.7.1), the product is finite since by Lemma 3.5.2 we have
$(W^{p\infty },\unicode[STIX]{x1D719}^{p\infty })$
. Note that on the right-hand side of (3.7.1), the product is finite since by Lemma 3.5.2 we have
 $\mathscr{R}_{v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v})=1$
identically on
$\mathscr{R}_{v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v})=1$
identically on
![]() $\mathscr{Y}^{\prime }$
if all the data are unramified. The analytic properties of
$\mathscr{Y}^{\prime }$
if all the data are unramified. The analytic properties of
 $L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})$
are then a consequence of the following claim. Let
$L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})$
are then a consequence of the following claim. Let
![]() $S$
be any finite set of places
$S$
be any finite set of places
![]() $v\nmid p\infty$
, containing all the ones such that either
$v\nmid p\infty$
, containing all the ones such that either
![]() $\unicode[STIX]{x1D70E}_{v}$
is ramified or the subgroup
$\unicode[STIX]{x1D70E}_{v}$
is ramified or the subgroup
 $V_{v}\subset \mathscr{O}_{E,v}^{\times }$
fixed in the Introduction is not maximal. Let
$V_{v}\subset \mathscr{O}_{E,v}^{\times }$
fixed in the Introduction is not maximal. Let
![]() $\mathscr{Y}^{\prime \circ }$
be a connected component and
$\mathscr{Y}^{\prime \circ }$
be a connected component and
![]() $\mathbf{B}$
be the associated quaternion algebra. Then for each
$\mathbf{B}$
be the associated quaternion algebra. Then for each
![]() $v\in S$
, there exists a finite set of pairs
$v\in S$
, there exists a finite set of pairs
 $(W_{v},\unicode[STIX]{x1D719}_{v})$
such that the locus of common vanishing of the corresponding functions
$(W_{v},\unicode[STIX]{x1D719}_{v})$
such that the locus of common vanishing of the corresponding functions
 $\mathscr{R}_{v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v})|_{\mathscr{Y}^{\circ }}$
is empty.
$\mathscr{R}_{v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v})|_{\mathscr{Y}^{\circ }}$
is empty.
We prove the claim. Let
 $\unicode[STIX]{x1D712}_{v}\in \mathscr{Y}_{v}^{\circ }$
be any closed point, where
$\unicode[STIX]{x1D712}_{v}\in \mathscr{Y}_{v}^{\circ }$
be any closed point, where
![]() $v\in S$
and
$v\in S$
and
 $\mathscr{Y}_{v}^{\circ }\subset \mathscr{Y}_{v}$
is the union of connected components corresponding to
$\mathscr{Y}_{v}^{\circ }\subset \mathscr{Y}_{v}$
is the union of connected components corresponding to
![]() $\mathscr{Y}^{\circ }$
. By Lemma 5.1.1 below, we have
$\mathscr{Y}^{\circ }$
. By Lemma 5.1.1 below, we have
 $\mathscr{R}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v})=Q_{v}(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713},v}(W_{v},\unicode[STIX]{x1D719}_{v}),\unicode[STIX]{x1D712}_{v})$
, where
$\mathscr{R}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v})=Q_{v}(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713},v}(W_{v},\unicode[STIX]{x1D719}_{v}),\unicode[STIX]{x1D712}_{v})$
, where
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713},v}$
is a Shimizu lift sending
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713},v}$
is a Shimizu lift sending
 $\unicode[STIX]{x1D70E}_{v}\times \mathscr{S}(\mathbf{V}_{v}\times F^{\times })$
onto
$\unicode[STIX]{x1D70E}_{v}\times \mathscr{S}(\mathbf{V}_{v}\times F^{\times })$
onto
 $\unicode[STIX]{x1D70B}_{v}\otimes \unicode[STIX]{x1D70B}_{v}^{\vee }$
, with
$\unicode[STIX]{x1D70B}_{v}\otimes \unicode[STIX]{x1D70B}_{v}^{\vee }$
, with
![]() $\unicode[STIX]{x1D70B}_{v}$
the Jacquet–Langlands transfer of
$\unicode[STIX]{x1D70B}_{v}$
the Jacquet–Langlands transfer of
![]() $\unicode[STIX]{x1D70E}_{v}$
to
$\unicode[STIX]{x1D70E}_{v}$
to
![]() $\mathbf{B}_{v}^{\times }$
. By construction of
$\mathbf{B}_{v}^{\times }$
. By construction of
![]() $\mathbf{B}_{v}$
and the result mentioned in § 1.1, the functional
$\mathbf{B}_{v}$
and the result mentioned in § 1.1, the functional
 $Q_{v}(\cdot ,\unicode[STIX]{x1D712}_{v})$
is non-vanishing. Therefore, given
$Q_{v}(\cdot ,\unicode[STIX]{x1D712}_{v})$
is non-vanishing. Therefore, given
 $\unicode[STIX]{x1D712}_{v}\in \mathscr{Y}_{v}^{\circ }$
, we can find
$\unicode[STIX]{x1D712}_{v}\in \mathscr{Y}_{v}^{\circ }$
, we can find
 $(W_{v},\unicode[STIX]{x1D719}_{v})$
such that
$(W_{v},\unicode[STIX]{x1D719}_{v})$
such that
 $\mathscr{R}_{v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v};\unicode[STIX]{x1D712}_{v})\neq 0$
.
$\mathscr{R}_{v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v};\unicode[STIX]{x1D712}_{v})\neq 0$
.
Consider the set of all functions
 $\mathscr{R}_{v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v})|_{\mathscr{Y}_{v}^{\circ }}$
for varying
$\mathscr{R}_{v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v})|_{\mathscr{Y}_{v}^{\circ }}$
for varying
 $(W_{v},\unicode[STIX]{x1D719}_{v})$
. As the locus of their common vanishing is empty, it follows by the Nullstellensatz that finitely many of them generate the unit ideal of
$(W_{v},\unicode[STIX]{x1D719}_{v})$
. As the locus of their common vanishing is empty, it follows by the Nullstellensatz that finitely many of them generate the unit ideal of
![]() $\mathscr{O}(\mathscr{Y}_{v}^{\circ })$
.Footnote
25
This completes the proof of the claim.
$\mathscr{O}(\mathscr{Y}_{v}^{\circ })$
.Footnote
25
This completes the proof of the claim.
We now move to the interpolation property. The algebraicity on
![]() $\mathscr{Y}_{M(\unicode[STIX]{x1D6FC})}^{\prime \,\text{l.c.}}$
is clear from the definition just given. By
$\mathscr{Y}_{M(\unicode[STIX]{x1D6FC})}^{\prime \,\text{l.c.}}$
is clear from the definition just given. By
![]() $\unicode[STIX]{x1D704}$
, which we will omit from the notation below, we can identify
$\unicode[STIX]{x1D704}$
, which we will omit from the notation below, we can identify
![]() $\unicode[STIX]{x1D711}$
with an antiholomorphic automorphic form
$\unicode[STIX]{x1D711}$
with an antiholomorphic automorphic form
![]() $\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D704}}$
. By the definitions and Proposition 3.5.3, we have
$\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D704}}$
. By the definitions and Proposition 3.5.3, we have
 $$\begin{eqnarray}\displaystyle L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})(\unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D713}_{p}) & = & \displaystyle \frac{\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\mathscr{I}(\unicode[STIX]{x1D719}^{p},\unicode[STIX]{x1D712}^{\prime }))}{\mathop{\prod }_{v\nmid p\infty }\mathscr{R}_{v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v};\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v})}\nonumber\\ \displaystyle & = & \displaystyle \frac{|D_{F}|^{1/2}\unicode[STIX]{x1D701}_{F}(2)}{2L(1,\unicode[STIX]{x1D70E},\operatorname{ad})}\cdot \frac{|D_{E}|^{1/2}|D_{F}|\unicode[STIX]{x1D6FC}^{-r}(\unicode[STIX]{x1D711},w_{r}^{-1}I(\unicode[STIX]{x1D719},\unicode[STIX]{x1D712}^{\prime }))}{\mathop{\prod }_{v\nmid p\infty }R_{v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D713}_{v})}\nonumber\\ \displaystyle & = & \displaystyle \frac{|D_{F}|^{1/2}\unicode[STIX]{x1D701}_{F}(2)}{2L(1,\unicode[STIX]{x1D70E},\operatorname{ad})}\cdot \frac{L^{(\infty )}(1/2,\unicode[STIX]{x1D70E}_{E},\unicode[STIX]{x1D712}^{\prime })}{\unicode[STIX]{x1D701}_{F}^{(\infty )}(2)L^{(\infty )}(1,\unicode[STIX]{x1D702})}\mathop{\prod }_{v|\infty }R_{v}^{\circ }(\unicode[STIX]{x1D719}_{v},W_{v},\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v})\mathop{\prod }_{v|p}R_{r,v}^{\natural }(\unicode[STIX]{x1D719}_{v},W_{v},\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v})\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D701}_{F,\infty }(2)}{2^{[F:\mathbf{Q}]}L(1,\unicode[STIX]{x1D70E}_{\infty },\operatorname{ad})}\cdot \frac{|D_{F}|^{1/2}L^{(\infty )}(1/2,\unicode[STIX]{x1D70E}_{E},\unicode[STIX]{x1D712}^{\prime })}{2L^{(\infty )}(1,\unicode[STIX]{x1D702})L^{(\infty )}(1,\unicode[STIX]{x1D70E},\operatorname{ad})}\mathop{\prod }_{v|p}R_{r,v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})(\unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D713}_{p}) & = & \displaystyle \frac{\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\mathscr{I}(\unicode[STIX]{x1D719}^{p},\unicode[STIX]{x1D712}^{\prime }))}{\mathop{\prod }_{v\nmid p\infty }\mathscr{R}_{v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v};\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v})}\nonumber\\ \displaystyle & = & \displaystyle \frac{|D_{F}|^{1/2}\unicode[STIX]{x1D701}_{F}(2)}{2L(1,\unicode[STIX]{x1D70E},\operatorname{ad})}\cdot \frac{|D_{E}|^{1/2}|D_{F}|\unicode[STIX]{x1D6FC}^{-r}(\unicode[STIX]{x1D711},w_{r}^{-1}I(\unicode[STIX]{x1D719},\unicode[STIX]{x1D712}^{\prime }))}{\mathop{\prod }_{v\nmid p\infty }R_{v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D713}_{v})}\nonumber\\ \displaystyle & = & \displaystyle \frac{|D_{F}|^{1/2}\unicode[STIX]{x1D701}_{F}(2)}{2L(1,\unicode[STIX]{x1D70E},\operatorname{ad})}\cdot \frac{L^{(\infty )}(1/2,\unicode[STIX]{x1D70E}_{E},\unicode[STIX]{x1D712}^{\prime })}{\unicode[STIX]{x1D701}_{F}^{(\infty )}(2)L^{(\infty )}(1,\unicode[STIX]{x1D702})}\mathop{\prod }_{v|\infty }R_{v}^{\circ }(\unicode[STIX]{x1D719}_{v},W_{v},\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v})\mathop{\prod }_{v|p}R_{r,v}^{\natural }(\unicode[STIX]{x1D719}_{v},W_{v},\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v})\nonumber\\ \displaystyle & = & \displaystyle \frac{\unicode[STIX]{x1D701}_{F,\infty }(2)}{2^{[F:\mathbf{Q}]}L(1,\unicode[STIX]{x1D70E}_{\infty },\operatorname{ad})}\cdot \frac{|D_{F}|^{1/2}L^{(\infty )}(1/2,\unicode[STIX]{x1D70E}_{E},\unicode[STIX]{x1D712}^{\prime })}{2L^{(\infty )}(1,\unicode[STIX]{x1D702})L^{(\infty )}(1,\unicode[STIX]{x1D70E},\operatorname{ad})}\mathop{\prod }_{v|p}R_{r,v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime },\unicode[STIX]{x1D713}_{v}).\nonumber\end{eqnarray}$$
Here
![]() $\unicode[STIX]{x1D713}^{p}$
is any additive character such that
$\unicode[STIX]{x1D713}^{p}$
is any additive character such that
 $\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}^{p}\unicode[STIX]{x1D713}_{p}\unicode[STIX]{x1D713}_{\infty }$
vanishes on
$\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}^{p}\unicode[STIX]{x1D713}_{p}\unicode[STIX]{x1D713}_{\infty }$
vanishes on
![]() $F$
. For
$F$
. For
![]() $v|\infty$
, we have
$v|\infty$
, we have
 $\unicode[STIX]{x1D701}_{F,v}(2)/L(1,\unicode[STIX]{x1D70E}_{v},\operatorname{ad})=\unicode[STIX]{x1D70B}^{-1}/(\unicode[STIX]{x1D70B}^{-3}/2)=2\unicode[STIX]{x1D70B}^{2}$
, so that the first fraction in the last line equals
$\unicode[STIX]{x1D701}_{F,v}(2)/L(1,\unicode[STIX]{x1D70E}_{v},\operatorname{ad})=\unicode[STIX]{x1D70B}^{-1}/(\unicode[STIX]{x1D70B}^{-3}/2)=2\unicode[STIX]{x1D70B}^{2}$
, so that the first fraction in the last line equals
![]() $\unicode[STIX]{x1D70B}^{2[F:\mathbf{Q}]}$
. The result follows.
$\unicode[STIX]{x1D70B}^{2[F:\mathbf{Q}]}$
. The result follows.
The proof is completed by the identification
 $R_{r,v}^{\natural }=Z_{v}^{\circ }$
for
$R_{r,v}^{\natural }=Z_{v}^{\circ }$
for
![]() $v|p$
carried out in Proposition A.2.2.◻
$v|p$
carried out in Proposition A.2.2.◻
4
 $p$
-adic heights
$p$
-adic heights
We recall the definition and properties of
![]() $p$
-adic heights and prove two integrality criteria for them. The material of §§ 4.2–4.3 will not be used until §§ 8–9.
$p$
-adic heights and prove two integrality criteria for them. The material of §§ 4.2–4.3 will not be used until §§ 8–9.
For background in
![]() $p$
-adic Hodge theory, see the summary in [Reference NekovářNek93, §1] and references therein. The notation we use is completely standard; it coincides with that of [Reference NekovářNek93] except that we shall prefer to write
$p$
-adic Hodge theory, see the summary in [Reference NekovářNek93, §1] and references therein. The notation we use is completely standard; it coincides with that of [Reference NekovářNek93] except that we shall prefer to write
![]() $\mathbf{D}_{\text{dR}}$
instead of
$\mathbf{D}_{\text{dR}}$
instead of
![]() $DR$
for the functor of de Rham periods.
$DR$
for the functor of de Rham periods.
4.1 Local and global height pairings
Let
![]() $F$
be a number field and
$F$
be a number field and
 $\mathscr{G}_{F}:=\operatorname{Gal}(\overline{F}/F)$
. Let
$\mathscr{G}_{F}:=\operatorname{Gal}(\overline{F}/F)$
. Let
![]() $L$
be a finite extension of
$L$
be a finite extension of
![]() $\mathbf{Q}_{p}$
, and let
$\mathbf{Q}_{p}$
, and let
![]() $V$
be a finite-dimensional
$V$
be a finite-dimensional
![]() $L$
-vector space with a continuous action of
$L$
-vector space with a continuous action of
![]() $\mathscr{G}_{F}$
. For each place
$\mathscr{G}_{F}$
. For each place
![]() $v$
of
$v$
of
![]() $F$
, we denote by
$F$
, we denote by
![]() $V_{v}$
the space
$V_{v}$
the space
![]() $V$
considered as a representation of
$V$
considered as a representation of
 $\mathscr{G}_{F,v}:=\operatorname{Gal}(\overline{F}_{v}/F_{v})$
.
$\mathscr{G}_{F,v}:=\operatorname{Gal}(\overline{F}_{v}/F_{v})$
.
Recall that the Bloch–Kato Selmer group of
![]() $V$
$V$
 $$\begin{eqnarray}H_{f}^{1}(F,V)\end{eqnarray}$$
$$\begin{eqnarray}H_{f}^{1}(F,V)\end{eqnarray}$$
is the subset of
 $H^{1}(F,V)=\operatorname{Ext}_{F}^{1}(L,V)$
(extensions in the category of continuous
$H^{1}(F,V)=\operatorname{Ext}_{F}^{1}(L,V)$
(extensions in the category of continuous
![]() $\mathscr{G}_{F}$
-representations over
$\mathscr{G}_{F}$
-representations over
![]() $L$
) consisting of the classes of those extensions
$L$
) consisting of the classes of those extensions
 $0\rightarrow V\rightarrow E_{1}\rightarrow L\rightarrow 0$
which are unramified at all
$0\rightarrow V\rightarrow E_{1}\rightarrow L\rightarrow 0$
which are unramified at all
![]() $v\nmid p$
and crystalline at all
$v\nmid p$
and crystalline at all
![]() $v|p$
(that is, such that
$v|p$
(that is, such that
![]() $E_{1}$
is).
$E_{1}$
is).
Suppose that:
-
–
 $V$
is unramified outside of a finite set of primes of
$V$
is unramified outside of a finite set of primes of
 $F$
;
$F$
; -
–
 $V_{v}$
is de Rham, and hence potentially semistable, for all
$V_{v}$
is de Rham, and hence potentially semistable, for all
 $v|p$
;
$v|p$
; -
–
 $H^{0}(F_{v},V)=H^{0}(F_{v},V^{\ast }(1))=0$
for all
$H^{0}(F_{v},V)=H^{0}(F_{v},V^{\ast }(1))=0$
for all
 $v\nmid p$
;
$v\nmid p$
; -
–
 $\mathbf{D}_{\text{crys}}(V_{v})^{\unicode[STIX]{x1D711}=1}=\mathbf{D}_{\text{crys}}(V_{v})^{\unicode[STIX]{x1D711}=1}=0$
for all
$\mathbf{D}_{\text{crys}}(V_{v})^{\unicode[STIX]{x1D711}=1}=\mathbf{D}_{\text{crys}}(V_{v})^{\unicode[STIX]{x1D711}=1}=0$
for all
 $v|p$
(where
$v|p$
(where
 $\unicode[STIX]{x1D711}$
denotes the crystalline Frobenius).
$\unicode[STIX]{x1D711}$
denotes the crystalline Frobenius).
Under those conditions, Nekovář [Reference NekovářNek93] (to which we refer for more details; see also [Reference NekovářNek06]) constructed a bilinear pairing on the Bloch–Kato Selmer groups
 $$\begin{eqnarray}\langle \,,\rangle :H_{f}^{1}(F,V)\times H_{f}^{1}(F,V^{\ast }(1))\rightarrow \unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L\end{eqnarray}$$
$$\begin{eqnarray}\langle \,,\rangle :H_{f}^{1}(F,V)\times H_{f}^{1}(F,V^{\ast }(1))\rightarrow \unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L\end{eqnarray}$$
depending on choices of
![]() $L$
-linear splittings of the Hodge filtration
$L$
-linear splittings of the Hodge filtration
 $$\begin{eqnarray}\text{Fil}^{0}\mathbf{D}_{\text{dR}}(V_{v})\subset \mathbf{D}_{\text{dR}}(V_{v})\end{eqnarray}$$
$$\begin{eqnarray}\text{Fil}^{0}\mathbf{D}_{\text{dR}}(V_{v})\subset \mathbf{D}_{\text{dR}}(V_{v})\end{eqnarray}$$
for the primes
![]() $v|p$
. In fact in [Reference NekovářNek93] it is assumed that
$v|p$
. In fact in [Reference NekovářNek93] it is assumed that
![]() $V_{v}$
is semistable; we will recall the definitions under this assumption, and at the same time see that they can be made compatible with extending the ground field (in particular, to reduce the potentially semistable case to the semistable case). Compare also [Reference BenoisBen14] for a very general treatment.
$V_{v}$
is semistable; we will recall the definitions under this assumption, and at the same time see that they can be made compatible with extending the ground field (in particular, to reduce the potentially semistable case to the semistable case). Compare also [Reference BenoisBen14] for a very general treatment.
Post-composing
![]() $\langle \,,\rangle$
with a continuous homomorphism
$\langle \,,\rangle$
with a continuous homomorphism
 $\ell :\unicode[STIX]{x1D6E4}_{F}\rightarrow L^{\prime }$
, for some
$\ell :\unicode[STIX]{x1D6E4}_{F}\rightarrow L^{\prime }$
, for some
![]() $L$
-vector space
$L$
-vector space
![]() $L^{\prime }$
, yields an
$L^{\prime }$
, yields an
![]() $L^{\prime }$
-valued pairing
$L^{\prime }$
-valued pairing
![]() $\langle \,,\rangle _{\ell }$
(the cases of interest to us are
$\langle \,,\rangle _{\ell }$
(the cases of interest to us are
![]() $L^{\prime }=L$
with any
$L^{\prime }=L$
with any
![]() $\ell$
, or
$\ell$
, or
 $L^{\prime }=\unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L$
with the tautological
$L^{\prime }=\unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L$
with the tautological
![]() $\ell$
). For such an
$\ell$
). For such an
![]() $\ell$
we write
$\ell$
we write
 $\ell _{v}:=\ell |_{F_{v}^{\times }}$
and we say that
$\ell _{v}:=\ell |_{F_{v}^{\times }}$
and we say that
![]() $\ell _{v}$
is unramified if it is trivial on
$\ell _{v}$
is unramified if it is trivial on
![]() $\mathscr{O}_{F,v}^{\times }$
(note that this is automatic if
$\mathscr{O}_{F,v}^{\times }$
(note that this is automatic if
![]() $v\nmid p$
).
$v\nmid p$
).
Let
 $x_{1}\in H_{f}^{1}(F,V)$
,
$x_{1}\in H_{f}^{1}(F,V)$
,
 $x_{2}\in H_{f}^{1}(F,V^{\ast }(1))$
and view them as classes
$x_{2}\in H_{f}^{1}(F,V^{\ast }(1))$
and view them as classes
 $x_{1}=e_{1}=[E_{1}]$
,
$x_{1}=e_{1}=[E_{1}]$
,
 $x_{2}=e_{2}=[E_{2}]$
of extensions of Galois representations
$x_{2}=e_{2}=[E_{2}]$
of extensions of Galois representations
 $$\begin{eqnarray}\displaystyle e_{1}:\quad 0 & \rightarrow & \displaystyle V\rightarrow E_{1}\rightarrow L\rightarrow 0,\nonumber\\ \displaystyle e_{2}:\quad 0 & \rightarrow & \displaystyle V^{\ast }(1)\rightarrow E_{2}\rightarrow L\rightarrow 0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle e_{1}:\quad 0 & \rightarrow & \displaystyle V\rightarrow E_{1}\rightarrow L\rightarrow 0,\nonumber\\ \displaystyle e_{2}:\quad 0 & \rightarrow & \displaystyle V^{\ast }(1)\rightarrow E_{2}\rightarrow L\rightarrow 0.\nonumber\end{eqnarray}$$
For any
![]() $e_{1}$
,
$e_{1}$
,
![]() $e_{2}$
as above, the set of Galois representations
$e_{2}$
as above, the set of Galois representations
![]() $E$
fitting into a commutative diagram
$E$
fitting into a commutative diagram

is an
 $H^{1}(F,L)$
-torsor [Reference NekovářNek93, Proposition 4.4]; any such
$H^{1}(F,L)$
-torsor [Reference NekovářNek93, Proposition 4.4]; any such
![]() $E$
is called a mixed extension of
$E$
is called a mixed extension of
![]() $e_{1}$
,
$e_{1}$
,
![]() $e_{2}^{\ast }(1)$
. Depending on the choice of (extensions
$e_{2}^{\ast }(1)$
. Depending on the choice of (extensions
![]() $e_{1}$
and
$e_{1}$
and
![]() $e_{2}$
and) a mixed extension
$e_{2}$
and) a mixed extension
![]() $E$
, there is a decomposition
$E$
, there is a decomposition
 $$\begin{eqnarray}\langle x_{1},x_{2}\rangle _{\ell }=\mathop{\sum }_{v\in S_{F}}\langle x_{1,v},x_{2,v}\rangle _{\ell _{v},E,v}\end{eqnarray}$$
$$\begin{eqnarray}\langle x_{1},x_{2}\rangle _{\ell }=\mathop{\sum }_{v\in S_{F}}\langle x_{1,v},x_{2,v}\rangle _{\ell _{v},E,v}\end{eqnarray}$$
of the height pairing into a (convergent) sum of local symbols indexed by the non-archimedean places of
![]() $F$
. We recall the definition of the latter [Reference NekovářNek93, §7.4]. The representation
$F$
. We recall the definition of the latter [Reference NekovářNek93, §7.4]. The representation
![]() $E$
can be shown to be automatically semistable at any
$E$
can be shown to be automatically semistable at any
![]() $v|p$
; for each
$v|p$
; for each
![]() $v$
it then yields a class
$v$
it then yields a class
 $[E_{v}]\in H_{\ast }^{1}(F_{v},E_{2})$
with
$[E_{v}]\in H_{\ast }^{1}(F_{v},E_{2})$
with
![]() $\ast =\emptyset$
if
$\ast =\emptyset$
if
![]() $v\nmid p$
,
$v\nmid p$
,
![]() $\ast =\text{st}$
if
$\ast =\text{st}$
if
![]() $v|p$
. This group sits in the following diagram of exact sequences.
$v|p$
. This group sits in the following diagram of exact sequences.

If
![]() $v|p$
, the chosen splitting of (4.1.2) uniquely determines a splitting
$v|p$
, the chosen splitting of (4.1.2) uniquely determines a splitting
 $s_{v}:H_{\ast }^{1}(F_{v},E_{2})\rightarrow$
$s_{v}:H_{\ast }^{1}(F_{v},E_{2})\rightarrow$
 $H^{1}(F_{v},L(1))$
; if
$H^{1}(F_{v},L(1))$
; if
![]() $v\nmid p$
, there is a canonical splitting independent of choices, also denoted by
$v\nmid p$
, there is a canonical splitting independent of choices, also denoted by
![]() $s_{v}$
. In both cases, the local symbol is
$s_{v}$
. In both cases, the local symbol is
 $$\begin{eqnarray}\langle x_{1,v},x_{2,v}\rangle _{\ell _{v},E,v}:=-\ell _{v}(s_{v}([E_{v}])),\end{eqnarray}$$
$$\begin{eqnarray}\langle x_{1,v},x_{2,v}\rangle _{\ell _{v},E,v}:=-\ell _{v}(s_{v}([E_{v}])),\end{eqnarray}$$
where we still denote by
![]() $\ell _{v}$
the composition
$\ell _{v}$
the composition
 $H^{1}(F_{v},L(1))\cong F_{v}^{\times }\,\hat{\otimes }\,L\rightarrow \unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L\rightarrow L^{\prime }$
. When
$H^{1}(F_{v},L(1))\cong F_{v}^{\times }\,\hat{\otimes }\,L\rightarrow \unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L\rightarrow L^{\prime }$
. When
![]() $v|p$
, we say that
$v|p$
, we say that
![]() $[E_{v}]$
is essentially crystalline if
$[E_{v}]$
is essentially crystalline if
 $[E_{v}]\in H_{f}^{1}(F_{v},E_{2})\subset H_{\text{st}}^{1}(F_{v},E_{2})$
; equivalently,
$[E_{v}]\in H_{f}^{1}(F_{v},E_{2})\subset H_{\text{st}}^{1}(F_{v},E_{2})$
; equivalently,
 $s_{v}([E_{v}])\in H_{f}^{1}(F_{v},L(1))$
.
$s_{v}([E_{v}])\in H_{f}^{1}(F_{v},L(1))$
.
Behaviour under field extensions. If
![]() $F_{w}^{\prime }/F_{v}$
is a finite extension of local non-archimedean fields, the pairing
$F_{w}^{\prime }/F_{v}$
is a finite extension of local non-archimedean fields, the pairing
 $$\begin{eqnarray}\langle \,,\rangle _{\ell _{v}\circ N_{F_{w}/F_{v}}}:H_{f}^{1}(F_{w}^{\prime },V_{w})\times H_{f}^{1}(F_{w}^{\prime },V_{w}^{\ast }(1))\rightarrow L^{\prime }\end{eqnarray}$$
$$\begin{eqnarray}\langle \,,\rangle _{\ell _{v}\circ N_{F_{w}/F_{v}}}:H_{f}^{1}(F_{w}^{\prime },V_{w})\times H_{f}^{1}(F_{w}^{\prime },V_{w}^{\ast }(1))\rightarrow L^{\prime }\end{eqnarray}$$
defined using the induced Hodge splittings and the map
 $\ell _{w}:=\ell _{v}\circ N_{F_{w}/F_{v}}$
satisfies
$\ell _{w}:=\ell _{v}\circ N_{F_{w}/F_{v}}$
satisfies
 $$\begin{eqnarray}\langle \text{cores}_{F_{v}}^{F_{w}^{\prime }}x_{1},x_{2}\rangle _{\ell _{v}}=\langle x_{1},\text{res}_{F_{v}}^{F_{w}^{\prime }}x_{2}\rangle _{\ell _{v}\circ N_{F_{w}/F_{v}}}\end{eqnarray}$$
$$\begin{eqnarray}\langle \text{cores}_{F_{v}}^{F_{w}^{\prime }}x_{1},x_{2}\rangle _{\ell _{v}}=\langle x_{1},\text{res}_{F_{v}}^{F_{w}^{\prime }}x_{2}\rangle _{\ell _{v}\circ N_{F_{w}/F_{v}}}\end{eqnarray}$$
for all
 $x_{1}\in H_{f}^{1}(F_{v},V_{v})$
,
$x_{1}\in H_{f}^{1}(F_{v},V_{v})$
,
 $x_{2}\in H_{f}^{1}(F_{w}^{\prime },V|_{\mathscr{G}_{F_{w}^{\prime }}}^{\ast }(1))$
.
$x_{2}\in H_{f}^{1}(F_{w}^{\prime },V|_{\mathscr{G}_{F_{w}^{\prime }}}^{\ast }(1))$
.
Back to the global situation, it follows that extending any
 $\ell :\unicode[STIX]{x1D6E4}_{F}\rightarrow L^{\prime }$
to the direct system
$\ell :\unicode[STIX]{x1D6E4}_{F}\rightarrow L^{\prime }$
to the direct system
 $(\unicode[STIX]{x1D6E4}_{F^{\prime }})_{F^{\prime }/F\text{ finite}}$
by
$(\unicode[STIX]{x1D6E4}_{F^{\prime }})_{F^{\prime }/F\text{ finite}}$
by
 $$\begin{eqnarray}\ell _{w}=\ell |_{F_{w}^{\prime \times }}:=\frac{1}{[F^{\prime }:F]}\ell _{v}\circ N_{F_{w}^{\prime }/F_{v}}\end{eqnarray}$$
$$\begin{eqnarray}\ell _{w}=\ell |_{F_{w}^{\prime \times }}:=\frac{1}{[F^{\prime }:F]}\ell _{v}\circ N_{F_{w}^{\prime }/F_{v}}\end{eqnarray}$$
we can extend
![]() $\langle \,,\rangle _{\ell }$
to a pairing
$\langle \,,\rangle _{\ell }$
to a pairing
 $$\begin{eqnarray}\langle \,,\rangle _{\ell }:\mathop{\varinjlim }\nolimits_{F^{\prime }}H_{f}^{1}(F^{\prime },V|_{\mathscr{ G}_{F^{\prime }}})\times H_{f}^{1}(F^{\prime },V|_{\mathscr{ G}_{F^{\prime }}}^{\ast }(1))\rightarrow L^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}\langle \,,\rangle _{\ell }:\mathop{\varinjlim }\nolimits_{F^{\prime }}H_{f}^{1}(F^{\prime },V|_{\mathscr{ G}_{F^{\prime }}})\times H_{f}^{1}(F^{\prime },V|_{\mathscr{ G}_{F^{\prime }}}^{\ast }(1))\rightarrow L^{\prime },\end{eqnarray}$$
where the limit is taken with respect to restriction maps. This allows us to define the pairing in the potentially semistable case as well.
Ordinariness. Let
![]() $v|p$
be a place of
$v|p$
be a place of
![]() $F$
.
$F$
.
Definition 4.1.1. We say that a de Rham representation
![]() $V_{v}$
of
$V_{v}$
of
![]() $\mathscr{G}_{F_{v}}$
satisfies the Panchishkin condition or that it is potentially ordinary if there is a (necessarily unique) exact sequence of de Rham
$\mathscr{G}_{F_{v}}$
satisfies the Panchishkin condition or that it is potentially ordinary if there is a (necessarily unique) exact sequence of de Rham
![]() $\mathscr{G}_{F_{v}}$
-representations
$\mathscr{G}_{F_{v}}$
-representations
 $$\begin{eqnarray}0\rightarrow V_{v}^{+}\rightarrow V_{v}\rightarrow V_{v}^{-}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow V_{v}^{+}\rightarrow V_{v}\rightarrow V_{v}^{-}\rightarrow 0\end{eqnarray}$$
with
 $\text{Fil}^{0}\mathbf{D}_{\text{dR}}(V_{v}^{+})=\mathbf{D}_{\text{dR}}(V_{v}^{-})/\text{Fil}^{0}=0$
.
$\text{Fil}^{0}\mathbf{D}_{\text{dR}}(V_{v}^{+})=\mathbf{D}_{\text{dR}}(V_{v}^{-})/\text{Fil}^{0}=0$
.
If
![]() $V_{v}$
is potentially ordinary, there is a canonical splitting of (4.1.2) given by
$V_{v}$
is potentially ordinary, there is a canonical splitting of (4.1.2) given by
 $$\begin{eqnarray}\mathbf{D}_{\text{dR}}(V_{v})\rightarrow \mathbf{D}_{\text{dR}}(V_{v}^{-})=\text{Fil}^{0}\mathbf{D}_{\text{dR}}(V_{v}).\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{D}_{\text{dR}}(V_{v})\rightarrow \mathbf{D}_{\text{dR}}(V_{v}^{-})=\text{Fil}^{0}\mathbf{D}_{\text{dR}}(V_{v}).\end{eqnarray}$$
Abelian varieties. If
![]() $A/F$
is an abelian variety with potentially semistable reduction at all
$A/F$
is an abelian variety with potentially semistable reduction at all
![]() $v|p$
, then the rational Tate module
$v|p$
, then the rational Tate module
 $V=V_{p}A$
satisfies the required assumptions, and there is a canonical isomorphism
$V=V_{p}A$
satisfies the required assumptions, and there is a canonical isomorphism
 $V^{\ast }(1)\cong V_{p}A^{\vee }$
. Suppose that there is an embedding of a number field
$V^{\ast }(1)\cong V_{p}A^{\vee }$
. Suppose that there is an embedding of a number field
 $M{\hookrightarrow}\operatorname{End}^{0}(A)$
; its action on
$M{\hookrightarrow}\operatorname{End}^{0}(A)$
; its action on
![]() $V$
induces a decomposition
$V$
induces a decomposition
 $V=\bigoplus _{\mathfrak{p}|p}V_{\mathfrak{p}}$
indexed by the primes of
$V=\bigoplus _{\mathfrak{p}|p}V_{\mathfrak{p}}$
indexed by the primes of
![]() $\mathscr{O}_{M}$
above
$\mathscr{O}_{M}$
above
![]() $p$
. Given such a prime
$p$
. Given such a prime
![]() $\mathfrak{p}$
, a finite extension
$\mathfrak{p}$
, a finite extension
![]() $L$
of
$L$
of
![]() $M_{\mathfrak{p}}$
, and splittings of the Hodge filtration on
$M_{\mathfrak{p}}$
, and splittings of the Hodge filtration on
 $\mathbf{D}_{\text{dR}}(V_{\mathfrak{p}}|_{\mathscr{G}_{F_{v}}})\otimes _{M_{\mathfrak{p}}}L$
for
$\mathbf{D}_{\text{dR}}(V_{\mathfrak{p}}|_{\mathscr{G}_{F_{v}}})\otimes _{M_{\mathfrak{p}}}L$
for
![]() $v|p$
, we obtain from the compatible pairings (4.1.8) a height pairing
$v|p$
, we obtain from the compatible pairings (4.1.8) a height pairing
 $$\begin{eqnarray}\langle \,,\rangle :A(\overline{F})\times A^{\vee }(\overline{F})\rightarrow \unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L\end{eqnarray}$$
$$\begin{eqnarray}\langle \,,\rangle :A(\overline{F})\times A^{\vee }(\overline{F})\rightarrow \unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L\end{eqnarray}$$
via the Kummer maps
 $\unicode[STIX]{x1D718}_{A,F^{\prime },\mathfrak{p}}:A(F^{\prime })\rightarrow H_{f}^{1}(F^{\prime },V)\rightarrow H_{f}^{1}(F^{\prime },V_{\mathfrak{p}})$
and
$\unicode[STIX]{x1D718}_{A,F^{\prime },\mathfrak{p}}:A(F^{\prime })\rightarrow H_{f}^{1}(F^{\prime },V)\rightarrow H_{f}^{1}(F^{\prime },V_{\mathfrak{p}})$
and
 $\unicode[STIX]{x1D718}_{A^{\vee },F^{\prime },\mathfrak{p}}:A(F^{\prime })\rightarrow H_{f}^{1}(F^{\prime },V_{\mathfrak{p}}^{\ast }(1))$
for any
$\unicode[STIX]{x1D718}_{A^{\vee },F^{\prime },\mathfrak{p}}:A(F^{\prime })\rightarrow H_{f}^{1}(F^{\prime },V_{\mathfrak{p}}^{\ast }(1))$
for any
 $F\subset F^{\prime }\subset \overline{F}$
.
$F\subset F^{\prime }\subset \overline{F}$
.
If
![]() $\mathfrak{p}$
is a prime of
$\mathfrak{p}$
is a prime of
![]() $M$
above
$M$
above
![]() $p$
and
$p$
and
 $V_{\mathfrak{p}}A\otimes L$
is potentially ordinary for all
$V_{\mathfrak{p}}A\otimes L$
is potentially ordinary for all
![]() $v|p$
, the height pairing (4.1.10) is then canonical (cf. [Reference NekovářNek06, §11.3]). Such is the situation of Theorem B. In that case we consider the restriction of (4.1.10) to
$v|p$
, the height pairing (4.1.10) is then canonical (cf. [Reference NekovářNek06, §11.3]). Such is the situation of Theorem B. In that case we consider the restriction of (4.1.10) to
![]() $A(\unicode[STIX]{x1D712})$
, coming from the Kummer maps
$A(\unicode[STIX]{x1D712})$
, coming from the Kummer maps
 $$\begin{eqnarray}\unicode[STIX]{x1D718}_{A(\unicode[STIX]{x1D712})}:A(\unicode[STIX]{x1D712})\rightarrow H_{f}^{1}(E,V_{\mathfrak{ p}}A(\unicode[STIX]{x1D712})),\quad \unicode[STIX]{x1D718}_{A^{\vee }(\unicode[STIX]{x1D712}^{-1})}:A^{\vee }(\unicode[STIX]{x1D712}^{-1})\rightarrow H_{f}^{1}(E,(V_{\mathfrak{ p}}A(\unicode[STIX]{x1D712})^{\ast })(1)),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D718}_{A(\unicode[STIX]{x1D712})}:A(\unicode[STIX]{x1D712})\rightarrow H_{f}^{1}(E,V_{\mathfrak{ p}}A(\unicode[STIX]{x1D712})),\quad \unicode[STIX]{x1D718}_{A^{\vee }(\unicode[STIX]{x1D712}^{-1})}:A^{\vee }(\unicode[STIX]{x1D712}^{-1})\rightarrow H_{f}^{1}(E,(V_{\mathfrak{ p}}A(\unicode[STIX]{x1D712})^{\ast })(1)),\end{eqnarray}$$
where
 $$\begin{eqnarray}V_{\mathfrak{p}}A(\unicode[STIX]{x1D712}):=V_{\mathfrak{p}}A|_{\mathscr{G}_{E}}\otimes L(\unicode[STIX]{x1D712})_{\unicode[STIX]{x1D712}}.\end{eqnarray}$$
$$\begin{eqnarray}V_{\mathfrak{p}}A(\unicode[STIX]{x1D712}):=V_{\mathfrak{p}}A|_{\mathscr{G}_{E}}\otimes L(\unicode[STIX]{x1D712})_{\unicode[STIX]{x1D712}}.\end{eqnarray}$$
Note that by the condition
 $\unicode[STIX]{x1D712}|_{\mathbf{A}^{\infty ,\times }}=\unicode[STIX]{x1D714}_{A}^{-1}$
, we have
$\unicode[STIX]{x1D712}|_{\mathbf{A}^{\infty ,\times }}=\unicode[STIX]{x1D714}_{A}^{-1}$
, we have
 $(V_{\mathfrak{p}}A(\unicode[STIX]{x1D712}))^{\ast }(1)\cong V_{\mathfrak{p}}A(\unicode[STIX]{x1D712})$
.
$(V_{\mathfrak{p}}A(\unicode[STIX]{x1D712}))^{\ast }(1)\cong V_{\mathfrak{p}}A(\unicode[STIX]{x1D712})$
.
4.2 Heights and intersections on curves
If
![]() $X/F$
is a (connected, smooth, proper) curve with semistable reduction at all
$X/F$
is a (connected, smooth, proper) curve with semistable reduction at all
![]() $v|p$
, let
$v|p$
, let
 $V:=H_{\acute{\text{e}}\text{t}}^{1}(X_{\overline{F}},\mathbf{Q}_{p}(1))$
. Then
$V:=H_{\acute{\text{e}}\text{t}}^{1}(X_{\overline{F}},\mathbf{Q}_{p}(1))$
. Then
![]() $V$
satisfies the relevant assumptions; moreover, it carries a non-degenerate symplectic form by Poincaré duality, inducing an isomorphism
$V$
satisfies the relevant assumptions; moreover, it carries a non-degenerate symplectic form by Poincaré duality, inducing an isomorphism
 $V\cong V^{\ast }(1)$
. For any finite extension
$V\cong V^{\ast }(1)$
. For any finite extension
![]() $L$
of
$L$
of
![]() $\mathbf{Q}_{p}$
, any Hodge splittings on
$\mathbf{Q}_{p}$
, any Hodge splittings on
 $(\mathbf{D}_{\text{dR}}(V_{v}\otimes L))_{v|p}$
, and any continuous homomorphism
$(\mathbf{D}_{\text{dR}}(V_{v}\otimes L))_{v|p}$
, and any continuous homomorphism
 $\ell :\unicode[STIX]{x1D6E4}_{F}\rightarrow L^{\prime }$
, we obtain a pairing
$\ell :\unicode[STIX]{x1D6E4}_{F}\rightarrow L^{\prime }$
, we obtain a pairing
 $$\begin{eqnarray}\langle \,,\rangle _{X,\ell }:\operatorname{Div}^{0}(X_{\overline{F}})\times \operatorname{Div}^{0}(X_{\overline{F}})\rightarrow L^{\prime }\end{eqnarray}$$
$$\begin{eqnarray}\langle \,,\rangle _{X,\ell }:\operatorname{Div}^{0}(X_{\overline{F}})\times \operatorname{Div}^{0}(X_{\overline{F}})\rightarrow L^{\prime }\end{eqnarray}$$
via the Kummer maps similarly to the above. The pairing factors through
 $\operatorname{Div}^{0}(X_{\overline{F}})\rightarrow J_{X}(\overline{F})$
, where
$\operatorname{Div}^{0}(X_{\overline{F}})\rightarrow J_{X}(\overline{F})$
, where
![]() $J_{X}$
is the Albanese variety; it corresponds to the height pairing on
$J_{X}$
is the Albanese variety; it corresponds to the height pairing on
 $J_{X}(\overline{F})\times J_{X}^{\vee }(\overline{F})$
via the canonical autoduality of
$J_{X}(\overline{F})\times J_{X}^{\vee }(\overline{F})$
via the canonical autoduality of
![]() $J_{X}$
.
$J_{X}$
.
The restriction of (4.2.1) to the set
 $(\operatorname{Div}^{0}(X_{\overline{F}})\times \operatorname{Div}^{0}(X_{\overline{F}}))^{\ast }$
of pairs of divisors with disjoint supports admits a canonical decomposition
$(\operatorname{Div}^{0}(X_{\overline{F}})\times \operatorname{Div}^{0}(X_{\overline{F}}))^{\ast }$
of pairs of divisors with disjoint supports admits a canonical decomposition
 $$\begin{eqnarray}\langle \,,\rangle _{X,\ell }=\mathop{\sum }_{w\in S_{F^{\prime }}}\langle \,,\rangle _{X,\ell _{w},w}.\end{eqnarray}$$
$$\begin{eqnarray}\langle \,,\rangle _{X,\ell }=\mathop{\sum }_{w\in S_{F^{\prime }}}\langle \,,\rangle _{X,\ell _{w},w}.\end{eqnarray}$$
Namely, the local symbols are continuous symmetric bi-additive maps given by
 $$\begin{eqnarray}\langle D_{1},D_{2}\rangle _{X,\ell _{w}}:=\langle x_{1},x_{2}\rangle _{\ell _{w},E,w},\end{eqnarray}$$
$$\begin{eqnarray}\langle D_{1},D_{2}\rangle _{X,\ell _{w}}:=\langle x_{1},x_{2}\rangle _{\ell _{w},E,w},\end{eqnarray}$$
where
![]() $x_{i}$
is the class of
$x_{i}$
is the class of
![]() $D_{i}$
in
$D_{i}$
in
 $H_{f}^{1}(F^{\prime },V)$
and, if
$H_{f}^{1}(F^{\prime },V)$
and, if
![]() $Z_{1}$
,
$Z_{1}$
,
 $Z_{2}\subset X_{\overline{F}}$
are disjoint proper closed subsets of
$Z_{2}\subset X_{\overline{F}}$
are disjoint proper closed subsets of
![]() $X_{\overline{F}}$
such that the support of
$X_{\overline{F}}$
such that the support of
![]() $D_{i}$
is contained in
$D_{i}$
is contained in
![]() $Z_{i}$
, then
$Z_{i}$
, then
![]() $E$
,
$E$
,
![]() $E_{1}$
,
$E_{1}$
,
![]() $E_{2}$
are the extensions obtained from the diagram of étale cohomology groups
$E_{2}$
are the extensions obtained from the diagram of étale cohomology groups

by pullback along
 $\text{cl}_{D_{1}}:L\rightarrow H_{Z_{1}}^{2}(X_{\overline{F}},L(1))$
and pushout along
$\text{cl}_{D_{1}}:L\rightarrow H_{Z_{1}}^{2}(X_{\overline{F}},L(1))$
and pushout along
 $-\operatorname{Tr}_{D_{2}}:H^{0}(Z_{2},L(1))\rightarrow L(1)$
.
$-\operatorname{Tr}_{D_{2}}:H^{0}(Z_{2},L(1))\rightarrow L(1)$
.
If
![]() $X$
does not have semistable reduction at the primes above
$X$
does not have semistable reduction at the primes above
![]() $p$
, we can still find a finite extension
$p$
, we can still find a finite extension
![]() $F^{\prime }/F$
such that
$F^{\prime }/F$
such that
![]() $X_{F^{\prime }}$
does, and define the pairing on
$X_{F^{\prime }}$
does, and define the pairing on
![]() $X_{F^{\prime }}$
. If
$X_{F^{\prime }}$
. If
 $X=\coprod _{i}X_{i}$
is a disjoint union of finitely many connected curves, then
$X=\coprod _{i}X_{i}$
is a disjoint union of finitely many connected curves, then
 $\operatorname{Div}^{0}(X_{\overline{F}})$
will denote the group of divisors having degree zero on each connected component; it affords local and global pairings by direct sum.
$\operatorname{Div}^{0}(X_{\overline{F}})$
will denote the group of divisors having degree zero on each connected component; it affords local and global pairings by direct sum.
A uniqueness principle. Suppose that
 $D_{1}=\operatorname{div}(h)$
is a principal divisor with support disjoint from the support of
$D_{1}=\operatorname{div}(h)$
is a principal divisor with support disjoint from the support of
![]() $D_{2}$
, and let
$D_{2}$
, and let
 $h(D_{2}):=\prod _{P}h(P)^{n_{P}}$
. Then the mixed extension
$h(D_{2}):=\prod _{P}h(P)^{n_{P}}$
. Then the mixed extension
 $[E_{w}]=[E_{D_{1},D_{2},w}]$
is the image of
$[E_{w}]=[E_{D_{1},D_{2},w}]$
is the image of
 $h(D_{2})\otimes 1\in F_{w}^{\prime \times }\,\hat{\otimes }\,L\cong H^{1}(F_{w}^{\prime },L(1))$
in
$h(D_{2})\otimes 1\in F_{w}^{\prime \times }\,\hat{\otimes }\,L\cong H^{1}(F_{w}^{\prime },L(1))$
in
 $H_{\ast }^{1}(F_{w}^{\prime },E_{2})$
under (4.1.4); it follows that
$H_{\ast }^{1}(F_{w}^{\prime },E_{2})$
under (4.1.4); it follows that
 $$\begin{eqnarray}\langle D_{1},D_{2}\rangle _{X,\ell _{w}}=\ell _{w}(h(D_{2}))\end{eqnarray}$$
$$\begin{eqnarray}\langle D_{1},D_{2}\rangle _{X,\ell _{w}}=\ell _{w}(h(D_{2}))\end{eqnarray}$$
independently of the choice of Hodge splittings. When
![]() $\ell _{w}$
is unramified, this property in fact suffices to characterise the pairing.
$\ell _{w}$
is unramified, this property in fact suffices to characterise the pairing.
Lemma 4.2.1. Let
![]() $X/F_{v}$
be a smooth proper curve over a local field
$X/F_{v}$
be a smooth proper curve over a local field
![]() $F_{v}$
and suppose that
$F_{v}$
and suppose that
 $\ell _{v}:F_{v}^{\times }\rightarrow L$
is unramified. Then there exists a unique locally constant symmetric bi-additive pairing
$\ell _{v}:F_{v}^{\times }\rightarrow L$
is unramified. Then there exists a unique locally constant symmetric bi-additive pairing
 $$\begin{eqnarray}\langle \,,\rangle _{X,\ell _{v}}:(\operatorname{Div}^{0}(X_{F_{v}})\times \operatorname{Div}^{0}(X_{F_{v}}))^{\ast }\rightarrow L\end{eqnarray}$$
$$\begin{eqnarray}\langle \,,\rangle _{X,\ell _{v}}:(\operatorname{Div}^{0}(X_{F_{v}})\times \operatorname{Div}^{0}(X_{F_{v}}))^{\ast }\rightarrow L\end{eqnarray}$$
such that
 $$\begin{eqnarray}\langle \operatorname{div}(h),D_{2}\rangle _{X,\ell _{v}}=\ell _{v}(h(D_{2}))\end{eqnarray}$$
$$\begin{eqnarray}\langle \operatorname{div}(h),D_{2}\rangle _{X,\ell _{v}}=\ell _{v}(h(D_{2}))\end{eqnarray}$$
whenever the two arguments have disjoint supports.
Proof. The result is well known, see e.g. [Reference Coleman and GrossCG89, Proposition 1.2], but for the reader’s convenience we recall the proof. A construction of such a pairing has just been recalled, and a second one will be given below. For the uniqueness, note that the difference of any two such pairings is a locally constant homomorphism
 $J(F_{v})\times J(F_{v})\rightarrow L$
. As the source is a compact group and the target is torsion free, such a homomorphism must be trivial.◻
$J(F_{v})\times J(F_{v})\rightarrow L$
. As the source is a compact group and the target is torsion free, such a homomorphism must be trivial.◻
Arithmetic intersections. Let
![]() $F^{\prime }\subset \overline{F}$
be a finite extension of
$F^{\prime }\subset \overline{F}$
be a finite extension of
![]() $F$
and
$F$
and
![]() $\mathscr{X}/\mathscr{O}_{F^{\prime }}$
be a regular integral model of
$\mathscr{X}/\mathscr{O}_{F^{\prime }}$
be a regular integral model of
![]() $X$
. For a divisor
$X$
. For a divisor
 $D\in \operatorname{Div}^{0}(X_{F^{\prime }})$
, we define its flat extension to the model
$D\in \operatorname{Div}^{0}(X_{F^{\prime }})$
, we define its flat extension to the model
![]() $\mathscr{X}$
to be the unique extension of
$\mathscr{X}$
to be the unique extension of
![]() $D$
which has intersection zero with any vertical divisor; it can be uniquely written as
$D$
which has intersection zero with any vertical divisor; it can be uniquely written as
![]() $\overline{D}+V$
, where
$\overline{D}+V$
, where
![]() $\overline{D}$
is the Zariski closure of
$\overline{D}$
is the Zariski closure of
![]() $D$
in
$D$
in
![]() $\mathscr{X}$
and
$\mathscr{X}$
and
![]() $V$
is a vertical divisor.
$V$
is a vertical divisor.
Let
![]() $D_{1}$
,
$D_{1}$
,
 $D_{2}\in \operatorname{Div}^{0}(X_{\overline{F}})$
be divisors with disjoint supports, with each
$D_{2}\in \operatorname{Div}^{0}(X_{\overline{F}})$
be divisors with disjoint supports, with each
![]() $D_{i}$
defined over a finite extension
$D_{i}$
defined over a finite extension
![]() $F_{i}$
; assume that
$F_{i}$
; assume that
 $F\subset F_{2}\subset F_{1}\subset \overline{F}$
. Let
$F\subset F_{2}\subset F_{1}\subset \overline{F}$
. Let
![]() $\mathscr{X}/\mathscr{O}_{F_{2}}$
be a regular and semistable model. Then, for each finite place
$\mathscr{X}/\mathscr{O}_{F_{2}}$
be a regular and semistable model. Then, for each finite place
 $w\in S_{F_{1}}$
, we can define partial local intersection multiplicities
$w\in S_{F_{1}}$
, we can define partial local intersection multiplicities
![]() $i_{w}$
,
$i_{w}$
,
![]() $j_{w}$
of the flat extensions
$j_{w}$
of the flat extensions
 $\overline{D}_{1}+V_{1}$
of
$\overline{D}_{1}+V_{1}$
of
![]() $D_{1}$
,
$D_{1}$
,
 $\overline{D}_{2}+V_{2}$
of
$\overline{D}_{2}+V_{2}$
of
![]() $D_{2}$
to
$D_{2}$
to
![]() $\mathscr{X}_{\mathscr{O}_{F_{1,w}}}$
. If the latter model is still regular, they are defined by
$\mathscr{X}_{\mathscr{O}_{F_{1,w}}}$
. If the latter model is still regular, they are defined by
 $$\begin{eqnarray}\begin{array}{@{}rcl@{}}i_{w}(D_{1},D_{2})\ & =\ & \displaystyle \frac{1}{[F_{1}:F]}(\overline{D}_{1}\cdot \overline{D}_{2})_{w},\\ j_{w}(D_{1},D_{2})\ & =\ & \displaystyle \frac{1}{[F_{1}:F]}(\overline{D}_{1}\cdot V_{2})_{w},\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rcl@{}}i_{w}(D_{1},D_{2})\ & =\ & \displaystyle \frac{1}{[F_{1}:F]}(\overline{D}_{1}\cdot \overline{D}_{2})_{w},\\ j_{w}(D_{1},D_{2})\ & =\ & \displaystyle \frac{1}{[F_{1}:F]}(\overline{D}_{1}\cdot V_{2})_{w},\end{array}\end{eqnarray}$$
where on the right-hand sides
![]() $(\,\cdot \,)_{w}$
are the usual
$(\,\cdot \,)_{w}$
are the usual
![]() $\mathbf{Z}$
-valued intersection multiplicities in
$\mathbf{Z}$
-valued intersection multiplicities in
![]() $\mathscr{X}_{\mathscr{O}_{F_{1,w}}}$
; see [Reference Yuan, Zhang and ZhangYZZ12, §7.1.7] for the generalisation of the definition to the case when
$\mathscr{X}_{\mathscr{O}_{F_{1,w}}}$
; see [Reference Yuan, Zhang and ZhangYZZ12, §7.1.7] for the generalisation of the definition to the case when
![]() $\mathscr{X}_{\mathscr{O}_{F_{1,w}}}$
is not regular. The total intersection
$\mathscr{X}_{\mathscr{O}_{F_{1,w}}}$
is not regular. The total intersection
 $$\begin{eqnarray}m_{w}(D_{1},D_{2})=i_{w}(D_{1},D_{2})+j_{w}(D_{1},D_{2})\end{eqnarray}$$
$$\begin{eqnarray}m_{w}(D_{1},D_{2})=i_{w}(D_{1},D_{2})+j_{w}(D_{1},D_{2})\end{eqnarray}$$
is of course independent of the choice of models.
Fix an extension
![]() $\overline{v}$
to
$\overline{v}$
to
![]() $\overline{F}$
of the valuation
$\overline{F}$
of the valuation
![]() $v$
on
$v$
on
![]() $F$
. Then we have pairings
$F$
. Then we have pairings
![]() $i_{\overline{v}}$
,
$i_{\overline{v}}$
,
![]() $j_{\overline{v}}$
on divisors on
$j_{\overline{v}}$
on divisors on
![]() $X_{\overline{F}_{\overline{v}}}$
with disjoint supports by the above formulas. We can group together the contributions of
$X_{\overline{F}_{\overline{v}}}$
with disjoint supports by the above formulas. We can group together the contributions of
![]() $i$
and
$i$
and
![]() $j$
according to the places of
$j$
according to the places of
![]() $F$
by
$F$
by
 $$\begin{eqnarray}\unicode[STIX]{x1D706}_{v}(D_{1},D_{2})=\unicode[STIX]{x2A0D}_{\operatorname{Gal}(\overline{F}/F)}\unicode[STIX]{x1D706}_{\overline{v}}(D_{1}^{\unicode[STIX]{x1D70E}},D_{2}^{\unicode[STIX]{x1D70E}})\,d\unicode[STIX]{x1D70E}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{v}(D_{1},D_{2})=\unicode[STIX]{x2A0D}_{\operatorname{Gal}(\overline{F}/F)}\unicode[STIX]{x1D706}_{\overline{v}}(D_{1}^{\unicode[STIX]{x1D70E}},D_{2}^{\unicode[STIX]{x1D70E}})\,d\unicode[STIX]{x1D70E}\end{eqnarray}$$
for
![]() $v$
any finite place of
$v$
any finite place of
![]() $F$
and
$F$
and
![]() $\unicode[STIX]{x1D706}=i$
,
$\unicode[STIX]{x1D706}=i$
,
![]() $j$
, or
$j$
, or
 $\unicode[STIX]{x1D706}_{v}(D_{1},D_{2})=\langle D_{1},D_{2}\rangle _{v}$
. Here the integral uses the Haar measure of total volume
$\unicode[STIX]{x1D706}_{v}(D_{1},D_{2})=\langle D_{1},D_{2}\rangle _{v}$
. Here the integral uses the Haar measure of total volume
![]() $1$
, and reduces to a finite weighted average for any fixed
$1$
, and reduces to a finite weighted average for any fixed
![]() $D_{1}$
,
$D_{1}$
,
![]() $D_{2}$
.
$D_{2}$
.
Proposition 4.2.2. Suppose that
![]() $D_{1}$
and
$D_{1}$
and
![]() $D_{2}$
are divisors of degree zero on
$D_{2}$
are divisors of degree zero on
![]() $X$
, defined over an extension
$X$
, defined over an extension
![]() $F^{\prime }$
of
$F^{\prime }$
of
![]() $F$
. Then, for all finite places
$F$
. Then, for all finite places
![]() $w\nmid p$
of
$w\nmid p$
of
![]() $F^{\prime }$
,
$F^{\prime }$
,
 $$\begin{eqnarray}\langle D_{1},D_{2}\rangle _{X,\ell _{w}}=m_{w}(D_{1},D_{2})\cdot \ell _{w}(\unicode[STIX]{x1D71B}_{w})=(i_{w}(D_{1},D_{2})+j_{w}(D_{1},D_{2}))\cdot \ell _{w}(\unicode[STIX]{x1D71B}_{w}).\end{eqnarray}$$
$$\begin{eqnarray}\langle D_{1},D_{2}\rangle _{X,\ell _{w}}=m_{w}(D_{1},D_{2})\cdot \ell _{w}(\unicode[STIX]{x1D71B}_{w})=(i_{w}(D_{1},D_{2})+j_{w}(D_{1},D_{2}))\cdot \ell _{w}(\unicode[STIX]{x1D71B}_{w}).\end{eqnarray}$$
Proof. This follows from Lemma 4.2.1 and (4.2.3); the verification that the arithmetic intersection pairing
![]() $m_{w}$
also satisfies the required properties can be found in [Reference GrossGro84].◻
$m_{w}$
also satisfies the required properties can be found in [Reference GrossGro84].◻
4.3 Integrality criteria
The result of Proposition 4.2.2 applies with the same proof if
![]() $w|p$
when
$w|p$
when
![]() $\ell _{w}$
is an unramified logarithm such as the valuation. In this case we will view it as a first integrality criterion for local heights.
$\ell _{w}$
is an unramified logarithm such as the valuation. In this case we will view it as a first integrality criterion for local heights.
Proposition 4.3.1. Let
 $\ell _{v}:F_{v}^{\times }\,\hat{\otimes }\,L\rightarrow \unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L$
be the tautological logarithm and let
$\ell _{v}:F_{v}^{\times }\,\hat{\otimes }\,L\rightarrow \unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L$
be the tautological logarithm and let
![]() $\ell _{w}$
be as in (4.1.7). Let
$\ell _{w}$
be as in (4.1.7). Let
 $v:F_{v}^{\times }\,\hat{\otimes }\,L\rightarrow L$
be the valuation. Then, for all
$v:F_{v}^{\times }\,\hat{\otimes }\,L\rightarrow L$
be the valuation. Then, for all
![]() $D_{1}$
,
$D_{1}$
,
 $D_{2}\in \operatorname{Div}^{0}(X_{F^{\prime }})$
, we have
$D_{2}\in \operatorname{Div}^{0}(X_{F^{\prime }})$
, we have
 $$\begin{eqnarray}v(\langle D_{1},D_{2}\rangle _{X,\ell _{w}})=[F_{w}^{\prime }:F_{v}]\cdot m_{w}(D_{1},D_{2}).\end{eqnarray}$$
$$\begin{eqnarray}v(\langle D_{1},D_{2}\rangle _{X,\ell _{w}})=[F_{w}^{\prime }:F_{v}]\cdot m_{w}(D_{1},D_{2}).\end{eqnarray}$$
In particular, if
 $m_{w}(D_{1},D_{2})=0$
, then
$m_{w}(D_{1},D_{2})=0$
, then
 $$\begin{eqnarray}\langle D_{1},D_{2}\rangle _{X,\ell _{w}}=\ell _{w}(s_{w}([E_{D_{1},D_{2},w}]))\in \mathscr{O}_{F,v}^{\times }\,\hat{\otimes }\,L=\ell _{w}(H_{f}^{1}(F_{w},L(1)));\end{eqnarray}$$
$$\begin{eqnarray}\langle D_{1},D_{2}\rangle _{X,\ell _{w}}=\ell _{w}(s_{w}([E_{D_{1},D_{2},w}]))\in \mathscr{O}_{F,v}^{\times }\,\hat{\otimes }\,L=\ell _{w}(H_{f}^{1}(F_{w},L(1)));\end{eqnarray}$$
equivalently, the mixed extension
 $[E_{D_{1},D_{2},w}]$
is essentially crystalline.
$[E_{D_{1},D_{2},w}]$
is essentially crystalline.
We need a finer integrality property for local heights, slightly generalising [Reference NekovářNek95, Proposition 1.11]. Let
![]() $F_{v}$
and
$F_{v}$
and
![]() $L$
be finite extensions of
$L$
be finite extensions of
![]() $\mathbf{Q}_{p}$
, let
$\mathbf{Q}_{p}$
, let
![]() $V$
be a
$V$
be a
![]() $\mathscr{G}_{F_{v}}$
-representation on an
$\mathscr{G}_{F_{v}}$
-representation on an
![]() $L$
-vector space equipped with a splitting of (4.1.2), and let
$L$
-vector space equipped with a splitting of (4.1.2), and let
 $\ell _{v}:F_{v}^{\times }\rightarrow L$
be a logarithm. Suppose that the following conditions are satisfied:
$\ell _{v}:F_{v}^{\times }\rightarrow L$
be a logarithm. Suppose that the following conditions are satisfied:
-
(a)
 $\ell _{v}:F_{v}^{\times }\rightarrow L$
is ramified;
$\ell _{v}:F_{v}^{\times }\rightarrow L$
is ramified; -
(b) the space
 $V$
admits a direct sum decomposition
$V$
admits a direct sum decomposition
 $V=V^{\prime }\oplus V^{\prime \prime }$
as
$V=V^{\prime }\oplus V^{\prime \prime }$
as
 $\mathscr{G}_{F_{v}}$
-representation, such that
$\mathscr{G}_{F_{v}}$
-representation, such that
 $V^{\prime }$
satisfies the Panchishkin condition, with a decomposition
$V^{\prime }$
satisfies the Panchishkin condition, with a decomposition
 $0\rightarrow V^{\prime +}\rightarrow V^{\prime }\rightarrow V^{\prime -}\rightarrow 0$
, and the restriction of the Hodge splitting of
$0\rightarrow V^{\prime +}\rightarrow V^{\prime }\rightarrow V^{\prime -}\rightarrow 0$
, and the restriction of the Hodge splitting of
 $\mathbf{D}_{\text{dR}}(V)$
to
$\mathbf{D}_{\text{dR}}(V)$
to
 $\mathbf{D}_{\text{dR}}(V^{\prime })$
coincides with the canonical one of (4.1.9);
$\mathbf{D}_{\text{dR}}(V^{\prime })$
coincides with the canonical one of (4.1.9); -
(c)
 $H^{0}(F_{v},V^{\prime -})=H^{0}(F_{v},V^{\prime +\ast }(1))=0$
.
$H^{0}(F_{v},V^{\prime -})=H^{0}(F_{v},V^{\prime +\ast }(1))=0$
.
By [Reference NekovářNek93, Proposition 1.28(3)], the last condition is equivalent to
 $\mathbf{D}_{\text{pst}}(V^{\prime })^{\unicode[STIX]{x1D711}=1}=\mathbf{D}_{\text{pst}}(V^{\prime \ast }(1))^{\unicode[STIX]{x1D711}=1}=0$
, where
$\mathbf{D}_{\text{pst}}(V^{\prime })^{\unicode[STIX]{x1D711}=1}=\mathbf{D}_{\text{pst}}(V^{\prime \ast }(1))^{\unicode[STIX]{x1D711}=1}=0$
, where
 $\mathbf{D}_{\text{pst}}(V^{\prime }):=\lim _{F\subset F^{\prime }}\mathbf{D}_{\text{st}}(V^{\prime }|_{\mathscr{G}_{F^{\prime }}})^{\operatorname{Gal}(F^{\prime }/F)}$
(the limit ranging over all sufficiently large finite Galois extensions
$\mathbf{D}_{\text{pst}}(V^{\prime }):=\lim _{F\subset F^{\prime }}\mathbf{D}_{\text{st}}(V^{\prime }|_{\mathscr{G}_{F^{\prime }}})^{\operatorname{Gal}(F^{\prime }/F)}$
(the limit ranging over all sufficiently large finite Galois extensions
![]() $F^{\prime }/F$
).
$F^{\prime }/F$
).
Let
![]() $T$
be a
$T$
be a
![]() $\mathscr{G}_{F,v}$
-stable
$\mathscr{G}_{F,v}$
-stable
![]() $\mathscr{O}_{L}$
-lattice in
$\mathscr{O}_{L}$
-lattice in
![]() $V$
,
$V$
,
 $T^{\prime }:=T\cap V^{\prime }$
,
$T^{\prime }:=T\cap V^{\prime }$
,
 $T^{\prime \prime }=T\cap V^{\prime \prime }$
; let
$T^{\prime \prime }=T\cap V^{\prime \prime }$
; let
![]() $d_{0}\geqslant 0$
be an integer such that
$d_{0}\geqslant 0$
be an integer such that
 $\mathfrak{p}_{L}^{d_{0}}T\subset T^{\prime }\oplus T^{\prime \prime }\subset T$
, where
$\mathfrak{p}_{L}^{d_{0}}T\subset T^{\prime }\oplus T^{\prime \prime }\subset T$
, where
![]() $\mathfrak{p}_{L}\in L$
is the maximal ideal of
$\mathfrak{p}_{L}\in L$
is the maximal ideal of
![]() $\mathscr{O}_{L}$
.
$\mathscr{O}_{L}$
.
Let
 $F_{v}\subset F_{v,\infty }\subset F_{v}^{\text{ab}}$
be the intermediate extension determined by
$F_{v}\subset F_{v,\infty }\subset F_{v}^{\text{ab}}$
be the intermediate extension determined by
 $\operatorname{Gal}(F_{v}^{\text{ab}}/F_{v,\infty })\cong \ker (\ell _{v})\subset F_{v}^{\times }$
under the reciprocity isomorphism. Let
$\operatorname{Gal}(F_{v}^{\text{ab}}/F_{v,\infty })\cong \ker (\ell _{v})\subset F_{v}^{\times }$
under the reciprocity isomorphism. Let
 $$\begin{eqnarray}N_{\infty ,\ell _{v}}H_{f}^{1}(F_{v},T^{\prime }):=\mathop{\bigcap }_{F_{w}^{\prime }}\text{cores}_{F_{v}}^{F_{w}^{\prime }}(H_{f}^{1}(F_{w}^{\prime },T^{\prime }))\end{eqnarray}$$
$$\begin{eqnarray}N_{\infty ,\ell _{v}}H_{f}^{1}(F_{v},T^{\prime }):=\mathop{\bigcap }_{F_{w}^{\prime }}\text{cores}_{F_{v}}^{F_{w}^{\prime }}(H_{f}^{1}(F_{w}^{\prime },T^{\prime }))\end{eqnarray}$$
be the subgroup of universal norms, where the intersection ranges over all finite extensions
 $F_{v}\subset F_{v^{\prime }}^{\prime }$
contained in
$F_{v}\subset F_{v^{\prime }}^{\prime }$
contained in
![]() $F_{v,\infty }$
.
$F_{v,\infty }$
.
Proposition 4.3.2. Let
 $x_{1}\in H_{f}^{1}(F_{v},T)$
,
$x_{1}\in H_{f}^{1}(F_{v},T)$
,
 $x_{2}\in H_{f}^{1}(F_{v},T^{\ast }(1))$
, and suppose that the image of
$x_{2}\in H_{f}^{1}(F_{v},T^{\ast }(1))$
, and suppose that the image of
![]() $x_{2}$
in
$x_{2}$
in
 $H_{f}^{1}(F_{v},T^{\prime \prime \ast }(1))$
vanishes. Let
$H_{f}^{1}(F_{v},T^{\prime \prime \ast }(1))$
vanishes. Let
![]() $d_{1}$
be the
$d_{1}$
be the
![]() $\mathscr{O}_{L}$
-length of
$\mathscr{O}_{L}$
-length of
 $H^{1}(F_{v},T^{\prime \prime \ast }(1))_{\text{tors}}$
and
$H^{1}(F_{v},T^{\prime \prime \ast }(1))_{\text{tors}}$
and
![]() $d_{2}$
the length of
$d_{2}$
the length of
 $H_{f}^{1}(F_{v},T^{\prime })/N_{\infty ,\ell _{v}}H_{f}^{1}(F_{v},T^{\prime })$
. Then
$H_{f}^{1}(F_{v},T^{\prime })/N_{\infty ,\ell _{v}}H_{f}^{1}(F_{v},T^{\prime })$
. Then
 $$\begin{eqnarray}\mathfrak{p}_{L}^{d_{0}+d_{1}+d_{2}}\langle x_{1},x_{2}\rangle _{\ell _{v},E,v}\subset \ell _{v}(F_{v}^{\times }\,\hat{\otimes }\,\mathscr{O}_{L})\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{p}_{L}^{d_{0}+d_{1}+d_{2}}\langle x_{1},x_{2}\rangle _{\ell _{v},E,v}\subset \ell _{v}(F_{v}^{\times }\,\hat{\otimes }\,\mathscr{O}_{L})\end{eqnarray}$$
for any mixed extension
![]() $E$
. If moreover
$E$
. If moreover
![]() $[E_{v}]$
is essentially crystalline, then
$[E_{v}]$
is essentially crystalline, then
 $$\begin{eqnarray}\mathfrak{p}_{L}^{d_{0}+d_{1}+d_{2}}\langle x_{1},x_{2}\rangle _{\ell _{v},E,v}\subset \ell _{v}(\mathscr{O}_{F,v}^{\times }\,\hat{\otimes }\,\mathscr{O}_{L}).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{p}_{L}^{d_{0}+d_{1}+d_{2}}\langle x_{1},x_{2}\rangle _{\ell _{v},E,v}\subset \ell _{v}(\mathscr{O}_{F,v}^{\times }\,\hat{\otimes }\,\mathscr{O}_{L}).\end{eqnarray}$$
Proof. The first assertion (which implicitly contains the assertion that
 $H_{f}^{1}(F_{v},T^{\prime })/$
$H_{f}^{1}(F_{v},T^{\prime })/$
 $N_{\infty ,\ell _{v}}H_{f}^{1}(F_{v},T^{\prime })$
is finite) is identical to [Reference NekovářNek95, Proposition 1.11], whose assumptions however are slightly more stringent. First,
$N_{\infty ,\ell _{v}}H_{f}^{1}(F_{v},T^{\prime })$
is finite) is identical to [Reference NekovářNek95, Proposition 1.11], whose assumptions however are slightly more stringent. First,
![]() $L$
is assumed to be
$L$
is assumed to be
![]() $\mathbf{Q}_{p}$
; this requires only cosmetic changes in the proof. Secondly, in [Reference NekovářNek95] the representation
$\mathbf{Q}_{p}$
; this requires only cosmetic changes in the proof. Secondly, in [Reference NekovářNek95] the representation
![]() $V$
(hence
$V$
(hence
![]() $V^{\prime }$
) is further assumed to be crystalline. This assumption is used via [Reference NekovářNek93, §6.6] to apply various consequences of the existence of the exact sequence
$V^{\prime }$
) is further assumed to be crystalline. This assumption is used via [Reference NekovářNek93, §6.6] to apply various consequences of the existence of the exact sequence
 $$\begin{eqnarray}0\rightarrow H_{f}^{1}(F_{v},V^{\prime +})\rightarrow H_{f}^{1}(F_{v},V^{\prime })\rightarrow H_{f}^{1}(F_{v},V^{\prime -})\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow H_{f}^{1}(F_{v},V^{\prime +})\rightarrow H_{f}^{1}(F_{v},V^{\prime })\rightarrow H_{f}^{1}(F_{v},V^{\prime -})\rightarrow 0,\end{eqnarray}$$
which is established in [Reference NekovářNek93, Proposition 1.25] under the assumption that
![]() $V^{\prime }$
is crystalline. However, (4.3.1) still exists under our assumption that
$V^{\prime }$
is crystalline. However, (4.3.1) still exists under our assumption that
 $H^{0}(F_{v},V^{\prime -})=0$
by [Reference BenoisBen11, Corollary 1.4.6].Footnote
26
$H^{0}(F_{v},V^{\prime -})=0$
by [Reference BenoisBen11, Corollary 1.4.6].Footnote
26
The second assertion follows from the proof of the first one: the height is the image under
![]() $\ell _{v}$
of an element of
$\ell _{v}$
of an element of
 $H^{1}(F_{v},L(1))=F_{v}^{\times }\,\hat{\otimes }\,L$
, which belongs to
$H^{1}(F_{v},L(1))=F_{v}^{\times }\,\hat{\otimes }\,L$
, which belongs to
 $H_{f}^{1}(F_{v},L(1))=\mathscr{O}_{F,v}^{\times }\,\hat{\otimes }\,L$
if
$H_{f}^{1}(F_{v},L(1))=\mathscr{O}_{F,v}^{\times }\,\hat{\otimes }\,L$
if
![]() $[E_{v}]$
is essentially crystalline.◻
$[E_{v}]$
is essentially crystalline.◻
5 Generating series and strategy of proof
We introduce the constructions that will serve to prove the main theorem. We have expressed the
![]() $p$
-adic
$p$
-adic
![]() $L$
-function as the
$L$
-function as the
![]() $p$
-adic Petersson product of a form
$p$
-adic Petersson product of a form
![]() $\unicode[STIX]{x1D711}$
in
$\unicode[STIX]{x1D711}$
in
![]() $\unicode[STIX]{x1D70E}_{A}$
and a certain kernel function depending on a Schwartz function
$\unicode[STIX]{x1D70E}_{A}$
and a certain kernel function depending on a Schwartz function
![]() $\unicode[STIX]{x1D719}$
. The connection between the data of
$\unicode[STIX]{x1D719}$
. The connection between the data of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D719})$
and the data of
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D719})$
and the data of
![]() $(f_{1},f_{2})$
appearing in the main theorem is given by the Shimizu lifting introduced in § 5.1. An arithmetic–geometric analogue of the latter allows us to express also the left-hand side of Theorem B as the image under the
$(f_{1},f_{2})$
appearing in the main theorem is given by the Shimizu lifting introduced in § 5.1. An arithmetic–geometric analogue of the latter allows us to express also the left-hand side of Theorem B as the image under the
![]() $p$
-adic Petersson product of another kernel function, introduced in § 5.3. The main result of this section is thus the reduction of Theorem B to an identity between the two kernel functions (§ 5.4).
$p$
-adic Petersson product of another kernel function, introduced in § 5.3. The main result of this section is thus the reduction of Theorem B to an identity between the two kernel functions (§ 5.4).
5.1 Shimizu’s theta lifting
Let
![]() $B$
be a quaternion algebra over a local or global field
$B$
be a quaternion algebra over a local or global field
![]() $F$
,
$F$
,
 $V=(B,q)$
with the reduced norm
$V=(B,q)$
with the reduced norm
![]() $q$
. The action
$q$
. The action
 $(h_{1},h_{2})\cdot x:=h_{1}xh_{2}^{-1}$
embeds
$(h_{1},h_{2})\cdot x:=h_{1}xh_{2}^{-1}$
embeds
 $(B^{\times }\times B^{\times })/F^{\times }$
inside
$(B^{\times }\times B^{\times })/F^{\times }$
inside
 $\mathbf{GO}(V)$
. If
$\mathbf{GO}(V)$
. If
![]() $F$
is a local field,
$F$
is a local field,
![]() $\unicode[STIX]{x1D70E}$
is a representation of
$\unicode[STIX]{x1D70E}$
is a representation of
 $\mathbf{GL}_{2}(F)$
, and
$\mathbf{GL}_{2}(F)$
, and
![]() $\unicode[STIX]{x1D70B}$
is a representation of
$\unicode[STIX]{x1D70B}$
is a representation of
![]() $B^{\times }$
, then the space of liftings
$B^{\times }$
, then the space of liftings
 $$\begin{eqnarray}\operatorname{Hom}_{\mathbf{GL}_{2}(F)\times B^{\times }\times B^{\times }}(\unicode[STIX]{x1D70E}\otimes \mathscr{S}(V\times F^{\times }),\unicode[STIX]{x1D70B}\otimes \unicode[STIX]{x1D70B}^{\vee })\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{\mathbf{GL}_{2}(F)\times B^{\times }\times B^{\times }}(\unicode[STIX]{x1D70E}\otimes \mathscr{S}(V\times F^{\times }),\unicode[STIX]{x1D70B}\otimes \unicode[STIX]{x1D70B}^{\vee })\end{eqnarray}$$
has dimension zero unless either
 $B=M_{2}(F)$
and
$B=M_{2}(F)$
and
![]() $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70E}$
or
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70E}$
or
![]() $\unicode[STIX]{x1D70E}$
is a discrete series and
$\unicode[STIX]{x1D70E}$
is a discrete series and
![]() $\unicode[STIX]{x1D70B}$
is its image under the Jacquet–Langlands correspondence; in the latter cases the dimension is one. An explicit generator was constructed by Shimizu in the global coherent case, and we can use it to normalise a generator in the local case and construct a generator in the global incoherent case.
$\unicode[STIX]{x1D70B}$
is its image under the Jacquet–Langlands correspondence; in the latter cases the dimension is one. An explicit generator was constructed by Shimizu in the global coherent case, and we can use it to normalise a generator in the local case and construct a generator in the global incoherent case.
Global lifting. Let
![]() $B$
be a quaternion algebra over a number field
$B$
be a quaternion algebra over a number field
![]() $F$
,
$F$
,
 $V=(B,q)$
with the reduced norm. Let
$V=(B,q)$
with the reduced norm. Let
![]() $\unicode[STIX]{x1D70E}$
be a cuspidal automorphic representation of
$\unicode[STIX]{x1D70E}$
be a cuspidal automorphic representation of
 $\mathbf{GL}_{2}(\mathbf{A}_{F})$
which is a discrete series at all places where
$\mathbf{GL}_{2}(\mathbf{A}_{F})$
which is a discrete series at all places where
![]() $B$
is ramified and
$B$
is ramified and
![]() $\unicode[STIX]{x1D70B}$
the automorphic representation of
$\unicode[STIX]{x1D70B}$
the automorphic representation of
![]() $B_{\mathbf{A}}^{\times }$
attached to
$B_{\mathbf{A}}^{\times }$
attached to
![]() $\unicode[STIX]{x1D70E}$
by the Jacquet–Langlands correspondence. Fix a non-trivial additive character
$\unicode[STIX]{x1D70E}$
by the Jacquet–Langlands correspondence. Fix a non-trivial additive character
 $\unicode[STIX]{x1D713}:\mathbf{A}/F\rightarrow \mathbf{C}^{\times }$
. Consider the theta series
$\unicode[STIX]{x1D713}:\mathbf{A}/F\rightarrow \mathbf{C}^{\times }$
. Consider the theta series
 $$\begin{eqnarray}\unicode[STIX]{x1D703}(g,h,\unicode[STIX]{x1D6F7})=\mathop{\sum }_{u\in F^{\times }}\mathop{\sum }_{x\in V}r_{\unicode[STIX]{x1D713}}(g,h)\unicode[STIX]{x1D6F7}(x,u),\quad g\in \mathbf{GL}_{2}(\mathbf{A}),h\in (B_{\mathbf{A}}^{\times }\times B_{\boldsymbol{ A}}^{\times })/\mathbf{A}^{\times }\subset \mathbf{GO}(V_{\boldsymbol{ A}})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}(g,h,\unicode[STIX]{x1D6F7})=\mathop{\sum }_{u\in F^{\times }}\mathop{\sum }_{x\in V}r_{\unicode[STIX]{x1D713}}(g,h)\unicode[STIX]{x1D6F7}(x,u),\quad g\in \mathbf{GL}_{2}(\mathbf{A}),h\in (B_{\mathbf{A}}^{\times }\times B_{\boldsymbol{ A}}^{\times })/\mathbf{A}^{\times }\subset \mathbf{GO}(V_{\boldsymbol{ A}})\end{eqnarray}$$
for
 $\unicode[STIX]{x1D6F7}\in \mathscr{S}(V_{\mathbf{A}}\times \mathbf{A}^{\times })$
. Then the Shimizu theta lift of any
$\unicode[STIX]{x1D6F7}\in \mathscr{S}(V_{\mathbf{A}}\times \mathbf{A}^{\times })$
. Then the Shimizu theta lift of any
![]() $\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D70E}$
is defined to be
$\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D70E}$
is defined to be
 $$\begin{eqnarray}\unicode[STIX]{x1D703}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6F7})(h):=\frac{\unicode[STIX]{x1D701}_{F}(2)}{2L(1,\unicode[STIX]{x1D70E},\operatorname{ad})}\int _{\mathbf{GL}_{2}(F)\backslash \mathbf{GL}_{2}(\mathbf{A})}\unicode[STIX]{x1D711}(g)\unicode[STIX]{x1D703}(g,h,\unicode[STIX]{x1D6F7})\,dg\quad \in \unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\vee }\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6F7})(h):=\frac{\unicode[STIX]{x1D701}_{F}(2)}{2L(1,\unicode[STIX]{x1D70E},\operatorname{ad})}\int _{\mathbf{GL}_{2}(F)\backslash \mathbf{GL}_{2}(\mathbf{A})}\unicode[STIX]{x1D711}(g)\unicode[STIX]{x1D703}(g,h,\unicode[STIX]{x1D6F7})\,dg\quad \in \unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\vee }\end{eqnarray}$$
and it is independent of the choice of
![]() $\unicode[STIX]{x1D713}$
.
$\unicode[STIX]{x1D713}$
.
If
![]() $F$
is totally real,
$F$
is totally real,
![]() $B$
is totally definite, and
$B$
is totally definite, and
 $\unicode[STIX]{x1D719}\in \overline{\mathscr{S}}(V_{\mathbf{A}}\times \mathbf{A}^{\times })$
, we denote
$\unicode[STIX]{x1D719}\in \overline{\mathscr{S}}(V_{\mathbf{A}}\times \mathbf{A}^{\times })$
, we denote
 $\unicode[STIX]{x1D703}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D719}):=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6F7})$
for any
$\unicode[STIX]{x1D703}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D719}):=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6F7})$
for any
![]() $\mathbf{O}(V_{\infty })$
-invariant preimage
$\mathbf{O}(V_{\infty })$
-invariant preimage
![]() $\unicode[STIX]{x1D6F7}$
of
$\unicode[STIX]{x1D6F7}$
of
![]() $\unicode[STIX]{x1D719}$
under (3.1.3). Let
$\unicode[STIX]{x1D719}$
under (3.1.3). Let
 $\mathscr{F}:\unicode[STIX]{x1D70B}\otimes \unicode[STIX]{x1D70B}^{\vee }\rightarrow \mathbf{C}$
be the duality defined by the Petersson bilinear pairing on
$\mathscr{F}:\unicode[STIX]{x1D70B}\otimes \unicode[STIX]{x1D70B}^{\vee }\rightarrow \mathbf{C}$
be the duality defined by the Petersson bilinear pairing on
![]() $B_{\mathbf{A}}^{\times }$
(for the Tamagawa measure). By [Reference WaldspurgerWal85, Proposition 5], we have
$B_{\mathbf{A}}^{\times }$
(for the Tamagawa measure). By [Reference WaldspurgerWal85, Proposition 5], we have
 $$\begin{eqnarray}\displaystyle \mathscr{F}\unicode[STIX]{x1D703}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6F7}) & = & \displaystyle \frac{(\unicode[STIX]{x1D70B}^{2}/2)^{[F:\mathbf{Q}]}}{|D|_{F}^{3/2}\unicode[STIX]{x1D701}_{F}^{\infty }(2)}\mathop{\prod }_{v\nmid \infty }\frac{|d_{v}|^{-3/2}\unicode[STIX]{x1D701}_{F,v}(2)^{2}}{L(1,\unicode[STIX]{x1D70E}_{v},\operatorname{ad})}\int _{N(F)_{v}\backslash \mathbf{GL}_{2}(F_{v})}W_{\unicode[STIX]{x1D711},-1,v}(g)r(g)\unicode[STIX]{x1D6F7}_{v}(1,1)\,dg\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{v|\infty }\frac{2\unicode[STIX]{x1D701}_{F,v}(2)}{\unicode[STIX]{x1D70B}^{2}L(1,\unicode[STIX]{x1D70E}_{v},\operatorname{ad})}\int _{N(F)_{v}\backslash \mathbf{GL}_{2}(F_{v})}W_{\unicode[STIX]{x1D711},-1,v}(g)r(g)\unicode[STIX]{x1D6F7}_{v}(1,1)\,dg.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{F}\unicode[STIX]{x1D703}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6F7}) & = & \displaystyle \frac{(\unicode[STIX]{x1D70B}^{2}/2)^{[F:\mathbf{Q}]}}{|D|_{F}^{3/2}\unicode[STIX]{x1D701}_{F}^{\infty }(2)}\mathop{\prod }_{v\nmid \infty }\frac{|d_{v}|^{-3/2}\unicode[STIX]{x1D701}_{F,v}(2)^{2}}{L(1,\unicode[STIX]{x1D70E}_{v},\operatorname{ad})}\int _{N(F)_{v}\backslash \mathbf{GL}_{2}(F_{v})}W_{\unicode[STIX]{x1D711},-1,v}(g)r(g)\unicode[STIX]{x1D6F7}_{v}(1,1)\,dg\nonumber\\ \displaystyle & & \displaystyle \times \,\mathop{\prod }_{v|\infty }\frac{2\unicode[STIX]{x1D701}_{F,v}(2)}{\unicode[STIX]{x1D70B}^{2}L(1,\unicode[STIX]{x1D70E}_{v},\operatorname{ad})}\int _{N(F)_{v}\backslash \mathbf{GL}_{2}(F_{v})}W_{\unicode[STIX]{x1D711},-1,v}(g)r(g)\unicode[STIX]{x1D6F7}_{v}(1,1)\,dg.\end{eqnarray}$$
The terms in the first line are all rational if
![]() $W_{\unicode[STIX]{x1D719},-1,v}$
and
$W_{\unicode[STIX]{x1D719},-1,v}$
and
![]() $\unicode[STIX]{x1D6F7}_{v}$
are, and almost all of the factors equal
$\unicode[STIX]{x1D6F7}_{v}$
are, and almost all of the factors equal
![]() $1$
.Footnote
27
For
$1$
.Footnote
27
For
![]() $v$
a real place, if
$v$
a real place, if
![]() $W_{\unicode[STIX]{x1D711},-1,v}$
is the standard antiholomorphic discrete series of weight
$W_{\unicode[STIX]{x1D711},-1,v}$
is the standard antiholomorphic discrete series of weight
![]() $2$
and
$2$
and
![]() $\unicode[STIX]{x1D6F7}_{v}$
is a preimage of the standard Schwartz function
$\unicode[STIX]{x1D6F7}_{v}$
is a preimage of the standard Schwartz function
 $\unicode[STIX]{x1D719}_{v}\in \overline{\mathscr{S}}(V_{v}\times F_{v}^{\times })$
under (3.1.2), the terms in the last line are rational too,Footnote
28
and in fact equal to
$\unicode[STIX]{x1D719}_{v}\in \overline{\mathscr{S}}(V_{v}\times F_{v}^{\times })$
under (3.1.2), the terms in the last line are rational too,Footnote
28
and in fact equal to
![]() $1$
by the calculation of Lemma 3.5.4.
$1$
by the calculation of Lemma 3.5.4.
Local lifting. In the local case, depending on the choice of
![]() $\unicode[STIX]{x1D713}_{v}$
, we can then normalise a generator
$\unicode[STIX]{x1D713}_{v}$
, we can then normalise a generator
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{v}=\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{v}}\in \operatorname{Hom}_{\mathbf{GL}_{2}(F_{v})\times B_{v}^{\times }\times B_{v}^{\times }}(\mathscr{W}(\unicode[STIX]{x1D70E}_{v},\overline{\unicode[STIX]{x1D713}}_{v})\otimes \mathscr{S}(V_{v}\times F_{v}^{\times }),\unicode[STIX]{x1D70B}_{v}\otimes \unicode[STIX]{x1D70B}_{v}^{\vee })\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{v}=\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{v}}\in \operatorname{Hom}_{\mathbf{GL}_{2}(F_{v})\times B_{v}^{\times }\times B_{v}^{\times }}(\mathscr{W}(\unicode[STIX]{x1D70E}_{v},\overline{\unicode[STIX]{x1D713}}_{v})\otimes \mathscr{S}(V_{v}\times F_{v}^{\times }),\unicode[STIX]{x1D70B}_{v}\otimes \unicode[STIX]{x1D70B}_{v}^{\vee })\end{eqnarray}$$
(where
 $\mathscr{W}(\unicode[STIX]{x1D70E}_{v},\overline{\unicode[STIX]{x1D713}}_{v})$
is the Whittaker model for
$\mathscr{W}(\unicode[STIX]{x1D70E}_{v},\overline{\unicode[STIX]{x1D713}}_{v})$
is the Whittaker model for
![]() $\unicode[STIX]{x1D70E}_{v}$
for the conjugate character
$\unicode[STIX]{x1D70E}_{v}$
for the conjugate character
![]() $\overline{\unicode[STIX]{x1D713}}_{v}$
) by
$\overline{\unicode[STIX]{x1D713}}_{v}$
) by
 $$\begin{eqnarray}\mathscr{F}_{v}\unicode[STIX]{x1D703}_{v}(W,\unicode[STIX]{x1D6F7})=\frac{c_{v}\unicode[STIX]{x1D701}_{F,v}(2)}{L(1,\unicode[STIX]{x1D70E}_{v},\operatorname{ad})}\int _{N(F)_{v}\backslash \mathbf{GL}_{2}(F_{v})}W(g)r(g)\unicode[STIX]{x1D6F7}(1,1)\,dg\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{F}_{v}\unicode[STIX]{x1D703}_{v}(W,\unicode[STIX]{x1D6F7})=\frac{c_{v}\unicode[STIX]{x1D701}_{F,v}(2)}{L(1,\unicode[STIX]{x1D70E}_{v},\operatorname{ad})}\int _{N(F)_{v}\backslash \mathbf{GL}_{2}(F_{v})}W(g)r(g)\unicode[STIX]{x1D6F7}(1,1)\,dg\end{eqnarray}$$
with
 $c_{v}=|d_{v}|^{-3/2}\unicode[STIX]{x1D701}_{F,v}(2)$
if
$c_{v}=|d_{v}|^{-3/2}\unicode[STIX]{x1D701}_{F,v}(2)$
if
![]() $v$
is finite and
$v$
is finite and
 $c_{v}=2\unicode[STIX]{x1D70B}^{-2}$
if
$c_{v}=2\unicode[STIX]{x1D70B}^{-2}$
if
![]() $v$
is archimedean. Here the decompositions
$v$
is archimedean. Here the decompositions
 $\unicode[STIX]{x1D70B}=\bigotimes _{v}\unicode[STIX]{x1D70B}_{v}$
,
$\unicode[STIX]{x1D70B}=\bigotimes _{v}\unicode[STIX]{x1D70B}_{v}$
,
 $\unicode[STIX]{x1D70B}^{\vee }=\bigotimes _{v}\unicode[STIX]{x1D70B}_{v}^{\vee }$
are taken to satisfy
$\unicode[STIX]{x1D70B}^{\vee }=\bigotimes _{v}\unicode[STIX]{x1D70B}_{v}^{\vee }$
are taken to satisfy
 $\mathscr{F}=\prod _{v}\mathscr{F}_{v}$
for the natural dualities
$\mathscr{F}=\prod _{v}\mathscr{F}_{v}$
for the natural dualities
 $\mathscr{F}_{v}:\unicode[STIX]{x1D70B}_{v}\otimes \unicode[STIX]{x1D70B}_{v}^{\vee }\rightarrow \mathbf{C}$
.
$\mathscr{F}_{v}:\unicode[STIX]{x1D70B}_{v}\otimes \unicode[STIX]{x1D70B}_{v}^{\vee }\rightarrow \mathbf{C}$
.
Then by (5.1.1) we have a decomposition
 $$\begin{eqnarray}\unicode[STIX]{x1D703}=\frac{(\unicode[STIX]{x1D70B}^{2}/2)^{[F:\mathbf{Q}]}}{|D|_{F}^{3/2}\unicode[STIX]{x1D701}_{F}^{\infty }(2)}\otimes _{v}\unicode[STIX]{x1D703}_{v}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}=\frac{(\unicode[STIX]{x1D70B}^{2}/2)^{[F:\mathbf{Q}]}}{|D|_{F}^{3/2}\unicode[STIX]{x1D701}_{F}^{\infty }(2)}\otimes _{v}\unicode[STIX]{x1D703}_{v}.\end{eqnarray}$$
As in the global case, we define
 $\unicode[STIX]{x1D703}_{v}(W,\unicode[STIX]{x1D719}):=\unicode[STIX]{x1D703}_{v}(W,\unicode[STIX]{x1D6F7})$
for
$\unicode[STIX]{x1D703}_{v}(W,\unicode[STIX]{x1D719}):=\unicode[STIX]{x1D703}_{v}(W,\unicode[STIX]{x1D6F7})$
for
 $\unicode[STIX]{x1D719}=\overline{\unicode[STIX]{x1D6F7}}\in \overline{\mathscr{S}}(V_{v}\times F_{v}^{\times })$
.
$\unicode[STIX]{x1D719}=\overline{\unicode[STIX]{x1D6F7}}\in \overline{\mathscr{S}}(V_{v}\times F_{v}^{\times })$
.
Incoherent lifting. Finally, suppose that
![]() $F$
is totally real and
$F$
is totally real and
![]() $\mathbf{B}$
is a totally definite incoherent quaternion algebra over
$\mathbf{B}$
is a totally definite incoherent quaternion algebra over
 $\mathbf{A}=\mathbf{A}_{F}$
, and let
$\mathbf{A}=\mathbf{A}_{F}$
, and let
 $\mathbf{V}=(\mathbf{B},q)$
. Let
$\mathbf{V}=(\mathbf{B},q)$
. Let
![]() $\unicode[STIX]{x1D70E}$
be a cuspidal automorphic representation of
$\unicode[STIX]{x1D70E}$
be a cuspidal automorphic representation of
 $\mathbf{GL}_{2}(\mathbf{A})$
which is a discrete series at all places of ramification of
$\mathbf{GL}_{2}(\mathbf{A})$
which is a discrete series at all places of ramification of
![]() $\mathbf{B}$
and let
$\mathbf{B}$
and let
 $\unicode[STIX]{x1D70B}=\bigotimes _{v}\unicode[STIX]{x1D70B}_{v}$
be the representation of
$\unicode[STIX]{x1D70B}=\bigotimes _{v}\unicode[STIX]{x1D70B}_{v}$
be the representation of
![]() $\mathbf{B}^{\times }$
associated to
$\mathbf{B}^{\times }$
associated to
![]() $\unicode[STIX]{x1D70E}$
by the local Jacquet–Langlands correspondence. Then (5.1.3) defines a lifting
$\unicode[STIX]{x1D70E}$
by the local Jacquet–Langlands correspondence. Then (5.1.3) defines a lifting
 $$\begin{eqnarray}\unicode[STIX]{x1D703}\in \operatorname{Hom}_{\mathbf{GL}_{2}(\mathbf{A})\times \mathbf{B}^{\times }\times \mathbf{B}^{\times }}(\unicode[STIX]{x1D70E}\otimes \mathscr{S}(\mathbf{V}\times \mathbf{A}^{\times }),\unicode[STIX]{x1D70B}\otimes \unicode[STIX]{x1D70B}^{\vee }).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}\in \operatorname{Hom}_{\mathbf{GL}_{2}(\mathbf{A})\times \mathbf{B}^{\times }\times \mathbf{B}^{\times }}(\unicode[STIX]{x1D70E}\otimes \mathscr{S}(\mathbf{V}\times \mathbf{A}^{\times }),\unicode[STIX]{x1D70B}\otimes \unicode[STIX]{x1D70B}^{\vee }).\end{eqnarray}$$
It coincides with the lifting denoted by the same name in [Reference Yuan, Zhang and ZhangYZZ12].
Rational liftings. If
![]() $M$
is a number field,
$M$
is a number field,
![]() $\unicode[STIX]{x1D70E}^{\infty }$
is an
$\unicode[STIX]{x1D70E}^{\infty }$
is an
![]() $M$
-rational cuspidal automorphic representation of
$M$
-rational cuspidal automorphic representation of
![]() $\mathbf{GL}_{2}$
of weight
$\mathbf{GL}_{2}$
of weight
![]() $2$
as in the Introduction, and
$2$
as in the Introduction, and
![]() $\unicode[STIX]{x1D70B}$
is its transfer to an
$\unicode[STIX]{x1D70B}$
is its transfer to an
![]() $M$
-rational representation of
$M$
-rational representation of
![]() $\mathbf{B}^{\infty \times }$
under the rational Jacquet–Langlands correspondence of [Reference Yuan, Zhang and ZhangYZZ12, Theorem 3.4], let
$\mathbf{B}^{\infty \times }$
under the rational Jacquet–Langlands correspondence of [Reference Yuan, Zhang and ZhangYZZ12, Theorem 3.4], let
![]() $\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D704}}$
be the associated complex automorphic representation, and
$\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D704}}$
be the associated complex automorphic representation, and
 $\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D704}}=\unicode[STIX]{x1D70B}\otimes _{M,\unicode[STIX]{x1D704}}\mathbf{C}$
for any
$\unicode[STIX]{x1D70B}^{\unicode[STIX]{x1D704}}=\unicode[STIX]{x1D70B}\otimes _{M,\unicode[STIX]{x1D704}}\mathbf{C}$
for any
 $\unicode[STIX]{x1D704}:M{\hookrightarrow}\mathbf{C}$
. Let
$\unicode[STIX]{x1D704}:M{\hookrightarrow}\mathbf{C}$
. Let
 $\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D704}}=\bigotimes _{v}\unicode[STIX]{x1D703}_{v}^{\unicode[STIX]{x1D704}}$
be the liftings just constructed. Then, if
$\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D704}}=\bigotimes _{v}\unicode[STIX]{x1D703}_{v}^{\unicode[STIX]{x1D704}}$
be the liftings just constructed. Then, if
![]() $\mathbf{B}$
is coherent, using the algebraic Petersson product of Lemma 2.4.2, there is a lifting
$\mathbf{B}$
is coherent, using the algebraic Petersson product of Lemma 2.4.2, there is a lifting
 $\unicode[STIX]{x1D703}:\unicode[STIX]{x1D70E}^{\infty }\otimes \overline{\mathscr{S}}(\mathbf{V}^{\infty }\times \mathbf{A}^{\infty ,\times })\rightarrow \unicode[STIX]{x1D70B}\otimes \unicode[STIX]{x1D70B}^{\vee }$
, which is defined over
$\unicode[STIX]{x1D703}:\unicode[STIX]{x1D70E}^{\infty }\otimes \overline{\mathscr{S}}(\mathbf{V}^{\infty }\times \mathbf{A}^{\infty ,\times })\rightarrow \unicode[STIX]{x1D70B}\otimes \unicode[STIX]{x1D70B}^{\vee }$
, which is defined over
![]() $M$
and satisfies
$M$
and satisfies
 $$\begin{eqnarray}\unicode[STIX]{x1D704}\unicode[STIX]{x1D703}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D719}^{\infty })=\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D704}}(\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D704}},\unicode[STIX]{x1D719}^{\infty }\unicode[STIX]{x1D719}_{\infty }^{\unicode[STIX]{x1D704}})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}\unicode[STIX]{x1D703}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D719}^{\infty })=\unicode[STIX]{x1D703}^{\unicode[STIX]{x1D704}}(\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D704}},\unicode[STIX]{x1D719}^{\infty }\unicode[STIX]{x1D719}_{\infty }^{\unicode[STIX]{x1D704}})\end{eqnarray}$$
if
![]() $\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D704}}$
is as described before Lemma 2.4.2 and
$\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D704}}$
is as described before Lemma 2.4.2 and
![]() $\unicode[STIX]{x1D719}_{\infty }^{\unicode[STIX]{x1D704}}$
is standard. On the left-hand side, we view
$\unicode[STIX]{x1D719}_{\infty }^{\unicode[STIX]{x1D704}}$
is standard. On the left-hand side, we view
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $\unicode[STIX]{x1D70B}^{\vee }$
indifferently as a representation of
$\unicode[STIX]{x1D70B}^{\vee }$
indifferently as a representation of
![]() $\mathbf{B}^{\infty \times }$
or
$\mathbf{B}^{\infty \times }$
or
![]() $\mathbf{B}^{\times }$
by tensoring on each with generators of the trivial representation at infinite places which pair to
$\mathbf{B}^{\times }$
by tensoring on each with generators of the trivial representation at infinite places which pair to
![]() $1$
under the duality (this ensures compatibility with the decomposition). After base-change to
$1$
under the duality (this ensures compatibility with the decomposition). After base-change to
 $M\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}(\unicode[STIX]{x1D6F9}_{v})$
, there are local liftings at finite places
$M\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}(\unicode[STIX]{x1D6F9}_{v})$
, there are local liftings at finite places
 $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{\text{univ}},v}:\mathscr{W}(\unicode[STIX]{x1D70E}_{v},\overline{\unicode[STIX]{x1D713}}_{\text{univ},v})\otimes \overline{\mathscr{S}}(V_{v}\times F_{v}^{\times })\rightarrow \unicode[STIX]{x1D70B}_{v}\otimes \unicode[STIX]{x1D70B}_{v}^{\vee }\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}(\unicode[STIX]{x1D6F9}_{v})$
satisfying
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{\text{univ}},v}:\mathscr{W}(\unicode[STIX]{x1D70E}_{v},\overline{\unicode[STIX]{x1D713}}_{\text{univ},v})\otimes \overline{\mathscr{S}}(V_{v}\times F_{v}^{\times })\rightarrow \unicode[STIX]{x1D70B}_{v}\otimes \unicode[STIX]{x1D70B}_{v}^{\vee }\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}(\unicode[STIX]{x1D6F9}_{v})$
satisfying
 $\unicode[STIX]{x1D704}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{\text{univ}},v}(W,\unicode[STIX]{x1D719})(\unicode[STIX]{x1D713}_{v})=\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713},v}^{\unicode[STIX]{x1D704}}(W^{\unicode[STIX]{x1D704}},\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D704}})$
. They induce an incoherent global lifting on
$\unicode[STIX]{x1D704}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{\text{univ}},v}(W,\unicode[STIX]{x1D719})(\unicode[STIX]{x1D713}_{v})=\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713},v}^{\unicode[STIX]{x1D704}}(W^{\unicode[STIX]{x1D704}},\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D704}})$
. They induce an incoherent global lifting on
 $\unicode[STIX]{x1D70E}^{\infty }\otimes \overline{\mathscr{S}}(\mathbf{V}^{\infty }\times \mathbf{A}^{\infty ,\times })$
, which is defined over
$\unicode[STIX]{x1D70E}^{\infty }\otimes \overline{\mathscr{S}}(\mathbf{V}^{\infty }\times \mathbf{A}^{\infty ,\times })$
, which is defined over
![]() $M$
independently of the choice of an additive character of
$M$
independently of the choice of an additive character of
![]() $\mathbf{A}$
trivial on
$\mathbf{A}$
trivial on
![]() $F$
,Footnote
29
and satisfies (5.1.4).
$F$
,Footnote
29
and satisfies (5.1.4).
Finally, for an embedding
 $\unicode[STIX]{x1D704}^{\prime }:M{\hookrightarrow}L$
with
$\unicode[STIX]{x1D704}^{\prime }:M{\hookrightarrow}L$
with
![]() $L$
a
$L$
a
![]() $p$
-adic field, we let
$p$
-adic field, we let
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D704}^{\prime }}:(\unicode[STIX]{x1D70E}^{\infty }\otimes \overline{\mathscr{S}}(\mathbf{V}^{\infty }\times \mathbf{A}^{\infty ,\times }))\otimes _{M}L\rightarrow (\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\vee })\otimes _{M,\unicode[STIX]{x1D704}^{\prime }}L\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D704}^{\prime }}:(\unicode[STIX]{x1D70E}^{\infty }\otimes \overline{\mathscr{S}}(\mathbf{V}^{\infty }\times \mathbf{A}^{\infty ,\times }))\otimes _{M}L\rightarrow (\unicode[STIX]{x1D70B}\times \unicode[STIX]{x1D70B}^{\vee })\otimes _{M,\unicode[STIX]{x1D704}^{\prime }}L\end{eqnarray}$$
be the base-change.
Local toric periods and zeta integrals. Recall from the Introduction that for any dual pair of representations
 $\unicode[STIX]{x1D70B}_{v}\otimes \unicode[STIX]{x1D70B}_{v}^{\vee }$
isomorphic (possibly after an extension of scalars) to the local component of
$\unicode[STIX]{x1D70B}_{v}\otimes \unicode[STIX]{x1D70B}_{v}^{\vee }$
isomorphic (possibly after an extension of scalars) to the local component of
![]() $\unicode[STIX]{x1D70B}\otimes \unicode[STIX]{x1D70B}^{\vee }$
, the normalised toric integrals of matrix coefficients of (1.1.2) are defined, for any
$\unicode[STIX]{x1D70B}\otimes \unicode[STIX]{x1D70B}^{\vee }$
, the normalised toric integrals of matrix coefficients of (1.1.2) are defined, for any
 $\unicode[STIX]{x1D712}\in \mathscr{Y}_{v}(\mathbf{C})$
, by
$\unicode[STIX]{x1D712}\in \mathscr{Y}_{v}(\mathbf{C})$
, by
 $$\begin{eqnarray}Q_{v}(f_{1,v},f_{2,v},\unicode[STIX]{x1D712})=|D|_{v}^{-1/2}|d|_{v}^{-1/2}\frac{L(1,\unicode[STIX]{x1D702}_{v})L(1,\unicode[STIX]{x1D70B}_{v},\operatorname{ad})}{\unicode[STIX]{x1D701}_{F,v}(2)L(1/2,\unicode[STIX]{x1D70B}_{E,v}^{\unicode[STIX]{x1D704}}\otimes \unicode[STIX]{x1D712}_{v})}Q_{v}^{\sharp }(f_{1,v},f_{2,v},\unicode[STIX]{x1D712}_{v}^{\unicode[STIX]{x1D704}}),\end{eqnarray}$$
$$\begin{eqnarray}Q_{v}(f_{1,v},f_{2,v},\unicode[STIX]{x1D712})=|D|_{v}^{-1/2}|d|_{v}^{-1/2}\frac{L(1,\unicode[STIX]{x1D702}_{v})L(1,\unicode[STIX]{x1D70B}_{v},\operatorname{ad})}{\unicode[STIX]{x1D701}_{F,v}(2)L(1/2,\unicode[STIX]{x1D70B}_{E,v}^{\unicode[STIX]{x1D704}}\otimes \unicode[STIX]{x1D712}_{v})}Q_{v}^{\sharp }(f_{1,v},f_{2,v},\unicode[STIX]{x1D712}_{v}^{\unicode[STIX]{x1D704}}),\end{eqnarray}$$
 $$\begin{eqnarray}Q_{v}^{\sharp }(f_{1,v},f_{2,v},\unicode[STIX]{x1D712}_{v})=\int _{E_{v}^{\times }/F_{v}^{\times }}\unicode[STIX]{x1D712}_{v}(t)(\unicode[STIX]{x1D70B}(t)f_{1,v},f_{2,v})\,dt.\end{eqnarray}$$
$$\begin{eqnarray}Q_{v}^{\sharp }(f_{1,v},f_{2,v},\unicode[STIX]{x1D712}_{v})=\int _{E_{v}^{\times }/F_{v}^{\times }}\unicode[STIX]{x1D712}_{v}(t)(\unicode[STIX]{x1D70B}(t)f_{1,v},f_{2,v})\,dt.\end{eqnarray}$$
The following lemma follows from the normalisation (5.1.2) and the definitions of the local toric zeta integrals
![]() $R_{r,v}^{\natural }$
in (3.5.2).
$R_{r,v}^{\natural }$
in (3.5.2).
Lemma 5.1.1. Let
 $\unicode[STIX]{x1D712}\in \mathscr{Y}_{M(\unicode[STIX]{x1D6FC})}^{\text{l.c.}}(\mathbf{C})$
and
$\unicode[STIX]{x1D712}\in \mathscr{Y}_{M(\unicode[STIX]{x1D6FC})}^{\text{l.c.}}(\mathbf{C})$
and
 $\unicode[STIX]{x1D713}=\bigotimes _{v}\unicode[STIX]{x1D713}_{v}:\mathbf{A}/F\rightarrow \mathbf{C}$
be a non-trivial additive character. Let
$\unicode[STIX]{x1D713}=\bigotimes _{v}\unicode[STIX]{x1D713}_{v}:\mathbf{A}/F\rightarrow \mathbf{C}$
be a non-trivial additive character. Let
![]() $Q_{v}$
and
$Q_{v}$
and
![]() $Q_{v}^{\sharp }$
be the pairings defined above for the representation
$Q_{v}^{\sharp }$
be the pairings defined above for the representation
 $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713},v}(\mathscr{W}(\unicode[STIX]{x1D70E}_{v},\overline{\unicode[STIX]{x1D713}}_{v})\otimes \overline{\mathscr{S}}(V_{v}\times F_{v}^{\times }))$
. Then, for all
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713},v}(\mathscr{W}(\unicode[STIX]{x1D70E}_{v},\overline{\unicode[STIX]{x1D713}}_{v})\otimes \overline{\mathscr{S}}(V_{v}\times F_{v}^{\times }))$
. Then, for all
![]() $v\nmid \infty$
, we have
$v\nmid \infty$
, we have
 $$\begin{eqnarray}|d|_{v}^{-3/2}R_{r,v}^{\circ }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v},\unicode[STIX]{x1D713}_{v})=Q_{v}^{\sharp }(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713},v}(W_{v},\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})^{-r_{v}}w_{r,v}^{-1}\unicode[STIX]{x1D719}_{v}),\unicode[STIX]{x1D712}_{v}),\end{eqnarray}$$
$$\begin{eqnarray}|d|_{v}^{-3/2}R_{r,v}^{\circ }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v},\unicode[STIX]{x1D713}_{v})=Q_{v}^{\sharp }(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713},v}(W_{v},\unicode[STIX]{x1D704}\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})^{-r_{v}}w_{r,v}^{-1}\unicode[STIX]{x1D719}_{v}),\unicode[STIX]{x1D712}_{v}),\end{eqnarray}$$
where as usual if
![]() $v\nmid p$
, we set
$v\nmid p$
, we set
![]() $\unicode[STIX]{x1D6FC}_{v}=1$
,
$\unicode[STIX]{x1D6FC}_{v}=1$
,
![]() $r_{v}=0$
,
$r_{v}=0$
,
 $w_{r,v}=1$
.
$w_{r,v}=1$
.
If
![]() $v\nmid p$
, we have
$v\nmid p$
, we have
 $$\begin{eqnarray}\mathscr{R}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v},\unicode[STIX]{x1D713}_{v})=Q_{v}(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713},v}(W_{v},\unicode[STIX]{x1D719}_{v}),\unicode[STIX]{x1D712}_{v})\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{R}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v},\unicode[STIX]{x1D713}_{v})=Q_{v}(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713},v}(W_{v},\unicode[STIX]{x1D719}_{v}),\unicode[STIX]{x1D712}_{v})\end{eqnarray}$$
and, for the product
 $Q^{p}=\prod _{v\nmid p\infty }Q_{v}$
, we have
$Q^{p}=\prod _{v\nmid p\infty }Q_{v}$
, we have
 $$\begin{eqnarray}\mathop{\prod }_{v\nmid p\infty }\mathscr{R}_{r,v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v},\unicode[STIX]{x1D713}_{v})=\frac{D_{F}^{3/2}\unicode[STIX]{x1D701}_{F}^{\infty }(2)}{(\unicode[STIX]{x1D70B}^{2}/2)^{[F:\mathbf{Q}]}}Q^{p}(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}w_{r}^{-1}\unicode[STIX]{x1D719}),\unicode[STIX]{x1D712}).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{v\nmid p\infty }\mathscr{R}_{r,v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v},\unicode[STIX]{x1D713}_{v})=\frac{D_{F}^{3/2}\unicode[STIX]{x1D701}_{F}^{\infty }(2)}{(\unicode[STIX]{x1D70B}^{2}/2)^{[F:\mathbf{Q}]}}Q^{p}(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}w_{r}^{-1}\unicode[STIX]{x1D719}),\unicode[STIX]{x1D712}).\end{eqnarray}$$
5.2 Hecke correspondences and generating series
Referring to [Reference Yuan, Zhang and ZhangYZZ12, §3.1] for more details, let us recall some basic notions on the Shimura curves
![]() $X_{U}$
. The set of geometrically connected components is
$X_{U}$
. The set of geometrically connected components is
 $\unicode[STIX]{x1D70B}_{0}(X_{U,\overline{F}})\cong F_{+}^{\times }\backslash \mathbf{A}^{\infty ,\times }/q(U)$
. The curve
$\unicode[STIX]{x1D70B}_{0}(X_{U,\overline{F}})\cong F_{+}^{\times }\backslash \mathbf{A}^{\infty ,\times }/q(U)$
. The curve
![]() $X_{U}$
admits a canonical divisor class (the Hodge class)
$X_{U}$
admits a canonical divisor class (the Hodge class)
 $\unicode[STIX]{x1D709}_{U}=(1/\text{deg}\,L_{U})L_{U}$
of degree
$\unicode[STIX]{x1D709}_{U}=(1/\text{deg}\,L_{U})L_{U}$
of degree
![]() $1$
on each geometrically connected component; here
$1$
on each geometrically connected component; here
 $$\begin{eqnarray}L_{U}=\unicode[STIX]{x1D714}_{X_{U}/F}+\mathop{\sum }_{x\in X_{U}(\overline{F})}(1-e_{x}^{-1})x,\end{eqnarray}$$
$$\begin{eqnarray}L_{U}=\unicode[STIX]{x1D714}_{X_{U}/F}+\mathop{\sum }_{x\in X_{U}(\overline{F})}(1-e_{x}^{-1})x,\end{eqnarray}$$
a line bundle defined over
![]() $F$
; here
$F$
; here
![]() $\unicode[STIX]{x1D714}_{X_{U}/F}$
is the canonical bundle and
$\unicode[STIX]{x1D714}_{X_{U}/F}$
is the canonical bundle and
![]() $e_{x}$
is the ramification index (see [Reference Yuan, Zhang and ZhangYZZ12, §3.1.3] for the precise definition) of the point
$e_{x}$
is the ramification index (see [Reference Yuan, Zhang and ZhangYZZ12, §3.1.3] for the precise definition) of the point
![]() $x$
.
$x$
.
Hecke correspondences. For
 $x\in \mathbf{B}^{\infty \times }$
, let
$x\in \mathbf{B}^{\infty \times }$
, let
 $\text{T}_{x}:X_{xUx^{-1}}\rightarrow X_{U}$
be the translation, given in the complex uniformisation by
$\text{T}_{x}:X_{xUx^{-1}}\rightarrow X_{U}$
be the translation, given in the complex uniformisation by
 $\text{T}_{x}([z,y])=[z,yx]$
. Let
$\text{T}_{x}([z,y])=[z,yx]$
. Let
 $\text{p}:X_{U\cap xUx^{-1}}\rightarrow X_{U}$
be the projection and let
$\text{p}:X_{U\cap xUx^{-1}}\rightarrow X_{U}$
be the projection and let
![]() $Z(x)_{U}$
be the image of
$Z(x)_{U}$
be the image of
 $$\begin{eqnarray}(\text{p},\text{p}\circ \text{T}_{x}):X_{U\cap xUx^{-1}}\rightarrow X_{U}\times X_{U}.\end{eqnarray}$$
$$\begin{eqnarray}(\text{p},\text{p}\circ \text{T}_{x}):X_{U\cap xUx^{-1}}\rightarrow X_{U}\times X_{U}.\end{eqnarray}$$
We view
![]() $Z(x)_{U}$
as a correspondence on
$Z(x)_{U}$
as a correspondence on
![]() $X_{U}$
, and we will sometimes use the same notation for the image of
$X_{U}$
, and we will sometimes use the same notation for the image of
![]() $Z(x)_{U}$
in
$Z(x)_{U}$
in
 $\operatorname{Pic}(X_{U}\times X_{U})$
(such abuses will be made clear in what follows).
$\operatorname{Pic}(X_{U}\times X_{U})$
(such abuses will be made clear in what follows).
We obtain an action of the Hecke algebra
 $\mathscr{H}_{\mathbf{B}^{\infty \times },U}:=C_{c}^{\infty }(\mathbf{B}^{\infty \times })^{U\times U}$
of
$\mathscr{H}_{\mathbf{B}^{\infty \times },U}:=C_{c}^{\infty }(\mathbf{B}^{\infty \times })^{U\times U}$
of
![]() $U$
-bi-invariant functions on
$U$
-bi-invariant functions on
![]() $\mathbf{B}^{\infty \times }$
by
$\mathbf{B}^{\infty \times }$
by
 $$\begin{eqnarray}\text{T}(h)_{U}=\mathop{\sum }_{x\in U\backslash \mathbf{B}^{\infty \times }/U}h(x)Z(x)_{U}.\end{eqnarray}$$
$$\begin{eqnarray}\text{T}(h)_{U}=\mathop{\sum }_{x\in U\backslash \mathbf{B}^{\infty \times }/U}h(x)Z(x)_{U}.\end{eqnarray}$$
Note the obvious relation
 $Z(x)_{U}=\text{T}(\mathbf{1}_{UxU})_{U}$
. The transpose
$Z(x)_{U}=\text{T}(\mathbf{1}_{UxU})_{U}$
. The transpose
![]() $\text{T}(h)^{\text{t}}$
equals
$\text{T}(h)^{\text{t}}$
equals
![]() $\text{T}(h^{\text{t}})$
with
$\text{T}(h^{\text{t}})$
with
 $h^{\text{t}}(x):=h(x^{-1})$
. It is then easy to verify that if
$h^{\text{t}}(x):=h(x^{-1})$
. It is then easy to verify that if
![]() $x$
has trivial components away from the set of places where
$x$
has trivial components away from the set of places where
![]() $U$
is maximal, we have
$U$
is maximal, we have
 $$\begin{eqnarray}Z(x)_{U}^{\text{t}}=Z(q(x)^{-1})_{U}Z(x)_{U}.\end{eqnarray}$$
$$\begin{eqnarray}Z(x)_{U}^{\text{t}}=Z(q(x)^{-1})_{U}Z(x)_{U}.\end{eqnarray}$$
Finally, for any simple quotient
![]() $A^{\prime }/F$
of
$A^{\prime }/F$
of
![]() $J$
with
$J$
with
 $M^{\prime }=\operatorname{End}^{0}(A^{\prime })$
, we have a
$M^{\prime }=\operatorname{End}^{0}(A^{\prime })$
, we have a
![]() $\mathbf{Q}$
-linear map
$\mathbf{Q}$
-linear map
 $$\begin{eqnarray}\displaystyle \text{T}_{\text{alg}}:\unicode[STIX]{x1D70B}_{A^{\prime }}\otimes _{M^{\prime }}\unicode[STIX]{x1D70B}_{A^{\prime \vee }} & \rightarrow & \displaystyle \operatorname{Hom}^{0}(J,J^{\vee })\nonumber\\ \displaystyle f_{1}\otimes f_{2} & \mapsto & \displaystyle f_{2}^{\vee }\circ f_{1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{T}_{\text{alg}}:\unicode[STIX]{x1D70B}_{A^{\prime }}\otimes _{M^{\prime }}\unicode[STIX]{x1D70B}_{A^{\prime \vee }} & \rightarrow & \displaystyle \operatorname{Hom}^{0}(J,J^{\vee })\nonumber\\ \displaystyle f_{1}\otimes f_{2} & \mapsto & \displaystyle f_{2}^{\vee }\circ f_{1}.\nonumber\end{eqnarray}$$
If
 $\unicode[STIX]{x1D704}:M^{\prime }{\hookrightarrow}L^{\prime }$
is any embedding into a
$\unicode[STIX]{x1D704}:M^{\prime }{\hookrightarrow}L^{\prime }$
is any embedding into a
![]() $p$
-adic field
$p$
-adic field
![]() $L^{\prime }$
, we denote by
$L^{\prime }$
, we denote by

the composition in which the first arrow is deduced from the unique
![]() $L^{\prime }$
-linear embedding
$L^{\prime }$
-linear embedding
 $L^{\prime }{\hookrightarrow}M^{\prime }\otimes _{\mathbf{Q}}L^{\prime }$
whose composition with
$L^{\prime }{\hookrightarrow}M^{\prime }\otimes _{\mathbf{Q}}L^{\prime }$
whose composition with
 $M^{\prime }\otimes _{\mathbf{Q}}L^{\prime }\rightarrow L^{\prime }$
,
$M^{\prime }\otimes _{\mathbf{Q}}L^{\prime }\rightarrow L^{\prime }$
,
 $x\otimes y\mapsto \unicode[STIX]{x1D704}(x)y$
, is
$x\otimes y\mapsto \unicode[STIX]{x1D704}(x)y$
, is
![]() $\text{id}_{L^{\prime }}$
.
$\text{id}_{L^{\prime }}$
.
Generating series. For any
 $\unicode[STIX]{x1D719}\in \overline{\mathscr{S}}(\mathbf{V}\times \mathbf{A}^{\times })$
invariant under
$\unicode[STIX]{x1D719}\in \overline{\mathscr{S}}(\mathbf{V}\times \mathbf{A}^{\times })$
invariant under
 $K=U\times U$
, define a generating series
$K=U\times U$
, define a generating series
 $$\begin{eqnarray}Z(\unicode[STIX]{x1D719}):=Z_{0}(\unicode[STIX]{x1D719})_{U}+Z_{\ast }(\unicode[STIX]{x1D719})_{U},\end{eqnarray}$$
$$\begin{eqnarray}Z(\unicode[STIX]{x1D719}):=Z_{0}(\unicode[STIX]{x1D719})_{U}+Z_{\ast }(\unicode[STIX]{x1D719})_{U},\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle Z_{0}(\unicode[STIX]{x1D719})_{U} & := & \displaystyle -\mathop{\sum }_{\unicode[STIX]{x1D6FD}\in F_{+}^{\times }\backslash \mathbf{A}^{\infty ,\times }/q(U)}\mathop{\sum }_{u\in \unicode[STIX]{x1D707}_{U^{p}}^{2}\backslash F^{\times }}E_{0}(\unicode[STIX]{x1D6FD}^{-1}u,\unicode[STIX]{x1D719})L_{K,\unicode[STIX]{x1D6FD}},\nonumber\\ \displaystyle Z_{a}(\unicode[STIX]{x1D719})_{U} & := & \displaystyle w_{U}\mathop{\sum }_{x\in K\backslash \mathbf{B}^{\infty \times }}\unicode[STIX]{x1D719}(x,aq(x)^{-1})Z(x)_{U}\quad \text{for}~a\in F^{\times },\nonumber\\ \displaystyle Z_{\ast }(\unicode[STIX]{x1D719})_{U} & := & \displaystyle \mathop{\sum }_{a\in F^{\times }}Z_{a}(\unicode[STIX]{x1D719})_{U}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Z_{0}(\unicode[STIX]{x1D719})_{U} & := & \displaystyle -\mathop{\sum }_{\unicode[STIX]{x1D6FD}\in F_{+}^{\times }\backslash \mathbf{A}^{\infty ,\times }/q(U)}\mathop{\sum }_{u\in \unicode[STIX]{x1D707}_{U^{p}}^{2}\backslash F^{\times }}E_{0}(\unicode[STIX]{x1D6FD}^{-1}u,\unicode[STIX]{x1D719})L_{K,\unicode[STIX]{x1D6FD}},\nonumber\\ \displaystyle Z_{a}(\unicode[STIX]{x1D719})_{U} & := & \displaystyle w_{U}\mathop{\sum }_{x\in K\backslash \mathbf{B}^{\infty \times }}\unicode[STIX]{x1D719}(x,aq(x)^{-1})Z(x)_{U}\quad \text{for}~a\in F^{\times },\nonumber\\ \displaystyle Z_{\ast }(\unicode[STIX]{x1D719})_{U} & := & \displaystyle \mathop{\sum }_{a\in F^{\times }}Z_{a}(\unicode[STIX]{x1D719})_{U}\nonumber\end{eqnarray}$$
with
 $w_{U}=|\{\pm 1\}\cap U|$
. Here
$w_{U}=|\{\pm 1\}\cap U|$
. Here
![]() $L_{K,\unicode[STIX]{x1D6FD}}$
denotes the component of a Hodge class in
$L_{K,\unicode[STIX]{x1D6FD}}$
denotes the component of a Hodge class in
 $\operatorname{Pic}(X_{U}\times X_{U})_{\mathbf{Q}}$
obtained from the classes
$\operatorname{Pic}(X_{U}\times X_{U})_{\mathbf{Q}}$
obtained from the classes
![]() $L_{U}$
(see [Reference Yuan, Zhang and ZhangYZZ12, §3.4.4]) and
$L_{U}$
(see [Reference Yuan, Zhang and ZhangYZZ12, §3.4.4]) and
 $$\begin{eqnarray}E_{0}(u,\unicode[STIX]{x1D719})=\unicode[STIX]{x1D719}(0,u)+W_{0}(u,\unicode[STIX]{x1D719})\end{eqnarray}$$
$$\begin{eqnarray}E_{0}(u,\unicode[STIX]{x1D719})=\unicode[STIX]{x1D719}(0,u)+W_{0}(u,\unicode[STIX]{x1D719})\end{eqnarray}$$
is the constant term of the standard Eisenstein series: its intertwining part
 $W_{0}(u,\unicode[STIX]{x1D719})$
is the value at
$W_{0}(u,\unicode[STIX]{x1D719})$
is the value at
![]() $s=0$
of
$s=0$
of
 $$\begin{eqnarray}W_{0}(s,u,\unicode[STIX]{x1D719})=\int _{\mathbf{A}}\unicode[STIX]{x1D6FF}(wn(b))^{s}r(wn(b))\unicode[STIX]{x1D719}(0,u)\,db,\end{eqnarray}$$
$$\begin{eqnarray}W_{0}(s,u,\unicode[STIX]{x1D719})=\int _{\mathbf{A}}\unicode[STIX]{x1D6FF}(wn(b))^{s}r(wn(b))\unicode[STIX]{x1D719}(0,u)\,db,\end{eqnarray}$$
where
 $\unicode[STIX]{x1D6FF}(g)=|a/d|^{1/2}$
if
$\unicode[STIX]{x1D6FF}(g)=|a/d|^{1/2}$
if
 $g=(\!\begin{smallmatrix}a & \ast \\ & d\end{smallmatrix}\!)k$
with
$g=(\!\begin{smallmatrix}a & \ast \\ & d\end{smallmatrix}\!)k$
with
 $k\in \mathbf{GL}_{2}(\widehat{\mathscr{O}}_{F})\mathbf{SO}(2,F_{\infty })$
.
$k\in \mathbf{GL}_{2}(\widehat{\mathscr{O}}_{F})\mathbf{SO}(2,F_{\infty })$
.
For
 $g\in \mathbf{GL}_{2}(\mathbf{A})$
, define
$g\in \mathbf{GL}_{2}(\mathbf{A})$
, define
 $$\begin{eqnarray}Z(g,\unicode[STIX]{x1D719})=Z(r(g)\unicode[STIX]{x1D719}),\end{eqnarray}$$
$$\begin{eqnarray}Z(g,\unicode[STIX]{x1D719})=Z(r(g)\unicode[STIX]{x1D719}),\end{eqnarray}$$
and similarly
 $Z_{0}(g,\unicode[STIX]{x1D719})_{U}$
,
$Z_{0}(g,\unicode[STIX]{x1D719})_{U}$
,
 $Z_{a}(g,\unicode[STIX]{x1D719})_{U}$
,
$Z_{a}(g,\unicode[STIX]{x1D719})_{U}$
,
 $Z_{\ast }(g,\unicode[STIX]{x1D719})_{U}$
.
$Z_{\ast }(g,\unicode[STIX]{x1D719})_{U}$
.
Let
 $U=U^{p}U_{p}$
and
$U=U^{p}U_{p}$
and
![]() $c_{U^{p}}$
be as in (3.4.3). By [Reference Yuan, Zhang and ZhangYZZ12, §3.4.6], the normalised versions
$c_{U^{p}}$
be as in (3.4.3). By [Reference Yuan, Zhang and ZhangYZZ12, §3.4.6], the normalised versions
 $$\begin{eqnarray}\widetilde{Z}(g,\unicode[STIX]{x1D719}):=c_{U^{p}}Z(g,\unicode[STIX]{x1D719})_{U},\quad \widetilde{Z}_{a}(g,\unicode[STIX]{x1D719}):=c_{U^{p}}Z_{a}(g,\unicode[STIX]{x1D719})_{U},\quad \ldots\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{Z}(g,\unicode[STIX]{x1D719}):=c_{U^{p}}Z(g,\unicode[STIX]{x1D719})_{U},\quad \widetilde{Z}_{a}(g,\unicode[STIX]{x1D719}):=c_{U^{p}}Z_{a}(g,\unicode[STIX]{x1D719})_{U},\quad \ldots\end{eqnarray}$$
are independent of
![]() $U^{p}$
. A key result, which is essentially a special case of the main theorem of [Reference Yuan, Zhang and ZhangYZ09], is that the series
$U^{p}$
. A key result, which is essentially a special case of the main theorem of [Reference Yuan, Zhang and ZhangYZ09], is that the series
![]() $\widetilde{Z}(g,\unicode[STIX]{x1D719})$
defines an automorphic form valued in
$\widetilde{Z}(g,\unicode[STIX]{x1D719})$
defines an automorphic form valued in
 $\operatorname{Pic}(X\times X)_{\mathbf{Q}}$
.
$\operatorname{Pic}(X\times X)_{\mathbf{Q}}$
.
Theorem 5.2.1. The map
 $$\begin{eqnarray}(\unicode[STIX]{x1D719},g)\mapsto \widetilde{Z}(g,\unicode[STIX]{x1D719})\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D719},g)\mapsto \widetilde{Z}(g,\unicode[STIX]{x1D719})\end{eqnarray}$$
defines an element
 $$\begin{eqnarray}\widetilde{Z}\in \operatorname{Hom}_{\mathbf{B}^{\times }\times \mathbf{B}^{\times }}(\overline{\mathscr{S}}(\mathbf{V}\times \mathbf{A}^{\times }),C^{\infty }(\mathbf{GL}_{2}(F)\backslash \mathbf{GL}_{2}(\mathbf{A}))\otimes \operatorname{Pic}(X\times X)_{\mathbf{Q}}).\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{Z}\in \operatorname{Hom}_{\mathbf{B}^{\times }\times \mathbf{B}^{\times }}(\overline{\mathscr{S}}(\mathbf{V}\times \mathbf{A}^{\times }),C^{\infty }(\mathbf{GL}_{2}(F)\backslash \mathbf{GL}_{2}(\mathbf{A}))\otimes \operatorname{Pic}(X\times X)_{\mathbf{Q}}).\end{eqnarray}$$
Here the target denotes the set of
 $\operatorname{Pic}(X\times X)$
-valued series
$\operatorname{Pic}(X\times X)$
-valued series
![]() $\widetilde{Z}$
such that for any linear functional
$\widetilde{Z}$
such that for any linear functional
 $\unicode[STIX]{x1D706}:\operatorname{Pic}(X\times X)_{\mathbf{Q}}\rightarrow \mathbf{Q}$
, the series
$\unicode[STIX]{x1D706}:\operatorname{Pic}(X\times X)_{\mathbf{Q}}\rightarrow \mathbf{Q}$
, the series
![]() $\unicode[STIX]{x1D706}(\widetilde{Z})$
is absolutely convergent and defines an automorphic form. Its constant term is non-holomorphic in general (in fact, only when
$\unicode[STIX]{x1D706}(\widetilde{Z})$
is absolutely convergent and defines an automorphic form. Its constant term is non-holomorphic in general (in fact, only when
![]() $F=\mathbf{Q}$
and
$F=\mathbf{Q}$
and
![]() $\unicode[STIX]{x1D6F4}=\infty$
). (However, the geometric kernel that we introduce next will always be a holomorphic cusp form of weight
$\unicode[STIX]{x1D6F4}=\infty$
). (However, the geometric kernel that we introduce next will always be a holomorphic cusp form of weight
![]() $2$
.) See [Reference Yuan, Zhang and ZhangYZZ12, Theorem 3.17 and Lemma 3.18] for the proof of the theorem.
$2$
.) See [Reference Yuan, Zhang and ZhangYZZ12, Theorem 3.17 and Lemma 3.18] for the proof of the theorem.
Assume from now on that
![]() $\unicode[STIX]{x1D719}_{\infty }$
is standard; we accordingly only write
$\unicode[STIX]{x1D719}_{\infty }$
is standard; we accordingly only write
![]() $Z(\unicode[STIX]{x1D719}^{\infty })$
,
$Z(\unicode[STIX]{x1D719}^{\infty })$
,
![]() $\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty })$
, …. Define, for each
$\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty })$
, …. Define, for each
![]() $a\in \mathbf{A}^{\times }$
,
$a\in \mathbf{A}^{\times }$
,
 $$\begin{eqnarray}\widetilde{Z}_{a}(\unicode[STIX]{x1D719}^{\infty }):=c_{U^{p}}w_{U}|a|\mathop{\sum }_{x\in K\backslash \mathbf{B}^{\infty \times }}\unicode[STIX]{x1D719}^{\infty }(x,aq(x)^{-1})Z(x)_{U}\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{Z}_{a}(\unicode[STIX]{x1D719}^{\infty }):=c_{U^{p}}w_{U}|a|\mathop{\sum }_{x\in K\backslash \mathbf{B}^{\infty \times }}\unicode[STIX]{x1D719}^{\infty }(x,aq(x)^{-1})Z(x)_{U}\end{eqnarray}$$
for any sufficiently small
![]() $U$
. This extends the previous definition for
$U$
. This extends the previous definition for
![]() $a\in F^{\times }$
, and it is easy to check that for every
$a\in F^{\times }$
, and it is easy to check that for every
 $y\in \mathbf{A}^{\infty ,\times }$
,
$y\in \mathbf{A}^{\infty ,\times }$
,
![]() $a\in F^{\times }$
, we have
$a\in F^{\times }$
, we have
 $$\begin{eqnarray}\widetilde{Z}_{a}((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!),\unicode[STIX]{x1D719}^{\infty })=|ay|_{\infty }\widetilde{Z}_{ay}(\unicode[STIX]{x1D719}^{\infty })\unicode[STIX]{x1D713}(iay_{\infty }).\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{Z}_{a}((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!),\unicode[STIX]{x1D719}^{\infty })=|ay|_{\infty }\widetilde{Z}_{ay}(\unicode[STIX]{x1D719}^{\infty })\unicode[STIX]{x1D713}(iay_{\infty }).\end{eqnarray}$$
In other words, the images in
 $\operatorname{Pic}(X_{U}\times X_{U})$
of the
$\operatorname{Pic}(X_{U}\times X_{U})$
of the
 $\widetilde{Z}_{a}(\unicode[STIX]{x1D719}^{\infty })$
are the reduced
$\widetilde{Z}_{a}(\unicode[STIX]{x1D719}^{\infty })$
are the reduced
![]() $q$
-expansion coefficients of
$q$
-expansion coefficients of
![]() $\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty })$
, in the following sense: for any functional
$\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty })$
, in the following sense: for any functional
![]() $\unicode[STIX]{x1D706}$
as above,
$\unicode[STIX]{x1D706}$
as above,
 $(\unicode[STIX]{x1D706}(\widetilde{Z}_{0}(y,\unicode[STIX]{x1D719})),(\unicode[STIX]{x1D706}(\widetilde{Z}_{a}(\unicode[STIX]{x1D719}^{\infty })))_{a})$
are the reduced
$(\unicode[STIX]{x1D706}(\widetilde{Z}_{0}(y,\unicode[STIX]{x1D719})),(\unicode[STIX]{x1D706}(\widetilde{Z}_{a}(\unicode[STIX]{x1D719}^{\infty })))_{a})$
are the reduced
![]() $q$
-expansion coefficients of the modular form
$q$
-expansion coefficients of the modular form
 $\unicode[STIX]{x1D706}(\widetilde{Z})(\unicode[STIX]{x1D719})$
.
$\unicode[STIX]{x1D706}(\widetilde{Z})(\unicode[STIX]{x1D719})$
.
Hecke operators and Hecke correspondences. For the following lemma, let
![]() $S$
be a set of finite places of
$S$
be a set of finite places of
![]() $F$
such that for all
$F$
such that for all
![]() $v\notin S$
,
$v\notin S$
,
![]() $\mathbf{B}_{v}$
is split,
$\mathbf{B}_{v}$
is split,
![]() $U_{v}$
is maximal, and
$U_{v}$
is maximal, and
![]() $\unicode[STIX]{x1D719}_{v}$
is standard. Fix any isomorphism
$\unicode[STIX]{x1D719}_{v}$
is standard. Fix any isomorphism
 $\unicode[STIX]{x1D6FE}:\mathbf{B}^{S}\rightarrow M_{2}(\mathbf{A}^{S})$
of
$\unicode[STIX]{x1D6FE}:\mathbf{B}^{S}\rightarrow M_{2}(\mathbf{A}^{S})$
of
![]() $\mathbf{A}^{S}$
-algebras carrying the reduced norm to the determinant and
$\mathbf{A}^{S}$
-algebras carrying the reduced norm to the determinant and
![]() $\mathscr{O}_{\mathbf{B}^{S}}$
to
$\mathscr{O}_{\mathbf{B}^{S}}$
to
 $M_{2}(\widehat{\mathscr{O}_{F}}\text{}^{S})$
; such an isomorphism is unique up to conjugation by
$M_{2}(\widehat{\mathscr{O}_{F}}\text{}^{S})$
; such an isomorphism is unique up to conjugation by
![]() $\mathscr{O}_{\mathbf{B}^{S}}^{\times }$
.
$\mathscr{O}_{\mathbf{B}^{S}}^{\times }$
.
Lemma 5.2.2. Let
 $U^{\prime }\text{}^{S}=\mathbf{GL}_{2}(\widehat{\mathscr{O}_{F}}\text{}^{S})$
, and identify the commutative algebras
$U^{\prime }\text{}^{S}=\mathbf{GL}_{2}(\widehat{\mathscr{O}_{F}}\text{}^{S})$
, and identify the commutative algebras
 $\mathscr{H}_{U^{\prime }\text{}^{S}}^{S}=\mathscr{H}_{\mathbf{GL}_{2}(\mathbf{A}^{\infty }),U^{\prime }\text{}^{S}}^{S}$
with
$\mathscr{H}_{U^{\prime }\text{}^{S}}^{S}=\mathscr{H}_{\mathbf{GL}_{2}(\mathbf{A}^{\infty }),U^{\prime }\text{}^{S}}^{S}$
with
 $\mathscr{H}_{\mathbf{B}^{\infty \times },U}^{S}$
via the isomorphism
$\mathscr{H}_{\mathbf{B}^{\infty \times },U}^{S}$
via the isomorphism
![]() $\unicode[STIX]{x1D6FE}^{\ast }$
induced by
$\unicode[STIX]{x1D6FE}^{\ast }$
induced by
![]() $\unicode[STIX]{x1D6FE}$
above. Then, for each
$\unicode[STIX]{x1D6FE}$
above. Then, for each
 $h\in \mathscr{H}_{U^{\prime }\text{}^{S}}^{S}$
, we have
$h\in \mathscr{H}_{U^{\prime }\text{}^{S}}^{S}$
, we have
 $$\begin{eqnarray}T(h)Z_{\ast }(\unicode[STIX]{x1D719}^{\infty })_{U}=\text{T}(\unicode[STIX]{x1D6FE}^{\ast }h)_{U}\circ Z_{\ast }(\unicode[STIX]{x1D719}^{\infty })_{U}.\end{eqnarray}$$
$$\begin{eqnarray}T(h)Z_{\ast }(\unicode[STIX]{x1D719}^{\infty })_{U}=\text{T}(\unicode[STIX]{x1D6FE}^{\ast }h)_{U}\circ Z_{\ast }(\unicode[STIX]{x1D719}^{\infty })_{U}.\end{eqnarray}$$
In the left-hand side, we view
 $Z_{\ast }(\unicode[STIX]{x1D719}^{\infty })$
as a reduced
$Z_{\ast }(\unicode[STIX]{x1D719}^{\infty })$
as a reduced
![]() $q$
-expansion of central character
$q$
-expansion of central character
 $z\mapsto Z(z)$
, and
$z\mapsto Z(z)$
, and
![]() $T(h)$
is the usual Hecke operator acting by (2.2.1); in the right-hand side, the symbol
$T(h)$
is the usual Hecke operator acting by (2.2.1); in the right-hand side, the symbol
![]() $\circ$
denotes composition of correspondences on
$\circ$
denotes composition of correspondences on
![]() $X_{U}$
.
$X_{U}$
.
In particular, the right-hand side is independent of the choice of
![]() $\unicode[STIX]{x1D6FE}$
.
$\unicode[STIX]{x1D6FE}$
.
Proof. It suffices to check the statements for the set of generators of the algebra
![]() $\mathscr{H}_{U^{\prime }\text{}^{S}}^{S}$
consisting of elements
$\mathscr{H}_{U^{\prime }\text{}^{S}}^{S}$
consisting of elements
 $h=h_{v}h^{vS}$
, with
$h=h_{v}h^{vS}$
, with
![]() $h^{vS}$
the unit of
$h^{vS}$
the unit of
![]() $\mathscr{H}_{U^{\prime }\text{}^{S}}^{vS}$
and
$\mathscr{H}_{U^{\prime }\text{}^{S}}^{vS}$
and
 $h_{v}=\mathbf{1}_{U_{v}x_{v}U_{v}}$
for
$h_{v}=\mathbf{1}_{U_{v}x_{v}U_{v}}$
for
 $x_{v}=(\!\begin{smallmatrix}\unicode[STIX]{x1D71B}_{v} & \\ & 1\end{smallmatrix}\!)$
or
$x_{v}=(\!\begin{smallmatrix}\unicode[STIX]{x1D71B}_{v} & \\ & 1\end{smallmatrix}\!)$
or
 $x_{v}=(\!\begin{smallmatrix}\unicode[STIX]{x1D71B}_{v}^{\pm 1} & \\ & \unicode[STIX]{x1D71B}_{v}^{\pm 1}\end{smallmatrix}\!)$
and
$x_{v}=(\!\begin{smallmatrix}\unicode[STIX]{x1D71B}_{v}^{\pm 1} & \\ & \unicode[STIX]{x1D71B}_{v}^{\pm 1}\end{smallmatrix}\!)$
and
![]() $v\notin S$
. In the second case the statement is clear.
$v\notin S$
. In the second case the statement is clear.
Suppose then that
 $x_{v}=(\!\begin{smallmatrix}\unicode[STIX]{x1D71B}_{v} & \\ & 1\end{smallmatrix}\!)$
. Decomposing
$x_{v}=(\!\begin{smallmatrix}\unicode[STIX]{x1D71B}_{v} & \\ & 1\end{smallmatrix}\!)$
. Decomposing
 $Z_{a}(\unicode[STIX]{x1D719})_{U}=Z_{a^{v}}(\unicode[STIX]{x1D719}^{v})_{U}Z_{a_{v}}(\unicode[STIX]{x1D719}_{v})_{U}$
, the
$Z_{a}(\unicode[STIX]{x1D719})_{U}=Z_{a^{v}}(\unicode[STIX]{x1D719}^{v})_{U}Z_{a_{v}}(\unicode[STIX]{x1D719}_{v})_{U}$
, the
![]() $a$
th coefficient of the left-hand side equals
$a$
th coefficient of the left-hand side equals
 $$\begin{eqnarray}Z_{a\unicode[STIX]{x1D71B}_{v}}(\unicode[STIX]{x1D719}^{\infty })_{U}+Z(\unicode[STIX]{x1D71B}_{v})_{U}Z_{a/\unicode[STIX]{x1D71B}_{v}}(\unicode[STIX]{x1D711}^{\infty })_{U}=Z_{a^{v}}(\unicode[STIX]{x1D719}^{v})_{U}\circ (Z_{a_{v}\unicode[STIX]{x1D71B}_{v}}(\unicode[STIX]{x1D719}_{v})_{U}+Z(\unicode[STIX]{x1D71B}_{v})_{U}Z_{a_{v}/\unicode[STIX]{x1D71B}_{v}}(\unicode[STIX]{x1D719}_{v})).\end{eqnarray}$$
$$\begin{eqnarray}Z_{a\unicode[STIX]{x1D71B}_{v}}(\unicode[STIX]{x1D719}^{\infty })_{U}+Z(\unicode[STIX]{x1D71B}_{v})_{U}Z_{a/\unicode[STIX]{x1D71B}_{v}}(\unicode[STIX]{x1D711}^{\infty })_{U}=Z_{a^{v}}(\unicode[STIX]{x1D719}^{v})_{U}\circ (Z_{a_{v}\unicode[STIX]{x1D71B}_{v}}(\unicode[STIX]{x1D719}_{v})_{U}+Z(\unicode[STIX]{x1D71B}_{v})_{U}Z_{a_{v}/\unicode[STIX]{x1D71B}_{v}}(\unicode[STIX]{x1D719}_{v})).\end{eqnarray}$$
It is not difficult to identify this with the
![]() $a$
th coefficient of the right-hand side using the Cartan decomposition
$a$
th coefficient of the right-hand side using the Cartan decomposition
 $$\begin{eqnarray}Z_{a_{v}}(\unicode[STIX]{x1D719}_{v})_{U}=\mathop{\sum }_{0\leqslant j\leqslant i\leqslant v(a),i+j=v(a)}Z\biggl(\biggl(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D71B}_{v}^{i} & \\ & \unicode[STIX]{x1D71B}_{v}^{j}\end{array}) \biggr)_{U}\end{eqnarray}$$
$$\begin{eqnarray}Z_{a_{v}}(\unicode[STIX]{x1D719}_{v})_{U}=\mathop{\sum }_{0\leqslant j\leqslant i\leqslant v(a),i+j=v(a)}Z\biggl(\biggl(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D71B}_{v}^{i} & \\ & \unicode[STIX]{x1D71B}_{v}^{j}\end{array}) \biggr)_{U}\end{eqnarray}$$
and the relation
 $$\begin{eqnarray}Z\biggl(\biggl(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D71B}_{v} & \\ & 1\end{array}) \biggr)_{U}\circ Z\biggl(\biggl(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D71B}_{v}^{i} & \\ & \unicode[STIX]{x1D71B}_{v}^{j}\end{array}) \biggr)_{U}=Z\biggl(\biggl(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D71B}_{v}^{i+1} & \\ & \unicode[STIX]{x1D71B}_{v}^{j}\end{array}) \biggr)_{U}+Z(\unicode[STIX]{x1D71B}_{v})_{U}Z\biggl(\biggl(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D71B}_{v}^{i-1} & \\ & \unicode[STIX]{x1D71B}_{v}^{j}\end{array}) \biggr)_{U}\end{eqnarray}$$
$$\begin{eqnarray}Z\biggl(\biggl(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D71B}_{v} & \\ & 1\end{array}) \biggr)_{U}\circ Z\biggl(\biggl(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D71B}_{v}^{i} & \\ & \unicode[STIX]{x1D71B}_{v}^{j}\end{array}) \biggr)_{U}=Z\biggl(\biggl(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D71B}_{v}^{i+1} & \\ & \unicode[STIX]{x1D71B}_{v}^{j}\end{array}) \biggr)_{U}+Z(\unicode[STIX]{x1D71B}_{v})_{U}Z\biggl(\biggl(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D71B}_{v}^{i-1} & \\ & \unicode[STIX]{x1D71B}_{v}^{j}\end{array}) \biggr)_{U}\end{eqnarray}$$
valid whenever
![]() $i>0$
.Footnote
30
◻
$i>0$
.Footnote
30
◻
5.3 Geometric kernel function
Fix a point
 $P\in X^{E^{\times }}(E^{\text{ab}})$
as in the Introduction and, for any
$P\in X^{E^{\times }}(E^{\text{ab}})$
as in the Introduction and, for any
 $h\in \mathbf{B}^{\infty \times }$
, denote
$h\in \mathbf{B}^{\infty \times }$
, denote
 $$\begin{eqnarray}[h]:=\text{T}_{h}P,\quad [h]^{\circ }=h-\unicode[STIX]{x1D709}_{q(h)},\end{eqnarray}$$
$$\begin{eqnarray}[h]:=\text{T}_{h}P,\quad [h]^{\circ }=h-\unicode[STIX]{x1D709}_{q(h)},\end{eqnarray}$$
where we identify
 $\unicode[STIX]{x1D70B}_{0}(X_{U,\overline{F}})\cong F_{+}^{\times }\backslash \mathbf{A}^{\times }/q(U)$
so that
$\unicode[STIX]{x1D70B}_{0}(X_{U,\overline{F}})\cong F_{+}^{\times }\backslash \mathbf{A}^{\times }/q(U)$
so that
![]() $P_{U}$
is in the component indexed by
$P_{U}$
is in the component indexed by
![]() $1$
(the point
$1$
(the point
![]() $T(h)P$
is then in the component indexed by
$T(h)P$
is then in the component indexed by
![]() $q(h)$
; see [Reference Yuan, Zhang and ZhangYZZ12, §3.1.2]).
$q(h)$
; see [Reference Yuan, Zhang and ZhangYZZ12, §3.1.2]).
Lemma 5.3.1. Fix
![]() $L$
-linear Hodge splittings on all the abelian varieties
$L$
-linear Hodge splittings on all the abelian varieties
![]() $A^{\prime }/F$
parametrised by
$A^{\prime }/F$
parametrised by
![]() $J$
and let
$J$
and let
![]() $\langle \,,\rangle _{A^{\prime },\ast }$
be the associated local (for
$\langle \,,\rangle _{A^{\prime },\ast }$
be the associated local (for
![]() $\ast =v$
) or global
$\ast =v$
) or global
![]() $(\ast =\emptyset )$
height pairings. There are unique local and global height pairings
$(\ast =\emptyset )$
height pairings. There are unique local and global height pairings
 $$\begin{eqnarray}\langle \,,\rangle _{J,\ast }:J^{\vee }(\overline{F})\times J(\overline{F})\rightarrow \unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L\end{eqnarray}$$
$$\begin{eqnarray}\langle \,,\rangle _{J,\ast }:J^{\vee }(\overline{F})\times J(\overline{F})\rightarrow \unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L\end{eqnarray}$$
such that for any
![]() $A^{\prime }$
and
$A^{\prime }$
and
 $f_{1}^{\prime }\in \unicode[STIX]{x1D70B}_{A^{\prime }}$
,
$f_{1}^{\prime }\in \unicode[STIX]{x1D70B}_{A^{\prime }}$
,
 $f_{2}^{\prime }\in \unicode[STIX]{x1D70B}_{A^{\prime }}^{\vee }$
, and any
$f_{2}^{\prime }\in \unicode[STIX]{x1D70B}_{A^{\prime }}^{\vee }$
, and any
 $P_{1}\in J^{\vee }(\overline{F})$
,
$P_{1}\in J^{\vee }(\overline{F})$
,
 $P_{2}\in J(\overline{F})$
,
$P_{2}\in J(\overline{F})$
,
 $$\begin{eqnarray}\langle P_{1},P_{2}\rangle _{\ast }=\langle f_{2}^{\prime \vee }\circ f_{1}^{\prime }(P_{1}),P_{2}\rangle _{A^{\prime },\ast }.\end{eqnarray}$$
$$\begin{eqnarray}\langle P_{1},P_{2}\rangle _{\ast }=\langle f_{2}^{\prime \vee }\circ f_{1}^{\prime }(P_{1}),P_{2}\rangle _{A^{\prime },\ast }.\end{eqnarray}$$
Proof. For each fixed level
![]() $U$
, there is a decomposition
$U$
, there is a decomposition
 $J_{U}^{\vee }{\sim}\bigoplus _{A^{\prime }}A^{\prime \vee }\otimes \unicode[STIX]{x1D70B}_{A^{\prime \vee }}^{\vee ,U}$
in the isogeny category of abelian varieties, induced by
$J_{U}^{\vee }{\sim}\bigoplus _{A^{\prime }}A^{\prime \vee }\otimes \unicode[STIX]{x1D70B}_{A^{\prime \vee }}^{\vee ,U}$
in the isogeny category of abelian varieties, induced by
 $P_{A^{\prime \vee }}\otimes f^{\prime \vee }\mapsto f^{\prime \vee }(P_{A^{\prime }})$
. Then the Hodge splittings on each
$P_{A^{\prime \vee }}\otimes f^{\prime \vee }\mapsto f^{\prime \vee }(P_{A^{\prime }})$
. Then the Hodge splittings on each
![]() $A^{\prime }$
induce Hodge splittings on
$A^{\prime }$
induce Hodge splittings on
![]() $J_{U}^{\vee }$
. The associated pairing on
$J_{U}^{\vee }$
. The associated pairing on
 $J_{U}^{\vee }\times J_{U}$
is then the unique one satisfying the required property by the projection formula for heights (see [Reference Mazur and TateMT83]). The same formula implies the compatibility with respect to changing
$J_{U}^{\vee }\times J_{U}$
is then the unique one satisfying the required property by the projection formula for heights (see [Reference Mazur and TateMT83]). The same formula implies the compatibility with respect to changing
![]() $U$
.◻
$U$
.◻
We consider the pairing given by the lemma associated with arbitrary Hodge splittings on
![]() $V_{p}A^{\prime }$
for
$V_{p}A^{\prime }$
for
![]() $A^{\prime }\neq A$
, and any splittings on
$A^{\prime }\neq A$
, and any splittings on
 $V_{p}A\otimes L=\bigoplus _{\mathfrak{p}^{\prime }}V_{\mathfrak{p}^{\prime }}A\otimes _{M_{\mathfrak{p}^{\prime }}}L$
which induce the canonical one on
$V_{p}A\otimes L=\bigoplus _{\mathfrak{p}^{\prime }}V_{\mathfrak{p}^{\prime }}A\otimes _{M_{\mathfrak{p}^{\prime }}}L$
which induce the canonical one on
![]() $V_{\mathfrak{p}}A$
. The subscript
$V_{\mathfrak{p}}A$
. The subscript
![]() $J$
will be generally omitted when there is no risk of confusion.
$J$
will be generally omitted when there is no risk of confusion.
Let
![]() $\unicode[STIX]{x1D719}$
be a Schwartz function and
$\unicode[STIX]{x1D719}$
be a Schwartz function and
![]() $\widetilde{Z}(\unicode[STIX]{x1D719})$
be as above. Each
$\widetilde{Z}(\unicode[STIX]{x1D719})$
be as above. Each
![]() $\widetilde{Z}_{a}(\unicode[STIX]{x1D719})$
gives a map
$\widetilde{Z}_{a}(\unicode[STIX]{x1D719})$
gives a map
 $$\begin{eqnarray}\widetilde{Z}_{a}(\unicode[STIX]{x1D719}):J(\overline{F})_{\mathbf{Q}}\rightarrow J^{\vee }(\overline{F})_{\boldsymbol{ Q}}\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{Z}_{a}(\unicode[STIX]{x1D719}):J(\overline{F})_{\mathbf{Q}}\rightarrow J^{\vee }(\overline{F})_{\boldsymbol{ Q}}\end{eqnarray}$$
by the action of Hecke correspondences. When
![]() $a$
has trivial components at infinity and
$a$
has trivial components at infinity and
![]() $\unicode[STIX]{x1D719}^{\infty }$
is standard, we write
$\unicode[STIX]{x1D719}^{\infty }$
is standard, we write
 $\widetilde{Z}_{a}(\unicode[STIX]{x1D719}^{\infty }):=\widetilde{Z}_{a}(\unicode[STIX]{x1D719})$
. Then, for
$\widetilde{Z}_{a}(\unicode[STIX]{x1D719}^{\infty }):=\widetilde{Z}_{a}(\unicode[STIX]{x1D719})$
. Then, for
 $g\in \mathbf{GL}_{2}(\mathbf{A}),h_{1},h_{2}\in \mathbf{B}^{\infty \times }$
, we define the height generating series
$g\in \mathbf{GL}_{2}(\mathbf{A}),h_{1},h_{2}\in \mathbf{B}^{\infty \times }$
, we define the height generating series
 $$\begin{eqnarray}\widetilde{Z}(g,h_{1},h_{2},\unicode[STIX]{x1D719}^{\infty }):=\langle \widetilde{Z}(g,\unicode[STIX]{x1D719})[h_{1}]^{\circ },[h_{2}]^{\circ }\rangle .\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{Z}(g,h_{1},h_{2},\unicode[STIX]{x1D719}^{\infty }):=\langle \widetilde{Z}(g,\unicode[STIX]{x1D719})[h_{1}]^{\circ },[h_{2}]^{\circ }\rangle .\end{eqnarray}$$
Proposition 5.3.2. The series
 $\widetilde{Z}(g,h_{1},h_{2},\unicode[STIX]{x1D719})$
is well defined independently of the choice of the point
$\widetilde{Z}(g,h_{1},h_{2},\unicode[STIX]{x1D719})$
is well defined independently of the choice of the point
![]() $P$
. It is invariant under the left action of
$P$
. It is invariant under the left action of
 $T(F)\times T(F)$
and it belongs to the space of weight-
$T(F)\times T(F)$
and it belongs to the space of weight-
![]() $2$
cuspforms
$2$
cuspforms
 $S_{2}(K^{\prime },\unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L)$
for a suitable open compact subgroup
$S_{2}(K^{\prime },\unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L)$
for a suitable open compact subgroup
 $K^{\prime }\subset \mathbf{GL}_{2}(\mathbf{A}^{\infty })$
.
$K^{\prime }\subset \mathbf{GL}_{2}(\mathbf{A}^{\infty })$
.
Proof. We explain the modularity with coefficients in the
![]() $p$
-adic vector space
$p$
-adic vector space
![]() $\unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L$
. Suppose that
$\unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L$
. Suppose that
![]() $U$
is small enough so that
$U$
is small enough so that
![]() $\unicode[STIX]{x1D719}$
is invariant under
$\unicode[STIX]{x1D719}$
is invariant under
![]() $U$
and
$U$
and
![]() $U$
is invariant under the conjugation action of
$U$
is invariant under the conjugation action of
![]() $h_{1}$
,
$h_{1}$
,
![]() $h_{2}$
. Pick a finite abelian extension
$h_{2}$
. Pick a finite abelian extension
![]() $E^{\prime }$
of
$E^{\prime }$
of
![]() $E$
such that
$E$
such that
 $P\in X_{U}(E^{\prime })$
and a basis
$P\in X_{U}(E^{\prime })$
and a basis
![]() $\{z_{i}\}$
of
$\{z_{i}\}$
of
 $J^{\vee }(E^{\prime })_{\mathbf{Q}}$
, and let
$J^{\vee }(E^{\prime })_{\mathbf{Q}}$
, and let
 $e_{i}:J^{\vee }(E^{\prime })_{\mathbf{Q}}\rightarrow \mathbf{Q}$
be the projection onto the line spanned by
$e_{i}:J^{\vee }(E^{\prime })_{\mathbf{Q}}\rightarrow \mathbf{Q}$
be the projection onto the line spanned by
![]() $z_{i}$
. Then we can write
$z_{i}$
. Then we can write
 $$\begin{eqnarray}\widetilde{Z}(g,(h_{1},h_{2}),\unicode[STIX]{x1D719}^{\infty })=\mathop{\sum }_{i}\langle z_{i},[h_{2}]^{0}\rangle \,\unicode[STIX]{x1D706}_{i}(\widetilde{Z}(g,\unicode[STIX]{x1D719}^{\infty })),\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{Z}(g,(h_{1},h_{2}),\unicode[STIX]{x1D719}^{\infty })=\mathop{\sum }_{i}\langle z_{i},[h_{2}]^{0}\rangle \,\unicode[STIX]{x1D706}_{i}(\widetilde{Z}(g,\unicode[STIX]{x1D719}^{\infty })),\end{eqnarray}$$
where
 $\unicode[STIX]{x1D706}_{i}(T)=e_{i}(T[h_{1}]^{\circ })$
. Each summand
$\unicode[STIX]{x1D706}_{i}(T)=e_{i}(T[h_{1}]^{\circ })$
. Each summand
 $\unicode[STIX]{x1D706}_{i}(\widetilde{Z}(g,\unicode[STIX]{x1D719}^{\infty }))$
is automorphic by Theorem 5.2.1, and in fact a holomorphic cuspform by [Reference Yuan, Zhang and ZhangYZZ12, Lemma 3.19] (the weight can be easily computed from the shape of
$\unicode[STIX]{x1D706}_{i}(\widetilde{Z}(g,\unicode[STIX]{x1D719}^{\infty }))$
is automorphic by Theorem 5.2.1, and in fact a holomorphic cuspform by [Reference Yuan, Zhang and ZhangYZZ12, Lemma 3.19] (the weight can be easily computed from the shape of
![]() $\unicode[STIX]{x1D719}_{\infty }$
). The other statements are also proved in [Reference Yuan, Zhang and ZhangYZZ12].◻
$\unicode[STIX]{x1D719}_{\infty }$
). The other statements are also proved in [Reference Yuan, Zhang and ZhangYZZ12].◻
Define
 $$\begin{eqnarray}\displaystyle \widetilde{Z}(g,\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712}) & := & \displaystyle \int _{T(F)\backslash T(\mathbf{A})/Z(A)}^{\ast }\unicode[STIX]{x1D712}(t)\widetilde{Z}(g,(t,1),\unicode[STIX]{x1D719}^{\infty })\,d^{\circ }t\nonumber\\ \displaystyle & = & \displaystyle \int _{T(F)\backslash T(\mathbf{A})/Z(A)}^{\ast }\unicode[STIX]{x1D712}(t)\widetilde{Z}(g,(1,t^{-1}),\unicode[STIX]{x1D719}^{\infty })\,d^{\circ }t\nonumber\\ \displaystyle & = & \displaystyle \int _{T(F)\backslash T(\mathbf{A})/Z(A)}\unicode[STIX]{x1D712}(t)\widetilde{Z}_{\unicode[STIX]{x1D714}^{-1}}(g,(1,t^{-1}),\unicode[STIX]{x1D719}^{\infty })\,d^{\circ }t,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{Z}(g,\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712}) & := & \displaystyle \int _{T(F)\backslash T(\mathbf{A})/Z(A)}^{\ast }\unicode[STIX]{x1D712}(t)\widetilde{Z}(g,(t,1),\unicode[STIX]{x1D719}^{\infty })\,d^{\circ }t\nonumber\\ \displaystyle & = & \displaystyle \int _{T(F)\backslash T(\mathbf{A})/Z(A)}^{\ast }\unicode[STIX]{x1D712}(t)\widetilde{Z}(g,(1,t^{-1}),\unicode[STIX]{x1D719}^{\infty })\,d^{\circ }t\nonumber\\ \displaystyle & = & \displaystyle \int _{T(F)\backslash T(\mathbf{A})/Z(A)}\unicode[STIX]{x1D712}(t)\widetilde{Z}_{\unicode[STIX]{x1D714}^{-1}}(g,(1,t^{-1}),\unicode[STIX]{x1D719}^{\infty })\,d^{\circ }t,\nonumber\end{eqnarray}$$
where
 $$\begin{eqnarray}\widetilde{Z}_{\unicode[STIX]{x1D714}^{-1}}(g,(1,t^{-1}),\unicode[STIX]{x1D719}^{\infty })=\unicode[STIX]{x2A0D}_{Z(\mathbf{A})}\unicode[STIX]{x1D714}^{-1}(z)\widetilde{Z}(g,(1,z^{-1}t^{-1}),\unicode[STIX]{x1D719}^{\infty })\,dz.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{Z}_{\unicode[STIX]{x1D714}^{-1}}(g,(1,t^{-1}),\unicode[STIX]{x1D719}^{\infty })=\unicode[STIX]{x2A0D}_{Z(\mathbf{A})}\unicode[STIX]{x1D714}^{-1}(z)\widetilde{Z}(g,(1,z^{-1}t^{-1}),\unicode[STIX]{x1D719}^{\infty })\,dz.\end{eqnarray}$$
Note that we have
 $$\begin{eqnarray}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})=|D_{E}|^{1/2}\widetilde{Z}^{[\text{YZZ}]}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})=|D_{E}|^{1/2}\widetilde{Z}^{[\text{YZZ}]}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})\end{eqnarray}$$
if
 $\widetilde{Z}^{[\text{YZZ}]}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})$
is the function denoted by
$\widetilde{Z}^{[\text{YZZ}]}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})$
is the function denoted by
![]() $\widetilde{Z}(\unicode[STIX]{x1D712},\unicode[STIX]{x1D719})$
in [Reference Yuan, Zhang and ZhangYZZ12, §§3.6.4 and 5.1.2].
$\widetilde{Z}(\unicode[STIX]{x1D712},\unicode[STIX]{x1D719})$
in [Reference Yuan, Zhang and ZhangYZZ12, §§3.6.4 and 5.1.2].
5.4 Arithmetic theta lifting and kernel identity
Similarly to [Reference Yuan, Zhang and ZhangYZZ12], we conclude this section by reducing our main theorem to the form which we will prove, namely as an identity between two kernel functions. The fundamental ingredient is the following theorem of Yuan–Zhang–Zhang.
Theorem 5.4.1 (Arithmetic theta lifting).
Let
![]() $\unicode[STIX]{x1D70E}_{A}^{\infty }$
be the
$\unicode[STIX]{x1D70E}_{A}^{\infty }$
be the
![]() $M$
-rational automorphic representation of
$M$
-rational automorphic representation of
 $\mathbf{GL}_{2}(\mathbf{A})$
attached to
$\mathbf{GL}_{2}(\mathbf{A})$
attached to
![]() $A$
. For any
$A$
. For any
![]() $\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D70E}^{\infty }$
, we have
$\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D70E}^{\infty }$
, we have
 $$\begin{eqnarray}(\unicode[STIX]{x1D711},\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty }))_{\unicode[STIX]{x1D70E}^{\infty }}=\text{T}_{\text{alg}}(\unicode[STIX]{x1D703}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D719}^{\infty }))\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D711},\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty }))_{\unicode[STIX]{x1D70E}^{\infty }}=\text{T}_{\text{alg}}(\unicode[STIX]{x1D703}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D719}^{\infty }))\end{eqnarray}$$
in
 $\operatorname{Hom}(J,J^{\vee })\otimes M$
.
$\operatorname{Hom}(J,J^{\vee })\otimes M$
.
For any
 $\unicode[STIX]{x1D711}^{\infty }\in \unicode[STIX]{x1D70E}^{\infty }$
, we have
$\unicode[STIX]{x1D711}^{\infty }\in \unicode[STIX]{x1D70E}^{\infty }$
, we have
 $$\begin{eqnarray}(\unicode[STIX]{x1D711},\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty }))_{\unicode[STIX]{x1D70E}^{\infty }}=|D_{F}|\text{T}_{\text{alg}}(\unicode[STIX]{x1D703}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D719}^{\infty }))\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D711},\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty }))_{\unicode[STIX]{x1D70E}^{\infty }}=|D_{F}|\text{T}_{\text{alg}}(\unicode[STIX]{x1D703}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D719}^{\infty }))\end{eqnarray}$$
in
 $\operatorname{Hom}(J,J^{\vee })\otimes M$
.
$\operatorname{Hom}(J,J^{\vee })\otimes M$
.
Let
 $\unicode[STIX]{x1D704}_{\mathfrak{p}}:M{\hookrightarrow}M_{\mathfrak{p}}\subset L$
. For each
$\unicode[STIX]{x1D704}_{\mathfrak{p}}:M{\hookrightarrow}M_{\mathfrak{p}}\subset L$
. For each
 $\unicode[STIX]{x1D711}^{p}\in \unicode[STIX]{x1D70E}_{A}^{p\infty }\otimes L$
, completing
$\unicode[STIX]{x1D711}^{p}\in \unicode[STIX]{x1D70E}_{A}^{p\infty }\otimes L$
, completing
![]() $\unicode[STIX]{x1D711}^{p}$
to a normalised
$\unicode[STIX]{x1D711}^{p}$
to a normalised
![]() $(\text{U}_{v}^{\ast })_{v|p}$
-eigenform
$(\text{U}_{v}^{\ast })_{v|p}$
-eigenform
 $\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D70E}\otimes L$
as before Proposition 2.4.4, we have
$\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D70E}\otimes L$
as before Proposition 2.4.4, we have
 $$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty }))=|D_{F}|\text{T}_{\text{alg}}(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}w_{r}\unicode[STIX]{x1D719}^{\infty }))\end{eqnarray}$$
$$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty }))=|D_{F}|\text{T}_{\text{alg}}(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}w_{r}\unicode[STIX]{x1D719}^{\infty }))\end{eqnarray}$$
for any sufficiently large
![]() $r\geqslant \text{}\underline{1}$
.
$r\geqslant \text{}\underline{1}$
.
Proof. In the first identity, both sides in fact belong to
![]() $M(\unicode[STIX]{x1D6FC})$
, and the result holds if and only if it holds after applying any embedding
$M(\unicode[STIX]{x1D6FC})$
, and the result holds if and only if it holds after applying any embedding
 $\unicode[STIX]{x1D704}:M(\unicode[STIX]{x1D6FC}){\hookrightarrow}\mathbf{C}$
. It is then equivalent to [Reference Yuan, Zhang and ZhangYZZ12, Theorem 3.22] via Proposition 2.4.4 and [Reference Yuan, Zhang and ZhangYZZ12, Proposition 3.16]. The second identity follows from the first one and the properties of
$\unicode[STIX]{x1D704}:M(\unicode[STIX]{x1D6FC}){\hookrightarrow}\mathbf{C}$
. It is then equivalent to [Reference Yuan, Zhang and ZhangYZZ12, Theorem 3.22] via Proposition 2.4.4 and [Reference Yuan, Zhang and ZhangYZZ12, Proposition 3.16]. The second identity follows from the first one and the properties of
![]() $\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
.◻
$\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
.◻
We can now rephrase the main theorem in the form of the following kernel identity.
Theorem 5.4.2 (Kernel identity).
Let
 $\unicode[STIX]{x1D711}^{p}\in \unicode[STIX]{x1D70E}_{A}^{p\infty }$
and let
$\unicode[STIX]{x1D711}^{p}\in \unicode[STIX]{x1D70E}_{A}^{p\infty }$
and let
 $\unicode[STIX]{x1D719}^{p\infty }\in \overline{\mathscr{S}}(\mathbf{V}^{p\infty }\times \mathbf{A}^{p\infty ,\times })$
. For any compact open subgroup
$\unicode[STIX]{x1D719}^{p\infty }\in \overline{\mathscr{S}}(\mathbf{V}^{p\infty }\times \mathbf{A}^{p\infty ,\times })$
. For any compact open subgroup
 $U_{T,p}=\prod _{v}U_{T,v}\subset 1+(\prod _{v|p}\unicode[STIX]{x1D71B}_{v})\mathscr{O}_{E,p}$
such that
$U_{T,p}=\prod _{v}U_{T,v}\subset 1+(\prod _{v|p}\unicode[STIX]{x1D71B}_{v})\mathscr{O}_{E,p}$
such that
 $\unicode[STIX]{x1D712}_{p}|_{U_{T,p}}=1$
, let
$\unicode[STIX]{x1D712}_{p}|_{U_{T,p}}=1$
, let
 $\unicode[STIX]{x1D719}^{\infty }=\unicode[STIX]{x1D719}^{p\infty }\unicode[STIX]{x1D719}_{p,U_{T,p}}$
, where
$\unicode[STIX]{x1D719}^{\infty }=\unicode[STIX]{x1D719}^{p\infty }\unicode[STIX]{x1D719}_{p,U_{T,p}}$
, where
 $\unicode[STIX]{x1D719}_{p,U_{T,p}}=\bigotimes _{v|p}\unicode[STIX]{x1D719}_{v,U_{T,v}}$
with
$\unicode[STIX]{x1D719}_{p,U_{T,p}}=\bigotimes _{v|p}\unicode[STIX]{x1D719}_{v,U_{T,v}}$
with
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{v,U_{T,v}}(x,u)=\unicode[STIX]{x1D6FF}_{1,U_{T,v}\cap \mathbf{V}_{1}}(x_{1})\mathbf{1}_{\mathscr{O}_{\mathbf{V}_{2}}}(x_{2})\mathbf{1}_{d_{v}^{-1}\mathscr{O}_{F,v}^{\times }}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{v,U_{T,v}}(x,u)=\unicode[STIX]{x1D6FF}_{1,U_{T,v}\cap \mathbf{V}_{1}}(x_{1})\mathbf{1}_{\mathscr{O}_{\mathbf{V}_{2}}}(x_{2})\mathbf{1}_{d_{v}^{-1}\mathscr{O}_{F,v}^{\times }}\end{eqnarray}$$
for
![]() $\unicode[STIX]{x1D6FF}_{1,U_{T,v}}$
as in (3.4.5).
$\unicode[STIX]{x1D6FF}_{1,U_{T,v}}$
as in (3.4.5).
Suppose that all primes
![]() $v|p$
split in
$v|p$
split in
![]() $E$
. Then we have
$E$
. Then we have
 $$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\text{d}_{F}\mathscr{I}(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712}))=2|D_{F}|L_{(p)}(1,\unicode[STIX]{x1D702})\cdot \ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})).\end{eqnarray}$$
$$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\text{d}_{F}\mathscr{I}(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712}))=2|D_{F}|L_{(p)}(1,\unicode[STIX]{x1D702})\cdot \ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})).\end{eqnarray}$$
The proof will occupy most of the rest of the paper (cf. the very end of § 8 below).
Proposition 5.4.3. If Theorem 5.4.2 is true for some
 $(\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D719}^{p\infty })$
such that for all
$(\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D719}^{p\infty })$
such that for all
![]() $v\nmid p\infty$
, the local integral
$v\nmid p\infty$
, the local integral
 $R_{v}(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v})\neq 0$
, then it is true for all
$R_{v}(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v})\neq 0$
, then it is true for all
 $(W^{p},\unicode[STIX]{x1D719}^{p\infty })$
, and Theorem B is true for all
$(W^{p},\unicode[STIX]{x1D719}^{p\infty })$
, and Theorem B is true for all
![]() $f_{1}\in \unicode[STIX]{x1D70B}$
,
$f_{1}\in \unicode[STIX]{x1D70B}$
,
 $f_{2}\in \unicode[STIX]{x1D70B}^{\vee }$
.
$f_{2}\in \unicode[STIX]{x1D70B}^{\vee }$
.
Proof. Consider the identity
 $$\begin{eqnarray}\displaystyle & & \displaystyle \langle \text{T}_{\text{alg},\unicode[STIX]{x1D704}_{\mathfrak{ p}}}(f_{1}\otimes f_{2})P_{\unicode[STIX]{x1D712}},P_{\unicode[STIX]{x1D712}^{-1}}\rangle _{J}\qquad \nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\unicode[STIX]{x1D701}_{F}^{\infty }(2)}{2(\unicode[STIX]{x1D70B}^{2}/2)^{[F:\mathbf{Q}]}|D_{E}|^{1/2}L(1,\unicode[STIX]{x1D702})}\mathop{\prod }_{v|p}Z_{v}^{\circ }(\unicode[STIX]{x1D6FC}_{v},\unicode[STIX]{x1D712}_{v})^{-1}\cdot \text{d}_{F}L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{A,E})(\unicode[STIX]{x1D712})\cdot Q(f_{1},f_{2},\unicode[STIX]{x1D712}),\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \langle \text{T}_{\text{alg},\unicode[STIX]{x1D704}_{\mathfrak{ p}}}(f_{1}\otimes f_{2})P_{\unicode[STIX]{x1D712}},P_{\unicode[STIX]{x1D712}^{-1}}\rangle _{J}\qquad \nonumber\\ \displaystyle & & \displaystyle \quad =\frac{\unicode[STIX]{x1D701}_{F}^{\infty }(2)}{2(\unicode[STIX]{x1D70B}^{2}/2)^{[F:\mathbf{Q}]}|D_{E}|^{1/2}L(1,\unicode[STIX]{x1D702})}\mathop{\prod }_{v|p}Z_{v}^{\circ }(\unicode[STIX]{x1D6FC}_{v},\unicode[STIX]{x1D712}_{v})^{-1}\cdot \text{d}_{F}L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{A,E})(\unicode[STIX]{x1D712})\cdot Q(f_{1},f_{2},\unicode[STIX]{x1D712}),\qquad\end{eqnarray}$$
where
 $\unicode[STIX]{x1D704}_{\mathfrak{p}}:M{\hookrightarrow}L(\unicode[STIX]{x1D712})$
, and we set
$\unicode[STIX]{x1D704}_{\mathfrak{p}}:M{\hookrightarrow}L(\unicode[STIX]{x1D712})$
, and we set
 $$\begin{eqnarray}P_{\unicode[STIX]{x1D712}}=\unicode[STIX]{x2A0D}_{[T]}\text{T}_{t}(P-\unicode[STIX]{x1D709}_{P})\unicode[STIX]{x1D712}(t)\,dt\in J(\overline{F})_{L(\unicode[STIX]{x1D712})}.\end{eqnarray}$$
$$\begin{eqnarray}P_{\unicode[STIX]{x1D712}}=\unicode[STIX]{x2A0D}_{[T]}\text{T}_{t}(P-\unicode[STIX]{x1D709}_{P})\unicode[STIX]{x1D712}(t)\,dt\in J(\overline{F})_{L(\unicode[STIX]{x1D712})}.\end{eqnarray}$$
The identity (5.4.1) is equivalent to Theorem B by Lemma 5.3.1, but it has the advantage of making sense, by linearity, for any element of
![]() $\unicode[STIX]{x1D70B}\otimes \unicode[STIX]{x1D70B}^{\vee }$
. By the multiplicity-one result, it suffices to prove it for a single element of this space which is not annihilated by the functional
$\unicode[STIX]{x1D70B}\otimes \unicode[STIX]{x1D70B}^{\vee }$
. By the multiplicity-one result, it suffices to prove it for a single element of this space which is not annihilated by the functional
![]() $Q(\cdot ,\unicode[STIX]{x1D712})$
. Such element will arise as a Shimizu lift. (The similar assertion on the validity of Theorem 5.4.2 for all
$Q(\cdot ,\unicode[STIX]{x1D712})$
. Such element will arise as a Shimizu lift. (The similar assertion on the validity of Theorem 5.4.2 for all
 $(\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D719}^{p\infty })$
follows from the uniqueness of the Shimizu lifting.)
$(\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D719}^{p\infty })$
follows from the uniqueness of the Shimizu lifting.)
By (3.7.1), we can write
 $$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\text{d}_{F}\mathscr{I}(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712}))=\text{d}_{F}L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})(\unicode[STIX]{x1D712})\mathop{\prod }_{v\nmid p\infty }\mathscr{R}_{v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v};\unicode[STIX]{x1D712}_{v})\end{eqnarray}$$
$$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\text{d}_{F}\mathscr{I}(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712}))=\text{d}_{F}L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})(\unicode[STIX]{x1D712})\mathop{\prod }_{v\nmid p\infty }\mathscr{R}_{v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v};\unicode[STIX]{x1D712}_{v})\end{eqnarray}$$
(note that as the functional
![]() $\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
is bounded, we can interchange it with the differentiation; the fact that the Leibniz rule does not introduce other terms follows from the vanishing of
$\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
is bounded, we can interchange it with the differentiation; the fact that the Leibniz rule does not introduce other terms follows from the vanishing of
 $\mathscr{I}(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712})$
, which will be shown in Proposition 7.1.1
(3) below). By Lemma 5.1.1, this equals
$\mathscr{I}(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712})$
, which will be shown in Proposition 7.1.1
(3) below). By Lemma 5.1.1, this equals
 $$\begin{eqnarray}\frac{|D_{F}|^{3/2}\unicode[STIX]{x1D701}_{F}^{\infty }(2)}{(\unicode[STIX]{x1D70B}^{2}/2)^{[F:\mathbf{Q}]}}\mathop{\prod }_{v|p}Q_{v}(\unicode[STIX]{x1D703}_{v}(W_{v},\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B}_{v})_{v}^{-r_{v}}w_{r,v}^{-1}\unicode[STIX]{x1D719}_{v}),\unicode[STIX]{x1D712}_{v})^{-1}\cdot \text{d}_{F}L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})(\unicode[STIX]{x1D712})\cdot Q(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}w_{r}^{-1}\unicode[STIX]{x1D719}),\unicode[STIX]{x1D712}).\end{eqnarray}$$
$$\begin{eqnarray}\frac{|D_{F}|^{3/2}\unicode[STIX]{x1D701}_{F}^{\infty }(2)}{(\unicode[STIX]{x1D70B}^{2}/2)^{[F:\mathbf{Q}]}}\mathop{\prod }_{v|p}Q_{v}(\unicode[STIX]{x1D703}_{v}(W_{v},\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B}_{v})_{v}^{-r_{v}}w_{r,v}^{-1}\unicode[STIX]{x1D719}_{v}),\unicode[STIX]{x1D712}_{v})^{-1}\cdot \text{d}_{F}L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})(\unicode[STIX]{x1D712})\cdot Q(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}w_{r}^{-1}\unicode[STIX]{x1D719}),\unicode[STIX]{x1D712}).\end{eqnarray}$$
For the geometric kernel, by Theorem 5.4.1 and the calculation of [Reference Yuan, Zhang and ZhangYZZ12, §3.6.4], we have
 $$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712}))=2|D_{F}|^{1/2}|D_{E}|^{1/2}L(1,\unicode[STIX]{x1D702})\langle \text{T}_{\text{alg},\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}w_{r}^{-1}\unicode[STIX]{x1D719}))P_{\unicode[STIX]{x1D712}},P_{\unicode[STIX]{x1D712}}^{-1}\rangle .\end{eqnarray}$$
$$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712}))=2|D_{F}|^{1/2}|D_{E}|^{1/2}L(1,\unicode[STIX]{x1D702})\langle \text{T}_{\text{alg},\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}w_{r}^{-1}\unicode[STIX]{x1D719}))P_{\unicode[STIX]{x1D712}},P_{\unicode[STIX]{x1D712}}^{-1}\rangle .\end{eqnarray}$$
Then (5.4.1) follows from Theorem 5.4.2 provided we show that, for all
![]() $v|p$
,
$v|p$
,
 $$\begin{eqnarray}Q_{v}(\unicode[STIX]{x1D703}_{v}(W_{v},\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})^{-r_{v}}w_{r,v}^{-1}\unicode[STIX]{x1D719}_{v}),\unicode[STIX]{x1D712}_{v})=L(1,\unicode[STIX]{x1D702}_{v})^{-1}\cdot Z_{v}^{\circ }(\unicode[STIX]{x1D712}_{v}).\end{eqnarray}$$
$$\begin{eqnarray}Q_{v}(\unicode[STIX]{x1D703}_{v}(W_{v},\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})^{-r_{v}}w_{r,v}^{-1}\unicode[STIX]{x1D719}_{v}),\unicode[STIX]{x1D712}_{v})=L(1,\unicode[STIX]{x1D702}_{v})^{-1}\cdot Z_{v}^{\circ }(\unicode[STIX]{x1D712}_{v}).\end{eqnarray}$$
This is proved by explicit computation in Proposition A.3.1. ◻
6 Local assumptions
We list here the local assumptions which simplify the computations, while implying the desired identity in general. We recall on the other hand the essential assumption, valid until the end of this paper, that all primes
![]() $v|p$
split in
$v|p$
split in
![]() $E$
.
$E$
.
Let
![]() $S_{F}$
be the set of finite places of
$S_{F}$
be the set of finite places of
![]() $F$
. We partition it as
$F$
. We partition it as
 $$\begin{eqnarray}S_{F}=S_{\text{non-split}}\cup S_{\text{split}}\end{eqnarray}$$
$$\begin{eqnarray}S_{F}=S_{\text{non-split}}\cup S_{\text{split}}\end{eqnarray}$$
with the obvious meaning according to the behaviour in
![]() $E$
, and further as
$E$
, and further as
 $$\begin{eqnarray}S_{F}=S_{p}\cup S_{1}\cup S_{2}\cup (S_{\text{non-split}}-S_{1})\cup (S_{\text{split}}-S_{p}-S_{2}),\end{eqnarray}$$
$$\begin{eqnarray}S_{F}=S_{p}\cup S_{1}\cup S_{2}\cup (S_{\text{non-split}}-S_{1})\cup (S_{\text{split}}-S_{p}-S_{2}),\end{eqnarray}$$
where:
-
–
 $S_{p}\subset S_{\text{split}}$
is the set of places above
$S_{p}\subset S_{\text{split}}$
is the set of places above
 $p$
;
$p$
; -
–
 $S_{1}$
is a finite subset of
$S_{1}$
is a finite subset of
 $S_{\text{non-split}}$
containing all places where
$S_{\text{non-split}}$
containing all places where
 $E/F$
or
$E/F$
or
 $F/\mathbf{Q}$
is ramified, or
$F/\mathbf{Q}$
is ramified, or
 $\unicode[STIX]{x1D70E}$
is not an unramified principal series, or
$\unicode[STIX]{x1D70E}$
is not an unramified principal series, or
 $\unicode[STIX]{x1D712}$
is ramified, or
$\unicode[STIX]{x1D712}$
is ramified, or
 $\mathbf{B}$
is ramified; we assume that
$\mathbf{B}$
is ramified; we assume that
 $|S_{1}|\geqslant 2$
;
$|S_{1}|\geqslant 2$
; -
–
 $S_{2}$
consists of two places in
$S_{2}$
consists of two places in
 $S_{\text{split}}-S_{p}$
at which
$S_{\text{split}}-S_{p}$
at which
 $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
 $\unicode[STIX]{x1D712}$
are unramified.
$\unicode[STIX]{x1D712}$
are unramified.
We further denote by
![]() $S_{\infty }$
the set of archimedean places of
$S_{\infty }$
the set of archimedean places of
![]() $F$
.
$F$
.
6.1 Assumptions away from
 $p$
$p$
Consider the following assumptions from [Reference Yuan, Zhang and ZhangYZZ12, §5.2].
Assumption 6.1.1 (Cf. [Reference Yuan, Zhang and ZhangYZZ12, Assumption 5.2]).
The Schwartz function
 $\unicode[STIX]{x1D719}=\bigotimes \unicode[STIX]{x1D719}_{v}\in \overline{\mathscr{S}}(\mathbf{B}\times \mathbf{A}^{\times })$
is a pure tensor,
$\unicode[STIX]{x1D719}=\bigotimes \unicode[STIX]{x1D719}_{v}\in \overline{\mathscr{S}}(\mathbf{B}\times \mathbf{A}^{\times })$
is a pure tensor,
![]() $\unicode[STIX]{x1D719}_{v}$
is standard for any
$\unicode[STIX]{x1D719}_{v}$
is standard for any
![]() $v\in S_{\infty }$
, and
$v\in S_{\infty }$
, and
![]() $\unicode[STIX]{x1D719}_{v}$
has values in
$\unicode[STIX]{x1D719}_{v}$
has values in
![]() $\mathbf{Q}$
for any
$\mathbf{Q}$
for any
![]() $v\in S_{F}$
.
$v\in S_{F}$
.
Assumption 6.1.2 [Reference Yuan, Zhang and ZhangYZZ12, Assumption 5.3].
For all
![]() $v\in S_{1}$
,
$v\in S_{1}$
,
![]() $\unicode[STIX]{x1D719}_{v}$
satisfies
$\unicode[STIX]{x1D719}_{v}$
satisfies
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{v}(x,u)=0\quad \text{if}~v(uq(x))\geqslant -v(d_{v})~\text{or}~v(uq(x_{2}))\geqslant -v(d_{v}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{v}(x,u)=0\quad \text{if}~v(uq(x))\geqslant -v(d_{v})~\text{or}~v(uq(x_{2}))\geqslant -v(d_{v}).\end{eqnarray}$$
Assumption 6.1.3 [Reference Yuan, Zhang and ZhangYZZ12, Assumption 5.4].
For all
![]() $v\in S_{2}$
,
$v\in S_{2}$
,
![]() $\unicode[STIX]{x1D719}_{v}$
satisfies
$\unicode[STIX]{x1D719}_{v}$
satisfies
 $$\begin{eqnarray}r(g)\unicode[STIX]{x1D719}_{v}(0,u)=0\quad \text{for all}~g\in \mathbf{GL}_{2}(F_{v}),u\in F_{v}^{\times }.\end{eqnarray}$$
$$\begin{eqnarray}r(g)\unicode[STIX]{x1D719}_{v}(0,u)=0\quad \text{for all}~g\in \mathbf{GL}_{2}(F_{v}),u\in F_{v}^{\times }.\end{eqnarray}$$
See [Reference Yuan, Zhang and ZhangYZZ12, Lemma 5.10] for an equivalent condition.
Assumption 6.1.4 [Reference Yuan, Zhang and ZhangYZZ12, Assumption 5.5].
For all
 $v\in S_{\text{non-split}}-S_{1}$
,
$v\in S_{\text{non-split}}-S_{1}$
,
![]() $\unicode[STIX]{x1D719}_{v}$
is the standard Schwartz function
$\unicode[STIX]{x1D719}_{v}$
is the standard Schwartz function
 $\unicode[STIX]{x1D719}_{v}(x,u)=\mathbf{1}_{\mathscr{O}_{\mathbf{B}_{v}}}(x)\mathbf{1}_{d_{v}^{-1}\mathscr{O}_{F,v}^{\times }}(u)$
.
$\unicode[STIX]{x1D719}_{v}(x,u)=\mathbf{1}_{\mathscr{O}_{\mathbf{B}_{v}}}(x)\mathbf{1}_{d_{v}^{-1}\mathscr{O}_{F,v}^{\times }}(u)$
.
Assumption 6.1.5 [Reference Yuan, Zhang and ZhangYZZ12, Assumption 5.6].
The open compact subgroup
 $U^{p}=\prod _{v\nmid p}U_{v}\subset \mathbf{B}(\mathbf{A}^{p\infty })$
satisfies the following:
$U^{p}=\prod _{v\nmid p}U_{v}\subset \mathbf{B}(\mathbf{A}^{p\infty })$
satisfies the following:
-
(i)
 $U_{v}$
is of the form
$U_{v}$
is of the form
 $(1+\unicode[STIX]{x1D71B}_{v}^{r}\mathscr{O}_{\mathbf{B}_{v}})^{\times }$
for some
$(1+\unicode[STIX]{x1D71B}_{v}^{r}\mathscr{O}_{\mathbf{B}_{v}})^{\times }$
for some
 $r\geqslant 0$
;
$r\geqslant 0$
; -
(ii)
 $\unicode[STIX]{x1D712}$
is invariant under
$\unicode[STIX]{x1D712}$
is invariant under
 $U_{T}^{p}:=U^{p}\cap T(\mathbf{A}^{p\infty })$
;
$U_{T}^{p}:=U^{p}\cap T(\mathbf{A}^{p\infty })$
; -
(iii)
 $\unicode[STIX]{x1D719}$
is invariant under
$\unicode[STIX]{x1D719}$
is invariant under
 $K^{p}=U^{p}\times U^{p}$
;
$K^{p}=U^{p}\times U^{p}$
; -
(iv)
 $U_{v}$
is maximal for all
$U_{v}$
is maximal for all
 $v\in S_{\text{non-split}}-S_{1}$
and all
$v\in S_{\text{non-split}}-S_{1}$
and all
 $v\in S_{2}$
;
$v\in S_{2}$
; -
(v)
 $U^{p}U_{0,p}$
does not contain
$U^{p}U_{0,p}$
does not contain
 $-1$
;
$-1$
; -
(vi)
 $U^{p}U_{0,p}$
is sufficiently small so that each connected component of the complex points of the Shimura curve
$U^{p}U_{0,p}$
is sufficiently small so that each connected component of the complex points of the Shimura curve
 $X_{U}$
is an unramified quotient of
$X_{U}$
is an unramified quotient of
 $\mathfrak{H}$
under the complex uniformisation.
$\mathfrak{H}$
under the complex uniformisation.
Here we have denoted by
 $U_{0,p}\subset \mathbf{B}_{p}^{\times }$
the maximal compact subgroup.
$U_{0,p}\subset \mathbf{B}_{p}^{\times }$
the maximal compact subgroup.
See [Reference Yuan, Zhang and ZhangYZZ12, §5.2.1] for an introductory discussion of the effect of those assumptions.
Lemma 6.1.6. For each
![]() $v\nmid p\infty$
, there exist
$v\nmid p\infty$
, there exist
 $W_{v}\in \unicode[STIX]{x1D70E}_{v}$
and a Schwartz function
$W_{v}\in \unicode[STIX]{x1D70E}_{v}$
and a Schwartz function
![]() $\unicode[STIX]{x1D719}_{v}$
satisfying all of Assumptions 6.1.1–6.1.5 such that
$\unicode[STIX]{x1D719}_{v}$
satisfying all of Assumptions 6.1.1–6.1.5 such that
 $$\begin{eqnarray}R_{v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v})\neq 0.\end{eqnarray}$$
$$\begin{eqnarray}R_{v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v})\neq 0.\end{eqnarray}$$
For all but finitely many places
![]() $v$
, we can take
$v$
, we can take
![]() $W_{v}$
to be an unramified vector and
$W_{v}$
to be an unramified vector and
![]() $\unicode[STIX]{x1D719}_{v}$
to be the standard Schwartz function.
$\unicode[STIX]{x1D719}_{v}$
to be the standard Schwartz function.
Proof. The existence of the sought-for pairs
 $(W_{v},\unicode[STIX]{x1D719}_{v})$
is proved in [Reference Yuan, Zhang and ZhangYZZ12, Proposition 5.8]. The second assertion follows from the unramified calculation, Lemma 3.5.2.◻
$(W_{v},\unicode[STIX]{x1D719}_{v})$
is proved in [Reference Yuan, Zhang and ZhangYZZ12, Proposition 5.8]. The second assertion follows from the unramified calculation, Lemma 3.5.2.◻
6.2 Assumptions at
 $p$
$p$
We make some further assumptions at the places
![]() $v\in S_{p}$
. After stating the restrictions on
$v\in S_{p}$
. After stating the restrictions on
![]() $\unicode[STIX]{x1D719}_{v}$
and
$\unicode[STIX]{x1D719}_{v}$
and
![]() $U_{v}$
, we will impose at the end of this section some restrictions on
$U_{v}$
, we will impose at the end of this section some restrictions on
![]() $\unicode[STIX]{x1D712}_{v}$
and on choices of a
$\unicode[STIX]{x1D712}_{v}$
and on choices of a
![]() $p$
-adic logarithm.
$p$
-adic logarithm.
Concerning
 $(\unicode[STIX]{x1D719}_{v},U_{v})$
, we need two conditions. On the one hand, that the centre of the open compact subgroup
$(\unicode[STIX]{x1D719}_{v},U_{v})$
, we need two conditions. On the one hand, that the centre of the open compact subgroup
![]() $U_{v}$
is sufficiently large so that, roughly speaking, for all but finitely many characters
$U_{v}$
is sufficiently large so that, roughly speaking, for all but finitely many characters
![]() $\unicode[STIX]{x1D712}$
, no non-zero vector in a
$\unicode[STIX]{x1D712}$
, no non-zero vector in a
![]() $T(F_{v})$
-representation can be both
$T(F_{v})$
-representation can be both
![]() $\unicode[STIX]{x1D712}_{v}$
-isotypic and invariant under
$\unicode[STIX]{x1D712}_{v}$
-isotypic and invariant under
 $U_{T,v}:=U\cap T(F_{v})$
; we will apply this in particular for the space generated by the Hodge classes on
$U_{T,v}:=U\cap T(F_{v})$
; we will apply this in particular for the space generated by the Hodge classes on
![]() $X_{U}$
. On the other hand, we need
$X_{U}$
. On the other hand, we need
![]() $\unicode[STIX]{x1D719}_{v}$
to be sufficiently close (a condition depending on
$\unicode[STIX]{x1D719}_{v}$
to be sufficiently close (a condition depending on
![]() $\unicode[STIX]{x1D712}_{v}$
) to a Dirac delta, so as to match the Schwartz functions used in the construction of the
$\unicode[STIX]{x1D712}_{v}$
) to a Dirac delta, so as to match the Schwartz functions used in the construction of the
![]() $p$
-adic analytic kernel. As stated, this is apparently incompatible with the previous condition. However, as
$p$
-adic analytic kernel. As stated, this is apparently incompatible with the previous condition. However, as
 $\unicode[STIX]{x1D712}_{v}|_{F_{v}^{\times }}=\unicode[STIX]{x1D714}_{v}^{-1}$
(fixed), an agreeable compromise can be found. We therefore state two distinct assumptions; while we will eventually work with the second assumption (the ‘compromise’), it will be convenient to reduce some proofs to the situation of the first one.
$\unicode[STIX]{x1D712}_{v}|_{F_{v}^{\times }}=\unicode[STIX]{x1D714}_{v}^{-1}$
(fixed), an agreeable compromise can be found. We therefore state two distinct assumptions; while we will eventually work with the second assumption (the ‘compromise’), it will be convenient to reduce some proofs to the situation of the first one.
Assumption 6.2.1. For each
![]() $v\in S_{p}$
,
$v\in S_{p}$
,
![]() $U_{v}$
and
$U_{v}$
and
![]() $\unicode[STIX]{x1D719}_{v}$
satisfy the following:
$\unicode[STIX]{x1D719}_{v}$
satisfy the following:
-
(i) the subgroup
 $U_{v}=1+\unicode[STIX]{x1D71B}_{v}^{r_{v}}\mathscr{O}_{\mathbf{B}_{v}}$
for some
$U_{v}=1+\unicode[STIX]{x1D71B}_{v}^{r_{v}}\mathscr{O}_{\mathbf{B}_{v}}$
for some
 $r_{v}\geqslant 1$
;
$r_{v}\geqslant 1$
; -
(ii)
 $\unicode[STIX]{x1D712}_{v}$
is invariant under
$\unicode[STIX]{x1D712}_{v}$
is invariant under
 $U_{T,v}$
;
$U_{T,v}$
; -
(iii)
 $\unicode[STIX]{x1D6FC}_{v}$
is invariant under
$\unicode[STIX]{x1D6FC}_{v}$
is invariant under
 $q(U_{v})$
;
$q(U_{v})$
; -
(iv) the Schwartz function is
where, as in (3.4.5), $$\begin{eqnarray}\unicode[STIX]{x1D719}_{v}(x,u)=\unicode[STIX]{x1D6FF}_{1,U_{T,v}}(x_{1})\mathbf{1}_{\mathscr{O}_{\mathbf{V}_{2}}}(x_{2})\unicode[STIX]{x1D6FF}_{q(U)}(u),\end{eqnarray}$$
and
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{v}(x,u)=\unicode[STIX]{x1D6FF}_{1,U_{T,v}}(x_{1})\mathbf{1}_{\mathscr{O}_{\mathbf{V}_{2}}}(x_{2})\unicode[STIX]{x1D6FF}_{q(U)}(u),\end{eqnarray}$$
and $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{1,U_{T,v}}(x_{1}):=\frac{\operatorname{vol}(E_{v})}{\operatorname{vol}(U_{T,v})}\mathbf{1}_{U_{T,v}}(x_{1})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{1,U_{T,v}}(x_{1}):=\frac{\operatorname{vol}(E_{v})}{\operatorname{vol}(U_{T,v})}\mathbf{1}_{U_{T,v}}(x_{1})\end{eqnarray}$$
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{q(U)}(u)=\frac{\operatorname{vol}(\mathscr{O}_{F}^{\times })}{\operatorname{vol}(q(U))}\mathbf{1}_{q(U)}(u).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{q(U)}(u)=\frac{\operatorname{vol}(\mathscr{O}_{F}^{\times })}{\operatorname{vol}(q(U))}\mathbf{1}_{q(U)}(u).\end{eqnarray}$$
Assumption 6.2.2. For each
![]() $v\in S_{p}$
,
$v\in S_{p}$
,
![]() $U_{v}$
and
$U_{v}$
and
![]() $\unicode[STIX]{x1D719}_{v}$
satisfy:
$\unicode[STIX]{x1D719}_{v}$
satisfy:
-
(i)
 $U_{v}=U_{F,v}^{\circ }\widetilde{U}_{v}$
with
$U_{v}=U_{F,v}^{\circ }\widetilde{U}_{v}$
with
 $U_{F,v}^{\circ }=(1+\unicode[STIX]{x1D71B}_{v}^{n_{v}}\mathscr{O}_{F,v})^{\times }\subset Z(F_{v})\subset \mathbf{B}_{v}^{\times }$
for some
$U_{F,v}^{\circ }=(1+\unicode[STIX]{x1D71B}_{v}^{n_{v}}\mathscr{O}_{F,v})^{\times }\subset Z(F_{v})\subset \mathbf{B}_{v}^{\times }$
for some
 $n_{v}\geqslant 1$
, and
$n_{v}\geqslant 1$
, and
 $\widetilde{U}_{v}=1+\unicode[STIX]{x1D71B}_{v}^{r_{v}}\mathscr{O}_{\mathbf{B},v}$
satisfies (i)–(ii) of Assumption 6.2.1;
$\widetilde{U}_{v}=1+\unicode[STIX]{x1D71B}_{v}^{r_{v}}\mathscr{O}_{\mathbf{B},v}$
satisfies (i)–(ii) of Assumption 6.2.1; -
(ii)
 $\unicode[STIX]{x1D714}_{v}$
is invariant under
$\unicode[STIX]{x1D714}_{v}$
is invariant under
 $U_{F,v}^{\circ }$
;
$U_{F,v}^{\circ }$
; -
(iii)
 $q(U_{v})\subset (U_{F,v}^{\circ })^{2}$
;
$q(U_{v})\subset (U_{F,v}^{\circ })^{2}$
; -
(iv)
 $\unicode[STIX]{x1D6FC}_{v}$
is invariant under
$\unicode[STIX]{x1D6FC}_{v}$
is invariant under
 $(U_{F,v}^{\circ })^{2}$
;
$(U_{F,v}^{\circ })^{2}$
; -
(v) the Schwartz function
 $\unicode[STIX]{x1D719}_{v}$
is (6.2.1)where
$\unicode[STIX]{x1D719}_{v}$
is (6.2.1)where $$\begin{eqnarray}\unicode[STIX]{x1D719}_{v}:=\unicode[STIX]{x2A0D}_{\mathscr{O}_{F,v}^{\times }}\unicode[STIX]{x1D714}_{v}(z)r((z,1))\widetilde{\unicode[STIX]{x1D719}}_{v}\,dz,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{v}:=\unicode[STIX]{x2A0D}_{\mathscr{O}_{F,v}^{\times }}\unicode[STIX]{x1D714}_{v}(z)r((z,1))\widetilde{\unicode[STIX]{x1D719}}_{v}\,dz,\end{eqnarray}$$
 $\widetilde{\unicode[STIX]{x1D719}}_{v}$
is as in Assumption 6.2.1 for
$\widetilde{\unicode[STIX]{x1D719}}_{v}$
is as in Assumption 6.2.1 for
 $\widetilde{U}_{v}$
.
$\widetilde{U}_{v}$
.
Remark 6.2.3. By (ii), the function
![]() $\unicode[STIX]{x1D719}_{v}$
in Assumption 6.2.2 is invariant under
$\unicode[STIX]{x1D719}_{v}$
in Assumption 6.2.2 is invariant under
 $K_{v}=U_{v}\times U_{v}$
. The subgroup
$K_{v}=U_{v}\times U_{v}$
. The subgroup
![]() $U_{F,v}^{\circ }$
in Assumption 6.2.2 can be chosen independently of
$U_{F,v}^{\circ }$
in Assumption 6.2.2 can be chosen independently of
![]() $\unicode[STIX]{x1D712}$
.
$\unicode[STIX]{x1D712}$
.
In view of the previous remark, we can introduce the following assumption after fixing
![]() $U_{F,v}^{\circ }$
.
$U_{F,v}^{\circ }$
.
Assumption 6.2.4. The character
![]() $\unicode[STIX]{x1D712}$
is not invariant under
$\unicode[STIX]{x1D712}$
is not invariant under
 $V_{p}^{\circ }:=\prod _{v|p}q^{-1}(U_{F,v}^{\circ })\subset \mathscr{O}_{E,p}^{\times }$
.
$V_{p}^{\circ }:=\prod _{v|p}q^{-1}(U_{F,v}^{\circ })\subset \mathscr{O}_{E,p}^{\times }$
.
Lemma 6.2.5. The set of finite-order characters
![]() $\unicode[STIX]{x1D712}\in \mathscr{Y}$
which do not satisfy Assumption 6.2.4 is finite.
$\unicode[STIX]{x1D712}\in \mathscr{Y}$
which do not satisfy Assumption 6.2.4 is finite.
Proof. Recall that by definition
 $\mathscr{Y}=\mathscr{Y}_{\unicode[STIX]{x1D714}}(V^{p})$
parametrises some
$\mathscr{Y}=\mathscr{Y}_{\unicode[STIX]{x1D714}}(V^{p})$
parametrises some
![]() $V^{p}$
-invariant characters for the open compact subgroup
$V^{p}$
-invariant characters for the open compact subgroup
 $V^{p}\subset E_{\mathbf{A}^{p\infty }}^{\times }$
fixed (arbitrarily) in the Introduction. Then a character
$V^{p}\subset E_{\mathbf{A}^{p\infty }}^{\times }$
fixed (arbitrarily) in the Introduction. Then a character
![]() $\unicode[STIX]{x1D712}$
as in the lemma factors through
$\unicode[STIX]{x1D712}$
as in the lemma factors through
 $$\begin{eqnarray}E_{\mathbf{A}^{\infty }}^{\times }/\overline{E^{\times }V^{p}V_{p}^{\circ }},\end{eqnarray}$$
$$\begin{eqnarray}E_{\mathbf{A}^{\infty }}^{\times }/\overline{E^{\times }V^{p}V_{p}^{\circ }},\end{eqnarray}$$
a finite group. ◻
 $p$
-adic logarithms
$p$
-adic logarithms
Recall that a
![]() $p$
-adic logarithm valued in a finite extension
$p$
-adic logarithm valued in a finite extension
![]() $L$
of
$L$
of
![]() $\mathbf{Q}_{p}$
is a continuous homomorphism
$\mathbf{Q}_{p}$
is a continuous homomorphism
 $$\begin{eqnarray}\ell :\unicode[STIX]{x1D6E4}_{F}\rightarrow L;\end{eqnarray}$$
$$\begin{eqnarray}\ell :\unicode[STIX]{x1D6E4}_{F}\rightarrow L;\end{eqnarray}$$
we call it ramified if for all
![]() $v|p$
the restriction
$v|p$
the restriction
 $\ell _{v}:=\ell |_{F_{v}^{\times }}$
is ramified, i.e. non-trivial on
$\ell _{v}:=\ell |_{F_{v}^{\times }}$
is ramified, i.e. non-trivial on
![]() $\mathscr{O}_{F,v}^{\times }$
.
$\mathscr{O}_{F,v}^{\times }$
.
Lemma 6.2.6. For any finite extension
![]() $L$
of
$L$
of
![]() $\mathbf{Q}_{p}$
, the vector space of continuous homomorphisms
$\mathbf{Q}_{p}$
, the vector space of continuous homomorphisms
 $\operatorname{Hom}(\unicode[STIX]{x1D6E4}_{F},L)$
admits a basis consisting of ramified logarithms.
$\operatorname{Hom}(\unicode[STIX]{x1D6E4}_{F},L)$
admits a basis consisting of ramified logarithms.
Proof. If
![]() $F=\mathbf{Q}$
, then
$F=\mathbf{Q}$
, then
 $\operatorname{Hom}(\unicode[STIX]{x1D6E4}_{\mathbf{Q}},L)$
is one dimensional with generator the cyclotomic logarithm
$\operatorname{Hom}(\unicode[STIX]{x1D6E4}_{\mathbf{Q}},L)$
is one dimensional with generator the cyclotomic logarithm
![]() $\ell _{\mathbf{Q}}$
, which is ramified. For general
$\ell _{\mathbf{Q}}$
, which is ramified. For general
![]() $F$
,
$F$
,
 $\ell _{\mathbf{Q}}\circ N_{F/\mathbf{Q}}:\unicode[STIX]{x1D6E4}_{F}\rightarrow \unicode[STIX]{x1D6E4}_{\mathbf{Q}}\rightarrow \mathbf{Q}_{p}$
is ramified (and it generates
$\ell _{\mathbf{Q}}\circ N_{F/\mathbf{Q}}:\unicode[STIX]{x1D6E4}_{F}\rightarrow \unicode[STIX]{x1D6E4}_{\mathbf{Q}}\rightarrow \mathbf{Q}_{p}$
is ramified (and it generates
 $\operatorname{Hom}(\unicode[STIX]{x1D6E4}_{F},L)$
if the Leopoldt conjecture for
$\operatorname{Hom}(\unicode[STIX]{x1D6E4}_{F},L)$
if the Leopoldt conjecture for
![]() $F$
holds). Any other logarithm
$F$
holds). Any other logarithm
![]() $\ell$
can be written as
$\ell$
can be written as
 $\ell =a\ell _{\mathbf{Q}}\circ N_{F/\mathbf{Q}}+(\ell -a\ell _{\mathbf{Q}}\circ N_{F/\mathbf{Q}})$
for any
$\ell =a\ell _{\mathbf{Q}}\circ N_{F/\mathbf{Q}}+(\ell -a\ell _{\mathbf{Q}}\circ N_{F/\mathbf{Q}})$
for any
![]() $a\in L$
; for all but finitely many values of
$a\in L$
; for all but finitely many values of
![]() $a$
, both summands are ramified.◻
$a$
, both summands are ramified.◻
7 Derivative of the analytic kernel
For this section, we retain all the notation of §§ 3.2–3.4, and we keep the assumption that
![]() $\mathbf{V}$
is incoherent. We assume that all
$\mathbf{V}$
is incoherent. We assume that all
![]() $v|p$
split in
$v|p$
split in
![]() $E$
.
$E$
.
7.1 Whittaker functions for the Eisenstein series
We start by studying the incoherent Eisenstein series
![]() $\mathscr{E}$
.
$\mathscr{E}$
.
Proposition 7.1.1.
-
(1) Let
 $a\in F_{v}^{\times }$
.
$a\in F_{v}^{\times }$
.-
(a) If
 $a$
is not represented by
$a$
is not represented by
 $(\mathbf{V}_{2,v},uq)$
, then
$(\mathbf{V}_{2,v},uq)$
, then
 $W_{a,v}^{\circ }(g,u,\mathbf{1})=0$
.
$W_{a,v}^{\circ }(g,u,\mathbf{1})=0$
. -
(b) (Local Siegel–Weil formula.) If there exists
 $x_{a}\in \mathbf{V}_{2,v}$
such that
$x_{a}\in \mathbf{V}_{2,v}$
such that
 $uq(x_{a})=a$
, then
$uq(x_{a})=a$
, then  $$\begin{eqnarray}W_{a,v}^{\circ }((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!),u,\mathbf{1})=\int _{E_{v}^{1}}r((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!),h)\unicode[STIX]{x1D719}_{2,v}(x_{a},u)\,dh.\end{eqnarray}$$
$$\begin{eqnarray}W_{a,v}^{\circ }((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!),u,\mathbf{1})=\int _{E_{v}^{1}}r((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!),h)\unicode[STIX]{x1D719}_{2,v}(x_{a},u)\,dh.\end{eqnarray}$$
-
-
(2) For any
 $a$
,
$a$
,
 $u\in F^{\times }$
, there is a place
$u\in F^{\times }$
, there is a place
 $v\nmid p$
of
$v\nmid p$
of
 $F$
such that
$F$
such that
 $a$
is not represented by
$a$
is not represented by
 $(\mathbf{V}_{2},uq)$
.
$(\mathbf{V}_{2},uq)$
. -
(3) For any
 $\unicode[STIX]{x1D719}_{2}^{p\infty }\in \mathscr{S}(\mathbf{V}_{2}^{p\infty }\times \mathbf{A}^{p\infty ,\times })$
,
$\unicode[STIX]{x1D719}_{2}^{p\infty }\in \mathscr{S}(\mathbf{V}_{2}^{p\infty }\times \mathbf{A}^{p\infty ,\times })$
,
 $u\in F^{\times }$
, we have and consequently
$u\in F^{\times }$
, we have and consequently $$\begin{eqnarray}\mathscr{E}(u,\unicode[STIX]{x1D719}_{2}^{p\infty };\mathbf{1})=0\end{eqnarray}$$
for any
$$\begin{eqnarray}\mathscr{E}(u,\unicode[STIX]{x1D719}_{2}^{p\infty };\mathbf{1})=0\end{eqnarray}$$
for any $$\begin{eqnarray}\mathscr{I}_{F}(\unicode[STIX]{x1D719}^{p\infty };\mathbf{1})=0,\quad \mathscr{I}(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712})=0\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{I}_{F}(\unicode[STIX]{x1D719}^{p\infty };\mathbf{1})=0,\quad \mathscr{I}(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712})=0\end{eqnarray}$$
 $\unicode[STIX]{x1D719}^{p\infty }\in \mathscr{S}(\mathbf{V}^{p\infty }\times \mathbf{A}^{p\infty ,\times })$
,
$\unicode[STIX]{x1D719}^{p\infty }\in \mathscr{S}(\mathbf{V}^{p\infty }\times \mathbf{A}^{p\infty ,\times })$
,
 $\unicode[STIX]{x1D712}\in \mathscr{Y}_{\unicode[STIX]{x1D714}}$
.
$\unicode[STIX]{x1D712}\in \mathscr{Y}_{\unicode[STIX]{x1D714}}$
.
Proof. Part (1) is [Reference Yuan, Zhang and ZhangYZZ12, Proposition 6.1] rewritten in our normalisation: except for (b) when
![]() $v|p$
, which is verified by explicit computation of both sides (recall that
$v|p$
, which is verified by explicit computation of both sides (recall that
![]() $\unicode[STIX]{x1D719}_{2,v}$
is standard when
$\unicode[STIX]{x1D719}_{2,v}$
is standard when
![]() $v|p$
). Part (2) is a crucial consequence of the incoherence, proved in [Reference Yuan, Zhang and ZhangYZZ12, Lemma 6.3]. In view of the expansion of Proposition 3.2.1, the vanishing is a consequence of the vanishing of the non-zero Whittaker functions (which is implied by the previous local results) and of
$v|p$
). Part (2) is a crucial consequence of the incoherence, proved in [Reference Yuan, Zhang and ZhangYZZ12, Lemma 6.3]. In view of the expansion of Proposition 3.2.1, the vanishing is a consequence of the vanishing of the non-zero Whittaker functions (which is implied by the previous local results) and of
 $$\begin{eqnarray}W_{0}(u,\mathbf{1})=-L^{(p)}(0,\unicode[STIX]{x1D702})\mathop{\prod }_{v}W_{0,v}^{\circ }(u,\mathbf{1})\!:\end{eqnarray}$$
$$\begin{eqnarray}W_{0}(u,\mathbf{1})=-L^{(p)}(0,\unicode[STIX]{x1D702})\mathop{\prod }_{v}W_{0,v}^{\circ }(u,\mathbf{1})\!:\end{eqnarray}$$
here we have
 $$\begin{eqnarray}L^{(p)}(0,\unicode[STIX]{x1D702})=\frac{L(0,\unicode[STIX]{x1D702})}{\mathop{\prod }_{v|p}L(0,\unicode[STIX]{x1D702}_{v})}=0\end{eqnarray}$$
$$\begin{eqnarray}L^{(p)}(0,\unicode[STIX]{x1D702})=\frac{L(0,\unicode[STIX]{x1D702})}{\mathop{\prod }_{v|p}L(0,\unicode[STIX]{x1D702}_{v})}=0\end{eqnarray}$$
as
![]() $L(0,\unicode[STIX]{x1D702})$
is defined and non-zero whereas
$L(0,\unicode[STIX]{x1D702})$
is defined and non-zero whereas
![]() $L(s,\unicode[STIX]{x1D702}_{v})$
has a pole at
$L(s,\unicode[STIX]{x1D702}_{v})$
has a pole at
![]() $s=0$
when
$s=0$
when
![]() $v$
splits in
$v$
splits in
![]() $E$
.◻
$E$
.◻
7.2 Decomposition of the derivative
Fix henceforth a tangent vector
 $\ell \in \operatorname{Hom}(\unicode[STIX]{x1D6E4}_{F},L(\unicode[STIX]{x1D712}))\cong T_{\mathbf{1}}\mathscr{Y}_{F}\otimes L(\unicode[STIX]{x1D712})\cong \mathscr{N}_{\mathscr{Y}/\mathscr{Y}^{\prime }}^{\ast }\text{}_{|\unicode[STIX]{x1D712}}$
; we assume that
$\ell \in \operatorname{Hom}(\unicode[STIX]{x1D6E4}_{F},L(\unicode[STIX]{x1D712}))\cong T_{\mathbf{1}}\mathscr{Y}_{F}\otimes L(\unicode[STIX]{x1D712})\cong \mathscr{N}_{\mathscr{Y}/\mathscr{Y}^{\prime }}^{\ast }\text{}_{|\unicode[STIX]{x1D712}}$
; we assume that
![]() $\ell$
is ramified when viewed as a
$\ell$
is ramified when viewed as a
![]() $p$
-adic logarithm (cf. Lemma 6.2.6). For any function
$p$
-adic logarithm (cf. Lemma 6.2.6). For any function
![]() $f$
on
$f$
on
![]() $\mathscr{Y}_{F}$
, we denote by
$\mathscr{Y}_{F}$
, we denote by
 $$\begin{eqnarray}f^{\prime }(\mathbf{1})=D_{\ell }f(\mathbf{1})\end{eqnarray}$$
$$\begin{eqnarray}f^{\prime }(\mathbf{1})=D_{\ell }f(\mathbf{1})\end{eqnarray}$$
the corresponding directional derivative.
Our goal is to compute, for any locally constant
![]() $\unicode[STIX]{x1D712}$
, the derivative
$\unicode[STIX]{x1D712}$
, the derivative
 $$\begin{eqnarray}\displaystyle \mathscr{I}^{\prime }(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712}) & = & \displaystyle \int _{[T]}^{\ast }\unicode[STIX]{x1D712}(t)\mathscr{I}_{F}^{\prime }((t,1),\unicode[STIX]{x1D719}^{p\infty };\mathbf{1})_{U}\,d^{\circ }t\nonumber\\ \displaystyle & = & \displaystyle \int _{[T]}^{\ast }\unicode[STIX]{x1D712}(t)\mathscr{I}_{F}^{\prime }((1,t^{-1}),\unicode[STIX]{x1D719}^{p\infty };\mathbf{1})_{U}\,d^{\circ }t,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{I}^{\prime }(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712}) & = & \displaystyle \int _{[T]}^{\ast }\unicode[STIX]{x1D712}(t)\mathscr{I}_{F}^{\prime }((t,1),\unicode[STIX]{x1D719}^{p\infty };\mathbf{1})_{U}\,d^{\circ }t\nonumber\\ \displaystyle & = & \displaystyle \int _{[T]}^{\ast }\unicode[STIX]{x1D712}(t)\mathscr{I}_{F}^{\prime }((1,t^{-1}),\unicode[STIX]{x1D719}^{p\infty };\mathbf{1})_{U}\,d^{\circ }t,\nonumber\end{eqnarray}$$
where the first identity (of
![]() $q$
-expansions) follows from the vanishing of the values
$q$
-expansions) follows from the vanishing of the values
 $\mathscr{I}_{F}(\unicode[STIX]{x1D719}^{p\infty };\mathbf{1})$
.
$\mathscr{I}_{F}(\unicode[STIX]{x1D719}^{p\infty };\mathbf{1})$
.
We can decompose the derivative into a sum of
![]() $q$
-expansions indexed by the non-split finite places
$q$
-expansions indexed by the non-split finite places
![]() $v$
. For each
$v$
. For each
![]() $u\in F^{\times }$
and each place
$u\in F^{\times }$
and each place
![]() $v$
of
$v$
of
![]() $F$
, let
$F$
, let
![]() $F_{u}(v)$
be the set of those
$F_{u}(v)$
be the set of those
![]() $a\in F^{\times }$
represented by
$a\in F^{\times }$
represented by
 $(\mathbf{V}_{2}^{v},uq)$
; by Proposition 7.1.1, we have
$(\mathbf{V}_{2}^{v},uq)$
; by Proposition 7.1.1, we have
 $W_{a,v}^{\circ }(u,\mathbf{1})=0$
for each
$W_{a,v}^{\circ }(u,\mathbf{1})=0$
for each
 $a\in F_{u}(v)$
, and moreover
$a\in F_{u}(v)$
, and moreover
![]() $F_{u}(v)$
is always empty if
$F_{u}(v)$
is always empty if
![]() $v$
splits in
$v$
splits in
![]() $E$
.
$E$
.
Then
 $$\begin{eqnarray}\mathscr{E}^{\prime }(u;\mathbf{1})=\frac{2^{[F:\mathbf{Q}]}|D_{F}|^{1/2}}{|D_{E}|^{1/2}L^{(p)}(1,\unicode[STIX]{x1D702})}\mathscr{W}_{0}^{\prime }(u;\mathbf{1})-\frac{2^{[F:\mathbf{Q}]|D|^{1/2}}}{|D_{E}|^{1/2}L^{(p)}(1,\unicode[STIX]{x1D702})}\mathop{\sum }_{\substack{ v\text{ non-split} \\ a\in F_{u}(v)}}\mathscr{W}_{a,v}^{\circ \;\prime }(u;\mathbf{1})\mathscr{W}_{a}^{\circ ,v}(u;\mathbf{1})\,\mathbf{q}^{a}.\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{E}^{\prime }(u;\mathbf{1})=\frac{2^{[F:\mathbf{Q}]}|D_{F}|^{1/2}}{|D_{E}|^{1/2}L^{(p)}(1,\unicode[STIX]{x1D702})}\mathscr{W}_{0}^{\prime }(u;\mathbf{1})-\frac{2^{[F:\mathbf{Q}]|D|^{1/2}}}{|D_{E}|^{1/2}L^{(p)}(1,\unicode[STIX]{x1D702})}\mathop{\sum }_{\substack{ v\text{ non-split} \\ a\in F_{u}(v)}}\mathscr{W}_{a,v}^{\circ \;\prime }(u;\mathbf{1})\mathscr{W}_{a}^{\circ ,v}(u;\mathbf{1})\,\mathbf{q}^{a}.\end{eqnarray}$$
For a non-split finite place
![]() $v$
, let
$v$
, let
 $$\begin{eqnarray}\displaystyle \mathscr{E}^{\prime }(u,\unicode[STIX]{x1D719}_{2}^{p\infty };\mathbf{1})(v) & := & \displaystyle -\frac{2^{[F:\mathbf{Q}]}|D_{F}|^{1/2}}{|D_{E/F}|^{1/2}L^{(p)}(1,\unicode[STIX]{x1D702})}\mathop{\sum }_{a\in F_{u}(v)}\mathscr{W}_{a,v}^{\prime }(u;\mathbf{1})\mathscr{W}_{a}^{\circ ,v}(u;\mathbf{1})\,\mathbf{q}^{a},\nonumber\\ \displaystyle \mathscr{I}_{F}^{\prime }((t_{1},t_{2}),\unicode[STIX]{x1D719}^{p\infty };\mathbf{1})(v) & := & \displaystyle c_{U^{p}}\mathop{\sum }_{u\in \unicode[STIX]{x1D707}_{U^{p}}^{2}\backslash F^{\times }}\unicode[STIX]{x1D703}(u,r(t_{1},t_{2})\unicode[STIX]{x1D719}_{1})\mathscr{E}^{\prime }(u,\unicode[STIX]{x1D719}_{2}^{p\infty };\mathbf{1})(v),\nonumber\\ \displaystyle \mathscr{I}^{\prime }(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712})(v) & := & \displaystyle \int _{[T]}^{\ast }\unicode[STIX]{x1D712}(t)\mathscr{I}_{F}^{\prime }((1,t^{-1}),\unicode[STIX]{x1D719}^{p\infty };\mathbf{1})(v)\,d^{\circ }t\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{E}^{\prime }(u,\unicode[STIX]{x1D719}_{2}^{p\infty };\mathbf{1})(v) & := & \displaystyle -\frac{2^{[F:\mathbf{Q}]}|D_{F}|^{1/2}}{|D_{E/F}|^{1/2}L^{(p)}(1,\unicode[STIX]{x1D702})}\mathop{\sum }_{a\in F_{u}(v)}\mathscr{W}_{a,v}^{\prime }(u;\mathbf{1})\mathscr{W}_{a}^{\circ ,v}(u;\mathbf{1})\,\mathbf{q}^{a},\nonumber\\ \displaystyle \mathscr{I}_{F}^{\prime }((t_{1},t_{2}),\unicode[STIX]{x1D719}^{p\infty };\mathbf{1})(v) & := & \displaystyle c_{U^{p}}\mathop{\sum }_{u\in \unicode[STIX]{x1D707}_{U^{p}}^{2}\backslash F^{\times }}\unicode[STIX]{x1D703}(u,r(t_{1},t_{2})\unicode[STIX]{x1D719}_{1})\mathscr{E}^{\prime }(u,\unicode[STIX]{x1D719}_{2}^{p\infty };\mathbf{1})(v),\nonumber\\ \displaystyle \mathscr{I}^{\prime }(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712})(v) & := & \displaystyle \int _{[T]}^{\ast }\unicode[STIX]{x1D712}(t)\mathscr{I}_{F}^{\prime }((1,t^{-1}),\unicode[STIX]{x1D719}^{p\infty };\mathbf{1})(v)\,d^{\circ }t\nonumber\end{eqnarray}$$
if
 $\unicode[STIX]{x1D719}^{p\infty }=\unicode[STIX]{x1D719}_{1}^{p\infty }\otimes \unicode[STIX]{x1D719}_{2}^{p\infty }$
, with
$\unicode[STIX]{x1D719}^{p\infty }=\unicode[STIX]{x1D719}_{1}^{p\infty }\otimes \unicode[STIX]{x1D719}_{2}^{p\infty }$
, with
![]() $\unicode[STIX]{x1D719}_{1}$
obtained from
$\unicode[STIX]{x1D719}_{1}$
obtained from
![]() $\unicode[STIX]{x1D719}_{1}^{p\infty }$
as in (3.4.5), and extended by linearity in general.
$\unicode[STIX]{x1D719}_{1}^{p\infty }$
as in (3.4.5), and extended by linearity in general.
Proposition 7.2.1. Under Assumption 6.1.2, we have
 $$\begin{eqnarray}\mathscr{I}_{F}^{\prime }(\unicode[STIX]{x1D719}^{p\infty };\mathbf{1})=\mathop{\sum }_{v~\text{non-split}}\mathscr{I}_{F}^{\prime }(\unicode[STIX]{x1D719}^{p\infty };\mathbf{1})(v).\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{I}_{F}^{\prime }(\unicode[STIX]{x1D719}^{p\infty };\mathbf{1})=\mathop{\sum }_{v~\text{non-split}}\mathscr{I}_{F}^{\prime }(\unicode[STIX]{x1D719}^{p\infty };\mathbf{1})(v).\end{eqnarray}$$
Proof. By the definitions, we only need to show that under our assumptions we have
 $$\begin{eqnarray}\mathscr{W}_{0}^{\prime }(u;\mathbf{1})=0.\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{W}_{0}^{\prime }(u;\mathbf{1})=0.\end{eqnarray}$$
This is proved similarly to [Reference Yuan, Zhang and ZhangYZZ12, Proposition 6.7]. ◻
7.3 Main result on the derivative
We give explicit expressions for the local components at good places, and identify the local components at bad places with certain coherent theta series coming from nearby quaternion algebras
![]() $\mathbf{B}(v)$
; these theta series will be orthogonal to all forms in
$\mathbf{B}(v)$
; these theta series will be orthogonal to all forms in
![]() $\unicode[STIX]{x1D70E}$
by the Waldspurger formula and the local dichotomy.
$\unicode[STIX]{x1D70E}$
by the Waldspurger formula and the local dichotomy.
Proposition 7.3.1. Let
![]() $v$
be a finite place non-split in
$v$
be a finite place non-split in
![]() $E$
. Then, for any
$E$
. Then, for any
 $(t_{1},t_{2})\in T(\mathbf{A})$
, we have
$(t_{1},t_{2})\in T(\mathbf{A})$
, we have
 $$\begin{eqnarray}\mathscr{I}_{F}^{\prime }((t_{1},t_{2}),\unicode[STIX]{x1D719}^{p\infty };\mathbf{1})(v)=2|D_{F}|L_{(p)}(1,\unicode[STIX]{x1D702})\unicode[STIX]{x2A0D}_{[T]}\mathscr{K}_{\unicode[STIX]{x1D719}^{p\infty }}^{(v)}((tt_{1},tt_{2}))\,dt\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{I}_{F}^{\prime }((t_{1},t_{2}),\unicode[STIX]{x1D719}^{p\infty };\mathbf{1})(v)=2|D_{F}|L_{(p)}(1,\unicode[STIX]{x1D702})\unicode[STIX]{x2A0D}_{[T]}\mathscr{K}_{\unicode[STIX]{x1D719}^{p\infty }}^{(v)}((tt_{1},tt_{2}))\,dt\end{eqnarray}$$
and
 $$\begin{eqnarray}\mathscr{I}^{\prime }(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712})(v)=2|D_{F}|L_{(p)}(1,\unicode[STIX]{x1D702})\int _{[T]}^{\ast }\unicode[STIX]{x2A0D}_{[T]}\mathscr{K}_{\unicode[STIX]{x1D719}^{p\infty }}^{(v)}((t,tt_{1}^{-1}))\,dt\,d^{\circ }t_{1},\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{I}^{\prime }(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712})(v)=2|D_{F}|L_{(p)}(1,\unicode[STIX]{x1D702})\int _{[T]}^{\ast }\unicode[STIX]{x2A0D}_{[T]}\mathscr{K}_{\unicode[STIX]{x1D719}^{p\infty }}^{(v)}((t,tt_{1}^{-1}))\,dt\,d^{\circ }t_{1},\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle \mathscr{K}_{\unicode[STIX]{x1D719}}^{(v)}(y,(t_{1},t_{2})) & = & \displaystyle \mathscr{K}_{r(t_{1},t_{2})\unicode[STIX]{x1D719}}^{(v)}(y)\nonumber\\ \displaystyle & = & \displaystyle c_{U^{p}}\mathop{\sum }_{u\in \unicode[STIX]{x1D707}_{U^{p}}^{2}\backslash F^{\times }}\mathop{\sum }_{x\in V-V_{1}}k_{r(t_{1},t_{2})\unicode[STIX]{x1D719}_{v}}(y,x,u)r((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!),(t_{1},t_{2}))\unicode[STIX]{x1D719}^{v\infty }(x,u)\,\mathbf{q}^{uq(x)}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{K}_{\unicode[STIX]{x1D719}}^{(v)}(y,(t_{1},t_{2})) & = & \displaystyle \mathscr{K}_{r(t_{1},t_{2})\unicode[STIX]{x1D719}}^{(v)}(y)\nonumber\\ \displaystyle & = & \displaystyle c_{U^{p}}\mathop{\sum }_{u\in \unicode[STIX]{x1D707}_{U^{p}}^{2}\backslash F^{\times }}\mathop{\sum }_{x\in V-V_{1}}k_{r(t_{1},t_{2})\unicode[STIX]{x1D719}_{v}}(y,x,u)r((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!),(t_{1},t_{2}))\unicode[STIX]{x1D719}^{v\infty }(x,u)\,\mathbf{q}^{uq(x)}\nonumber\end{eqnarray}$$
with
 $k_{\unicode[STIX]{x1D719}_{v}}(y,x,u)$
the linear function in
$k_{\unicode[STIX]{x1D719}_{v}}(y,x,u)$
the linear function in
![]() $\unicode[STIX]{x1D719}_{v}$
given when
$\unicode[STIX]{x1D719}_{v}$
given when
 $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}_{1,v}\otimes \unicode[STIX]{x1D719}_{2,v}$
by
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}_{1,v}\otimes \unicode[STIX]{x1D719}_{2,v}$
by
 $$\begin{eqnarray}k_{\unicode[STIX]{x1D719}_{v}}(y,x,u):=-\frac{|d|_{v}^{1/2}|D|_{v}^{1/2}}{\operatorname{vol}(E_{v}^{1})}r((\!\begin{smallmatrix}y_{v} & \\ & 1\end{smallmatrix}\!))\unicode[STIX]{x1D719}_{1,v}(x_{1},u)\mathscr{W}_{uq(y_{2}),v}^{\circ \;\prime }(y,u,\unicode[STIX]{x1D719}_{2,v}).\end{eqnarray}$$
$$\begin{eqnarray}k_{\unicode[STIX]{x1D719}_{v}}(y,x,u):=-\frac{|d|_{v}^{1/2}|D|_{v}^{1/2}}{\operatorname{vol}(E_{v}^{1})}r((\!\begin{smallmatrix}y_{v} & \\ & 1\end{smallmatrix}\!))\unicode[STIX]{x1D719}_{1,v}(x_{1},u)\mathscr{W}_{uq(y_{2}),v}^{\circ \;\prime }(y,u,\unicode[STIX]{x1D719}_{2,v}).\end{eqnarray}$$
Proof. This follows from the definitions and the Siegel–Weil formula (Proposition 7.1.1 (b)). The computation is as in [Reference Yuan, Zhang and ZhangYZZ12, Proposition 6.5]. ◻
Lemma 7.3.2. Assume that
![]() $\unicode[STIX]{x1D719}^{\infty }$
is
$\unicode[STIX]{x1D719}^{\infty }$
is
![]() $\mathbf{Q}$
-valued. For each non-split finite place
$\mathbf{Q}$
-valued. For each non-split finite place
![]() $v$
, the values of the function
$v$
, the values of the function
 $$\begin{eqnarray}k_{\unicode[STIX]{x1D719}_{v}}^{\natural }(y,x,u):=\ell (\unicode[STIX]{x1D71B}_{v})^{-1}k_{\unicode[STIX]{x1D719}_{v}}(y,x,u)\end{eqnarray}$$
$$\begin{eqnarray}k_{\unicode[STIX]{x1D719}_{v}}^{\natural }(y,x,u):=\ell (\unicode[STIX]{x1D71B}_{v})^{-1}k_{\unicode[STIX]{x1D719}_{v}}(y,x,u)\end{eqnarray}$$
and the coefficients of the reduced
![]() $q$
-expansions
$q$
-expansions
 $$\begin{eqnarray}\displaystyle \mathscr{K}_{\unicode[STIX]{x1D719}^{p\infty }}^{(v)\,\natural } & := & \displaystyle \ell (\unicode[STIX]{x1D71B}_{v})^{-1}\mathscr{K}_{\unicode[STIX]{x1D719}^{p\infty }}^{(v)},\nonumber\\ \displaystyle \mathscr{I}_{F}^{\prime }\text{}^{\natural }(\unicode[STIX]{x1D719}^{p\infty })(v) & := & \displaystyle \ell (\unicode[STIX]{x1D71B}_{v})^{-1}\mathscr{I}_{F}^{\prime }(\unicode[STIX]{x1D719}^{p\infty })(v)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{K}_{\unicode[STIX]{x1D719}^{p\infty }}^{(v)\,\natural } & := & \displaystyle \ell (\unicode[STIX]{x1D71B}_{v})^{-1}\mathscr{K}_{\unicode[STIX]{x1D719}^{p\infty }}^{(v)},\nonumber\\ \displaystyle \mathscr{I}_{F}^{\prime }\text{}^{\natural }(\unicode[STIX]{x1D719}^{p\infty })(v) & := & \displaystyle \ell (\unicode[STIX]{x1D71B}_{v})^{-1}\mathscr{I}_{F}^{\prime }(\unicode[STIX]{x1D719}^{p\infty })(v)\nonumber\end{eqnarray}$$
belong to
![]() $\mathbf{Q}$
.
$\mathbf{Q}$
.
Proof. By Lemma 3.3.1, the local Whittaker function
 $\mathscr{W}_{a,v}^{\circ }(y,u,\unicode[STIX]{x1D719}_{2,v};\unicode[STIX]{x1D712}_{F})$
belongs to
$\mathscr{W}_{a,v}^{\circ }(y,u,\unicode[STIX]{x1D719}_{2,v};\unicode[STIX]{x1D712}_{F})$
belongs to
 $\mathscr{O}(\mathscr{Y}_{F,v})\cong M[X_{v}^{\pm 1}]$
and actually to
$\mathscr{O}(\mathscr{Y}_{F,v})\cong M[X_{v}^{\pm 1}]$
and actually to
 $\mathbf{Q}[X_{v}^{\pm 1}]$
, where
$\mathbf{Q}[X_{v}^{\pm 1}]$
, where
 $X_{v}(\unicode[STIX]{x1D712}_{F,v}):=\unicode[STIX]{x1D712}_{F,v}(\unicode[STIX]{x1D71B}_{v})$
for any uniformiser
$X_{v}(\unicode[STIX]{x1D712}_{F,v}):=\unicode[STIX]{x1D712}_{F,v}(\unicode[STIX]{x1D71B}_{v})$
for any uniformiser
![]() $\unicode[STIX]{x1D71B}_{v}$
. (Recall that the scheme
$\unicode[STIX]{x1D71B}_{v}$
. (Recall that the scheme
![]() $\mathscr{Y}_{F,v}$
of (3.3.1) parametrises unramified characters of
$\mathscr{Y}_{F,v}$
of (3.3.1) parametrises unramified characters of
![]() $F_{v}^{\times }$
.) Therefore, its derivative in the direction
$F_{v}^{\times }$
.) Therefore, its derivative in the direction
![]() $\ell$
is a rational multiple of
$\ell$
is a rational multiple of
 $D_{\ell }X_{v}=\ell (\unicode[STIX]{x1D71B}_{v})$
.◻
$D_{\ell }X_{v}=\ell (\unicode[STIX]{x1D71B}_{v})$
.◻
The following is the main result of this section. It is the direct analogue of [Reference Yuan, Zhang and ZhangYZZ12, Proposition 6.8 and Corollary 6.9] and it is proved in the same way, using Proposition 3.2.3
(1). To compare signs with [Reference Yuan, Zhang and ZhangYZZ12], note that in Proposition 7.3.1 we have preferred to place the minus sign in the definition of
![]() $k_{\unicode[STIX]{x1D719}_{v}}$
; and that our
$k_{\unicode[STIX]{x1D719}_{v}}$
; and that our
![]() $\ell (\unicode[STIX]{x1D71B}_{v})$
, which is the derivative at
$\ell (\unicode[STIX]{x1D71B}_{v})$
, which is the derivative at
![]() $s=0$
of
$s=0$
of
 $\unicode[STIX]{x1D712}_{F}(\unicode[STIX]{x1D71B}_{v})^{s}$
, should be compared with
$\unicode[STIX]{x1D712}_{F}(\unicode[STIX]{x1D71B}_{v})^{s}$
, should be compared with
 $-\log \,q_{F,v}$
in [Reference Yuan, Zhang and ZhangYZZ12] (denoted by
$-\log \,q_{F,v}$
in [Reference Yuan, Zhang and ZhangYZZ12] (denoted by
 $-\log \,N_{v}$
there), which is the derivative at
$-\log \,N_{v}$
there), which is the derivative at
![]() $s=0$
of
$s=0$
of
![]() $|\unicode[STIX]{x1D71B}_{v}|^{s}$
.
$|\unicode[STIX]{x1D71B}_{v}|^{s}$
.
Proposition 7.3.3. Let
![]() $v$
be a non-split finite place of
$v$
be a non-split finite place of
![]() $F$
, and let
$F$
, and let
![]() $B_{v}$
be the quaternion algebra over
$B_{v}$
be the quaternion algebra over
![]() $F_{v}$
which is not isomorphic to
$F_{v}$
which is not isomorphic to
![]() $\mathbf{B}_{v}$
.
$\mathbf{B}_{v}$
.
-
(1) If
 $v\in S_{\text{non-split}}-S_{1}$
, then
$v\in S_{\text{non-split}}-S_{1}$
, then  $$\begin{eqnarray}k_{\unicode[STIX]{x1D719}_{v}}^{\natural }(1,x,u)=\mathbf{1}_{\mathscr{ O}_{B_{v}}\times \mathscr{O}_{F_{v}}^{\times }}(x,u)\frac{v(q(x_{2}))+1}{2}.\end{eqnarray}$$
$$\begin{eqnarray}k_{\unicode[STIX]{x1D719}_{v}}^{\natural }(1,x,u)=\mathbf{1}_{\mathscr{ O}_{B_{v}}\times \mathscr{O}_{F_{v}}^{\times }}(x,u)\frac{v(q(x_{2}))+1}{2}.\end{eqnarray}$$
-
(2) If
 $v\in S_{1}$
and
$v\in S_{1}$
and
 $\unicode[STIX]{x1D719}_{v}$
satisfies Assumption 6.1.2, then
$\unicode[STIX]{x1D719}_{v}$
satisfies Assumption 6.1.2, then
 $k_{\unicode[STIX]{x1D719}_{v}}^{\natural }(y,x,u)$
extends to a rational Schwartz function of
$k_{\unicode[STIX]{x1D719}_{v}}^{\natural }(y,x,u)$
extends to a rational Schwartz function of
 $(x,u)\in B_{v}\times F_{v}^{\times }$
, and we have the identity of
$(x,u)\in B_{v}\times F_{v}^{\times }$
, and we have the identity of
 $q$
-expansions where, for any
$q$
-expansions where, for any $$\begin{eqnarray}\mathscr{K}_{\unicode[STIX]{x1D719}}^{(v)\,\natural }((t_{1},t_{2}))=\text{}^{\mathbf{q}}\unicode[STIX]{x1D703}((t_{1},t_{2}),k_{\unicode[STIX]{x1D719}_{v}}^{\natural }\otimes \unicode[STIX]{x1D719}^{v}),\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{K}_{\unicode[STIX]{x1D719}}^{(v)\,\natural }((t_{1},t_{2}))=\text{}^{\mathbf{q}}\unicode[STIX]{x1D703}((t_{1},t_{2}),k_{\unicode[STIX]{x1D719}_{v}}^{\natural }\otimes \unicode[STIX]{x1D719}^{v}),\end{eqnarray}$$
 $\unicode[STIX]{x1D719}^{\prime }$
, is the usual theta series.
$\unicode[STIX]{x1D719}^{\prime }$
, is the usual theta series. $$\begin{eqnarray}\unicode[STIX]{x1D703}(g,(t_{1},t_{2}),\unicode[STIX]{x1D719}^{\prime })=c_{U^{p}}\mathop{\sum }_{u\in \unicode[STIX]{x1D707}_{U^{p}}^{2}\backslash F^{\times }}\mathop{\sum }_{x\in V}r(g,(t_{1},t_{2}))\unicode[STIX]{x1D719}^{\prime }(x,u)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}(g,(t_{1},t_{2}),\unicode[STIX]{x1D719}^{\prime })=c_{U^{p}}\mathop{\sum }_{u\in \unicode[STIX]{x1D707}_{U^{p}}^{2}\backslash F^{\times }}\mathop{\sum }_{x\in V}r(g,(t_{1},t_{2}))\unicode[STIX]{x1D719}^{\prime }(x,u)\end{eqnarray}$$
8 Decomposition of the geometric kernel and comparison
We establish a decomposition of the geometric kernel according to the places of
![]() $F$
, and compare its local terms away from
$F$
, and compare its local terms away from
![]() $p$
with the corresponding local terms in the expansion of the analytic kernel. Together with a result on the local components of the geometric kernel at
$p$
with the corresponding local terms in the expansion of the analytic kernel. Together with a result on the local components of the geometric kernel at
![]() $p$
proved in § 9, this proves the kernel identity of Theorem 5.4.2 (hence Theorem B) when
$p$
proved in § 9, this proves the kernel identity of Theorem 5.4.2 (hence Theorem B) when
![]() $\unicode[STIX]{x1D712}$
satisfies Assumption 6.2.4.
$\unicode[STIX]{x1D712}$
satisfies Assumption 6.2.4.
8.1 Vanishing of the contribution of the Hodge classes
Fix a level
![]() $U$
as in Assumptions 6.1.5 and 6.2.2.
$U$
as in Assumptions 6.1.5 and 6.2.2.
Recall the height generating series
 $$\begin{eqnarray}\widetilde{Z}((t_{1},t_{2}),\unicode[STIX]{x1D719}^{\infty })=\langle \widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })(t_{1}-\unicode[STIX]{x1D709}_{q(t_{1})}),t_{2}-\unicode[STIX]{x1D709}_{q(t_{2})}\rangle\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{Z}((t_{1},t_{2}),\unicode[STIX]{x1D719}^{\infty })=\langle \widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })(t_{1}-\unicode[STIX]{x1D709}_{q(t_{1})}),t_{2}-\unicode[STIX]{x1D709}_{q(t_{2})}\rangle\end{eqnarray}$$
and the geometric kernel function
 $$\begin{eqnarray}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})=\int _{[T]}^{\ast }\unicode[STIX]{x1D712}(t)\widetilde{Z}((1,t^{-1}),\unicode[STIX]{x1D719}^{\infty })\,dt.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})=\int _{[T]}^{\ast }\unicode[STIX]{x1D712}(t)\widetilde{Z}((1,t^{-1}),\unicode[STIX]{x1D719}^{\infty })\,dt.\end{eqnarray}$$
They are modular cuspforms with coefficients in
 $\unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L(\unicode[STIX]{x1D712})$
.
$\unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L(\unicode[STIX]{x1D712})$
.
Proposition 8.1.1.
-
(1) If Assumption 6.1.3 is satisfied, then
for all $$\begin{eqnarray}\deg \widetilde{Z}(\unicode[STIX]{x1D719}^{\infty })_{U,\unicode[STIX]{x1D6FC}}=0\end{eqnarray}$$
$$\begin{eqnarray}\deg \widetilde{Z}(\unicode[STIX]{x1D719}^{\infty })_{U,\unicode[STIX]{x1D6FC}}=0\end{eqnarray}$$
 $\unicode[STIX]{x1D6FC}\in F_{+}^{\times }\backslash \mathbf{A}^{\times }/q(U)$
.
$\unicode[STIX]{x1D6FC}\in F_{+}^{\times }\backslash \mathbf{A}^{\times }/q(U)$
.
-
(2) If Assumption 6.1.3 is satisfied, then
for all $$\begin{eqnarray}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty })\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FC}}=0\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty })\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FC}}=0\end{eqnarray}$$
 $\unicode[STIX]{x1D6FC}\in F_{+}^{\times }\backslash \mathbf{A}^{\times }/q(U)$
.
$\unicode[STIX]{x1D6FC}\in F_{+}^{\times }\backslash \mathbf{A}^{\times }/q(U)$
.
-
(3) If Assumption 6.2.4 is satisfied, then
 $$\begin{eqnarray}\int _{[T]}^{\ast }\unicode[STIX]{x1D712}(t)\unicode[STIX]{x1D709}_{U,q(t)}\,dt=0.\end{eqnarray}$$
$$\begin{eqnarray}\int _{[T]}^{\ast }\unicode[STIX]{x1D712}(t)\unicode[STIX]{x1D709}_{U,q(t)}\,dt=0.\end{eqnarray}$$
-
(4) If Assumptions 6.1.3 and 6.2.4 are both satisfied, then
where $$\begin{eqnarray}\text{}^{\mathbf{q}}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})_{U}=\langle \text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })1,t_{\unicode[STIX]{x1D712}}\rangle ,\end{eqnarray}$$
$$\begin{eqnarray}\text{}^{\mathbf{q}}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})_{U}=\langle \text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })1,t_{\unicode[STIX]{x1D712}}\rangle ,\end{eqnarray}$$
 $$\begin{eqnarray}t_{\unicode[STIX]{x1D712}}=\int _{[T]}^{\ast }\unicode[STIX]{x1D712}(t)[t^{-1}]_{U}\,d^{\circ }t\in \operatorname{Div}^{0}(X_{U})_{L(\unicode[STIX]{x1D712})}.\end{eqnarray}$$
$$\begin{eqnarray}t_{\unicode[STIX]{x1D712}}=\int _{[T]}^{\ast }\unicode[STIX]{x1D712}(t)[t^{-1}]_{U}\,d^{\circ }t\in \operatorname{Div}^{0}(X_{U})_{L(\unicode[STIX]{x1D712})}.\end{eqnarray}$$
Proof. Note first that part (4) follows from parts (2) and (3) after expanding and bringing the integration inside. Part (2) follows from part (1) as in [Reference Yuan, Zhang and ZhangYZZ12, §7.3.1], and part (1) is proved in [Reference Yuan, Zhang and ZhangYZZ12, Lemma 7.6].
For part (3), note first that the group
![]() $V_{p}^{\circ }$
of Assumption 6.2.4 acts trivially on the Hodge classes; in fact, we have
$V_{p}^{\circ }$
of Assumption 6.2.4 acts trivially on the Hodge classes; in fact, we have
 $r(1,t^{-1})\unicode[STIX]{x1D709}_{U,\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D709}_{U,\unicode[STIX]{x1D6FC}q(t)}$
and, by definition,
$r(1,t^{-1})\unicode[STIX]{x1D709}_{U,\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D709}_{U,\unicode[STIX]{x1D6FC}q(t)}$
and, by definition,
 $q(V_{p}^{\circ })\subset U$
. On the other hand, we are assuming that the character
$q(V_{p}^{\circ })\subset U$
. On the other hand, we are assuming that the character
![]() $\unicode[STIX]{x1D712}$
is non-trivial on
$\unicode[STIX]{x1D712}$
is non-trivial on
![]() $V_{p}^{\circ }$
. It follows that the integration against
$V_{p}^{\circ }$
. It follows that the integration against
![]() $\unicode[STIX]{x1D712}$
on
$\unicode[STIX]{x1D712}$
on
 $V_{p}^{\circ }\subset T(\mathbf{A})$
annihilates the Hodge classes.◻
$V_{p}^{\circ }\subset T(\mathbf{A})$
annihilates the Hodge classes.◻
8.2 Decomposition
Let
 $$\begin{eqnarray}\ell :\unicode[STIX]{x1D6E4}_{F}\rightarrow L(\unicode[STIX]{x1D712})\end{eqnarray}$$
$$\begin{eqnarray}\ell :\unicode[STIX]{x1D6E4}_{F}\rightarrow L(\unicode[STIX]{x1D712})\end{eqnarray}$$
be the ramified logarithm fixed in § 7.2. For the rest of this section and in § 9, we will abuse notation by writing
 $\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})$
for the image of
$\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})$
for the image of
 $\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})$
under
$\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})$
under
 $\ell :\unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L(\unicode[STIX]{x1D712})\rightarrow L(\unicode[STIX]{x1D712})$
.
$\ell :\unicode[STIX]{x1D6E4}_{F}\,\hat{\otimes }\,L(\unicode[STIX]{x1D712})\rightarrow L(\unicode[STIX]{x1D712})$
.
Lemma 8.2.1. If Assumption 6.1.2 is satisfied, then for all
 $a\in \mathbf{A}^{S_{1}\infty ,\times }$
and for all
$a\in \mathbf{A}^{S_{1}\infty ,\times }$
and for all
![]() $t_{1}$
,
$t_{1}$
,
 $t_{2}\in T(\mathbf{A}^{\infty })$
, the support of
$t_{2}\in T(\mathbf{A}^{\infty })$
, the support of
 $Z_{a}(\unicode[STIX]{x1D719}^{\infty })t_{1}$
does not contain
$Z_{a}(\unicode[STIX]{x1D719}^{\infty })t_{1}$
does not contain
![]() $[t_{2}]$
.
$[t_{2}]$
.
Proof. This is shown in [Reference Yuan, Zhang and ZhangYZZ12, §7.2.2]. ◻
Let
 $\overline{\mathbf{S}}^{\prime }=\overline{\mathbf{S}}_{S_{1}}^{\prime }(L(\unicode[STIX]{x1D712}))$
be the quotient space, relative to the set of primes
$\overline{\mathbf{S}}^{\prime }=\overline{\mathbf{S}}_{S_{1}}^{\prime }(L(\unicode[STIX]{x1D712}))$
be the quotient space, relative to the set of primes
![]() $S_{1}$
, introduced after the approximation lemma (Lemma 2.1.2).
$S_{1}$
, introduced after the approximation lemma (Lemma 2.1.2).
Proposition 8.2.2. Suppose that Assumptions 6.1.2, 6.1.3, and 6.2.4 are satisfied. If
![]() $H$
is any sufficiently large finite extension of
$H$
is any sufficiently large finite extension of
![]() $E$
and
$E$
and
![]() $w$
is a place of
$w$
is a place of
![]() $H$
, let
$H$
, let
![]() $\langle \,,\rangle _{\ell ,w}$
be the pairing on
$\langle \,,\rangle _{\ell ,w}$
be the pairing on
 $\operatorname{Div}^{0}(X_{U,H})$
associated with
$\operatorname{Div}^{0}(X_{U,H})$
associated with
![]() $\ell _{w}$
of (4.1.7). Let
$\ell _{w}$
of (4.1.7). Let
 $\text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })$
be the image of
$\text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })$
be the image of
![]() $\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })$
in
$\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })$
in
 $\overline{\mathbf{S}}^{\prime }\otimes \text{Corr}\,(X\times X)_{\mathbf{Q}}$
. Then in
$\overline{\mathbf{S}}^{\prime }\otimes \text{Corr}\,(X\times X)_{\mathbf{Q}}$
. Then in
![]() $\overline{\mathbf{S}}^{\prime }$
we have the decomposition
$\overline{\mathbf{S}}^{\prime }$
we have the decomposition
 $$\begin{eqnarray}\text{}^{\mathbf{q}}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})=\mathop{\sum }_{v}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(v)\end{eqnarray}$$
$$\begin{eqnarray}\text{}^{\mathbf{q}}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})=\mathop{\sum }_{v}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(v)\end{eqnarray}$$
where
 $$\begin{eqnarray}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(v)=\mathop{\sum }_{w|v}\langle \text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })1,t_{\unicode[STIX]{x1D712}}\rangle _{\ell ,w}.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(v)=\mathop{\sum }_{w|v}\langle \text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })1,t_{\unicode[STIX]{x1D712}}\rangle _{\ell ,w}.\end{eqnarray}$$
Proof. By Proposition 8.1.1
(4), we have
 $\widetilde{Z}_{a}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})=\langle \widetilde{Z}_{a}(\unicode[STIX]{x1D719}^{\infty })1,t_{\unicode[STIX]{x1D712}}\rangle$
for all
$\widetilde{Z}_{a}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})=\langle \widetilde{Z}_{a}(\unicode[STIX]{x1D719}^{\infty })1,t_{\unicode[STIX]{x1D712}}\rangle$
for all
 $a\in \mathbf{A}^{\infty ,\times }$
. If
$a\in \mathbf{A}^{\infty ,\times }$
. If
 $a\in \mathbf{A}^{S_{1}\infty ,\times }$
, the two divisors have disjoint supports by Lemma 8.2.1, and we can decompose their local height according to (4.2.2).◻
$a\in \mathbf{A}^{S_{1}\infty ,\times }$
, the two divisors have disjoint supports by Lemma 8.2.1, and we can decompose their local height according to (4.2.2).◻
For each place
![]() $w$
of
$w$
of
![]() $E$
, fix an extension
$E$
, fix an extension
![]() $\overline{w}$
of
$\overline{w}$
of
![]() $w$
to
$w$
to
![]() $\overline{F}\supset E$
and, for each finite extension
$\overline{F}\supset E$
and, for each finite extension
![]() $H\subset \overline{F}$
of
$H\subset \overline{F}$
of
![]() $E$
, let
$E$
, let
![]() $\langle \,,\rangle _{\overline{w}}$
be the pairing associated with
$\langle \,,\rangle _{\overline{w}}$
be the pairing associated with
 $\ell _{\overline{w}}:=(1/[H_{\overline{w}}:F_{v}])\ell _{v}\circ N_{H_{\overline{w}}/F_{v}}$
. The absence of the field
$\ell _{\overline{w}}:=(1/[H_{\overline{w}}:F_{v}])\ell _{v}\circ N_{H_{\overline{w}}/F_{v}}$
. The absence of the field
![]() $H$
from the notation is justified by the compatibility deriving from (4.1.6). By the explicit description of the Galois action on CM points, we have
$H$
from the notation is justified by the compatibility deriving from (4.1.6). By the explicit description of the Galois action on CM points, we have
 $$\begin{eqnarray}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(v)=\frac{1}{|S_{E_{v}}|}\mathop{\sum }_{w\in S_{E_{v}}}\unicode[STIX]{x2A0D}_{[T]}\langle \text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })t,tt_{\unicode[STIX]{x1D712}}\rangle _{\overline{w}}\;dt\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(v)=\frac{1}{|S_{E_{v}}|}\mathop{\sum }_{w\in S_{E_{v}}}\unicode[STIX]{x2A0D}_{[T]}\langle \text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })t,tt_{\unicode[STIX]{x1D712}}\rangle _{\overline{w}}\;dt\end{eqnarray}$$
in
![]() $\overline{\mathbf{S}}^{\prime }$
and, if
$\overline{\mathbf{S}}^{\prime }$
and, if
![]() $v\nmid p$
, by Proposition 4.2.2, we can further write
$v\nmid p$
, by Proposition 4.2.2, we can further write
 $$\begin{eqnarray}\displaystyle \widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(v) & = & \displaystyle \frac{\ell (\unicode[STIX]{x1D71B}_{v})}{|S_{E_{v}}|}\mathop{\sum }_{w\in S_{E_{v}}}\int _{[T]}^{\ast }\unicode[STIX]{x2A0D}_{[T]}i_{\overline{w}}(\text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719})t,tt_{1}^{-1})\unicode[STIX]{x1D712}(t_{1})\,dt\,d^{\circ }t_{1}\nonumber\\ \displaystyle & & \displaystyle +\,\int _{[T]}^{\ast }\unicode[STIX]{x2A0D}_{[T]}j_{\overline{w}}(\text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719})t,tt_{1}^{-1})\unicode[STIX]{x1D712}(t_{1})\,dt\,d^{\circ }t_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(v) & = & \displaystyle \frac{\ell (\unicode[STIX]{x1D71B}_{v})}{|S_{E_{v}}|}\mathop{\sum }_{w\in S_{E_{v}}}\int _{[T]}^{\ast }\unicode[STIX]{x2A0D}_{[T]}i_{\overline{w}}(\text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719})t,tt_{1}^{-1})\unicode[STIX]{x1D712}(t_{1})\,dt\,d^{\circ }t_{1}\nonumber\\ \displaystyle & & \displaystyle +\,\int _{[T]}^{\ast }\unicode[STIX]{x2A0D}_{[T]}j_{\overline{w}}(\text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719})t,tt_{1}^{-1})\unicode[STIX]{x1D712}(t_{1})\,dt\,d^{\circ }t_{1}.\end{eqnarray}$$
8.3 Comparison of kernels
Recall that we want to show the kernel identity
 $$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\mathscr{I}^{\prime }(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712}))=2L_{(p)}(1,\unicode[STIX]{x1D702})\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712}))\end{eqnarray}$$
$$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\mathscr{I}^{\prime }(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712}))=2L_{(p)}(1,\unicode[STIX]{x1D702})\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712}))\end{eqnarray}$$
of Theorem 5.4.2 (more precisely, we have here projected both sides of that identity to
![]() $L(\unicode[STIX]{x1D712})$
via
$L(\unicode[STIX]{x1D712})$
via
![]() $\ell$
).
$\ell$
).
Similarly to Proposition 8.2.2, we have by Propositions 7.2.1 and 7.3.1 a decomposition of reduced
![]() $q$
-expansions
$q$
-expansions
 $$\begin{eqnarray}\mathscr{I}^{\prime }(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712})=\mathop{\sum }_{v~\text{non-split}}\mathscr{I}^{\prime }(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712})(v)\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{I}^{\prime }(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712})=\mathop{\sum }_{v~\text{non-split}}\mathscr{I}^{\prime }(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712})(v)\end{eqnarray}$$
with
 $$\begin{eqnarray}\mathscr{I}^{\prime }(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712})(v)=2|D_{F}|L_{(p)}(1,\unicode[STIX]{x1D702})\int _{[T]}^{\ast }\unicode[STIX]{x2A0D}_{[T]}\mathscr{K}_{\unicode[STIX]{x1D719}^{p\infty }}^{(v)}(t,tt_{1}^{-1})\unicode[STIX]{x1D712}(t_{1})\,dt\,d^{\circ }t_{1},\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{I}^{\prime }(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712})(v)=2|D_{F}|L_{(p)}(1,\unicode[STIX]{x1D702})\int _{[T]}^{\ast }\unicode[STIX]{x2A0D}_{[T]}\mathscr{K}_{\unicode[STIX]{x1D719}^{p\infty }}^{(v)}(t,tt_{1}^{-1})\unicode[STIX]{x1D712}(t_{1})\,dt\,d^{\circ }t_{1},\end{eqnarray}$$
and the
![]() $q$
-expansion
$q$
-expansion
 $\mathscr{K}_{\unicode[STIX]{x1D719}^{p\infty }}^{(v)\natural }=\mathscr{K}_{\unicode[STIX]{x1D719}^{p\infty }}^{(v)}\cdot \ell (\unicode[STIX]{x1D71B}_{v})^{-1}$
has rational coefficients.
$\mathscr{K}_{\unicode[STIX]{x1D719}^{p\infty }}^{(v)\natural }=\mathscr{K}_{\unicode[STIX]{x1D719}^{p\infty }}^{(v)}\cdot \ell (\unicode[STIX]{x1D71B}_{v})^{-1}$
has rational coefficients.
We thus state the main theorem on the local components of the kernel function from which the identity (8.3.1) will follow, preceded by a result on the components away from
![]() $p$
which facilitates the comparison with [Reference Yuan, Zhang and ZhangYZZ12].
$p$
which facilitates the comparison with [Reference Yuan, Zhang and ZhangYZZ12].
Proposition 8.3.1. Suppose that all of the assumptions of § 6.1 are satisfied together with Assumptions 6.2.2. Then for all
 $t_{1},t_{2}\in T(\mathbf{A})$
we have the following identities of reduced
$t_{1},t_{2}\in T(\mathbf{A})$
we have the following identities of reduced
![]() $q$
-expansions in
$q$
-expansions in
![]() $\overline{\mathbf{S}}^{\prime }$
.
$\overline{\mathbf{S}}^{\prime }$
.
-
(1) If
 $v\in S_{\text{split}}-S_{p}$
, then
$v\in S_{\text{split}}-S_{p}$
, then  $$\begin{eqnarray}i_{\overline{v}}(\text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })t_{1},t_{2})=j_{\overline{v}}(\text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })t_{1},t_{2})=0.\end{eqnarray}$$
$$\begin{eqnarray}i_{\overline{v}}(\text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })t_{1},t_{2})=j_{\overline{v}}(\text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })t_{1},t_{2})=0.\end{eqnarray}$$
-
(2) If
 $v\in S_{\text{non-split}}-S_{1}$
, then
$v\in S_{\text{non-split}}-S_{1}$
, then  $$\begin{eqnarray}i_{\overline{v}}(\text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })t_{1},t_{2})=\mathscr{K}_{\unicode[STIX]{x1D719}^{p\infty }}^{(v)\natural }(t_{1},t_{2}),\quad j_{\overline{v}}(\text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })t_{1},t_{2})=0.\end{eqnarray}$$
$$\begin{eqnarray}i_{\overline{v}}(\text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })t_{1},t_{2})=\mathscr{K}_{\unicode[STIX]{x1D719}^{p\infty }}^{(v)\natural }(t_{1},t_{2}),\quad j_{\overline{v}}(\text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })t_{1},t_{2})=0.\end{eqnarray}$$
-
(3) If
 $v\in S_{1}$
, then there exist Schwartz functions
$v\in S_{1}$
, then there exist Schwartz functions
 $k_{\unicode[STIX]{x1D719}_{v}}$
,
$k_{\unicode[STIX]{x1D719}_{v}}$
,
 $m_{\unicode[STIX]{x1D719}_{v}}$
,
$m_{\unicode[STIX]{x1D719}_{v}}$
,
 $l_{\unicode[STIX]{x1D719}_{v}}\in \overline{\mathscr{S}}(B(v)_{v}\times F_{v}^{\times })$
depending on
$l_{\unicode[STIX]{x1D719}_{v}}\in \overline{\mathscr{S}}(B(v)_{v}\times F_{v}^{\times })$
depending on
 $\unicode[STIX]{x1D719}_{v}$
and
$\unicode[STIX]{x1D719}_{v}$
and
 $U_{v}$
such that
$U_{v}$
such that  $$\begin{eqnarray}\displaystyle \mathscr{K}_{\unicode[STIX]{x1D719}^{p\infty }}^{(v)\natural }(t_{1},t_{2}) & = & \displaystyle \text{}^{\mathbf{q}}\unicode[STIX]{x1D703}((t_{1},t_{2}),k_{\unicode[STIX]{x1D719}_{v}}\otimes \unicode[STIX]{x1D719}^{v}),\nonumber\\ \displaystyle i_{\overline{v}}(\text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })t_{1},t_{2}) & = & \displaystyle \text{}^{\mathbf{q}}\unicode[STIX]{x1D703}((t_{1},t_{2}),m_{\unicode[STIX]{x1D719}_{v}}\otimes \unicode[STIX]{x1D719}^{v}),\nonumber\\ \displaystyle j_{\overline{v}}(\text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })t_{1},t_{2}) & = & \displaystyle \text{}^{\mathbf{q}}\unicode[STIX]{x1D703}((t_{1},t_{2}),l_{\unicode[STIX]{x1D719}_{v}}\otimes \unicode[STIX]{x1D719}^{v}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{K}_{\unicode[STIX]{x1D719}^{p\infty }}^{(v)\natural }(t_{1},t_{2}) & = & \displaystyle \text{}^{\mathbf{q}}\unicode[STIX]{x1D703}((t_{1},t_{2}),k_{\unicode[STIX]{x1D719}_{v}}\otimes \unicode[STIX]{x1D719}^{v}),\nonumber\\ \displaystyle i_{\overline{v}}(\text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })t_{1},t_{2}) & = & \displaystyle \text{}^{\mathbf{q}}\unicode[STIX]{x1D703}((t_{1},t_{2}),m_{\unicode[STIX]{x1D719}_{v}}\otimes \unicode[STIX]{x1D719}^{v}),\nonumber\\ \displaystyle j_{\overline{v}}(\text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })t_{1},t_{2}) & = & \displaystyle \text{}^{\mathbf{q}}\unicode[STIX]{x1D703}((t_{1},t_{2}),l_{\unicode[STIX]{x1D719}_{v}}\otimes \unicode[STIX]{x1D719}^{v}).\nonumber\end{eqnarray}$$
Here
![]() $B(v)$
is the coherent nearby quaternion algebra to
$B(v)$
is the coherent nearby quaternion algebra to
![]() $\mathbf{B}$
obtained by changing invariants at
$\mathbf{B}$
obtained by changing invariants at
![]() $v$
and, for
$v$
and, for
 $\unicode[STIX]{x1D719}^{\prime }\in \overline{\mathscr{S}}(B(v)_{\mathbf{A}}\times \mathbf{A}^{\times })$
, we have the automorphic theta series
$\unicode[STIX]{x1D719}^{\prime }\in \overline{\mathscr{S}}(B(v)_{\mathbf{A}}\times \mathbf{A}^{\times })$
, we have the automorphic theta series
 $$\begin{eqnarray}\unicode[STIX]{x1D703}(g,(t_{1},t_{2}),\unicode[STIX]{x1D719}^{\prime })=c_{U^{p}}\mathop{\sum }_{u\in \unicode[STIX]{x1D707}_{U^{p}}^{2}\backslash F^{\times }}\mathop{\sum }_{x\in B(v)}r(g,(t_{1},t_{2}))\unicode[STIX]{x1D719}^{\prime }(x,u).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}(g,(t_{1},t_{2}),\unicode[STIX]{x1D719}^{\prime })=c_{U^{p}}\mathop{\sum }_{u\in \unicode[STIX]{x1D707}_{U^{p}}^{2}\backslash F^{\times }}\mathop{\sum }_{x\in B(v)}r(g,(t_{1},t_{2}))\unicode[STIX]{x1D719}^{\prime }(x,u).\end{eqnarray}$$
We denote by
 $$\begin{eqnarray}I(\unicode[STIX]{x1D719}^{\prime },\unicode[STIX]{x1D712})(g):=\int _{[T]}^{\ast }\unicode[STIX]{x2A0D}_{[T]}\unicode[STIX]{x1D712}(t_{1})\unicode[STIX]{x1D703}(g,(t,t_{1}^{-1}t),\unicode[STIX]{x1D719}^{\prime })\,dt\,d^{\circ }t_{1}\end{eqnarray}$$
$$\begin{eqnarray}I(\unicode[STIX]{x1D719}^{\prime },\unicode[STIX]{x1D712})(g):=\int _{[T]}^{\ast }\unicode[STIX]{x2A0D}_{[T]}\unicode[STIX]{x1D712}(t_{1})\unicode[STIX]{x1D703}(g,(t,t_{1}^{-1}t),\unicode[STIX]{x1D719}^{\prime })\,dt\,d^{\circ }t_{1}\end{eqnarray}$$
the associated coherent theta function.
Proof. Part (1) is [Reference Yuan, Zhang and ZhangYZZ12, Theorem 7.8(1)]. In part (2), the vanishing of
![]() $j_{\overline{v}}$
follows by the definitions; the other identity is obtained by explicit computation of both sides as in [Reference Yuan, Zhang and ZhangYZZ12, Proposition 8.8], which gives the expression for the geometric side;Footnote
31
on the analytic side we use the result of Proposition 7.3.3
(1). Part (3) for
$j_{\overline{v}}$
follows by the definitions; the other identity is obtained by explicit computation of both sides as in [Reference Yuan, Zhang and ZhangYZZ12, Proposition 8.8], which gives the expression for the geometric side;Footnote
31
on the analytic side we use the result of Proposition 7.3.3
(1). Part (3) for
![]() $\mathscr{K}_{\unicode[STIX]{x1D719}^{p\infty }}^{(v)\natural }$
is Proposition 7.3.3
(2), whereas for
$\mathscr{K}_{\unicode[STIX]{x1D719}^{p\infty }}^{(v)\natural }$
is Proposition 7.3.3
(2), whereas for
![]() $i_{\overline{v}}$
and
$i_{\overline{v}}$
and
![]() $j_{\overline{v}}$
it is [Reference Yuan, Zhang and ZhangYZZ12, Theorem 7.8(4)].◻
$j_{\overline{v}}$
it is [Reference Yuan, Zhang and ZhangYZZ12, Theorem 7.8(4)].◻
Theorem 8.3.2. Suppose that all of the assumptions of § 6.1 are satisfied together with Assumptions 6.2.2 and 6.2.4. Then we have the following identities of reduced
![]() $q$
-expansions in
$q$
-expansions in
![]() $\overline{\mathbf{S}}^{\prime }$
.
$\overline{\mathbf{S}}^{\prime }$
.
-
(1) If
 $v\in S_{\text{split}}-S_{p}$
, then
$v\in S_{\text{split}}-S_{p}$
, then  $$\begin{eqnarray}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(v)=0.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(v)=0.\end{eqnarray}$$
-
(2) If
 $v\in S_{\text{non-split}}-S_{1}$
, then
$v\in S_{\text{non-split}}-S_{1}$
, then  $$\begin{eqnarray}\mathscr{I}^{\prime }(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712})(v)=2|D_{F}|L_{(p)}(1,\unicode[STIX]{x1D702})\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(v).\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{I}^{\prime }(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712})(v)=2|D_{F}|L_{(p)}(1,\unicode[STIX]{x1D702})\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(v).\end{eqnarray}$$
-
(3) If
 $v\in S_{1}$
, then there exist Schwartz functions
$v\in S_{1}$
, then there exist Schwartz functions
 $k_{\unicode[STIX]{x1D719}_{v}}$
,
$k_{\unicode[STIX]{x1D719}_{v}}$
,
 $n_{\unicode[STIX]{x1D719}_{v}}\in \overline{\mathscr{S}}(B(v)_{v}\times F_{v}^{\times })$
depending on
$n_{\unicode[STIX]{x1D719}_{v}}\in \overline{\mathscr{S}}(B(v)_{v}\times F_{v}^{\times })$
depending on
 $\unicode[STIX]{x1D719}_{v}$
and
$\unicode[STIX]{x1D719}_{v}$
and
 $U_{v}$
such that, with the notation (8.3.3),
$U_{v}$
such that, with the notation (8.3.3),  $$\begin{eqnarray}\displaystyle \mathscr{I}^{\prime }(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712})(v) & = & \displaystyle \text{}^{\mathbf{q}}I(k_{\unicode[STIX]{x1D719}_{v}}\otimes \unicode[STIX]{x1D719}^{v},\unicode[STIX]{x1D712}),\nonumber\\ \displaystyle \widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(v) & = & \displaystyle \text{}^{\mathbf{q}}I(n_{\unicode[STIX]{x1D719}_{v}}\otimes \unicode[STIX]{x1D719}^{v},\unicode[STIX]{x1D712}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{I}^{\prime }(\unicode[STIX]{x1D719}^{p\infty };\unicode[STIX]{x1D712})(v) & = & \displaystyle \text{}^{\mathbf{q}}I(k_{\unicode[STIX]{x1D719}_{v}}\otimes \unicode[STIX]{x1D719}^{v},\unicode[STIX]{x1D712}),\nonumber\\ \displaystyle \widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(v) & = & \displaystyle \text{}^{\mathbf{q}}I(n_{\unicode[STIX]{x1D719}_{v}}\otimes \unicode[STIX]{x1D719}^{v},\unicode[STIX]{x1D712}).\nonumber\end{eqnarray}$$
-
(4) The sum
belongs to the isomorphic image $$\begin{eqnarray}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(p):=\mathop{\sum }_{v\in S_{p}}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(v)\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(p):=\mathop{\sum }_{v\in S_{p}}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(v)\end{eqnarray}$$
 $\overline{\mathbf{S}}\subset \overline{\mathbf{S}}^{\prime }$
of the space of
$\overline{\mathbf{S}}\subset \overline{\mathbf{S}}^{\prime }$
of the space of
 $p$
-adic modular forms
$p$
-adic modular forms
 $\mathbf{S}$
, and we have
$\mathbf{S}$
, and we have  $$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(p))=0.\end{eqnarray}$$
$$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(p))=0.\end{eqnarray}$$
Proof (to be completed in § 9).
Parts (1)–(3) follow from Proposition 8.3.1 by integration via (8.2.1) and (8.3.2). They imply the identity in
![]() $\overline{\mathbf{S}}^{\prime }$
$\overline{\mathbf{S}}^{\prime }$
 $$\begin{eqnarray}\displaystyle 2|D_{F}|L_{(p)}(1,\unicode[STIX]{x1D702})\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(p) & = & \displaystyle 2|D_{F}|L_{(p)}(1,\unicode[STIX]{x1D702})\text{}^{\mathbf{q}}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})-\mathop{\sum }_{v\nmid p}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(v)\nonumber\\ \displaystyle & = & \displaystyle 2|D_{F}|L_{(p)}(1,\unicode[STIX]{x1D702})\text{}^{\mathbf{q}}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})-\mathscr{I}^{\prime }(\unicode[STIX]{x1D719}^{\infty };\unicode[STIX]{x1D712})\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{v\in S_{1}}\text{}^{\mathbf{q}}I(\unicode[STIX]{x1D719}^{v}\otimes d_{\unicode[STIX]{x1D719}_{v}}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2|D_{F}|L_{(p)}(1,\unicode[STIX]{x1D702})\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(p) & = & \displaystyle 2|D_{F}|L_{(p)}(1,\unicode[STIX]{x1D702})\text{}^{\mathbf{q}}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})-\mathop{\sum }_{v\nmid p}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(v)\nonumber\\ \displaystyle & = & \displaystyle 2|D_{F}|L_{(p)}(1,\unicode[STIX]{x1D702})\text{}^{\mathbf{q}}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})-\mathscr{I}^{\prime }(\unicode[STIX]{x1D719}^{\infty };\unicode[STIX]{x1D712})\nonumber\\ \displaystyle & & \displaystyle -\,\mathop{\sum }_{v\in S_{1}}\text{}^{\mathbf{q}}I(\unicode[STIX]{x1D719}^{v}\otimes d_{\unicode[STIX]{x1D719}_{v}}),\end{eqnarray}$$
where
 $d_{\unicode[STIX]{x1D719}_{v}}=2|D_{F}|L_{(p)}(1,\unicode[STIX]{x1D702})n_{\unicode[STIX]{x1D719}_{v}}-k_{\unicode[STIX]{x1D719}_{v}}$
for
$d_{\unicode[STIX]{x1D719}_{v}}=2|D_{F}|L_{(p)}(1,\unicode[STIX]{x1D702})n_{\unicode[STIX]{x1D719}_{v}}-k_{\unicode[STIX]{x1D719}_{v}}$
for
![]() $v\in S_{1}$
. As all terms in the right-hand side belong to
$v\in S_{1}$
. As all terms in the right-hand side belong to
![]() $\overline{\mathbf{S}}$
, so does
$\overline{\mathbf{S}}$
, so does
 $\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(p)$
. The proof of the vanishing statement of part (4) will be given in § 9.◻
$\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(p)$
. The proof of the vanishing statement of part (4) will be given in § 9.◻
Proof of Theorem 5.4.2 under Assumption 6.2.4.
We show that Theorem 5.4.2 follows from Theorem 8.3.2, under the same assumptions. By Proposition 5.4.3 and Lemma 6.1.6, only Assumption 6.2.4 on the character
![]() $\unicode[STIX]{x1D712}$
is restrictive. Moreover by Lemma 6.2.6 it is equivalent to show that the desired kernel identity holds after applying to both sides a ramified logarithm
$\unicode[STIX]{x1D712}$
is restrictive. Moreover by Lemma 6.2.6 it is equivalent to show that the desired kernel identity holds after applying to both sides a ramified logarithm
 $\ell :\unicode[STIX]{x1D6E4}_{F}\rightarrow L(\unicode[STIX]{x1D712})$
.
$\ell :\unicode[STIX]{x1D6E4}_{F}\rightarrow L(\unicode[STIX]{x1D712})$
.
By (8.3.4),
 $$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(2|D_{F}|L(1,\unicode[STIX]{x1D702})\cdot \text{}^{\mathbf{q}}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})-\mathscr{I}^{\prime }(\unicode[STIX]{x1D719}^{\infty };\unicode[STIX]{x1D712}))=\mathop{\sum }_{v\in S_{1}}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\text{}^{\mathbf{q}}I(\unicode[STIX]{x1D719}^{v}\otimes d_{\unicode[STIX]{x1D719}_{v}}))+\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(p)).\end{eqnarray}$$
$$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(2|D_{F}|L(1,\unicode[STIX]{x1D702})\cdot \text{}^{\mathbf{q}}\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})-\mathscr{I}^{\prime }(\unicode[STIX]{x1D719}^{\infty };\unicode[STIX]{x1D712}))=\mathop{\sum }_{v\in S_{1}}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\text{}^{\mathbf{q}}I(\unicode[STIX]{x1D719}^{v}\otimes d_{\unicode[STIX]{x1D719}_{v}}))+\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(p)).\end{eqnarray}$$
The vanishing of the terms indexed by
![]() $S_{1}$
can be shown as in [Reference Yuan, Zhang and ZhangYZZ12, §7.4.3] to follow from the local result of Tunnell and Saito together with Waldspurger’s formula. The term
$S_{1}$
can be shown as in [Reference Yuan, Zhang and ZhangYZZ12, §7.4.3] to follow from the local result of Tunnell and Saito together with Waldspurger’s formula. The term
 $\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(p))=0$
by part (4) of Theorem 8.3.2.◻
$\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(p))=0$
by part (4) of Theorem 8.3.2.◻
9 Local heights at
 $p$
$p$
After some preparation in § 9.1, in § 9.2 we prove the vanishing statement of part 4 of Theorem 8.3.2. We follow a strategy of Nekovář [Reference NekovářNek95] and Shnidman [Reference ShnidmanShn16].
For each
![]() $v|p$
, fix isomorphisms
$v|p$
, fix isomorphisms
 $$\begin{eqnarray}E_{v}:=E\otimes _{F}F_{v}\cong F_{v}\oplus F_{v}\end{eqnarray}$$
$$\begin{eqnarray}E_{v}:=E\otimes _{F}F_{v}\cong F_{v}\oplus F_{v}\end{eqnarray}$$
and
 $B_{v}\cong M_{2}(F_{v})$
such that the embedding of quadratic spaces
$B_{v}\cong M_{2}(F_{v})$
such that the embedding of quadratic spaces
 $E_{v}{\hookrightarrow}B_{v}$
is identified with
$E_{v}{\hookrightarrow}B_{v}$
is identified with
 $(a,d)\mapsto (\!\begin{smallmatrix}a & \\ & d\end{smallmatrix}\!)$
; then for the decomposition
$(a,d)\mapsto (\!\begin{smallmatrix}a & \\ & d\end{smallmatrix}\!)$
; then for the decomposition
 $\mathbf{B}_{v}=\mathbf{V}_{1,v}\oplus \mathbf{V}_{2,v}=E_{v}\oplus E_{v}^{\bot }$
, the first (respectively second) factor consists of the diagonal (respectively antidiagonal) matrices. Let
$\mathbf{B}_{v}=\mathbf{V}_{1,v}\oplus \mathbf{V}_{2,v}=E_{v}\oplus E_{v}^{\bot }$
, the first (respectively second) factor consists of the diagonal (respectively antidiagonal) matrices. Let
![]() $w$
,
$w$
,
![]() $w^{\ast }$
be the places of
$w^{\ast }$
be the places of
![]() $E$
above
$E$
above
![]() $v$
such that
$v$
such that
![]() $E_{w}$
(respectively
$E_{w}$
(respectively
![]() $E_{w^{\ast }}$
) corresponds to the projection onto the first (respectively second) factor under (9.0.5). We fix the extension
$E_{w^{\ast }}$
) corresponds to the projection onto the first (respectively second) factor under (9.0.5). We fix the extension
![]() $\overline{v}=\overline{w}$
of
$\overline{v}=\overline{w}$
of
![]() $v$
to
$v$
to
![]() $\overline{F}\supset E$
to be any one inducing
$\overline{F}\supset E$
to be any one inducing
![]() $w$
on
$w$
on
![]() $E$
, and we will accordingly view the local reciprocity maps
$E$
, and we will accordingly view the local reciprocity maps
 $\text{rec}_{w}:E_{w}^{\times }=F_{v}^{\times }\rightarrow \operatorname{Gal}(\overline{F}_{\overline{v}}/F_{v})^{\text{ab}}=\operatorname{Gal}(\overline{F}_{\overline{v}}/E_{w})^{\text{ab}}$
.
$\text{rec}_{w}:E_{w}^{\times }=F_{v}^{\times }\rightarrow \operatorname{Gal}(\overline{F}_{\overline{v}}/F_{v})^{\text{ab}}=\operatorname{Gal}(\overline{F}_{\overline{v}}/E_{w})^{\text{ab}}$
.
9.1 Local Hecke and Galois actions on CM points
Let
 $U=U_{F}^{\circ }\widetilde{U}=\prod _{v}U_{v}\subset \mathbf{B}^{\infty \times }$
be an open compact subgroup and
$U=U_{F}^{\circ }\widetilde{U}=\prod _{v}U_{v}\subset \mathbf{B}^{\infty \times }$
be an open compact subgroup and
 $\unicode[STIX]{x1D719}\in \overline{\mathscr{S}}(\mathbf{B}\times \mathbf{A}^{\times })$
satisfy Assumption 6.2.2 for integers
$\unicode[STIX]{x1D719}\in \overline{\mathscr{S}}(\mathbf{B}\times \mathbf{A}^{\times })$
satisfy Assumption 6.2.2 for integers
 $r=(r_{v})_{v|p}$
. Fix throughout this subsection a prime
$r=(r_{v})_{v|p}$
. Fix throughout this subsection a prime
![]() $v|p$
.
$v|p$
.
By Lemma 3.1.1, the generating series
![]() $\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty })$
is invariant under
$\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty })$
is invariant under
 $K^{1}(\unicode[STIX]{x1D71B}^{r^{\prime }})_{v}$
for some
$K^{1}(\unicode[STIX]{x1D71B}^{r^{\prime }})_{v}$
for some
![]() $r^{\prime }>0$
. We compute the action of the operator
$r^{\prime }>0$
. We compute the action of the operator
![]() $\text{U}_{v,\ast }$
on it.
$\text{U}_{v,\ast }$
on it.
Lemma 9.1.1. For each
![]() $a\in \mathbf{A}^{\times }$
,
$a\in \mathbf{A}^{\times }$
,
![]() $v|p$
, the
$v|p$
, the
![]() $a$
th reduced
$a$
th reduced
![]() $q$
-expansion coefficient of
$q$
-expansion coefficient of
 $\text{U}_{v,\ast }\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty })$
equals
$\text{U}_{v,\ast }\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty })$
equals
 $$\begin{eqnarray}Z(\unicode[STIX]{x1D71B}_{v}^{-1})\widetilde{Z}_{a\unicode[STIX]{x1D71B}_{v}}(\unicode[STIX]{x1D719}^{\infty }),\end{eqnarray}$$
$$\begin{eqnarray}Z(\unicode[STIX]{x1D71B}_{v}^{-1})\widetilde{Z}_{a\unicode[STIX]{x1D71B}_{v}}(\unicode[STIX]{x1D719}^{\infty }),\end{eqnarray}$$
where the
![]() $(a\unicode[STIX]{x1D71B}_{v})$
th
$(a\unicode[STIX]{x1D71B}_{v})$
th
![]() $q$
-expansion coefficient of
$q$
-expansion coefficient of
![]() $\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty })$
is given in (5.2.2).
$\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty })$
is given in (5.2.2).
Proof. We have
 $$\begin{eqnarray}\displaystyle \text{U}_{v,\ast }\unicode[STIX]{x1D719}_{v}(x,u) & = & \displaystyle |\unicode[STIX]{x1D71B}_{v}|\mathop{\sum }_{j\in \mathscr{O}_{F,v}/\unicode[STIX]{x1D71B}_{v}}r((\!\begin{smallmatrix}\unicode[STIX]{x1D71B}_{v} & j\\ & 1\end{smallmatrix}\!))\unicode[STIX]{x1D719}_{v}(x,u)\nonumber\\ \displaystyle & = & \displaystyle |\unicode[STIX]{x1D71B}_{v}|\unicode[STIX]{x1D719}_{v}(\unicode[STIX]{x1D71B}_{v}x,\unicode[STIX]{x1D71B}_{v}^{-1}u)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{U}_{v,\ast }\unicode[STIX]{x1D719}_{v}(x,u) & = & \displaystyle |\unicode[STIX]{x1D71B}_{v}|\mathop{\sum }_{j\in \mathscr{O}_{F,v}/\unicode[STIX]{x1D71B}_{v}}r((\!\begin{smallmatrix}\unicode[STIX]{x1D71B}_{v} & j\\ & 1\end{smallmatrix}\!))\unicode[STIX]{x1D719}_{v}(x,u)\nonumber\\ \displaystyle & = & \displaystyle |\unicode[STIX]{x1D71B}_{v}|\unicode[STIX]{x1D719}_{v}(\unicode[STIX]{x1D71B}_{v}x,\unicode[STIX]{x1D71B}_{v}^{-1}u)\nonumber\end{eqnarray}$$
under our assumptions on
![]() $\unicode[STIX]{x1D719}_{v}$
.
$\unicode[STIX]{x1D719}_{v}$
.
Inserting this in the definition of
![]() $\widetilde{Z}$
and performing the change of variables
$\widetilde{Z}$
and performing the change of variables
 $x^{\prime }=\unicode[STIX]{x1D71B}_{v}x$
, we obtain the result.◻
$x^{\prime }=\unicode[STIX]{x1D71B}_{v}x$
, we obtain the result.◻
We wish to give a more explicit expression for
 $$\begin{eqnarray}\widetilde{Z}_{a\unicode[STIX]{x1D71B}_{v}^{s}}(\unicode[STIX]{x1D719}^{\infty })[1]_{U}=c_{U^{p}}|a\unicode[STIX]{x1D71B}^{s}|\mathop{\sum }_{x\in U\backslash \mathbf{B}^{\infty \times }/U}\unicode[STIX]{x1D719}^{\infty }(x,a\unicode[STIX]{x1D71B}_{v}^{s}q(x)^{-1})[x]_{U}\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{Z}_{a\unicode[STIX]{x1D71B}_{v}^{s}}(\unicode[STIX]{x1D719}^{\infty })[1]_{U}=c_{U^{p}}|a\unicode[STIX]{x1D71B}^{s}|\mathop{\sum }_{x\in U\backslash \mathbf{B}^{\infty \times }/U}\unicode[STIX]{x1D719}^{\infty }(x,a\unicode[STIX]{x1D71B}_{v}^{s}q(x)^{-1})[x]_{U}\end{eqnarray}$$
as
![]() $s$
varies. Let
$s$
varies. Let
 $$\begin{eqnarray}\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D71B}_{v}^{r_{v}})=\left\{\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\in M_{2}(\mathscr{O}_{F,v})\,\biggm\vert\,a,d\in 1+\unicode[STIX]{x1D71B}_{v}^{r_{v}}\mathscr{O}_{F,v}\right\}U_{F,v}^{\circ }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D71B}_{v}^{r_{v}})=\left\{\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)\in M_{2}(\mathscr{O}_{F,v})\,\biggm\vert\,a,d\in 1+\unicode[STIX]{x1D71B}_{v}^{r_{v}}\mathscr{O}_{F,v}\right\}U_{F,v}^{\circ }.\end{eqnarray}$$
Then
 $\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D71B}_{v}^{r_{v}})\subset \mathbf{B}_{v}$
is the image of the support of
$\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D71B}_{v}^{r_{v}})\subset \mathbf{B}_{v}$
is the image of the support of
![]() $\unicode[STIX]{x1D719}_{v}$
under the natural projection
$\unicode[STIX]{x1D719}_{v}$
under the natural projection
 $\mathbf{B}_{v}\times F_{v}^{\times }\rightarrow \mathbf{B}_{v}$
; and, for each
$\mathbf{B}_{v}\times F_{v}^{\times }\rightarrow \mathbf{B}_{v}$
; and, for each
 $x_{v}\in U_{v}\backslash \mathbf{B}_{v}^{\times }/U_{v}$
, some
$x_{v}\in U_{v}\backslash \mathbf{B}_{v}^{\times }/U_{v}$
, some
 $x^{v}\in \mathbf{B}^{v\infty ,\times }$
such that
$x^{v}\in \mathbf{B}^{v\infty ,\times }$
such that
![]() $x^{v}x_{v}$
contributes to the sum (9.1.1) exists if and only if
$x^{v}x_{v}$
contributes to the sum (9.1.1) exists if and only if
![]() $x_{v}$
belongs to
$x_{v}$
belongs to
 $$\begin{eqnarray}\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D71B}_{v}^{r_{v}})_{a\unicode[STIX]{x1D71B}_{v}^{s_{v}}}:=\{x_{v}\in \unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D71B}_{v}^{r_{v}}),q(x_{v})\in a\unicode[STIX]{x1D71B}_{v}^{s_{v}}(1+\unicode[STIX]{x1D71B}^{r}\mathscr{O}_{F,v})\}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D71B}_{v}^{r_{v}})_{a\unicode[STIX]{x1D71B}_{v}^{s_{v}}}:=\{x_{v}\in \unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D71B}_{v}^{r_{v}}),q(x_{v})\in a\unicode[STIX]{x1D71B}_{v}^{s_{v}}(1+\unicode[STIX]{x1D71B}^{r}\mathscr{O}_{F,v})\}.\end{eqnarray}$$
Lemma 9.1.2. Let
![]() $U_{v}$
,
$U_{v}$
,
![]() $\unicode[STIX]{x1D719}_{v}$
be as in Assumption 6.2.2, and let
$\unicode[STIX]{x1D719}_{v}$
be as in Assumption 6.2.2, and let
![]() $a\in F_{v}^{\times }$
with
$a\in F_{v}^{\times }$
with
 $s_{v}=v(a)\geqslant r_{v}$
. Then the quotient sets
$s_{v}=v(a)\geqslant r_{v}$
. Then the quotient sets
 $U_{v}\backslash \unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D71B}_{v}^{r_{v}})_{a}/U_{v}$
,
$U_{v}\backslash \unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D71B}_{v}^{r_{v}})_{a}/U_{v}$
,
 $\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D71B}_{v}^{r_{v}})_{a}/U_{v}$
, and
$\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D71B}_{v}^{r_{v}})_{a}/U_{v}$
, and
 $U_{v}\backslash \unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D71B}_{v}^{r_{v}})_{a}$
are in bijection and, for each of them, the set of elements
$U_{v}\backslash \unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D71B}_{v}^{r_{v}})_{a}$
are in bijection and, for each of them, the set of elements
 $$\begin{eqnarray}x_{v}(b_{v},a):=\left(\begin{array}{@{}cc@{}}1 & b_{v}\\ b_{v}^{-1}(1-a) & 1\end{array}\right)\in M_{2}(F_{v})=\mathbf{B}_{v},\quad b_{v}\in (\mathscr{O}_{F,v}/\unicode[STIX]{x1D71B}_{v}^{r_{v}+s_{v}})^{\times }\end{eqnarray}$$
$$\begin{eqnarray}x_{v}(b_{v},a):=\left(\begin{array}{@{}cc@{}}1 & b_{v}\\ b_{v}^{-1}(1-a) & 1\end{array}\right)\in M_{2}(F_{v})=\mathbf{B}_{v},\quad b_{v}\in (\mathscr{O}_{F,v}/\unicode[STIX]{x1D71B}_{v}^{r_{v}+s_{v}})^{\times }\end{eqnarray}$$
is a complete set of representatives.
Proof. We drop the subscripts
![]() $v$
. By acting on the right with diagonal elements belonging to
$v$
. By acting on the right with diagonal elements belonging to
![]() $U$
, we can bring any element
$U$
, we can bring any element
 $x\in \unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D71B}^{r})_{a}$
to one of the form
$x\in \unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D71B}^{r})_{a}$
to one of the form
![]() $x(b,a^{\prime })$
with
$x(b,a^{\prime })$
with
![]() $b\in \mathscr{O}_{F}^{\times }$
,
$b\in \mathscr{O}_{F}^{\times }$
,
 $a^{\prime }\in a(1+\unicode[STIX]{x1D71B}^{r}\mathscr{O}_{F})$
. The right action of an element
$a^{\prime }\in a(1+\unicode[STIX]{x1D71B}^{r}\mathscr{O}_{F})$
. The right action of an element
![]() $\unicode[STIX]{x1D6FE}\in U$
sends an element
$\unicode[STIX]{x1D6FE}\in U$
sends an element
![]() $x(b,a)$
to one of the same form
$x(b,a)$
to one of the same form
![]() $x(b^{\prime },a^{\prime })$
if and only if
$x(b^{\prime },a^{\prime })$
if and only if
 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}=\left(\begin{array}{@{}cc@{}}1+\unicode[STIX]{x1D706}\unicode[STIX]{x1D71B}^{r} & \displaystyle \frac{-b\unicode[STIX]{x1D707}\unicode[STIX]{x1D71B}^{r}}{1-a}\\ \displaystyle \frac{-\unicode[STIX]{x1D706}\unicode[STIX]{x1D71B}^{r}}{b} & 1+\unicode[STIX]{x1D71B}^{r}\unicode[STIX]{x1D707}\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}=\left(\begin{array}{@{}cc@{}}1+\unicode[STIX]{x1D706}\unicode[STIX]{x1D71B}^{r} & \displaystyle \frac{-b\unicode[STIX]{x1D707}\unicode[STIX]{x1D71B}^{r}}{1-a}\\ \displaystyle \frac{-\unicode[STIX]{x1D706}\unicode[STIX]{x1D71B}^{r}}{b} & 1+\unicode[STIX]{x1D71B}^{r}\unicode[STIX]{x1D707}\end{array}\right)\end{eqnarray}$$
for some
 $\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \mathscr{O}_{F}$
; in this case, we have
$\unicode[STIX]{x1D706},\unicode[STIX]{x1D707}\in \mathscr{O}_{F}$
; in this case, we have
 $$\begin{eqnarray}b^{\prime }=b\frac{1-a\unicode[STIX]{x1D707}\unicode[STIX]{x1D71B}^{r}}{1-a},\quad a^{\prime }=a\biggl(1-\unicode[STIX]{x1D71B}^{r}(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D707})-\unicode[STIX]{x1D71B}^{2r}\frac{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}a}{1-a\unicode[STIX]{x1D71B}^{r}}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}b^{\prime }=b\frac{1-a\unicode[STIX]{x1D707}\unicode[STIX]{x1D71B}^{r}}{1-a},\quad a^{\prime }=a\biggl(1-\unicode[STIX]{x1D71B}^{r}(\unicode[STIX]{x1D706}+\unicode[STIX]{x1D707})-\unicode[STIX]{x1D71B}^{2r}\frac{\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}a}{1-a\unicode[STIX]{x1D71B}^{r}}\biggr).\end{eqnarray}$$
The situation when considering the left action of
![]() $U$
is analogous (as can be seen by the symmetry
$U$
is analogous (as can be seen by the symmetry
 $b\leftrightarrow b^{-1}(1-u\unicode[STIX]{x1D71B}^{s})$
). The lemma follows.◻
$b\leftrightarrow b^{-1}(1-u\unicode[STIX]{x1D71B}^{s})$
). The lemma follows.◻
Henceforth we will just write
![]() $x_{v}(b_{v})$
for
$x_{v}(b_{v})$
for
 $x_{v}(b_{v},a)$
unless there is risk of confusion.
$x_{v}(b_{v},a)$
unless there is risk of confusion.
Lemma 9.1.3. Fix
![]() $a\in F_{v}^{\times }$
with
$a\in F_{v}^{\times }$
with
 $v(a)\geqslant r_{v}$
.
$v(a)\geqslant r_{v}$
.
-
(1) Let
 $x=x^{v}x_{v}(b_{v})$
,
$x=x^{v}x_{v}(b_{v})$
,
 $c_{v}\in \mathscr{O}_{F,v}=\mathscr{O}_{E_{w}}$
. The action of the Galois element
$c_{v}\in \mathscr{O}_{F,v}=\mathscr{O}_{E_{w}}$
. The action of the Galois element
 $\text{rec}_{E}(1+c_{v}\unicode[STIX]{x1D71B}_{v}^{r_{v}})$
is (9.1.2)
$\text{rec}_{E}(1+c_{v}\unicode[STIX]{x1D71B}_{v}^{r_{v}})$
is (9.1.2) $$\begin{eqnarray}\text{rec}(1+c_{v}\unicode[STIX]{x1D71B}_{v}^{r_{v}})[x]_{U}=[x^{v}x_{v}(b_{v}(1+c_{v}\unicode[STIX]{x1D71B}_{v}^{r_{v}}))]_{U}.\end{eqnarray}$$
$$\begin{eqnarray}\text{rec}(1+c_{v}\unicode[STIX]{x1D71B}_{v}^{r_{v}})[x]_{U}=[x^{v}x_{v}(b_{v}(1+c_{v}\unicode[STIX]{x1D71B}_{v}^{r_{v}}))]_{U}.\end{eqnarray}$$
-
(2) We have
where $$\begin{eqnarray}\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D71B}_{v}^{r_{v}})_{a}/U_{v}=\coprod _{\overline{b}\in (\mathscr{O}_{F}/\unicode[STIX]{x1D71B}_{v}^{r})^{\times }}\text{rec}_{E}((1+\unicode[STIX]{x1D71B}^{r_{v}}\mathscr{O}_{F,v}/1+\unicode[STIX]{x1D71B}^{s_{v}}\mathscr{O}_{F,v}))x_{v}(b)U_{v},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D71B}_{v}^{r_{v}})_{a}/U_{v}=\coprod _{\overline{b}\in (\mathscr{O}_{F}/\unicode[STIX]{x1D71B}_{v}^{r})^{\times }}\text{rec}_{E}((1+\unicode[STIX]{x1D71B}^{r_{v}}\mathscr{O}_{F,v}/1+\unicode[STIX]{x1D71B}^{s_{v}}\mathscr{O}_{F,v}))x_{v}(b)U_{v},\end{eqnarray}$$
 $b$
is any lift of
$b$
is any lift of
 $\overline{b}$
to
$\overline{b}$
to
 $\mathscr{O}_{F,v}/\unicode[STIX]{x1D71B}^{r_{v}+s_{v}}$
.
$\mathscr{O}_{F,v}/\unicode[STIX]{x1D71B}^{r_{v}+s_{v}}$
.
Proof. Both assertions follow from the explicit description of the Galois action on CM points: we have
 $$\begin{eqnarray}\text{rec}_{E}(1+c_{v}\unicode[STIX]{x1D71B}_{v}^{r_{v}})[x]_{U}=\left[\left(\begin{array}{@{}cc@{}}1+c_{v}\unicode[STIX]{x1D71B}_{v}^{r} & \\ & 1\end{array}\right)x\right]_{U},\end{eqnarray}$$
$$\begin{eqnarray}\text{rec}_{E}(1+c_{v}\unicode[STIX]{x1D71B}_{v}^{r_{v}})[x]_{U}=\left[\left(\begin{array}{@{}cc@{}}1+c_{v}\unicode[STIX]{x1D71B}_{v}^{r} & \\ & 1\end{array}\right)x\right]_{U},\end{eqnarray}$$
and a calculation establishes part (1). In view of Lemma 9.1.2, part (2) is then a restatement of the obvious identity
 $(\mathscr{O}_{F_{v}}/\unicode[STIX]{x1D71B}_{v}^{r+s})^{\times }=((1+\unicode[STIX]{x1D71B}^{r}\mathscr{O}_{F,v})/(1+\unicode[STIX]{x1D71B}^{s}\mathscr{O}_{F,v}))(\mathscr{O}_{F_{v}}/\unicode[STIX]{x1D71B}_{v}^{r})^{\times }$
.◻
$(\mathscr{O}_{F_{v}}/\unicode[STIX]{x1D71B}_{v}^{r+s})^{\times }=((1+\unicode[STIX]{x1D71B}^{r}\mathscr{O}_{F,v})/(1+\unicode[STIX]{x1D71B}^{s}\mathscr{O}_{F,v}))(\mathscr{O}_{F_{v}}/\unicode[STIX]{x1D71B}_{v}^{r})^{\times }$
.◻
Norm relation for the generating series. Let
 $$\begin{eqnarray}\widetilde{Z}_{a}^{v}(\unicode[STIX]{x1D719}^{v}):=c_{U^{p}}\mathop{\sum }_{x^{v}\in \mathbf{B}^{v\infty \times }/U}\unicode[STIX]{x1D719}^{v\infty }(x^{v},aq(x^{v})^{-1})Z(x^{v})_{U}.\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{Z}_{a}^{v}(\unicode[STIX]{x1D719}^{v}):=c_{U^{p}}\mathop{\sum }_{x^{v}\in \mathbf{B}^{v\infty \times }/U}\unicode[STIX]{x1D719}^{v\infty }(x^{v},aq(x^{v})^{-1})Z(x^{v})_{U}.\end{eqnarray}$$
Then we have
 $$\begin{eqnarray}\widetilde{Z}_{a\unicode[STIX]{x1D71B}^{s}}(\unicode[STIX]{x1D719})[1]_{U}=|\unicode[STIX]{x1D71B}_{v}|_{v}^{-2r_{v}}\mathop{\sum }_{x_{v}}\widetilde{Z}_{a}^{v}(\unicode[STIX]{x1D719}^{v})[x_{v}]_{U},\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{Z}_{a\unicode[STIX]{x1D71B}^{s}}(\unicode[STIX]{x1D719})[1]_{U}=|\unicode[STIX]{x1D71B}_{v}|_{v}^{-2r_{v}}\mathop{\sum }_{x_{v}}\widetilde{Z}_{a}^{v}(\unicode[STIX]{x1D719}^{v})[x_{v}]_{U},\end{eqnarray}$$
where the sum runs over
 $x_{v}\in \unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D71B}_{v}^{r_{v}})_{v(a)+v(d)+s_{v}}/U_{v}$
.
$x_{v}\in \unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D71B}_{v}^{r_{v}})_{v(a)+v(d)+s_{v}}/U_{v}$
.
For
![]() $s\geqslant r_{v}$
, let
$s\geqslant r_{v}$
, let
 $H_{s}\subset E^{\text{ab}}$
be the extension of
$H_{s}\subset E^{\text{ab}}$
be the extension of
![]() $E$
with norm group
$E$
with norm group
 $$\begin{eqnarray}U_{F}^{\circ }U_{T}^{v}(1+\unicode[STIX]{x1D71B}_{w}^{s}\mathscr{O}_{E,w}),\end{eqnarray}$$
$$\begin{eqnarray}U_{F}^{\circ }U_{T}^{v}(1+\unicode[STIX]{x1D71B}_{w}^{s}\mathscr{O}_{E,w}),\end{eqnarray}$$
where
 $U_{T}=U\cap E_{\mathbf{A}^{\infty }}^{\times }$
. Let
$U_{T}=U\cap E_{\mathbf{A}^{\infty }}^{\times }$
. Let
 $H_{\infty }=\bigcup _{s\geqslant r_{v}}H_{s}$
. If
$H_{\infty }=\bigcup _{s\geqslant r_{v}}H_{s}$
. If
![]() $r_{v}$
is sufficiently large, for all
$r_{v}$
is sufficiently large, for all
![]() $s\geqslant r_{v}$
the extension
$s\geqslant r_{v}$
the extension
 $H_{s}/H_{r_{v}}$
is totally ramified at
$H_{s}/H_{r_{v}}$
is totally ramified at
![]() $\overline{w}$
, and we have
$\overline{w}$
, and we have
 $$\begin{eqnarray}\operatorname{Gal}(H_{s}/H_{r})\cong \operatorname{Gal}(H_{s_{v},\overline{w}}/H_{r_{v},\overline{w}})\cong (1+\unicode[STIX]{x1D71B}_{v}^{r_{v}}\mathscr{O}_{F,v})/(1+\unicode[STIX]{x1D71B}_{v}^{s}\mathscr{O}_{F,v}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Gal}(H_{s}/H_{r})\cong \operatorname{Gal}(H_{s_{v},\overline{w}}/H_{r_{v},\overline{w}})\cong (1+\unicode[STIX]{x1D71B}_{v}^{r_{v}}\mathscr{O}_{F,v})/(1+\unicode[STIX]{x1D71B}_{v}^{s}\mathscr{O}_{F,v}).\end{eqnarray}$$
For convenience, we set
 $$\begin{eqnarray}H_{s}^{\prime }:=H_{r_{v}+s}\end{eqnarray}$$
$$\begin{eqnarray}H_{s}^{\prime }:=H_{r_{v}+s}\end{eqnarray}$$
for any
 $s\in \{0,1,\ldots ,\infty \}$
and, when
$s\in \{0,1,\ldots ,\infty \}$
and, when
![]() $s<\infty$
, we denote by
$s<\infty$
, we denote by
![]() $\operatorname{Tr}_{s}$
, and similarly later
$\operatorname{Tr}_{s}$
, and similarly later
![]() $N_{s}$
, the trace (respectively norm) with respect to the field extension
$N_{s}$
, the trace (respectively norm) with respect to the field extension
![]() $H_{s}^{\prime }/H_{0}^{\prime }$
.
$H_{s}^{\prime }/H_{0}^{\prime }$
.
Proposition 9.1.4. Fix any
 $a\in \mathbf{A}^{\infty ,\times }$
with
$a\in \mathbf{A}^{\infty ,\times }$
with
 $v(a)=r_{v}$
. With the notation just defined, we have
$v(a)=r_{v}$
. With the notation just defined, we have
 $$\begin{eqnarray}\widetilde{Z}_{a\unicode[STIX]{x1D71B}^{s}}(\unicode[STIX]{x1D719})[1]_{U}=\mathop{\sum }_{i\in I}\mathop{\sum }_{\overline{b}\in (\mathscr{O}_{F,v}/\unicode[STIX]{x1D71B}^{r})^{\times }}\operatorname{Tr}_{s}c_{i}[x_{i}^{v}x_{v}(b,a\unicode[STIX]{x1D71B}^{s})]_{U},\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{Z}_{a\unicode[STIX]{x1D71B}^{s}}(\unicode[STIX]{x1D719})[1]_{U}=\mathop{\sum }_{i\in I}\mathop{\sum }_{\overline{b}\in (\mathscr{O}_{F,v}/\unicode[STIX]{x1D71B}^{r})^{\times }}\operatorname{Tr}_{s}c_{i}[x_{i}^{v}x_{v}(b,a\unicode[STIX]{x1D71B}^{s})]_{U},\end{eqnarray}$$
where the finite indexing set
![]() $I$
, the constants
$I$
, the constants
![]() $c_{i}\in \mathbf{Q}$
, and the cosets
$c_{i}\in \mathbf{Q}$
, and the cosets
![]() $x_{i}^{v}U^{v}$
are independent of
$x_{i}^{v}U^{v}$
are independent of
![]() $s$
. Moreover, there exists an integer
$s$
. Moreover, there exists an integer
![]() $d\neq 0$
independent of
$d\neq 0$
independent of
![]() $a$
such that
$a$
such that
 $c_{i}\in d^{-1}\mathbf{Z}$
for all
$c_{i}\in d^{-1}\mathbf{Z}$
for all
![]() $i$
.
$i$
.
Proof. By Lemma 9.1.3, we can write
 $$\begin{eqnarray}\displaystyle \widetilde{Z}_{a\unicode[STIX]{x1D71B}^{s}}(\unicode[STIX]{x1D719})[1]_{U} & = & \displaystyle |\unicode[STIX]{x1D71B}_{v}|_{v}^{-2r_{v}}\mathop{\sum }_{\overline{b}\in (\mathscr{O}_{F}/\unicode[STIX]{x1D71B}_{v}^{r_{v}})^{\times }}\widetilde{Z}_{a}^{v}(\unicode[STIX]{x1D719}^{v})[\operatorname{Gal}(H_{s,\overline{w}}^{\prime }/H_{0,\overline{w}}^{\prime })\cdot x_{v}(b,a\unicode[STIX]{x1D71B}^{s})]_{U}\nonumber\\ \displaystyle & = & \displaystyle |\unicode[STIX]{x1D71B}_{v}|_{v}^{-2r_{v}}\mathop{\sum }_{\overline{b}\in (\mathscr{O}_{F}/\unicode[STIX]{x1D71B}_{v}^{r_{v}})^{\times }}\operatorname{Tr}_{s}(\widetilde{Z}_{a}^{v}(\unicode[STIX]{x1D719}^{v})[x_{v}(b,a\unicode[STIX]{x1D71B}^{s})]_{U})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \widetilde{Z}_{a\unicode[STIX]{x1D71B}^{s}}(\unicode[STIX]{x1D719})[1]_{U} & = & \displaystyle |\unicode[STIX]{x1D71B}_{v}|_{v}^{-2r_{v}}\mathop{\sum }_{\overline{b}\in (\mathscr{O}_{F}/\unicode[STIX]{x1D71B}_{v}^{r_{v}})^{\times }}\widetilde{Z}_{a}^{v}(\unicode[STIX]{x1D719}^{v})[\operatorname{Gal}(H_{s,\overline{w}}^{\prime }/H_{0,\overline{w}}^{\prime })\cdot x_{v}(b,a\unicode[STIX]{x1D71B}^{s})]_{U}\nonumber\\ \displaystyle & = & \displaystyle |\unicode[STIX]{x1D71B}_{v}|_{v}^{-2r_{v}}\mathop{\sum }_{\overline{b}\in (\mathscr{O}_{F}/\unicode[STIX]{x1D71B}_{v}^{r_{v}})^{\times }}\operatorname{Tr}_{s}(\widetilde{Z}_{a}^{v}(\unicode[STIX]{x1D719}^{v})[x_{v}(b,a\unicode[STIX]{x1D71B}^{s})]_{U})\nonumber\end{eqnarray}$$
using (9.1.3), as by construction the correspondence
 $\widetilde{Z}_{a}^{v}(\unicode[STIX]{x1D719}^{v})_{U}$
is defined over
$\widetilde{Z}_{a}^{v}(\unicode[STIX]{x1D719}^{v})_{U}$
is defined over
![]() $H_{0}^{\prime }$
. We obtain the result by writing
$H_{0}^{\prime }$
. We obtain the result by writing
 $\widetilde{Z}_{a}^{v}(\unicode[STIX]{x1D719}^{v})_{U}=\sum _{i\in I}c_{i}Z(x_{i}^{v})_{U}$
.
$\widetilde{Z}_{a}^{v}(\unicode[STIX]{x1D719}^{v})_{U}=\sum _{i\in I}c_{i}Z(x_{i}^{v})_{U}$
.
Finally, the existence of
![]() $d$
follows from the fact that
$d$
follows from the fact that
![]() $\unicode[STIX]{x1D719}^{\infty }$
is a Schwartz function.◻
$\unicode[STIX]{x1D719}^{\infty }$
is a Schwartz function.◻
The extension
 $H_{\infty ,\overline{w}}/E_{w}$
. After de Shalit [Reference de ShalitdSha85], given a non-archimedean local field
$H_{\infty ,\overline{w}}/E_{w}$
. After de Shalit [Reference de ShalitdSha85], given a non-archimedean local field
![]() $K$
, we say that an extension
$K$
, we say that an extension
 $K^{\prime }\subset K^{\text{ab}}$
of
$K^{\prime }\subset K^{\text{ab}}$
of
![]() $K$
is a relative Lubin–Tate extension if there is a (necessarily unique) finite unramified extension
$K$
is a relative Lubin–Tate extension if there is a (necessarily unique) finite unramified extension
 $K\subset K^{\circ }\subset K^{\prime }$
such that
$K\subset K^{\circ }\subset K^{\prime }$
such that
 $K^{\prime }\subset K^{\text{ab}}$
is maximal for the property of being totally ramified above
$K^{\prime }\subset K^{\text{ab}}$
is maximal for the property of being totally ramified above
![]() $K^{\circ }$
. By local class field theory, for any relative Lubin–Tate extension
$K^{\circ }$
. By local class field theory, for any relative Lubin–Tate extension
![]() $K^{\prime }$
, there exists a unique element
$K^{\prime }$
, there exists a unique element
 $\unicode[STIX]{x1D71B}\in K^{\times }$
with
$\unicode[STIX]{x1D71B}\in K^{\times }$
with
 $v_{K}(\unicode[STIX]{x1D71B})=[K^{\circ }:K]$
(where
$v_{K}(\unicode[STIX]{x1D71B})=[K^{\circ }:K]$
(where
![]() $v_{K}$
is the valuation of
$v_{K}$
is the valuation of
![]() $K$
) such that
$K$
) such that
 $K^{\prime }\subset K^{\text{ab}}$
is the subfield cut out by
$K^{\prime }\subset K^{\text{ab}}$
is the subfield cut out by
 $\langle \unicode[STIX]{x1D71B}\rangle \subset K^{\times }$
via the reciprocity map of
$\langle \unicode[STIX]{x1D71B}\rangle \subset K^{\times }$
via the reciprocity map of
![]() $K$
. We call
$K$
. We call
![]() $\unicode[STIX]{x1D71B}$
the pseudo-uniformiser associated with
$\unicode[STIX]{x1D71B}$
the pseudo-uniformiser associated with
![]() $K^{\prime }$
.
$K^{\prime }$
.
Lemma 9.1.5. The field
![]() $H_{\infty ,\overline{w}}$
is the relative Lubin–Tate extension of
$H_{\infty ,\overline{w}}$
is the relative Lubin–Tate extension of
![]() $E_{w}$
associated with a pseudo-uniformiser
$E_{w}$
associated with a pseudo-uniformiser
 $\unicode[STIX]{x1D71B}_{\text{LT}}\in E_{w}^{\times }$
which is algebraic over
$\unicode[STIX]{x1D71B}_{\text{LT}}\in E_{w}^{\times }$
which is algebraic over
![]() $E$
and satisfies
$E$
and satisfies
 $q_{w}(\unicode[STIX]{x1D71B}_{\text{LT}})=1$
.
$q_{w}(\unicode[STIX]{x1D71B}_{\text{LT}})=1$
.
Proof. It is easy to verify that
![]() $H_{\infty ,\overline{w}}$
is a relative Lubin–Tate extension. We only need to identify the corresponding pseudo-uniformiser
$H_{\infty ,\overline{w}}$
is a relative Lubin–Tate extension. We only need to identify the corresponding pseudo-uniformiser
![]() $\unicode[STIX]{x1D71B}_{\text{LT}}$
. It suffices in fact to find an element
$\unicode[STIX]{x1D71B}_{\text{LT}}$
. It suffices in fact to find an element
![]() $\unicode[STIX]{x1D703}\in E^{\times }$
satisfying
$\unicode[STIX]{x1D703}\in E^{\times }$
satisfying
 $q(\unicode[STIX]{x1D703})=1$
and lying in the kernel of
$q(\unicode[STIX]{x1D703})=1$
and lying in the kernel of
 $\text{rec}_{E_{w}}:E_{w}^{\times }\rightarrow \operatorname{Gal}(H_{\infty ,\overline{w}}/E_{w})$
, as then
$\text{rec}_{E_{w}}:E_{w}^{\times }\rightarrow \operatorname{Gal}(H_{\infty ,\overline{w}}/E_{w})$
, as then
![]() $\unicode[STIX]{x1D71B}_{\text{LT}}$
must be a root of
$\unicode[STIX]{x1D71B}_{\text{LT}}$
must be a root of
![]() $\unicode[STIX]{x1D703}$
and hence also satisfies the required property.
$\unicode[STIX]{x1D703}$
and hence also satisfies the required property.
Let
 $\unicode[STIX]{x1D71B}_{w}\in E_{w}$
be a uniformiser at
$\unicode[STIX]{x1D71B}_{w}\in E_{w}$
be a uniformiser at
![]() $w$
, and let
$w$
, and let
 $d=[E_{\mathbf{A}^{\infty }}^{\times }:E^{\times }U_{T}]$
, where
$d=[E_{\mathbf{A}^{\infty }}^{\times }:E^{\times }U_{T}]$
, where
![]() $U_{T}^{v}$
is as before,
$U_{T}^{v}$
is as before,
 $U_{T,w}\subset \mathscr{O}_{E,w}^{\times }$
is arbitrary, and
$U_{T,w}\subset \mathscr{O}_{E,w}^{\times }$
is arbitrary, and
![]() $U_{T,w^{\ast }}$
is identified with
$U_{T,w^{\ast }}$
is identified with
![]() $U_{F,v}^{\circ }$
under
$U_{F,v}^{\circ }$
under
 $F_{v}\cong E_{w^{\ast }}$
. Then we can find
$F_{v}\cong E_{w^{\ast }}$
. Then we can find
![]() $t\in E^{\times }$
,
$t\in E^{\times }$
,
![]() $u\in U_{T}$
such that
$u\in U_{T}$
such that
 $\unicode[STIX]{x1D71B}_{w}^{d}=tu$
. We show that the image of
$\unicode[STIX]{x1D71B}_{w}^{d}=tu$
. We show that the image of
 $\unicode[STIX]{x1D703}:=t/\overline{t}$
in
$\unicode[STIX]{x1D703}:=t/\overline{t}$
in
![]() $E_{w}^{\times }$
lies in the kernel of
$E_{w}^{\times }$
lies in the kernel of
 $\text{rec}_{E_{w}}:E_{w}^{\times }\rightarrow \operatorname{Gal}(H_{\infty ,\overline{w}}/E_{w})$
. Letting
$\text{rec}_{E_{w}}:E_{w}^{\times }\rightarrow \operatorname{Gal}(H_{\infty ,\overline{w}}/E_{w})$
. Letting
 $\unicode[STIX]{x1D704}_{w}:E_{w}^{\times }{\hookrightarrow}E_{\mathbf{A}^{\infty }}^{\times }$
be the inclusion, we show equivalently that
$\unicode[STIX]{x1D704}_{w}:E_{w}^{\times }{\hookrightarrow}E_{\mathbf{A}^{\infty }}^{\times }$
be the inclusion, we show equivalently that
![]() $\unicode[STIX]{x1D704}_{w}(\unicode[STIX]{x1D703})$
is in the kernel of
$\unicode[STIX]{x1D704}_{w}(\unicode[STIX]{x1D703})$
is in the kernel of
 $\text{rec}_{E}:E_{\mathbf{A}^{\infty }}^{\times }\rightarrow \operatorname{Gal}(H_{\infty ,\overline{w}}/E)$
or concretely that
$\text{rec}_{E}:E_{\mathbf{A}^{\infty }}^{\times }\rightarrow \operatorname{Gal}(H_{\infty ,\overline{w}}/E)$
or concretely that
 $i_{w}(t/\overline{t})\in E^{\times }U_{T}^{v}U_{F}^{\circ }$
. Now we have
$i_{w}(t/\overline{t})\in E^{\times }U_{T}^{v}U_{F}^{\circ }$
. Now we have
 $$\begin{eqnarray}\unicode[STIX]{x1D704}_{w}(t/\overline{t})=t\cdot u^{v}\unicode[STIX]{x1D704}_{w}(u_{w^{\ast }})\unicode[STIX]{x1D704}_{w^{\ast }}(u_{w^{\ast }}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}_{w}(t/\overline{t})=t\cdot u^{v}\unicode[STIX]{x1D704}_{w}(u_{w^{\ast }})\unicode[STIX]{x1D704}_{w^{\ast }}(u_{w^{\ast }}).\end{eqnarray}$$
By construction,
 $u^{v}\in U_{T}^{v}$
, and
$u^{v}\in U_{T}^{v}$
, and
 $\unicode[STIX]{x1D704}_{w}(u_{w^{\ast }})\unicode[STIX]{x1D704}_{w^{\ast }}(u_{w^{\ast }})$
belongs to
$\unicode[STIX]{x1D704}_{w}(u_{w^{\ast }})\unicode[STIX]{x1D704}_{w^{\ast }}(u_{w^{\ast }})$
belongs to
![]() $U_{F,v}^{\circ }$
. This completes the proof.◻
$U_{F,v}^{\circ }$
. This completes the proof.◻
9.2 Annihilation of local heights
Suppose still that the open compact
![]() $U$
and the Schwartz function
$U$
and the Schwartz function
![]() $\unicode[STIX]{x1D719}^{\infty }$
satisfy all of the assumptions of § 6.1 together with Assumption 6.2.2. In this subsection, we complete the proof of Theorem 8.3.2 by showing that the element
$\unicode[STIX]{x1D719}^{\infty }$
satisfy all of the assumptions of § 6.1 together with Assumption 6.2.2. In this subsection, we complete the proof of Theorem 8.3.2 by showing that the element
 $\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(p)\in \overline{\mathbf{S}}$
is annihilated by
$\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(p)\in \overline{\mathbf{S}}$
is annihilated by
![]() $\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
. Let
$\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
. Let
![]() $S$
be a finite set of non-archimedean places of
$S$
be a finite set of non-archimedean places of
![]() $F$
such that, for all
$F$
such that, for all
![]() $v\notin S$
, all the data are unramified,
$v\notin S$
, all the data are unramified,
![]() $U_{v}$
is maximal, and
$U_{v}$
is maximal, and
![]() $\unicode[STIX]{x1D719}_{v}$
is standard. Let
$\unicode[STIX]{x1D719}_{v}$
is standard. Let
 $K=K^{p}K_{p}$
be the level of the modular form
$K=K^{p}K_{p}$
be the level of the modular form
![]() $\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty })$
, and let
$\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty })$
, and let
 $T_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })\in \mathscr{H}^{S}(L)=\mathscr{H}^{S}(M)\otimes _{M,\unicode[STIX]{x1D704}_{\mathfrak{p}}}L$
be any element as in Proposition 2.4.4
(4). By that result, it suffices to prove that
$T_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })\in \mathscr{H}^{S}(L)=\mathscr{H}^{S}(M)\otimes _{M,\unicode[STIX]{x1D704}_{\mathfrak{p}}}L$
be any element as in Proposition 2.4.4
(4). By that result, it suffices to prove that
 $$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(T_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(p))=0.\end{eqnarray}$$
$$\begin{eqnarray}\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}(T_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(p))=0.\end{eqnarray}$$
We will in fact prove the following.
Proposition 9.2.1. For all
![]() $v|p$
, the element
$v|p$
, the element
 $T_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(v)\in \overline{\mathbf{S}}^{\prime }$
is
$T_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(v)\in \overline{\mathbf{S}}^{\prime }$
is
![]() $v$
-critical in the sense of Definition 2.4.1.
$v$
-critical in the sense of Definition 2.4.1.
Recall from § 2.2 that the commutative ring
 $\mathscr{H}^{S}(M)$
acts on the space of reduced
$\mathscr{H}^{S}(M)$
acts on the space of reduced
![]() $q$
-expansions
$q$
-expansions
![]() $\mathbf{S}^{\prime }(K^{p})$
and its quotient
$\mathbf{S}^{\prime }(K^{p})$
and its quotient
 $\overline{\mathbf{S}}_{S_{1}}^{\prime }(K^{p})$
, so that the expression
$\overline{\mathbf{S}}_{S_{1}}^{\prime }(K^{p})$
, so that the expression
 $T_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(v)$
makes sense. Proposition 9.2.1 implies that
$T_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(v)$
makes sense. Proposition 9.2.1 implies that
 $T_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(p)$
is a
$T_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})(p)$
is a
![]() $p$
-critical element of
$p$
-critical element of
![]() $\overline{\mathbf{S}}$
and hence it is annihilated by
$\overline{\mathbf{S}}$
and hence it is annihilated by
![]() $\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
by Proposition 2.4.4
(3), establishing (9.2.1).
$\ell _{\unicode[STIX]{x1D711}^{p},\unicode[STIX]{x1D6FC}}$
by Proposition 2.4.4
(3), establishing (9.2.1).
By Lemma 5.2.2, there is a Hecke correspondence
 $\text{T}(\unicode[STIX]{x1D70E}^{\vee })_{U}$
on
$\text{T}(\unicode[STIX]{x1D70E}^{\vee })_{U}$
on
![]() $X_{U}$
(with coefficients in
$X_{U}$
(with coefficients in
![]() $M$
) such that
$M$
) such that
 $$\begin{eqnarray}T_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })\text{}^{\mathbf{q}}Z_{\ast }(\unicode[STIX]{x1D719}^{\infty })_{U}=\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}\circ Z_{\ast }(\unicode[STIX]{x1D719}^{\infty })_{U}\end{eqnarray}$$
$$\begin{eqnarray}T_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })\text{}^{\mathbf{q}}Z_{\ast }(\unicode[STIX]{x1D719}^{\infty })_{U}=\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}\circ Z_{\ast }(\unicode[STIX]{x1D719}^{\infty })_{U}\end{eqnarray}$$
as correspondences on
![]() $X_{U}$
. Then
$X_{U}$
. Then
 $T_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})_{U}(v)$
is an average of
$T_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })\widetilde{Z}(\unicode[STIX]{x1D719}^{\infty },\unicode[STIX]{x1D712})_{U}(v)$
is an average of
 $$\begin{eqnarray}\langle \text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}\text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })_{U}[1],t_{\unicode[STIX]{x1D712}}\rangle _{\overline{w}}=\langle \text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })_{U}[1],\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}t_{\unicode[STIX]{x1D712}}\rangle _{\overline{w}}\end{eqnarray}$$
$$\begin{eqnarray}\langle \text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}\text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })_{U}[1],t_{\unicode[STIX]{x1D712}}\rangle _{\overline{w}}=\langle \text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })_{U}[1],\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}t_{\unicode[STIX]{x1D712}}\rangle _{\overline{w}}\end{eqnarray}$$
for
![]() $\overline{w}|v$
.
$\overline{w}|v$
.
We study the class of
 $\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}t_{\unicode[STIX]{x1D712}}$
in
$\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}t_{\unicode[STIX]{x1D712}}$
in
 $H_{f}^{1}(E,\operatorname{Ind}_{E}^{H}V_{p}J_{U}|_{\mathscr{G}_{E}})$
, where
$H_{f}^{1}(E,\operatorname{Ind}_{E}^{H}V_{p}J_{U}|_{\mathscr{G}_{E}})$
, where
 $H\subset E^{\text{ab}}$
is any sufficiently large finite extension. Let
$H\subset E^{\text{ab}}$
is any sufficiently large finite extension. Let
![]() $L^{\prime }$
denote
$L^{\prime }$
denote
![]() $\overline{\mathbf{Q}}_{p}$
or any sufficiently large finite extension of
$\overline{\mathbf{Q}}_{p}$
or any sufficiently large finite extension of
![]() $\mathbf{Q}_{p}$
. As
$\mathbf{Q}_{p}$
. As
![]() $\mathscr{G}_{F}$
-representations, we have
$\mathscr{G}_{F}$
-representations, we have
 $$\begin{eqnarray}V_{p}J_{U}\otimes _{\mathbf{Q}_{p}}L^{\prime }=\bigoplus _{A^{\prime },\unicode[STIX]{x1D704}^{\prime }:M_{A^{\prime }}{\hookrightarrow}L^{\prime }}\unicode[STIX]{x1D70B}_{A^{\prime }}^{U}\otimes _{M_{A^{\prime }}}V_{p}A^{\prime \unicode[STIX]{x1D704}}\end{eqnarray}$$
$$\begin{eqnarray}V_{p}J_{U}\otimes _{\mathbf{Q}_{p}}L^{\prime }=\bigoplus _{A^{\prime },\unicode[STIX]{x1D704}^{\prime }:M_{A^{\prime }}{\hookrightarrow}L^{\prime }}\unicode[STIX]{x1D70B}_{A^{\prime }}^{U}\otimes _{M_{A^{\prime }}}V_{p}A^{\prime \unicode[STIX]{x1D704}}\end{eqnarray}$$
for some pairwise non-isogenous simple abelian varieties
![]() $A^{\prime }/F$
with
$A^{\prime }/F$
with
 $\operatorname{End}^{0}A^{\prime }=M_{A^{\prime }}$
; here
$\operatorname{End}^{0}A^{\prime }=M_{A^{\prime }}$
; here
 $V_{p}A^{\prime \unicode[STIX]{x1D704}}:=V_{p}A^{\prime }\otimes _{M_{A^{\prime }},\unicode[STIX]{x1D704}}L^{\prime }$
. More generally, let
$V_{p}A^{\prime \unicode[STIX]{x1D704}}:=V_{p}A^{\prime }\otimes _{M_{A^{\prime }},\unicode[STIX]{x1D704}}L^{\prime }$
. More generally, let
 $$\begin{eqnarray}V:=\operatorname{Ind}_{E}^{H}V_{p}J_{U}|_{\mathscr{G}_{H}}\end{eqnarray}$$
$$\begin{eqnarray}V:=\operatorname{Ind}_{E}^{H}V_{p}J_{U}|_{\mathscr{G}_{H}}\end{eqnarray}$$
for a finite extension
![]() $H$
of
$H$
of
![]() $E$
as above; then we have
$E$
as above; then we have
 $$\begin{eqnarray}V\otimes _{\mathbf{Q}_{p}}L^{\prime }=\bigoplus _{A^{\prime },\unicode[STIX]{x1D704}^{\prime }:M_{A^{\prime }}{\hookrightarrow}L^{\prime },\unicode[STIX]{x1D712}^{\prime }:\operatorname{Gal}(H/E)\rightarrow L^{\prime \times }}\unicode[STIX]{x1D70B}_{A^{\prime }}^{U}\otimes _{M_{A^{\prime }}}V_{p}A^{\prime \unicode[STIX]{x1D704}}(\unicode[STIX]{x1D712}^{\prime }),\end{eqnarray}$$
$$\begin{eqnarray}V\otimes _{\mathbf{Q}_{p}}L^{\prime }=\bigoplus _{A^{\prime },\unicode[STIX]{x1D704}^{\prime }:M_{A^{\prime }}{\hookrightarrow}L^{\prime },\unicode[STIX]{x1D712}^{\prime }:\operatorname{Gal}(H/E)\rightarrow L^{\prime \times }}\unicode[STIX]{x1D70B}_{A^{\prime }}^{U}\otimes _{M_{A^{\prime }}}V_{p}A^{\prime \unicode[STIX]{x1D704}}(\unicode[STIX]{x1D712}^{\prime }),\end{eqnarray}$$
where
 $V_{p}A^{\prime \unicode[STIX]{x1D704}}(\unicode[STIX]{x1D712}^{\prime }):=V_{p}A^{\prime }\otimes _{M_{A^{\prime }},\unicode[STIX]{x1D704}}L_{\unicode[STIX]{x1D712}}^{\prime }.$
$V_{p}A^{\prime \unicode[STIX]{x1D704}}(\unicode[STIX]{x1D712}^{\prime }):=V_{p}A^{\prime }\otimes _{M_{A^{\prime }},\unicode[STIX]{x1D704}}L_{\unicode[STIX]{x1D712}}^{\prime }.$
Let
 $V^{\prime }:=\unicode[STIX]{x1D70B}_{A^{\vee }}^{U}\otimes _{M}V_{p}A^{\vee \unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D712}^{-1})\subset V$
, where
$V^{\prime }:=\unicode[STIX]{x1D70B}_{A^{\vee }}^{U}\otimes _{M}V_{p}A^{\vee \unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D712}^{-1})\subset V$
, where
 $\unicode[STIX]{x1D704}_{\mathfrak{p}}:M{\hookrightarrow}L\subset L(\unicode[STIX]{x1D712})$
is the usual embedding. Let
$\unicode[STIX]{x1D704}_{\mathfrak{p}}:M{\hookrightarrow}L\subset L(\unicode[STIX]{x1D712})$
is the usual embedding. Let
 $V^{\prime \prime }\subset V$
be its complement in the direct sum (9.2.4),
$V^{\prime \prime }\subset V$
be its complement in the direct sum (9.2.4),
 $V=V^{\prime }\oplus V^{\prime \prime }$
.
$V=V^{\prime }\oplus V^{\prime \prime }$
.
Proposition 9.2.2. The class of
 $\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}t_{\unicode[STIX]{x1D712}}$
in
$\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}t_{\unicode[STIX]{x1D712}}$
in
 $H_{f}^{1}(E,V)$
belongs to the subspace
$H_{f}^{1}(E,V)$
belongs to the subspace
 $H_{f}^{1}(E,V^{\prime })$
.
$H_{f}^{1}(E,V^{\prime })$
.
Proof. We may and do replace
![]() $L(\unicode[STIX]{x1D712})$
by a sufficiently large finite extension
$L(\unicode[STIX]{x1D712})$
by a sufficiently large finite extension
![]() $L^{\prime }$
. It is clear that the class of
$L^{\prime }$
. It is clear that the class of
![]() $t_{\unicode[STIX]{x1D712}}$
belongs to
$t_{\unicode[STIX]{x1D712}}$
belongs to
 $H_{f}^{1}(E,V_{p}J_{U}(\unicode[STIX]{x1D712}^{-1}))$
. Then it is enough to verify that
$H_{f}^{1}(E,V_{p}J_{U}(\unicode[STIX]{x1D712}^{-1}))$
. Then it is enough to verify that
 $\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}$
annihilates
$\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}$
annihilates
 $\bigoplus _{(A^{\prime },\unicode[STIX]{x1D704})\neq (A^{\vee },\unicode[STIX]{x1D704}_{\mathfrak{p}})}(V_{p}A^{\prime \unicode[STIX]{x1D704}})^{m_{A^{\prime }}}$
. Equivalently, we show that for any
$\bigoplus _{(A^{\prime },\unicode[STIX]{x1D704})\neq (A^{\vee },\unicode[STIX]{x1D704}_{\mathfrak{p}})}(V_{p}A^{\prime \unicode[STIX]{x1D704}})^{m_{A^{\prime }}}$
. Equivalently, we show that for any
 $(A^{\prime },\unicode[STIX]{x1D704})\neq (A,\unicode[STIX]{x1D704}_{\mathfrak{p}})$
and any
$(A^{\prime },\unicode[STIX]{x1D704})\neq (A,\unicode[STIX]{x1D704}_{\mathfrak{p}})$
and any
 $f_{1}\in \unicode[STIX]{x1D70B}_{A^{\prime }}$
,
$f_{1}\in \unicode[STIX]{x1D70B}_{A^{\prime }}$
,
 $f_{2}\in \unicode[STIX]{x1D70B}_{A^{\prime }}$
,
$f_{2}\in \unicode[STIX]{x1D70B}_{A^{\prime }}$
,
 $$\begin{eqnarray}\text{T}_{\text{alg},\unicode[STIX]{x1D704}}(f_{1},f_{2})\circ \text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}=0\end{eqnarray}$$
$$\begin{eqnarray}\text{T}_{\text{alg},\unicode[STIX]{x1D704}}(f_{1},f_{2})\circ \text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}=0\end{eqnarray}$$
in
 $\operatorname{Hom}(J_{U},J_{U}^{\vee })$
.
$\operatorname{Hom}(J_{U},J_{U}^{\vee })$
.
We have
 $$\begin{eqnarray}\text{T}_{\text{alg},\unicode[STIX]{x1D704}}(f_{1},f_{2})\circ \text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}=\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{ p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}\circ \text{T}_{\text{alg},\unicode[STIX]{x1D704}}(f_{1},f_{2})=\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}\circ \text{T}_{\text{alg},\unicode[STIX]{x1D704}}(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D704}}(\unicode[STIX]{x1D711}^{\prime },{\unicode[STIX]{x1D719}^{\infty }}^{\prime }))\end{eqnarray}$$
$$\begin{eqnarray}\text{T}_{\text{alg},\unicode[STIX]{x1D704}}(f_{1},f_{2})\circ \text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}=\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{ p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}\circ \text{T}_{\text{alg},\unicode[STIX]{x1D704}}(f_{1},f_{2})=\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}\circ \text{T}_{\text{alg},\unicode[STIX]{x1D704}}(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D704}}(\unicode[STIX]{x1D711}^{\prime },{\unicode[STIX]{x1D719}^{\infty }}^{\prime }))\end{eqnarray}$$
for some
 $\unicode[STIX]{x1D711}^{\prime }\in \unicode[STIX]{x1D70E}_{A^{\prime }}^{\infty }$
and some rational Schwartz function
$\unicode[STIX]{x1D711}^{\prime }\in \unicode[STIX]{x1D70E}_{A^{\prime }}^{\infty }$
and some rational Schwartz function
![]() ${\unicode[STIX]{x1D719}^{\infty }}^{\prime }$
. By Theorem 5.4.1, this can be rewritten as
${\unicode[STIX]{x1D719}^{\infty }}^{\prime }$
. By Theorem 5.4.1, this can be rewritten as
 $$\begin{eqnarray}\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}\circ (\unicode[STIX]{x1D704}\unicode[STIX]{x1D711}^{\prime },\widetilde{Z}_{\ast }({\unicode[STIX]{x1D719}^{\infty }}^{\prime }))_{\unicode[STIX]{x1D70E}_{A^{\prime }}^{\infty }}=(\unicode[STIX]{x1D704}\unicode[STIX]{x1D711}^{\prime },\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}\circ \widetilde{Z}_{\ast }({\unicode[STIX]{x1D719}^{\infty }}^{\prime }))_{\unicode[STIX]{x1D70E}_{A^{\prime }}^{\infty }}\end{eqnarray}$$
$$\begin{eqnarray}\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}\circ (\unicode[STIX]{x1D704}\unicode[STIX]{x1D711}^{\prime },\widetilde{Z}_{\ast }({\unicode[STIX]{x1D719}^{\infty }}^{\prime }))_{\unicode[STIX]{x1D70E}_{A^{\prime }}^{\infty }}=(\unicode[STIX]{x1D704}\unicode[STIX]{x1D711}^{\prime },\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}\circ \widetilde{Z}_{\ast }({\unicode[STIX]{x1D719}^{\infty }}^{\prime }))_{\unicode[STIX]{x1D70E}_{A^{\prime }}^{\infty }}\end{eqnarray}$$
using an obvious commutativity. Applying Lemma 5.2.2 again, we have
 $$\begin{eqnarray}\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}\circ \widetilde{Z}_{\ast }({\unicode[STIX]{x1D719}^{\infty }}^{\prime })=\unicode[STIX]{x1D704}_{\mathfrak{ p}}T(\unicode[STIX]{x1D70E})\widetilde{Z}_{\ast }({\unicode[STIX]{x1D719}^{\infty }}^{\prime }),\end{eqnarray}$$
$$\begin{eqnarray}\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}\circ \widetilde{Z}_{\ast }({\unicode[STIX]{x1D719}^{\infty }}^{\prime })=\unicode[STIX]{x1D704}_{\mathfrak{ p}}T(\unicode[STIX]{x1D70E})\widetilde{Z}_{\ast }({\unicode[STIX]{x1D719}^{\infty }}^{\prime }),\end{eqnarray}$$
where in view of (5.2.1), it is easy to see that we are justified in calling
![]() $T(\unicode[STIX]{x1D70E})$
the Hecke operator corresponding to
$T(\unicode[STIX]{x1D70E})$
the Hecke operator corresponding to
 $T(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}$
; i.e. this Hecke operator acts as the idempotent projection onto
$T(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}$
; i.e. this Hecke operator acts as the idempotent projection onto
 $\unicode[STIX]{x1D70E}^{K}\subset M_{2}(K,M)$
for the appropriate level
$\unicode[STIX]{x1D70E}^{K}\subset M_{2}(K,M)$
for the appropriate level
![]() $K$
. It is then clear that modular forms in the image of
$K$
. It is then clear that modular forms in the image of
![]() $T(\unicode[STIX]{x1D70E})$
are in the right kernel of
$T(\unicode[STIX]{x1D70E})$
are in the right kernel of
![]() $(\,,\,)_{\unicode[STIX]{x1D70E}_{A^{\prime }}^{\infty }}$
if
$(\,,\,)_{\unicode[STIX]{x1D70E}_{A^{\prime }}^{\infty }}$
if
 $\unicode[STIX]{x1D70E}_{A^{\prime }}\neq \unicode[STIX]{x1D70E}_{A^{\vee }}$
or equivalently (as
$\unicode[STIX]{x1D70E}_{A^{\prime }}\neq \unicode[STIX]{x1D70E}_{A^{\vee }}$
or equivalently (as
 $A^{\prime }\mapsto \unicode[STIX]{x1D70E}_{A^{\prime }}$
is injective) if
$A^{\prime }\mapsto \unicode[STIX]{x1D70E}_{A^{\prime }}$
is injective) if
 $A^{\prime }\neq A^{\vee }$
.
$A^{\prime }\neq A^{\vee }$
.
If
 $A^{\prime }=A^{\vee }$
, then the expression of interest is the image of
$A^{\prime }=A^{\vee }$
, then the expression of interest is the image of
 $\unicode[STIX]{x1D711}^{\prime }\otimes T(\unicode[STIX]{x1D70E})\widetilde{Z}_{\ast }({\unicode[STIX]{x1D719}^{\infty }}^{\prime })\in \unicode[STIX]{x1D70E}_{A^{\vee }}\otimes (\operatorname{Hom}(J_{U},J_{U}^{\vee })\otimes S_{2}(M))$
under the
$\unicode[STIX]{x1D711}^{\prime }\otimes T(\unicode[STIX]{x1D70E})\widetilde{Z}_{\ast }({\unicode[STIX]{x1D719}^{\infty }}^{\prime })\in \unicode[STIX]{x1D70E}_{A^{\vee }}\otimes (\operatorname{Hom}(J_{U},J_{U}^{\vee })\otimes S_{2}(M))$
under the
![]() $M$
-linear algebraic Petersson product and two projections applied to the two factors, induced respectively from
$M$
-linear algebraic Petersson product and two projections applied to the two factors, induced respectively from
 $\unicode[STIX]{x1D704}:M\otimes L^{\prime }\rightarrow L^{\prime }$
and
$\unicode[STIX]{x1D704}:M\otimes L^{\prime }\rightarrow L^{\prime }$
and
 $\unicode[STIX]{x1D704}_{\mathfrak{p}}:M\otimes L^{\prime }\rightarrow L^{\prime }$
. If
$\unicode[STIX]{x1D704}_{\mathfrak{p}}:M\otimes L^{\prime }\rightarrow L^{\prime }$
. If
![]() $\unicode[STIX]{x1D704}\neq \unicode[STIX]{x1D704}_{\mathfrak{p}}$
, their combination is zero.◻
$\unicode[STIX]{x1D704}\neq \unicode[STIX]{x1D704}_{\mathfrak{p}}$
, their combination is zero.◻
Proposition 9.2.3. For each
![]() $\overline{w}|p$
and each
$\overline{w}|p$
and each
 $a\in \mathbf{A}^{S_{1}\infty ,\times }$
, the mixed extension
$a\in \mathbf{A}^{S_{1}\infty ,\times }$
, the mixed extension
![]() $E$
associated with the divisors
$E$
associated with the divisors
 $\widetilde{Z}_{a}(\unicode[STIX]{x1D719}^{\infty })_{U}[1]$
and
$\widetilde{Z}_{a}(\unicode[STIX]{x1D719}^{\infty })_{U}[1]$
and
 $\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })t_{\unicode[STIX]{x1D712}}$
is essentially crystalline at
$\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })t_{\unicode[STIX]{x1D712}}$
is essentially crystalline at
![]() $\overline{w}$
.
$\overline{w}$
.
Proof. By Proposition 4.3.1, it is equivalent to show that
 $$\begin{eqnarray}m_{\overline{w}}(\widetilde{Z}_{a}(\unicode[STIX]{x1D719}^{\infty })_{U}[1],\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })t_{\unicode[STIX]{x1D712}})=0.\end{eqnarray}$$
$$\begin{eqnarray}m_{\overline{w}}(\widetilde{Z}_{a}(\unicode[STIX]{x1D719}^{\infty })_{U}[1],\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })t_{\unicode[STIX]{x1D712}})=0.\end{eqnarray}$$
Under Assumptions 6.1.2 and 6.1.3 (which are local at
![]() $S_{1}\cup S_{2}$
and hence unaffected by the action of
$S_{1}\cup S_{2}$
and hence unaffected by the action of
 $\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })$
), this is proved in [Reference Yuan, Zhang and ZhangYZZ12, Proposition 8.15, §8.5.1].◻
$\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })$
), this is proved in [Reference Yuan, Zhang and ZhangYZZ12, Proposition 8.15, §8.5.1].◻
Proof of Proposition 9.2.1.
For each
![]() $\overline{w}|v$
, by the discussion preceding (9.2.2) it suffices to show that
$\overline{w}|v$
, by the discussion preceding (9.2.2) it suffices to show that
 $$\begin{eqnarray}\langle \text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })_{U}[1],\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}t_{\unicode[STIX]{x1D712}}\rangle _{\overline{w}}\end{eqnarray}$$
$$\begin{eqnarray}\langle \text{}^{\mathbf{q}}\widetilde{Z}_{\ast }(\unicode[STIX]{x1D719}^{\infty })_{U}[1],\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}t_{\unicode[STIX]{x1D712}}\rangle _{\overline{w}}\end{eqnarray}$$
is a
![]() $v$
-critical element of
$v$
-critical element of
![]() $\overline{\mathbf{S}}^{\prime }$
, that is (by the definition and Lemma 9.1.1), that
$\overline{\mathbf{S}}^{\prime }$
, that is (by the definition and Lemma 9.1.1), that
 $$\begin{eqnarray}\langle \widetilde{Z}_{a\unicode[STIX]{x1D71B}^{s}}(\unicode[STIX]{x1D719}^{\infty })_{U}[1],\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}t_{\unicode[STIX]{x1D712}}\rangle _{\overline{w}}\in q_{F,v}^{s-c}\mathscr{O}_{L(\unicode[STIX]{x1D712})}\end{eqnarray}$$
$$\begin{eqnarray}\langle \widetilde{Z}_{a\unicode[STIX]{x1D71B}^{s}}(\unicode[STIX]{x1D719}^{\infty })_{U}[1],\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}t_{\unicode[STIX]{x1D712}}\rangle _{\overline{w}}\in q_{F,v}^{s-c}\mathscr{O}_{L(\unicode[STIX]{x1D712})}\end{eqnarray}$$
for all
![]() $a$
with
$a$
with
 $v(a)=r_{v}$
and some constant
$v(a)=r_{v}$
and some constant
![]() $c$
independent of
$c$
independent of
![]() $a$
and
$a$
and
![]() $s$
.
$s$
.
We may assume that
![]() $\overline{w}$
extends the place
$\overline{w}$
extends the place
![]() $w$
of
$w$
of
![]() $E$
fixed above.
$E$
fixed above.
By Proposition 9.1.4, when
 $v(a)=r_{v}$
, the divisor
$v(a)=r_{v}$
, the divisor
 $\widetilde{Z}_{a\unicode[STIX]{x1D71B}^{s}}(\unicode[STIX]{x1D719}^{\infty })_{U}[1]$
is a finite sum, with
$\widetilde{Z}_{a\unicode[STIX]{x1D71B}^{s}}(\unicode[STIX]{x1D719}^{\infty })_{U}[1]$
is a finite sum, with
![]() $p$
-adically bounded coefficients, of elements
$p$
-adically bounded coefficients, of elements
 $\operatorname{Tr}_{s}[x_{j,s}]_{U}$
, where
$\operatorname{Tr}_{s}[x_{j,s}]_{U}$
, where
![]() $\operatorname{Tr}_{s}$
denotes the trace map on divisors for the field extension
$\operatorname{Tr}_{s}$
denotes the trace map on divisors for the field extension
![]() $H_{s}^{\prime }/H_{0}^{\prime }$
, and
$H_{s}^{\prime }/H_{0}^{\prime }$
, and
 $[x_{j,s}]_{U}\in \operatorname{Div}^{0}(X_{U,H_{s}^{\prime }})$
.
$[x_{j,s}]_{U}\in \operatorname{Div}^{0}(X_{U,H_{s}^{\prime }})$
.
Recall that
 $\langle \,,\rangle _{\overline{w}}=\langle \,,\rangle _{\ell _{\overline{w}}}$
for a fixed
$\langle \,,\rangle _{\overline{w}}=\langle \,,\rangle _{\ell _{\overline{w}}}$
for a fixed
 $\ell _{\overline{w}}:\overline{F}_{\overline{w}}^{\times }\rightarrow L(\unicode[STIX]{x1D712})$
.Footnote
32
By (4.1.6), we have
$\ell _{\overline{w}}:\overline{F}_{\overline{w}}^{\times }\rightarrow L(\unicode[STIX]{x1D712})$
.Footnote
32
By (4.1.6), we have
 $$\begin{eqnarray}\langle \operatorname{Tr}_{s}[x_{j,s}]_{U},\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}t_{\unicode[STIX]{x1D712}}\rangle _{\ell _{\overline{w}}}=\langle [x_{j,s}]_{U},\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}t_{\unicode[STIX]{x1D712}}\rangle _{\ell _{\overline{w}}\circ N_{s,\overline{w}}},\end{eqnarray}$$
$$\begin{eqnarray}\langle \operatorname{Tr}_{s}[x_{j,s}]_{U},\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}t_{\unicode[STIX]{x1D712}}\rangle _{\ell _{\overline{w}}}=\langle [x_{j,s}]_{U},\text{T}_{\unicode[STIX]{x1D704}_{\mathfrak{p}}}(\unicode[STIX]{x1D70E}^{\vee })_{U}^{\text{t}}t_{\unicode[STIX]{x1D712}}\rangle _{\ell _{\overline{w}}\circ N_{s,\overline{w}}},\end{eqnarray}$$
where we recall that
 $N_{s}=N_{s,\overline{w}}$
is the norm for
$N_{s}=N_{s,\overline{w}}$
is the norm for
 $H_{s,\overline{w}}^{\prime }/H_{0,\overline{w}}^{\prime }$
.
$H_{s,\overline{w}}^{\prime }/H_{0,\overline{w}}^{\prime }$
.
Now take the field
![]() $H$
of (9.2.3) to be
$H$
of (9.2.3) to be
 $H=H_{s}^{\prime }$
, and consider the
$H=H_{s}^{\prime }$
, and consider the
![]() $\mathscr{G}_{E_{w}}$
-representations
$\mathscr{G}_{E_{w}}$
-representations
 $V^{\prime }\subset V=V_{s}$
over
$V^{\prime }\subset V=V_{s}$
over
![]() $L(\unicode[STIX]{x1D712})$
defined above Proposition 9.2.2. By our assumptions,
$L(\unicode[STIX]{x1D712})$
defined above Proposition 9.2.2. By our assumptions,
![]() $V^{\prime }$
satisfies the condition
$V^{\prime }$
satisfies the condition
 $\mathbf{D}_{\text{pst}}(V^{\prime })^{\unicode[STIX]{x1D711}=1}=0$
and the Panchishkin condition, with an exact sequence of
$\mathbf{D}_{\text{pst}}(V^{\prime })^{\unicode[STIX]{x1D711}=1}=0$
and the Panchishkin condition, with an exact sequence of
![]() $\mathscr{G}_{E_{w}}$
-representations
$\mathscr{G}_{E_{w}}$
-representations
 $$\begin{eqnarray}0\rightarrow V^{\prime +}\rightarrow V^{\prime }\rightarrow V^{\prime -}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow V^{\prime +}\rightarrow V^{\prime }\rightarrow V^{\prime -}\rightarrow 0.\end{eqnarray}$$
The representation
![]() $V_{s}$
has a natural
$V_{s}$
has a natural
![]() $\mathscr{G}_{E}$
-stable lattice, namely
$\mathscr{G}_{E}$
-stable lattice, namely
 $T_{s}:=\operatorname{Ind}_{E}^{H_{s}^{\prime }}T_{p}J_{U}|_{\mathscr{G}_{H_{s}^{\prime }}}$
. Let
$T_{s}:=\operatorname{Ind}_{E}^{H_{s}^{\prime }}T_{p}J_{U}|_{\mathscr{G}_{H_{s}^{\prime }}}$
. Let
 $T^{\prime }:=T\cap V^{\prime }$
,
$T^{\prime }:=T\cap V^{\prime }$
,
 $T_{s}^{\prime \prime }:=T_{s}\cap V^{\prime \prime }$
,
$T_{s}^{\prime \prime }:=T_{s}\cap V^{\prime \prime }$
,
 $T^{\prime +}:=T^{\prime }\cap V^{\prime +}$
,
$T^{\prime +}:=T^{\prime }\cap V^{\prime +}$
,
 $T^{\prime -}=T^{\prime }/T^{\prime +}$
; note that
$T^{\prime -}=T^{\prime }/T^{\prime +}$
; note that
![]() $V^{\prime }$
,
$V^{\prime }$
,
![]() $T^{\prime }$
,
$T^{\prime }$
,
![]() $T^{\prime \pm }$
are independent of
$T^{\prime \pm }$
are independent of
![]() $s$
(hence the notation).
$s$
(hence the notation).
Let
![]() $\widetilde{E}_{\overline{w}}/E_{w}$
be a finite extension over which
$\widetilde{E}_{\overline{w}}/E_{w}$
be a finite extension over which
![]() $V_{\mathfrak{p}}A$
(hence
$V_{\mathfrak{p}}A$
(hence
![]() $V^{\prime }$
) becomes semistable. We may assume that the extension
$V^{\prime }$
) becomes semistable. We may assume that the extension
 $\widetilde{E}_{\overline{w}}\subset E^{\text{ab}}$
is abelian and totally ramified (see [Reference NekovářNek06, Propositions 12.11.5(iv) and 12.5.10 and their proofs]). For
$\widetilde{E}_{\overline{w}}\subset E^{\text{ab}}$
is abelian and totally ramified (see [Reference NekovářNek06, Propositions 12.11.5(iv) and 12.5.10 and their proofs]). For
 $s\in \{0,1,\ldots ,\infty \}$
, let
$s\in \{0,1,\ldots ,\infty \}$
, let
 $\widetilde{H}_{s,\overline{w}}^{\prime }:=\widetilde{E}_{\overline{w}}H_{s,\overline{w}}^{\prime }$
be the compositum.
$\widetilde{H}_{s,\overline{w}}^{\prime }:=\widetilde{E}_{\overline{w}}H_{s,\overline{w}}^{\prime }$
be the compositum.
We can then apply Proposition 4.3.2, with the fields
![]() $\widetilde{H}_{s}^{\prime }$
playing the role of the field denoted there by ‘
$\widetilde{H}_{s}^{\prime }$
playing the role of the field denoted there by ‘
![]() $F_{v}$
’; together with Proposition 9.2.3, it implies that (9.2.5) belongs to
$F_{v}$
’; together with Proposition 9.2.3, it implies that (9.2.5) belongs to
 $$\begin{eqnarray}\mathfrak{p}_{L(\unicode[STIX]{x1D712})}^{-(d_{0}+d_{1,s}+d_{2})}\ell _{\overline{w}}\circ \widetilde{N}_{s}(\mathscr{O}_{H_{s}^{\prime },\overline{w}}^{\times }\,\hat{\otimes }\,\mathscr{O}_{L(\unicode[STIX]{x1D712})})\subset \mathfrak{p}_{L(\unicode[STIX]{x1D712})}^{-(d_{0}+d_{1,s}+d_{2}+d^{\prime })}q_{F,v}^{s-c_{0}}\mathscr{O}_{L(\unicode[STIX]{x1D712})},\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{p}_{L(\unicode[STIX]{x1D712})}^{-(d_{0}+d_{1,s}+d_{2})}\ell _{\overline{w}}\circ \widetilde{N}_{s}(\mathscr{O}_{H_{s}^{\prime },\overline{w}}^{\times }\,\hat{\otimes }\,\mathscr{O}_{L(\unicode[STIX]{x1D712})})\subset \mathfrak{p}_{L(\unicode[STIX]{x1D712})}^{-(d_{0}+d_{1,s}+d_{2}+d^{\prime })}q_{F,v}^{s-c_{0}}\mathscr{O}_{L(\unicode[STIX]{x1D712})},\end{eqnarray}$$
where
![]() $d_{0}$
,
$d_{0}$
,
![]() $d_{1,s}$
,
$d_{1,s}$
,
![]() $d_{2}$
are the integers of Proposition 4.3.2,Footnote
33
$d_{2}$
are the integers of Proposition 4.3.2,Footnote
33
![]() $\widetilde{N}_{s}$
is the norm of
$\widetilde{N}_{s}$
is the norm of
![]() $\widetilde{H}_{s}^{\prime }/\widetilde{H}_{0}^{\prime }$
, and
$\widetilde{H}_{s}^{\prime }/\widetilde{H}_{0}^{\prime }$
, and
![]() $d^{\prime }$
accounts for the denominators coming from (4.1.7). The containment follows from the fact that the extension
$d^{\prime }$
accounts for the denominators coming from (4.1.7). The containment follows from the fact that the extension
![]() $H_{s}^{\prime }/H_{0}^{\prime }$
is totally ramified at
$H_{s}^{\prime }/H_{0}^{\prime }$
is totally ramified at
![]() $\overline{w}$
of degree
$\overline{w}$
of degree
![]() $q_{F,v}^{s}$
, so that
$q_{F,v}^{s}$
, so that
![]() $\widetilde{H}_{s}^{\prime }/\widetilde{H}_{0}^{\prime }$
has ramification degree at least
$\widetilde{H}_{s}^{\prime }/\widetilde{H}_{0}^{\prime }$
has ramification degree at least
![]() $q_{F,v}^{s-c_{0}}$
for some constant
$q_{F,v}^{s-c_{0}}$
for some constant
![]() $c_{0}$
.
$c_{0}$
.
To complete the proof, we need to establish the boundedness of the integer sequence
 $$\begin{eqnarray}d_{1,s}=\text{length}_{\mathscr{O}_{L(\unicode[STIX]{x1D712})}}H^{1}(\widetilde{H}_{0,\overline{w}}^{\prime },T_{s}^{\prime \prime \ast }(1)\otimes L(\unicode[STIX]{x1D712})/\mathscr{O}_{L(\unicode[STIX]{x1D712})})_{\text{tors}}.\end{eqnarray}$$
$$\begin{eqnarray}d_{1,s}=\text{length}_{\mathscr{O}_{L(\unicode[STIX]{x1D712})}}H^{1}(\widetilde{H}_{0,\overline{w}}^{\prime },T_{s}^{\prime \prime \ast }(1)\otimes L(\unicode[STIX]{x1D712})/\mathscr{O}_{L(\unicode[STIX]{x1D712})})_{\text{tors}}.\end{eqnarray}$$
As
 $$\begin{eqnarray}\displaystyle & & \displaystyle H^{1}(\widetilde{H}_{0,\overline{w}}^{\prime },T_{s}^{\prime \prime \ast }(1)\otimes L(\unicode[STIX]{x1D712})/\mathscr{O}_{L(\unicode[STIX]{x1D712})})_{\text{tors}}\nonumber\\ \displaystyle & & \displaystyle \quad \cong H^{0}(\widetilde{H}_{0,\overline{w}}^{\prime },T_{s}^{\prime \prime \ast }(1))\subset H^{0}(E_{w},T_{p}J_{U}^{\ast }(1)\otimes \mathscr{O}_{L(\unicode[STIX]{x1D712})}[\operatorname{Gal}(\widetilde{H}_{s,\overline{w}}^{\prime }/E_{w})]),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle H^{1}(\widetilde{H}_{0,\overline{w}}^{\prime },T_{s}^{\prime \prime \ast }(1)\otimes L(\unicode[STIX]{x1D712})/\mathscr{O}_{L(\unicode[STIX]{x1D712})})_{\text{tors}}\nonumber\\ \displaystyle & & \displaystyle \quad \cong H^{0}(\widetilde{H}_{0,\overline{w}}^{\prime },T_{s}^{\prime \prime \ast }(1))\subset H^{0}(E_{w},T_{p}J_{U}^{\ast }(1)\otimes \mathscr{O}_{L(\unicode[STIX]{x1D712})}[\operatorname{Gal}(\widetilde{H}_{s,\overline{w}}^{\prime }/E_{w})]),\nonumber\end{eqnarray}$$
the boundedness follows from the next lemma. ◻
Lemma 9.2.4. Let
 $\unicode[STIX]{x1D6E4}_{\text{LT}}^{\prime }:=\operatorname{Gal}(\widetilde{H}_{\infty ,\overline{w}}^{\prime }/E_{w})$
. Then
$\unicode[STIX]{x1D6E4}_{\text{LT}}^{\prime }:=\operatorname{Gal}(\widetilde{H}_{\infty ,\overline{w}}^{\prime }/E_{w})$
. Then
 $$\begin{eqnarray}H^{0}(E_{w},V_{p}J_{U}^{\ast }(1)\otimes \mathscr{O}_{L(\unicode[STIX]{x1D712})}\unicode[STIX]{x27E6}\unicode[STIX]{x1D6E4}_{\text{LT}}^{\prime }\unicode[STIX]{x27E7})=0.\end{eqnarray}$$
$$\begin{eqnarray}H^{0}(E_{w},V_{p}J_{U}^{\ast }(1)\otimes \mathscr{O}_{L(\unicode[STIX]{x1D712})}\unicode[STIX]{x27E6}\unicode[STIX]{x1D6E4}_{\text{LT}}^{\prime }\unicode[STIX]{x27E7})=0.\end{eqnarray}$$
Proof. We use the results and notation of Lemma 9.1.5. Note first that we may safely replace
![]() $L(\unicode[STIX]{x1D712})$
by a finite extension
$L(\unicode[STIX]{x1D712})$
by a finite extension
![]() $L^{\prime }$
splitting
$L^{\prime }$
splitting
![]() $E_{w}/\mathbf{Q}_{p}$
. As
$E_{w}/\mathbf{Q}_{p}$
. As
 $V_{p}J_{U}=V_{p}J_{U}^{\ast }(1)$
is Hodge–Tate, we have
$V_{p}J_{U}=V_{p}J_{U}^{\ast }(1)$
is Hodge–Tate, we have
 $$\begin{eqnarray}H^{0}(E_{w},V_{p}J_{U}\otimes _{\mathscr{O}_{L(\unicode[STIX]{x1D712})}}\mathscr{O}_{L(\unicode[STIX]{x1D712})}\unicode[STIX]{x27E6}\unicode[STIX]{x1D6E4}_{\text{LT}}^{\prime }\unicode[STIX]{x27E7})\subset \bigoplus _{\unicode[STIX]{x1D713}}H^{0}(E_{w},V_{p}J_{U}(\unicode[STIX]{x1D713}))(\unicode[STIX]{x1D713}^{-1}),\end{eqnarray}$$
$$\begin{eqnarray}H^{0}(E_{w},V_{p}J_{U}\otimes _{\mathscr{O}_{L(\unicode[STIX]{x1D712})}}\mathscr{O}_{L(\unicode[STIX]{x1D712})}\unicode[STIX]{x27E6}\unicode[STIX]{x1D6E4}_{\text{LT}}^{\prime }\unicode[STIX]{x27E7})\subset \bigoplus _{\unicode[STIX]{x1D713}}H^{0}(E_{w},V_{p}J_{U}(\unicode[STIX]{x1D713}))(\unicode[STIX]{x1D713}^{-1}),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D713}$
runs through the Hodge–Tate characters of
$\unicode[STIX]{x1D713}$
runs through the Hodge–Tate characters of
![]() $\mathscr{G}_{E}$
factoring through
$\mathscr{G}_{E}$
factoring through
![]() $\unicode[STIX]{x1D6E4}_{\text{LT}}^{\prime }$
. Since the latter is a quotient of
$\unicode[STIX]{x1D6E4}_{\text{LT}}^{\prime }$
. Since the latter is a quotient of
![]() $E_{w}^{\times }$
dominating
$E_{w}^{\times }$
dominating
 $\unicode[STIX]{x1D6E4}_{\text{LT}}=\operatorname{Gal}(H_{\infty ,\overline{w}}/E_{w})\cong E_{w}^{\times }/\langle \unicode[STIX]{x1D71B}_{\text{LT}}\rangle$
, we have
$\unicode[STIX]{x1D6E4}_{\text{LT}}=\operatorname{Gal}(H_{\infty ,\overline{w}}/E_{w})\cong E_{w}^{\times }/\langle \unicode[STIX]{x1D71B}_{\text{LT}}\rangle$
, we have
 $\unicode[STIX]{x1D6E4}_{\text{LT}}^{\prime }\cong E_{w}^{\times }/\langle \unicode[STIX]{x1D71B}_{\text{LT}}^{e}\rangle$
for some
$\unicode[STIX]{x1D6E4}_{\text{LT}}^{\prime }\cong E_{w}^{\times }/\langle \unicode[STIX]{x1D71B}_{\text{LT}}^{e}\rangle$
for some
![]() $e\geqslant 1$
. Then the condition that
$e\geqslant 1$
. Then the condition that
![]() $\unicode[STIX]{x1D713}$
factors through
$\unicode[STIX]{x1D713}$
factors through
![]() $\unicode[STIX]{x1D6E4}_{\text{LT}}^{\prime }$
is equivalent to
$\unicode[STIX]{x1D6E4}_{\text{LT}}^{\prime }$
is equivalent to
 $\unicode[STIX]{x1D713}\circ \text{rec}_{E,w}(\unicode[STIX]{x1D71B}_{\text{LT}}^{e})=1$
for the pseudo-uniformiser
$\unicode[STIX]{x1D713}\circ \text{rec}_{E,w}(\unicode[STIX]{x1D71B}_{\text{LT}}^{e})=1$
for the pseudo-uniformiser
 $\unicode[STIX]{x1D714}_{\text{LT}}\in E_{w}^{\times }$
.
$\unicode[STIX]{x1D714}_{\text{LT}}\in E_{w}^{\times }$
.
By [Reference SerreSer68, Appendix III.A], a character
![]() $\unicode[STIX]{x1D713}$
of
$\unicode[STIX]{x1D713}$
of
![]() $\mathscr{G}_{E,w}$
is Hodge–Tate of some weight
$\mathscr{G}_{E,w}$
is Hodge–Tate of some weight
 $\text{}\underline{n}\in \mathbf{Z}[\operatorname{Hom}(E_{w},L^{\prime })]$
if and only if the maps
$\text{}\underline{n}\in \mathbf{Z}[\operatorname{Hom}(E_{w},L^{\prime })]$
if and only if the maps
 $E_{w}^{\times }\rightarrow L^{\prime \times }$
given by
$E_{w}^{\times }\rightarrow L^{\prime \times }$
given by
 $\unicode[STIX]{x1D713}\circ \text{rec}_{E,w}$
and
$\unicode[STIX]{x1D713}\circ \text{rec}_{E,w}$
and
 $x\mapsto x^{-\text{}\underline{n}}:=\prod _{\unicode[STIX]{x1D70F}\in \operatorname{Hom}(E_{w},L^{\prime })}\unicode[STIX]{x1D70F}(x)^{-\text{}\underline{n}(\unicode[STIX]{x1D70F})}$
coincide near
$x\mapsto x^{-\text{}\underline{n}}:=\prod _{\unicode[STIX]{x1D70F}\in \operatorname{Hom}(E_{w},L^{\prime })}\unicode[STIX]{x1D70F}(x)^{-\text{}\underline{n}(\unicode[STIX]{x1D70F})}$
coincide near
![]() $1\in E_{w}^{\times }$
. By [Reference ConradCon, Proposition B.4(i)],
$1\in E_{w}^{\times }$
. By [Reference ConradCon, Proposition B.4(i)],
![]() $\unicode[STIX]{x1D713}$
is crystalline if and only if those maps coincide on
$\unicode[STIX]{x1D713}$
is crystalline if and only if those maps coincide on
![]() $\mathscr{O}_{E,w}^{\times }$
; therefore, we may write any Hodge–Tate character
$\mathscr{O}_{E,w}^{\times }$
; therefore, we may write any Hodge–Tate character
![]() $\unicode[STIX]{x1D713}$
as
$\unicode[STIX]{x1D713}$
as
 $\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}_{0}\unicode[STIX]{x1D713}_{1}$
with
$\unicode[STIX]{x1D713}=\unicode[STIX]{x1D713}_{0}\unicode[STIX]{x1D713}_{1}$
with
![]() $\unicode[STIX]{x1D713}_{0}$
of finite order and
$\unicode[STIX]{x1D713}_{0}$
of finite order and
![]() $\unicode[STIX]{x1D713}_{1}$
crystalline.
$\unicode[STIX]{x1D713}_{1}$
crystalline.
Then, letting
![]() $E_{w,0}$
be the maximal unramified extension of
$E_{w,0}$
be the maximal unramified extension of
![]() $\mathbf{Q}_{p}$
contained in
$\mathbf{Q}_{p}$
contained in
![]() $E_{w}$
and
$E_{w}$
and
 $d=[E_{w}:E_{w,0}]$
, we can first write
$d=[E_{w}:E_{w,0}]$
, we can first write
 $$\begin{eqnarray}H^{0}(E_{w},V_{p}J_{U}(\unicode[STIX]{x1D713}))=\mathbf{D}_{\text{crys}}(V_{p}J_{U}(\unicode[STIX]{x1D713}))^{\unicode[STIX]{x1D711}=1}\subset \mathbf{D}_{\text{crys}}(V_{p}J_{U}(\unicode[STIX]{x1D713}))^{\unicode[STIX]{x1D711}^{d}=1}\end{eqnarray}$$
$$\begin{eqnarray}H^{0}(E_{w},V_{p}J_{U}(\unicode[STIX]{x1D713}))=\mathbf{D}_{\text{crys}}(V_{p}J_{U}(\unicode[STIX]{x1D713}))^{\unicode[STIX]{x1D711}=1}\subset \mathbf{D}_{\text{crys}}(V_{p}J_{U}(\unicode[STIX]{x1D713}))^{\unicode[STIX]{x1D711}^{d}=1}\end{eqnarray}$$
for the
![]() $E_{w,0}$
-linear endomorphism
$E_{w,0}$
-linear endomorphism
![]() $\unicode[STIX]{x1D711}^{d}$
(where
$\unicode[STIX]{x1D711}^{d}$
(where
![]() $\unicode[STIX]{x1D711}$
is the crystalline Frobenius) and then
$\unicode[STIX]{x1D711}$
is the crystalline Frobenius) and then
 $$\begin{eqnarray}\mathbf{D}_{\text{crys}}(V_{p}J_{U}(\unicode[STIX]{x1D713}))^{\unicode[STIX]{x1D711}^{d}=1}=\mathbf{D}_{\text{crys}}(V_{p}J_{U}(\unicode[STIX]{x1D713}_{0}))^{\unicode[STIX]{x1D711}^{d}=\unicode[STIX]{x1D706}_{1}^{-1}},\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{D}_{\text{crys}}(V_{p}J_{U}(\unicode[STIX]{x1D713}))^{\unicode[STIX]{x1D711}^{d}=1}=\mathbf{D}_{\text{crys}}(V_{p}J_{U}(\unicode[STIX]{x1D713}_{0}))^{\unicode[STIX]{x1D711}^{d}=\unicode[STIX]{x1D706}_{1}^{-1}},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D706}_{1}\in L^{\prime }$
is the scalar giving the action of
$\unicode[STIX]{x1D706}_{1}\in L^{\prime }$
is the scalar giving the action of
![]() $\unicode[STIX]{x1D711}^{d}$
on
$\unicode[STIX]{x1D711}^{d}$
on
 $\mathbf{D}_{\text{crys}}(\unicode[STIX]{x1D713}_{1})$
.
$\mathbf{D}_{\text{crys}}(\unicode[STIX]{x1D713}_{1})$
.
By [Reference MokraneMok93, Theorem 5.3], all eigenvalues of
![]() $\unicode[STIX]{x1D711}^{d}$
on
$\unicode[STIX]{x1D711}^{d}$
on
 $\mathbf{D}_{\text{crys}}(V_{p}J_{U}(\unicode[STIX]{x1D713}_{0}))$
are Weil
$\mathbf{D}_{\text{crys}}(V_{p}J_{U}(\unicode[STIX]{x1D713}_{0}))$
are Weil
![]() $q_{E,w}$
-numbers of strictly negative weight. To conclude that
$q_{E,w}$
-numbers of strictly negative weight. To conclude that
 $\mathbf{D}_{\text{crys}}(V_{p}J_{U}(\unicode[STIX]{x1D713}))^{\unicode[STIX]{x1D711}^{d}=1}=0$
, it thus suffices to show that
$\mathbf{D}_{\text{crys}}(V_{p}J_{U}(\unicode[STIX]{x1D713}))^{\unicode[STIX]{x1D711}^{d}=1}=0$
, it thus suffices to show that
![]() $\unicode[STIX]{x1D706}_{1}$
is an algebraic number of weight
$\unicode[STIX]{x1D706}_{1}$
is an algebraic number of weight
![]() $0$
.
$0$
.
By [Reference ConradCon, Proposition B.4(ii)], we have
 $$\begin{eqnarray}\unicode[STIX]{x1D706}_{1}=\unicode[STIX]{x1D713}_{1}\circ \text{rec}_{E,w}(\unicode[STIX]{x1D71B}_{w})^{-1}\cdot \unicode[STIX]{x1D71B}_{w}^{-\text{}\underline{n}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{1}=\unicode[STIX]{x1D713}_{1}\circ \text{rec}_{E,w}(\unicode[STIX]{x1D71B}_{w})^{-1}\cdot \unicode[STIX]{x1D71B}_{w}^{-\text{}\underline{n}},\end{eqnarray}$$
where
 $\unicode[STIX]{x1D71B}_{w}\in E_{w}^{\times }$
is any uniformiser and
$\unicode[STIX]{x1D71B}_{w}\in E_{w}^{\times }$
is any uniformiser and
![]() $\text{}\underline{n}$
are the Hodge–Tate weights. Writing
$\text{}\underline{n}$
are the Hodge–Tate weights. Writing
 $\unicode[STIX]{x1D71B}^{m}=u\unicode[STIX]{x1D71B}_{\text{LT}}$
for
$\unicode[STIX]{x1D71B}^{m}=u\unicode[STIX]{x1D71B}_{\text{LT}}$
for
 $m=w(\unicode[STIX]{x1D71B}_{\text{LT}})$
and some
$m=w(\unicode[STIX]{x1D71B}_{\text{LT}})$
and some
 $u\in \mathscr{O}_{E,w}^{\times }$
, we have
$u\in \mathscr{O}_{E,w}^{\times }$
, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D706}_{1}^{m}=\unicode[STIX]{x1D713}_{1}\circ \text{rec}_{E,w}(u\unicode[STIX]{x1D71B}_{\text{LT}})^{-1}\cdot u^{-\text{}\underline{n}}\unicode[STIX]{x1D71B}_{\text{LT}}^{-\text{}\underline{n}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{1}^{m}=\unicode[STIX]{x1D713}_{1}\circ \text{rec}_{E,w}(u\unicode[STIX]{x1D71B}_{\text{LT}})^{-1}\cdot u^{-\text{}\underline{n}}\unicode[STIX]{x1D71B}_{\text{LT}}^{-\text{}\underline{n}}.\end{eqnarray}$$
Now
 $\unicode[STIX]{x1D713}_{1}\circ \text{rec}_{E,w}(u)=u^{-\text{}\underline{n}}$
by the crystalline condition, and
$\unicode[STIX]{x1D713}_{1}\circ \text{rec}_{E,w}(u)=u^{-\text{}\underline{n}}$
by the crystalline condition, and
 $\unicode[STIX]{x1D713}_{1}^{e}\circ \text{rec}_{E,w}(\unicode[STIX]{x1D71B}_{\text{LT}})=1$
as
$\unicode[STIX]{x1D713}_{1}^{e}\circ \text{rec}_{E,w}(\unicode[STIX]{x1D71B}_{\text{LT}})=1$
as
![]() $\unicode[STIX]{x1D713}_{1}$
factors through
$\unicode[STIX]{x1D713}_{1}$
factors through
![]() $\unicode[STIX]{x1D6E4}_{\text{LT}}^{\prime }$
. Hence,
$\unicode[STIX]{x1D6E4}_{\text{LT}}^{\prime }$
. Hence,
 $\unicode[STIX]{x1D706}_{1}^{em}=\unicode[STIX]{x1D71B}_{\text{LT}}^{-e\text{}\underline{n}}$
. By Lemma 9.1.5,
$\unicode[STIX]{x1D706}_{1}^{em}=\unicode[STIX]{x1D71B}_{\text{LT}}^{-e\text{}\underline{n}}$
. By Lemma 9.1.5,
![]() $\unicode[STIX]{x1D71B}_{\text{LT}}$
is an algebraic number of weight
$\unicode[STIX]{x1D71B}_{\text{LT}}$
is an algebraic number of weight
![]() $0$
and hence so is
$0$
and hence so is
![]() $\unicode[STIX]{x1D706}_{1}$
.◻
$\unicode[STIX]{x1D706}_{1}$
.◻
10 Formulas in anticyclotomic families
In §§ 10.1–10.2, we prove Theorem C after filling in some details in its setup. It is largely a corollary of Theorem B (which we have proved for all but finitely many characters), once a construction of the Heegner–theta elements interpolating automorphic toric periods and Heegner points is carried out. Finally, Theorem B for the missing characters will be recovered as a corollary of Theorem C.
In § 10.3, we prove Theorem D.
We invite the reader to go back to § 1.4 for the setup and notation that we are going to use in this section (except for the preliminary lemma (Lemma 10.1.1)).
10.1 A local construction
Let
![]() $L$
and
$L$
and
![]() $F$
be finite extensions of
$F$
be finite extensions of
![]() $\mathbf{Q}_{p}$
, and denote by
$\mathbf{Q}_{p}$
, and denote by
![]() $v$
the valuation of
$v$
the valuation of
![]() $F$
and by
$F$
and by
![]() $\unicode[STIX]{x1D71B}\in F$
a fixed uniformiser. Let
$\unicode[STIX]{x1D71B}\in F$
a fixed uniformiser. Let
![]() $\unicode[STIX]{x1D70B}$
be a smooth representation of
$\unicode[STIX]{x1D70B}$
be a smooth representation of
 $\mathbf{GL}_{2}(F)$
on an
$\mathbf{GL}_{2}(F)$
on an
![]() $L$
-vector space with central character
$L$
-vector space with central character
![]() $\unicode[STIX]{x1D714}$
and a stable
$\unicode[STIX]{x1D714}$
and a stable
![]() $\mathscr{O}_{L}$
-lattice
$\mathscr{O}_{L}$
-lattice
![]() $\unicode[STIX]{x1D70B}_{\mathscr{O}_{L}}$
. Let
$\unicode[STIX]{x1D70B}_{\mathscr{O}_{L}}$
. Let
 $E^{\times }\subset \mathbf{GL}_{2}(F)$
be the diagonal torus. Assume that
$E^{\times }\subset \mathbf{GL}_{2}(F)$
be the diagonal torus. Assume that
![]() $\unicode[STIX]{x1D70B}$
is nearly ordinary in the sense of Definition 1.2.2 with unit character
$\unicode[STIX]{x1D70B}$
is nearly ordinary in the sense of Definition 1.2.2 with unit character
 $\unicode[STIX]{x1D6FC}:F^{\times }\rightarrow L^{\times }$
. Let
$\unicode[STIX]{x1D6FC}:F^{\times }\rightarrow L^{\times }$
. Let
 $f_{\unicode[STIX]{x1D6FC}}^{\circ }\in \unicode[STIX]{x1D70B}-\{0\}$
be any non-zero element satisfying
$f_{\unicode[STIX]{x1D6FC}}^{\circ }\in \unicode[STIX]{x1D70B}-\{0\}$
be any non-zero element satisfying
 $\text{U}_{v}^{\ast }f_{\unicode[STIX]{x1D6FC}}^{\circ }=\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})f_{\unicode[STIX]{x1D6FC}}^{\circ }$
, which is unique up to multiplication by
$\text{U}_{v}^{\ast }f_{\unicode[STIX]{x1D6FC}}^{\circ }=\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})f_{\unicode[STIX]{x1D6FC}}^{\circ }$
, which is unique up to multiplication by
![]() $L^{\times }$
. For
$L^{\times }$
. For
![]() $r\geqslant 1$
, let
$r\geqslant 1$
, let
 $s_{r}=(\!\begin{smallmatrix}\unicode[STIX]{x1D71B}^{r} & 1\\ & 1\end{smallmatrix}\!)$
and
$s_{r}=(\!\begin{smallmatrix}\unicode[STIX]{x1D71B}^{r} & 1\\ & 1\end{smallmatrix}\!)$
and
 $$\begin{eqnarray}f_{\unicode[STIX]{x1D6FC},r}:=|\unicode[STIX]{x1D71B}|^{-r}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}s_{r}f_{\unicode[STIX]{x1D6FC}}^{\circ }.\end{eqnarray}$$
$$\begin{eqnarray}f_{\unicode[STIX]{x1D6FC},r}:=|\unicode[STIX]{x1D71B}|^{-r}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}s_{r}f_{\unicode[STIX]{x1D6FC}}^{\circ }.\end{eqnarray}$$
It is easy to check that
![]() $f_{\unicode[STIX]{x1D6FC},r}$
is independent of the choice of
$f_{\unicode[STIX]{x1D6FC},r}$
is independent of the choice of
![]() $\unicode[STIX]{x1D71B}$
, and it is invariant under
$\unicode[STIX]{x1D71B}$
, and it is invariant under
 $V_{r}=(\!\begin{smallmatrix}1+\unicode[STIX]{x1D71B}^{r}\mathscr{O}_{F,v} & \\ & 1\end{smallmatrix}\!)V_{F}$
, where
$V_{r}=(\!\begin{smallmatrix}1+\unicode[STIX]{x1D71B}^{r}\mathscr{O}_{F,v} & \\ & 1\end{smallmatrix}\!)V_{F}$
, where
 $V_{F}:=\operatorname{Ker}(\unicode[STIX]{x1D714})\subset Z(F)$
.
$V_{F}:=\operatorname{Ker}(\unicode[STIX]{x1D714})\subset Z(F)$
.
Lemma 10.1.1.
-
(1) The collection
 $f_{\unicode[STIX]{x1D6FC},V_{r}}:=f_{\unicode[STIX]{x1D6FC},r}$
, for
$f_{\unicode[STIX]{x1D6FC},V_{r}}:=f_{\unicode[STIX]{x1D6FC},r}$
, for
 $r\geqslant 0$
, defines an element where the inverse system runs over compact open subgroups
$r\geqslant 0$
, defines an element where the inverse system runs over compact open subgroups $$\begin{eqnarray}f_{\unicode[STIX]{x1D6FC}}=(f_{\unicode[STIX]{x1D6FC},V})\in \underset{V}{\varprojlim }\,\unicode[STIX]{x1D70B}^{V},\end{eqnarray}$$
$$\begin{eqnarray}f_{\unicode[STIX]{x1D6FC}}=(f_{\unicode[STIX]{x1D6FC},V})\in \underset{V}{\varprojlim }\,\unicode[STIX]{x1D70B}^{V},\end{eqnarray}$$
 $V_{F}\subset V\subset E^{\times }$
, and the transition maps
$V_{F}\subset V\subset E^{\times }$
, and the transition maps
 $\unicode[STIX]{x1D70B}^{V^{\prime }}\rightarrow \unicode[STIX]{x1D70B}^{V}$
are given by
$\unicode[STIX]{x1D70B}^{V^{\prime }}\rightarrow \unicode[STIX]{x1D70B}^{V}$
are given by  $$\begin{eqnarray}f\mapsto \unicode[STIX]{x2A0D}_{V/V^{\prime }}\unicode[STIX]{x1D70B}(t)f\,dt.\end{eqnarray}$$
$$\begin{eqnarray}f\mapsto \unicode[STIX]{x2A0D}_{V/V^{\prime }}\unicode[STIX]{x1D70B}(t)f\,dt.\end{eqnarray}$$
-
(2) Let
 $\unicode[STIX]{x1D70B}_{\mathscr{O}_{L}}\subset \unicode[STIX]{x1D70B}$
be a
$\unicode[STIX]{x1D70B}_{\mathscr{O}_{L}}\subset \unicode[STIX]{x1D70B}$
be a
 $\mathbf{GL}_{2}(F)$
-stable
$\mathbf{GL}_{2}(F)$
-stable
 $\mathscr{O}_{L}$
-lattice containing
$\mathscr{O}_{L}$
-lattice containing
 $f_{\unicode[STIX]{x1D6FC}}^{\circ }$
. The collection of elements
$f_{\unicode[STIX]{x1D6FC}}^{\circ }$
. The collection of elements
 $\tilde{f}_{\unicode[STIX]{x1D6FC},V_{r}}:=|\unicode[STIX]{x1D71B}|^{r}f_{\unicode[STIX]{x1D6FC},r}=\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}s_{r}f_{\unicode[STIX]{x1D6FC}}^{\circ }$
defines an element where the transition maps
$\tilde{f}_{\unicode[STIX]{x1D6FC},V_{r}}:=|\unicode[STIX]{x1D71B}|^{r}f_{\unicode[STIX]{x1D6FC},r}=\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}s_{r}f_{\unicode[STIX]{x1D6FC}}^{\circ }$
defines an element where the transition maps $$\begin{eqnarray}\tilde{f}_{\unicode[STIX]{x1D6FC}}\in \underset{V}{\varprojlim }\,\unicode[STIX]{x1D70B}_{\mathscr{O}_{L}}^{V},\end{eqnarray}$$
$$\begin{eqnarray}\tilde{f}_{\unicode[STIX]{x1D6FC}}\in \underset{V}{\varprojlim }\,\unicode[STIX]{x1D70B}_{\mathscr{O}_{L}}^{V},\end{eqnarray}$$
 $\unicode[STIX]{x1D70B}^{V^{\prime }}\rightarrow \unicode[STIX]{x1D70B}^{V}$
are given by
$\unicode[STIX]{x1D70B}^{V^{\prime }}\rightarrow \unicode[STIX]{x1D70B}^{V}$
are given by  $$\begin{eqnarray}f\mapsto \mathop{\sum }_{t\in V/V^{\prime }}\unicode[STIX]{x1D70B}(t)f.\end{eqnarray}$$
$$\begin{eqnarray}f\mapsto \mathop{\sum }_{t\in V/V^{\prime }}\unicode[STIX]{x1D70B}(t)f.\end{eqnarray}$$
Proof. We need to prove that
 $$\begin{eqnarray}\unicode[STIX]{x2A0D}_{V_{r}/V_{r+1}}\unicode[STIX]{x1D70B}(t)f_{\unicode[STIX]{x1D6FC},r+1}\,dt=f_{\unicode[STIX]{x1D6FC},r}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2A0D}_{V_{r}/V_{r+1}}\unicode[STIX]{x1D70B}(t)f_{\unicode[STIX]{x1D6FC},r+1}\,dt=f_{\unicode[STIX]{x1D6FC},r}.\end{eqnarray}$$
A set of representatives for
 $V_{r}/V_{r+1}$
is
$V_{r}/V_{r+1}$
is
 $\{\!(\!\begin{smallmatrix}1+j\unicode[STIX]{x1D71B}^{r} & \\ & 1\end{smallmatrix}\!)\!\}_{j\in \mathscr{O}_{F}/\unicode[STIX]{x1D71B}}$
; on the other hand, recall that
$\{\!(\!\begin{smallmatrix}1+j\unicode[STIX]{x1D71B}^{r} & \\ & 1\end{smallmatrix}\!)\!\}_{j\in \mathscr{O}_{F}/\unicode[STIX]{x1D71B}}$
; on the other hand, recall that
 $\text{U}_{v}^{\ast }=\sum _{j\in \mathscr{O}_{F}/\unicode[STIX]{x1D71B}_{v}}(\!\begin{smallmatrix}\unicode[STIX]{x1D71B} & j\\ & 1\end{smallmatrix}\!)$
. From the identity
$\text{U}_{v}^{\ast }=\sum _{j\in \mathscr{O}_{F}/\unicode[STIX]{x1D71B}_{v}}(\!\begin{smallmatrix}\unicode[STIX]{x1D71B} & j\\ & 1\end{smallmatrix}\!)$
. From the identity
 $$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}1+j\unicode[STIX]{x1D71B}^{r} & \\ & 1\end{array}\right)\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D71B}^{r+1} & 1\\ & 1\end{array}\right)=\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D71B}^{r} & 1\\ & 1\end{array}\right)\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D71B} & j\\ & 1\end{array}\right)\left(\begin{array}{@{}cc@{}}1+j\unicode[STIX]{x1D71B}^{r} & \\ & 1\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}1+j\unicode[STIX]{x1D71B}^{r} & \\ & 1\end{array}\right)\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D71B}^{r+1} & 1\\ & 1\end{array}\right)=\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D71B}^{r} & 1\\ & 1\end{array}\right)\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D71B} & j\\ & 1\end{array}\right)\left(\begin{array}{@{}cc@{}}1+j\unicode[STIX]{x1D71B}^{r} & \\ & 1\end{array}\right),\end{eqnarray}$$
we obtain
 $$\begin{eqnarray}\unicode[STIX]{x2A0D}_{V_{r}/V_{r+1}}\unicode[STIX]{x1D70B}(t)s_{r+1}f_{\unicode[STIX]{x1D6FC}}^{\circ }=q_{F,v}^{-1}s_{r}\text{U}_{v}^{\ast }f_{\unicode[STIX]{x1D6FC}}^{\circ }=|\unicode[STIX]{x1D71B}|^{-1}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})s_{r}f_{\unicode[STIX]{x1D6FC}}^{\circ },\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2A0D}_{V_{r}/V_{r+1}}\unicode[STIX]{x1D70B}(t)s_{r+1}f_{\unicode[STIX]{x1D6FC}}^{\circ }=q_{F,v}^{-1}s_{r}\text{U}_{v}^{\ast }f_{\unicode[STIX]{x1D6FC}}^{\circ }=|\unicode[STIX]{x1D71B}|^{-1}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})s_{r}f_{\unicode[STIX]{x1D6FC}}^{\circ },\end{eqnarray}$$
as desired. The integrality statement of part 2 is clear as
 $\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})\in \mathscr{O}_{L}^{\times }$
.◻
$\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})\in \mathscr{O}_{L}^{\times }$
.◻
Let us restore the notation
![]() $\unicode[STIX]{x1D70B}^{+}=\unicode[STIX]{x1D70B}$
,
$\unicode[STIX]{x1D70B}^{+}=\unicode[STIX]{x1D70B}$
,
 $\unicode[STIX]{x1D70B}^{-}=\unicode[STIX]{x1D70B}^{\vee }$
, employing it in the current local setting. Then if
$\unicode[STIX]{x1D70B}^{-}=\unicode[STIX]{x1D70B}^{\vee }$
, employing it in the current local setting. Then if
![]() $\unicode[STIX]{x1D70B}^{+}$
is as in the previous lemma, it is easy to check that
$\unicode[STIX]{x1D70B}^{+}$
is as in the previous lemma, it is easy to check that
![]() $\unicode[STIX]{x1D70B}^{-}$
is also nearly
$\unicode[STIX]{x1D70B}^{-}$
is also nearly
![]() $\mathfrak{p}$
ordinary. Explicitly, the element
$\mathfrak{p}$
ordinary. Explicitly, the element
 $$\begin{eqnarray}f_{\unicode[STIX]{x1D6FC}}^{+,\circ }(y)=\mathbf{1}_{\mathscr{ O}_{F}-\{0\}}(y)|y|_{v}\unicode[STIX]{x1D6FC}_{v}(y)\end{eqnarray}$$
$$\begin{eqnarray}f_{\unicode[STIX]{x1D6FC}}^{+,\circ }(y)=\mathbf{1}_{\mathscr{ O}_{F}-\{0\}}(y)|y|_{v}\unicode[STIX]{x1D6FC}_{v}(y)\end{eqnarray}$$
in the
![]() $L$
-rational subspaceFootnote
34
of any Kirillov model of
$L$
-rational subspaceFootnote
34
of any Kirillov model of
![]() $\unicode[STIX]{x1D70B}_{v}^{+}$
satisfies
$\unicode[STIX]{x1D70B}_{v}^{+}$
satisfies
 $\text{U}_{v}^{\ast }f_{\unicode[STIX]{x1D6FC}}^{+,\circ }=\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})f_{\unicode[STIX]{x1D6FC}}^{+,\circ }$
, and the element
$\text{U}_{v}^{\ast }f_{\unicode[STIX]{x1D6FC}}^{+,\circ }=\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})f_{\unicode[STIX]{x1D6FC}}^{+,\circ }$
, and the element
 $$\begin{eqnarray}f_{\unicode[STIX]{x1D6FC}}^{-,\circ }(y)=\mathbf{1}_{\mathscr{ O}_{F}-\{0\}}(y)|y|_{v}\unicode[STIX]{x1D714}^{-1}(y)\unicode[STIX]{x1D6FC}_{v}(y)\end{eqnarray}$$
$$\begin{eqnarray}f_{\unicode[STIX]{x1D6FC}}^{-,\circ }(y)=\mathbf{1}_{\mathscr{ O}_{F}-\{0\}}(y)|y|_{v}\unicode[STIX]{x1D714}^{-1}(y)\unicode[STIX]{x1D6FC}_{v}(y)\end{eqnarray}$$
in the
![]() $L$
-rational subspace of any Kirillov model of
$L$
-rational subspace of any Kirillov model of
![]() $\unicode[STIX]{x1D70B}_{v}^{-}$
satisfies
$\unicode[STIX]{x1D70B}_{v}^{-}$
satisfies
 $\text{U}_{v,\ast }f_{\unicode[STIX]{x1D6FC}}^{-,\circ }=\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})f_{\unicode[STIX]{x1D6FC}}^{-,\circ }$
.
$\text{U}_{v,\ast }f_{\unicode[STIX]{x1D6FC}}^{-,\circ }=\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})f_{\unicode[STIX]{x1D6FC}}^{-,\circ }$
.
We can then construct an element
 $f_{\unicode[STIX]{x1D6FC}}^{-}=(f_{\unicode[STIX]{x1D6FC},V}^{-})_{V}=(f_{\unicode[STIX]{x1D6FC},r}^{-})_{r}$
with the property of the previous lemma as
$f_{\unicode[STIX]{x1D6FC}}^{-}=(f_{\unicode[STIX]{x1D6FC},V}^{-})_{V}=(f_{\unicode[STIX]{x1D6FC},r}^{-})_{r}$
with the property of the previous lemma as
 $f_{\unicode[STIX]{x1D6FC},r}^{-}:=|\unicode[STIX]{x1D71B}|^{-r}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}s_{r}^{\ast }f_{\unicode[STIX]{x1D6FC}}^{-,\circ }$
with
$f_{\unicode[STIX]{x1D6FC},r}^{-}:=|\unicode[STIX]{x1D71B}|^{-r}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}s_{r}^{\ast }f_{\unicode[STIX]{x1D6FC}}^{-,\circ }$
with
 $s_{r}^{\ast }=(\!\begin{smallmatrix}1 & \unicode[STIX]{x1D71B}^{-r}\\ & \unicode[STIX]{x1D71B}^{-r}\end{smallmatrix}\!)$
.
$s_{r}^{\ast }=(\!\begin{smallmatrix}1 & \unicode[STIX]{x1D71B}^{-r}\\ & \unicode[STIX]{x1D71B}^{-r}\end{smallmatrix}\!)$
.
Local toric periods. Let us restore the subscripts
![]() $v$
. Recall the universal Kirillov models
$v$
. Recall the universal Kirillov models
 $\mathscr{K}(\unicode[STIX]{x1D70B}_{v}^{\pm },\unicode[STIX]{x1D713}_{\text{univ},v})$
of § 2.3. Then the elements
$\mathscr{K}(\unicode[STIX]{x1D70B}_{v}^{\pm },\unicode[STIX]{x1D713}_{\text{univ},v})$
of § 2.3. Then the elements
![]() $f_{\unicode[STIX]{x1D6FC},v}^{\pm ,\circ }$
of (10.1.2) and (10.1.3) yield, by the proof of the lemma, explicit elements
$f_{\unicode[STIX]{x1D6FC},v}^{\pm ,\circ }$
of (10.1.2) and (10.1.3) yield, by the proof of the lemma, explicit elements
 $$\begin{eqnarray}f_{\unicode[STIX]{x1D6FC},v}^{\pm }\in \underset{V}{\varprojlim }\,\mathscr{K}(\unicode[STIX]{x1D70B}_{v}^{\pm },\unicode[STIX]{x1D713}_{\text{univ},v})^{V},\end{eqnarray}$$
$$\begin{eqnarray}f_{\unicode[STIX]{x1D6FC},v}^{\pm }\in \underset{V}{\varprojlim }\,\mathscr{K}(\unicode[STIX]{x1D70B}_{v}^{\pm },\unicode[STIX]{x1D713}_{\text{univ},v})^{V},\end{eqnarray}$$
where the transition maps are given by averages.
Recall the local toric period
 $Q_{v}(f_{v}^{+},f_{v}^{-},\unicode[STIX]{x1D712}_{v})$
of (1.1.2), for a character
$Q_{v}(f_{v}^{+},f_{v}^{-},\unicode[STIX]{x1D712}_{v})$
of (1.1.2), for a character
 $\unicode[STIX]{x1D712}_{v}\in \mathscr{Y}_{v}^{\text{l.c.}}$
, which we define on
$\unicode[STIX]{x1D712}_{v}\in \mathscr{Y}_{v}^{\text{l.c.}}$
, which we define on
 $\mathscr{K}(\unicode[STIX]{x1D70B}_{v}^{+},\unicode[STIX]{x1D713}_{\text{univ},v})\otimes \mathscr{K}(\unicode[STIX]{x1D70B}_{v}^{-},\unicode[STIX]{x1D713}_{\text{univ},v})$
using the canonical pairing of Lemma 2.3.2 on the universal Kirillov models.
$\mathscr{K}(\unicode[STIX]{x1D70B}_{v}^{+},\unicode[STIX]{x1D713}_{\text{univ},v})\otimes \mathscr{K}(\unicode[STIX]{x1D70B}_{v}^{-},\unicode[STIX]{x1D713}_{\text{univ},v})$
using the canonical pairing of Lemma 2.3.2 on the universal Kirillov models.
By the previous discussion and the defining property of
![]() $f_{\unicode[STIX]{x1D6FC}}^{\pm }$
, for any character
$f_{\unicode[STIX]{x1D6FC}}^{\pm }$
, for any character
 $\unicode[STIX]{x1D712}_{v}\in \mathscr{Y}_{v}^{\text{l.c.}}$
, the element
$\unicode[STIX]{x1D712}_{v}\in \mathscr{Y}_{v}^{\text{l.c.}}$
, the element
 $$\begin{eqnarray}Q_{v}(f_{\unicode[STIX]{x1D6FC},v}^{+},f_{\unicode[STIX]{x1D6FC},v}^{-},\unicode[STIX]{x1D712}_{v}):=\lim _{V}\frac{L(1,\unicode[STIX]{x1D702}_{v})L(1,\unicode[STIX]{x1D70B}_{v},\operatorname{ad})}{\unicode[STIX]{x1D701}_{F,v}(2)L(1/2,\unicode[STIX]{x1D70B}_{E,v}\otimes \unicode[STIX]{x1D712}_{v})_{v}}\int _{E_{v}^{\times }/F_{v}^{\times }}\unicode[STIX]{x1D712}_{v}(t)(\unicode[STIX]{x1D70B}(t)f_{\unicode[STIX]{x1D6FC},v,V}^{+},f_{\unicode[STIX]{x1D6FC},v,V}^{-})\,d^{\circ }t\end{eqnarray}$$
$$\begin{eqnarray}Q_{v}(f_{\unicode[STIX]{x1D6FC},v}^{+},f_{\unicode[STIX]{x1D6FC},v}^{-},\unicode[STIX]{x1D712}_{v}):=\lim _{V}\frac{L(1,\unicode[STIX]{x1D702}_{v})L(1,\unicode[STIX]{x1D70B}_{v},\operatorname{ad})}{\unicode[STIX]{x1D701}_{F,v}(2)L(1/2,\unicode[STIX]{x1D70B}_{E,v}\otimes \unicode[STIX]{x1D712}_{v})_{v}}\int _{E_{v}^{\times }/F_{v}^{\times }}\unicode[STIX]{x1D712}_{v}(t)(\unicode[STIX]{x1D70B}(t)f_{\unicode[STIX]{x1D6FC},v,V}^{+},f_{\unicode[STIX]{x1D6FC},v,V}^{-})\,d^{\circ }t\end{eqnarray}$$
is well defined and it belongs to
 $M(\unicode[STIX]{x1D712}_{v})\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}(\unicode[STIX]{x1D714}_{v})$
. In fact, if
$M(\unicode[STIX]{x1D712}_{v})\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{v}}(\unicode[STIX]{x1D714}_{v})$
. In fact, if
 $M(\unicode[STIX]{x1D6FC}_{v},\unicode[STIX]{x1D712}_{v})\subset L$
is a subfield containing the values of
$M(\unicode[STIX]{x1D6FC}_{v},\unicode[STIX]{x1D712}_{v})\subset L$
is a subfield containing the values of
![]() $\unicode[STIX]{x1D6FC}_{v}$
,
$\unicode[STIX]{x1D6FC}_{v}$
,
![]() $\unicode[STIX]{x1D714}_{v}$
, and
$\unicode[STIX]{x1D714}_{v}$
, and
![]() $\unicode[STIX]{x1D712}_{v}$
, then
$\unicode[STIX]{x1D712}_{v}$
, then
 $Q_{v}(f_{\unicode[STIX]{x1D6FC},v}^{+},f_{\unicode[STIX]{x1D6FC},v}^{-},\unicode[STIX]{x1D712}_{v})$
belongs to
$Q_{v}(f_{\unicode[STIX]{x1D6FC},v}^{+},f_{\unicode[STIX]{x1D6FC},v}^{-},\unicode[STIX]{x1D712}_{v})$
belongs to
 $\mathscr{O}_{\unicode[STIX]{x1D6F9}_{v,M(\unicode[STIX]{x1D6FC}_{v},\unicode[STIX]{x1D712}_{v})}}(\unicode[STIX]{x1D714}_{v})$
.
$\mathscr{O}_{\unicode[STIX]{x1D6F9}_{v,M(\unicode[STIX]{x1D6FC}_{v},\unicode[STIX]{x1D712}_{v})}}(\unicode[STIX]{x1D714}_{v})$
.
Lemma 10.1.2. With notation as above, we have
 $$\begin{eqnarray}Q_{v}(f_{\unicode[STIX]{x1D6FC},v}^{+},f_{\unicode[STIX]{x1D6FC},v}^{-})=\unicode[STIX]{x1D701}_{F,v}(2)^{-1}\cdot Z_{v}^{\circ }\end{eqnarray}$$
$$\begin{eqnarray}Q_{v}(f_{\unicode[STIX]{x1D6FC},v}^{+},f_{\unicode[STIX]{x1D6FC},v}^{-})=\unicode[STIX]{x1D701}_{F,v}(2)^{-1}\cdot Z_{v}^{\circ }\end{eqnarray}$$
as sections of
 $\mathscr{O}_{\mathscr{Y}_{v}\times \unicode[STIX]{x1D6F9}_{v}}(\unicode[STIX]{x1D714}_{v})$
; here
$\mathscr{O}_{\mathscr{Y}_{v}\times \unicode[STIX]{x1D6F9}_{v}}(\unicode[STIX]{x1D714}_{v})$
; here
![]() $Z_{v}^{\circ }$
is as in Theorem A.
$Z_{v}^{\circ }$
is as in Theorem A.
Proof. It suffices to show that the result holds at any complex geometric point
 $(\unicode[STIX]{x1D712}_{v},\unicode[STIX]{x1D713}_{v})\in \mathscr{Y}_{v}^{\text{l.c.}}\times \unicode[STIX]{x1D6F9}_{v}(\mathbf{C})$
. Drop all subscripts
$(\unicode[STIX]{x1D712}_{v},\unicode[STIX]{x1D713}_{v})\in \mathscr{Y}_{v}^{\text{l.c.}}\times \unicode[STIX]{x1D6F9}_{v}(\mathbf{C})$
. Drop all subscripts
![]() $v$
, and fix a sufficiently large integer
$v$
, and fix a sufficiently large integer
![]() $r$
(depending on
$r$
(depending on
![]() $\unicode[STIX]{x1D712}$
). Recalling the pairing of Lemma 2.3.2, we have by definition
$\unicode[STIX]{x1D712}$
). Recalling the pairing of Lemma 2.3.2, we have by definition
 $$\begin{eqnarray}Q(f_{\unicode[STIX]{x1D6FC}}^{+},f_{\unicode[STIX]{x1D6FC}}^{-},\unicode[STIX]{x1D712})=\frac{L(1,\unicode[STIX]{x1D702})L(1,\unicode[STIX]{x1D70B},\text{ad})}{\unicode[STIX]{x1D701}_{F}(2)L(1/2,\unicode[STIX]{x1D70B}_{E},\unicode[STIX]{x1D712})}\int _{E^{\times }/F^{\times }}\unicode[STIX]{x1D712}(t)(\unicode[STIX]{x1D70B}(t)f_{\unicode[STIX]{x1D6FC}}^{+},f_{\unicode[STIX]{x1D6FC}}^{-})\,\frac{dt}{|d|^{1/2}}.\end{eqnarray}$$
$$\begin{eqnarray}Q(f_{\unicode[STIX]{x1D6FC}}^{+},f_{\unicode[STIX]{x1D6FC}}^{-},\unicode[STIX]{x1D712})=\frac{L(1,\unicode[STIX]{x1D702})L(1,\unicode[STIX]{x1D70B},\text{ad})}{\unicode[STIX]{x1D701}_{F}(2)L(1/2,\unicode[STIX]{x1D70B}_{E},\unicode[STIX]{x1D712})}\int _{E^{\times }/F^{\times }}\unicode[STIX]{x1D712}(t)(\unicode[STIX]{x1D70B}(t)f_{\unicode[STIX]{x1D6FC}}^{+},f_{\unicode[STIX]{x1D6FC}}^{-})\,\frac{dt}{|d|^{1/2}}.\end{eqnarray}$$
We denote by
![]() $E_{w}$
(respectively
$E_{w}$
(respectively
![]() $E_{w^{\ast }}$
) the image of
$E_{w^{\ast }}$
) the image of
![]() $F$
under the map
$F$
under the map
 $F\rightarrow M_{2}(F)$
sending
$F\rightarrow M_{2}(F)$
sending
 $t\mapsto (\!\begin{smallmatrix}t & \\ & 1\end{smallmatrix}\!)$
(respectively
$t\mapsto (\!\begin{smallmatrix}t & \\ & 1\end{smallmatrix}\!)$
(respectively
 $t\mapsto (\!\begin{smallmatrix}1 & \\ & t\end{smallmatrix}\!)$
), and by
$t\mapsto (\!\begin{smallmatrix}1 & \\ & t\end{smallmatrix}\!)$
), and by
![]() $\unicode[STIX]{x1D712}_{w}$
(respectively
$\unicode[STIX]{x1D712}_{w}$
(respectively
![]() $\unicode[STIX]{x1D712}_{w^{\ast }}$
) the restriction of
$\unicode[STIX]{x1D712}_{w^{\ast }}$
) the restriction of
![]() $\unicode[STIX]{x1D712}$
to
$\unicode[STIX]{x1D712}$
to
![]() $E_{w}^{\times }$
(respectively
$E_{w}^{\times }$
(respectively
![]() $E_{w^{\ast }}^{\times }$
).
$E_{w^{\ast }}^{\times }$
).
We can then compute that
 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D701}_{F}(1)L(1/2,\unicode[STIX]{x1D70B}_{E},\unicode[STIX]{x1D712})}{L(1,\unicode[STIX]{x1D702})}Q(f_{\unicode[STIX]{x1D6FC}}^{+},f_{\unicode[STIX]{x1D6FC}}^{-},\unicode[STIX]{x1D712})\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D701}_{F}(1)L(1/2,\unicode[STIX]{x1D70B}_{E},\unicode[STIX]{x1D712})}{L(1,\unicode[STIX]{x1D702})}Q(f_{\unicode[STIX]{x1D6FC}}^{+},f_{\unicode[STIX]{x1D6FC}}^{-},\unicode[STIX]{x1D712})\end{eqnarray}$$
equals
 $$\begin{eqnarray}\displaystyle & & \displaystyle |d|^{-1}\int _{F^{\times }}\int _{F^{\times }}|\unicode[STIX]{x1D71B}|^{-r}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}s_{r}f_{\unicode[STIX]{x1D6FC}}^{+,\circ }(ty)\cdot |\unicode[STIX]{x1D71B}|^{-r}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}s_{r}^{\ast }f_{\unicode[STIX]{x1D6FC}}^{-,\circ }(y)\unicode[STIX]{x1D712}_{w}(t)\,d^{\times }y\,d^{\times }t\nonumber\\ \displaystyle & & \displaystyle \quad =|d|^{-1}\int _{F^{\times }}\int _{F^{\times }}|\unicode[STIX]{x1D71B}|^{-r}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}\unicode[STIX]{x1D713}(-ty)|ty\unicode[STIX]{x1D71B}^{r}|\unicode[STIX]{x1D6FC}(ty\unicode[STIX]{x1D71B}^{r})\mathbf{1}_{\mathscr{O}_{F}-\{0\}}(ty\unicode[STIX]{x1D71B}^{r})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,|\unicode[STIX]{x1D71B}|^{-r}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}\unicode[STIX]{x1D713}(y)\unicode[STIX]{x1D714}(\unicode[STIX]{x1D71B})^{r}|y\unicode[STIX]{x1D71B}^{r}|\unicode[STIX]{x1D6FC}(y\unicode[STIX]{x1D71B}^{r})\unicode[STIX]{x1D714}^{-1}(y\unicode[STIX]{x1D71B}^{r})\mathbf{1}_{\mathscr{O}_{F}-\{0\}}(y\unicode[STIX]{x1D71B}^{r})\unicode[STIX]{x1D712}_{w}(t)\,d^{\times }y\,d^{\times }t.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |d|^{-1}\int _{F^{\times }}\int _{F^{\times }}|\unicode[STIX]{x1D71B}|^{-r}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}s_{r}f_{\unicode[STIX]{x1D6FC}}^{+,\circ }(ty)\cdot |\unicode[STIX]{x1D71B}|^{-r}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}s_{r}^{\ast }f_{\unicode[STIX]{x1D6FC}}^{-,\circ }(y)\unicode[STIX]{x1D712}_{w}(t)\,d^{\times }y\,d^{\times }t\nonumber\\ \displaystyle & & \displaystyle \quad =|d|^{-1}\int _{F^{\times }}\int _{F^{\times }}|\unicode[STIX]{x1D71B}|^{-r}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}\unicode[STIX]{x1D713}(-ty)|ty\unicode[STIX]{x1D71B}^{r}|\unicode[STIX]{x1D6FC}(ty\unicode[STIX]{x1D71B}^{r})\mathbf{1}_{\mathscr{O}_{F}-\{0\}}(ty\unicode[STIX]{x1D71B}^{r})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,|\unicode[STIX]{x1D71B}|^{-r}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}\unicode[STIX]{x1D713}(y)\unicode[STIX]{x1D714}(\unicode[STIX]{x1D71B})^{r}|y\unicode[STIX]{x1D71B}^{r}|\unicode[STIX]{x1D6FC}(y\unicode[STIX]{x1D71B}^{r})\unicode[STIX]{x1D714}^{-1}(y\unicode[STIX]{x1D71B}^{r})\mathbf{1}_{\mathscr{O}_{F}-\{0\}}(y\unicode[STIX]{x1D71B}^{r})\unicode[STIX]{x1D712}_{w}(t)\,d^{\times }y\,d^{\times }t.\nonumber\end{eqnarray}$$
We now perform the change of variables
![]() $t^{\prime }=ty$
and observe that
$t^{\prime }=ty$
and observe that
 $\unicode[STIX]{x1D712}_{w}(t)=\unicode[STIX]{x1D712}_{w}(t^{\prime })\unicode[STIX]{x1D712}_{w}^{-1}(y)=\unicode[STIX]{x1D712}_{w}(t^{\prime })\unicode[STIX]{x1D714}(y)\unicode[STIX]{x1D712}_{w^{\ast }}(y)$
; we conclude after simplification that the above expression equals
$\unicode[STIX]{x1D712}_{w}(t)=\unicode[STIX]{x1D712}_{w}(t^{\prime })\unicode[STIX]{x1D712}_{w}^{-1}(y)=\unicode[STIX]{x1D712}_{w}(t^{\prime })\unicode[STIX]{x1D714}(y)\unicode[STIX]{x1D712}_{w^{\ast }}(y)$
; we conclude after simplification that the above expression equals
 $$\begin{eqnarray}|d|^{-1}\int _{v(t^{\prime })\geqslant -r}\unicode[STIX]{x1D713}(-t^{\prime })|t^{\prime }|\unicode[STIX]{x1D6FC}(t^{\prime })\unicode[STIX]{x1D712}_{w}(t^{\prime })\,d^{\times }t^{\prime }\int _{v(y)\geqslant -r}\unicode[STIX]{x1D713}(-y)|y|\unicode[STIX]{x1D6FC}(y)\unicode[STIX]{x1D712}_{w^{\ast }}(y)\,d^{\times }y.\end{eqnarray}$$
$$\begin{eqnarray}|d|^{-1}\int _{v(t^{\prime })\geqslant -r}\unicode[STIX]{x1D713}(-t^{\prime })|t^{\prime }|\unicode[STIX]{x1D6FC}(t^{\prime })\unicode[STIX]{x1D712}_{w}(t^{\prime })\,d^{\times }t^{\prime }\int _{v(y)\geqslant -r}\unicode[STIX]{x1D713}(-y)|y|\unicode[STIX]{x1D6FC}(y)\unicode[STIX]{x1D712}_{w^{\ast }}(y)\,d^{\times }y.\end{eqnarray}$$
If
![]() $r$
is sufficiently large, the domains of integration can be replaced by
$r$
is sufficiently large, the domains of integration can be replaced by
![]() $F^{\times }$
. The computation of the integrals is carried out in Lemma A.1.1. We obtain
$F^{\times }$
. The computation of the integrals is carried out in Lemma A.1.1. We obtain
 $$\begin{eqnarray}Q_{v}(f_{\unicode[STIX]{x1D6FC},v}^{+},f_{\unicode[STIX]{x1D6FC},v}^{-},\unicode[STIX]{x1D712}_{v})=\frac{L(1,\unicode[STIX]{x1D702}_{v})}{\unicode[STIX]{x1D701}_{F,v}(1)L(1/2,\unicode[STIX]{x1D70B}_{E,v},\unicode[STIX]{x1D712}_{v})}\unicode[STIX]{x1D701}_{E,v}(1)\mathop{\prod }_{w|v}Z_{w}(\unicode[STIX]{x1D712}_{w})=\unicode[STIX]{x1D701}_{F,v}(2)^{-1}\cdot Z_{v}^{\circ }(\unicode[STIX]{x1D712}_{v}).\Box\end{eqnarray}$$
$$\begin{eqnarray}Q_{v}(f_{\unicode[STIX]{x1D6FC},v}^{+},f_{\unicode[STIX]{x1D6FC},v}^{-},\unicode[STIX]{x1D712}_{v})=\frac{L(1,\unicode[STIX]{x1D702}_{v})}{\unicode[STIX]{x1D701}_{F,v}(1)L(1/2,\unicode[STIX]{x1D70B}_{E,v},\unicode[STIX]{x1D712}_{v})}\unicode[STIX]{x1D701}_{E,v}(1)\mathop{\prod }_{w|v}Z_{w}(\unicode[STIX]{x1D712}_{w})=\unicode[STIX]{x1D701}_{F,v}(2)^{-1}\cdot Z_{v}^{\circ }(\unicode[STIX]{x1D712}_{v}).\Box\end{eqnarray}$$
10.2 Gross–Zagier and Waldspurger formulas
Here we prove Theorem C. We continue with the notation of the previous subsection, and we suppose that
![]() $\unicode[STIX]{x1D70B}_{v}^{\pm }$
is isomorphic to the local component at
$\unicode[STIX]{x1D70B}_{v}^{\pm }$
is isomorphic to the local component at
![]() $v|p$
of the representation
$v|p$
of the representation
![]() $\unicode[STIX]{x1D70B}^{\pm }$
of the Introduction. Let
$\unicode[STIX]{x1D70B}^{\pm }$
of the Introduction. Let
![]() $w$
,
$w$
,
![]() $w^{\ast }$
be the two places of
$w^{\ast }$
be the two places of
![]() $E$
above
$E$
above
![]() $v$
, and fix an isomorphism
$v$
, and fix an isomorphism
 $\mathbf{B}_{v}\cong M_{2}(F_{v})$
such that the map
$\mathbf{B}_{v}\cong M_{2}(F_{v})$
such that the map
 $E_{v}\cong E_{w}\oplus E_{w^{\ast }}\rightarrow \mathbf{B}_{v}$
is identified with the map
$E_{v}\cong E_{w}\oplus E_{w^{\ast }}\rightarrow \mathbf{B}_{v}$
is identified with the map
 $F_{v}\oplus F_{v}\rightarrow M_{2}(F_{v})$
given by
$F_{v}\oplus F_{v}\rightarrow M_{2}(F_{v})$
given by
 $(t_{1},t_{2})\mapsto (\!\begin{smallmatrix}t_{1} & \\ & t_{2}\end{smallmatrix}\!)$
.
$(t_{1},t_{2})\mapsto (\!\begin{smallmatrix}t_{1} & \\ & t_{2}\end{smallmatrix}\!)$
.
We go back to the global situation with the notation and assumption of § 1.4. Choose a universal Whittaker (or Kirillov) functional for
![]() $\unicode[STIX]{x1D70B}^{+}$
at
$\unicode[STIX]{x1D70B}^{+}$
at
![]() $p$
, that is, a
$p$
, that is, a
![]() $\mathbf{B}_{p}^{\times }$
-equivariant map
$\mathbf{B}_{p}^{\times }$
-equivariant map
 $\mathscr{K}_{p}^{+}:\unicode[STIX]{x1D70B}^{+}\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D6F9}_{p})\rightarrow \bigotimes _{v|p}\mathscr{K}(\unicode[STIX]{x1D70B}^{+},\unicode[STIX]{x1D713}_{\text{univ},v})$
. By the natural dualities of
$\mathscr{K}_{p}^{+}:\unicode[STIX]{x1D70B}^{+}\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D6F9}_{p})\rightarrow \bigotimes _{v|p}\mathscr{K}(\unicode[STIX]{x1D70B}^{+},\unicode[STIX]{x1D713}_{\text{univ},v})$
. By the natural dualities of
![]() $\unicode[STIX]{x1D70B}^{\pm }$
and the Kirillov models, it induces a
$\unicode[STIX]{x1D70B}^{\pm }$
and the Kirillov models, it induces a
![]() $\mathbf{B}_{p}^{\times }$
-equivariant map
$\mathbf{B}_{p}^{\times }$
-equivariant map
 $\mathscr{K}_{p}^{+\vee }:\bigotimes _{v|p}\mathscr{K}(\unicode[STIX]{x1D70B}^{-},\unicode[STIX]{x1D713}_{\text{univ},v})\rightarrow \unicode[STIX]{x1D70B}^{-}\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D6F9}_{p})$
, whose inverse
$\mathscr{K}_{p}^{+\vee }:\bigotimes _{v|p}\mathscr{K}(\unicode[STIX]{x1D70B}^{-},\unicode[STIX]{x1D713}_{\text{univ},v})\rightarrow \unicode[STIX]{x1D70B}^{-}\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D6F9}_{p})$
, whose inverse
![]() $\mathscr{K}_{p}^{-}$
is a universal Kirillov functional for
$\mathscr{K}_{p}^{-}$
is a universal Kirillov functional for
![]() $\unicode[STIX]{x1D70B}_{p}^{-}$
. Letting
$\unicode[STIX]{x1D70B}_{p}^{-}$
. Letting
 $\unicode[STIX]{x1D70B}_{p,\mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D6F9}_{p})}^{\pm }:=\bigotimes _{v|p}\mathscr{K}(\unicode[STIX]{x1D70B}^{\pm },\unicode[STIX]{x1D713}_{\text{univ},v})$
, we obtain a unique decomposition
$\unicode[STIX]{x1D70B}_{p,\mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D6F9}_{p})}^{\pm }:=\bigotimes _{v|p}\mathscr{K}(\unicode[STIX]{x1D70B}^{\pm },\unicode[STIX]{x1D713}_{\text{univ},v})$
, we obtain a unique decomposition
 $\unicode[STIX]{x1D70B}^{\pm }\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D6F9}_{p})\cong \unicode[STIX]{x1D70B}_{\mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D6F9}_{p})}^{\pm ,p}\otimes \unicode[STIX]{x1D70B}_{p,\mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D6F9}_{p})}^{\pm }$
. The decomposition arises from a decomposition of the natural
$\unicode[STIX]{x1D70B}^{\pm }\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D6F9}_{p})\cong \unicode[STIX]{x1D70B}_{\mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D6F9}_{p})}^{\pm ,p}\otimes \unicode[STIX]{x1D70B}_{p,\mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D6F9}_{p})}^{\pm }$
. The decomposition arises from a decomposition of the natural
![]() $M$
-rational subspaces
$M$
-rational subspaces
 $\unicode[STIX]{x1D70B}^{\pm }\cong \unicode[STIX]{x1D70B}^{\pm ,p}\otimes \unicode[STIX]{x1D70B}_{p}^{\pm }$
.Footnote
35
$\unicode[STIX]{x1D70B}^{\pm }\cong \unicode[STIX]{x1D70B}^{\pm ,p}\otimes \unicode[STIX]{x1D70B}_{p}^{\pm }$
.Footnote
35
Heegner–theta elements. For each
 $f^{\pm ,p}\in \unicode[STIX]{x1D70B}^{\pm p}\otimes M(\unicode[STIX]{x1D6FC})$
, let
$f^{\pm ,p}\in \unicode[STIX]{x1D70B}^{\pm p}\otimes M(\unicode[STIX]{x1D6FC})$
, let
 $$\begin{eqnarray}f_{\unicode[STIX]{x1D6FC}}^{\pm ,p}:=f^{\pm p}\otimes f_{\unicode[STIX]{x1D6FC},p}^{\pm }\in \unicode[STIX]{x1D70B}_{M(\unicode[STIX]{x1D6FC})}^{\pm ,p}\otimes \underset{V\subset \mathscr{O}_{E,p}^{\times }}{\varprojlim }\,\unicode[STIX]{x1D70B}_{p,\mathscr{O}_{M(\unicode[STIX]{x1D6FC})}}^{\pm ,V},\end{eqnarray}$$
$$\begin{eqnarray}f_{\unicode[STIX]{x1D6FC}}^{\pm ,p}:=f^{\pm p}\otimes f_{\unicode[STIX]{x1D6FC},p}^{\pm }\in \unicode[STIX]{x1D70B}_{M(\unicode[STIX]{x1D6FC})}^{\pm ,p}\otimes \underset{V\subset \mathscr{O}_{E,p}^{\times }}{\varprojlim }\,\unicode[STIX]{x1D70B}_{p,\mathscr{O}_{M(\unicode[STIX]{x1D6FC})}}^{\pm ,V},\end{eqnarray}$$
where
 $f_{\unicode[STIX]{x1D6FC},p}^{\pm }=\bigotimes _{v|p}f_{\unicode[STIX]{x1D6FC},v}^{\pm }$
with
$f_{\unicode[STIX]{x1D6FC},p}^{\pm }=\bigotimes _{v|p}f_{\unicode[STIX]{x1D6FC},v}^{\pm }$
with
![]() $f_{\unicode[STIX]{x1D6FC},v}^{\pm }$
the elements (10.1.4).
$f_{\unicode[STIX]{x1D6FC},v}^{\pm }$
the elements (10.1.4).
Fix a component
 $\mathscr{Y}_{\pm }^{\circ }\subset \mathscr{Y}_{\pm }$
of type
$\mathscr{Y}_{\pm }^{\circ }\subset \mathscr{Y}_{\pm }$
of type
 $\unicode[STIX]{x1D700}\in \{+1,-1\}$
as in § 1.4. Then the elements
$\unicode[STIX]{x1D700}\in \{+1,-1\}$
as in § 1.4. Then the elements
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6FC}}^{\pm }(f^{\pm ,p}) & := & \displaystyle \unicode[STIX]{x2A0D}_{E^{\times }\backslash E_{\mathbf{A}^{\infty }}^{\times }}f_{\unicode[STIX]{x1D6FC}}^{p,\pm }(i(t))\unicode[STIX]{x1D712}_{\text{univ}}(t)\,dt\in \mathscr{O}_{\mathscr{Y}_{\pm }}(\mathscr{Y}_{\pm })^{\text{b}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6FC}}^{\pm }(f^{\pm ,p}) & := & \displaystyle \unicode[STIX]{x2A0D}_{E^{\times }\backslash E_{\mathbf{A}^{\infty }}^{\times }}f_{\unicode[STIX]{x1D6FC}}^{p,\pm }(i(t))\unicode[STIX]{x1D712}_{\text{univ}}(t)\,dt\in \mathscr{O}_{\mathscr{Y}_{\pm }}(\mathscr{Y}_{\pm })^{\text{b}},\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{\pm }(f^{\pm ,p}) & := & \displaystyle \lim _{U_{T,p}\rightarrow \{1\}}\unicode[STIX]{x2A0D}_{E^{\times }\backslash E_{\mathbf{A}^{\infty }}^{\times }/U_{T}}\unicode[STIX]{x1D705}(f_{\unicode[STIX]{x1D6FC}}^{p,\pm }(\text{rec}_{E}(t)\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D709}}(P))\otimes \unicode[STIX]{x1D712}_{\text{univ},U_{T}}^{\pm }(t))\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \in \mathbf{S}_{\mathfrak{p}}(A_{E},\unicode[STIX]{x1D712}_{\text{univ}}^{\pm },\mathscr{Y}_{\pm })^{\text{b}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{\pm }(f^{\pm ,p}) & := & \displaystyle \lim _{U_{T,p}\rightarrow \{1\}}\unicode[STIX]{x2A0D}_{E^{\times }\backslash E_{\mathbf{A}^{\infty }}^{\times }/U_{T}}\unicode[STIX]{x1D705}(f_{\unicode[STIX]{x1D6FC}}^{p,\pm }(\text{rec}_{E}(t)\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D709}}(P))\otimes \unicode[STIX]{x1D712}_{\text{univ},U_{T}}^{\pm }(t))\,dt\nonumber\\ \displaystyle & & \displaystyle \quad \in \mathbf{S}_{\mathfrak{p}}(A_{E},\unicode[STIX]{x1D712}_{\text{univ}}^{\pm },\mathscr{Y}_{\pm })^{\text{b}},\end{eqnarray}$$
or rather their restriction to
 $\mathscr{Y}_{\pm }^{\circ }\subset \mathscr{Y}_{\pm }$
, satisfy the property of Theorem C
(1). Here
$\mathscr{Y}_{\pm }^{\circ }\subset \mathscr{Y}_{\pm }$
, satisfy the property of Theorem C
(1). Here
 $\unicode[STIX]{x1D712}_{\text{univ},U_{T}}^{\pm }:\unicode[STIX]{x1D6E4}\rightarrow \mathscr{O}^{\times }(\mathscr{Y}_{\pm })^{U_{T}}$
is the convolution of
$\unicode[STIX]{x1D712}_{\text{univ},U_{T}}^{\pm }:\unicode[STIX]{x1D6E4}\rightarrow \mathscr{O}^{\times }(\mathscr{Y}_{\pm })^{U_{T}}$
is the convolution of
![]() $\unicode[STIX]{x1D712}_{\text{univ}}^{\pm }$
with the finest
$\unicode[STIX]{x1D712}_{\text{univ}}^{\pm }$
with the finest
![]() $U_{T}$
-invariant approximation to a delta function at
$U_{T}$
-invariant approximation to a delta function at
![]() $\mathbf{1}\in \unicode[STIX]{x1D6E4}$
.
$\mathbf{1}\in \unicode[STIX]{x1D6E4}$
.
We explain the boundedness in the case of
 $\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{\pm }(f^{\pm ,p})$
. The rigid space
$\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{\pm }(f^{\pm ,p})$
. The rigid space
![]() $\mathscr{Y}_{\pm }$
is the generic fibre of an
$\mathscr{Y}_{\pm }$
is the generic fibre of an
![]() $\mathscr{O}_{L}$
-formal scheme
$\mathscr{O}_{L}$
-formal scheme
 $\mathfrak{Y}_{\pm }:=\text{Spf}\mathscr{O}_{L}\unicode[STIX]{x27E6}\unicode[STIX]{x1D6E4}\unicode[STIX]{x27E7}/((\unicode[STIX]{x1D714}^{\pm 1}(\unicode[STIX]{x1D6FE})[\unicode[STIX]{x1D6FE}]-[1])_{\unicode[STIX]{x1D6FE}\in \mathbf{A}^{\infty ,\times }})$
.Footnote
36
(Similarly, each geometric connected component
$\mathfrak{Y}_{\pm }:=\text{Spf}\mathscr{O}_{L}\unicode[STIX]{x27E6}\unicode[STIX]{x1D6E4}\unicode[STIX]{x27E7}/((\unicode[STIX]{x1D714}^{\pm 1}(\unicode[STIX]{x1D6FE})[\unicode[STIX]{x1D6FE}]-[1])_{\unicode[STIX]{x1D6FE}\in \mathbf{A}^{\infty ,\times }})$
.Footnote
36
(Similarly, each geometric connected component
![]() $\mathscr{Y}_{\pm }^{\circ }$
has a formal model
$\mathscr{Y}_{\pm }^{\circ }$
has a formal model
 $\mathfrak{Y}_{\pm }^{\circ }\subset \mathfrak{Y}$
.) This identifies
$\mathfrak{Y}_{\pm }^{\circ }\subset \mathfrak{Y}$
.) This identifies
 $\mathscr{O}_{\mathscr{Y}_{\pm }}(\mathscr{Y}_{\pm })^{\text{b}}=\mathscr{O}_{\mathfrak{\{}}(\mathfrak{\{})\otimes _{\mathscr{O}_{L}}L$
. By Lemma 10.1.1
(2) applied to the natural lattice
$\mathscr{O}_{\mathscr{Y}_{\pm }}(\mathscr{Y}_{\pm })^{\text{b}}=\mathscr{O}_{\mathfrak{\{}}(\mathfrak{\{})\otimes _{\mathscr{O}_{L}}L$
. By Lemma 10.1.1
(2) applied to the natural lattice
 $\unicode[STIX]{x1D70B}_{\mathscr{O}_{L}}^{\pm }\subset \unicode[STIX]{x1D70B}^{\pm }\otimes L$
given by
$\unicode[STIX]{x1D70B}_{\mathscr{O}_{L}}^{\pm }\subset \unicode[STIX]{x1D70B}^{\pm }\otimes L$
given by
 $\operatorname{Hom}(J,A^{\pm })\otimes _{\operatorname{End}(A)}\mathscr{O}_{L}\subset \operatorname{Hom}^{0}(J,A^{\pm })\otimes L$
, after possibly replacing
$\operatorname{Hom}(J,A^{\pm })\otimes _{\operatorname{End}(A)}\mathscr{O}_{L}\subset \operatorname{Hom}^{0}(J,A^{\pm })\otimes L$
, after possibly replacing
![]() $f^{\pm ,p}$
by a fixed multiple, the elements
$f^{\pm ,p}$
by a fixed multiple, the elements
 $\tilde{f}_{\unicode[STIX]{x1D6FC}}^{p,\pm }(\text{T}_{t}\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D709}}(P))$
belong to
$\tilde{f}_{\unicode[STIX]{x1D6FC}}^{p,\pm }(\text{T}_{t}\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D709}}(P))$
belong to
 $A^{\pm }(E^{\text{ab}})$
. Then each term in the sequence at the right-hand side of (10.2.2) is a fixed multiple of
$A^{\pm }(E^{\text{ab}})$
. Then each term in the sequence at the right-hand side of (10.2.2) is a fixed multiple of
 $$\begin{eqnarray}\mathop{\sum }_{t\in E^{\times }\backslash E_{\mathbf{A}^{\infty }}^{\times }/U_{T}}\unicode[STIX]{x1D705}(\tilde{f}_{\unicode[STIX]{x1D6FC}}^{p,\pm }(\text{rec}_{E}(t)\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D709}}(P))\otimes \unicode[STIX]{x1D712}_{\text{univ},U_{T}}^{\pm }(t)),\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{t\in E^{\times }\backslash E_{\mathbf{A}^{\infty }}^{\times }/U_{T}}\unicode[STIX]{x1D705}(\tilde{f}_{\unicode[STIX]{x1D6FC}}^{p,\pm }(\text{rec}_{E}(t)\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D709}}(P))\otimes \unicode[STIX]{x1D712}_{\text{univ},U_{T}}^{\pm }(t)),\end{eqnarray}$$
which belongs to the
![]() $\mathscr{O}_{L}$
-module
$\mathscr{O}_{L}$
-module
 $H_{f}^{1}(E,T_{\mathfrak{p}}A^{\pm }\otimes \mathscr{O}_{\mathfrak{\{}}(\mathfrak{\{})^{U_{T}}(\unicode[STIX]{x1D712}_{\text{univ},U_{T}}^{\pm }))$
. Hence, some non-zero multiple of
$H_{f}^{1}(E,T_{\mathfrak{p}}A^{\pm }\otimes \mathscr{O}_{\mathfrak{\{}}(\mathfrak{\{})^{U_{T}}(\unicode[STIX]{x1D712}_{\text{univ},U_{T}}^{\pm }))$
. Hence, some non-zero multiple of
 $\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{\pm }(f^{\pm ,p})$
belongs to the limit
$\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{\pm }(f^{\pm ,p})$
belongs to the limit
 $\mathop{\varprojlim }\nolimits_{U_{T}}H_{f}^{1}(E,T_{\mathfrak{p}}A^{\pm }\otimes \mathscr{O}_{\mathfrak{\{}}(\mathfrak{\{})^{U_{T}}(\unicode[STIX]{x1D712}_{\text{univ},U_{T}}^{\pm }))$
, whose tensor product with
$\mathop{\varprojlim }\nolimits_{U_{T}}H_{f}^{1}(E,T_{\mathfrak{p}}A^{\pm }\otimes \mathscr{O}_{\mathfrak{\{}}(\mathfrak{\{})^{U_{T}}(\unicode[STIX]{x1D712}_{\text{univ},U_{T}}^{\pm }))$
, whose tensor product with
![]() $L$
is indeed
$L$
is indeed
 $\mathbf{S}_{\mathfrak{p}}(A_{E},\unicode[STIX]{x1D712}_{\text{univ}}^{\pm },\mathscr{Y}_{\pm })^{\text{b}}$
.
$\mathbf{S}_{\mathfrak{p}}(A_{E},\unicode[STIX]{x1D712}_{\text{univ}}^{\pm },\mathscr{Y}_{\pm })^{\text{b}}$
.
Local toric periods away from
![]() $p$
. Given the chosen decomposition
$p$
. Given the chosen decomposition
 $\unicode[STIX]{x1D6FE}^{\pm }:\unicode[STIX]{x1D70B}^{\pm }\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D6F9}_{p})\cong \unicode[STIX]{x1D70B}_{\mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D6F9}_{p})}^{\pm ,p}\otimes \unicode[STIX]{x1D70B}_{p,\mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D6F9}_{p})}^{\pm }$
, let
$\unicode[STIX]{x1D6FE}^{\pm }:\unicode[STIX]{x1D70B}^{\pm }\otimes \mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D6F9}_{p})\cong \unicode[STIX]{x1D70B}_{\mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D6F9}_{p})}^{\pm ,p}\otimes \unicode[STIX]{x1D70B}_{p,\mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D6F9}_{p})}^{\pm }$
, let
![]() $(\,,\,)^{p}$
be the unique pairing on
$(\,,\,)^{p}$
be the unique pairing on
 $\unicode[STIX]{x1D70B}_{\mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}}^{+,p}\otimes \unicode[STIX]{x1D70B}_{\mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}}^{-,p}$
which makes
$\unicode[STIX]{x1D70B}_{\mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}}^{+,p}\otimes \unicode[STIX]{x1D70B}_{\mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}}^{-,p}$
which makes
 $\unicode[STIX]{x1D6FE}^{+}\otimes \unicode[STIX]{x1D6FE}^{-}$
into an isometry for the natural pairings on
$\unicode[STIX]{x1D6FE}^{+}\otimes \unicode[STIX]{x1D6FE}^{-}$
into an isometry for the natural pairings on
![]() $\unicode[STIX]{x1D70B}^{\pm }$
and
$\unicode[STIX]{x1D70B}^{\pm }$
and
 $\unicode[STIX]{x1D70B}_{p,\mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D6F9}_{p})}^{\pm }$
.Footnote
37
Then, for each
$\unicode[STIX]{x1D70B}_{p,\mathscr{O}_{\unicode[STIX]{x1D6F9}_{p}}(\unicode[STIX]{x1D6F9}_{p})}^{\pm }$
.Footnote
37
Then, for each
 $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}^{p}\unicode[STIX]{x1D712}_{p}\in \mathscr{Y}^{\circ \,\text{l.c.}}$
, the toric period
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}^{p}\unicode[STIX]{x1D712}_{p}\in \mathscr{Y}^{\circ \,\text{l.c.}}$
, the toric period
![]() $Q^{p}$
of (1.4.7) is defined. By Lemma 5.1.1, Theorem C
(2) then follows from Proposition 3.6.1. It is also proved in slightly different language in [Reference Liu, Zhang and ZhangLZZ15, Lemma 4.6(ii)].
$Q^{p}$
of (1.4.7) is defined. By Lemma 5.1.1, Theorem C
(2) then follows from Proposition 3.6.1. It is also proved in slightly different language in [Reference Liu, Zhang and ZhangLZZ15, Lemma 4.6(ii)].
Formulas. We prove the anticyclotomic formulas of Theorem C, and at the same time complete the proof of Theorem B for the characters who do not satisfy Assumption 6.2.4.
Lemma 10.2.1. Let
![]() $L$
be a non-archimedean local field with ring of integers
$L$
be a non-archimedean local field with ring of integers
![]() $\mathscr{O}_{L}$
,
$\mathscr{O}_{L}$
,
![]() $n\geqslant 1$
, and let
$n\geqslant 1$
, and let
![]() $\mathscr{D}_{n}$
be the rigid analytic polydisc over
$\mathscr{D}_{n}$
be the rigid analytic polydisc over
![]() $L$
in
$L$
in
![]() $n$
variables, that is, the generic fibre of
$n$
variables, that is, the generic fibre of
 $\text{Spf}\,\mathscr{O}_{L}\unicode[STIX]{x27E6}X_{1},\ldots ,X_{n}\unicode[STIX]{x27E7}$
. Let
$\text{Spf}\,\mathscr{O}_{L}\unicode[STIX]{x27E6}X_{1},\ldots ,X_{n}\unicode[STIX]{x27E7}$
. Let
 $\unicode[STIX]{x1D6F4}_{n}\subset \mathscr{D}_{n}(\overline{L})$
be the set of points of the form
$\unicode[STIX]{x1D6F4}_{n}\subset \mathscr{D}_{n}(\overline{L})$
be the set of points of the form
 $x=(\unicode[STIX]{x1D701}_{1}-1,\ldots ,\unicode[STIX]{x1D701}_{n}-1)$
with each
$x=(\unicode[STIX]{x1D701}_{1}-1,\ldots ,\unicode[STIX]{x1D701}_{n}-1)$
with each
![]() $\unicode[STIX]{x1D701}_{i}$
a root of unity of
$\unicode[STIX]{x1D701}_{i}$
a root of unity of
![]() $p$
-power order. Let
$p$
-power order. Let
 $$\begin{eqnarray}f\in \mathscr{O}(\mathscr{D}_{n})^{\text{b}}=\mathscr{O}_{L}\unicode[STIX]{x27E6}X_{1},\ldots ,X_{n}\unicode[STIX]{x27E7}\otimes L\end{eqnarray}$$
$$\begin{eqnarray}f\in \mathscr{O}(\mathscr{D}_{n})^{\text{b}}=\mathscr{O}_{L}\unicode[STIX]{x27E6}X_{1},\ldots ,X_{n}\unicode[STIX]{x27E7}\otimes L\end{eqnarray}$$
be such that
 $f(x)=0$
for all but finitely may
$f(x)=0$
for all but finitely may
![]() $x\in \unicode[STIX]{x1D6F4}_{n}$
. Then
$x\in \unicode[STIX]{x1D6F4}_{n}$
. Then
![]() $f=0$
.
$f=0$
.
Proof. This is by induction on
![]() $n$
, the case
$n$
, the case
![]() $n=1$
being well known [Reference Amice and VéluAV75]; we will abbreviate
$n=1$
being well known [Reference Amice and VéluAV75]; we will abbreviate
 $X=(X_{1},\ldots ,X_{n})$
and
$X=(X_{1},\ldots ,X_{n})$
and
 $X^{\prime }=(X_{1},\ldots ,X_{n-1})$
. Up to multiplying
$X^{\prime }=(X_{1},\ldots ,X_{n-1})$
. Up to multiplying
![]() $f$
by a suitable non-zero polynomial, we may assume that
$f$
by a suitable non-zero polynomial, we may assume that
 $f\in \mathscr{O}_{L}\unicode[STIX]{x27E6}X\unicode[STIX]{x27E7}$
and that it vanishes on all of
$f\in \mathscr{O}_{L}\unicode[STIX]{x27E6}X\unicode[STIX]{x27E7}$
and that it vanishes on all of
![]() $\unicode[STIX]{x1D6F4}_{n}$
. We may write, with multi-index notation,
$\unicode[STIX]{x1D6F4}_{n}$
. We may write, with multi-index notation,
 $f=\sum _{J\subset \mathbf{N}^{n}}a_{J}X^{J}$
(where
$f=\sum _{J\subset \mathbf{N}^{n}}a_{J}X^{J}$
(where
 $\mathbf{N}=\{0,1,2,\ldots ,\}$
) with each
$\mathbf{N}=\{0,1,2,\ldots ,\}$
) with each
 $a_{J}\in \mathscr{O}_{L}$
. Let
$a_{J}\in \mathscr{O}_{L}$
. Let
 $f_{j}(X^{\prime }):=\sum _{J^{\prime }\subset \mathbf{N}^{n-1}}a_{J^{\prime }j}(X^{\prime })^{J^{\prime }}\in \mathscr{O}_{L}\unicode[STIX]{x27E6}X^{\prime }\unicode[STIX]{x27E7}$
; then
$f_{j}(X^{\prime }):=\sum _{J^{\prime }\subset \mathbf{N}^{n-1}}a_{J^{\prime }j}(X^{\prime })^{J^{\prime }}\in \mathscr{O}_{L}\unicode[STIX]{x27E6}X^{\prime }\unicode[STIX]{x27E7}$
; then
 $$\begin{eqnarray}f(X)=\mathop{\sum }_{j=0}^{\infty }f_{j}(X^{\prime })X_{n}^{j}.\end{eqnarray}$$
$$\begin{eqnarray}f(X)=\mathop{\sum }_{j=0}^{\infty }f_{j}(X^{\prime })X_{n}^{j}.\end{eqnarray}$$
By assumption,
 $f_{0}(X^{\prime })=f(X^{\prime },0)$
vanishes on all of
$f_{0}(X^{\prime })=f(X^{\prime },0)$
vanishes on all of
![]() $\unicode[STIX]{x1D6F4}_{n-1}$
and hence by the induction hypothesis
$\unicode[STIX]{x1D6F4}_{n-1}$
and hence by the induction hypothesis
![]() $f_{0}=0$
and
$f_{0}=0$
and
![]() $X_{n}|f$
. By induction on
$X_{n}|f$
. By induction on
![]() $j$
, repeatedly replacing
$j$
, repeatedly replacing
![]() $f$
by
$f$
by
![]() $X_{n}^{-1}f$
, we find that each
$X_{n}^{-1}f$
, we find that each
![]() $f_{j}=0$
and hence
$f_{j}=0$
and hence
![]() $f=0$
.◻
$f=0$
.◻
Lemma 10.2.2. Let
 $\mathscr{Y}^{\circ }\subset \mathscr{Y}$
be a connected component of type
$\mathscr{Y}^{\circ }\subset \mathscr{Y}$
be a connected component of type
![]() $\unicode[STIX]{x1D700}=-1$
, and let
$\unicode[STIX]{x1D700}=-1$
, and let
 ${\mathscr{Y}^{\circ }}^{\prime }\subset \mathscr{Y}^{\prime }$
be the connected component containing
${\mathscr{Y}^{\circ }}^{\prime }\subset \mathscr{Y}^{\prime }$
be the connected component containing
![]() $\mathscr{Y}^{\circ }$
. The
$\mathscr{Y}^{\circ }$
. The
![]() $p$
-adic
$p$
-adic
![]() $L$
-function
$L$
-function
 $L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})|_{{\mathscr{Y}^{\circ }}^{\prime }}$
is a section of
$L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})|_{{\mathscr{Y}^{\circ }}^{\prime }}$
is a section of
 $\mathscr{I}_{\mathscr{Y}}\subset \mathscr{O}_{\mathscr{Y}^{\prime }}$
.
$\mathscr{I}_{\mathscr{Y}}\subset \mathscr{O}_{\mathscr{Y}^{\prime }}$
.
Proof. By the interpolation property and the functional equation,
 $L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})$
vanishes on
$L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})$
vanishes on
 $\mathscr{Y}^{\circ }\cap \mathscr{Y}^{\text{l.c.},\text{an}}(\overline{L})$
. We conclude by applying Lemma 10.2.1, noting that after base-change to a finite extension of
$\mathscr{Y}^{\circ }\cap \mathscr{Y}^{\text{l.c.},\text{an}}(\overline{L})$
. We conclude by applying Lemma 10.2.1, noting that after base-change to a finite extension of
![]() $L$
, there is an isomorphism
$L$
, there is an isomorphism
 $\mathscr{Y}\rightarrow \coprod _{i\in I}\mathscr{D}_{[F:\mathbf{Q}]}^{(i)}$
to a finite disjoint union of rigid polydiscs, taking
$\mathscr{Y}\rightarrow \coprod _{i\in I}\mathscr{D}_{[F:\mathbf{Q}]}^{(i)}$
to a finite disjoint union of rigid polydiscs, taking
 $\mathscr{Y}^{\text{l.c.},\text{an}}(\overline{L})$
to
$\mathscr{Y}^{\text{l.c.},\text{an}}(\overline{L})$
to
 $\coprod _{i\in I}\unicode[STIX]{x1D6F4}_{[F:\mathbf{Q}]}^{(i)}$
.◻
$\coprod _{i\in I}\unicode[STIX]{x1D6F4}_{[F:\mathbf{Q}]}^{(i)}$
.◻
Proposition 10.2.3. The following are equivalent:
-
(1) Theorem B is true for all
 $f_{1}$
,
$f_{1}$
,
 $f_{2}$
, and all locally constant characters
$f_{2}$
, and all locally constant characters
 $\unicode[STIX]{x1D712}\in \mathscr{Y}_{L}^{\text{l.c.}}$
;
$\unicode[STIX]{x1D712}\in \mathscr{Y}_{L}^{\text{l.c.}}$
; -
(2) Theorem B is true for all
 $f_{1}$
,
$f_{1}$
,
 $f_{2}$
, and all but finitely many locally constant characters
$f_{2}$
, and all but finitely many locally constant characters
 $\unicode[STIX]{x1D712}\in \mathscr{Y}_{L}^{\text{l.c.}}$
;
$\unicode[STIX]{x1D712}\in \mathscr{Y}_{L}^{\text{l.c.}}$
;
Proof. It is clear that (1) implies (2). That (2) implies (3) follows from Lemma 10.2.1 applied to the difference of the two sides of the desired equality, together with the interpolation properties and the evaluation of the local toric integrals in Lemma 10.1.2. Finally, the multiplicity-one result together with Lemma 10.1.2 shows that (3) implies (1). ◻
Since we have already shown at the end of § 8.3 that Theorem B is true for all but finitely many finite-order characters, this completes the proof of Theorem B in general and proves Theorem C (4). Finally, the anticyclotomic Waldspurger formula of Theorem C (3) follows from the Waldspurger formula at finite-order characters (1.4.2) by the argument in the proof of Proposition 10.2.3.
10.3 Birch and Swinnerton-Dyer formula
Theorem D follows immediately from combining the first and second parts of the following proposition. We abbreviate
 $\mathbf{S}_{\mathfrak{p}}^{\pm }:=\mathbf{S}_{\mathfrak{p}}(A_{E}^{\pm },\unicode[STIX]{x1D712}_{\text{univ}}^{\pm },\mathscr{Y}^{\circ })^{\text{b}}$
and remark that, under the assumption
$\mathbf{S}_{\mathfrak{p}}^{\pm }:=\mathbf{S}_{\mathfrak{p}}(A_{E}^{\pm },\unicode[STIX]{x1D712}_{\text{univ}}^{\pm },\mathscr{Y}^{\circ })^{\text{b}}$
and remark that, under the assumption
![]() $\unicode[STIX]{x1D714}=\mathbf{1}$
of Theorem D, we have
$\unicode[STIX]{x1D714}=\mathbf{1}$
of Theorem D, we have
 $A=A^{+}=A^{-}$
and
$A=A^{+}=A^{-}$
and
 $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}^{+}=\unicode[STIX]{x1D70B}^{-}$
.
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}^{+}=\unicode[STIX]{x1D70B}^{-}$
.
Proposition 10.3.1. Under the assumptions and notation of Theorem D, the following hold.
-
(1) Let
be the saturated $$\begin{eqnarray}\text{}\underline{\mathscr{H}}\subset \mathbf{S}_{\mathfrak{p}}^{+}\otimes \mathbf{S}_{\mathfrak{ p}}^{-,\unicode[STIX]{x1D704}}\end{eqnarray}$$
$$\begin{eqnarray}\text{}\underline{\mathscr{H}}\subset \mathbf{S}_{\mathfrak{p}}^{+}\otimes \mathbf{S}_{\mathfrak{ p}}^{-,\unicode[STIX]{x1D704}}\end{eqnarray}$$
 $\unicode[STIX]{x1D6EC}$
-submodule generated by the Heegner points
$\unicode[STIX]{x1D6EC}$
-submodule generated by the Heegner points
 $\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f^{p})\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-}(f^{p})$
for
$\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f^{p})\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-}(f^{p})$
for
 $f^{p}\in \unicode[STIX]{x1D70B}^{p}$
. The
$f^{p}\in \unicode[STIX]{x1D70B}^{p}$
. The
 $\unicode[STIX]{x1D6EC}$
-modules
$\unicode[STIX]{x1D6EC}$
-modules
 $\mathbf{S}_{\mathfrak{p}}^{\pm }$
are generically of rank
$\mathbf{S}_{\mathfrak{p}}^{\pm }$
are generically of rank
 $1$
, and moreover
$1$
, and moreover
 $\text{}\underline{\mathscr{H}}$
is free of rank
$\text{}\underline{\mathscr{H}}$
is free of rank
 $1$
over
$1$
over
 $\unicode[STIX]{x1D6EC}$
, generated by an explicit element
$\unicode[STIX]{x1D6EC}$
, generated by an explicit element
 $\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-,\unicode[STIX]{x1D704}}$
.
$\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-,\unicode[STIX]{x1D704}}$
.
-
(2) We have the divisibility of
 $\unicode[STIX]{x1D6EC}$
-ideals
$\unicode[STIX]{x1D6EC}$
-ideals  $$\begin{eqnarray}\operatorname{char}_{\unicode[STIX]{x1D6EC}}\widetilde{H}_{f}^{2}(E,V_{\mathfrak{ p}}A\otimes \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D712}_{\text{univ}}))_{\text{tors}}\quad \mid \quad \operatorname{char}_{\unicode[STIX]{x1D6EC}}(\mathbf{S}_{\mathfrak{p}}^{+}\otimes _{\unicode[STIX]{x1D6EC}}\mathbf{S}_{\mathfrak{ p}}^{-,\unicode[STIX]{x1D704}}/\text{}\underline{\mathscr{H}}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{char}_{\unicode[STIX]{x1D6EC}}\widetilde{H}_{f}^{2}(E,V_{\mathfrak{ p}}A\otimes \unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D712}_{\text{univ}}))_{\text{tors}}\quad \mid \quad \operatorname{char}_{\unicode[STIX]{x1D6EC}}(\mathbf{S}_{\mathfrak{p}}^{+}\otimes _{\unicode[STIX]{x1D6EC}}\mathbf{S}_{\mathfrak{ p}}^{-,\unicode[STIX]{x1D704}}/\text{}\underline{\mathscr{H}}).\end{eqnarray}$$
-
(3) Letting
 $\langle \,\,\rangle$
denote the height pairing (1.4.6), we have
$\langle \,\,\rangle$
denote the height pairing (1.4.6), we have  $$\begin{eqnarray}\langle \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-,\unicode[STIX]{x1D704}}\rangle =\frac{c_{E}}{2}\cdot \text{d}_{F}L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})|_{\mathscr{Y}^{\circ }}.\end{eqnarray}$$
$$\begin{eqnarray}\langle \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-,\unicode[STIX]{x1D704}}\rangle =\frac{c_{E}}{2}\cdot \text{d}_{F}L_{p,\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70E}_{E})|_{\mathscr{Y}^{\circ }}.\end{eqnarray}$$
Proof. We define
 $\widetilde{Q}_{v}(f_{v},\unicode[STIX]{x1D712}_{v}):=Q_{v}(f_{v},f_{v},\unicode[STIX]{x1D712}_{v})$
for
$\widetilde{Q}_{v}(f_{v},\unicode[STIX]{x1D712}_{v}):=Q_{v}(f_{v},f_{v},\unicode[STIX]{x1D712}_{v})$
for
![]() $f_{v}\in \unicode[STIX]{x1D70B}_{v}$
, and similarly
$f_{v}\in \unicode[STIX]{x1D70B}_{v}$
, and similarly
 $\widetilde{Q}(f,\unicode[STIX]{x1D712}):=\prod _{v}\widetilde{Q}(f_{v},\unicode[STIX]{x1D712}_{v})$
if
$\widetilde{Q}(f,\unicode[STIX]{x1D712}):=\prod _{v}\widetilde{Q}(f_{v},\unicode[STIX]{x1D712}_{v})$
if
 $f=\bigotimes _{v}f_{v}\in \unicode[STIX]{x1D70B}$
. By [Reference WaldspurgerWal85, Lemme 13] (possibly applied to twists
$f=\bigotimes _{v}f_{v}\in \unicode[STIX]{x1D70B}$
. By [Reference WaldspurgerWal85, Lemme 13] (possibly applied to twists
 $(\unicode[STIX]{x1D70B}_{v}\otimes \unicode[STIX]{x1D707}_{v}^{-\text{`}},\unicode[STIX]{x1D712}_{v}\cdot (\unicode[STIX]{x1D707}_{v}\circ q_{w}))$
for some character
$(\unicode[STIX]{x1D70B}_{v}\otimes \unicode[STIX]{x1D707}_{v}^{-\text{`}},\unicode[STIX]{x1D712}_{v}\cdot (\unicode[STIX]{x1D707}_{v}\circ q_{w}))$
for some character
![]() $\unicode[STIX]{x1D707}_{v}$
of
$\unicode[STIX]{x1D707}_{v}$
of
![]() $F_{v}^{\times }$
), the spaces
$F_{v}^{\times }$
), the spaces
 $\text{H}(\unicode[STIX]{x1D70B}_{v},\unicode[STIX]{x1D712}_{v})=\operatorname{Hom}_{E_{v}^{\times }}(\unicode[STIX]{x1D70B}_{v}\otimes \unicode[STIX]{x1D712}_{v},L(\unicode[STIX]{x1D712}_{v}))$
are non-zero if and only if
$\text{H}(\unicode[STIX]{x1D70B}_{v},\unicode[STIX]{x1D712}_{v})=\operatorname{Hom}_{E_{v}^{\times }}(\unicode[STIX]{x1D70B}_{v}\otimes \unicode[STIX]{x1D712}_{v},L(\unicode[STIX]{x1D712}_{v}))$
are non-zero if and only if
 $\widetilde{Q}_{v}(\cdot ,\unicode[STIX]{x1D712}_{v})$
is non-zero on
$\widetilde{Q}_{v}(\cdot ,\unicode[STIX]{x1D712}_{v})$
is non-zero on
![]() $\unicode[STIX]{x1D70B}_{v}$
. We also define
$\unicode[STIX]{x1D70B}_{v}$
. We also define
 $\widetilde{\mathscr{Q}}_{v}(f_{v}):=\mathscr{Q}_{v}(f_{v},f_{v})$
and
$\widetilde{\mathscr{Q}}_{v}(f_{v}):=\mathscr{Q}_{v}(f_{v},f_{v})$
and
 $\widetilde{\mathscr{Q}}(f^{p}):=\unicode[STIX]{x1D701}_{F,p}(2)^{-1}\prod _{v\nmid p}\widetilde{\mathscr{Q}}(f_{v})\in \unicode[STIX]{x1D6EC}$
for
$\widetilde{\mathscr{Q}}(f^{p}):=\unicode[STIX]{x1D701}_{F,p}(2)^{-1}\prod _{v\nmid p}\widetilde{\mathscr{Q}}(f_{v})\in \unicode[STIX]{x1D6EC}$
for
 $f^{p}=\otimes f_{v}\in \unicode[STIX]{x1D70B}^{p}$
. If the local conditions (1.1.1) are satisfied, as we assume, then the spaces
$f^{p}=\otimes f_{v}\in \unicode[STIX]{x1D70B}^{p}$
. If the local conditions (1.1.1) are satisfied, as we assume, then the spaces
 $\text{H}(\unicode[STIX]{x1D70B}_{v},\unicode[STIX]{x1D712}_{v})$
are non-zero for all
$\text{H}(\unicode[STIX]{x1D70B}_{v},\unicode[STIX]{x1D712}_{v})$
are non-zero for all
![]() $\unicode[STIX]{x1D712}\in \mathscr{Y}^{\circ }$
, and
$\unicode[STIX]{x1D712}\in \mathscr{Y}^{\circ }$
, and
![]() $\widetilde{\mathscr{Q}}$
is not identically zero on
$\widetilde{\mathscr{Q}}$
is not identically zero on
![]() $\unicode[STIX]{x1D70B}^{p}$
.
$\unicode[STIX]{x1D70B}^{p}$
.
We will invoke the results of Fouquet in [Reference FouquetFou13] after comparing our setup with his. Let
 $U_{r}=U^{p}\prod _{v|p}U_{r,v}\subset \mathbf{B}^{\infty ,\times }$
be such that
$U_{r}=U^{p}\prod _{v|p}U_{r,v}\subset \mathbf{B}^{\infty ,\times }$
be such that
 $U_{r,v}=K_{0}(\unicode[STIX]{x1D71B}_{v}^{r_{v}})$
for
$U_{r,v}=K_{0}(\unicode[STIX]{x1D71B}_{v}^{r_{v}})$
for
![]() $v|p$
,
$v|p$
,
![]() $r_{v}\geqslant 1$
. Let
$r_{v}\geqslant 1$
. Let
 $eH_{\acute{\text{e}}\text{t}}^{1}(X_{U_{r},\overline{F}},\mathscr{O}_{L}(1))$
be the image of
$eH_{\acute{\text{e}}\text{t}}^{1}(X_{U_{r},\overline{F}},\mathscr{O}_{L}(1))$
be the image of
 $H_{\acute{\text{e}}\text{t}}^{1}(X_{U_{r},\overline{F}},\mathscr{O}_{L}(1))$
under the product
$H_{\acute{\text{e}}\text{t}}^{1}(X_{U_{r},\overline{F}},\mathscr{O}_{L}(1))$
under the product
![]() $e$
of the projectors
$e$
of the projectors
 $e_{v}:=\lim _{n}\text{U}_{v}^{n!}$
. Let
$e_{v}:=\lim _{n}\text{U}_{v}^{n!}$
. Let
 $\mathscr{J}_{\unicode[STIX]{x1D70B}}\subset \mathscr{H}_{\mathbf{B}^{\infty \times }}^{\text{sph}}$
be the annihilator of
$\mathscr{J}_{\unicode[STIX]{x1D70B}}\subset \mathscr{H}_{\mathbf{B}^{\infty \times }}^{\text{sph}}$
be the annihilator of
![]() $\unicode[STIX]{x1D70B}$
viewed as a module over the spherical Hecke algebra
$\unicode[STIX]{x1D70B}$
viewed as a module over the spherical Hecke algebra
![]() $\mathscr{H}_{\mathbf{B}^{\infty \times }}^{\text{sph}}$
for
$\mathscr{H}_{\mathbf{B}^{\infty \times }}^{\text{sph}}$
for
![]() $\mathbf{B}^{\infty \times }$
, and let
$\mathbf{B}^{\infty \times }$
, and let
 $$\begin{eqnarray}eH_{\acute{\text{e}}\text{t}}^{1}(X_{U^{p},\overline{F}},\mathscr{O}_{L}(1))[\unicode[STIX]{x1D70B}]:=eH_{\acute{\text{e}}\text{t}}^{1}(X_{U_{r},\overline{F}},\mathscr{O}_{L}(1))/\mathscr{J}_{\unicode[STIX]{x1D70B}},\end{eqnarray}$$
$$\begin{eqnarray}eH_{\acute{\text{e}}\text{t}}^{1}(X_{U^{p},\overline{F}},\mathscr{O}_{L}(1))[\unicode[STIX]{x1D70B}]:=eH_{\acute{\text{e}}\text{t}}^{1}(X_{U_{r},\overline{F}},\mathscr{O}_{L}(1))/\mathscr{J}_{\unicode[STIX]{x1D70B}},\end{eqnarray}$$
a Galois module which is independent of
![]() $r\geqslant \text{}\underline{1}$
. The operators
$r\geqslant \text{}\underline{1}$
. The operators
![]() $\text{U}_{v}$
act invertibly on
$\text{U}_{v}$
act invertibly on
 $eH^{1}(X_{U_{r},\overline{F}},\mathscr{O}_{L}(1))$
, and in fact by
$eH^{1}(X_{U_{r},\overline{F}},\mathscr{O}_{L}(1))$
, and in fact by
![]() $\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})$
on
$\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})$
on
 $eH_{\acute{\text{e}}\text{t}}^{1}(X_{U^{p},\overline{F}},\mathscr{O}_{L}(1))[\unicode[STIX]{x1D70B}]$
. Let
$eH_{\acute{\text{e}}\text{t}}^{1}(X_{U^{p},\overline{F}},\mathscr{O}_{L}(1))[\unicode[STIX]{x1D70B}]$
. Let
![]() $f^{p}\in \unicode[STIX]{x1D70B}^{p}$
be such that
$f^{p}\in \unicode[STIX]{x1D70B}^{p}$
be such that
 $\widetilde{\mathscr{Q}}(f^{p})\neq 0$
. Denote by
$\widetilde{\mathscr{Q}}(f^{p})\neq 0$
. Denote by
![]() $\unicode[STIX]{x1D705}$
the Abel–Jacobi functor and by
$\unicode[STIX]{x1D705}$
the Abel–Jacobi functor and by
 $f_{\unicode[STIX]{x1D6FC}}^{\circ }:=f^{p}\otimes f_{\unicode[STIX]{x1D6FC},p}^{\circ }$
, with
$f_{\unicode[STIX]{x1D6FC}}^{\circ }:=f^{p}\otimes f_{\unicode[STIX]{x1D6FC},p}^{\circ }$
, with
![]() $f_{\unicode[STIX]{x1D6FC},p}^{\circ }$
, the product of the elements
$f_{\unicode[STIX]{x1D6FC},p}^{\circ }$
, the product of the elements
![]() $f_{\unicode[STIX]{x1D6FC},v}^{\circ }$
of (10.1.2) for
$f_{\unicode[STIX]{x1D6FC},v}^{\circ }$
of (10.1.2) for
![]() $v|p$
. Then, up to a fixed non-zero multiple, the class
$v|p$
. Then, up to a fixed non-zero multiple, the class
 $\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f^{p})$
is the image under
$\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f^{p})$
is the image under
![]() $\unicode[STIX]{x1D705}(f_{\unicode[STIX]{x1D6FC}}^{\circ })$
of the limit of the compatible sequence
$\unicode[STIX]{x1D705}(f_{\unicode[STIX]{x1D6FC}}^{\circ })$
of the limit of the compatible sequence
 $$\begin{eqnarray}\mathscr{P}_{\unicode[STIX]{x1D6FC},r}:=\text{U}_{p}^{-r}\mathop{\sum }_{t\in E^{\times }\backslash E_{\mathbf{A}^{\infty }}^{\times }/U_{T}}\unicode[STIX]{x1D705}(\text{rec}_{E}(t)\text{T}_{s_{r}}\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D709}}(P))\otimes \unicode[STIX]{x1D712}_{\text{univ},U_{T}}^{\pm }(t)\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{P}_{\unicode[STIX]{x1D6FC},r}:=\text{U}_{p}^{-r}\mathop{\sum }_{t\in E^{\times }\backslash E_{\mathbf{A}^{\infty }}^{\times }/U_{T}}\unicode[STIX]{x1D705}(\text{rec}_{E}(t)\text{T}_{s_{r}}\unicode[STIX]{x1D704}_{\unicode[STIX]{x1D709}}(P))\otimes \unicode[STIX]{x1D712}_{\text{univ},U_{T}}^{\pm }(t)\end{eqnarray}$$
of integral elements of
 $H_{f}^{1}(E,eH_{\acute{\text{e}}\text{t}}^{1}(X_{U^{p},\overline{F}},\mathscr{O}_{L}(1))\otimes \unicode[STIX]{x1D6EC}^{U_{T}}(\unicode[STIX]{x1D712}_{\text{univ},U_{T}}))$
. Fouquet takes as input a certain compatible sequence
$H_{f}^{1}(E,eH_{\acute{\text{e}}\text{t}}^{1}(X_{U^{p},\overline{F}},\mathscr{O}_{L}(1))\otimes \unicode[STIX]{x1D6EC}^{U_{T}}(\unicode[STIX]{x1D712}_{\text{univ},U_{T}}))$
. Fouquet takes as input a certain compatible sequence
 $(z(\mathfrak{c}_{p},S))_{S}$
[Reference FouquetFou13, Definitions 4.11 and 4.14] of classes in the latter space to construct, via suitable local modifications according to the method of Kolyvagin, an Euler system [Reference FouquetFou13, §5]. Noting that the local modifications occur at well-chosen, good primes
$(z(\mathfrak{c}_{p},S))_{S}$
[Reference FouquetFou13, Definitions 4.11 and 4.14] of classes in the latter space to construct, via suitable local modifications according to the method of Kolyvagin, an Euler system [Reference FouquetFou13, §5]. Noting that the local modifications occur at well-chosen, good primes
![]() $\ell$
of
$\ell$
of
![]() $E$
, his construction can equally well be applied to the sequence
$E$
, his construction can equally well be applied to the sequence
 $(\mathscr{P}_{\unicode[STIX]{x1D6FC},r})_{r}$
in place of
$(\mathscr{P}_{\unicode[STIX]{x1D6FC},r})_{r}$
in place of
 $(z(\mathfrak{c}_{p},S))_{S}$
. This Euler system can then be projected via
$(z(\mathfrak{c}_{p},S))_{S}$
. This Euler system can then be projected via
![]() $\unicode[STIX]{x1D705}(f_{\unicode[STIX]{x1D6FC}})$
to yield an Euler system for
$\unicode[STIX]{x1D705}(f_{\unicode[STIX]{x1D6FC}})$
to yield an Euler system for
 $V_{\mathfrak{p}}A\,\otimes \,\unicode[STIX]{x1D6EC}$
. Under the condition that the first element
$V_{\mathfrak{p}}A\,\otimes \,\unicode[STIX]{x1D6EC}$
. Under the condition that the first element
 $\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f^{p})\in \mathbf{S}_{\mathfrak{p}}^{+}$
(corresponding to
$\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f^{p})\in \mathbf{S}_{\mathfrak{p}}^{+}$
(corresponding to
![]() $z_{f,\infty }$
in [Reference FouquetFou13]) of the projected Euler system is non-torsion, it is proved in [Reference FouquetFou13, Theorem B(ii)] that
$z_{f,\infty }$
in [Reference FouquetFou13]) of the projected Euler system is non-torsion, it is proved in [Reference FouquetFou13, Theorem B(ii)] that
![]() $\mathbf{S}_{\mathfrak{p}}^{\pm }$
have generic rank
$\mathbf{S}_{\mathfrak{p}}^{\pm }$
have generic rank
![]() $1$
over
$1$
over
![]() $\unicode[STIX]{x1D6EC}$
. By the main result of [Reference Aflalo and NekovářAN10], generalising [Reference Cornut and VatsalCV05], the family of points
$\unicode[STIX]{x1D6EC}$
. By the main result of [Reference Aflalo and NekovářAN10], generalising [Reference Cornut and VatsalCV05], the family of points
 $\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f^{p})\in \mathbf{S}_{\mathfrak{p}}^{+}$
is indeed not
$\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f^{p})\in \mathbf{S}_{\mathfrak{p}}^{+}$
is indeed not
![]() $\unicode[STIX]{x1D6EC}$
-torsion provided
$\unicode[STIX]{x1D6EC}$
-torsion provided
 $\widetilde{\mathscr{Q}}(f^{p})\neq 0$
(i.e.
$\widetilde{\mathscr{Q}}(f^{p})\neq 0$
(i.e.
![]() $f_{v}$
is a ‘local test vector’ for all
$f_{v}$
is a ‘local test vector’ for all
![]() $v\nmid p$
). We conclude as desired that
$v\nmid p$
). We conclude as desired that
![]() $\mathbf{S}_{\mathfrak{p}}^{\pm }$
have generic rank
$\mathbf{S}_{\mathfrak{p}}^{\pm }$
have generic rank
![]() $1$
over
$1$
over
![]() $\unicode[STIX]{x1D6EC}$
and that the same is true of the submodule
$\unicode[STIX]{x1D6EC}$
and that the same is true of the submodule
![]() $\text{}\underline{\mathscr{H}}$
.
$\text{}\underline{\mathscr{H}}$
.
We now proceed to complete the proof of part 1 by showing that the ‘Heegner submodule’
![]() $\text{}\underline{\mathscr{H}}$
is in fact free of rank
$\text{}\underline{\mathscr{H}}$
is in fact free of rank
![]() $1$
and constructing a ‘canonical’ generator. First we note that by [Reference FouquetFou13, Theorem 6.1], each special fibre
$1$
and constructing a ‘canonical’ generator. First we note that by [Reference FouquetFou13, Theorem 6.1], each special fibre
![]() $\text{}\underline{\mathscr{H}}_{|\unicode[STIX]{x1D712}}$
(for arbitrary
$\text{}\underline{\mathscr{H}}_{|\unicode[STIX]{x1D712}}$
(for arbitrary
![]() $\unicode[STIX]{x1D712}\in \mathscr{Y}^{\circ }$
) has dimension either
$\unicode[STIX]{x1D712}\in \mathscr{Y}^{\circ }$
) has dimension either
![]() $0$
(we will soon exclude this case) or
$0$
(we will soon exclude this case) or
![]() $1$
over
$1$
over
![]() $L(\unicode[STIX]{x1D712})$
. Let
$L(\unicode[STIX]{x1D712})$
. Let
 $\{\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f_{i}^{p})\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-}(f_{i}^{p})^{\unicode[STIX]{x1D704}}:i\in I\}$
be finitely many sections of
$\{\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f_{i}^{p})\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-}(f_{i}^{p})^{\unicode[STIX]{x1D704}}:i\in I\}$
be finitely many sections of
![]() $\text{}\underline{\mathscr{H}}$
. By [Reference Yuan, Zhang and ZhangYZZ12], for each
$\text{}\underline{\mathscr{H}}$
. By [Reference Yuan, Zhang and ZhangYZZ12], for each
 $\unicode[STIX]{x1D712}\in \mathscr{Y}^{\circ ,\text{l.c.}}:=\mathscr{Y}^{\circ }\cap \mathscr{Y}^{\text{l.c.},\text{an}}$
, the specialisation
$\unicode[STIX]{x1D712}\in \mathscr{Y}^{\circ ,\text{l.c.}}:=\mathscr{Y}^{\circ }\cap \mathscr{Y}^{\text{l.c.},\text{an}}$
, the specialisation
 $\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f_{i}^{p})\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-}(f_{i}^{p})^{\unicode[STIX]{x1D704}}(\unicode[STIX]{x1D712})$
is non-zero if and only if
$\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f_{i}^{p})\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-}(f_{i}^{p})^{\unicode[STIX]{x1D704}}(\unicode[STIX]{x1D712})$
is non-zero if and only if
 $\widetilde{\mathscr{Q}}(f_{i}^{p})(\unicode[STIX]{x1D712})\neq 0$
, and moreover the images of the specialisations at
$\widetilde{\mathscr{Q}}(f_{i}^{p})(\unicode[STIX]{x1D712})\neq 0$
, and moreover the images of the specialisations at
![]() $\unicode[STIX]{x1D712}$
of the global sections of
$\unicode[STIX]{x1D712}$
of the global sections of
![]() $\text{}\underline{\mathscr{H}}$
$\text{}\underline{\mathscr{H}}$
 $$\begin{eqnarray}\mathop{\prod }_{j\in I,j\neq i}\widetilde{\mathscr{Q}}(f_{j}^{p})\cdot \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f_{i}^{p})\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-}(f_{i}^{p})^{\unicode[STIX]{x1D704}}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{j\in I,j\neq i}\widetilde{\mathscr{Q}}(f_{j}^{p})\cdot \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f_{i}^{p})\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-}(f_{i}^{p})^{\unicode[STIX]{x1D704}}\end{eqnarray}$$
under the Néron–Tate height pairing (after choosing any embedding
 $L(\unicode[STIX]{x1D712}){\hookrightarrow}\mathbf{C}$
) coincide. As
$L(\unicode[STIX]{x1D712}){\hookrightarrow}\mathbf{C}$
) coincide. As
![]() $\text{}\underline{\mathscr{H}}_{|\unicode[STIX]{x1D712}}$
has dimension at most
$\text{}\underline{\mathscr{H}}_{|\unicode[STIX]{x1D712}}$
has dimension at most
![]() $1$
, the Néron–Tate height pairing on
$1$
, the Néron–Tate height pairing on
 $\text{}\underline{\mathscr{H}}_{\unicode[STIX]{x1D712}}\otimes \mathbf{C}$
is an isomorphism onto its image in
$\text{}\underline{\mathscr{H}}_{\unicode[STIX]{x1D712}}\otimes \mathbf{C}$
is an isomorphism onto its image in
![]() $\mathbf{C}$
, and we deduce that that the elements (10.3.1) coincide over
$\mathbf{C}$
, and we deduce that that the elements (10.3.1) coincide over
![]() $\mathscr{Y}^{\circ ,\text{l.c.}}$
. Since the latter set is dense in
$\mathscr{Y}^{\circ ,\text{l.c.}}$
. Since the latter set is dense in
![]() $\operatorname{Spec}\unicode[STIX]{x1D6EC}$
by Lemma 10.2.1, they coincide everywhere and glue to a global section
$\operatorname{Spec}\unicode[STIX]{x1D6EC}$
by Lemma 10.2.1, they coincide everywhere and glue to a global section
 $(\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-,\unicode[STIX]{x1D704}})^{\prime }$
of
$(\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-,\unicode[STIX]{x1D704}})^{\prime }$
of
![]() $\text{}\underline{\mathscr{H}}$
over
$\text{}\underline{\mathscr{H}}$
over
![]() $\mathscr{Y}^{\circ }$
.Footnote
38
$\mathscr{Y}^{\circ }$
.Footnote
38
Similarly to what is claimed in the proof of Theorem 3.7.1, there exists a finite set
 $\{f_{i}^{p}:i\in I\}\subset \unicode[STIX]{x1D70B}^{p}$
such that the open sets
$\{f_{i}^{p}:i\in I\}\subset \unicode[STIX]{x1D70B}^{p}$
such that the open sets
 $\mathscr{U}_{f_{i}^{p}}:=\{\widetilde{\mathscr{Q}}(f_{i}^{p})\neq 0\}\subset \mathscr{Y}^{\circ }$
cover
$\mathscr{U}_{f_{i}^{p}}:=\{\widetilde{\mathscr{Q}}(f_{i}^{p})\neq 0\}\subset \mathscr{Y}^{\circ }$
cover
![]() $\mathscr{Y}^{\circ }$
. Then the section
$\mathscr{Y}^{\circ }$
. Then the section
 $$\begin{eqnarray}\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-,\unicode[STIX]{x1D704}}:=\mathop{\prod }_{i\in I}\widetilde{\mathscr{Q}}(f_{i}^{p})^{-1}\cdot (\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-,\unicode[STIX]{x1D704}})^{\prime }\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-,\unicode[STIX]{x1D704}}:=\mathop{\prod }_{i\in I}\widetilde{\mathscr{Q}}(f_{i}^{p})^{-1}\cdot (\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-,\unicode[STIX]{x1D704}})^{\prime }\end{eqnarray}$$
is nowhere vanishing and a generator of
![]() $\text{}\underline{\mathscr{H}}$
. It is independent of choices since for any
$\text{}\underline{\mathscr{H}}$
. It is independent of choices since for any
 $f^{p}\in \unicode[STIX]{x1D70B}^{p}$
it coincides with
$f^{p}\in \unicode[STIX]{x1D70B}^{p}$
it coincides with
 $\widetilde{\mathscr{Q}}(f^{p})^{-1}\cdot \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f^{p})\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-}(f^{p})^{\unicode[STIX]{x1D704}}$
over
$\widetilde{\mathscr{Q}}(f^{p})^{-1}\cdot \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f^{p})\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-}(f^{p})^{\unicode[STIX]{x1D704}}$
over
![]() $\mathscr{U}_{f^{p}}$
. This completes the proof of Part 1.
$\mathscr{U}_{f^{p}}$
. This completes the proof of Part 1.
Part 2 is [Reference FouquetFou13, Theorem B(ii)] with
![]() $\text{}\underline{\mathscr{H}}$
replaced by its submodule generated by a non-torsion element
$\text{}\underline{\mathscr{H}}$
replaced by its submodule generated by a non-torsion element
 $z_{f,\infty }\otimes z_{f,\infty }\in \text{}\underline{\mathscr{H}}$
; as noted above, we can replace this element by any of the elements
$z_{f,\infty }\otimes z_{f,\infty }\in \text{}\underline{\mathscr{H}}$
; as noted above, we can replace this element by any of the elements
 $\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f^{p})\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-}(f^{p})^{\unicode[STIX]{x1D704}}$
, and by a glueing argument with
$\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}(f^{p})\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-}(f^{p})^{\unicode[STIX]{x1D704}}$
, and by a glueing argument with
 $\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-,\unicode[STIX]{x1D704}}$
.
$\mathscr{P}_{\unicode[STIX]{x1D6FC}}^{+}\otimes \mathscr{P}_{\unicode[STIX]{x1D6FC}}^{-,\unicode[STIX]{x1D704}}$
.
Acknowledgements
I would like to thank S. Zhang for warm encouragement and A. Burungale, M. Chida, O. Fouquet, M.-L. Hsieh, A. Iovita, S. Kudla, V. Pilloni, E. Urban, Y. Tian, X. Yuan, and W. Zhang for useful conversations or correspondence. I am especially grateful to S. Shah for his help with the chirality of Haar measures and to A. Shnidman for extended discussions on heights. Finally, I would like to thank the referee for a careful reading and A. Besser for kindly agreeing to study the compatibility between
![]() $p$
-adic heights and Arakelov theory on curves of bad reduction: his work gave me confidence at a time when I had not found the alternative argument used here. Parts of the present paper were written while the author was a postdoctoral fellow at MSRI, funded under NSF grant 0932078000, and at the CRM (Montreal). Final revisions were made when the author was a postdoctoral fellow funded by the Fondation Mathématique Jacques Hadamard.
$p$
-adic heights and Arakelov theory on curves of bad reduction: his work gave me confidence at a time when I had not found the alternative argument used here. Parts of the present paper were written while the author was a postdoctoral fellow at MSRI, funded under NSF grant 0932078000, and at the CRM (Montreal). Final revisions were made when the author was a postdoctoral fellow funded by the Fondation Mathématique Jacques Hadamard.
Appendix Local integrals
A.1 Basic integral
All the integrals computed in the appendix will ultimately reduce to the following.
Lemma A.1.1. Let
![]() $F_{v}$
be a non-archimedean local field, and let
$F_{v}$
be a non-archimedean local field, and let
![]() $E_{w}/F_{v}$
be an extension of degree
$E_{w}/F_{v}$
be an extension of degree
![]() $fe\leqslant 2$
, with
$fe\leqslant 2$
, with
![]() $f$
the inertia degree and
$f$
the inertia degree and
![]() $e$
the ramification degree. Let
$e$
the ramification degree. Let
![]() $q_{w}$
be the relative norm and
$q_{w}$
be the relative norm and
 $D\in \mathscr{O}_{F,v}$
be a generator of the relative discriminant.
$D\in \mathscr{O}_{F,v}$
be a generator of the relative discriminant.
Let
![]() $L$
be a field of characteristic zero, let
$L$
be a field of characteristic zero, let
 $\unicode[STIX]{x1D6FC}_{v}:F_{v}^{\times }\rightarrow L^{\times }$
and
$\unicode[STIX]{x1D6FC}_{v}:F_{v}^{\times }\rightarrow L^{\times }$
and
 $\unicode[STIX]{x1D712}^{\prime }:E_{w}^{\times }\rightarrow L^{\times }$
be multiplicative characters,
$\unicode[STIX]{x1D712}^{\prime }:E_{w}^{\times }\rightarrow L^{\times }$
be multiplicative characters,
 $\unicode[STIX]{x1D713}_{v}:F_{v}\rightarrow L^{\times }$
be an additive character of level
$\unicode[STIX]{x1D713}_{v}:F_{v}\rightarrow L^{\times }$
be an additive character of level
![]() $0$
, and
$0$
, and
 $\unicode[STIX]{x1D713}_{E,w}=\unicode[STIX]{x1D713}_{v}\circ \operatorname{Tr}_{E_{w}/F_{v}}$
. Define
$\unicode[STIX]{x1D713}_{E,w}=\unicode[STIX]{x1D713}_{v}\circ \operatorname{Tr}_{E_{w}/F_{v}}$
. Define
 $$\begin{eqnarray}Z_{w}(\unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D713}_{v}):=\int _{E_{w}^{\times }}\unicode[STIX]{x1D6FC}\circ q(t)\unicode[STIX]{x1D712}^{\prime }(t)\unicode[STIX]{x1D713}_{E_{w}}(t)\,\frac{dt}{|D|^{1/2}|d|_{v}^{f/2}},\end{eqnarray}$$
$$\begin{eqnarray}Z_{w}(\unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D713}_{v}):=\int _{E_{w}^{\times }}\unicode[STIX]{x1D6FC}\circ q(t)\unicode[STIX]{x1D712}^{\prime }(t)\unicode[STIX]{x1D713}_{E_{w}}(t)\,\frac{dt}{|D|^{1/2}|d|_{v}^{f/2}},\end{eqnarray}$$
where
![]() $dt$
is the restriction of the standard measure on
$dt$
is the restriction of the standard measure on
![]() $E_{w}$
.
$E_{w}$
.
Then we have
 $$\begin{eqnarray}Z_{w}(\unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D713}_{v})=\left\{\begin{array}{@{}ll@{}}\displaystyle \unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})^{-v(D)}\unicode[STIX]{x1D712}_{w}^{\prime }(\unicode[STIX]{x1D71B}_{w})^{-v(D)}\frac{1-\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})^{-f}\unicode[STIX]{x1D712}_{w}^{\prime }(\unicode[STIX]{x1D71B}_{w})^{-1}}{1-\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})^{f}\unicode[STIX]{x1D712}_{w}^{\prime }(\unicode[STIX]{x1D71B}_{w})q_{F,v}^{-f}}\quad & \text{if }\unicode[STIX]{x1D712}_{w}^{\prime }\cdot \unicode[STIX]{x1D6FC}_{v}\circ q\text{ is unramified},\\ \unicode[STIX]{x1D70F}(\unicode[STIX]{x1D712}_{w}^{\prime }\cdot \unicode[STIX]{x1D6FC}_{v}\circ q,\unicode[STIX]{x1D713}_{E_{w}})\quad & \text{if }\unicode[STIX]{x1D712}_{w}^{\prime }\cdot \unicode[STIX]{x1D6FC}_{v}\circ q\text{ is ramified}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}Z_{w}(\unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D713}_{v})=\left\{\begin{array}{@{}ll@{}}\displaystyle \unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})^{-v(D)}\unicode[STIX]{x1D712}_{w}^{\prime }(\unicode[STIX]{x1D71B}_{w})^{-v(D)}\frac{1-\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})^{-f}\unicode[STIX]{x1D712}_{w}^{\prime }(\unicode[STIX]{x1D71B}_{w})^{-1}}{1-\unicode[STIX]{x1D6FC}_{v}(\unicode[STIX]{x1D71B}_{v})^{f}\unicode[STIX]{x1D712}_{w}^{\prime }(\unicode[STIX]{x1D71B}_{w})q_{F,v}^{-f}}\quad & \text{if }\unicode[STIX]{x1D712}_{w}^{\prime }\cdot \unicode[STIX]{x1D6FC}_{v}\circ q\text{ is unramified},\\ \unicode[STIX]{x1D70F}(\unicode[STIX]{x1D712}_{w}^{\prime }\cdot \unicode[STIX]{x1D6FC}_{v}\circ q,\unicode[STIX]{x1D713}_{E_{w}})\quad & \text{if }\unicode[STIX]{x1D712}_{w}^{\prime }\cdot \unicode[STIX]{x1D6FC}_{v}\circ q\text{ is ramified}.\end{array}\right.\end{eqnarray}$$
Here for any character
![]() $\widetilde{\unicode[STIX]{x1D712}}_{w}^{\prime }$
of conductor
$\widetilde{\unicode[STIX]{x1D712}}_{w}^{\prime }$
of conductor
![]() $\mathfrak{f}$
,
$\mathfrak{f}$
,
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}(\widetilde{\unicode[STIX]{x1D712}}^{\prime },\unicode[STIX]{x1D713}_{E_{w}})=\int _{w(t)=-w(\mathfrak{f})}\widetilde{\unicode[STIX]{x1D712}}_{w}(t)\unicode[STIX]{x1D713}_{E,w}(t)\,\frac{dt}{|D|^{1/2}|d|_{v}^{f/2}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}(\widetilde{\unicode[STIX]{x1D712}}^{\prime },\unicode[STIX]{x1D713}_{E_{w}})=\int _{w(t)=-w(\mathfrak{f})}\widetilde{\unicode[STIX]{x1D712}}_{w}(t)\unicode[STIX]{x1D713}_{E,w}(t)\,\frac{dt}{|D|^{1/2}|d|_{v}^{f/2}},\end{eqnarray}$$
with
 $n=-w(\mathfrak{f}(\unicode[STIX]{x1D712}_{w}^{\prime }))-w(d_{E,w})$
.
$n=-w(\mathfrak{f}(\unicode[STIX]{x1D712}_{w}^{\prime }))-w(d_{E,w})$
.
Proof. If
![]() $\unicode[STIX]{x1D712}^{\prime }$
is unramified, only the subset
$\unicode[STIX]{x1D712}^{\prime }$
is unramified, only the subset
 $\{w(t)\geqslant -1-w(d)-v(D)\}\subset E_{w}^{\times }$
contributes to the integral, and we have
$\{w(t)\geqslant -1-w(d)-v(D)\}\subset E_{w}^{\times }$
contributes to the integral, and we have
 $$\begin{eqnarray}\displaystyle Z_{w}(\unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D713}) & = & \displaystyle \unicode[STIX]{x1D6FC}^{-v(D)}\unicode[STIX]{x1D712}_{w}^{\prime }(\unicode[STIX]{x1D71B}_{w})^{-ev(d)-v(D)}\biggl(\frac{\unicode[STIX]{x1D701}_{E}(1)^{-1}}{1-\unicode[STIX]{x1D6FC}^{f}\unicode[STIX]{x1D712}^{\prime }(\unicode[STIX]{x1D71B})}-\frac{1}{q_{F,v}^{f}}\unicode[STIX]{x1D6FC}^{-f}\unicode[STIX]{x1D712}^{\prime }(\unicode[STIX]{x1D71B})^{-1}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FC}^{-v(D)}\unicode[STIX]{x1D712}_{w}^{\prime }(\unicode[STIX]{x1D71B}_{w})^{-ev(d)-v(D)}\frac{1-\unicode[STIX]{x1D6FC}^{-f}\unicode[STIX]{x1D712}^{\prime }(\unicode[STIX]{x1D71B})^{-1}q_{F,v}^{-f}}{1-\unicode[STIX]{x1D6FC}^{f}\unicode[STIX]{x1D712}^{\prime }(\unicode[STIX]{x1D71B})}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Z_{w}(\unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D713}) & = & \displaystyle \unicode[STIX]{x1D6FC}^{-v(D)}\unicode[STIX]{x1D712}_{w}^{\prime }(\unicode[STIX]{x1D71B}_{w})^{-ev(d)-v(D)}\biggl(\frac{\unicode[STIX]{x1D701}_{E}(1)^{-1}}{1-\unicode[STIX]{x1D6FC}^{f}\unicode[STIX]{x1D712}^{\prime }(\unicode[STIX]{x1D71B})}-\frac{1}{q_{F,v}^{f}}\unicode[STIX]{x1D6FC}^{-f}\unicode[STIX]{x1D712}^{\prime }(\unicode[STIX]{x1D71B})^{-1}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FC}^{-v(D)}\unicode[STIX]{x1D712}_{w}^{\prime }(\unicode[STIX]{x1D71B}_{w})^{-ev(d)-v(D)}\frac{1-\unicode[STIX]{x1D6FC}^{-f}\unicode[STIX]{x1D712}^{\prime }(\unicode[STIX]{x1D71B})^{-1}q_{F,v}^{-f}}{1-\unicode[STIX]{x1D6FC}^{f}\unicode[STIX]{x1D712}^{\prime }(\unicode[STIX]{x1D71B})}.\nonumber\end{eqnarray}$$
If
![]() $\unicode[STIX]{x1D712}^{\prime }$
is ramified of conductor
$\unicode[STIX]{x1D712}^{\prime }$
is ramified of conductor
 $\mathfrak{f}=\mathfrak{f}(\unicode[STIX]{x1D712}^{\prime })$
, then only the annulus
$\mathfrak{f}=\mathfrak{f}(\unicode[STIX]{x1D712}^{\prime })$
, then only the annulus
 $w(t)=-w(\mathfrak{f})-w(d)-v(D)$
contributes, and we get
$w(t)=-w(\mathfrak{f})-w(d)-v(D)$
contributes, and we get
 $$\begin{eqnarray}Z_{w}(\unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D713})=\unicode[STIX]{x1D6FC}_{v}^{-fw(\mathfrak{f})-fv(D)}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D713}_{E}).\Box\end{eqnarray}$$
$$\begin{eqnarray}Z_{w}(\unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D713})=\unicode[STIX]{x1D6FC}_{v}^{-fw(\mathfrak{f})-fv(D)}\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D712}^{\prime },\unicode[STIX]{x1D713}_{E}).\Box\end{eqnarray}$$
A.2 Interpolation factor
We compute the integral giving the interpolation factor for the
![]() $p$
-adic
$p$
-adic
![]() $L$
-function.
$L$
-function.
The following Iwahori decomposition can be proved similarly to [Reference HuHu16, Lemma A.1].
Lemma A.2.1. For a local field
![]() $F$
with uniformiser
$F$
with uniformiser
![]() $\unicode[STIX]{x1D71B}$
and for any
$\unicode[STIX]{x1D71B}$
and for any
![]() $r\geqslant 1$
, the double quotient
$r\geqslant 1$
, the double quotient
 $$\begin{eqnarray}N(F)A(F)Z(F)\backslash \mathbf{GL}_{2}(F)/K_{1}^{1}(\unicode[STIX]{x1D71B}^{r})\end{eqnarray}$$
$$\begin{eqnarray}N(F)A(F)Z(F)\backslash \mathbf{GL}_{2}(F)/K_{1}^{1}(\unicode[STIX]{x1D71B}^{r})\end{eqnarray}$$
admits the set of representatives
 $$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}1 & \\ & 1\end{array}\right),\quad \left(\begin{array}{@{}cc@{}}1 & \\ c^{(i)}\unicode[STIX]{x1D71B}^{r-i} & 1\end{array}\right),\quad 1\leqslant i\leqslant r,~c^{(i)}\in (\mathscr{O}_{F}/\unicode[STIX]{x1D71B}^{i})^{\times }.\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}1 & \\ & 1\end{array}\right),\quad \left(\begin{array}{@{}cc@{}}1 & \\ c^{(i)}\unicode[STIX]{x1D71B}^{r-i} & 1\end{array}\right),\quad 1\leqslant i\leqslant r,~c^{(i)}\in (\mathscr{O}_{F}/\unicode[STIX]{x1D71B}^{i})^{\times }.\end{eqnarray}$$
Note that we may also replace the first representative by
 $(\!\begin{smallmatrix}1 & \\ \unicode[STIX]{x1D71B}^{r} & 1\end{smallmatrix}\!)\in K_{1}^{1}(\unicode[STIX]{x1D71B}^{r})$
.
$(\!\begin{smallmatrix}1 & \\ \unicode[STIX]{x1D71B}^{r} & 1\end{smallmatrix}\!)\in K_{1}^{1}(\unicode[STIX]{x1D71B}^{r})$
.
Proposition A.2.2. Let
 $\unicode[STIX]{x1D712}^{\prime }\in \mathscr{Y}_{M(\unicode[STIX]{x1D6FC})}^{\prime \,\text{l.c.}}(\mathbf{C})$
and let
$\unicode[STIX]{x1D712}^{\prime }\in \mathscr{Y}_{M(\unicode[STIX]{x1D6FC})}^{\prime \,\text{l.c.}}(\mathbf{C})$
and let
 $\unicode[STIX]{x1D704}:M(\unicode[STIX]{x1D6FC}){\hookrightarrow}\mathbf{C}$
be the induced embedding. Let
$\unicode[STIX]{x1D704}:M(\unicode[STIX]{x1D6FC}){\hookrightarrow}\mathbf{C}$
be the induced embedding. Let
![]() $v|p$
, and let
$v|p$
, and let
![]() $\unicode[STIX]{x1D719}_{v}$
be either as in Assumption 6.2.1 for some sufficiently small
$\unicode[STIX]{x1D719}_{v}$
be either as in Assumption 6.2.1 for some sufficiently small
 $U_{T,v}\subset \mathscr{O}_{E,v}^{\times }$
, or as in Assumption 6.2.2. Then, for any sufficiently large integer
$U_{T,v}\subset \mathscr{O}_{E,v}^{\times }$
, or as in Assumption 6.2.2. Then, for any sufficiently large integer
![]() $r$
, the normalised integral
$r$
, the normalised integral
 $R_{r,v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime })$
of (3.5.2) equals
$R_{r,v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime })$
of (3.5.2) equals
 $$\begin{eqnarray}R_{r,v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime }\text{}^{\unicode[STIX]{x1D704}})=Z_{v}^{\circ }(\unicode[STIX]{x1D712}_{v}^{\prime }):=\frac{\unicode[STIX]{x1D701}_{F,v}(2)L(1,\unicode[STIX]{x1D702}_{v})^{2}}{L(1/2,\unicode[STIX]{x1D70E}_{E,v}^{\unicode[STIX]{x1D704}},\unicode[STIX]{x1D712}_{v}^{\prime })}\mathop{\prod }_{w|v}Z_{w}(\unicode[STIX]{x1D712}_{w}^{\prime }),\end{eqnarray}$$
$$\begin{eqnarray}R_{r,v}^{\natural }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}^{\prime }\text{}^{\unicode[STIX]{x1D704}})=Z_{v}^{\circ }(\unicode[STIX]{x1D712}_{v}^{\prime }):=\frac{\unicode[STIX]{x1D701}_{F,v}(2)L(1,\unicode[STIX]{x1D702}_{v})^{2}}{L(1/2,\unicode[STIX]{x1D70E}_{E,v}^{\unicode[STIX]{x1D704}},\unicode[STIX]{x1D712}_{v}^{\prime })}\mathop{\prod }_{w|v}Z_{w}(\unicode[STIX]{x1D712}_{w}^{\prime }),\end{eqnarray}$$
with
 $Z_{w}(\unicode[STIX]{x1D712}_{w}^{\prime })$
as in Lemma A.1.1.
$Z_{w}(\unicode[STIX]{x1D712}_{w}^{\prime })$
as in Lemma A.1.1.
Proof. We omit the subscripts
![]() $v$
and the embedding
$v$
and the embedding
![]() $\unicode[STIX]{x1D704}$
in the calculations which follow. By definition, we need to show that the integral
$\unicode[STIX]{x1D704}$
in the calculations which follow. By definition, we need to show that the integral
![]() $R_{r,v}^{\circ }$
of Proposition 3.5.1 equals
$R_{r,v}^{\circ }$
of Proposition 3.5.1 equals
 $$\begin{eqnarray}R_{r,v}^{\circ }=R_{r}^{\circ }(W,\unicode[STIX]{x1D719},\unicode[STIX]{x1D712}^{\prime })=|D|^{1/2}|d|^{2}L(1,\unicode[STIX]{x1D702})\mathop{\prod }_{w|v}Z_{w}(\unicode[STIX]{x1D712}_{w}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}R_{r,v}^{\circ }=R_{r}^{\circ }(W,\unicode[STIX]{x1D719},\unicode[STIX]{x1D712}^{\prime })=|D|^{1/2}|d|^{2}L(1,\unicode[STIX]{x1D702})\mathop{\prod }_{w|v}Z_{w}(\unicode[STIX]{x1D712}_{w}^{\prime }).\end{eqnarray}$$
Note that the assertion in the case of Assumption 6.2.2 is implied by the assertion in the case of Assumption 6.2.1 by (6.2.1), so we will place ourselves in the latter situation.
By the decomposition of Lemma A.2.1, and observing that
![]() $\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{F},r}$
vanishes on
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{F},r}$
vanishes on
 $K-K_{0}(\unicode[STIX]{x1D71B}^{r})$
, we have
$K-K_{0}(\unicode[STIX]{x1D71B}^{r})$
, we have
 $$\begin{eqnarray}\displaystyle R_{r,v}^{\circ } & = & \displaystyle \unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}\int _{F^{\times }}W_{-1}((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!))\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{F},r}((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!))\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{T(F)}\unicode[STIX]{x1D712}^{\prime }(t)\int _{P(\unicode[STIX]{x1D71B}^{r})\backslash K_{1}^{1}(\unicode[STIX]{x1D71B}^{r})}|y|r(kw_{r}^{-1})\unicode[STIX]{x1D719}(yt^{-1},y^{-1}q(t))\,dk\,d^{\times }t\,\frac{d^{\times }y}{|y|},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R_{r,v}^{\circ } & = & \displaystyle \unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}\int _{F^{\times }}W_{-1}((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!))\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D712}_{F},r}((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!))\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{T(F)}\unicode[STIX]{x1D712}^{\prime }(t)\int _{P(\unicode[STIX]{x1D71B}^{r})\backslash K_{1}^{1}(\unicode[STIX]{x1D71B}^{r})}|y|r(kw_{r}^{-1})\unicode[STIX]{x1D719}(yt^{-1},y^{-1}q(t))\,dk\,d^{\times }t\,\frac{d^{\times }y}{|y|},\nonumber\end{eqnarray}$$
where
 $P(\unicode[STIX]{x1D71B}^{r})=P\cap K_{1}^{1}(\unicode[STIX]{x1D71B}^{r})$
(recall that
$P(\unicode[STIX]{x1D71B}^{r})=P\cap K_{1}^{1}(\unicode[STIX]{x1D71B}^{r})$
(recall that
 $P=NZA$
). Here we have preferred to denote by
$P=NZA$
). Here we have preferred to denote by
![]() $d^{\times }t$
the standard Haar measure on
$d^{\times }t$
the standard Haar measure on
 $T(F_{v})=E_{v}^{\times }$
; later
$T(F_{v})=E_{v}^{\times }$
; later
![]() $dt$
will denote the additive measure on
$dt$
will denote the additive measure on
![]() $E_{v}$
.
$E_{v}$
.
Changing variables
 $k^{\prime }=w_{r}kw_{r}^{-1}$
, we observe that by Lemma 3.1.1 the group
$k^{\prime }=w_{r}kw_{r}^{-1}$
, we observe that by Lemma 3.1.1 the group
 $K_{1}^{1}(\unicode[STIX]{x1D71B}^{r})$
acts trivially for sufficiently large
$K_{1}^{1}(\unicode[STIX]{x1D71B}^{r})$
acts trivially for sufficiently large
![]() $r$
. Then we can insert
$r$
. Then we can insert
 $$\begin{eqnarray}W_{-1}((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!))=\mathbf{1}_{\mathscr{O}_{F}-\{0\}}(y)|y|\unicode[STIX]{x1D6FC}(y)\end{eqnarray}$$
$$\begin{eqnarray}W_{-1}((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!))=\mathbf{1}_{\mathscr{O}_{F}-\{0\}}(y)|y|\unicode[STIX]{x1D6FC}(y)\end{eqnarray}$$
and
 $$\begin{eqnarray}r(w_{r}^{-1})\unicode[STIX]{x1D719}(x,u)=|\unicode[STIX]{x1D71B}^{-r}|\unicode[STIX]{x1D713}_{E,U}(ux_{1})\mathbf{1}_{\mathscr{O}_{\mathbf{V}_{2}}}(x_{2})\unicode[STIX]{x1D6FF}_{q(U)}(\unicode[STIX]{x1D71B}^{r}u),\end{eqnarray}$$
$$\begin{eqnarray}r(w_{r}^{-1})\unicode[STIX]{x1D719}(x,u)=|\unicode[STIX]{x1D71B}^{-r}|\unicode[STIX]{x1D713}_{E,U}(ux_{1})\mathbf{1}_{\mathscr{O}_{\mathbf{V}_{2}}}(x_{2})\unicode[STIX]{x1D6FF}_{q(U)}(\unicode[STIX]{x1D71B}^{r}u),\end{eqnarray}$$
where
 $\unicode[STIX]{x1D713}_{E,U}=r(\operatorname{vol}(U)^{-1}\mathbf{1}_{U})\unicode[STIX]{x1D713}_{E}$
for the extension of
$\unicode[STIX]{x1D713}_{E,U}=r(\operatorname{vol}(U)^{-1}\mathbf{1}_{U})\unicode[STIX]{x1D713}_{E}$
for the extension of
![]() $r$
to functions on
$r$
to functions on
![]() $K$
(so that
$K$
(so that
![]() $\unicode[STIX]{x1D713}_{E,U}$
is the finest
$\unicode[STIX]{x1D713}_{E,U}$
is the finest
![]() $U$
-invariant approximation to
$U$
-invariant approximation to
![]() $\unicode[STIX]{x1D713}_{E}$
). We obtain
$\unicode[STIX]{x1D713}_{E}$
). We obtain
 $$\begin{eqnarray}R_{r,v}^{\circ }=\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}|d|^{1/2}\unicode[STIX]{x1D701}_{F,v}(1)^{-1}\int _{\mathscr{O}_{F}-\{0\}}|y|\unicode[STIX]{x1D6FC}(y)\int _{T(F)}\unicode[STIX]{x1D712}^{\prime }(t)\unicode[STIX]{x1D713}_{E,U}(t)\unicode[STIX]{x1D6FF}_{q(U)}(\unicode[STIX]{x1D71B}^{r}y^{-1}q(t))\,dt\,d^{\times }y,\end{eqnarray}$$
$$\begin{eqnarray}R_{r,v}^{\circ }=\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}|d|^{1/2}\unicode[STIX]{x1D701}_{F,v}(1)^{-1}\int _{\mathscr{O}_{F}-\{0\}}|y|\unicode[STIX]{x1D6FC}(y)\int _{T(F)}\unicode[STIX]{x1D712}^{\prime }(t)\unicode[STIX]{x1D713}_{E,U}(t)\unicode[STIX]{x1D6FF}_{q(U)}(\unicode[STIX]{x1D71B}^{r}y^{-1}q(t))\,dt\,d^{\times }y,\end{eqnarray}$$
where
 $|d|^{1/2}\unicode[STIX]{x1D701}_{F,v}(1)^{-1}$
appears as
$|d|^{1/2}\unicode[STIX]{x1D701}_{F,v}(1)^{-1}$
appears as
 $\operatorname{vol}(P(\unicode[STIX]{x1D71B}^{r})\backslash K_{1}^{1}(\unicode[STIX]{x1D71B}^{r}))|\unicode[STIX]{x1D71B}|^{-r}$
. We get
$\operatorname{vol}(P(\unicode[STIX]{x1D71B}^{r})\backslash K_{1}^{1}(\unicode[STIX]{x1D71B}^{r}))|\unicode[STIX]{x1D71B}|^{-r}$
. We get
 $$\begin{eqnarray}R_{r,v}^{\circ }=|d|\unicode[STIX]{x1D701}_{F,v}(1)^{-1}\int _{v(q(t))\geqslant -r}|q(t)|\unicode[STIX]{x1D6FC}(q(t))\unicode[STIX]{x1D712}^{\prime }(t)\unicode[STIX]{x1D713}_{E}(t)\,d^{\times }t.\end{eqnarray}$$
$$\begin{eqnarray}R_{r,v}^{\circ }=|d|\unicode[STIX]{x1D701}_{F,v}(1)^{-1}\int _{v(q(t))\geqslant -r}|q(t)|\unicode[STIX]{x1D6FC}(q(t))\unicode[STIX]{x1D712}^{\prime }(t)\unicode[STIX]{x1D713}_{E}(t)\,d^{\times }t.\end{eqnarray}$$
If
![]() $r$
is sufficiently large, the domain of integration can be replaced with all of
$r$
is sufficiently large, the domain of integration can be replaced with all of
![]() $T(F)$
. Switching to the additive measure, and using the isomorphism
$T(F)$
. Switching to the additive measure, and using the isomorphism
 $E_{v}^{\times }=E_{w}^{\times }\times E_{w^{\ast }}^{\times }$
in the split case, the integral equals
$E_{v}^{\times }=E_{w}^{\times }\times E_{w^{\ast }}^{\times }$
in the split case, the integral equals
 $$\begin{eqnarray}R_{r,v}^{\circ }=|d|L(1,\unicode[STIX]{x1D702})\int _{E_{v}^{\times }}\unicode[STIX]{x1D6FC}(q(t))\unicode[STIX]{x1D712}^{\prime }(t)\unicode[STIX]{x1D713}_{E}(t)\,dt=|D|^{1/2}|d|^{2}L(1,\unicode[STIX]{x1D702})\mathop{\prod }_{w|v}Z_{w}(\unicode[STIX]{x1D712}_{w}^{\prime }),\end{eqnarray}$$
$$\begin{eqnarray}R_{r,v}^{\circ }=|d|L(1,\unicode[STIX]{x1D702})\int _{E_{v}^{\times }}\unicode[STIX]{x1D6FC}(q(t))\unicode[STIX]{x1D712}^{\prime }(t)\unicode[STIX]{x1D713}_{E}(t)\,dt=|D|^{1/2}|d|^{2}L(1,\unicode[STIX]{x1D702})\mathop{\prod }_{w|v}Z_{w}(\unicode[STIX]{x1D712}_{w}^{\prime }),\end{eqnarray}$$
as desired. ◻
A.3 Toric period
We compare the normalised toric periods with the interpolation factor.
Proposition A.3.1. Suppose that
![]() $v|p$
splits in
$v|p$
splits in
![]() $E$
. Then, for any finite-order character
$E$
. Then, for any finite-order character
 $\unicode[STIX]{x1D712}\in \mathscr{Y}^{\text{l.c.}}$
, we have
$\unicode[STIX]{x1D712}\in \mathscr{Y}^{\text{l.c.}}$
, we have
 $$\begin{eqnarray}Q_{v}(\unicode[STIX]{x1D703}_{v}(W_{v},\unicode[STIX]{x1D6FC}_{v}^{-r_{v}}w_{r,v}^{-1}\unicode[STIX]{x1D719}_{v}),\unicode[STIX]{x1D712}_{v})=L(1,\unicode[STIX]{x1D702}_{v})^{-1}\cdot Z_{v}^{\circ }(\unicode[STIX]{x1D6FC}_{v},\unicode[STIX]{x1D712}_{v})\end{eqnarray}$$
$$\begin{eqnarray}Q_{v}(\unicode[STIX]{x1D703}_{v}(W_{v},\unicode[STIX]{x1D6FC}_{v}^{-r_{v}}w_{r,v}^{-1}\unicode[STIX]{x1D719}_{v}),\unicode[STIX]{x1D712}_{v})=L(1,\unicode[STIX]{x1D702}_{v})^{-1}\cdot Z_{v}^{\circ }(\unicode[STIX]{x1D6FC}_{v},\unicode[STIX]{x1D712}_{v})\end{eqnarray}$$
for any
![]() $\unicode[STIX]{x1D719}_{v}$
as in Proposition A.2.2 and any sufficiently large
$\unicode[STIX]{x1D719}_{v}$
as in Proposition A.2.2 and any sufficiently large
![]() $r_{v}\geqslant 1$
.
$r_{v}\geqslant 1$
.
For consistency with the proof of Proposition A.2.2, in the proof we will denote by
![]() $d^{\times }t$
the Haar measure on
$d^{\times }t$
the Haar measure on
![]() $T(F)$
denoted by
$T(F)$
denoted by
![]() $dt$
in the rest of the paper.
$dt$
in the rest of the paper.
Proof. By the definitions and Proposition A.2.2, it suffices to show that for any
 $\unicode[STIX]{x1D712}\in \mathscr{Y}^{\text{l.c.}}(\mathbf{C})$
, we have
$\unicode[STIX]{x1D712}\in \mathscr{Y}^{\text{l.c.}}(\mathbf{C})$
, we have
 $$\begin{eqnarray}|d|_{v}^{3/2}Q_{v}^{\sharp }(\unicode[STIX]{x1D703}_{v}(W_{v},\unicode[STIX]{x1D6FC}_{v}^{-r_{v}}w_{r,v}^{-1}\unicode[STIX]{x1D719}_{v}),\unicode[STIX]{x1D712}_{v})=L(1,\unicode[STIX]{x1D702}_{v})^{-1}\cdot R_{r,v}^{\circ }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}),\end{eqnarray}$$
$$\begin{eqnarray}|d|_{v}^{3/2}Q_{v}^{\sharp }(\unicode[STIX]{x1D703}_{v}(W_{v},\unicode[STIX]{x1D6FC}_{v}^{-r_{v}}w_{r,v}^{-1}\unicode[STIX]{x1D719}_{v}),\unicode[STIX]{x1D712}_{v})=L(1,\unicode[STIX]{x1D702}_{v})^{-1}\cdot R_{r,v}^{\circ }(W_{v},\unicode[STIX]{x1D719}_{v},\unicode[STIX]{x1D712}_{v}),\end{eqnarray}$$
where
![]() $Q_{v}^{\sharp }$
is the toric integral of (5.1.5).
$Q_{v}^{\sharp }$
is the toric integral of (5.1.5).
By the Shimizu lifting (Lemma 5.1.1) and Lemma A.2.1, we can write
 $$\begin{eqnarray}Q_{v}^{\sharp }:=|d|_{v}^{3/2}Q_{v}(\unicode[STIX]{x1D703}_{v}(W_{v},\unicode[STIX]{x1D6FC}_{v}^{-r_{v}}w_{r,v}^{-1}\unicode[STIX]{x1D719}_{v}),\unicode[STIX]{x1D712}_{v})=Q_{v}^{\sharp \,(0,1)}+\mathop{\sum }_{i=1}^{r}\mathop{\sum }_{c\in (\mathscr{O}_{F}/\unicode[STIX]{x1D71B}^{i})^{\times }}Q_{v}^{\sharp \,(i,c)},\end{eqnarray}$$
$$\begin{eqnarray}Q_{v}^{\sharp }:=|d|_{v}^{3/2}Q_{v}(\unicode[STIX]{x1D703}_{v}(W_{v},\unicode[STIX]{x1D6FC}_{v}^{-r_{v}}w_{r,v}^{-1}\unicode[STIX]{x1D719}_{v}),\unicode[STIX]{x1D712}_{v})=Q_{v}^{\sharp \,(0,1)}+\mathop{\sum }_{i=1}^{r}\mathop{\sum }_{c\in (\mathscr{O}_{F}/\unicode[STIX]{x1D71B}^{i})^{\times }}Q_{v}^{\sharp \,(i,c)},\end{eqnarray}$$
where, for each
![]() $(i,c)$
, omitting the subscripts
$(i,c)$
, omitting the subscripts
![]() $v$
,
$v$
,
 $$\begin{eqnarray}\displaystyle Q_{v}^{\sharp \,(i,c)} & := & \displaystyle \unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}\int _{F^{\times }}W_{-1}((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!)n^{-}(c\unicode[STIX]{x1D71B}^{r-i}))\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{T(F)}\unicode[STIX]{x1D712}^{\prime }(t)\int _{P(\unicode[STIX]{x1D71B}^{r})\backslash K_{1}^{1}(\unicode[STIX]{x1D71B}^{r})}|y|r(n^{-}(c\unicode[STIX]{x1D71B}^{r-i})kw_{r}^{-1})\unicode[STIX]{x1D719}(yt^{-1},y^{-1}q(t))\,dk\,d^{\times }t\,\frac{d^{\times }y}{|y|}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Q_{v}^{\sharp \,(i,c)} & := & \displaystyle \unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}\int _{F^{\times }}W_{-1}((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!)n^{-}(c\unicode[STIX]{x1D71B}^{r-i}))\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{T(F)}\unicode[STIX]{x1D712}^{\prime }(t)\int _{P(\unicode[STIX]{x1D71B}^{r})\backslash K_{1}^{1}(\unicode[STIX]{x1D71B}^{r})}|y|r(n^{-}(c\unicode[STIX]{x1D71B}^{r-i})kw_{r}^{-1})\unicode[STIX]{x1D719}(yt^{-1},y^{-1}q(t))\,dk\,d^{\times }t\,\frac{d^{\times }y}{|y|}.\nonumber\end{eqnarray}$$
Note that
 $Q_{v}^{\sharp \,(0,1)}=R_{v}^{\circ }$
, where
$Q_{v}^{\sharp \,(0,1)}=R_{v}^{\circ }$
, where
![]() $R_{v}^{\circ }$
is as in the previous proposition, since
$R_{v}^{\circ }$
is as in the previous proposition, since
 $n^{-}(\unicode[STIX]{x1D71B}^{r})\in K_{1}^{1}(\unicode[STIX]{x1D71B}^{r})$
. We will compute the other terms.
$n^{-}(\unicode[STIX]{x1D71B}^{r})\in K_{1}^{1}(\unicode[STIX]{x1D71B}^{r})$
. We will compute the other terms.
We have
 $(\!\begin{smallmatrix}1 & \\ c\unicode[STIX]{x1D71B}^{r-i} & 1\end{smallmatrix}\!)w_{r}^{-1}=w_{r}^{-1}(\!\begin{smallmatrix}1 & -c\unicode[STIX]{x1D71B}^{-i}\\ & 1\end{smallmatrix}\!)$
and, when
$(\!\begin{smallmatrix}1 & \\ c\unicode[STIX]{x1D71B}^{r-i} & 1\end{smallmatrix}\!)w_{r}^{-1}=w_{r}^{-1}(\!\begin{smallmatrix}1 & -c\unicode[STIX]{x1D71B}^{-i}\\ & 1\end{smallmatrix}\!)$
and, when
 $x=(x_{1},x_{2})$
with
$x=(x_{1},x_{2})$
with
![]() $x_{2}=0$
,
$x_{2}=0$
,
 $$\begin{eqnarray}\displaystyle r(n^{-}(c\unicode[STIX]{x1D71B}^{r-i})w_{r}^{-1})\unicode[STIX]{x1D719}(x,u) & = & \displaystyle |\unicode[STIX]{x1D71B}^{-r}|\int _{E}\unicode[STIX]{x1D713}_{E}(ux_{1}\unicode[STIX]{x1D709}_{1})\unicode[STIX]{x1D713}(-uc\unicode[STIX]{x1D71B}^{r-i}q(\unicode[STIX]{x1D709}_{1}))\unicode[STIX]{x1D6FF}_{U}(\unicode[STIX]{x1D709}_{1})\unicode[STIX]{x1D6FF}_{q(U)}(\unicode[STIX]{x1D71B}^{r}u)\,d\unicode[STIX]{x1D709}_{1}\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\mathscr{O}_{\mathbf{V}_{2}}}\unicode[STIX]{x1D713}(-uc\unicode[STIX]{x1D71B}^{r-i}q(\unicode[STIX]{x1D709}_{2}))\unicode[STIX]{x1D6FF}_{q(U)}(\unicode[STIX]{x1D71B}^{r}u)\,d\unicode[STIX]{x1D709}_{2}\nonumber\\ \displaystyle & = & \displaystyle |\unicode[STIX]{x1D71B}|^{i-r}\unicode[STIX]{x1D713}_{E,U}(ux_{1})\unicode[STIX]{x1D713}_{q(U)}(-c\unicode[STIX]{x1D71B}^{-i})\unicode[STIX]{x1D6FF}_{q(U)}(\unicode[STIX]{x1D71B}^{r}u).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle r(n^{-}(c\unicode[STIX]{x1D71B}^{r-i})w_{r}^{-1})\unicode[STIX]{x1D719}(x,u) & = & \displaystyle |\unicode[STIX]{x1D71B}^{-r}|\int _{E}\unicode[STIX]{x1D713}_{E}(ux_{1}\unicode[STIX]{x1D709}_{1})\unicode[STIX]{x1D713}(-uc\unicode[STIX]{x1D71B}^{r-i}q(\unicode[STIX]{x1D709}_{1}))\unicode[STIX]{x1D6FF}_{U}(\unicode[STIX]{x1D709}_{1})\unicode[STIX]{x1D6FF}_{q(U)}(\unicode[STIX]{x1D71B}^{r}u)\,d\unicode[STIX]{x1D709}_{1}\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{\mathscr{O}_{\mathbf{V}_{2}}}\unicode[STIX]{x1D713}(-uc\unicode[STIX]{x1D71B}^{r-i}q(\unicode[STIX]{x1D709}_{2}))\unicode[STIX]{x1D6FF}_{q(U)}(\unicode[STIX]{x1D71B}^{r}u)\,d\unicode[STIX]{x1D709}_{2}\nonumber\\ \displaystyle & = & \displaystyle |\unicode[STIX]{x1D71B}|^{i-r}\unicode[STIX]{x1D713}_{E,U}(ux_{1})\unicode[STIX]{x1D713}_{q(U)}(-c\unicode[STIX]{x1D71B}^{-i})\unicode[STIX]{x1D6FF}_{q(U)}(\unicode[STIX]{x1D71B}^{r}u).\nonumber\end{eqnarray}$$
Inserting this, we obtain
 $$\begin{eqnarray}\displaystyle Q_{v}^{\sharp \,(i,c)} & = & \displaystyle |\unicode[STIX]{x1D71B}|^{i}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}|d|^{1/2}\unicode[STIX]{x1D701}_{F,v}(1)^{-1}\int _{F^{\times }}W((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!)n^{-}(c\unicode[STIX]{x1D71B}^{r-i}))\int _{T(F)}\unicode[STIX]{x1D712}(t)\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D713}_{E,U}(t)\unicode[STIX]{x1D713}_{q(U)}(-c\unicode[STIX]{x1D71B}^{-i})\unicode[STIX]{x1D6FF}_{q(U)}(\unicode[STIX]{x1D71B}^{r}y^{-1}q(t))\,d^{\times }t\,d^{\times }y.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Q_{v}^{\sharp \,(i,c)} & = & \displaystyle |\unicode[STIX]{x1D71B}|^{i}\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D71B})^{-r}|d|^{1/2}\unicode[STIX]{x1D701}_{F,v}(1)^{-1}\int _{F^{\times }}W((\!\begin{smallmatrix}y & \\ & 1\end{smallmatrix}\!)n^{-}(c\unicode[STIX]{x1D71B}^{r-i}))\int _{T(F)}\unicode[STIX]{x1D712}(t)\nonumber\\ \displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D713}_{E,U}(t)\unicode[STIX]{x1D713}_{q(U)}(-c\unicode[STIX]{x1D71B}^{-i})\unicode[STIX]{x1D6FF}_{q(U)}(\unicode[STIX]{x1D71B}^{r}y^{-1}q(t))\,d^{\times }t\,d^{\times }y.\nonumber\end{eqnarray}$$
We have already noted that
 $Q_{v}^{\sharp (0,1)}=R_{v}^{\circ }$
. For
$Q_{v}^{\sharp (0,1)}=R_{v}^{\circ }$
. For
![]() $i=1$
, if
$i=1$
, if
![]() $r$
is sufficiently large, then
$r$
is sufficiently large, then
![]() $W$
is still invariant under
$W$
is still invariant under
 $K_{1}^{1}(\unicode[STIX]{x1D71B}^{r-1})$
; then
$K_{1}^{1}(\unicode[STIX]{x1D71B}^{r-1})$
; then
 $\sum _{c}Q_{v}^{\sharp (1,c)}$
equals
$\sum _{c}Q_{v}^{\sharp (1,c)}$
equals
![]() $C\cdot R_{v}^{\circ }$
with
$C\cdot R_{v}^{\circ }$
with
 $C=|\unicode[STIX]{x1D71B}|\sum _{c\in (\mathscr{O}/\unicode[STIX]{x1D71B})^{\times }}\unicode[STIX]{x1D713}_{q(U)}(-c\unicode[STIX]{x1D71B}^{-1})=-|\unicode[STIX]{x1D71B}|$
.
$C=|\unicode[STIX]{x1D71B}|\sum _{c\in (\mathscr{O}/\unicode[STIX]{x1D71B})^{\times }}\unicode[STIX]{x1D713}_{q(U)}(-c\unicode[STIX]{x1D71B}^{-1})=-|\unicode[STIX]{x1D71B}|$
.
Finally, we claim that for each
![]() $i\geqslant 2$
,
$i\geqslant 2$
,
 $\sum _{c}Q_{v}^{\sharp (i,c)}=0$
. Indeed, let
$\sum _{c}Q_{v}^{\sharp (i,c)}=0$
. Indeed, let
 $q(U)=1+\unicode[STIX]{x1D71B}^{n}\mathscr{O}_{F,v}$
. If
$q(U)=1+\unicode[STIX]{x1D71B}^{n}\mathscr{O}_{F,v}$
. If
 $i\geqslant n+1$
, then
$i\geqslant n+1$
, then
 $\unicode[STIX]{x1D713}_{q(U)}(-c\unicode[STIX]{x1D71B}^{-i})=0$
; if
$\unicode[STIX]{x1D713}_{q(U)}(-c\unicode[STIX]{x1D71B}^{-i})=0$
; if
![]() $i\leqslant n$
, then if
$i\leqslant n$
, then if
![]() $r$
is sufficiently large
$r$
is sufficiently large
![]() $W$
is still invariant under
$W$
is still invariant under
 $K_{1}^{1}(\unicode[STIX]{x1D71B}^{r-i})\subset K_{1}^{1}(\unicode[STIX]{x1D71B}^{r-n})$
, and summing the only terms depending on
$K_{1}^{1}(\unicode[STIX]{x1D71B}^{r-i})\subset K_{1}^{1}(\unicode[STIX]{x1D71B}^{r-n})$
, and summing the only terms depending on
![]() $c$
produces a factor
$c$
produces a factor
 $\sum _{c\in (\mathscr{O}/\unicode[STIX]{x1D71B}^{i})^{\times }}\unicode[STIX]{x1D713}(c\unicode[STIX]{x1D71B}^{-i})=0$
.
$\sum _{c\in (\mathscr{O}/\unicode[STIX]{x1D71B}^{i})^{\times }}\unicode[STIX]{x1D713}(c\unicode[STIX]{x1D71B}^{-i})=0$
.
Summing up, we have
 $$\begin{eqnarray}Q_{v}^{\sharp }=Q_{v}^{\sharp (0,1)}+\mathop{\sum }_{c\in (\mathscr{O}_{F}/\unicode[STIX]{x1D71B}_{v})^{\times }}Q_{v}^{\sharp (1,c)}=(1-|\unicode[STIX]{x1D71B}|)R_{r,v}^{\circ }=L(1,\unicode[STIX]{x1D702}_{v})^{-1}\cdot R_{r,v}^{\circ },\end{eqnarray}$$
$$\begin{eqnarray}Q_{v}^{\sharp }=Q_{v}^{\sharp (0,1)}+\mathop{\sum }_{c\in (\mathscr{O}_{F}/\unicode[STIX]{x1D71B}_{v})^{\times }}Q_{v}^{\sharp (1,c)}=(1-|\unicode[STIX]{x1D71B}|)R_{r,v}^{\circ }=L(1,\unicode[STIX]{x1D702}_{v})^{-1}\cdot R_{r,v}^{\circ },\end{eqnarray}$$
as desired. ◻
Question A.3.2. A comparison between Propositions 10.1.2 and A.3.1 suggests that the identity
 $$\begin{eqnarray}\lim _{r\rightarrow \infty }L(1,\unicode[STIX]{x1D702}_{v})\cdot \unicode[STIX]{x1D703}_{v}(W_{v},\unicode[STIX]{x1D6FC}_{v}^{-r}w_{r}^{-1}\unicode[STIX]{x1D719}_{v})=\unicode[STIX]{x1D701}_{F,v}(2)\cdot f_{\unicode[STIX]{x1D6FC},v}^{+}\otimes f_{\unicode[STIX]{x1D6FC},v}^{-}\end{eqnarray}$$
$$\begin{eqnarray}\lim _{r\rightarrow \infty }L(1,\unicode[STIX]{x1D702}_{v})\cdot \unicode[STIX]{x1D703}_{v}(W_{v},\unicode[STIX]{x1D6FC}_{v}^{-r}w_{r}^{-1}\unicode[STIX]{x1D719}_{v})=\unicode[STIX]{x1D701}_{F,v}(2)\cdot f_{\unicode[STIX]{x1D6FC},v}^{+}\otimes f_{\unicode[STIX]{x1D6FC},v}^{-}\end{eqnarray}$$
might hold in
 $\mathop{\varprojlim }\nolimits_{V}(\unicode[STIX]{x1D70B}_{v}^{+})^{V}\otimes \mathop{\varprojlim }\nolimits_{V}(\unicode[STIX]{x1D70B}_{v}^{-})^{V}$
(with notation as in Lemma 10.1.1). Is this the case?
$\mathop{\varprojlim }\nolimits_{V}(\unicode[STIX]{x1D70B}_{v}^{+})^{V}\otimes \mathop{\varprojlim }\nolimits_{V}(\unicode[STIX]{x1D70B}_{v}^{-})^{V}$
(with notation as in Lemma 10.1.1). Is this the case?