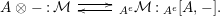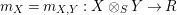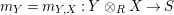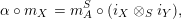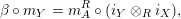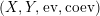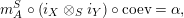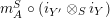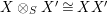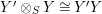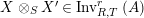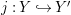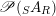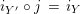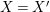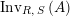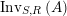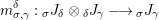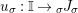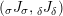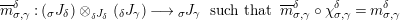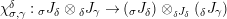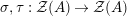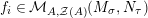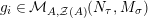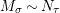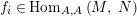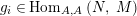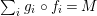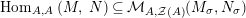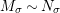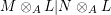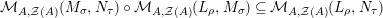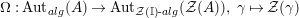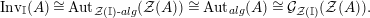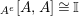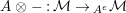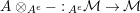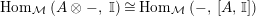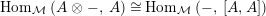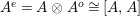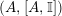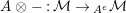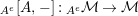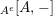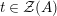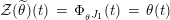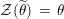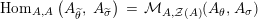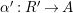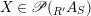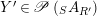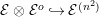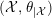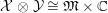Introduction
0.1 Motivation and overview
The notion of what is nowadays known as an Azumaya algebra was first formulated by Azumaya in [Reference Azumaya4, page 128] where he introduced the Brauer group of a local ring [Reference Azumaya4, page 138], generalizing by this the classical notion of Brauer group of a field which was extremely important in developing the arithmetic study of fields.
For a general commutative base ring, this notion was recovered later on by Auslander and Goldman in [Reference Auslander and Goldman3], where several new properties of Azumaya algebras were displayed; see for instance [Reference Auslander and Goldman3, Section 3]. In [Reference Auslander2], Auslander extended this notion to ringed spaces, in the case of a topological space endowed with its structural sheaf of rings of continuous complex valued functions; Azumaya algebrasFootnote
1
are interpreted as locally trivial algebra bundles whose fibers are central simple complex algebras (that is, square matrixes over complex numbers). As was shown by Grothendieck in [Reference Grothendieck19, 1.1], the set of isomorphic classes of Azumaya algebras with constant rank
![]() $n^{2}$
over a topological space, is identified with the set of isomorphic classes of
$n^{2}$
over a topological space, is identified with the set of isomorphic classes of
![]() $GP(n)$
-principal bundles with base this space. Here
$GP(n)$
-principal bundles with base this space. Here
![]() $GP(n)$
is the projective group with
$GP(n)$
is the projective group with
![]() $n$
variables over the complex numbers. By using the classifying space of this group, a homotopic interpretation of these Azumaya algebras over
$n$
variables over the complex numbers. By using the classifying space of this group, a homotopic interpretation of these Azumaya algebras over
![]() $CW$
-complexes, is also possible [Reference Grothendieck19, 1.1].
$CW$
-complexes, is also possible [Reference Grothendieck19, 1.1].
Naturally, with a compact base space, the global sections of an Azumaya algebra bundle give rise to an Azumaya algebra over the ring of continuous complex valued functions (the base ring). In this way, those Azumaya algebra bundles of rank
![]() $n^{2}$
lead to Azumaya algebras which are finitely generated and projective of locally constant rank
$n^{2}$
lead to Azumaya algebras which are finitely generated and projective of locally constant rank
![]() $n^{2}$
as modules over the base ring. By the classification theorem [Reference Knus and Ojanguren18, Théorème 6.6, Corollaire 6.7], a given Azumaya algebra is of this form if and only if it is a twisted form [Reference Knus and Ojanguren18, (c) page 29] of an
$n^{2}$
as modules over the base ring. By the classification theorem [Reference Knus and Ojanguren18, Théorème 6.6, Corollaire 6.7], a given Azumaya algebra is of this form if and only if it is a twisted form [Reference Knus and Ojanguren18, (c) page 29] of an
![]() $n$
-square matrixes algebra with coefficients in the base ring. The latter condition can be interpreted in the case of smooth manifoldsFootnote
2
, by saying that there is a surjective submersion to the base manifold such that the induced bundle of any Azumaya algebra bundle of rank
$n$
-square matrixes algebra with coefficients in the base ring. The latter condition can be interpreted in the case of smooth manifoldsFootnote
2
, by saying that there is a surjective submersion to the base manifold such that the induced bundle of any Azumaya algebra bundle of rank
![]() $n^{2}$
is a trivial bundle.
$n^{2}$
is a trivial bundle.
There is no doubt then that Azumaya algebras are extremely rich objects which, along the last decades, have attracted the attention of several mathematicians from different areas. Unfortunately, we have the feeling that Azumaya algebras have not been deeply investigated in the general setting of abelian monoidal categories. However, the concept of an Azumaya monoid in symmetric monoidal categories has been earlier introduced in the literature, [Reference Fisher-Palmquist11, Reference Pareigis26, Reference Vitale30].
The main motivation of this paper is to try to fulfil this lack of investigation by introducing and studying Miyashita action on Azumaya monoids in abelian symmetric monoidal categories. Although the results displayed here can be applied to other situations, we limit ourselves to a concrete application concerning the category of comodules over commutative (flat) Hopf algebroids which up to our knowledge seems not to have been treated before.
0.2 Description of the main results
In the first part of this paper, that is Sections 1 and 2, we introduce and study Miyashita actions in monoidal categories. To be precise, let
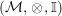 $({\mathcal{M}},\otimes _{},\mathbb{I})$
be a Penrose abelian locally small monoidal category whose tensor products
$({\mathcal{M}},\otimes _{},\mathbb{I})$
be a Penrose abelian locally small monoidal category whose tensor products
![]() $\otimes _{}$
are right exact functors (on both arguments), and consider two morphisms of monoids
$\otimes _{}$
are right exact functors (on both arguments), and consider two morphisms of monoids
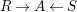 $R\rightarrow A\leftarrow S$
which are monomorphisms in
$R\rightarrow A\leftarrow S$
which are monomorphisms in
![]() ${\mathcal{M}}$
. We first consider the set
${\mathcal{M}}$
. We first consider the set
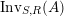 $\text{Inv}_{S,R}(A)$
which consists of two-sided invertible
$\text{Inv}_{S,R}(A)$
which consists of two-sided invertible
![]() $(R,S)$
-sub-bimodules of
$(R,S)$
-sub-bimodules of
![]() $A$
. These are isomorphic classes
$A$
. These are isomorphic classes
![]() $(X,i_{X})$
of
$(X,i_{X})$
of
![]() $(R,S)$
-sub-bimodules with monomorphism
$(R,S)$
-sub-bimodules with monomorphism
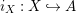 $i_{X}:X{\hookrightarrow}A$
such that there exists another sub-bimodule
$i_{X}:X{\hookrightarrow}A$
such that there exists another sub-bimodule
![]() $(Y,i_{Y})$
with compatible isomorphisms
$(Y,i_{Y})$
with compatible isomorphisms
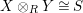 $X\otimes _{R}Y\cong S$
and
$X\otimes _{R}Y\cong S$
and
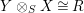 $Y\otimes _{S}X\cong R$
, each in the appropriate category of bimodules, which are defined via the multiplications of
$Y\otimes _{S}X\cong R$
, each in the appropriate category of bimodules, which are defined via the multiplications of
![]() $A$
with respect to
$A$
with respect to
![]() $R$
and
$R$
and
![]() $S$
(the pair
$S$
(the pair
![]() $(X,Y)$
with the two isomorphisms is also referred to as a two-sided dualizable datum). Section 1 is entirely devoted to the properties of these data which will be used in the proofs of results stated in the forthcoming sections. It is noteworthy to mention here that the set
$(X,Y)$
with the two isomorphisms is also referred to as a two-sided dualizable datum). Section 1 is entirely devoted to the properties of these data which will be used in the proofs of results stated in the forthcoming sections. It is noteworthy to mention here that the set
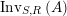 $\text{Inv}_{S,R}\left(A\right)$
is quite different from the one already considered in the literature; see Remark 1.8 and Appendix A where this difference is made clearer.
$\text{Inv}_{S,R}\left(A\right)$
is quite different from the one already considered in the literature; see Remark 1.8 and Appendix A where this difference is made clearer.
Our goal in Section 2 is to construct the map
![]() $\unicode[STIX]{x1D6F7}$
:
$\unicode[STIX]{x1D6F7}$
:
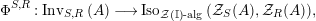 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}^{S,R}:\text{Inv}_{S,R}\left(A\right)\longrightarrow \text{Iso}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}\left({\mathcal{Z}}_{S}(A),{\mathcal{Z}}_{R}(A)\right)\!,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}^{S,R}:\text{Inv}_{S,R}\left(A\right)\longrightarrow \text{Iso}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}\left({\mathcal{Z}}_{S}(A),{\mathcal{Z}}_{R}(A)\right)\!,\end{eqnarray}$$
where
![]() ${\mathcal{Z}}$
,
${\mathcal{Z}}$
,
![]() ${\mathcal{Z}}_{R}$
and
${\mathcal{Z}}_{R}$
and
![]() ${\mathcal{Z}}_{S}$
are the functors
${\mathcal{Z}}_{S}$
are the functors
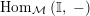 $\text{Hom}_{{\mathcal{M}}}\left(\mathbb{I},\,-\right)$
,
$\text{Hom}_{{\mathcal{M}}}\left(\mathbb{I},\,-\right)$
,
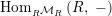 $\text{Hom}_{\text{}_{R}{\mathcal{M}}_{R}}\left(R,\,-\right)$
and
$\text{Hom}_{\text{}_{R}{\mathcal{M}}_{R}}\left(R,\,-\right)$
and
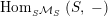 $\text{Hom}_{\text{}_{S}{\mathcal{M}}_{S}}\left(S,\,-\right)$
, respectively (here
$\text{Hom}_{\text{}_{S}{\mathcal{M}}_{S}}\left(S,\,-\right)$
, respectively (here
![]() $\text{}_{R}{\mathcal{M}}_{R}$
denotes the category of
$\text{}_{R}{\mathcal{M}}_{R}$
denotes the category of
![]() $R$
-bimodules). The codomain of
$R$
-bimodules). The codomain of
![]() $\unicode[STIX]{x1D6F7}^{S,R}$
is the set of
$\unicode[STIX]{x1D6F7}^{S,R}$
is the set of
![]() ${\mathcal{Z}}(\mathbb{I})$
-algebra isomorphisms between the invariant algebras
${\mathcal{Z}}(\mathbb{I})$
-algebra isomorphisms between the invariant algebras
![]() ${\mathcal{Z}}_{S}(A)$
and
${\mathcal{Z}}_{S}(A)$
and
![]() ${\mathcal{Z}}_{R}(A)$
. In particular, when
${\mathcal{Z}}_{R}(A)$
. In particular, when
![]() $R=S$
, we show in Proposition 2.3 that the morphism
$R=S$
, we show in Proposition 2.3 that the morphism
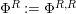 $\unicode[STIX]{x1D6F7}^{R}:=\unicode[STIX]{x1D6F7}^{R,R}$
factors as a composition of group homomorphisms:
$\unicode[STIX]{x1D6F7}^{R}:=\unicode[STIX]{x1D6F7}^{R,R}$
factors as a composition of group homomorphisms:
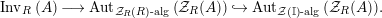 $$\begin{eqnarray}\text{Inv}_{R}\left(A\right)\longrightarrow \text{Aut}_{{\mathcal{Z}}_{R}(R)\text{-alg}}\left({\mathcal{Z}}_{R}(A)\right){\hookrightarrow}\text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}\left({\mathcal{Z}}_{R}(A)\right)\!.\end{eqnarray}$$
$$\begin{eqnarray}\text{Inv}_{R}\left(A\right)\longrightarrow \text{Aut}_{{\mathcal{Z}}_{R}(R)\text{-alg}}\left({\mathcal{Z}}_{R}(A)\right){\hookrightarrow}\text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}\left({\mathcal{Z}}_{R}(A)\right)\!.\end{eqnarray}$$
The morphism
![]() $\unicode[STIX]{x1D6F7}^{R}$
is known in the literature as Miyashita action. For
$\unicode[STIX]{x1D6F7}^{R}$
is known in the literature as Miyashita action. For
![]() $R=\mathbb{I}$
, we clearly have a morphism of groups
$R=\mathbb{I}$
, we clearly have a morphism of groups
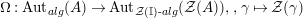 $\unicode[STIX]{x1D6FA}:\text{Aut}_{alg}(A)\rightarrow \text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-}alg}({\mathcal{Z}}(A)),,\unicode[STIX]{x1D6FE}\mapsto {\mathcal{Z}}(\unicode[STIX]{x1D6FE})$
, where
$\unicode[STIX]{x1D6FA}:\text{Aut}_{alg}(A)\rightarrow \text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-}alg}({\mathcal{Z}}(A)),,\unicode[STIX]{x1D6FE}\mapsto {\mathcal{Z}}(\unicode[STIX]{x1D6FE})$
, where
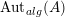 $\text{Aut}_{alg}(A)$
is the group of monoid automorphisms of
$\text{Aut}_{alg}(A)$
is the group of monoid automorphisms of
![]() $A$
.
$A$
.
The main aim of the second part of the paper, that is Sections 3 and 4, is to give conditions under which the map
![]() $\unicode[STIX]{x1D6F7}^{\mathbb{I}}$
, or some of its factors, becomes bijective. Explicitly in Theorem 3.4, we show that
$\unicode[STIX]{x1D6F7}^{\mathbb{I}}$
, or some of its factors, becomes bijective. Explicitly in Theorem 3.4, we show that
![]() $\unicode[STIX]{x1D6F7}^{\mathbb{I}}$
is injective when the base category
$\unicode[STIX]{x1D6F7}^{\mathbb{I}}$
is injective when the base category
![]() ${\mathcal{M}}$
is bicomplete and
${\mathcal{M}}$
is bicomplete and
![]() $\mathbb{I}$
is isomorphic to a specific submonoid of
$\mathbb{I}$
is isomorphic to a specific submonoid of
![]() $A$
. If we further assume that
$A$
. If we further assume that
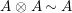 $A\otimes _{}A\sim A$
(i.e.,
$A\otimes _{}A\sim A$
(i.e.,
![]() $A$
and
$A$
and
![]() $A\otimes _{}A$
are direct summand of a product of finite copies of each other as
$A\otimes _{}A$
are direct summand of a product of finite copies of each other as
![]() $A$
-bimodules),
$A$
-bimodules),
![]() $\unicode[STIX]{x1D6FA}$
is surjective and the functor
$\unicode[STIX]{x1D6FA}$
is surjective and the functor
![]() $-\otimes _{}A$
is exact, then
$-\otimes _{}A$
is exact, then
![]() $\unicode[STIX]{x1D6F7}^{\mathbb{I}}$
comes out to be bijective; see Theorem 3.12 where other bijections were also established, when
$\unicode[STIX]{x1D6F7}^{\mathbb{I}}$
comes out to be bijective; see Theorem 3.12 where other bijections were also established, when
![]() ${\mathcal{Z}}$
is faithful (i.e., the unit object
${\mathcal{Z}}$
is faithful (i.e., the unit object
![]() $\mathbb{I}$
is a generator).
$\mathbb{I}$
is a generator).
In Section 4, we study the behavior of
![]() $\unicode[STIX]{x1D6F7}^{\mathbb{I}}$
in the case when
$\unicode[STIX]{x1D6F7}^{\mathbb{I}}$
in the case when
![]() ${\mathcal{M}}$
is also symmetric. In Proposition 4.1, we construct a morphism of groups
${\mathcal{M}}$
is also symmetric. In Proposition 4.1, we construct a morphism of groups
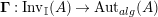 $\boldsymbol{\unicode[STIX]{x1D6E4}}:\text{Inv}_{\mathbb{I}}(A)\rightarrow \text{Aut}_{alg}(A)$
, and show that
$\boldsymbol{\unicode[STIX]{x1D6E4}}:\text{Inv}_{\mathbb{I}}(A)\rightarrow \text{Aut}_{alg}(A)$
, and show that
![]() $\unicode[STIX]{x1D6F7}^{\mathbb{I}}$
decomposes as
$\unicode[STIX]{x1D6F7}^{\mathbb{I}}$
decomposes as
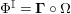 $\unicode[STIX]{x1D6F7}^{\mathbb{I}}=\boldsymbol{\unicode[STIX]{x1D6E4}}\circ \unicode[STIX]{x1D6FA}$
. After that, in Corollary 4.9, we show that
$\unicode[STIX]{x1D6F7}^{\mathbb{I}}=\boldsymbol{\unicode[STIX]{x1D6E4}}\circ \unicode[STIX]{x1D6FA}$
. After that, in Corollary 4.9, we show that
![]() $\boldsymbol{\unicode[STIX]{x1D6E4}}$
is bijective for any Azumaya monoid
$\boldsymbol{\unicode[STIX]{x1D6E4}}$
is bijective for any Azumaya monoid
![]() $A$
whose enveloping monoid
$A$
whose enveloping monoid
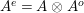 $A^{e}=A\otimes _{}A^{o}$
is, as an
$A^{e}=A\otimes _{}A^{o}$
is, as an
![]() $A$
-bimodule, a direct summand of a product of finite copies of
$A$
-bimodule, a direct summand of a product of finite copies of
![]() $A$
, and always under the hypothesis that
$A$
, and always under the hypothesis that
![]() ${\mathcal{Z}}$
is faithful.
${\mathcal{Z}}$
is faithful.
Our main application, given in Section 5, deals with the category of (right)
![]() $H$
-comodules over a commutative flat Hopf algebroid
$H$
-comodules over a commutative flat Hopf algebroid
![]() $(R,H)$
, where the base ring
$(R,H)$
, where the base ring
![]() $R$
is assumed to be a generator. In fact, we show that the group of
$R$
is assumed to be a generator. In fact, we show that the group of
![]() $H$
-automorphisms of an Azumaya
$H$
-automorphisms of an Azumaya
![]() $H$
-comodule
$H$
-comodule
![]() $R$
-algebra which satisfies the above condition is isomorphic to the group of all invertible
$R$
-algebra which satisfies the above condition is isomorphic to the group of all invertible
![]() $H$
-subcomodules; see Corollary 5.5. The particular case of split Hopf algebroid is one of the best places where this application could have some geometric meaning. For instance, let us consider a compact Lie group
$H$
-subcomodules; see Corollary 5.5. The particular case of split Hopf algebroid is one of the best places where this application could have some geometric meaning. For instance, let us consider a compact Lie group
![]() $G$
acting freely and smoothly on a manifold
$G$
acting freely and smoothly on a manifold
![]() $\mathfrak{M}$
. Assume that this action converts the ring
$\mathfrak{M}$
. Assume that this action converts the ring
![]() ${\mathcal{C}}^{\infty }(\mathfrak{M})$
of smooth (complex valued) functions into an
${\mathcal{C}}^{\infty }(\mathfrak{M})$
of smooth (complex valued) functions into an
![]() $\mathscr{R}_{\mathbb{C}}(G)$
-comodule
$\mathscr{R}_{\mathbb{C}}(G)$
-comodule
![]() $\mathbb{C}$
-algebra, where
$\mathbb{C}$
-algebra, where
![]() $\mathscr{R}_{\mathbb{C}}(G)$
is the commutative Hopf
$\mathscr{R}_{\mathbb{C}}(G)$
is the commutative Hopf
![]() $\mathbb{C}$
-algebra of representative smooth functions on
$\mathbb{C}$
-algebra of representative smooth functions on
![]() $G$
. Now, consider the Hopf algebroid
$G$
. Now, consider the Hopf algebroid
![]() $(R,H)$
with
$(R,H)$
with
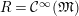 $R={\mathcal{C}}^{\infty }(\mathfrak{M})$
and
$R={\mathcal{C}}^{\infty }(\mathfrak{M})$
and
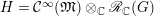 $H={\mathcal{C}}^{\infty }(\mathfrak{M})\otimes _{\mathbb{C}}\mathscr{R}_{\mathbb{C}}(G)$
. In this way the
$H={\mathcal{C}}^{\infty }(\mathfrak{M})\otimes _{\mathbb{C}}\mathscr{R}_{\mathbb{C}}(G)$
. In this way the
![]() $R$
-module of smooth global sections of any
$R$
-module of smooth global sections of any
![]() $G$
-equivariant complex vector bundle turns out to be an
$G$
-equivariant complex vector bundle turns out to be an
![]() $H$
-comodule. Hence an interpretation of our result in this setting can be given as follows. Take an Azumaya
$H$
-comodule. Hence an interpretation of our result in this setting can be given as follows. Take an Azumaya
![]() $G$
-equivariant algebra bundle
$G$
-equivariant algebra bundle
![]() $({\mathcal{E}},\unicode[STIX]{x1D703})$
of constant rank
$({\mathcal{E}},\unicode[STIX]{x1D703})$
of constant rank
![]() $n^{2}$
and consider its
$n^{2}$
and consider its
![]() $G$
-equivariant enveloping algebra bundleFootnote
3
$G$
-equivariant enveloping algebra bundleFootnote
3
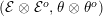 $({\mathcal{E}}\otimes _{}{\mathcal{E}}^{o},\unicode[STIX]{x1D703}\otimes _{}\unicode[STIX]{x1D703}^{o})$
such that the canonical splitting
$({\mathcal{E}}\otimes _{}{\mathcal{E}}^{o},\unicode[STIX]{x1D703}\otimes _{}\unicode[STIX]{x1D703}^{o})$
such that the canonical splitting
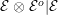 ${\mathcal{E}}\otimes _{}{\mathcal{E}}^{o}|{\mathcal{E}}$
in vector bundles is also
${\mathcal{E}}\otimes _{}{\mathcal{E}}^{o}|{\mathcal{E}}$
in vector bundles is also
![]() $G$
-equivariantFootnote
4
. Then we can affirm that the group of
$G$
-equivariantFootnote
4
. Then we can affirm that the group of
![]() $G$
-equivariant algebra automorphisms of
$G$
-equivariant algebra automorphisms of
![]() ${\mathcal{E}}$
is isomorphic to the group of (isomorphic classes) of all invertible
${\mathcal{E}}$
is isomorphic to the group of (isomorphic classes) of all invertible
![]() $G$
-equivariant subbundlesFootnote
5
of
$G$
-equivariant subbundlesFootnote
5
of
![]() ${\mathcal{E}}$
. Analogous affirmations take place in the context of affine algebraic varieties. In fact, we have an analogue result when
${\mathcal{E}}$
. Analogous affirmations take place in the context of affine algebraic varieties. In fact, we have an analogue result when
![]() $G$
is an affine algebraic group acting freely (and algebraically) on an affine algebraic variety
$G$
is an affine algebraic group acting freely (and algebraically) on an affine algebraic variety
![]() ${\mathcal{X}}$
, by taking the split Hopf algebroid
${\mathcal{X}}$
, by taking the split Hopf algebroid
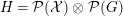 $H={\mathcal{P}}({\mathcal{X}})\otimes _{}{\mathcal{P}}(G)$
, where
$H={\mathcal{P}}({\mathcal{X}})\otimes _{}{\mathcal{P}}(G)$
, where
![]() ${\mathcal{P}}({\mathcal{X}})$
is the commutative algebra of polynomial functions on
${\mathcal{P}}({\mathcal{X}})$
is the commutative algebra of polynomial functions on
![]() ${\mathcal{X}}$
, and
${\mathcal{X}}$
, and
![]() ${\mathcal{P}}(G)$
is the Hopf algebra of polynomial functions on
${\mathcal{P}}(G)$
is the Hopf algebra of polynomial functions on
![]() $G$
.
$G$
.
0.3 Basic notions, notations and general assumptions
Let
![]() ${\mathcal{M}}$
be an additive category. The notation
${\mathcal{M}}$
be an additive category. The notation
![]() $X\in {\mathcal{M}}$
means that
$X\in {\mathcal{M}}$
means that
![]() $X$
is an object in
$X$
is an object in
![]() ${\mathcal{M}}$
. The identity arrow
${\mathcal{M}}$
. The identity arrow
![]() $\text{Id}_{X}$
of
$\text{Id}_{X}$
of
![]() $X\in {\mathcal{M}}$
will be denoted by the object itself if there is no danger of misunderstanding. The sets of morphisms are denoted by
$X\in {\mathcal{M}}$
will be denoted by the object itself if there is no danger of misunderstanding. The sets of morphisms are denoted by
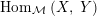 $\text{Hom}_{{\mathcal{M}}}\left(X,\,Y\right)$
, for
$\text{Hom}_{{\mathcal{M}}}\left(X,\,Y\right)$
, for
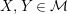 $X,Y\in {\mathcal{M}}$
. For two functors
$X,Y\in {\mathcal{M}}$
. For two functors
![]() ${\mathcal{F}}$
and
${\mathcal{F}}$
and
![]() ${\mathcal{G}}$
the notation
${\mathcal{G}}$
the notation
![]() ${\mathcal{F}}\dashv {\mathcal{G}}$
means that
${\mathcal{F}}\dashv {\mathcal{G}}$
means that
![]() ${\mathcal{F}}$
is a left adjoint to
${\mathcal{F}}$
is a left adjoint to
![]() ${\mathcal{G}}$
.
${\mathcal{G}}$
.
Let
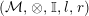 $({\mathcal{M}},\otimes _{},\mathbb{I},l,r)$
be a monoidal additive (resp. abelian) category, that is,
$({\mathcal{M}},\otimes _{},\mathbb{I},l,r)$
be a monoidal additive (resp. abelian) category, that is,
![]() ${\mathcal{M}}$
is an additive (resp. abelian) category such that the tensor product
${\mathcal{M}}$
is an additive (resp. abelian) category such that the tensor product
![]() $\otimes$
is an additive bi-functor. Denote by
$\otimes$
is an additive bi-functor. Denote by
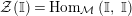 ${\mathcal{Z}}(\mathbb{I})=\text{Hom}_{{\mathcal{M}}}\left(\mathbb{I},\,\mathbb{I}\right)$
the commutative endomorphisms ring of the identity object
${\mathcal{Z}}(\mathbb{I})=\text{Hom}_{{\mathcal{M}}}\left(\mathbb{I},\,\mathbb{I}\right)$
the commutative endomorphisms ring of the identity object
![]() $\mathbb{I}$
. Clearly, each of the abelian groups
$\mathbb{I}$
. Clearly, each of the abelian groups
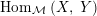 $\text{Hom}_{{\mathcal{M}}}\left(X,\,Y\right)$
admits a canonical structure of
$\text{Hom}_{{\mathcal{M}}}\left(X,\,Y\right)$
admits a canonical structure of
![]() ${\mathcal{Z}}(\mathbb{I})$
-bimodule. A
${\mathcal{Z}}(\mathbb{I})$
-bimodule. A
![]() ${\mathcal{Z}}(\mathbb{I})$
-bimodule is called central if the left
${\mathcal{Z}}(\mathbb{I})$
-bimodule is called central if the left
![]() ${\mathcal{Z}}(\mathbb{I})$
-module structure coincides with the right one.
${\mathcal{Z}}(\mathbb{I})$
-module structure coincides with the right one.
Recall from [Reference Bruguières5, page 5825] that
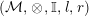 $({\mathcal{M}},\otimes _{},\mathbb{I},l,r)$
is said to be Penrose if the abelian groups of morphisms are central
$({\mathcal{M}},\otimes _{},\mathbb{I},l,r)$
is said to be Penrose if the abelian groups of morphisms are central
![]() ${\mathcal{Z}}(\mathbb{I})$
-bimodules. This in particular implies that
${\mathcal{Z}}(\mathbb{I})$
-bimodules. This in particular implies that
![]() ${\mathcal{M}}$
is a
${\mathcal{M}}$
is a
![]() ${\mathcal{Z}}(\mathbb{I})$
-linear category (i.e.,
${\mathcal{Z}}(\mathbb{I})$
-linear category (i.e.,
![]() ${\mathcal{M}}$
is enriched in the monoidal category of
${\mathcal{M}}$
is enriched in the monoidal category of
![]() ${\mathcal{Z}}(\mathbb{I})$
-modules). Notice that a braided monoidal additive category is always Penrose, cf. [Reference Bruguières5, remark on page 5825].
${\mathcal{Z}}(\mathbb{I})$
-modules). Notice that a braided monoidal additive category is always Penrose, cf. [Reference Bruguières5, remark on page 5825].
In this paper
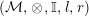 $({\mathcal{M}},\otimes _{},\mathbb{I},l,r)$
is a Penrose monoidal abelian category, where tensor products are right exact on both factors, and the underlying category
$({\mathcal{M}},\otimes _{},\mathbb{I},l,r)$
is a Penrose monoidal abelian category, where tensor products are right exact on both factors, and the underlying category
![]() ${\mathcal{M}}$
is locally small, that is the class of subobjects of any object is a set.
${\mathcal{M}}$
is locally small, that is the class of subobjects of any object is a set.
For a monoid
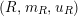 $(R,m_{R},u_{R})$
(or simply
$(R,m_{R},u_{R})$
(or simply
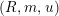 $(R,m,u)$
when no confusion can be made), we denote by
$(R,m,u)$
when no confusion can be made), we denote by
![]() $\text{}_{R}{\mathcal{M}}$
,
$\text{}_{R}{\mathcal{M}}$
,
![]() ${\mathcal{M}}_{R}$
and
${\mathcal{M}}_{R}$
and
![]() $\text{}_{R}{\mathcal{M}}_{R}$
its categories of left
$\text{}_{R}{\mathcal{M}}_{R}$
its categories of left
![]() $R$
-modules, right
$R$
-modules, right
![]() $R$
-modules and
$R$
-modules and
![]() $R$
-bimodules, respectively. The category
$R$
-bimodules, respectively. The category
![]() $\text{}_{R}{\mathcal{M}}_{R}$
inherits then a structure of monoidal abelian (also bicomplete if
$\text{}_{R}{\mathcal{M}}_{R}$
inherits then a structure of monoidal abelian (also bicomplete if
![]() ${\mathcal{M}}$
is) category with right exact tensor products denoted by
${\mathcal{M}}$
is) category with right exact tensor products denoted by
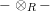 $-\otimes _{R}-$
; the unit object is
$-\otimes _{R}-$
; the unit object is
![]() $R$
and the left, right constraints are denoted, respectively by
$R$
and the left, right constraints are denoted, respectively by
![]() $l^{R}$
and
$l^{R}$
and
![]() $r^{R}$
. Furthermore, the forgetful functor
$r^{R}$
. Furthermore, the forgetful functor
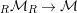 $\text{}_{R}{\mathcal{M}}_{R}\rightarrow {\mathcal{M}}$
is faithful and exact. We denote by
$\text{}_{R}{\mathcal{M}}_{R}\rightarrow {\mathcal{M}}$
is faithful and exact. We denote by
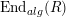 $\text{End}_{alg}(R)$
the ring of monoid endomorphisms of
$\text{End}_{alg}(R)$
the ring of monoid endomorphisms of
![]() $R$
and by
$R$
and by
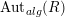 $\text{Aut}_{alg}(R)$
its group of units.
$\text{Aut}_{alg}(R)$
its group of units.
Given a second monoid
![]() $S$
, we use the classical notation for morphisms of left, right and bimodules. That is, we denote by
$S$
, we use the classical notation for morphisms of left, right and bimodules. That is, we denote by
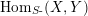 $\text{Hom}_{S\text{-}}(X,Y)$
the set of left
$\text{Hom}_{S\text{-}}(X,Y)$
the set of left
![]() $S$
-module morphisms, by
$S$
-module morphisms, by
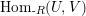 $\text{Hom}_{\text{-}R}(U,V)$
the set of right
$\text{Hom}_{\text{-}R}(U,V)$
the set of right
![]() $R$
-module morphisms, and by
$R$
-module morphisms, and by
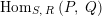 $\text{Hom}_{S,\,R}\left(P,\,Q\right)$
the set of
$\text{Hom}_{S,\,R}\left(P,\,Q\right)$
the set of
![]() $(S,R)$
-bimodule morphisms (
$(S,R)$
-bimodule morphisms (
![]() $S$
on the left and
$S$
on the left and
![]() $R$
on the right). We will use the notation
$R$
on the right). We will use the notation
![]() ${\mathcal{Z}}_{R}(-)$
for the functor
${\mathcal{Z}}_{R}(-)$
for the functor
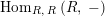 $\text{Hom}_{R,\,R}\left(R,\,-\right)$
and similarly for
$\text{Hom}_{R,\,R}\left(R,\,-\right)$
and similarly for
![]() ${\mathcal{Z}}_{S}(-)$
.
${\mathcal{Z}}_{S}(-)$
.
An object
![]() $X$
in
$X$
in
![]() ${\mathcal{M}}$
is called left (resp. right) flat, if the functor
${\mathcal{M}}$
is called left (resp. right) flat, if the functor
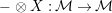 $-\otimes _{}X:{\mathcal{M}}\rightarrow {\mathcal{M}}$
(resp.
$-\otimes _{}X:{\mathcal{M}}\rightarrow {\mathcal{M}}$
(resp.
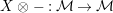 $X\otimes _{}-:{\mathcal{M}}\rightarrow {\mathcal{M}}$
) is left exact. Obviously, if
$X\otimes _{}-:{\mathcal{M}}\rightarrow {\mathcal{M}}$
) is left exact. Obviously, if
![]() ${\mathcal{M}}$
is symmetric, then left flat is equivalent to right flat, and the adjective left or right is omitted.
${\mathcal{M}}$
is symmetric, then left flat is equivalent to right flat, and the adjective left or right is omitted.
1 Invertible bimodules and dualizable data, revisited
Let
![]() $A,R,S$
be monoids in
$A,R,S$
be monoids in
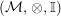 $({\mathcal{M}},\otimes ,\mathbb{I})$
and let
$({\mathcal{M}},\otimes ,\mathbb{I})$
and let
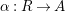 $\unicode[STIX]{x1D6FC}:R\rightarrow A$
,
$\unicode[STIX]{x1D6FC}:R\rightarrow A$
,
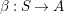 $\unicode[STIX]{x1D6FD}:S\rightarrow A$
be morphisms of monoids. One can consider in a canonical way
$\unicode[STIX]{x1D6FD}:S\rightarrow A$
be morphisms of monoids. One can consider in a canonical way
![]() $A$
as a monoid simultaneously in the monoidal categories of bimodules
$A$
as a monoid simultaneously in the monoidal categories of bimodules
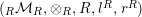 $(\text{}_{R}{\mathcal{M}}_{R},\otimes _{R},R,l^{R},r^{R})$
and
$(\text{}_{R}{\mathcal{M}}_{R},\otimes _{R},R,l^{R},r^{R})$
and
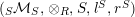 $(\text{}_{S}{\mathcal{M}}_{S},\otimes _{R},S,l^{S},r^{S})$
. To distinguish the multiplications of
$(\text{}_{S}{\mathcal{M}}_{S},\otimes _{R},S,l^{S},r^{S})$
. To distinguish the multiplications of
![]() $A$
in these different categories, we use the following notations:
$A$
in these different categories, we use the following notations:
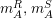 $m_{A}^{R},m_{A}^{S}$
.
$m_{A}^{R},m_{A}^{S}$
.
Consider
![]() $A$
as an
$A$
as an
![]() $(R,S)$
-bimodule via
$(R,S)$
-bimodule via
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
. By an
$\unicode[STIX]{x1D6FD}$
. By an
![]() $(R,S)$
-sub-bimodule of
$(R,S)$
-sub-bimodule of
![]() $A$
, we mean a pair
$A$
, we mean a pair
![]() $(X,i_{X})$
where
$(X,i_{X})$
where
![]() $X$
is an
$X$
is an
![]() $(R,S)$
-bimodule and
$(R,S)$
-bimodule and
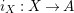 $i_{X}:X\rightarrow A$
a monomorphism of
$i_{X}:X\rightarrow A$
a monomorphism of
![]() $(R,S)$
-bimodules. Consider
$(R,S)$
-bimodules. Consider
 $$\begin{eqnarray}\mathscr{P}\left(\text{}_{R}A_{S}\right):=\Big\{(R,S)\text{-sub-bimodules }\left(X,i_{X}\right)\text{ of }_{R}A_{S}\Big\}.\end{eqnarray}$$
$$\begin{eqnarray}\mathscr{P}\left(\text{}_{R}A_{S}\right):=\Big\{(R,S)\text{-sub-bimodules }\left(X,i_{X}\right)\text{ of }_{R}A_{S}\Big\}.\end{eqnarray}$$
Since the base category
![]() ${\mathcal{M}}$
is locally small,
${\mathcal{M}}$
is locally small,
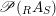 $\mathscr{P}(\text{}_{R}A_{S})$
is a skeletally small category, where a morphism
$\mathscr{P}(\text{}_{R}A_{S})$
is a skeletally small category, where a morphism
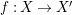 $f:X\rightarrow X^{\prime }$
is a morphism of
$f:X\rightarrow X^{\prime }$
is a morphism of
![]() $(R,S)$
-bimodules satisfying
$(R,S)$
-bimodules satisfying
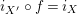 $i_{X^{\prime }}\circ f=i_{X}$
. We will not make a difference between the category
$i_{X^{\prime }}\circ f=i_{X}$
. We will not make a difference between the category
 $\mathscr{P}(\text{}_{R}A_{S})$
and its skeleton set, that is, between an object
$\mathscr{P}(\text{}_{R}A_{S})$
and its skeleton set, that is, between an object
![]() $X$
and its representing element
$X$
and its representing element
![]() $(X,i_{X})$
. In this way, an element (or an object)
$(X,i_{X})$
. In this way, an element (or an object)
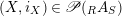 $(X,i_{X})\in \mathscr{P}(\text{}_{R}A_{S})$
will be simply denoted by
$(X,i_{X})\in \mathscr{P}(\text{}_{R}A_{S})$
will be simply denoted by
![]() $X$
, where the (fixed) monomorphism of
$X$
, where the (fixed) monomorphism of
![]() $(R,S)$
-bimodules
$(R,S)$
-bimodules
![]() $i_{X}$
is implicitly understood. Similar conventions and considerations are applied to the set
$i_{X}$
is implicitly understood. Similar conventions and considerations are applied to the set
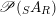 $\mathscr{P}(\text{}_{S}A_{R})$
.
$\mathscr{P}(\text{}_{S}A_{R})$
.
Given
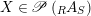 $X\in \mathscr{P}\left(\text{}_{R}A_{S}\right)$
and
$X\in \mathscr{P}\left(\text{}_{R}A_{S}\right)$
and
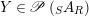 $Y\in \mathscr{P}\left(\text{}_{S}A_{R}\right)$
, one defines
$Y\in \mathscr{P}\left(\text{}_{S}A_{R}\right)$
, one defines
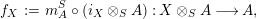 $$\begin{eqnarray}\displaystyle f_{X} & := & \displaystyle m_{A}^{S}\circ \left(i_{X}\otimes _{S}A\right):X\otimes _{S}A\longrightarrow A,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{X} & := & \displaystyle m_{A}^{S}\circ \left(i_{X}\otimes _{S}A\right):X\otimes _{S}A\longrightarrow A,\end{eqnarray}$$
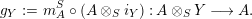 $$\begin{eqnarray}\displaystyle g_{Y} & := & \displaystyle m_{A}^{S}\circ \left(A\otimes _{S}i_{Y}\right):A\otimes _{S}Y\longrightarrow A.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g_{Y} & := & \displaystyle m_{A}^{S}\circ \left(A\otimes _{S}i_{Y}\right):A\otimes _{S}Y\longrightarrow A.\end{eqnarray}$$
Using this time the multiplication
![]() $m_{A}^{R}$
, one analogously defines
$m_{A}^{R}$
, one analogously defines
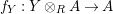 $f_{Y}:Y\otimes _{R}A\rightarrow A$
and
$f_{Y}:Y\otimes _{R}A\rightarrow A$
and
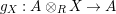 $g_{X}:A\otimes _{R}X\rightarrow A$
.
$g_{X}:A\otimes _{R}X\rightarrow A$
.
Recall the following two definitions which will play a central role in this section.
Definition 1.1. A right inverse for
 $X\in \mathscr{P}(\text{}_{R}A_{S})$
consists of an element
$X\in \mathscr{P}(\text{}_{R}A_{S})$
consists of an element
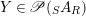 $Y\in \mathscr{P}(\text{}_{S}A_{R})$
such that
$Y\in \mathscr{P}(\text{}_{S}A_{R})$
such that
-
∙ there are morphisms
 $m_{X}=m_{X,Y}:X\otimes _{S}Y\rightarrow R$
in
$m_{X}=m_{X,Y}:X\otimes _{S}Y\rightarrow R$
in
 $_{R}{\mathcal{M}}_{R}$
and
$_{R}{\mathcal{M}}_{R}$
and
 $m_{Y}=m_{Y,X}:Y\otimes _{R}X\rightarrow S$
in
$m_{Y}=m_{Y,X}:Y\otimes _{R}X\rightarrow S$
in
 $_{S}{\mathcal{M}}_{S}$
fulfilling (3)
$_{S}{\mathcal{M}}_{S}$
fulfilling (3) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}\circ m_{X} & = & \displaystyle m_{A}^{S}\circ \left(i_{X}\otimes _{S}i_{Y}\right)\!,\end{eqnarray}$$
(4)
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}\circ m_{X} & = & \displaystyle m_{A}^{S}\circ \left(i_{X}\otimes _{S}i_{Y}\right)\!,\end{eqnarray}$$
(4) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FD}\circ m_{Y} & = & \displaystyle m_{A}^{R}\circ \left(i_{Y}\otimes _{R}i_{X}\right)\!,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FD}\circ m_{Y} & = & \displaystyle m_{A}^{R}\circ \left(i_{Y}\otimes _{R}i_{X}\right)\!,\end{eqnarray}$$
-
∙
 $m_{X}$
is an isomorphism.
$m_{X}$
is an isomorphism.
We also say that
![]() $X$
is a right invertible sub-bimodule. Left and two-sided inverses are obviously defined.
$X$
is a right invertible sub-bimodule. Left and two-sided inverses are obviously defined.
Definition 1.2. An
![]() $(R,S)$
-bimodule
$(R,S)$
-bimodule
![]() $X$
is called right dualizable if there exist an
$X$
is called right dualizable if there exist an
![]() $(S,R)$
-bimodule
$(S,R)$
-bimodule
![]() $Y$
and morphisms
$Y$
and morphisms
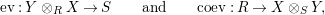 $$\begin{eqnarray}\text{ev}:Y\otimes _{R}X\rightarrow S\qquad \text{and}\qquad \text{coev}:R\rightarrow X\otimes _{S}Y,\end{eqnarray}$$
$$\begin{eqnarray}\text{ev}:Y\otimes _{R}X\rightarrow S\qquad \text{and}\qquad \text{coev}:R\rightarrow X\otimes _{S}Y,\end{eqnarray}$$
of
![]() $S$
-bimodules and
$S$
-bimodules and
![]() $R$
-bimodules respectively, such that the following equalities hold true
$R$
-bimodules respectively, such that the following equalities hold true
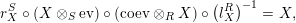 $$\begin{eqnarray}\displaystyle r_{X}^{S}\circ \left(X\otimes _{S}\text{ev}\right)\circ \left(\text{ coev}\otimes _{R}X\right)\circ \left(l_{X}^{R}\right)^{-1} & = & \displaystyle X,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle r_{X}^{S}\circ \left(X\otimes _{S}\text{ev}\right)\circ \left(\text{ coev}\otimes _{R}X\right)\circ \left(l_{X}^{R}\right)^{-1} & = & \displaystyle X,\end{eqnarray}$$
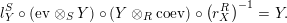 $$\begin{eqnarray}\displaystyle l_{Y}^{S}\circ \left(\text{ev}\otimes _{S}Y\right)\circ \left(Y\otimes _{R}\text{coev}\right)\circ \left(r_{X}^{R}\right)^{-1} & = & \displaystyle Y.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle l_{Y}^{S}\circ \left(\text{ev}\otimes _{S}Y\right)\circ \left(Y\otimes _{R}\text{coev}\right)\circ \left(r_{X}^{R}\right)^{-1} & = & \displaystyle Y.\end{eqnarray}$$
We will also say that
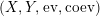 $\left(X,Y,\text{ev},\text{coev}\right)$
is a right dualizable datum in this case. Notice, that the same definition was given in [Reference Pareigis27, Definition 2.1] with different terminology, where condition (ii) in that definition always holds true under our assumptions. If
$\left(X,Y,\text{ev},\text{coev}\right)$
is a right dualizable datum in this case. Notice, that the same definition was given in [Reference Pareigis27, Definition 2.1] with different terminology, where condition (ii) in that definition always holds true under our assumptions. If
![]() $R=S$
, then of course we have that
$R=S$
, then of course we have that
![]() $Y$
is a (left) dual object of
$Y$
is a (left) dual object of
![]() $X$
in the monoidal category of bimodules
$X$
in the monoidal category of bimodules
![]() $\text{}_{R}{\mathcal{M}}_{R}$
. In such case, if
$\text{}_{R}{\mathcal{M}}_{R}$
. In such case, if
![]() $Y$
exists, it is unique up to isomorphism.
$Y$
exists, it is unique up to isomorphism.
The following standard diagrammatic notation will be used in the sequel.
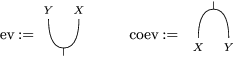
In terms of these diagrams, equations (5) and (6) are represented as follows (notice that several kinds of tensor products are involved)
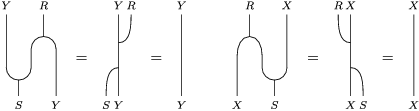
which we use in the following form, where, as customary, we get rid of the unit constraints.
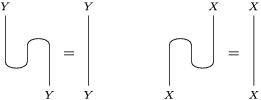
1.1 Right inverse versus right dualizable datum, and adjunctions
The main aim of this subsection is to check that the right inverse, if it exists, is unique up to isomorphism. To this end, we first show that the existence of a right inverse leads in fact to a right dualizable datum. The converse holds true under some more assumptions; see Section A.1. Secondly we show, as it might be expected, that a dualizable datum entails adjunctions.
Proposition 1.3. Let
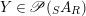 $Y\in \mathscr{P}(\text{}_{S}A_{R})$
be a right inverse of
$Y\in \mathscr{P}(\text{}_{S}A_{R})$
be a right inverse of
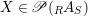 $X\in \mathscr{P}(\text{}_{R}A_{S})$
, as in Definition 1.1. Set
$X\in \mathscr{P}(\text{}_{R}A_{S})$
, as in Definition 1.1. Set
 $$\begin{eqnarray}\text{ev}:=m_{Y}:Y\otimes _{R}X\rightarrow S\qquad \text{and}\qquad \text{coev}:=\left(m_{X}\right)^{-1}:R\rightarrow X\otimes _{S}Y.\end{eqnarray}$$
$$\begin{eqnarray}\text{ev}:=m_{Y}:Y\otimes _{R}X\rightarrow S\qquad \text{and}\qquad \text{coev}:=\left(m_{X}\right)^{-1}:R\rightarrow X\otimes _{S}Y.\end{eqnarray}$$
Then
-
(i)
 $\left(X,Y,\text{ev},\text{coev}\right)$
is a right dualizable datum;
$\left(X,Y,\text{ev},\text{coev}\right)$
is a right dualizable datum; -
(ii) we have that
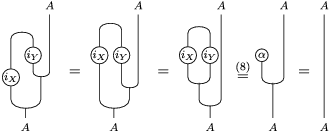
(8) $$\begin{eqnarray}\displaystyle & m_{A}^{S}\circ \left(i_{X}\otimes _{S}i_{Y}\right)\circ \text{coev}=\unicode[STIX]{x1D6FC}, & \displaystyle\end{eqnarray}$$
(9)
$$\begin{eqnarray}\displaystyle & m_{A}^{S}\circ \left(i_{X}\otimes _{S}i_{Y}\right)\circ \text{coev}=\unicode[STIX]{x1D6FC}, & \displaystyle\end{eqnarray}$$
(9) $$\begin{eqnarray}\displaystyle & m_{A}^{R}\circ \left(i_{Y}\otimes _{R}i_{X}\right)=\unicode[STIX]{x1D6FD}\circ \text{ev}\text{.} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & m_{A}^{R}\circ \left(i_{Y}\otimes _{R}i_{X}\right)=\unicode[STIX]{x1D6FD}\circ \text{ev}\text{.} & \displaystyle\end{eqnarray}$$
Proof. (i) Assume that there is another
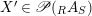 $X^{\prime }\in \mathscr{P}(\text{}_{R}A_{S})$
with right inverse
$X^{\prime }\in \mathscr{P}(\text{}_{R}A_{S})$
with right inverse
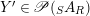 $Y^{\prime }\in \mathscr{P}(\text{}_{S}A_{R})$
. Then, for any pair of morphisms
$Y^{\prime }\in \mathscr{P}(\text{}_{S}A_{R})$
. Then, for any pair of morphisms
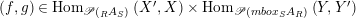 $(f,g)\in \text{Hom}_{\mathscr{P}\left(\text{}_{R}A_{S}\right)}\left(X^{\prime },X\right)\times \text{Hom}_{\mathscr{P}\left(mbox_{S}A_{R}\right)}\left(Y,Y^{\prime }\right)$
, we define
$(f,g)\in \text{Hom}_{\mathscr{P}\left(\text{}_{R}A_{S}\right)}\left(X^{\prime },X\right)\times \text{Hom}_{\mathscr{P}\left(mbox_{S}A_{R}\right)}\left(Y,Y^{\prime }\right)$
, we define
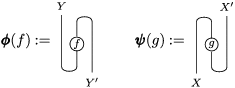
Explicitly,
![]() $\pmb{\unicode[STIX]{x1D719}}$
and
$\pmb{\unicode[STIX]{x1D719}}$
and
![]() $\pmb{\unicode[STIX]{x1D713}}$
are given by
$\pmb{\unicode[STIX]{x1D713}}$
are given by
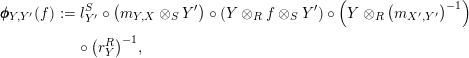 $$\begin{eqnarray}\displaystyle \pmb{\unicode[STIX]{x1D719}}_{Y,Y^{\prime }}(f) & := & \displaystyle l_{Y^{\prime }}^{S}\circ \left(m_{Y,X}\otimes _{S}Y^{\prime }\right)\circ (Y\otimes _{R}f\otimes _{S}Y^{\prime })\circ \left(Y\otimes _{R}\left(m_{X^{\prime },Y^{\prime }}\right)^{-1}\right)\nonumber\\ \displaystyle & & \displaystyle \circ \left(r_{Y}^{R}\right)^{-1}\!,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \pmb{\unicode[STIX]{x1D719}}_{Y,Y^{\prime }}(f) & := & \displaystyle l_{Y^{\prime }}^{S}\circ \left(m_{Y,X}\otimes _{S}Y^{\prime }\right)\circ (Y\otimes _{R}f\otimes _{S}Y^{\prime })\circ \left(Y\otimes _{R}\left(m_{X^{\prime },Y^{\prime }}\right)^{-1}\right)\nonumber\\ \displaystyle & & \displaystyle \circ \left(r_{Y}^{R}\right)^{-1}\!,\end{eqnarray}$$
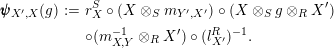 $$\begin{eqnarray}\displaystyle \pmb{\unicode[STIX]{x1D713}}_{X^{\prime },X}(g) & := & \displaystyle r_{X}^{S}\circ (X\otimes _{S}m_{Y^{\prime },X^{\prime }})\circ (X\otimes _{S}g\otimes _{R}X^{\prime })\nonumber\\ \displaystyle & & \displaystyle \circ (m_{X,Y}^{-1}\otimes _{R}X^{\prime })\circ (l_{X^{\prime }}^{R})^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \pmb{\unicode[STIX]{x1D713}}_{X^{\prime },X}(g) & := & \displaystyle r_{X}^{S}\circ (X\otimes _{S}m_{Y^{\prime },X^{\prime }})\circ (X\otimes _{S}g\otimes _{R}X^{\prime })\nonumber\\ \displaystyle & & \displaystyle \circ (m_{X,Y}^{-1}\otimes _{R}X^{\prime })\circ (l_{X^{\prime }}^{R})^{-1}.\end{eqnarray}$$
Therefore, we have
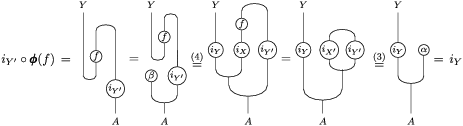
Similarly, one obtains the equality
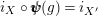 $i_{X}\circ \pmb{\unicode[STIX]{x1D713}}(g)=i_{X^{\prime }}$
. Now, for
$i_{X}\circ \pmb{\unicode[STIX]{x1D713}}(g)=i_{X^{\prime }}$
. Now, for
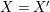 $X=X^{\prime }$
,
$X=X^{\prime }$
,
![]() $Y=Y^{\prime }$
and
$Y=Y^{\prime }$
and
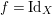 $f=\text{Id}_{X}$
, we get
$f=\text{Id}_{X}$
, we get
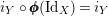 $i_{Y}\circ \pmb{\unicode[STIX]{x1D719}}(\text{Id}_{X})=i_{Y}$
which implies that
$i_{Y}\circ \pmb{\unicode[STIX]{x1D719}}(\text{Id}_{X})=i_{Y}$
which implies that
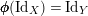 $\pmb{\unicode[STIX]{x1D719}}(\text{Id}_{X})=\text{Id}_{Y}$
, since
$\pmb{\unicode[STIX]{x1D719}}(\text{Id}_{X})=\text{Id}_{Y}$
, since
![]() $i_{Y}$
is a monomorphism. Taking now
$i_{Y}$
is a monomorphism. Taking now
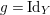 $g=\text{Id}_{Y}$
, we obtain
$g=\text{Id}_{Y}$
, we obtain
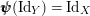 $\pmb{\unicode[STIX]{x1D713}}(\text{Id}_{Y})=\text{Id}_{X}$
. Both equalities
$\pmb{\unicode[STIX]{x1D713}}(\text{Id}_{Y})=\text{Id}_{X}$
. Both equalities
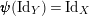 $\pmb{\unicode[STIX]{x1D713}}(\text{Id}_{Y})=\text{Id}_{X}$
and
$\pmb{\unicode[STIX]{x1D713}}(\text{Id}_{Y})=\text{Id}_{X}$
and
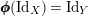 $\pmb{\unicode[STIX]{x1D719}}(\text{Id}_{X})=\text{Id}_{Y}$
form precisely equation (7), and this finishes the proof of this item.
$\pmb{\unicode[STIX]{x1D719}}(\text{Id}_{X})=\text{Id}_{Y}$
form precisely equation (7), and this finishes the proof of this item.
(ii) Equalities (8) and (9) are just (3) and (4) rewritten with respect to
![]() $\text{ev}$
and
$\text{ev}$
and
![]() $\text{coev}$
.◻
$\text{coev}$
.◻
The following result is inspired by the equivalence between (ii) and (iii) in [Reference May22, Theorem 2.6]; see also [Reference Pareigis27, Proposition 2.2]. For the reader’s sake we give here a diagrammatic proof.
Proposition 1.4. Let
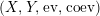 $\left(X,Y,\text{ev},\text{coev}\right)$
be a right dualizable datum, as in Definition 1.2. Then the assignments
$\left(X,Y,\text{ev},\text{coev}\right)$
be a right dualizable datum, as in Definition 1.2. Then the assignments
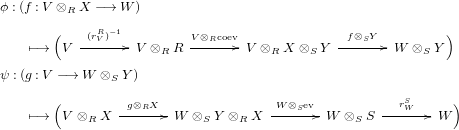
yield a natural isomorphism
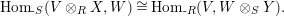 $$\begin{eqnarray}\text{Hom}_{\text{-}S}(V\otimes _{R}X,W)\cong \text{Hom}_{\text{-}R}(V,W\otimes _{S}Y).\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}_{\text{-}S}(V\otimes _{R}X,W)\cong \text{Hom}_{\text{-}R}(V,W\otimes _{S}Y).\end{eqnarray}$$
In other words the functor
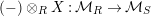 $\left(-\right)\otimes _{R}X:{\mathcal{M}}_{R}\rightarrow {\mathcal{M}}_{S}$
is left adjoint to the functor
$\left(-\right)\otimes _{R}X:{\mathcal{M}}_{R}\rightarrow {\mathcal{M}}_{S}$
is left adjoint to the functor
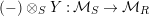 $(-)\otimes _{S}Y:{\mathcal{M}}_{S}\rightarrow {\mathcal{M}}_{R}$
. We also have that
$(-)\otimes _{S}Y:{\mathcal{M}}_{S}\rightarrow {\mathcal{M}}_{R}$
. We also have that
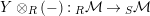 $Y\otimes _{R}(-):\text{}_{R}{\mathcal{M}}\rightarrow \text{}_{S}{\mathcal{M}}$
is a left adjoint of
$Y\otimes _{R}(-):\text{}_{R}{\mathcal{M}}\rightarrow \text{}_{S}{\mathcal{M}}$
is a left adjoint of
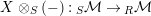 $X\otimes _{S}(-):\text{}_{S}{\mathcal{M}}\rightarrow \text{}_{R}{\mathcal{M}}$
.
$X\otimes _{S}(-):\text{}_{S}{\mathcal{M}}\rightarrow \text{}_{R}{\mathcal{M}}$
.
Proof. The naturality of both
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D713}$
is clear. Now, for
$\unicode[STIX]{x1D713}$
is clear. Now, for
![]() $f$
as above we have
$f$
as above we have
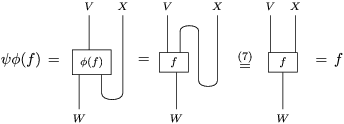
If we reflect horizontally the diagrams above and we apply the substitutions
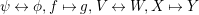 $\unicode[STIX]{x1D713}\leftrightarrow \unicode[STIX]{x1D719},f\mapsto g,V\leftrightarrow W,X\mapsto Y$
, we get the diagrammatic proof for the equality
$\unicode[STIX]{x1D713}\leftrightarrow \unicode[STIX]{x1D719},f\mapsto g,V\leftrightarrow W,X\mapsto Y$
, we get the diagrammatic proof for the equality
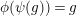 $\unicode[STIX]{x1D719}(\unicode[STIX]{x1D713}(g))=g$
. The last adjunction is similarly proved.◻
$\unicode[STIX]{x1D719}(\unicode[STIX]{x1D713}(g))=g$
. The last adjunction is similarly proved.◻
As a consequence of Propositions 1.3 and 1.4, we obtain the desired uniqueness of the right inverse, since we know that a right adjoint functor is unique up to a natural isomorphism.
Corollary 1.5. Let
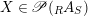 $X\in \mathscr{P}(\text{}_{R}A_{S})$
. Then a right inverse of
$X\in \mathscr{P}(\text{}_{R}A_{S})$
. Then a right inverse of
![]() $X$
, if it exists, is unique up to an isomorphism in
$X$
, if it exists, is unique up to an isomorphism in
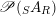 $\mathscr{P}(\text{}_{S}A_{R})$
. More precisely, assume that
$\mathscr{P}(\text{}_{S}A_{R})$
. More precisely, assume that
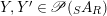 $Y,Y^{\prime }\in \mathscr{P}(\text{}_{S}A_{R})$
are two right inverses of
$Y,Y^{\prime }\in \mathscr{P}(\text{}_{S}A_{R})$
are two right inverses of
![]() $X$
. Then
$X$
. Then
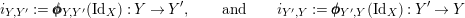 $$\begin{eqnarray}i_{Y,Y^{\prime }}:=\pmb{\unicode[STIX]{x1D719}}_{Y,Y^{\prime }}(\text{Id}_{X}):Y\rightarrow Y^{\prime },\qquad \text{and}\qquad i_{Y^{\prime },Y}:=\pmb{\unicode[STIX]{x1D719}}_{Y^{\prime },Y}(\text{Id}_{X}):Y^{\prime }\rightarrow Y\end{eqnarray}$$
$$\begin{eqnarray}i_{Y,Y^{\prime }}:=\pmb{\unicode[STIX]{x1D719}}_{Y,Y^{\prime }}(\text{Id}_{X}):Y\rightarrow Y^{\prime },\qquad \text{and}\qquad i_{Y^{\prime },Y}:=\pmb{\unicode[STIX]{x1D719}}_{Y^{\prime },Y}(\text{Id}_{X}):Y^{\prime }\rightarrow Y\end{eqnarray}$$
are mutual inverses in
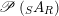 $\mathscr{P}\left(\text{}_{S}A_{R}\right)$
, where
$\mathscr{P}\left(\text{}_{S}A_{R}\right)$
, where
![]() $\pmb{\unicode[STIX]{x1D719}}$
is as in (11). Moreover, if
$\pmb{\unicode[STIX]{x1D719}}$
is as in (11). Moreover, if
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
are monomorphisms, we also have
$\unicode[STIX]{x1D6FD}$
are monomorphisms, we also have
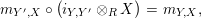 $$\begin{eqnarray}\displaystyle m_{Y^{\prime },X}\circ \left(i_{Y,Y^{\prime }}\otimes _{R}X\right) & = & \displaystyle m_{Y,X},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle m_{Y^{\prime },X}\circ \left(i_{Y,Y^{\prime }}\otimes _{R}X\right) & = & \displaystyle m_{Y,X},\end{eqnarray}$$
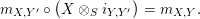 $$\begin{eqnarray}\displaystyle m_{X,Y^{\prime }}\circ \left(X\otimes _{S}i_{Y,Y^{\prime }}\right) & = & \displaystyle m_{X,Y}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle m_{X,Y^{\prime }}\circ \left(X\otimes _{S}i_{Y,Y^{\prime }}\right) & = & \displaystyle m_{X,Y}.\end{eqnarray}$$
Proof. We only show the last statement. The equality (13) is shown as follows:
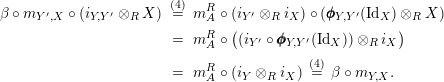 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FD}\circ m_{Y^{\prime },X}\circ (i_{Y,Y^{\prime }}\otimes _{R}X) & \,\overset{(4)}{=}\, & \displaystyle m_{A}^{R}\circ (i_{Y^{\prime }}\otimes _{R}i_{X})\circ (\pmb{\unicode[STIX]{x1D719}}_{Y,Y^{\prime }}(\text{Id}_{X})\otimes _{R}X)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \big((i_{Y^{\prime }}\circ \pmb{\unicode[STIX]{x1D719}}_{Y,Y^{\prime }}(\text{Id}_{X}))\otimes _{R}i_{X}\big)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ (i_{Y}\otimes _{R}i_{X})\,\overset{(4)}{=}\,\unicode[STIX]{x1D6FD}\circ m_{Y,X}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FD}\circ m_{Y^{\prime },X}\circ (i_{Y,Y^{\prime }}\otimes _{R}X) & \,\overset{(4)}{=}\, & \displaystyle m_{A}^{R}\circ (i_{Y^{\prime }}\otimes _{R}i_{X})\circ (\pmb{\unicode[STIX]{x1D719}}_{Y,Y^{\prime }}(\text{Id}_{X})\otimes _{R}X)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \big((i_{Y^{\prime }}\circ \pmb{\unicode[STIX]{x1D719}}_{Y,Y^{\prime }}(\text{Id}_{X}))\otimes _{R}i_{X}\big)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ (i_{Y}\otimes _{R}i_{X})\,\overset{(4)}{=}\,\unicode[STIX]{x1D6FD}\circ m_{Y,X}.\nonumber\end{eqnarray}$$
Equality (14) follows similarly.◻
We finish this subsection by giving more properties of dualizable datum which in fact lead to a characterization of right invertible sub-bimodules.
Proposition 1.6. Let
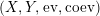 $(X,Y,\text{ev},\text{coev})$
be a right dualizable datum such that
$(X,Y,\text{ev},\text{coev})$
be a right dualizable datum such that
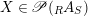 $X\in \mathscr{P}(\text{}_{R}A_{S})$
and
$X\in \mathscr{P}(\text{}_{R}A_{S})$
and
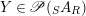 $Y\in \mathscr{P}(\text{}_{S}A_{R})$
with associated monomorphisms
$Y\in \mathscr{P}(\text{}_{S}A_{R})$
with associated monomorphisms
![]() $i_{X},i_{Y}$
satisfying equations (8) and (9). Then the morphisms
$i_{X},i_{Y}$
satisfying equations (8) and (9). Then the morphisms
![]() $f_{X}$
and
$f_{X}$
and
![]() $g_{Y}$
of equations (1) and (2) are isomorphisms with inverses
$g_{Y}$
of equations (1) and (2) are isomorphisms with inverses
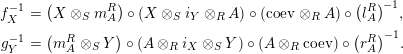 $$\begin{eqnarray}\displaystyle f_{X}^{-1} & = & \displaystyle \left(X\otimes _{S}m_{A}^{R}\right)\circ \left(X\otimes _{S}i_{Y}\otimes _{R}A\right)\circ \left(\text{coev}\otimes _{R}A\right)\circ \left(l_{A}^{R}\right)^{-1}\!,\nonumber\\ \displaystyle g_{Y}^{-1} & = & \displaystyle \left(m_{A}^{R}\otimes _{S}Y\right)\circ \left(A\otimes _{R}i_{X}\otimes _{S}Y\right)\circ \left(A\otimes _{R}\text{coev}\right)\circ \left(r_{A}^{R}\right)^{-1}\!.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{X}^{-1} & = & \displaystyle \left(X\otimes _{S}m_{A}^{R}\right)\circ \left(X\otimes _{S}i_{Y}\otimes _{R}A\right)\circ \left(\text{coev}\otimes _{R}A\right)\circ \left(l_{A}^{R}\right)^{-1}\!,\nonumber\\ \displaystyle g_{Y}^{-1} & = & \displaystyle \left(m_{A}^{R}\otimes _{S}Y\right)\circ \left(A\otimes _{R}i_{X}\otimes _{S}Y\right)\circ \left(A\otimes _{R}\text{coev}\right)\circ \left(r_{A}^{R}\right)^{-1}\!.\nonumber\end{eqnarray}$$
Proof. Let us prove that
![]() $f_{X}$
and
$f_{X}$
and
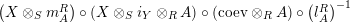 $\left(X\otimes _{S}m_{A}^{R}\right)\circ \left(X\otimes _{S}i_{Y}\otimes _{R}A\right)\circ \left(\text{coev}\otimes _{R}A\right)\circ \left(l_{A}^{R}\right)^{-1}$
are mutual inverses (the proof for
$\left(X\otimes _{S}m_{A}^{R}\right)\circ \left(X\otimes _{S}i_{Y}\otimes _{R}A\right)\circ \left(\text{coev}\otimes _{R}A\right)\circ \left(l_{A}^{R}\right)^{-1}$
are mutual inverses (the proof for
![]() $g_{Y}$
is analogous). One composition can be computed by means of the following tangle diagrams.
$g_{Y}$
is analogous). One composition can be computed by means of the following tangle diagrams.
The other composition is computed as follows.

◻
Combining Proposition 1.3 with Proposition 1.6, we obtain
Corollary 1.7. Let
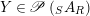 $Y\in \mathscr{P}\left(\text{}_{S}A_{R}\right)$
be a right inverse of
$Y\in \mathscr{P}\left(\text{}_{S}A_{R}\right)$
be a right inverse of
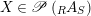 $X\in \mathscr{P}\left(\text{}_{R}A_{S}\right)$
. Then the morphisms
$X\in \mathscr{P}\left(\text{}_{R}A_{S}\right)$
. Then the morphisms
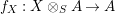 $f_{X}:X\otimes _{S}A\rightarrow A$
and
$f_{X}:X\otimes _{S}A\rightarrow A$
and
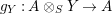 $g_{Y}:A\otimes _{S}Y\rightarrow A$
defined in (1) and (2) are isomorphisms.
$g_{Y}:A\otimes _{S}Y\rightarrow A$
defined in (1) and (2) are isomorphisms.
Remark 1.8. Corollary 1.7 says that, if
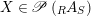 $X\in \mathscr{P}\left(\text{}_{R}A_{S}\right)$
has a right inverse, then
$X\in \mathscr{P}\left(\text{}_{R}A_{S}\right)$
has a right inverse, then
![]() $f_{X}$
is an isomorphism. Implicitly, an analogous statement holds true for left invertible elements in
$f_{X}$
is an isomorphism. Implicitly, an analogous statement holds true for left invertible elements in
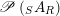 $\mathscr{P}\left(\text{}_{S}A_{R}\right)$
. At this level of generality the converse of this implication is not at all a trivial question. However, once assumed that
$\mathscr{P}\left(\text{}_{S}A_{R}\right)$
. At this level of generality the converse of this implication is not at all a trivial question. However, once assumed that
![]() $X$
belongs to a right dualizable datum
$X$
belongs to a right dualizable datum
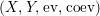 $(X,Y,\text{ev},\text{coev})$
with
$(X,Y,\text{ev},\text{coev})$
with
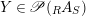 $Y\in \mathscr{P}(\text{}_{R}A_{S})$
such that
$Y\in \mathscr{P}(\text{}_{R}A_{S})$
such that
![]() $f_{X}$
is an isomorphism and that
$f_{X}$
is an isomorphism and that
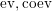 $\text{ev},\text{coev}$
satisfy equations (8) and (9), then one can construct a new submonoid
$\text{ev},\text{coev}$
satisfy equations (8) and (9), then one can construct a new submonoid
![]() $R^{\prime }$
of
$R^{\prime }$
of
![]() $A$
in such a way that
$A$
in such a way that
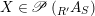 $X\in \mathscr{P}\left(\text{}_{R^{\prime }}A_{S}\right)$
is right invertible. The complete proof of this fact is included in the Appendix; see Theorem A.4. On the other hand, one can define a right invertible
$X\in \mathscr{P}\left(\text{}_{R^{\prime }}A_{S}\right)$
is right invertible. The complete proof of this fact is included in the Appendix; see Theorem A.4. On the other hand, one can define a right invertible
![]() $(R,S)$
-sub-bimodule as a sub-bimodule
$(R,S)$
-sub-bimodule as a sub-bimodule
![]() $X$
of
$X$
of
![]() $A$
whose associated morphism
$A$
whose associated morphism
![]() $f_{X}$
is an isomorphism. This was in fact the approach adopted in [Reference EL Kaoutit and Gómez-Torrecillas8, Reference Gómez-Torrecillas and Mesablishvili12, Reference Masuoka21]. It is noteworthy to mention that these arguments show in fact that our approach runs in a different direction.
$f_{X}$
is an isomorphism. This was in fact the approach adopted in [Reference EL Kaoutit and Gómez-Torrecillas8, Reference Gómez-Torrecillas and Mesablishvili12, Reference Masuoka21]. It is noteworthy to mention that these arguments show in fact that our approach runs in a different direction.
1.2 The group of invertible sub-bimodules
Before introducing the set of two-sided invertible sub-bimodules, which will be our main object of study in the forthcoming sections, this lemma is needed:
Lemma 1.9. Let
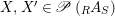 $X,X^{\prime }\in \mathscr{P}\left(\text{}_{R}A_{S}\right)$
have right inverses
$X,X^{\prime }\in \mathscr{P}\left(\text{}_{R}A_{S}\right)$
have right inverses
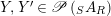 $Y,Y^{\prime }\in \mathscr{P}\left(\text{}_{S}A_{R}\right)$
respectively, as in Definition 1.1. Then the maps
$Y,Y^{\prime }\in \mathscr{P}\left(\text{}_{S}A_{R}\right)$
respectively, as in Definition 1.1. Then the maps
![]() $\pmb{\unicode[STIX]{x1D719}}_{Y,Y^{\prime }}$
and
$\pmb{\unicode[STIX]{x1D719}}_{Y,Y^{\prime }}$
and
![]() $\pmb{\unicode[STIX]{x1D713}}_{X^{\prime },X}$
given by the formulas (11), (12), yield an isomorphism
$\pmb{\unicode[STIX]{x1D713}}_{X^{\prime },X}$
given by the formulas (11), (12), yield an isomorphism
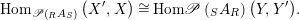 $$\begin{eqnarray}\text{Hom}_{\mathscr{P}\left(\text{}_{R}A_{S}\right)}\left(X^{\prime },X\right)\cong \text{Hom}\mathscr{P}\left(\text{}_{S}A_{R}\right)\left(Y,Y^{\prime }\right)\!.\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}_{\mathscr{P}\left(\text{}_{R}A_{S}\right)}\left(X^{\prime },X\right)\cong \text{Hom}\mathscr{P}\left(\text{}_{S}A_{R}\right)\left(Y,Y^{\prime }\right)\!.\end{eqnarray}$$
Moreover, we have
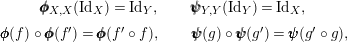 $$\begin{eqnarray}\displaystyle & \pmb{\unicode[STIX]{x1D719}}_{X,X}(\text{Id}_{X})=\text{Id}_{Y},\qquad \pmb{\unicode[STIX]{x1D713}}_{Y,Y}(\text{Id}_{Y})=\text{Id}_{X}, & \displaystyle \nonumber\\ \displaystyle & \pmb{\unicode[STIX]{x1D719}}(f)\circ \pmb{\unicode[STIX]{x1D719}}(f^{\prime })=\pmb{\unicode[STIX]{x1D719}}(f^{\prime }\circ f),\qquad \pmb{\unicode[STIX]{x1D713}}(g)\circ \pmb{\unicode[STIX]{x1D713}}(g^{\prime })=\pmb{\unicode[STIX]{x1D713}}(g^{\prime }\circ g), & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \pmb{\unicode[STIX]{x1D719}}_{X,X}(\text{Id}_{X})=\text{Id}_{Y},\qquad \pmb{\unicode[STIX]{x1D713}}_{Y,Y}(\text{Id}_{Y})=\text{Id}_{X}, & \displaystyle \nonumber\\ \displaystyle & \pmb{\unicode[STIX]{x1D719}}(f)\circ \pmb{\unicode[STIX]{x1D719}}(f^{\prime })=\pmb{\unicode[STIX]{x1D719}}(f^{\prime }\circ f),\qquad \pmb{\unicode[STIX]{x1D713}}(g)\circ \pmb{\unicode[STIX]{x1D713}}(g^{\prime })=\pmb{\unicode[STIX]{x1D713}}(g^{\prime }\circ g), & \displaystyle \nonumber\end{eqnarray}$$
where in the last two equations different
![]() $\pmb{\unicode[STIX]{x1D719}}$
’s and
$\pmb{\unicode[STIX]{x1D719}}$
’s and
![]() $\pmb{\unicode[STIX]{x1D713}}$
’s are employed.
$\pmb{\unicode[STIX]{x1D713}}$
’s are employed.
Proof. First note that the required isomorphism is obtained, using the adjunctions of Proposition 1.4, as follows:
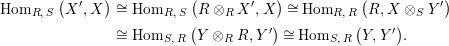 $$\begin{eqnarray}\displaystyle \text{Hom}_{R,\,S}\left(X^{\prime },X\right) & \cong & \displaystyle \text{Hom}_{R,\,S}\left(R\otimes _{R}X^{\prime },X\right)\cong \text{Hom}_{R,\,R}\left(R,X\otimes _{S}Y^{\prime }\right)\nonumber\\ \displaystyle & \cong & \displaystyle \text{Hom}_{S,\,R}\left(Y\otimes _{R}R,Y^{\prime }\right)\cong \text{Hom}_{S,\,R}\left(Y,Y^{\prime }\right)\!.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{Hom}_{R,\,S}\left(X^{\prime },X\right) & \cong & \displaystyle \text{Hom}_{R,\,S}\left(R\otimes _{R}X^{\prime },X\right)\cong \text{Hom}_{R,\,R}\left(R,X\otimes _{S}Y^{\prime }\right)\nonumber\\ \displaystyle & \cong & \displaystyle \text{Hom}_{S,\,R}\left(Y\otimes _{R}R,Y^{\prime }\right)\cong \text{Hom}_{S,\,R}\left(Y,Y^{\prime }\right)\!.\nonumber\end{eqnarray}$$
By (7), it is clear that
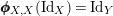 $\pmb{\unicode[STIX]{x1D719}}_{X,X}(\text{Id}_{X})=\text{Id}_{Y}$
and
$\pmb{\unicode[STIX]{x1D719}}_{X,X}(\text{Id}_{X})=\text{Id}_{Y}$
and
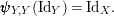 $\pmb{\unicode[STIX]{x1D713}}_{Y,Y}(\text{Id}_{Y})=\text{Id}_{X}.$
The following diagrams show that
$\pmb{\unicode[STIX]{x1D713}}_{Y,Y}(\text{Id}_{Y})=\text{Id}_{X}.$
The following diagrams show that
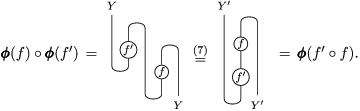
If we reflect horizontally the diagrammatic proof above we get
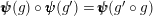 $\pmb{\unicode[STIX]{x1D713}}(g)\circ \pmb{\unicode[STIX]{x1D713}}(g^{\prime })=\pmb{\unicode[STIX]{x1D713}}(g^{\prime }\circ g)$
.◻
$\pmb{\unicode[STIX]{x1D713}}(g)\circ \pmb{\unicode[STIX]{x1D713}}(g^{\prime })=\pmb{\unicode[STIX]{x1D713}}(g^{\prime }\circ g)$
.◻
Definition 1.10. Let
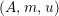 $(A,m,u)$
be a monoid in
$(A,m,u)$
be a monoid in
![]() ${\mathcal{M}}$
and
${\mathcal{M}}$
and
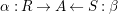 $\unicode[STIX]{x1D6FC}:R\rightarrow A\leftarrow S:\unicode[STIX]{x1D6FD}$
two morphisms of monoids. We define
$\unicode[STIX]{x1D6FC}:R\rightarrow A\leftarrow S:\unicode[STIX]{x1D6FD}$
two morphisms of monoids. We define
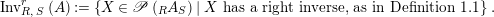 $$\begin{eqnarray}\text{Inv}_{R,\,S}^{r}\left(A\right):=\left\{X\in \mathscr{P}\left(\text{}_{R}A_{S}\right)\mid X\text{ has a right inverse, as in Definition 1.1}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\text{Inv}_{R,\,S}^{r}\left(A\right):=\left\{X\in \mathscr{P}\left(\text{}_{R}A_{S}\right)\mid X\text{ has a right inverse, as in Definition 1.1}\right\}.\end{eqnarray}$$
Similarly, one can define
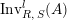 $\text{Inv}_{R,\,S}^{l}(A)$
; interchanging
$\text{Inv}_{R,\,S}^{l}(A)$
; interchanging
![]() $R$
by
$R$
by
![]() $S$
, one defines
$S$
, one defines
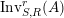 $\text{Inv}_{S,R}^{r}(A)$
and
$\text{Inv}_{S,R}^{r}(A)$
and
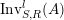 $\text{Inv}_{S,R}^{l}(A)$
.
$\text{Inv}_{S,R}^{l}(A)$
.
The following lemma establishes a functorial relation between the left- and right-hand sides versions of the previous definition.
Lemma 1.11. Consider
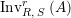 $\text{Inv}_{R,\,S}^{r}\left(A\right)$
and
$\text{Inv}_{R,\,S}^{r}\left(A\right)$
and
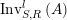 $\text{Inv}_{S,R}^{l}\left(A\right)$
as full subcategories of
$\text{Inv}_{S,R}^{l}\left(A\right)$
as full subcategories of
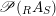 $\mathscr{P}(\text{}_{R}A_{S})$
and
$\mathscr{P}(\text{}_{R}A_{S})$
and
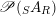 $\mathscr{P}(\text{}_{S}A_{R})$
, respectively. Then there is an isomorphism of categories
$\mathscr{P}(\text{}_{S}A_{R})$
, respectively. Then there is an isomorphism of categories
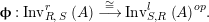 $$\begin{eqnarray}\boldsymbol{\boldsymbol{\unicode[STIX]{x1D719}}}:\text{Inv}_{R,\,S}^{r}\left(A\right)\overset{\cong }{\longrightarrow }\text{Inv}_{S,R}^{l}\left(A\right)^{op}\!.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{\boldsymbol{\unicode[STIX]{x1D719}}}:\text{Inv}_{R,\,S}^{r}\left(A\right)\overset{\cong }{\longrightarrow }\text{Inv}_{S,R}^{l}\left(A\right)^{op}\!.\end{eqnarray}$$
Proof. First notice that both
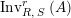 $\text{Inv}_{R,\,S}^{r}\left(A\right)$
and
$\text{Inv}_{R,\,S}^{r}\left(A\right)$
and
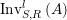 $\text{Inv}_{S,R}^{l}\left(A\right)$
are regarded as skeletal categories, in the sense that any two isomorphic objects are identical [Reference Lane20, page 91]. Therefore, in view of Lemma 1.5, if
$\text{Inv}_{S,R}^{l}\left(A\right)$
are regarded as skeletal categories, in the sense that any two isomorphic objects are identical [Reference Lane20, page 91]. Therefore, in view of Lemma 1.5, if
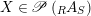 $X\in \mathscr{P}\left(\text{}_{R}A_{S}\right)$
has a right inverse, then this inverse is unique and denoted by
$X\in \mathscr{P}\left(\text{}_{R}A_{S}\right)$
has a right inverse, then this inverse is unique and denoted by
![]() $X^{r}$
. Thus to each object
$X^{r}$
. Thus to each object
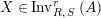 $X\in \text{Inv}_{R,\,S}^{r}\left(A\right)$
it corresponds a unique object
$X\in \text{Inv}_{R,\,S}^{r}\left(A\right)$
it corresponds a unique object
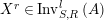 $X^{r}\in \text{Inv}_{S,R}^{l}\left(A\right)$
. This establishes a bijection at the level of objects. By Lemma 1.9 we know that the maps
$X^{r}\in \text{Inv}_{S,R}^{l}\left(A\right)$
. This establishes a bijection at the level of objects. By Lemma 1.9 we know that the maps
![]() $\pmb{\unicode[STIX]{x1D719}}$
of equation (11) induce isomorphisms
$\pmb{\unicode[STIX]{x1D719}}$
of equation (11) induce isomorphisms
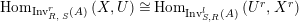 $\text{Hom}_{\text{Inv}_{R,\,S}^{r}\left(A\right)}\left(X,U\right)\cong \text{Hom}_{\text{Inv}_{S,R}^{l}\left(A\right)}\left(U^{r},X^{r}\right)$
, which, by the last equations of that Lemma, give the desired contravariant category isomorphism
$\text{Hom}_{\text{Inv}_{R,\,S}^{r}\left(A\right)}\left(X,U\right)\cong \text{Hom}_{\text{Inv}_{S,R}^{l}\left(A\right)}\left(U^{r},X^{r}\right)$
, which, by the last equations of that Lemma, give the desired contravariant category isomorphism
![]() $\boldsymbol{\boldsymbol{\unicode[STIX]{x1D719}}}.$
◻
$\boldsymbol{\boldsymbol{\unicode[STIX]{x1D719}}}.$
◻
The image of an element
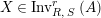 $X\in \text{Inv}_{R,\,S}^{r}\left(A\right)$
by the functor
$X\in \text{Inv}_{R,\,S}^{r}\left(A\right)$
by the functor
![]() $\boldsymbol{\boldsymbol{\unicode[STIX]{x1D719}}}$
of Lemma 1.11 will be denoted by
$\boldsymbol{\boldsymbol{\unicode[STIX]{x1D719}}}$
of Lemma 1.11 will be denoted by
![]() $X^{r}$
. The set of two-sided invertible sub-bimodules is then defined in the following way:
$X^{r}$
. The set of two-sided invertible sub-bimodules is then defined in the following way:
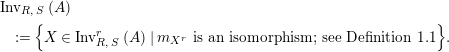 $$\begin{eqnarray}\displaystyle & & \displaystyle \text{Inv}_{R,\,S}\left(A\right)\nonumber\\ \displaystyle & & \displaystyle \quad :=\Big\{X\in \text{Inv}_{R,\,S}^{r}\left(A\right)\mid m_{X^{r}}\text{ is an isomorphism; see Definition 1.1}\Big\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{Inv}_{R,\,S}\left(A\right)\nonumber\\ \displaystyle & & \displaystyle \quad :=\Big\{X\in \text{Inv}_{R,\,S}^{r}\left(A\right)\mid m_{X^{r}}\text{ is an isomorphism; see Definition 1.1}\Big\}.\end{eqnarray}$$
One shows the following equivalent description of this set
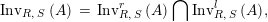 $$\begin{eqnarray}\text{Inv}_{R,\,S}\left(A\right)\,=\,\text{Inv}_{R,\,S}^{r}\left(A\right)\bigcap \mathop{\text{Inv}}_{R,\,S}^{l}\left(A\right)\!,\end{eqnarray}$$
$$\begin{eqnarray}\text{Inv}_{R,\,S}\left(A\right)\,=\,\text{Inv}_{R,\,S}^{r}\left(A\right)\bigcap \mathop{\text{Inv}}_{R,\,S}^{l}\left(A\right)\!,\end{eqnarray}$$
where the intersection is that of two subsets of
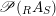 $\mathscr{P}(\text{}_{R}A_{S})$
.
$\mathscr{P}(\text{}_{R}A_{S})$
.
Let
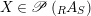 $X\in \mathscr{P}\left(\text{}_{R}A_{S}\right)$
and
$X\in \mathscr{P}\left(\text{}_{R}A_{S}\right)$
and
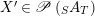 $X^{\prime }\in \mathscr{P}\left(\text{}_{S}A_{T}\right)$
, where
$X^{\prime }\in \mathscr{P}\left(\text{}_{S}A_{T}\right)$
, where
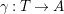 $\unicode[STIX]{x1D6FE}:T\rightarrow A$
is another morphism of monoids. The image of the morphism
$\unicode[STIX]{x1D6FE}:T\rightarrow A$
is another morphism of monoids. The image of the morphism
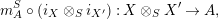 $$\begin{eqnarray}m_{A}^{S}\circ (i_{X}\otimes _{S}i_{X^{\prime }}):X\otimes _{S}X^{\prime }\rightarrow A,\end{eqnarray}$$
$$\begin{eqnarray}m_{A}^{S}\circ (i_{X}\otimes _{S}i_{X^{\prime }}):X\otimes _{S}X^{\prime }\rightarrow A,\end{eqnarray}$$
will be denoted by
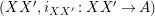 $(XX^{\prime },i_{XX^{\prime }}:XX^{\prime }\rightarrow A)$
, which will be considered as an element in
$(XX^{\prime },i_{XX^{\prime }}:XX^{\prime }\rightarrow A)$
, which will be considered as an element in
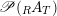 $\mathscr{P}(\text{}_{R}A_{T})$
.
$\mathscr{P}(\text{}_{R}A_{T})$
.
Proposition 1.12. Let
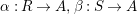 $\unicode[STIX]{x1D6FC}:R\rightarrow A,\unicode[STIX]{x1D6FD}:S\rightarrow A$
and
$\unicode[STIX]{x1D6FC}:R\rightarrow A,\unicode[STIX]{x1D6FD}:S\rightarrow A$
and
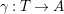 $\unicode[STIX]{x1D6FE}:T\rightarrow A$
be morphisms of monoids in
$\unicode[STIX]{x1D6FE}:T\rightarrow A$
be morphisms of monoids in
![]() ${\mathcal{M}}$
. Let
${\mathcal{M}}$
. Let
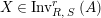 $X\in \text{Inv}_{R,\,S}^{r}\left(A\right)$
and
$X\in \text{Inv}_{R,\,S}^{r}\left(A\right)$
and
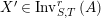 $X^{\prime }\in \text{Inv}_{S,T}^{r}\left(A\right)$
with right inverses
$X^{\prime }\in \text{Inv}_{S,T}^{r}\left(A\right)$
with right inverses
![]() $Y$
and
$Y$
and
![]() $Y^{\prime }$
, respectively. Then
$Y^{\prime }$
, respectively. Then
-
(i)
 $m_{A}^{S}\circ (i_{X}\otimes _{S}i_{X^{\prime }})$
and
$m_{A}^{S}\circ (i_{X}\otimes _{S}i_{X^{\prime }})$
and
 $m_{A}^{S}\circ (i_{Y^{\prime }}\otimes _{S}i_{Y})$
are monomorphisms that is
$m_{A}^{S}\circ (i_{Y^{\prime }}\otimes _{S}i_{Y})$
are monomorphisms that is
 $X\otimes _{S}X^{\prime }\cong XX^{\prime }$
and
$X\otimes _{S}X^{\prime }\cong XX^{\prime }$
and
 $Y^{\prime }\otimes _{S}Y\cong Y^{\prime }Y$
, as
$Y^{\prime }\otimes _{S}Y\cong Y^{\prime }Y$
, as
 $(R,T)$
-bimodules.
$(R,T)$
-bimodules. -
(ii)
 $X\otimes _{S}X^{\prime }\in \text{Inv}_{R,T}^{r}\left(A\right)$
and its right inverse is
$X\otimes _{S}X^{\prime }\in \text{Inv}_{R,T}^{r}\left(A\right)$
and its right inverse is
 $Y^{\prime }\otimes _{S}Y$
.
$Y^{\prime }\otimes _{S}Y$
.
Moreover, we have a functor
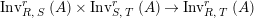 $\text{Inv}_{R,\,S}^{r}\left(A\right)\times \text{Inv}_{S,\,T}^{r}\left(A\right)\rightarrow \text{Inv}_{R,\,T}^{r}\left(A\right)$
.
$\text{Inv}_{R,\,S}^{r}\left(A\right)\times \text{Inv}_{S,\,T}^{r}\left(A\right)\rightarrow \text{Inv}_{R,\,T}^{r}\left(A\right)$
.
Proof.
![]() $(1)$
By Proposition 1.4, the functor
$(1)$
By Proposition 1.4, the functor
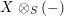 $X\otimes _{S}(-)$
is a right adjoint and hence left exact so that
$X\otimes _{S}(-)$
is a right adjoint and hence left exact so that
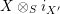 $X\otimes _{S}i_{X^{\prime }}$
is a monomorphism. By Corollary 1.7, the morphism
$X\otimes _{S}i_{X^{\prime }}$
is a monomorphism. By Corollary 1.7, the morphism
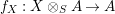 $f_{X}:X\otimes _{S}A\rightarrow A$
is an isomorphism. Thus
$f_{X}:X\otimes _{S}A\rightarrow A$
is an isomorphism. Thus
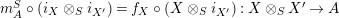 $m_{A}^{S}\circ (i_{X}\otimes _{S}i_{X^{\prime }})=f_{X}\circ (X\otimes _{S}i_{X^{\prime }}):X\otimes _{S}X^{\prime }\rightarrow A$
is a monomorphism. Similarly, using the fact that the functor
$m_{A}^{S}\circ (i_{X}\otimes _{S}i_{X^{\prime }})=f_{X}\circ (X\otimes _{S}i_{X^{\prime }}):X\otimes _{S}X^{\prime }\rightarrow A$
is a monomorphism. Similarly, using the fact that the functor
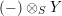 $(-)\otimes _{S}Y$
is a right adjoint (Proposition 1.4) and that
$(-)\otimes _{S}Y$
is a right adjoint (Proposition 1.4) and that
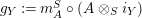 $g_{Y}:=m_{A}^{S}\circ (A\otimes _{S}i_{Y})$
is an isomorphism (Corollary 1.7) one gets that
$g_{Y}:=m_{A}^{S}\circ (A\otimes _{S}i_{Y})$
is an isomorphism (Corollary 1.7) one gets that
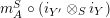 $m_{A}^{S}\circ (i_{Y^{\prime }}\otimes _{S}i_{Y})$
is a monomorphism too.
$m_{A}^{S}\circ (i_{Y^{\prime }}\otimes _{S}i_{Y})$
is a monomorphism too.
![]() $(2)$
Define
$(2)$
Define
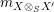 $m_{X\otimes _{S}X^{\prime }}$
and
$m_{X\otimes _{S}X^{\prime }}$
and
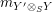 $m_{Y^{\prime }\otimes _{S}Y}$
diagrammatically by setting
$m_{Y^{\prime }\otimes _{S}Y}$
diagrammatically by setting

Now, using equation (3) for
![]() $X^{\prime }$
and
$X^{\prime }$
and
![]() $X$
, one gets the same equality for
$X$
, one gets the same equality for
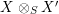 $X\otimes _{S}X^{\prime }$
as follows.
$X\otimes _{S}X^{\prime }$
as follows.
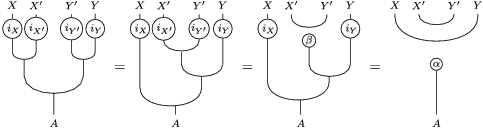
The same diagrammatic proof, once applied the substitutions
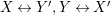 $X\leftrightarrow Y^{\prime },Y\leftrightarrow X^{\prime }$
and
$X\leftrightarrow Y^{\prime },Y\leftrightarrow X^{\prime }$
and
![]() $\unicode[STIX]{x1D6FC}\leftrightarrow \unicode[STIX]{x1D6FE}$
, yields (4) for
$\unicode[STIX]{x1D6FC}\leftrightarrow \unicode[STIX]{x1D6FE}$
, yields (4) for
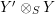 $Y^{\prime }\otimes _{S}Y$
using the corresponding equality for
$Y^{\prime }\otimes _{S}Y$
using the corresponding equality for
![]() $Y$
and
$Y$
and
![]() $Y^{\prime }$
. The last statement is clear.◻
$Y^{\prime }$
. The last statement is clear.◻
Corollary 1.13. Assume that
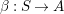 $\unicode[STIX]{x1D6FD}:S\rightarrow A$
is a monomorphism. Then
$\unicode[STIX]{x1D6FD}:S\rightarrow A$
is a monomorphism. Then
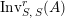 $\text{Inv}_{S,\,S}^{r}(A)$
is a monoid where the multiplication of
$\text{Inv}_{S,\,S}^{r}(A)$
is a monoid where the multiplication of
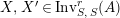 $X,X^{\prime }\in \text{Inv}_{S,\,S}^{r}(A)$
is given by
$X,X^{\prime }\in \text{Inv}_{S,\,S}^{r}(A)$
is given by
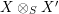 $X\otimes _{S}X^{\prime }$
with monomorphism
$X\otimes _{S}X^{\prime }$
with monomorphism
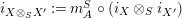 $i_{X\otimes _{S}X^{\prime }}:=m_{A}^{S}\circ (i_{X}\otimes _{S}i_{X^{\prime }})$
. The neutral element is
$i_{X\otimes _{S}X^{\prime }}:=m_{A}^{S}\circ (i_{X}\otimes _{S}i_{X^{\prime }})$
. The neutral element is
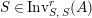 $S\in \text{Inv}_{S,\,S}^{r}(A)$
via
$S\in \text{Inv}_{S,\,S}^{r}(A)$
via
![]() $\unicode[STIX]{x1D6FD}$
. Moreover,
$\unicode[STIX]{x1D6FD}$
. Moreover,
 $\text{Inv}_{S,\,S}(A)$
is the group of units of this monoid.
$\text{Inv}_{S,\,S}(A)$
is the group of units of this monoid.
Proof. Let
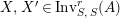 $X,X^{\prime }\in \text{Inv}_{S,\,S}^{r}(A)$
. By Proposition 1.12, we have
$X,X^{\prime }\in \text{Inv}_{S,\,S}^{r}(A)$
. By Proposition 1.12, we have
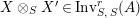 $X\otimes _{S}X^{\prime }\in \text{Inv}_{S,\,S}^{r}(A)$
, with monomorphism
$X\otimes _{S}X^{\prime }\in \text{Inv}_{S,\,S}^{r}(A)$
, with monomorphism
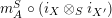 $m_{A}^{S}\circ (i_{X}\otimes _{S}i_{X^{\prime }})$
, so that
$m_{A}^{S}\circ (i_{X}\otimes _{S}i_{X^{\prime }})$
, so that
![]() $\otimes _{S}$
is a well-defined multiplication for
$\otimes _{S}$
is a well-defined multiplication for
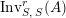 $\text{Inv}_{S,\,S}^{r}(A)$
. It is clearly associative. Note that
$\text{Inv}_{S,\,S}^{r}(A)$
. It is clearly associative. Note that
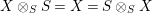 $X\otimes _{S}S=X=S\otimes _{S}X$
as sub-bimodules of
$X\otimes _{S}S=X=S\otimes _{S}X$
as sub-bimodules of
![]() $A$
(these equalities make sense as the definition of subobject is given up to isomorphism, cf. [Reference Lane20, page 122]). Thus
$A$
(these equalities make sense as the definition of subobject is given up to isomorphism, cf. [Reference Lane20, page 122]). Thus
![]() $S$
is the neutral element for this operation.
$S$
is the neutral element for this operation.
Let us check the last statement. For this consider
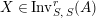 $X\in \text{Inv}_{S,\,S}^{r}(A)$
and
$X\in \text{Inv}_{S,\,S}^{r}(A)$
and
![]() $Y$
its right inverse (as in Definition 1.1). Then, by equation (3), we have
$Y$
its right inverse (as in Definition 1.1). Then, by equation (3), we have
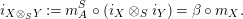 $$\begin{eqnarray}i_{X\otimes _{S}Y}:=m_{A}^{S}\circ (i_{X}\otimes _{S}i_{Y})=\unicode[STIX]{x1D6FD}\circ m_{X}.\end{eqnarray}$$
$$\begin{eqnarray}i_{X\otimes _{S}Y}:=m_{A}^{S}\circ (i_{X}\otimes _{S}i_{Y})=\unicode[STIX]{x1D6FD}\circ m_{X}.\end{eqnarray}$$
This means that
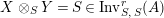 $X\otimes _{S}Y=S\in \text{Inv}_{S,\,S}^{r}(A)$
, as
$X\otimes _{S}Y=S\in \text{Inv}_{S,\,S}^{r}(A)$
, as
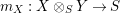 $m_{X}:X\otimes _{S}Y\rightarrow S$
is an isomorphism. Therefore, any element in
$m_{X}:X\otimes _{S}Y\rightarrow S$
is an isomorphism. Therefore, any element in
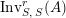 $\text{Inv}_{S,\,S}^{r}(A)$
is already right invertible w.r.t. to the multiplication
$\text{Inv}_{S,\,S}^{r}(A)$
is already right invertible w.r.t. to the multiplication
![]() $\otimes _{S}$
. Thus an element
$\otimes _{S}$
. Thus an element
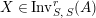 $X\in \text{Inv}_{S,\,S}^{r}(A)$
belongs to the group of units if and only if it has a left
$X\in \text{Inv}_{S,\,S}^{r}(A)$
belongs to the group of units if and only if it has a left
![]() $\otimes _{S}$
-inverse. Note that, in this case, the left and the right inverses should coincide as we are in a monoid. Therefore, the element
$\otimes _{S}$
-inverse. Note that, in this case, the left and the right inverses should coincide as we are in a monoid. Therefore, the element
![]() $X$
is
$X$
is
![]() $\otimes _{S}$
-invertible if and only if
$\otimes _{S}$
-invertible if and only if
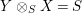 $Y\otimes _{S}X=S$
. Now,
$Y\otimes _{S}X=S$
. Now,
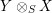 $Y\otimes _{S}X$
is sub-bimodule of
$Y\otimes _{S}X$
is sub-bimodule of
![]() $A$
via
$A$
via
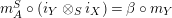 $m_{A}^{S}\circ (i_{Y}\otimes _{S}i_{X})=\unicode[STIX]{x1D6FD}\circ m_{Y}$
by equation (4). Thus, the equality
$m_{A}^{S}\circ (i_{Y}\otimes _{S}i_{X})=\unicode[STIX]{x1D6FD}\circ m_{Y}$
by equation (4). Thus, the equality
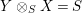 $Y\otimes _{S}X=S$
holds if and only if there is an isomorphism
$Y\otimes _{S}X=S$
holds if and only if there is an isomorphism
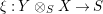 $\unicode[STIX]{x1D709}:Y\otimes _{S}X\rightarrow S$
of bimodules over
$\unicode[STIX]{x1D709}:Y\otimes _{S}X\rightarrow S$
of bimodules over
![]() $S$
such that
$S$
such that
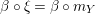 $\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D709}=\unicode[STIX]{x1D6FD}\circ m_{Y}$
. Since we are assuming
$\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D709}=\unicode[STIX]{x1D6FD}\circ m_{Y}$
. Since we are assuming
![]() $\unicode[STIX]{x1D6FD}$
to be a monomorphism, this equality is equivalent to say that
$\unicode[STIX]{x1D6FD}$
to be a monomorphism, this equality is equivalent to say that
![]() $m_{Y}$
is an isomorphism. This entails that
$m_{Y}$
is an isomorphism. This entails that
![]() $X$
is
$X$
is
![]() $\otimes _{S}$
- invertible if and only if
$\otimes _{S}$
- invertible if and only if
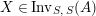 $X\in \text{Inv}_{S,\,S}(A)$
.◻
$X\in \text{Inv}_{S,\,S}(A)$
.◻
The group
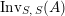 $\text{Inv}_{S,\,S}(A)$
, considered in Corollary 1.13, will also be denoted by
$\text{Inv}_{S,\,S}(A)$
, considered in Corollary 1.13, will also be denoted by
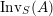 $\text{Inv}_{S}(A)$
.
$\text{Inv}_{S}(A)$
.
Proposition 1.14. Let
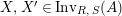 $X,X^{\prime }\in \text{Inv}_{R,\,S}(A)$
be two-sided invertible sub-bimodules of
$X,X^{\prime }\in \text{Inv}_{R,\,S}(A)$
be two-sided invertible sub-bimodules of
![]() $A$
with inverses
$A$
with inverses
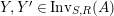 $Y,Y^{\prime }\in \text{Inv}_{S,R}(A)$
, respectively. Consider the category isomorphism
$Y,Y^{\prime }\in \text{Inv}_{S,R}(A)$
, respectively. Consider the category isomorphism
![]() $\boldsymbol{\boldsymbol{\unicode[STIX]{x1D719}}}$
of Lemma 1.11, and assume that there is a monomorphism
$\boldsymbol{\boldsymbol{\unicode[STIX]{x1D719}}}$
of Lemma 1.11, and assume that there is a monomorphism
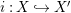 $i:X{\hookrightarrow}X^{\prime }$
of bimodules in
$i:X{\hookrightarrow}X^{\prime }$
of bimodules in
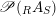 $\mathscr{P}(\text{}_{R}A_{S})$
(i.e., satisfying
$\mathscr{P}(\text{}_{R}A_{S})$
(i.e., satisfying
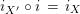 $i_{X^{\prime }}\circ i\,=\,i_{X}$
).
$i_{X^{\prime }}\circ i\,=\,i_{X}$
).
-
(1) The morphism
 $i$
is an isomorphism if and only if
$i$
is an isomorphism if and only if
 $\boldsymbol{\boldsymbol{\unicode[STIX]{x1D719}}}(i)$
is.
$\boldsymbol{\boldsymbol{\unicode[STIX]{x1D719}}}(i)$
is. -
(2) Assume further that there is a monomorphism of bimodules
 $j:Y{\hookrightarrow}Y^{\prime }$
in
$j:Y{\hookrightarrow}Y^{\prime }$
in
 $\mathscr{P}(\text{}_{S}A_{R})$
(i.e., satisfying
$\mathscr{P}(\text{}_{S}A_{R})$
(i.e., satisfying
 $i_{Y^{\prime }}\circ j\,=\,i_{Y}$
). Then both
$i_{Y^{\prime }}\circ j\,=\,i_{Y}$
). Then both
 $i$
and
$i$
and
 $j$
are isomorphisms that is
$j$
are isomorphisms that is
 $X=X^{\prime }$
and
$X=X^{\prime }$
and
 $Y=Y^{\prime }$
as elements in
$Y=Y^{\prime }$
as elements in
 $\text{Inv}_{R,\,S}\left(A\right)$
and
$\text{Inv}_{R,\,S}\left(A\right)$
and
 $\text{Inv}_{S,R}\left(A\right)$
, respectively.
$\text{Inv}_{S,R}\left(A\right)$
, respectively.
Proof.
![]() $(1)$
is trivial.
$(1)$
is trivial.
![]() $(2)$
From Lemma 1.11 we know that
$(2)$
From Lemma 1.11 we know that
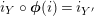 $i_{Y}\circ \boldsymbol{\boldsymbol{\unicode[STIX]{x1D719}}}(i)=i_{Y^{\prime }}$
. Thus
$i_{Y}\circ \boldsymbol{\boldsymbol{\unicode[STIX]{x1D719}}}(i)=i_{Y^{\prime }}$
. Thus
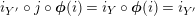 $i_{Y^{\prime }}\circ j\circ \boldsymbol{\boldsymbol{\unicode[STIX]{x1D719}}}(i)=i_{Y}\circ \boldsymbol{\boldsymbol{\unicode[STIX]{x1D719}}}(i)=i_{Y^{\prime }}$
. Since
$i_{Y^{\prime }}\circ j\circ \boldsymbol{\boldsymbol{\unicode[STIX]{x1D719}}}(i)=i_{Y}\circ \boldsymbol{\boldsymbol{\unicode[STIX]{x1D719}}}(i)=i_{Y^{\prime }}$
. Since
![]() $i_{Y^{\prime }}$
is a monomorphism, we get
$i_{Y^{\prime }}$
is a monomorphism, we get
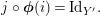 $j\circ \boldsymbol{\boldsymbol{\unicode[STIX]{x1D719}}}(i)=\text{Id}_{Y^{\prime }}.$
Similarly one proves that
$j\circ \boldsymbol{\boldsymbol{\unicode[STIX]{x1D719}}}(i)=\text{Id}_{Y^{\prime }}.$
Similarly one proves that
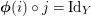 $\boldsymbol{\boldsymbol{\unicode[STIX]{x1D719}}}(i)\circ j=\text{Id}_{Y}$
. Thus
$\boldsymbol{\boldsymbol{\unicode[STIX]{x1D719}}}(i)\circ j=\text{Id}_{Y}$
. Thus
![]() $j$
and
$j$
and
![]() $\boldsymbol{\boldsymbol{\unicode[STIX]{x1D719}}}(i)$
are isomorphisms. By
$\boldsymbol{\boldsymbol{\unicode[STIX]{x1D719}}}(i)$
are isomorphisms. By
![]() $(1)$
, the morphism
$(1)$
, the morphism
![]() $i$
is an isomorphism too, and this finishes the proof.◻
$i$
is an isomorphism too, and this finishes the proof.◻
2 Miyashita action and invariant subobjects
In this section we assume that our base monoidal category
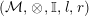 $({\mathcal{M}},\otimes _{},\mathbb{I},l,r)$
is also bicomplete. In what follows let
$({\mathcal{M}},\otimes _{},\mathbb{I},l,r)$
is also bicomplete. In what follows let
![]() $A,R$
and
$A,R$
and
![]() $S$
be three monoids in
$S$
be three monoids in
![]() ${\mathcal{M}}$
and
${\mathcal{M}}$
and
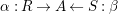 $\unicode[STIX]{x1D6FC}:R\rightarrow A\leftarrow S:\unicode[STIX]{x1D6FD}$
be morphisms of monoids which are monomorphisms in
$\unicode[STIX]{x1D6FC}:R\rightarrow A\leftarrow S:\unicode[STIX]{x1D6FD}$
be morphisms of monoids which are monomorphisms in
![]() ${\mathcal{M}}$
. We denote by
${\mathcal{M}}$
. We denote by
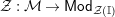 ${\mathcal{Z}}:{\mathcal{M}}\rightarrow \mathsf{Mod}_{{\mathcal{Z}}(\mathbb{I})}$
the functor
${\mathcal{Z}}:{\mathcal{M}}\rightarrow \mathsf{Mod}_{{\mathcal{Z}}(\mathbb{I})}$
the functor
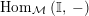 $\text{Hom}_{{\mathcal{M}}}\left(\mathbb{I},\,-\right)$
, where
$\text{Hom}_{{\mathcal{M}}}\left(\mathbb{I},\,-\right)$
, where
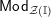 $\mathsf{Mod}_{{\mathcal{Z}}(\mathbb{I})}$
denotes the category of
$\mathsf{Mod}_{{\mathcal{Z}}(\mathbb{I})}$
denotes the category of
![]() ${\mathcal{Z}}(\mathbb{I})$
-modules. Analogously, we denote by
${\mathcal{Z}}(\mathbb{I})$
-modules. Analogously, we denote by
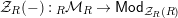 ${\mathcal{Z}}_{R}(-):\text{}_{R}{\mathcal{M}}_{R}\rightarrow \mathsf{Mod}_{{\mathcal{Z}}_{R}(R)}$
the functor
${\mathcal{Z}}_{R}(-):\text{}_{R}{\mathcal{M}}_{R}\rightarrow \mathsf{Mod}_{{\mathcal{Z}}_{R}(R)}$
the functor
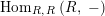 $\text{Hom}_{R,\,R}\left(R,\,-\right)$
, and similarly we consider
$\text{Hom}_{R,\,R}\left(R,\,-\right)$
, and similarly we consider
![]() ${\mathcal{Z}}_{S}(-)$
.
${\mathcal{Z}}_{S}(-)$
.
2.1 Miyashita action: Definition
In this subsection we introduce the Miyashita action in the context of monoidal categories. This is a map (group homomorphism) which connects
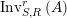 $\text{Inv}_{S,R}^{r}\left(A\right)$
(resp.
$\text{Inv}_{S,R}^{r}\left(A\right)$
(resp.
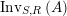 $\text{Inv}_{S,R}\left(A\right)$
) with the set of (iso)morphisms of
$\text{Inv}_{S,R}\left(A\right)$
) with the set of (iso)morphisms of
![]() ${\mathcal{Z}}(\mathbb{I})$
-algebras from
${\mathcal{Z}}(\mathbb{I})$
-algebras from
![]() ${\mathcal{Z}}_{S}(A)$
to
${\mathcal{Z}}_{S}(A)$
to
![]() ${\mathcal{Z}}_{R}(A)$
. The latter can be seen as the invariants (subalgebra) of
${\mathcal{Z}}_{R}(A)$
. The latter can be seen as the invariants (subalgebra) of
![]() $A$
with respect to
$A$
with respect to
![]() $S$
and
$S$
and
![]() $R$
, respectively (usually they are denoted by
$R$
, respectively (usually they are denoted by
![]() $A^{S}$
and
$A^{S}$
and
![]() $A^{R}$
respectively in the classical case).
$A^{R}$
respectively in the classical case).
Let
![]() $M$
be a left
$M$
be a left
![]() $S$
-module and let
$S$
-module and let
![]() $N$
be an
$N$
be an
![]() $A$
-bimodule. Consider the action
$A$
-bimodule. Consider the action
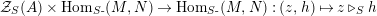 ${\mathcal{Z}}_{S}(A)\times \text{Hom}_{S\text{-}}(M,N)\rightarrow \text{Hom}_{S\text{-}}(M,N):(z,h)\mapsto z\rhd _{S}h$
defined by setting
${\mathcal{Z}}_{S}(A)\times \text{Hom}_{S\text{-}}(M,N)\rightarrow \text{Hom}_{S\text{-}}(M,N):(z,h)\mapsto z\rhd _{S}h$
defined by setting
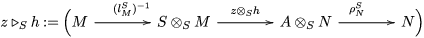
Similarly one defines the action
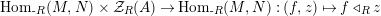 $\text{Hom}_{\text{-}R}(M,N)\times {\mathcal{Z}}_{R}(A)\rightarrow \text{Hom}_{\text{-}R}(M,N):(f,z)\mapsto f\lhd _{R}z$
. When
$\text{Hom}_{\text{-}R}(M,N)\times {\mathcal{Z}}_{R}(A)\rightarrow \text{Hom}_{\text{-}R}(M,N):(f,z)\mapsto f\lhd _{R}z$
. When
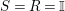 $S=R=\mathbb{I}$
we omit the subscripts and write
$S=R=\mathbb{I}$
we omit the subscripts and write
![]() $f\lhd z$
and
$f\lhd z$
and
![]() $z\rhd f$
.
$z\rhd f$
.
Lemma 2.1. Let
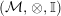 $({\mathcal{M}},\otimes ,\mathbb{I})$
be a monoidal category. Let
$({\mathcal{M}},\otimes ,\mathbb{I})$
be a monoidal category. Let
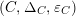 $(C,\unicode[STIX]{x1D6E5}_{C},\unicode[STIX]{x1D700}_{C})$
be a comonoid in
$(C,\unicode[STIX]{x1D6E5}_{C},\unicode[STIX]{x1D700}_{C})$
be a comonoid in
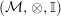 $({\mathcal{M}},\otimes ,\mathbb{I})$
and let
$({\mathcal{M}},\otimes ,\mathbb{I})$
and let
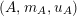 $\left(A,m_{A},u_{A}\right)$
be a monoid in
$\left(A,m_{A},u_{A}\right)$
be a monoid in
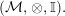 $({\mathcal{M}},\otimes ,\mathbb{I}).$
Then
$({\mathcal{M}},\otimes ,\mathbb{I}).$
Then
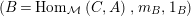 $$\begin{eqnarray}\left(B=\text{Hom}_{{\mathcal{M}}}\left(C,A\right),m_{B},1_{B}\right)\end{eqnarray}$$
$$\begin{eqnarray}\left(B=\text{Hom}_{{\mathcal{M}}}\left(C,A\right),m_{B},1_{B}\right)\end{eqnarray}$$
is a
![]() $\mathbb{Z}$
-algebra where, for all
$\mathbb{Z}$
-algebra where, for all
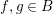 $f,g\in B$
$f,g\in B$
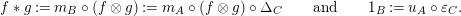 $$\begin{eqnarray}f\ast g:=m_{B}\circ \left(f\otimes g\right):=m_{A}\circ \left(f\otimes g\right)\circ \unicode[STIX]{x1D6E5}_{C}\qquad \text{and}\qquad 1_{B}:=u_{A}\circ \unicode[STIX]{x1D700}_{C}.\end{eqnarray}$$
$$\begin{eqnarray}f\ast g:=m_{B}\circ \left(f\otimes g\right):=m_{A}\circ \left(f\otimes g\right)\circ \unicode[STIX]{x1D6E5}_{C}\qquad \text{and}\qquad 1_{B}:=u_{A}\circ \unicode[STIX]{x1D700}_{C}.\end{eqnarray}$$
Proof. Straightforward. ◻
Since
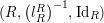 $(R,\left(l_{R}^{R}\right)^{-1}\!,\text{Id}_{R})$
is a comonoid and
$(R,\left(l_{R}^{R}\right)^{-1}\!,\text{Id}_{R})$
is a comonoid and
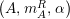 $\left(A,m_{A}^{R},\unicode[STIX]{x1D6FC}\right)$
is a monoid, both in
$\left(A,m_{A}^{R},\unicode[STIX]{x1D6FC}\right)$
is a monoid, both in
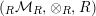 $\left(\text{}_{R}{\mathcal{M}}_{R},\otimes _{R},R\right)$
, we have that
$\left(\text{}_{R}{\mathcal{M}}_{R},\otimes _{R},R\right)$
, we have that
![]() ${\mathcal{Z}}_{R}(A)$
is a
${\mathcal{Z}}_{R}(A)$
is a
![]() $\mathbb{Z}$
-algebra by Lemma 2.1. Furthermore, since the base category is assumed to be Penrose, we have that
$\mathbb{Z}$
-algebra by Lemma 2.1. Furthermore, since the base category is assumed to be Penrose, we have that
 $R\otimes _{}t=t\otimes _{}R$
for every element
$R\otimes _{}t=t\otimes _{}R$
for every element
![]() $t$
in
$t$
in
![]() ${\mathcal{Z}}(\mathbb{I})$
which in fact defines an algebra map
${\mathcal{Z}}(\mathbb{I})$
which in fact defines an algebra map
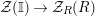 ${\mathcal{Z}}(\mathbb{I})\rightarrow {\mathcal{Z}}_{R}(R)$
so that
${\mathcal{Z}}(\mathbb{I})\rightarrow {\mathcal{Z}}_{R}(R)$
so that
![]() ${\mathcal{Z}}_{R}(R)$
becomes a commutative
${\mathcal{Z}}_{R}(R)$
becomes a commutative
![]() ${\mathcal{Z}}(\mathbb{I})$
-algebra. In this way, the map
${\mathcal{Z}}(\mathbb{I})$
-algebra. In this way, the map
![]() ${\mathcal{Z}}_{R}(\unicode[STIX]{x1D6FC})$
clearly induces a structure of
${\mathcal{Z}}_{R}(\unicode[STIX]{x1D6FC})$
clearly induces a structure of
![]() ${\mathcal{Z}}(\mathbb{I})$
-algebra on
${\mathcal{Z}}(\mathbb{I})$
-algebra on
![]() ${\mathcal{Z}}_{R}(A)$
. Explicitly, the unit
${\mathcal{Z}}_{R}(A)$
. Explicitly, the unit
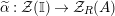 $\widetilde{\unicode[STIX]{x1D6FC}}:{\mathcal{Z}}(\mathbb{I})\rightarrow {\mathcal{Z}}_{R}(A)$
of this algebra maps an element
$\widetilde{\unicode[STIX]{x1D6FC}}:{\mathcal{Z}}(\mathbb{I})\rightarrow {\mathcal{Z}}_{R}(A)$
of this algebra maps an element
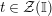 $t\in {\mathcal{Z}}(\mathbb{I})$
to
$t\in {\mathcal{Z}}(\mathbb{I})$
to
 $\unicode[STIX]{x1D6FC}\circ (R\otimes _{}t)\,=\,\unicode[STIX]{x1D6FC}\circ (t\otimes _{}R)$
which is an element in
$\unicode[STIX]{x1D6FC}\circ (R\otimes _{}t)\,=\,\unicode[STIX]{x1D6FC}\circ (t\otimes _{}R)$
which is an element in
![]() ${\mathcal{Z}}_{R}(A)$
. Similarly, one constructs
${\mathcal{Z}}_{R}(A)$
. Similarly, one constructs
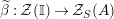 $\widetilde{\unicode[STIX]{x1D6FD}}:{\mathcal{Z}}(\mathbb{I})\rightarrow {\mathcal{Z}}_{S}(A)$
. On the other hand, one shows that the map
$\widetilde{\unicode[STIX]{x1D6FD}}:{\mathcal{Z}}(\mathbb{I})\rightarrow {\mathcal{Z}}_{S}(A)$
. On the other hand, one shows that the map
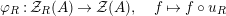 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{R}:{\mathcal{Z}}_{R}(A)\rightarrow {\mathcal{Z}}(A),\quad f\mapsto f\circ u_{R}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{R}:{\mathcal{Z}}_{R}(A)\rightarrow {\mathcal{Z}}(A),\quad f\mapsto f\circ u_{R}\end{eqnarray}$$
is multiplicative and satisfies
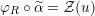 $\unicode[STIX]{x1D711}_{R}\circ \widetilde{\unicode[STIX]{x1D6FC}}={\mathcal{Z}}(u)$
, so that it is a
$\unicode[STIX]{x1D711}_{R}\circ \widetilde{\unicode[STIX]{x1D6FC}}={\mathcal{Z}}(u)$
, so that it is a
![]() ${\mathcal{Z}}(\mathbb{I})$
-algebras map. Moreover, by using that morphisms in
${\mathcal{Z}}(\mathbb{I})$
-algebras map. Moreover, by using that morphisms in
![]() ${\mathcal{Z}}_{R}(A)$
are of
${\mathcal{Z}}_{R}(A)$
are of
![]() $R$
-bimodules, one also gets that
$R$
-bimodules, one also gets that
![]() $\unicode[STIX]{x1D711}_{R}$
is always injective. In this way, both
$\unicode[STIX]{x1D711}_{R}$
is always injective. In this way, both
![]() ${\mathcal{Z}}_{R}(A)$
and
${\mathcal{Z}}_{R}(A)$
and
![]() ${\mathcal{Z}}_{S}(A)$
become
${\mathcal{Z}}_{S}(A)$
become
![]() ${\mathcal{Z}}(\mathbb{I})$
-subalgebras of
${\mathcal{Z}}(\mathbb{I})$
-subalgebras of
![]() ${\mathcal{Z}}(A)$
.
${\mathcal{Z}}(A)$
.
Proposition 2.2. For any
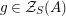 $g\in {\mathcal{Z}}_{S}(A)$
and
$g\in {\mathcal{Z}}_{S}(A)$
and
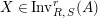 $X\in \text{Inv}_{R,\,S}^{r}(A)$
let
$X\in \text{Inv}_{R,\,S}^{r}(A)$
let
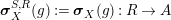 $\boldsymbol{\unicode[STIX]{x1D70E}}_{X}^{S,R}(g):=\boldsymbol{\unicode[STIX]{x1D70E}}_{X}(g):R\rightarrow A$
be defined by
$\boldsymbol{\unicode[STIX]{x1D70E}}_{X}^{S,R}(g):=\boldsymbol{\unicode[STIX]{x1D70E}}_{X}(g):R\rightarrow A$
be defined by
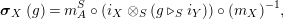 $$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D70E}}_{X}\left(g\right)=m_{A}^{S}\circ \left(i_{X}\otimes _{S}(g\rhd _{S}i_{Y})\right)\circ \left(m_{X}\right)^{-1}\!,\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D70E}}_{X}\left(g\right)=m_{A}^{S}\circ \left(i_{X}\otimes _{S}(g\rhd _{S}i_{Y})\right)\circ \left(m_{X}\right)^{-1}\!,\end{eqnarray}$$
where
![]() $Y$
is a right inverse of
$Y$
is a right inverse of
![]() $X$
. Then,
$X$
. Then,
![]() $\boldsymbol{\unicode[STIX]{x1D70E}}_{X}$
does not depend on the choice of
$\boldsymbol{\unicode[STIX]{x1D70E}}_{X}$
does not depend on the choice of
![]() $Y$
and the map
$Y$
and the map
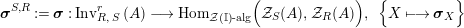 $$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D70E}}^{S,R}:=\boldsymbol{\unicode[STIX]{x1D70E}}:\text{Inv}_{R,\,S}^{r}\left(A\right)\longrightarrow \text{Hom}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}\Big({\mathcal{Z}}_{S}(A),{\mathcal{Z}}_{R}(A)\Big),\;\;\Big\{X\longmapsto \boldsymbol{\unicode[STIX]{x1D70E}}_{X}\Big\}\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D70E}}^{S,R}:=\boldsymbol{\unicode[STIX]{x1D70E}}:\text{Inv}_{R,\,S}^{r}\left(A\right)\longrightarrow \text{Hom}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}\Big({\mathcal{Z}}_{S}(A),{\mathcal{Z}}_{R}(A)\Big),\;\;\Big\{X\longmapsto \boldsymbol{\unicode[STIX]{x1D70E}}_{X}\Big\}\end{eqnarray}$$
is well defined.
Proof. First note that the right inverse
![]() $Y$
of
$Y$
of
![]() $X$
is unique up to isomorphism as shown in Lemma 1.5. Let us check that
$X$
is unique up to isomorphism as shown in Lemma 1.5. Let us check that
![]() $\boldsymbol{\unicode[STIX]{x1D70E}}_{X}\left(g\right)$
does not depend on this isomorphism. Thus, given another right inverse
$\boldsymbol{\unicode[STIX]{x1D70E}}_{X}\left(g\right)$
does not depend on this isomorphism. Thus, given another right inverse
![]() $Z$
of
$Z$
of
![]() $X$
, we want to check that the formula (18) is the same for both
$X$
, we want to check that the formula (18) is the same for both
![]() $Y$
and
$Y$
and
![]() $Z$
. That is, we need to check the following equality
$Z$
. That is, we need to check the following equality
 $$\begin{eqnarray}\displaystyle \boldsymbol{\unicode[STIX]{x1D70E}}_{X,Y}\left(g\right) & := & \displaystyle m_{A}^{S}\circ \left(i_{X}\otimes _{S}(g\rhd _{S}i_{Y})\right)\circ \left(m_{X}\right)^{-1}\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{S}\circ \left(i_{X}\otimes _{S}(g\rhd _{S}i_{Z})\right)\circ \left(m_{X}\right)^{-1}:=\boldsymbol{\unicode[STIX]{x1D70E}}_{X,Z}\left(g\right)\!.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{\unicode[STIX]{x1D70E}}_{X,Y}\left(g\right) & := & \displaystyle m_{A}^{S}\circ \left(i_{X}\otimes _{S}(g\rhd _{S}i_{Y})\right)\circ \left(m_{X}\right)^{-1}\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{S}\circ \left(i_{X}\otimes _{S}(g\rhd _{S}i_{Z})\right)\circ \left(m_{X}\right)^{-1}:=\boldsymbol{\unicode[STIX]{x1D70E}}_{X,Z}\left(g\right)\!.\nonumber\end{eqnarray}$$
The map
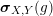 $\boldsymbol{\unicode[STIX]{x1D70E}}_{X,Y}(g)$
can be represented by the following diagram:
$\boldsymbol{\unicode[STIX]{x1D70E}}_{X,Y}(g)$
can be represented by the following diagram:
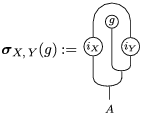
Using the isomorphisms stated in Corollary 1.5, we then have
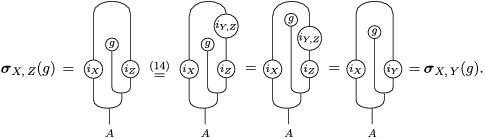
By a similar argument, one proves that the definition of this map does not depend on the representative of the equivalence class
![]() $(X,i_{X})$
. In other words if
$(X,i_{X})$
. In other words if
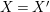 $X=X^{\prime }$
(i.e., there is an isomorphism
$X=X^{\prime }$
(i.e., there is an isomorphism
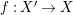 $f:X^{\prime }\rightarrow X$
such that
$f:X^{\prime }\rightarrow X$
such that
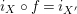 $i_{X}\circ f=i_{X^{\prime }}$
), then
$i_{X}\circ f=i_{X^{\prime }}$
), then
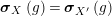 $\boldsymbol{\unicode[STIX]{x1D70E}}_{X}\left(g\right)=\boldsymbol{\unicode[STIX]{x1D70E}}_{X^{\prime }}\left(g\right)$
. On the other hand, the morphism
$\boldsymbol{\unicode[STIX]{x1D70E}}_{X}\left(g\right)=\boldsymbol{\unicode[STIX]{x1D70E}}_{X^{\prime }}\left(g\right)$
. On the other hand, the morphism
![]() $\boldsymbol{\unicode[STIX]{x1D70E}}_{X}\left(g\right)$
is a morphism in
$\boldsymbol{\unicode[STIX]{x1D70E}}_{X}\left(g\right)$
is a morphism in
![]() $_{R}{\mathcal{M}}_{R}$
being the composition of morphisms in
$_{R}{\mathcal{M}}_{R}$
being the composition of morphisms in
![]() $_{R}{\mathcal{M}}_{R}$
. Therefore,
$_{R}{\mathcal{M}}_{R}$
. Therefore,
![]() $\boldsymbol{\unicode[STIX]{x1D70E}}_{X}\left(g\right)$
is an element in
$\boldsymbol{\unicode[STIX]{x1D70E}}_{X}\left(g\right)$
is an element in
![]() ${\mathcal{Z}}_{R}(A)$
.
${\mathcal{Z}}_{R}(A)$
.
We have to check that
![]() $\boldsymbol{\unicode[STIX]{x1D70E}}_{X}$
is a
$\boldsymbol{\unicode[STIX]{x1D70E}}_{X}$
is a
![]() ${\mathcal{Z}}(\mathbb{I})$
-algebra map. To this aim, given
${\mathcal{Z}}(\mathbb{I})$
-algebra map. To this aim, given
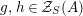 $g,h\in {\mathcal{Z}}_{S}(A)$
, we first show that
$g,h\in {\mathcal{Z}}_{S}(A)$
, we first show that
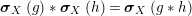 $\boldsymbol{\unicode[STIX]{x1D70E}}_{X}\left(g\right)\ast \boldsymbol{\unicode[STIX]{x1D70E}}_{X}\left(h\right)=\boldsymbol{\unicode[STIX]{x1D70E}}_{X}\left(g\ast h\right)$
. Using the diagrammatic notation, we have
$\boldsymbol{\unicode[STIX]{x1D70E}}_{X}\left(g\right)\ast \boldsymbol{\unicode[STIX]{x1D70E}}_{X}\left(h\right)=\boldsymbol{\unicode[STIX]{x1D70E}}_{X}\left(g\ast h\right)$
. Using the diagrammatic notation, we have
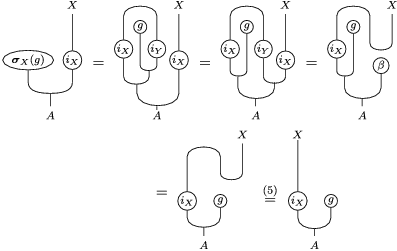
so that we get
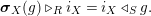 $$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D70E}}_{X}(g)\rhd _{R}i_{X}=i_{X}\lhd _{S}g.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D70E}}_{X}(g)\rhd _{R}i_{X}=i_{X}\lhd _{S}g.\end{eqnarray}$$
Using this equality, we obtain
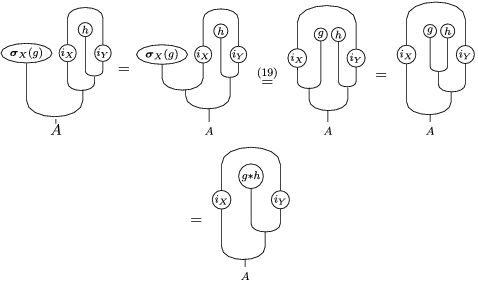
which means that
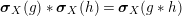 $\boldsymbol{\unicode[STIX]{x1D70E}}_{X}(g)\ast \boldsymbol{\unicode[STIX]{x1D70E}}_{X}(h)=\boldsymbol{\unicode[STIX]{x1D70E}}_{X}(g\ast h)$
. Moreover, we have
$\boldsymbol{\unicode[STIX]{x1D70E}}_{X}(g)\ast \boldsymbol{\unicode[STIX]{x1D70E}}_{X}(h)=\boldsymbol{\unicode[STIX]{x1D70E}}_{X}(g\ast h)$
. Moreover, we have
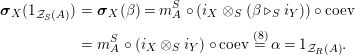 $$\begin{eqnarray}\displaystyle \boldsymbol{\unicode[STIX]{x1D70E}}_{X}(1_{{\mathcal{Z}}_{S}(A)}) & = & \displaystyle \boldsymbol{\unicode[STIX]{x1D70E}}_{X}(\unicode[STIX]{x1D6FD})=m_{A}^{S}\circ (i_{X}\otimes _{S}(\unicode[STIX]{x1D6FD}\rhd _{S}i_{Y}))\circ \text{coev}\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{S}\circ (i_{X}\otimes _{S}i_{Y})\circ \text{coev}\overset{(8)}{=}\unicode[STIX]{x1D6FC}=1_{{\mathcal{Z}}_{R}(A)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{\unicode[STIX]{x1D70E}}_{X}(1_{{\mathcal{Z}}_{S}(A)}) & = & \displaystyle \boldsymbol{\unicode[STIX]{x1D70E}}_{X}(\unicode[STIX]{x1D6FD})=m_{A}^{S}\circ (i_{X}\otimes _{S}(\unicode[STIX]{x1D6FD}\rhd _{S}i_{Y}))\circ \text{coev}\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{S}\circ (i_{X}\otimes _{S}i_{Y})\circ \text{coev}\overset{(8)}{=}\unicode[STIX]{x1D6FC}=1_{{\mathcal{Z}}_{R}(A)}.\nonumber\end{eqnarray}$$
We still need to check that
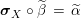 $\boldsymbol{\unicode[STIX]{x1D70E}}_{X}\circ \widetilde{\unicode[STIX]{x1D6FD}}\,=\,\widetilde{\unicode[STIX]{x1D6FC}}$
. To this aim, given
$\boldsymbol{\unicode[STIX]{x1D70E}}_{X}\circ \widetilde{\unicode[STIX]{x1D6FD}}\,=\,\widetilde{\unicode[STIX]{x1D6FC}}$
. To this aim, given
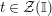 $t\in {\mathcal{Z}}(\mathbb{I})$
, we have
$t\in {\mathcal{Z}}(\mathbb{I})$
, we have
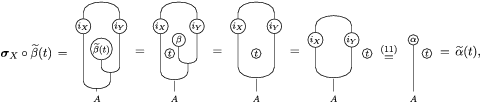
and this completes the proof.◻
The map defined in the following proposition is an extension, to the general framework of monoidal categories, of the so-called Miyashita action which was originally introduced by Miyashita in [Reference Miyashita23, page 100]. Further developments on this action appeared in various studies: Hopf–Galois extensions,
![]() $H$
-separable extensions, comodules over corings with grouplike elements and so forth; see [Reference EL Kaoutit and Gómez-Torrecillas8, Reference Kadison15–Reference Kadison and Külshammer17, Reference Masuoka21, Reference Schauenburg29]. Our general definition aims to provide a common and unifying context for all these studies.
$H$
-separable extensions, comodules over corings with grouplike elements and so forth; see [Reference EL Kaoutit and Gómez-Torrecillas8, Reference Kadison15–Reference Kadison and Külshammer17, Reference Masuoka21, Reference Schauenburg29]. Our general definition aims to provide a common and unifying context for all these studies.
Proposition 2.3. The map
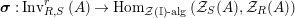 $$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D70E}}:\text{Inv}_{R,S}^{r}\left(A\right)\rightarrow \text{Hom}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}\left({\mathcal{Z}}_{S}(A),{\mathcal{Z}}_{R}(A)\right)\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D70E}}:\text{Inv}_{R,S}^{r}\left(A\right)\rightarrow \text{Hom}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}\left({\mathcal{Z}}_{S}(A),{\mathcal{Z}}_{R}(A)\right)\end{eqnarray}$$
of Proposition 2.2 induces a map
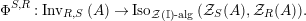 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}^{S,R}:\text{Inv}_{R,S}\left(A\right)\rightarrow \text{Iso}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}\left({\mathcal{Z}}_{S}(A),{\mathcal{Z}}_{R}(A)\right)\!.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}^{S,R}:\text{Inv}_{R,S}\left(A\right)\rightarrow \text{Iso}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}\left({\mathcal{Z}}_{S}(A),{\mathcal{Z}}_{R}(A)\right)\!.\end{eqnarray}$$
In particular, when
![]() $R=S$
we have a morphism of groups
$R=S$
we have a morphism of groups
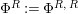 $\unicode[STIX]{x1D6F7}^{R}:=\unicode[STIX]{x1D6F7}^{R,\,R}$
. Moreover,
$\unicode[STIX]{x1D6F7}^{R}:=\unicode[STIX]{x1D6F7}^{R,\,R}$
. Moreover,
![]() $\unicode[STIX]{x1D6F7}^{R}$
factors as the composition
$\unicode[STIX]{x1D6F7}^{R}$
factors as the composition
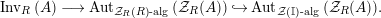 $$\begin{eqnarray}\text{Inv}_{R}\left(A\right)\longrightarrow \text{Aut}_{{\mathcal{Z}}_{R}(R)\text{-alg}}\left({\mathcal{Z}}_{R}(A)\right){\hookrightarrow}\text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}\left({\mathcal{Z}}_{R}(A)\right)\!.\end{eqnarray}$$
$$\begin{eqnarray}\text{Inv}_{R}\left(A\right)\longrightarrow \text{Aut}_{{\mathcal{Z}}_{R}(R)\text{-alg}}\left({\mathcal{Z}}_{R}(A)\right){\hookrightarrow}\text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}\left({\mathcal{Z}}_{R}(A)\right)\!.\end{eqnarray}$$
Proof. Consider both
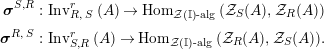 $$\begin{eqnarray}\displaystyle \boldsymbol{\unicode[STIX]{x1D70E}}^{S,R} & : & \displaystyle \text{Inv}_{R,\,S}^{r}\left(A\right)\rightarrow \text{Hom}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}\left({\mathcal{Z}}_{S}(A),{\mathcal{Z}}_{R}(A)\right)\nonumber\\ \displaystyle \boldsymbol{\unicode[STIX]{x1D70E}}^{R,\,S} & : & \displaystyle \text{Inv}_{S,R}^{r}\left(A\right)\rightarrow \text{Hom}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}\left({\mathcal{Z}}_{R}(A),{\mathcal{Z}}_{S}(A)\right)\!.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{\unicode[STIX]{x1D70E}}^{S,R} & : & \displaystyle \text{Inv}_{R,\,S}^{r}\left(A\right)\rightarrow \text{Hom}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}\left({\mathcal{Z}}_{S}(A),{\mathcal{Z}}_{R}(A)\right)\nonumber\\ \displaystyle \boldsymbol{\unicode[STIX]{x1D70E}}^{R,\,S} & : & \displaystyle \text{Inv}_{S,R}^{r}\left(A\right)\rightarrow \text{Hom}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}\left({\mathcal{Z}}_{R}(A),{\mathcal{Z}}_{S}(A)\right)\!.\nonumber\end{eqnarray}$$
Take
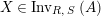 $X\in \text{Inv}_{R,\,S}\left(A\right)$
as in (15). Since
$X\in \text{Inv}_{R,\,S}\left(A\right)$
as in (15). Since
![]() $m_{X^{r}}$
is an isomorphism, we have that
$m_{X^{r}}$
is an isomorphism, we have that
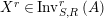 $X^{r}\in \text{Inv}_{S,R}^{r}\left(A\right)$
. Hence we can consider both
$X^{r}\in \text{Inv}_{S,R}^{r}\left(A\right)$
. Hence we can consider both
![]() $\boldsymbol{\unicode[STIX]{x1D70E}}_{X}^{S,R}$
and
$\boldsymbol{\unicode[STIX]{x1D70E}}_{X}^{S,R}$
and
![]() $\boldsymbol{\unicode[STIX]{x1D70E}}_{X^{r}}^{R,\,S}$
. Let us check that these maps are mutual inverses. For
$\boldsymbol{\unicode[STIX]{x1D70E}}_{X^{r}}^{R,\,S}$
. Let us check that these maps are mutual inverses. For
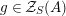 $g\in {\mathcal{Z}}_{S}(A)$
, we have
$g\in {\mathcal{Z}}_{S}(A)$
, we have
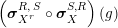 $\left(\boldsymbol{\unicode[STIX]{x1D70E}}_{X^{r}}^{R,\,S}\circ \boldsymbol{\unicode[STIX]{x1D70E}}_{X}^{S,R}\right)\left(g\right)$
is equal to
$\left(\boldsymbol{\unicode[STIX]{x1D70E}}_{X^{r}}^{R,\,S}\circ \boldsymbol{\unicode[STIX]{x1D70E}}_{X}^{S,R}\right)\left(g\right)$
is equal to
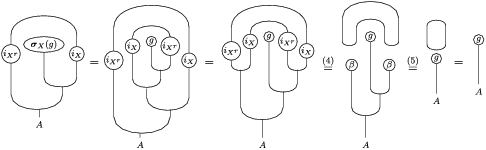
Thus
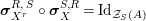 $\boldsymbol{\unicode[STIX]{x1D70E}}_{X^{r}}^{R,\,S}\circ \boldsymbol{\unicode[STIX]{x1D70E}}_{X}^{S,R}=\text{Id}_{{\mathcal{Z}}_{S}(A)}$
. Similarly one gets
$\boldsymbol{\unicode[STIX]{x1D70E}}_{X^{r}}^{R,\,S}\circ \boldsymbol{\unicode[STIX]{x1D70E}}_{X}^{S,R}=\text{Id}_{{\mathcal{Z}}_{S}(A)}$
. Similarly one gets
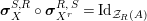 $\boldsymbol{\unicode[STIX]{x1D70E}}_{X}^{S,R}\circ \boldsymbol{\unicode[STIX]{x1D70E}}_{X^{r}}^{R,\,S}=\text{Id}_{{\mathcal{Z}}_{R}(A)}$
. Therefore,
$\boldsymbol{\unicode[STIX]{x1D70E}}_{X}^{S,R}\circ \boldsymbol{\unicode[STIX]{x1D70E}}_{X^{r}}^{R,\,S}=\text{Id}_{{\mathcal{Z}}_{R}(A)}$
. Therefore,
![]() $\boldsymbol{\unicode[STIX]{x1D70E}}_{X}^{S,R}$
is an isomorphism. This proves that
$\boldsymbol{\unicode[STIX]{x1D70E}}_{X}^{S,R}$
is an isomorphism. This proves that
![]() $\unicode[STIX]{x1D6F7}^{S,R}$
is well defined.
$\unicode[STIX]{x1D6F7}^{S,R}$
is well defined.
Now assume that
![]() $R=S$
. By Corollary 1.13, we know that
$R=S$
. By Corollary 1.13, we know that
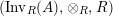 $(\text{Inv}_{R}(A),\otimes _{R},R)$
is a group. Let us check that
$(\text{Inv}_{R}(A),\otimes _{R},R)$
is a group. Let us check that
![]() $\unicode[STIX]{x1D6F7}^{R}$
is a group morphism. Take
$\unicode[STIX]{x1D6F7}^{R}$
is a group morphism. Take
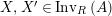 $X,X^{\prime }\in \text{Inv}_{R}\left(A\right)$
with two-sided inverses
$X,X^{\prime }\in \text{Inv}_{R}\left(A\right)$
with two-sided inverses
![]() $Y$
and
$Y$
and
![]() $Y^{\prime }$
, respectively. We have
$Y^{\prime }$
, respectively. We have
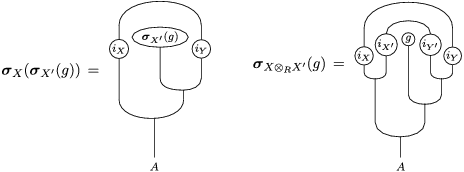
where
![]() $g$
is as above. The second equality in diagram (22) implies that
$g$
is as above. The second equality in diagram (22) implies that
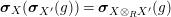 $\boldsymbol{\unicode[STIX]{x1D70E}}_{X}(\boldsymbol{\unicode[STIX]{x1D70E}}_{X^{\prime }}(g))=\boldsymbol{\unicode[STIX]{x1D70E}}_{X\otimes _{R}X^{\prime }}(g)$
. In other words
$\boldsymbol{\unicode[STIX]{x1D70E}}_{X}(\boldsymbol{\unicode[STIX]{x1D70E}}_{X^{\prime }}(g))=\boldsymbol{\unicode[STIX]{x1D70E}}_{X\otimes _{R}X^{\prime }}(g)$
. In other words
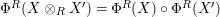 $\unicode[STIX]{x1D6F7}^{R}(X\otimes _{R}X^{\prime })=\unicode[STIX]{x1D6F7}^{R}(X)\circ \unicode[STIX]{x1D6F7}^{R}(X^{\prime })$
. Moreover,
$\unicode[STIX]{x1D6F7}^{R}(X\otimes _{R}X^{\prime })=\unicode[STIX]{x1D6F7}^{R}(X)\circ \unicode[STIX]{x1D6F7}^{R}(X^{\prime })$
. Moreover,
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{R}(R)(g) & = & \displaystyle \boldsymbol{\unicode[STIX]{x1D70E}}_{R}(g)\overset{(18)}{=}m_{A}^{R}\circ (\unicode[STIX]{x1D6FC}\otimes _{R}(g\rhd _{R}\unicode[STIX]{x1D6FC}))\circ (r_{R}^{R})^{-1}\nonumber\\ \displaystyle & \overset{(\ast )}{=} & \displaystyle m_{A}^{R}\circ (\unicode[STIX]{x1D6FC}\otimes _{R}g)\circ (r_{R}^{R})^{-1}=\unicode[STIX]{x1D6FC}\rhd _{R}g=g\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{R}(R)(g) & = & \displaystyle \boldsymbol{\unicode[STIX]{x1D70E}}_{R}(g)\overset{(18)}{=}m_{A}^{R}\circ (\unicode[STIX]{x1D6FC}\otimes _{R}(g\rhd _{R}\unicode[STIX]{x1D6FC}))\circ (r_{R}^{R})^{-1}\nonumber\\ \displaystyle & \overset{(\ast )}{=} & \displaystyle m_{A}^{R}\circ (\unicode[STIX]{x1D6FC}\otimes _{R}g)\circ (r_{R}^{R})^{-1}=\unicode[STIX]{x1D6FC}\rhd _{R}g=g\nonumber\end{eqnarray}$$
so that
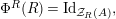 $\unicode[STIX]{x1D6F7}^{R}(R)=\text{Id}_{{\mathcal{Z}}_{R}(A)},$
where in
$\unicode[STIX]{x1D6F7}^{R}(R)=\text{Id}_{{\mathcal{Z}}_{R}(A)},$
where in
![]() $(\ast )$
we applied the definition of
$(\ast )$
we applied the definition of
![]() $\rhd _{R}$
.
$\rhd _{R}$
.
Let us check that
![]() $\unicode[STIX]{x1D6F7}^{R}$
factors as stated. Take
$\unicode[STIX]{x1D6F7}^{R}$
factors as stated. Take
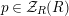 $p\in {\mathcal{Z}}_{R}(R)$
and set
$p\in {\mathcal{Z}}_{R}(R)$
and set
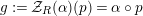 $g:={\mathcal{Z}}_{R}(\unicode[STIX]{x1D6FC})(p)=\unicode[STIX]{x1D6FC}\circ p$
. Since we already know that
$g:={\mathcal{Z}}_{R}(\unicode[STIX]{x1D6FC})(p)=\unicode[STIX]{x1D6FC}\circ p$
. Since we already know that
![]() $\unicode[STIX]{x1D70E}_{X}$
is multiplicative, in order to conclude that
$\unicode[STIX]{x1D70E}_{X}$
is multiplicative, in order to conclude that
![]() $\unicode[STIX]{x1D70E}_{X}$
is
$\unicode[STIX]{x1D70E}_{X}$
is
![]() ${\mathcal{Z}}_{R}(R)$
-bilinear, it suffices to check that
${\mathcal{Z}}_{R}(R)$
-bilinear, it suffices to check that
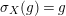 $\unicode[STIX]{x1D70E}_{X}(g)=g$
. As
$\unicode[STIX]{x1D70E}_{X}(g)=g$
. As
![]() $p$
is an endomorphism of the unit
$p$
is an endomorphism of the unit
![]() $R$
of the monoidal category
$R$
of the monoidal category
![]() $\text{}_{R}{\mathcal{M}}_{R}$
, we have
$\text{}_{R}{\mathcal{M}}_{R}$
, we have
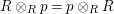 $R\otimes _{R}p=p\otimes _{R}R$
. Hence, by using the same arguments of diagram (20), we get the desired equality.◻
$R\otimes _{R}p=p\otimes _{R}R$
. Hence, by using the same arguments of diagram (20), we get the desired equality.◻
Remark 2.4. Submonoids of
![]() $A$
are
$A$
are
![]() $0$
-cells in a bicategory
$0$
-cells in a bicategory
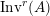 $\text{Inv}^{r}(A)$
, where for any two
$\text{Inv}^{r}(A)$
, where for any two
![]() $0$
-cells
$0$
-cells
![]() $R$
and
$R$
and
![]() $S$
the associated hom-category from
$S$
the associated hom-category from
![]() $R$
to
$R$
to
![]() $S$
is given by
$S$
is given by
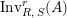 $\text{Inv}_{R,\,S}^{r}(A)$
with horizontal and vertical multiplications given by the functors of Proposition 1.12. Similarly, one defines the bicategories
$\text{Inv}_{R,\,S}^{r}(A)$
with horizontal and vertical multiplications given by the functors of Proposition 1.12. Similarly, one defines the bicategories
![]() $\text{Inv}^{l}(A)$
and
$\text{Inv}^{l}(A)$
and
![]() $\text{Inv}(A)$
. Now, if we restrict to submonoids
$\text{Inv}(A)$
. Now, if we restrict to submonoids
![]() $R$
of
$R$
of
![]() $A$
for which the functor
$A$
for which the functor
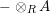 $-\otimes _{R}A$
reflects isomorphisms and denote this new bicategory by
$-\otimes _{R}A$
reflects isomorphisms and denote this new bicategory by
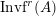 $\text{Invf}^{r}(A)$
, then any morphism in the hom-category
$\text{Invf}^{r}(A)$
, then any morphism in the hom-category
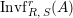 $\text{Invf}_{R,\,S}^{r}(A)$
is an isomorphism. Indeed, given a morphism
$\text{Invf}_{R,\,S}^{r}(A)$
is an isomorphism. Indeed, given a morphism
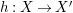 $h:X\rightarrow X^{\prime }$
in
$h:X\rightarrow X^{\prime }$
in
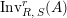 $\text{Inv}_{R,\,S}^{r}(A)$
, then
$\text{Inv}_{R,\,S}^{r}(A)$
, then
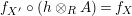 $f_{X^{\prime }}\circ (h\otimes _{R}A)=f_{X}$
, where
$f_{X^{\prime }}\circ (h\otimes _{R}A)=f_{X}$
, where
![]() $f_{-}$
is as in equation (1). Therefore, by Corollary 1.7, we have
$f_{-}$
is as in equation (1). Therefore, by Corollary 1.7, we have
![]() $h\otimes _{R}A$
is an isomorphism and hence
$h\otimes _{R}A$
is an isomorphism and hence
![]() $h$
is an isomorphism as well.
$h$
is an isomorphism as well.
In this way, the bicategory
![]() $\text{Invf}(A)$
, corresponding to
$\text{Invf}(A)$
, corresponding to
![]() $\text{Inv}(A)$
, can be regarded as a 2-groupoid, that is, a bicategory where
$\text{Inv}(A)$
, can be regarded as a 2-groupoid, that is, a bicategory where
![]() $1$
-cells and
$1$
-cells and
![]() $2$
-cells are invertible (i.e., each
$2$
-cells are invertible (i.e., each
![]() $1$
-cell is a member of an internal equivalence and any
$1$
-cell is a member of an internal equivalence and any
![]() $2$
-cell is an isomorphism). However,
$2$
-cell is an isomorphism). However,
![]() $\text{Inv}(A)$
viewed as a small category with hom-sets
$\text{Inv}(A)$
viewed as a small category with hom-sets
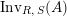 $\text{Inv}_{R,\,S}(A)$
and composition given by the tensor products
$\text{Inv}_{R,\,S}(A)$
and composition given by the tensor products
![]() $\otimes _{R}$
, is clearly a groupoid.
$\otimes _{R}$
, is clearly a groupoid.
On the other hand, there is another
![]() $2$
-category with
$2$
-category with
![]() $0$
-cells given by
$0$
-cells given by
![]() ${\mathcal{Z}}(\mathbb{I})$
-subalgebras of
${\mathcal{Z}}(\mathbb{I})$
-subalgebras of
![]() ${\mathcal{Z}}(A)$
, and hom-category from
${\mathcal{Z}}(A)$
, and hom-category from
![]() $E$
and
$E$
and
![]() $E^{\prime }$
given by the set
$E^{\prime }$
given by the set
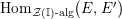 $\text{Hom}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}\big(E,E^{\prime }\big)$
(objects are edges and arrows are squares). Clearly, one assigns to any
$\text{Hom}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}\big(E,E^{\prime }\big)$
(objects are edges and arrows are squares). Clearly, one assigns to any
![]() $1$
-cell
$1$
-cell
![]() $R$
in
$R$
in
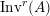 $\text{Inv}^{r}(A)$
a
$\text{Inv}^{r}(A)$
a
![]() $1$
-cell
$1$
-cell
![]() ${\mathcal{Z}}_{R}(A)$
in this
${\mathcal{Z}}_{R}(A)$
in this
![]() $2$
-category, by using the map
$2$
-category, by using the map
![]() $\unicode[STIX]{x1D711}_{R}$
of (17). However, it is not clear to us whether the family of maps
$\unicode[STIX]{x1D711}_{R}$
of (17). However, it is not clear to us whether the family of maps
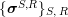 $\{\boldsymbol{\unicode[STIX]{x1D70E}}^{S,R}\}_{S,\,R}$
defined in Proposition 2.2 together with this assignment, give rise to a family of functors and thus to a morphism of bicategories. Nevertheless, using the maps
$\{\boldsymbol{\unicode[STIX]{x1D70E}}^{S,R}\}_{S,\,R}$
defined in Proposition 2.2 together with this assignment, give rise to a family of functors and thus to a morphism of bicategories. Nevertheless, using the maps
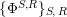 $\{\unicode[STIX]{x1D6F7}^{S,R}\}_{S,\,R}$
given in Proposition 2.3, one shows, as in the classical case [Reference Miyashita23, Theorem 1.3], that
$\{\unicode[STIX]{x1D6F7}^{S,R}\}_{S,\,R}$
given in Proposition 2.3, one shows, as in the classical case [Reference Miyashita23, Theorem 1.3], that
![]() $\unicode[STIX]{x1D6F7}$
establishes a homomorphism of groupoids.
$\unicode[STIX]{x1D6F7}$
establishes a homomorphism of groupoids.
2.2 Invariant subobjects
Let
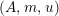 $(A,m,u)$
be a monoid in
$(A,m,u)$
be a monoid in
![]() ${\mathcal{M}}$
and consider
${\mathcal{M}}$
and consider
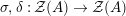 $\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}:{\mathcal{Z}}(A)\rightarrow {\mathcal{Z}}(A)$
two
$\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}:{\mathcal{Z}}(A)\rightarrow {\mathcal{Z}}(A)$
two
![]() ${\mathcal{Z}}(\mathbb{I})$
-linear maps. For each element
${\mathcal{Z}}(\mathbb{I})$
-linear maps. For each element
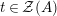 $t\in {\mathcal{Z}}(A)$
, define the following equalizer:
$t\in {\mathcal{Z}}(A)$
, define the following equalizer:
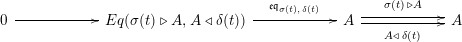
Now, since
![]() ${\mathcal{M}}$
is an abelian and bicomplete category, we can take the intersection of all those equalizes:
${\mathcal{M}}$
is an abelian and bicomplete category, we can take the intersection of all those equalizes:
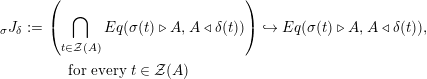 $$\begin{eqnarray}\displaystyle \text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}} & := & \displaystyle \left(\mathop{\bigcap }_{t\in {\mathcal{Z}}(A)}Eq(\unicode[STIX]{x1D70E}(t)\rhd A,A\lhd \unicode[STIX]{x1D6FF}(t))\right){\hookrightarrow}Eq(\unicode[STIX]{x1D70E}(t)\rhd A,A\lhd \unicode[STIX]{x1D6FF}(t)),\nonumber\\ \displaystyle & & \displaystyle \quad \text{for every }t\in {\mathcal{Z}}(A)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}} & := & \displaystyle \left(\mathop{\bigcap }_{t\in {\mathcal{Z}}(A)}Eq(\unicode[STIX]{x1D70E}(t)\rhd A,A\lhd \unicode[STIX]{x1D6FF}(t))\right){\hookrightarrow}Eq(\unicode[STIX]{x1D70E}(t)\rhd A,A\lhd \unicode[STIX]{x1D6FF}(t)),\nonumber\\ \displaystyle & & \displaystyle \quad \text{for every }t\in {\mathcal{Z}}(A)\end{eqnarray}$$
with structure monomorphism denoted by
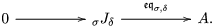
We view
![]() $\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}}$
as an element in
$\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}}$
as an element in
![]() $\mathscr{P}(\text{}_{\mathbb{I}}A_{\mathbb{I}})$
with monomorphism
$\mathscr{P}(\text{}_{\mathbb{I}}A_{\mathbb{I}})$
with monomorphism
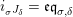 $i_{\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}}}=\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}$
as in Section 1. The pair
$i_{\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}}}=\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}$
as in Section 1. The pair
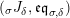 $(\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}},\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}})$
is in fact an universal object with respect to the following equations:
$(\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}},\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}})$
is in fact an universal object with respect to the following equations:
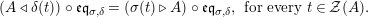 $$\begin{eqnarray}(A\lhd \unicode[STIX]{x1D6FF}(t))\circ \mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}=(\unicode[STIX]{x1D70E}(t)\rhd A)\circ \mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}},\text{ for every }t\in {\mathcal{Z}}(A).\end{eqnarray}$$
$$\begin{eqnarray}(A\lhd \unicode[STIX]{x1D6FF}(t))\circ \mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}=(\unicode[STIX]{x1D70E}(t)\rhd A)\circ \mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}},\text{ for every }t\in {\mathcal{Z}}(A).\end{eqnarray}$$
In other words any other morphism which satisfies these equations (parameterized by elements in
![]() ${\mathcal{Z}}(A)$
) factors uniquely throughout the monomorphism
${\mathcal{Z}}(A)$
) factors uniquely throughout the monomorphism
![]() $\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}$
. For every
$\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}$
. For every
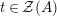 $t\in {\mathcal{Z}}(A)$
, equation (25) will be used in the following form
$t\in {\mathcal{Z}}(A)$
, equation (25) will be used in the following form
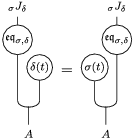
For simplicity we write
![]() $\text{}_{1}J_{1}$
,
$\text{}_{1}J_{1}$
,
![]() $\text{}_{\unicode[STIX]{x1D70E}}J_{1}$
and
$\text{}_{\unicode[STIX]{x1D70E}}J_{1}$
and
![]() $\text{}_{1}J_{\unicode[STIX]{x1D6FF}}$
when one or both the involved
$\text{}_{1}J_{\unicode[STIX]{x1D6FF}}$
when one or both the involved
![]() ${\mathcal{Z}}(\mathbb{I})$
-linear maps are identity.
${\mathcal{Z}}(\mathbb{I})$
-linear maps are identity.
Proposition 2.5. Let
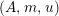 $(A,m,u)$
be a monoid in
$(A,m,u)$
be a monoid in
![]() ${\mathcal{M}}$
and let
${\mathcal{M}}$
and let
![]() $\unicode[STIX]{x1D70E}$
,
$\unicode[STIX]{x1D70E}$
,
![]() $\unicode[STIX]{x1D6FF}$
,
$\unicode[STIX]{x1D6FF}$
,
![]() $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
![]() $\unicode[STIX]{x1D706}$
be in
$\unicode[STIX]{x1D706}$
be in
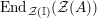 $\text{End}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
. Consider the family of subobjects
$\text{End}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
. Consider the family of subobjects
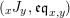 $(\text{}_{x}J_{y},\mathfrak{eq}_{x,y})$
of
$(\text{}_{x}J_{y},\mathfrak{eq}_{x,y})$
of
![]() $A$
, for
$A$
, for
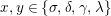 $x,y\in \{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D706}\}$
. Then
$x,y\in \{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D706}\}$
. Then
-
(i) There is a morphism
such that $$\begin{eqnarray}m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}:\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}}\otimes \text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FE}}\longrightarrow \text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
(27)
$$\begin{eqnarray}m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}:\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}}\otimes \text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FE}}\longrightarrow \text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
(27) $$\begin{eqnarray}\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}\circ m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}=m\circ (\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE}}).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}\circ m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}=m\circ (\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE}}).\end{eqnarray}$$
-
(ii) We have
(28) $$\begin{eqnarray}m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D6FE}}\circ (m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}\otimes \text{}_{\unicode[STIX]{x1D6FE}}J_{\unicode[STIX]{x1D706}})=m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D6FF}}\circ (\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}}\otimes m_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D6FE}}).\end{eqnarray}$$
$$\begin{eqnarray}m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D6FE}}\circ (m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}\otimes \text{}_{\unicode[STIX]{x1D6FE}}J_{\unicode[STIX]{x1D706}})=m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D6FF}}\circ (\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}}\otimes m_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D6FE}}).\end{eqnarray}$$
-
(iii) There exists a unique morphism
 $u_{\unicode[STIX]{x1D70E}}:\mathbb{I}\rightarrow \text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D70E}}$
such that
$u_{\unicode[STIX]{x1D70E}}:\mathbb{I}\rightarrow \text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D70E}}$
such that
 $\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}}\circ u_{\unicode[STIX]{x1D70E}}=u.$
Furthermore
$\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}}\circ u_{\unicode[STIX]{x1D70E}}=u.$
Furthermore
 $(\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D70E}},m_{\unicode[STIX]{x1D70E}},u_{\unicode[STIX]{x1D70E}})$
is a monoid, for every
$(\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D70E}},m_{\unicode[STIX]{x1D70E}},u_{\unicode[STIX]{x1D70E}})$
is a monoid, for every
 ${\mathcal{Z}}(\mathbb{I})$
-linear map
${\mathcal{Z}}(\mathbb{I})$
-linear map
 $\unicode[STIX]{x1D70E}$
, where we set
$\unicode[STIX]{x1D70E}$
, where we set
 $m_{\unicode[STIX]{x1D70E}}:=m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D70E}}$
.
$m_{\unicode[STIX]{x1D70E}}:=m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D70E}}$
. -
(iv) The morphisms
 $m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}^{\unicode[STIX]{x1D70E}}$
and
$m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}^{\unicode[STIX]{x1D70E}}$
and
 $m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}^{\unicode[STIX]{x1D6FF}}$
turn
$m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}^{\unicode[STIX]{x1D6FF}}$
turn
 $\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}}$
into a
$\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}}$
into a
 $(\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D70E}},\text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FF}})$
-bimodule.
$(\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D70E}},\text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FF}})$
-bimodule. -
(v) There is a unique morphism
(29)where $$\begin{eqnarray}\overline{m}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}:(\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}})\otimes _{\text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FF}}}(\text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FE}})\longrightarrow \text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FE}}\,\text{ such that }\,\overline{m}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}\circ \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}=m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}\end{eqnarray}$$
$$\begin{eqnarray}\overline{m}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}:(\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}})\otimes _{\text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FF}}}(\text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FE}})\longrightarrow \text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FE}}\,\text{ such that }\,\overline{m}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}\circ \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}=m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}\end{eqnarray}$$
 $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}:\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}}\otimes \text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FE}}\rightarrow (\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}})\otimes _{\text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FF}}}(\text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FE}})$
denotes the canonical morphism defining the tensor product over the monoid
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}:\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}}\otimes \text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FE}}\rightarrow (\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}})\otimes _{\text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FF}}}(\text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FE}})$
denotes the canonical morphism defining the tensor product over the monoid
 $\text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FF}}$
.
$\text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FF}}$
.
Proof. (i) Fixing an element
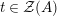 $t\in {\mathcal{Z}}(A)$
, we have
$t\in {\mathcal{Z}}(A)$
, we have
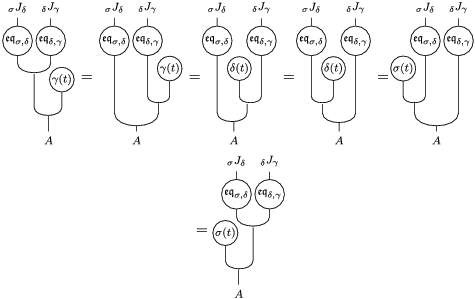
which shows that
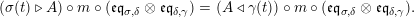 $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D70E}(t)\rhd A)\circ m\circ (\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE}}) & = & \displaystyle (A\lhd \unicode[STIX]{x1D6FE}(t))\circ m\circ (\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D70E}(t)\rhd A)\circ m\circ (\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE}}) & = & \displaystyle (A\lhd \unicode[STIX]{x1D6FE}(t))\circ m\circ (\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE}}).\nonumber\end{eqnarray}$$
Hence, by the universal property, the desired morphism is the one which turns commutative the diagrams
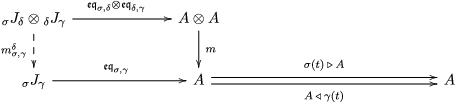
for every
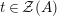 $t\in {\mathcal{Z}}(A)$
.
$t\in {\mathcal{Z}}(A)$
.
(ii) The equation follows from the fact that
![]() $\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D706}}$
is a monomorphism and the computation:
$\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D706}}$
is a monomorphism and the computation:
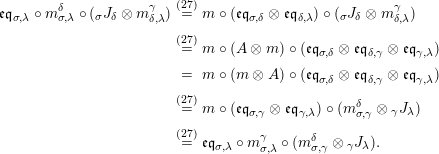 $$\begin{eqnarray}\displaystyle \mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D706}}\circ m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D6FF}}\circ (\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}}\otimes m_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D6FE}}) & \overset{(27)}{=} & \displaystyle m\circ (\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D706}})\circ (\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}}\otimes m_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D6FE}})\nonumber\\ \displaystyle & \overset{(27)}{=} & \displaystyle m\circ (A\otimes _{}m)\circ (\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D706}})\nonumber\\ \displaystyle & = & \displaystyle m\circ (m\otimes _{}A)\circ (\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D706}})\nonumber\\ \displaystyle & \overset{(27)}{=} & \displaystyle m\circ (\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D706}})\circ (m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}\otimes \text{}_{\unicode[STIX]{x1D6FE}}J_{\unicode[STIX]{x1D706}})\nonumber\\ \displaystyle & \overset{(27)}{=} & \displaystyle \mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D706}}\circ m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D6FE}}\circ (m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}\otimes \text{}_{\unicode[STIX]{x1D6FE}}J_{\unicode[STIX]{x1D706}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D706}}\circ m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D6FF}}\circ (\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}}\otimes m_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D6FE}}) & \overset{(27)}{=} & \displaystyle m\circ (\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D706}})\circ (\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}}\otimes m_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D6FE}})\nonumber\\ \displaystyle & \overset{(27)}{=} & \displaystyle m\circ (A\otimes _{}m)\circ (\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D706}})\nonumber\\ \displaystyle & = & \displaystyle m\circ (m\otimes _{}A)\circ (\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D706}})\nonumber\\ \displaystyle & \overset{(27)}{=} & \displaystyle m\circ (\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D706}})\circ (m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}\otimes \text{}_{\unicode[STIX]{x1D6FE}}J_{\unicode[STIX]{x1D706}})\nonumber\\ \displaystyle & \overset{(27)}{=} & \displaystyle \mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D706}}\circ m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D6FE}}\circ (m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}\otimes \text{}_{\unicode[STIX]{x1D6FE}}J_{\unicode[STIX]{x1D706}}).\nonumber\end{eqnarray}$$
(iii) The associativity follows by (28). Denote
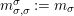 $m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D70E}}:=m_{\unicode[STIX]{x1D70E}}$
and
$m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}}^{\unicode[STIX]{x1D70E}}:=m_{\unicode[STIX]{x1D70E}}$
and
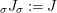 $\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D70E}}:=J$
. Now, we show that there is a morphism
$\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D70E}}:=J$
. Now, we show that there is a morphism
![]() $u_{\unicode[STIX]{x1D70E}}$
such that the following diagrams commute
$u_{\unicode[STIX]{x1D70E}}$
such that the following diagrams commute

We compute
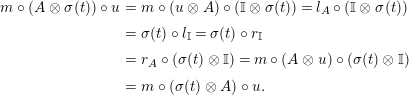 $$\begin{eqnarray}\displaystyle m\circ (A\otimes _{}\unicode[STIX]{x1D70E}(t))\circ u & = & \displaystyle m\circ (u\otimes _{}A)\circ (\mathbb{I}\otimes _{}\unicode[STIX]{x1D70E}(t))=l_{A}\circ (\mathbb{I}\otimes _{}\unicode[STIX]{x1D70E}(t))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70E}(t)\circ l_{\mathbb{I}}=\unicode[STIX]{x1D70E}(t)\circ r_{\mathbb{I}}\nonumber\\ \displaystyle & = & \displaystyle r_{A}\circ (\unicode[STIX]{x1D70E}(t)\otimes _{}\mathbb{I})=m\circ (A\otimes _{}u)\circ (\unicode[STIX]{x1D70E}(t)\otimes _{}\mathbb{I})\nonumber\\ \displaystyle & = & \displaystyle m\circ (\unicode[STIX]{x1D70E}(t)\otimes _{}A)\circ u.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle m\circ (A\otimes _{}\unicode[STIX]{x1D70E}(t))\circ u & = & \displaystyle m\circ (u\otimes _{}A)\circ (\mathbb{I}\otimes _{}\unicode[STIX]{x1D70E}(t))=l_{A}\circ (\mathbb{I}\otimes _{}\unicode[STIX]{x1D70E}(t))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70E}(t)\circ l_{\mathbb{I}}=\unicode[STIX]{x1D70E}(t)\circ r_{\mathbb{I}}\nonumber\\ \displaystyle & = & \displaystyle r_{A}\circ (\unicode[STIX]{x1D70E}(t)\otimes _{}\mathbb{I})=m\circ (A\otimes _{}u)\circ (\unicode[STIX]{x1D70E}(t)\otimes _{}\mathbb{I})\nonumber\\ \displaystyle & = & \displaystyle m\circ (\unicode[STIX]{x1D70E}(t)\otimes _{}A)\circ u.\nonumber\end{eqnarray}$$
We now prove that the multiplication of
![]() $J$
is unitary:
$J$
is unitary:
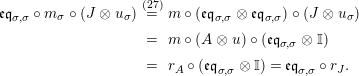 $$\begin{eqnarray}\displaystyle \mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}}\circ m_{\unicode[STIX]{x1D70E}}\circ (J\otimes _{}u_{\unicode[STIX]{x1D70E}}) & \overset{(27)}{=} & \displaystyle m\circ (\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}})\circ (J\otimes _{}u_{\unicode[STIX]{x1D70E}})\nonumber\\ \displaystyle & = & \displaystyle m\circ (A\otimes _{}u)\circ (\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}}\otimes _{}\mathbb{I})\nonumber\\ \displaystyle & = & \displaystyle r_{A}\circ (\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}}\otimes _{}\mathbb{I})=\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}}\circ r_{J}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}}\circ m_{\unicode[STIX]{x1D70E}}\circ (J\otimes _{}u_{\unicode[STIX]{x1D70E}}) & \overset{(27)}{=} & \displaystyle m\circ (\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}})\circ (J\otimes _{}u_{\unicode[STIX]{x1D70E}})\nonumber\\ \displaystyle & = & \displaystyle m\circ (A\otimes _{}u)\circ (\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}}\otimes _{}\mathbb{I})\nonumber\\ \displaystyle & = & \displaystyle r_{A}\circ (\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}}\otimes _{}\mathbb{I})=\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}}\circ r_{J}.\nonumber\end{eqnarray}$$
Since
![]() $\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}}$
is a monomorphism we obtain
$\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}}$
is a monomorphism we obtain
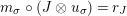 $m_{\unicode[STIX]{x1D70E}}\circ (J\otimes _{}u_{\unicode[STIX]{x1D70E}})=r_{J}$
. In a similar manner one gets
$m_{\unicode[STIX]{x1D70E}}\circ (J\otimes _{}u_{\unicode[STIX]{x1D70E}})=r_{J}$
. In a similar manner one gets
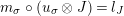 $m_{\unicode[STIX]{x1D70E}}\circ (u_{\unicode[STIX]{x1D70E}}\otimes _{}J)=l_{J}$
. We have so proved that
$m_{\unicode[STIX]{x1D70E}}\circ (u_{\unicode[STIX]{x1D70E}}\otimes _{}J)=l_{J}$
. We have so proved that
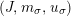 $(J,m_{\unicode[STIX]{x1D70E}},u_{\unicode[STIX]{x1D70E}})$
is a monoid.
$(J,m_{\unicode[STIX]{x1D70E}},u_{\unicode[STIX]{x1D70E}})$
is a monoid.
(iv) It follows by (28).
(v) From (28) one gets that
![]() $m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}$
is balanced over
$m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}$
is balanced over
![]() $_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FF}}$
.◻
$_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FF}}$
.◻
3 The bijectivity of Miyashita action
The aim of this section is to seek for conditions under which the Miyashita action, that is the map of Proposition 2.3, or some of its factors are bijective. We work, as before, over a Penrose monoidal abelian, locally small and bicomplete category
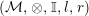 $({\mathcal{M}},\otimes _{},\mathbb{I},l,r)$
, where the tensor product is right exact on both factors.
$({\mathcal{M}},\otimes _{},\mathbb{I},l,r)$
, where the tensor product is right exact on both factors.
3.1 The case when
 $\unicode[STIX]{x1D6F7}$
is a monomorphism of groups
$\unicode[STIX]{x1D6F7}$
is a monomorphism of groups
Take
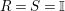 $R=S=\mathbb{I}$
in Proposition 2.3 and consider an invertible subobject
$R=S=\mathbb{I}$
in Proposition 2.3 and consider an invertible subobject
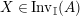 $X\in \text{Inv}_{\mathbb{I}}(A)$
with two-sided inverse
$X\in \text{Inv}_{\mathbb{I}}(A)$
with two-sided inverse
![]() $Y$
. The image of any
$Y$
. The image of any
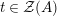 $t\in {\mathcal{Z}}(A)$
through the map
$t\in {\mathcal{Z}}(A)$
through the map
![]() $\unicode[STIX]{x1D6F7}_{X}$
of equation (21) is given by
$\unicode[STIX]{x1D6F7}_{X}$
of equation (21) is given by
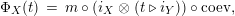 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{X}(t)\,=\,m\circ \left(i_{X}\otimes _{}(t\rhd i_{Y})\right)\circ \text{coev},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{X}(t)\,=\,m\circ \left(i_{X}\otimes _{}(t\rhd i_{Y})\right)\circ \text{coev},\end{eqnarray}$$
where,
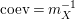 $\text{coev}=m_{X}^{-1}$
is as in Proposition 1.3.
$\text{coev}=m_{X}^{-1}$
is as in Proposition 1.3.
Lemma 3.1. Let
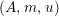 $(A,m,u)$
be a monoid in
$(A,m,u)$
be a monoid in
![]() ${\mathcal{M}}$
and let
${\mathcal{M}}$
and let
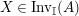 $X\in \text{Inv}_{\mathbb{I}}(A)$
with inverse
$X\in \text{Inv}_{\mathbb{I}}(A)$
with inverse
![]() $Y$
. Consider the associated automorphism
$Y$
. Consider the associated automorphism
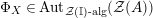 $\unicode[STIX]{x1D6F7}_{X}\in \text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}({\mathcal{Z}}(A))$
defined as in Proposition 2.3 with
$\unicode[STIX]{x1D6F7}_{X}\in \text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}({\mathcal{Z}}(A))$
defined as in Proposition 2.3 with
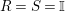 $R=S=\mathbb{I}$
. Then we have monomorphisms
$R=S=\mathbb{I}$
. Then we have monomorphisms

satisfying
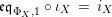 $\mathfrak{eq}_{\unicode[STIX]{x1D6F7}_{X},1}\circ \unicode[STIX]{x1D704}_{X}\,=\,i_{X}$
, and
$\mathfrak{eq}_{\unicode[STIX]{x1D6F7}_{X},1}\circ \unicode[STIX]{x1D704}_{X}\,=\,i_{X}$
, and
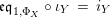 $\mathfrak{eq}_{1,\unicode[STIX]{x1D6F7}_{X}}\circ \unicode[STIX]{x1D704}_{Y}\,=\,i_{Y}$
.
$\mathfrak{eq}_{1,\unicode[STIX]{x1D6F7}_{X}}\circ \unicode[STIX]{x1D704}_{Y}\,=\,i_{Y}$
.
Proof. By applying equation (19) to our situation we obtain
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{X}(t)\rhd i_{X}=i_{X}\lhd t,\quad \text{for every }t\in {\mathcal{Z}}(A).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{X}(t)\rhd i_{X}=i_{X}\lhd t,\quad \text{for every }t\in {\mathcal{Z}}(A).\end{eqnarray}$$
Equivalently
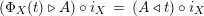 $(\unicode[STIX]{x1D6F7}_{X}(t)\rhd A)\circ i_{X}\,=\,(A\lhd t)\circ i_{X}$
for every
$(\unicode[STIX]{x1D6F7}_{X}(t)\rhd A)\circ i_{X}\,=\,(A\lhd t)\circ i_{X}$
for every
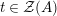 $t\in {\mathcal{Z}}(A)$
, which by the universal property of
$t\in {\mathcal{Z}}(A)$
, which by the universal property of
![]() $\text{}_{\unicode[STIX]{x1D6F7}_{X}}J_{1}$
gives the desired monomorphism. Replacing
$\text{}_{\unicode[STIX]{x1D6F7}_{X}}J_{1}$
gives the desired monomorphism. Replacing
![]() $X$
by
$X$
by
![]() $Y$
one gets the other monomorphism.◻
$Y$
one gets the other monomorphism.◻
Notice that for any
![]() ${\mathcal{Z}}(\mathbb{I})$
-algebra automorphism
${\mathcal{Z}}(\mathbb{I})$
-algebra automorphism
![]() $\unicode[STIX]{x1D703}$
of
$\unicode[STIX]{x1D703}$
of
![]() ${\mathcal{Z}}(A)$
, we have that for each
${\mathcal{Z}}(A)$
, we have that for each
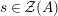 $s\in {\mathcal{Z}}(A)$
, there exists a unique
$s\in {\mathcal{Z}}(A)$
, there exists a unique
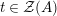 $t\in {\mathcal{Z}}(A)$
such that
$t\in {\mathcal{Z}}(A)$
such that
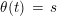 $\unicode[STIX]{x1D703}(t)\,=\,s$
. Hence
$\unicode[STIX]{x1D703}(t)\,=\,s$
. Hence
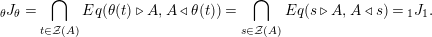 $$\begin{eqnarray}\text{}_{\unicode[STIX]{x1D703}}J_{\unicode[STIX]{x1D703}}=\mathop{\bigcap }_{t\in {\mathcal{Z}}(A)}Eq(\unicode[STIX]{x1D703}(t)\rhd A,A\lhd \unicode[STIX]{x1D703}(t))=\mathop{\bigcap }_{s\in {\mathcal{Z}}(A)}Eq(s\rhd A,A\lhd s)=\text{}_{1}J_{1}.\end{eqnarray}$$
$$\begin{eqnarray}\text{}_{\unicode[STIX]{x1D703}}J_{\unicode[STIX]{x1D703}}=\mathop{\bigcap }_{t\in {\mathcal{Z}}(A)}Eq(\unicode[STIX]{x1D703}(t)\rhd A,A\lhd \unicode[STIX]{x1D703}(t))=\mathop{\bigcap }_{s\in {\mathcal{Z}}(A)}Eq(s\rhd A,A\lhd s)=\text{}_{1}J_{1}.\end{eqnarray}$$
This observation is implicitly used in the foregoing.
Proposition 3.2. Let
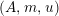 $(A,m,u)$
be a monoid in
$(A,m,u)$
be a monoid in
![]() ${\mathcal{M}}$
and assume that
${\mathcal{M}}$
and assume that
![]() $u$
is a monomorphism. Let
$u$
is a monomorphism. Let
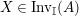 $X\in \text{Inv}_{\mathbb{I}}(A)$
be an invertible subobject with associated automorphism
$X\in \text{Inv}_{\mathbb{I}}(A)$
be an invertible subobject with associated automorphism
![]() $\unicode[STIX]{x1D6F7}_{X}$
as in (32). Then
$\unicode[STIX]{x1D6F7}_{X}$
as in (32). Then
![]() $\text{}_{\unicode[STIX]{x1D6F7}_{X}}J_{1}$
is a two-sided invertible
$\text{}_{\unicode[STIX]{x1D6F7}_{X}}J_{1}$
is a two-sided invertible
![]() $\text{}_{1}J_{1}$
-sub-bimodule of
$\text{}_{1}J_{1}$
-sub-bimodule of
![]() $A$
, that is an element of
$A$
, that is an element of
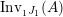 $\text{Inv}_{\text{}_{1}J_{1}}(A)$
with inverse
$\text{Inv}_{\text{}_{1}J_{1}}(A)$
with inverse
![]() $\text{}_{1}J_{\unicode[STIX]{x1D6F7}_{X}}$
.
$\text{}_{1}J_{\unicode[STIX]{x1D6F7}_{X}}$
.
Proof. Along this proof we abbreviate
![]() $\unicode[STIX]{x1D6F7}_{X}$
to
$\unicode[STIX]{x1D6F7}_{X}$
to
![]() $\unicode[STIX]{x1D719}$
. The morphisms
$\unicode[STIX]{x1D719}$
. The morphisms
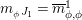 $m_{\text{}_{\unicode[STIX]{x1D719}}J_{1}}=\overline{m}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}}^{1}$
and
$m_{\text{}_{\unicode[STIX]{x1D719}}J_{1}}=\overline{m}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}}^{1}$
and
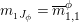 $m_{\text{}_{1}J_{\unicode[STIX]{x1D719}}}=\overline{m}_{1,1}^{\unicode[STIX]{x1D719}}$
defined in Proposition 1.3 for the pair
$m_{\text{}_{1}J_{\unicode[STIX]{x1D719}}}=\overline{m}_{1,1}^{\unicode[STIX]{x1D719}}$
defined in Proposition 1.3 for the pair
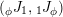 $(\text{}_{\unicode[STIX]{x1D719}}J_{1},\text{}_{1}J_{\unicode[STIX]{x1D719}})$
, are given by Proposition 2.5(v), where the compatibility constrains are shown using equations (28) and (29). Consider the morphism
$(\text{}_{\unicode[STIX]{x1D719}}J_{1},\text{}_{1}J_{\unicode[STIX]{x1D719}})$
, are given by Proposition 2.5(v), where the compatibility constrains are shown using equations (28) and (29). Consider the morphism
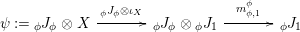
where
![]() $\unicode[STIX]{x1D704}_{X}$
was defined in Lemma 3.1. Now let us check that
$\unicode[STIX]{x1D704}_{X}$
was defined in Lemma 3.1. Now let us check that
![]() $m_{\text{}_{\unicode[STIX]{x1D719}}J_{1}}$
is invertible with inverse
$m_{\text{}_{\unicode[STIX]{x1D719}}J_{1}}$
is invertible with inverse
![]() $\unicode[STIX]{x1D708}$
defined as the following composition of morphisms:
$\unicode[STIX]{x1D708}$
defined as the following composition of morphisms:
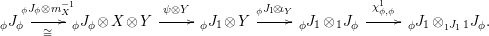
We have
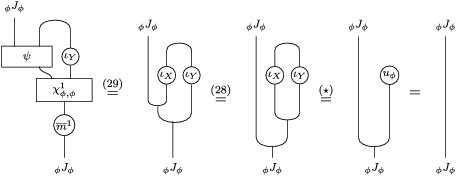
where the last equality is given by Proposition 2.5(iii), while equality
![]() $(\star )$
is proved as follows:
$(\star )$
is proved as follows:
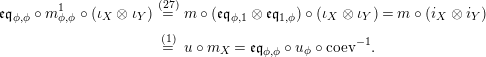 $$\begin{eqnarray}\displaystyle \mathfrak{eq}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}}\circ m_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}}^{1}\circ (\unicode[STIX]{x1D704}_{X}\otimes \unicode[STIX]{x1D704}_{Y}) & \overset{(27)}{=} & \displaystyle m\circ (\mathfrak{eq}_{\unicode[STIX]{x1D719},1}\otimes \mathfrak{eq}_{1,\unicode[STIX]{x1D719}})\circ (\unicode[STIX]{x1D704}_{X}\otimes \unicode[STIX]{x1D704}_{Y})=m\circ (i_{X}\otimes i_{Y})\nonumber\\ \displaystyle & \overset{(1)}{=} & \displaystyle u\circ m_{X}=\mathfrak{eq}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}}\circ u_{\unicode[STIX]{x1D719}}\circ \text{coev}^{-1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathfrak{eq}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}}\circ m_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}}^{1}\circ (\unicode[STIX]{x1D704}_{X}\otimes \unicode[STIX]{x1D704}_{Y}) & \overset{(27)}{=} & \displaystyle m\circ (\mathfrak{eq}_{\unicode[STIX]{x1D719},1}\otimes \mathfrak{eq}_{1,\unicode[STIX]{x1D719}})\circ (\unicode[STIX]{x1D704}_{X}\otimes \unicode[STIX]{x1D704}_{Y})=m\circ (i_{X}\otimes i_{Y})\nonumber\\ \displaystyle & \overset{(1)}{=} & \displaystyle u\circ m_{X}=\mathfrak{eq}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}}\circ u_{\unicode[STIX]{x1D719}}\circ \text{coev}^{-1}.\nonumber\end{eqnarray}$$
This proves that
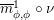 $\overline{m}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}}^{1}\circ \unicode[STIX]{x1D708}$
is the identity. A similar computation, which uses composition with the epimorphism
$\overline{m}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}}^{1}\circ \unicode[STIX]{x1D708}$
is the identity. A similar computation, which uses composition with the epimorphism
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}}^{1}$
, shows that
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}}^{1}$
, shows that
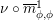 $\unicode[STIX]{x1D708}\circ \overline{m}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}}^{1}$
is the identity too so that
$\unicode[STIX]{x1D708}\circ \overline{m}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}}^{1}$
is the identity too so that
![]() $\overline{m}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}}^{1}$
is invertible. Replacing
$\overline{m}_{\unicode[STIX]{x1D719},\unicode[STIX]{x1D719}}^{1}$
is invertible. Replacing
![]() $\unicode[STIX]{x1D719}$
by
$\unicode[STIX]{x1D719}$
by
![]() $\unicode[STIX]{x1D719}^{-1}$
will show that
$\unicode[STIX]{x1D719}^{-1}$
will show that
![]() $m_{\text{}_{\unicode[STIX]{x1D719}^{-1}}J_{1}}$
is an isomorphism which means that
$m_{\text{}_{\unicode[STIX]{x1D719}^{-1}}J_{1}}$
is an isomorphism which means that
![]() $m_{\text{}_{1}J_{\unicode[STIX]{x1D719}}}$
is an isomorphism, since
$m_{\text{}_{1}J_{\unicode[STIX]{x1D719}}}$
is an isomorphism, since
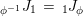 $_{\unicode[STIX]{x1D719}^{-1}}J_{1}\,=\,\text{}_{1}J_{\unicode[STIX]{x1D719}}$
.◻
$_{\unicode[STIX]{x1D719}^{-1}}J_{1}\,=\,\text{}_{1}J_{\unicode[STIX]{x1D719}}$
.◻
Lemma 3.3. Let
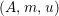 $(A,m,u)$
be a monoid in
$(A,m,u)$
be a monoid in
![]() ${\mathcal{M}}$
. Assume that the unit
${\mathcal{M}}$
. Assume that the unit
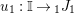 $u_{1}:\mathbb{I}\rightarrow \text{}_{1}J_{1}$
is an isomorphism and consider a two-sided invertible object
$u_{1}:\mathbb{I}\rightarrow \text{}_{1}J_{1}$
is an isomorphism and consider a two-sided invertible object
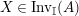 $X\in \text{Inv}_{\mathbb{I}}(A)$
with inverse
$X\in \text{Inv}_{\mathbb{I}}(A)$
with inverse
![]() $Y$
and associated automorphism
$Y$
and associated automorphism
![]() $\unicode[STIX]{x1D6F7}_{X}$
as in (32). Then, we have
$\unicode[STIX]{x1D6F7}_{X}$
as in (32). Then, we have
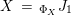 $X\,=\,\text{}_{\unicode[STIX]{x1D6F7}_{X}}J_{1}$
and
$X\,=\,\text{}_{\unicode[STIX]{x1D6F7}_{X}}J_{1}$
and
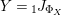 $Y=\text{}_{1}J_{\unicode[STIX]{x1D6F7}_{X}}$
.
$Y=\text{}_{1}J_{\unicode[STIX]{x1D6F7}_{X}}$
.
Proof. Under the assumption made on
![]() $u_{1}$
, the unit
$u_{1}$
, the unit
![]() $u$
is a monomorphism by Proposition 2.5(iii). Hence, by Proposition 3.2, we know that
$u$
is a monomorphism by Proposition 2.5(iii). Hence, by Proposition 3.2, we know that
![]() $_{\unicode[STIX]{x1D6F7}_{X}}J_{1}$
is invertible with inverse
$_{\unicode[STIX]{x1D6F7}_{X}}J_{1}$
is invertible with inverse
![]() $\text{}_{1}J_{\unicode[STIX]{x1D6F7}_{X}}$
. Therefore, we have that
$\text{}_{1}J_{\unicode[STIX]{x1D6F7}_{X}}$
. Therefore, we have that
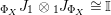 $\text{}_{\unicode[STIX]{x1D6F7}_{X}}J_{1}\otimes \text{}_{1}J_{\unicode[STIX]{x1D6F7}_{X}}\cong \mathbb{I}$
and
$\text{}_{\unicode[STIX]{x1D6F7}_{X}}J_{1}\otimes \text{}_{1}J_{\unicode[STIX]{x1D6F7}_{X}}\cong \mathbb{I}$
and
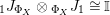 $\text{}_{1}J_{\unicode[STIX]{x1D6F7}_{X}}\otimes \text{}_{\unicode[STIX]{x1D6F7}_{X}}J_{1}\cong \mathbb{I}$
. Now, by Lemma 3.1, we know that
$\text{}_{1}J_{\unicode[STIX]{x1D6F7}_{X}}\otimes \text{}_{\unicode[STIX]{x1D6F7}_{X}}J_{1}\cong \mathbb{I}$
. Now, by Lemma 3.1, we know that
![]() $X$
is injected in
$X$
is injected in
![]() $\text{}_{\unicode[STIX]{x1D6F7}_{X}}J_{1}$
while
$\text{}_{\unicode[STIX]{x1D6F7}_{X}}J_{1}$
while
![]() $Y$
is injected in
$Y$
is injected in
![]() $\text{}_{1}J_{\unicode[STIX]{x1D6F7}_{X}}$
. Summing up, we have shown that the elements
$\text{}_{1}J_{\unicode[STIX]{x1D6F7}_{X}}$
. Summing up, we have shown that the elements
![]() $X$
and
$X$
and
![]() $\text{}_{\unicode[STIX]{x1D6F7}_{X}}J_{1}$
satisfy the assumptions of Proposition 1.14(2) so that we obtain the equalities
$\text{}_{\unicode[STIX]{x1D6F7}_{X}}J_{1}$
satisfy the assumptions of Proposition 1.14(2) so that we obtain the equalities
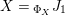 $X=\text{}_{\unicode[STIX]{x1D6F7}_{X}}J_{1}$
and
$X=\text{}_{\unicode[STIX]{x1D6F7}_{X}}J_{1}$
and
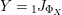 $Y=\text{}_{1}J_{\unicode[STIX]{x1D6F7}_{X}}$
.◻
$Y=\text{}_{1}J_{\unicode[STIX]{x1D6F7}_{X}}$
.◻
Given a monoid
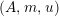 $(A,m,u)$
in
$(A,m,u)$
in
![]() ${\mathcal{M}}$
, we define the set
${\mathcal{M}}$
, we define the set
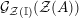 ${\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
as follows:
${\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
as follows:
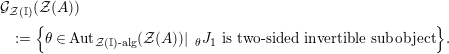 $$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))\nonumber\\ \displaystyle & & \displaystyle \quad :=\Bigl\{\unicode[STIX]{x1D703}\in \text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}({\mathcal{Z}}(A))|\,\,\text{}_{\unicode[STIX]{x1D703}}J_{1}\text{ is two-sided invertible subobject}\Bigr\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))\nonumber\\ \displaystyle & & \displaystyle \quad :=\Bigl\{\unicode[STIX]{x1D703}\in \text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}({\mathcal{Z}}(A))|\,\,\text{}_{\unicode[STIX]{x1D703}}J_{1}\text{ is two-sided invertible subobject}\Bigr\}.\end{eqnarray}$$
Here by
![]() $\text{}_{\unicode[STIX]{x1D703}}J_{1}$
invertible we mean that the morphisms
$\text{}_{\unicode[STIX]{x1D703}}J_{1}$
invertible we mean that the morphisms
![]() $\overline{m}_{\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}}^{1}$
and
$\overline{m}_{\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}}^{1}$
and
![]() $\overline{m}_{1,1}^{\unicode[STIX]{x1D703}}$
given in equation (29) are isomorphisms, which, in view of equation (34), shows that
$\overline{m}_{1,1}^{\unicode[STIX]{x1D703}}$
given in equation (29) are isomorphisms, which, in view of equation (34), shows that
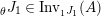 $\text{}_{\unicode[STIX]{x1D703}}J_{1}\in \text{Inv}_{\text{}_{1}J_{1}}(A)$
. In this case, the two-sided inverse of
$\text{}_{\unicode[STIX]{x1D703}}J_{1}\in \text{Inv}_{\text{}_{1}J_{1}}(A)$
. In this case, the two-sided inverse of
![]() $\text{}_{\unicode[STIX]{x1D703}}J_{1}$
is
$\text{}_{\unicode[STIX]{x1D703}}J_{1}$
is
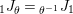 $\text{}_{1}J_{\unicode[STIX]{x1D703}}=\text{}_{\unicode[STIX]{x1D703}^{-1}}J_{1}$
. As we will see below the set
$\text{}_{1}J_{\unicode[STIX]{x1D703}}=\text{}_{\unicode[STIX]{x1D703}^{-1}}J_{1}$
. As we will see below the set
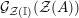 ${\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
is in fact a subgroup of the automorphisms group
${\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
is in fact a subgroup of the automorphisms group
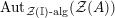 $\text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}({\mathcal{Z}}(A))$
.
$\text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}({\mathcal{Z}}(A))$
.
The following is one of our main results.
Theorem 3.4. Let
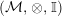 $({\mathcal{M}},\otimes _{},\mathbb{I})$
be a Penrose monoidal abelian, locally small and bicomplete category with right exact tensor products functors. Let
$({\mathcal{M}},\otimes _{},\mathbb{I})$
be a Penrose monoidal abelian, locally small and bicomplete category with right exact tensor products functors. Let
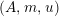 $(A,m,u)$
be a monoid such that the morphism
$(A,m,u)$
be a monoid such that the morphism
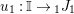 $u_{1}:\mathbb{I}\rightarrow \text{}_{1}J_{1}$
is an isomorphism. Then the map
$u_{1}:\mathbb{I}\rightarrow \text{}_{1}J_{1}$
is an isomorphism. Then the map
![]() $\unicode[STIX]{x1D6F7}$
of Proposition 2.3 induces an isomorphism of groups
$\unicode[STIX]{x1D6F7}$
of Proposition 2.3 induces an isomorphism of groups
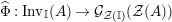 $\widehat{\unicode[STIX]{x1D6F7}}:\text{Inv}_{\mathbb{I}}(A)\rightarrow {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
which makes the following triangle commutative
$\widehat{\unicode[STIX]{x1D6F7}}:\text{Inv}_{\mathbb{I}}(A)\rightarrow {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
which makes the following triangle commutative
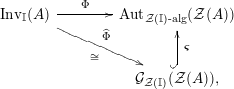
where
![]() $\boldsymbol{\unicode[STIX]{x1D70D}}$
denotes the canonical injection. Moreover,
$\boldsymbol{\unicode[STIX]{x1D70D}}$
denotes the canonical injection. Moreover,
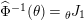 $\widehat{\unicode[STIX]{x1D6F7}}^{-1}(\unicode[STIX]{x1D703})=\text{}_{\unicode[STIX]{x1D703}}J_{1}$
, for every
$\widehat{\unicode[STIX]{x1D6F7}}^{-1}(\unicode[STIX]{x1D703})=\text{}_{\unicode[STIX]{x1D703}}J_{1}$
, for every
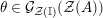 $\unicode[STIX]{x1D703}\in {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
.
$\unicode[STIX]{x1D703}\in {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
.
Proof. In view of Proposition 3.2, it is clear that
![]() $\unicode[STIX]{x1D6F7}$
corestricts to a map
$\unicode[STIX]{x1D6F7}$
corestricts to a map
![]() $\widehat{\unicode[STIX]{x1D6F7}}$
such that
$\widehat{\unicode[STIX]{x1D6F7}}$
such that
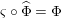 $\unicode[STIX]{x1D70D}\circ \widehat{\unicode[STIX]{x1D6F7}}=\unicode[STIX]{x1D6F7}$
and, by Lemma 3.3, we have that
$\unicode[STIX]{x1D70D}\circ \widehat{\unicode[STIX]{x1D6F7}}=\unicode[STIX]{x1D6F7}$
and, by Lemma 3.3, we have that
![]() $\widehat{\unicode[STIX]{x1D6F7}}$
is injective. Let us check that it is also surjective that is that
$\widehat{\unicode[STIX]{x1D6F7}}$
is injective. Let us check that it is also surjective that is that
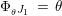 $\unicode[STIX]{x1D6F7}_{\text{}_{\unicode[STIX]{x1D703}}J_{1}}\,=\,\unicode[STIX]{x1D703}$
, for every
$\unicode[STIX]{x1D6F7}_{\text{}_{\unicode[STIX]{x1D703}}J_{1}}\,=\,\unicode[STIX]{x1D703}$
, for every
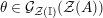 $\unicode[STIX]{x1D703}\in {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
. Recall that, for a given
$\unicode[STIX]{x1D703}\in {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
. Recall that, for a given
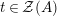 $t\in {\mathcal{Z}}(A)$
, we have
$t\in {\mathcal{Z}}(A)$
, we have
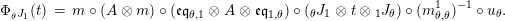 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\text{}_{\unicode[STIX]{x1D703}}J_{1}}(t)\,=\,m\circ (A\otimes _{}m)\circ (\mathfrak{eq}_{\unicode[STIX]{x1D703},1}\otimes _{}A\otimes _{}\mathfrak{eq}_{1,\unicode[STIX]{x1D703}})\circ (\text{}_{\unicode[STIX]{x1D703}}J_{1}\otimes _{}t\otimes \text{}_{1}J_{\unicode[STIX]{x1D703}})\circ (m_{\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}}^{1})^{-1}\circ u_{\unicode[STIX]{x1D703}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\text{}_{\unicode[STIX]{x1D703}}J_{1}}(t)\,=\,m\circ (A\otimes _{}m)\circ (\mathfrak{eq}_{\unicode[STIX]{x1D703},1}\otimes _{}A\otimes _{}\mathfrak{eq}_{1,\unicode[STIX]{x1D703}})\circ (\text{}_{\unicode[STIX]{x1D703}}J_{1}\otimes _{}t\otimes \text{}_{1}J_{\unicode[STIX]{x1D703}})\circ (m_{\unicode[STIX]{x1D703},\unicode[STIX]{x1D703}}^{1})^{-1}\circ u_{\unicode[STIX]{x1D703}}.\end{eqnarray}$$
The desired equality can be checked by diagrams as follows
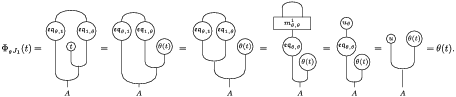
We have so proved that the map
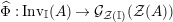 $\widehat{\unicode[STIX]{x1D6F7}}:\text{Inv}_{\mathbb{I}}(A)\rightarrow {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
is bijective. As a consequence, since
$\widehat{\unicode[STIX]{x1D6F7}}:\text{Inv}_{\mathbb{I}}(A)\rightarrow {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
is bijective. As a consequence, since
![]() $\unicode[STIX]{x1D6F7}$
is a group morphism, we have for free that
$\unicode[STIX]{x1D6F7}$
is a group morphism, we have for free that
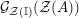 ${\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
is a subgroup of the automorphisms group
${\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
is a subgroup of the automorphisms group
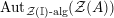 $\text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}({\mathcal{Z}}(A))$
and that both
$\text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-alg}}({\mathcal{Z}}(A))$
and that both
![]() $\widehat{\unicode[STIX]{x1D6F7}}$
and
$\widehat{\unicode[STIX]{x1D6F7}}$
and
![]() $\unicode[STIX]{x1D70D}$
are group morphisms.◻
$\unicode[STIX]{x1D70D}$
are group morphisms.◻
3.2 The case when
 $\unicode[STIX]{x1D6F7}$
is an isomorphism of groups
$\unicode[STIX]{x1D6F7}$
is an isomorphism of groups
Let
![]() $M$
and
$M$
and
![]() $N$
be two
$N$
be two
![]() $A$
-bimodules. Consider the action
$A$
-bimodules. Consider the action
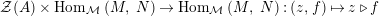 ${\mathcal{Z}}(A)\times \text{Hom}_{{\mathcal{M}}}\left(M,\,N\right)\rightarrow \text{Hom}_{{\mathcal{M}}}\left(M,\,N\right):(z,f)\mapsto z\rhd f$
, defined by (16) for
${\mathcal{Z}}(A)\times \text{Hom}_{{\mathcal{M}}}\left(M,\,N\right)\rightarrow \text{Hom}_{{\mathcal{M}}}\left(M,\,N\right):(z,f)\mapsto z\rhd f$
, defined by (16) for
![]() $S=\mathbb{I}$
, and its right-hand version
$S=\mathbb{I}$
, and its right-hand version
![]() $f\lhd z$
. These actions turns in fact the
$f\lhd z$
. These actions turns in fact the
![]() ${\mathcal{Z}}(\mathbb{I})$
-module
${\mathcal{Z}}(\mathbb{I})$
-module
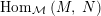 $\text{Hom}_{{\mathcal{M}}}\left(M,\,N\right)$
into a
$\text{Hom}_{{\mathcal{M}}}\left(M,\,N\right)$
into a
![]() ${\mathcal{Z}}(A)$
-bimodule. Note that for
${\mathcal{Z}}(A)$
-bimodule. Note that for
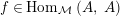 $f\in \text{Hom}_{{\mathcal{M}}}\left(A,\,A\right)$
one easily checks that
$f\in \text{Hom}_{{\mathcal{M}}}\left(A,\,A\right)$
one easily checks that
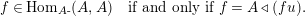 $$\begin{eqnarray}f\in \text{Hom}_{A\text{-}}(A,A)\quad \text{if and only if }f=A\lhd (fu).\end{eqnarray}$$
$$\begin{eqnarray}f\in \text{Hom}_{A\text{-}}(A,A)\quad \text{if and only if }f=A\lhd (fu).\end{eqnarray}$$
Here the notation
![]() $fu$
stands for the composition. Given
$fu$
stands for the composition. Given
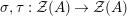 $\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}:{\mathcal{Z}}(A)\rightarrow {\mathcal{Z}}(A)$
two
$\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}:{\mathcal{Z}}(A)\rightarrow {\mathcal{Z}}(A)$
two
![]() ${\mathcal{Z}}(I)$
-linear maps, we set
${\mathcal{Z}}(I)$
-linear maps, we set
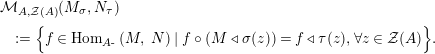 $$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(M_{\unicode[STIX]{x1D70E}},N_{\unicode[STIX]{x1D70F}})\nonumber\\ \displaystyle & & \displaystyle \quad :=\Bigl\{f\in \text{Hom}_{A\text{-}}\left(M,\,N\right)\mid f\circ (M\lhd \unicode[STIX]{x1D70E}(z))=f\lhd \unicode[STIX]{x1D70F}(z),\forall z\in {\mathcal{Z}}(A)\Bigr\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(M_{\unicode[STIX]{x1D70E}},N_{\unicode[STIX]{x1D70F}})\nonumber\\ \displaystyle & & \displaystyle \quad :=\Bigl\{f\in \text{Hom}_{A\text{-}}\left(M,\,N\right)\mid f\circ (M\lhd \unicode[STIX]{x1D70E}(z))=f\lhd \unicode[STIX]{x1D70F}(z),\forall z\in {\mathcal{Z}}(A)\Bigr\}.\nonumber\end{eqnarray}$$
For every
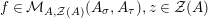 $f\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(A_{\unicode[STIX]{x1D70E}},A_{\unicode[STIX]{x1D70F}}),z\in {\mathcal{Z}}(A)$
, we have
$f\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(A_{\unicode[STIX]{x1D70E}},A_{\unicode[STIX]{x1D70F}}),z\in {\mathcal{Z}}(A)$
, we have
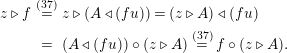 $$\begin{eqnarray}\displaystyle z\rhd f & \overset{(37)}{=} & \displaystyle z\rhd (A\lhd (fu))=(z\rhd A)\lhd (fu)\nonumber\\ \displaystyle & = & \displaystyle (A\lhd (fu))\circ (z\rhd A)\overset{(37)}{=}f\circ (z\rhd A).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle z\rhd f & \overset{(37)}{=} & \displaystyle z\rhd (A\lhd (fu))=(z\rhd A)\lhd (fu)\nonumber\\ \displaystyle & = & \displaystyle (A\lhd (fu))\circ (z\rhd A)\overset{(37)}{=}f\circ (z\rhd A).\end{eqnarray}$$
Let
![]() $\unicode[STIX]{x1D70C}$
be another
$\unicode[STIX]{x1D70C}$
be another
![]() ${\mathcal{Z}}(\mathbb{I})$
-linear endomorphism of
${\mathcal{Z}}(\mathbb{I})$
-linear endomorphism of
![]() ${\mathcal{Z}}(A)$
. We then compute
${\mathcal{Z}}(A)$
. We then compute
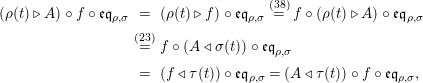 $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D70C}(t)\rhd A)\circ f\circ \mathfrak{eq}_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70E}} & = & \displaystyle (\unicode[STIX]{x1D70C}(t)\rhd f)\circ \mathfrak{eq}_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70E}}\overset{(38)}{=}f\circ (\unicode[STIX]{x1D70C}(t)\rhd A)\circ \mathfrak{eq}_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70E}}\nonumber\\ \displaystyle & \overset{(23)}{=} & \displaystyle f\circ (A\lhd \unicode[STIX]{x1D70E}(t))\circ \mathfrak{eq}_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70E}}\nonumber\\ \displaystyle & = & \displaystyle (f\lhd \unicode[STIX]{x1D70F}(t))\circ \mathfrak{eq}_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70E}}=(A\lhd \unicode[STIX]{x1D70F}(t))\circ f\circ \mathfrak{eq}_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70E}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D70C}(t)\rhd A)\circ f\circ \mathfrak{eq}_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70E}} & = & \displaystyle (\unicode[STIX]{x1D70C}(t)\rhd f)\circ \mathfrak{eq}_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70E}}\overset{(38)}{=}f\circ (\unicode[STIX]{x1D70C}(t)\rhd A)\circ \mathfrak{eq}_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70E}}\nonumber\\ \displaystyle & \overset{(23)}{=} & \displaystyle f\circ (A\lhd \unicode[STIX]{x1D70E}(t))\circ \mathfrak{eq}_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70E}}\nonumber\\ \displaystyle & = & \displaystyle (f\lhd \unicode[STIX]{x1D70F}(t))\circ \mathfrak{eq}_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70E}}=(A\lhd \unicode[STIX]{x1D70F}(t))\circ f\circ \mathfrak{eq}_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70E}},\nonumber\end{eqnarray}$$
for any
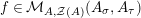 $f\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(A_{\unicode[STIX]{x1D70E}},A_{\unicode[STIX]{x1D70F}})$
and
$f\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(A_{\unicode[STIX]{x1D70E}},A_{\unicode[STIX]{x1D70F}})$
and
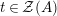 $t\in {\mathcal{Z}}(A)$
. Using the universal property of
$t\in {\mathcal{Z}}(A)$
. Using the universal property of
![]() $\mathfrak{eq}_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70F}}$
, we so get a unique morphism
$\mathfrak{eq}_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70F}}$
, we so get a unique morphism
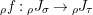 $\text{}_{\unicode[STIX]{x1D70C}}f:\text{}_{\unicode[STIX]{x1D70C}}J_{\unicode[STIX]{x1D70E}}\rightarrow \text{}_{\unicode[STIX]{x1D70C}}J_{\unicode[STIX]{x1D70F}}$
such that
$\text{}_{\unicode[STIX]{x1D70C}}f:\text{}_{\unicode[STIX]{x1D70C}}J_{\unicode[STIX]{x1D70E}}\rightarrow \text{}_{\unicode[STIX]{x1D70C}}J_{\unicode[STIX]{x1D70F}}$
such that
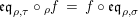 $\mathfrak{eq}_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70F}}\circ \text{}_{\unicode[STIX]{x1D70C}}f\,=\,f\circ \mathfrak{eq}_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70E}}$
which in diagrammatic form is expressed by
$\mathfrak{eq}_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70F}}\circ \text{}_{\unicode[STIX]{x1D70C}}f\,=\,f\circ \mathfrak{eq}_{\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70E}}$
which in diagrammatic form is expressed by
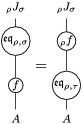
In this way we have defined a map
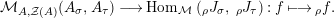 $$\begin{eqnarray}{\mathcal{M}}_{A,{\mathcal{Z}}(A)}(A_{\unicode[STIX]{x1D70E}},A_{\unicode[STIX]{x1D70F}})\longrightarrow \text{Hom}_{{\mathcal{M}}}\left(\text{}_{\unicode[STIX]{x1D70C}}J_{\unicode[STIX]{x1D70E}},\,\text{}_{\unicode[STIX]{x1D70C}}J_{\unicode[STIX]{x1D70F}}\right):f\longmapsto \text{}_{\unicode[STIX]{x1D70C}}f.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{M}}_{A,{\mathcal{Z}}(A)}(A_{\unicode[STIX]{x1D70E}},A_{\unicode[STIX]{x1D70F}})\longrightarrow \text{Hom}_{{\mathcal{M}}}\left(\text{}_{\unicode[STIX]{x1D70C}}J_{\unicode[STIX]{x1D70E}},\,\text{}_{\unicode[STIX]{x1D70C}}J_{\unicode[STIX]{x1D70F}}\right):f\longmapsto \text{}_{\unicode[STIX]{x1D70C}}f.\end{eqnarray}$$
Definition 3.5. Let
![]() $M$
and
$M$
and
![]() $N$
be two
$N$
be two
![]() $A$
-bimodules.
$A$
-bimodules.
-
(1) For
 $\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}:{\mathcal{Z}}(A)\rightarrow {\mathcal{Z}}(A)$
, we will write
$\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}:{\mathcal{Z}}(A)\rightarrow {\mathcal{Z}}(A)$
, we will write
 $M_{\unicode[STIX]{x1D70E}}|N_{\unicode[STIX]{x1D70F}}$
whenever there is
$M_{\unicode[STIX]{x1D70E}}|N_{\unicode[STIX]{x1D70F}}$
whenever there is
 $k\geqslant 1$
and morphisms
$k\geqslant 1$
and morphisms
 $f_{i}\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(M_{\unicode[STIX]{x1D70E}},N_{\unicode[STIX]{x1D70F}})$
,
$f_{i}\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(M_{\unicode[STIX]{x1D70E}},N_{\unicode[STIX]{x1D70F}})$
,
 $g_{i}\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(N_{\unicode[STIX]{x1D70F}},M_{\unicode[STIX]{x1D70E}})$
, for
$g_{i}\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(N_{\unicode[STIX]{x1D70F}},M_{\unicode[STIX]{x1D70E}})$
, for
 $i=1,\ldots ,k$
, such that
$i=1,\ldots ,k$
, such that
 $\sum _{i}g_{i}\circ f_{i}=M$
. We will write
$\sum _{i}g_{i}\circ f_{i}=M$
. We will write
 $M_{\unicode[STIX]{x1D70E}}\sim N_{\unicode[STIX]{x1D70F}}$
whenever both
$M_{\unicode[STIX]{x1D70E}}\sim N_{\unicode[STIX]{x1D70F}}$
whenever both
 $M_{\unicode[STIX]{x1D70E}}|N_{\unicode[STIX]{x1D70F}}$
and
$M_{\unicode[STIX]{x1D70E}}|N_{\unicode[STIX]{x1D70F}}$
and
 $N_{\unicode[STIX]{x1D70F}}|M_{\unicode[STIX]{x1D70E}}$
.
$N_{\unicode[STIX]{x1D70F}}|M_{\unicode[STIX]{x1D70E}}$
. -
(2) If there is
 $k\geqslant 1$
and morphisms
$k\geqslant 1$
and morphisms
 $f_{i}\in \text{Hom}_{A,A}\left(M,\,N\right)$
,
$f_{i}\in \text{Hom}_{A,A}\left(M,\,N\right)$
,
 $g_{i}\in \text{Hom}_{A,A}\left(N,\,M\right)$
, for
$g_{i}\in \text{Hom}_{A,A}\left(N,\,M\right)$
, for
 $i=1,\ldots ,k$
, such that
$i=1,\ldots ,k$
, such that
 $\sum _{i}g_{i}\circ f_{i}=M$
, then we will write
$\sum _{i}g_{i}\circ f_{i}=M$
, then we will write
 $M|N$
. Since our base category
$M|N$
. Since our base category
 ${\mathcal{M}}$
is an abelian category, this is equivalent to say that
${\mathcal{M}}$
is an abelian category, this is equivalent to say that
 $M$
, as an
$M$
, as an
 $A$
-bimodule, is direct summand of a finite direct sum of copies of
$A$
-bimodule, is direct summand of a finite direct sum of copies of
 $N$
. We will write
$N$
. We will write
 $M\sim N$
whenever both
$M\sim N$
whenever both
 $M|N$
and
$M|N$
and
 $N|M$
. The same notation was used for bimodules over rings by Miyashita in [Reference Miyashita23] which in fact goes back to a Hirata [Reference Hirata13], although with different symbols.
$N|M$
. The same notation was used for bimodules over rings by Miyashita in [Reference Miyashita23] which in fact goes back to a Hirata [Reference Hirata13], although with different symbols.
The possible relation between the items
![]() $(1)$
and
$(1)$
and
![]() $(2)$
in the previous Definition will be explored in Proposition 3.8 below. Part of the following Theorem can be compared with [Reference Pareigis25, Theorem 5.3].
$(2)$
in the previous Definition will be explored in Proposition 3.8 below. Part of the following Theorem can be compared with [Reference Pareigis25, Theorem 5.3].
Theorem 3.6. Let
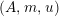 $(A,m,u)$
be a monoid in
$(A,m,u)$
be a monoid in
![]() ${\mathcal{M}}$
. Let
${\mathcal{M}}$
. Let
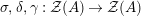 $\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE}:{\mathcal{Z}}(A)\rightarrow {\mathcal{Z}}(A)$
be
$\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE}:{\mathcal{Z}}(A)\rightarrow {\mathcal{Z}}(A)$
be
![]() ${\mathcal{Z}}(\mathbb{I})$
-linear maps and assume that
${\mathcal{Z}}(\mathbb{I})$
-linear maps and assume that
![]() $A_{\unicode[STIX]{x1D6FE}}|A_{\unicode[STIX]{x1D6FF}}$
. Then the morphism
$A_{\unicode[STIX]{x1D6FE}}|A_{\unicode[STIX]{x1D6FF}}$
. Then the morphism
![]() $m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}$
is a split epimorphism. If we further assume that
$m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}$
is a split epimorphism. If we further assume that
![]() $A$
is right flat and that
$A$
is right flat and that
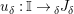 $u_{\unicode[STIX]{x1D6FF}}:\mathbb{I}\rightarrow \text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FF}}$
is an isomorphism, then
$u_{\unicode[STIX]{x1D6FF}}:\mathbb{I}\rightarrow \text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FF}}$
is an isomorphism, then
![]() $m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}$
is an isomorphism.
$m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}$
is an isomorphism.
Proof. Let
![]() $g_{i}$
denote the resulting maps from the assumption
$g_{i}$
denote the resulting maps from the assumption
![]() $A_{\unicode[STIX]{x1D6FE}}|A_{\unicode[STIX]{x1D6FF}}$
. Since each
$A_{\unicode[STIX]{x1D6FE}}|A_{\unicode[STIX]{x1D6FF}}$
. Since each
![]() $g_{i}$
is left
$g_{i}$
is left
![]() $A$
-linear, we have
$A$
-linear, we have
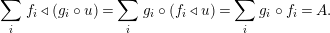 $$\begin{eqnarray}\mathop{\sum }_{i}f_{i}\lhd (g_{i}\circ u)=\mathop{\sum }_{i}g_{i}\circ (f_{i}\lhd u)=\mathop{\sum }_{i}g_{i}\circ f_{i}=A.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i}f_{i}\lhd (g_{i}\circ u)=\mathop{\sum }_{i}g_{i}\circ (f_{i}\lhd u)=\mathop{\sum }_{i}g_{i}\circ f_{i}=A.\end{eqnarray}$$
We set
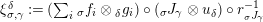 $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}:=({\sum _{i}}_{\unicode[STIX]{x1D70E}}f_{i}\,\otimes \,_{\unicode[STIX]{x1D6FF}}g_{i})\circ (\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FE}}\otimes u_{\unicode[STIX]{x1D6FF}})\circ r_{_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FE}}}^{-1}$
, where
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}:=({\sum _{i}}_{\unicode[STIX]{x1D70E}}f_{i}\,\otimes \,_{\unicode[STIX]{x1D6FF}}g_{i})\circ (\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FE}}\otimes u_{\unicode[STIX]{x1D6FF}})\circ r_{_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FE}}}^{-1}$
, where
![]() $_{\unicode[STIX]{x1D70E}}f_{i}$
and
$_{\unicode[STIX]{x1D70E}}f_{i}$
and
![]() $_{\unicode[STIX]{x1D6FF}}g_{j}$
are defined as in equation (39). By its own definition the morphism
$_{\unicode[STIX]{x1D6FF}}g_{j}$
are defined as in equation (39). By its own definition the morphism
![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}$
satisfies
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}$
satisfies
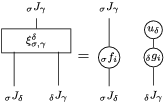
where the summation is understood. So we compute
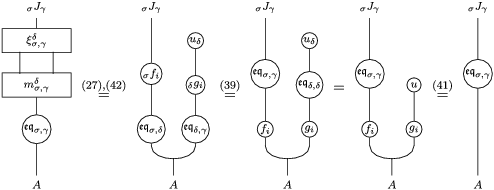
Since
![]() $\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}$
is a monomorphism, we conclude that
$\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}$
is a monomorphism, we conclude that
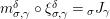 $m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}\circ \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}=\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FE}}$
and hence
$m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}\circ \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}=\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FE}}$
and hence
![]() $m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}$
is a split epimorphism. Now let us check, under the assumptions
$m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}$
is a split epimorphism. Now let us check, under the assumptions
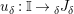 $u_{\unicode[STIX]{x1D6FF}}:\mathbb{I}\rightarrow \text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FF}}$
is an isomorphism and
$u_{\unicode[STIX]{x1D6FF}}:\mathbb{I}\rightarrow \text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FF}}$
is an isomorphism and
![]() $A$
is right flat, that
$A$
is right flat, that
![]() $m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}$
is indeed an isomorphism. Using diagrams, with summation understood again, we have
$m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}$
is indeed an isomorphism. Using diagrams, with summation understood again, we have
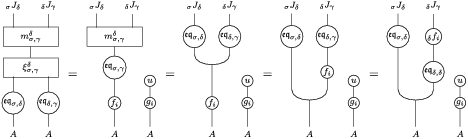
where in the first equality we have used simultaneously equations (42), (39) and the fact that the unit
![]() $u_{\unicode[STIX]{x1D6FF}}$
of
$u_{\unicode[STIX]{x1D6FF}}$
of
![]() $\text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FF}}$
satisfies
$\text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FF}}$
satisfies
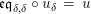 $\mathfrak{eq}_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}}\circ u_{\unicode[STIX]{x1D6FF}}\,=\,u$
the unit of
$\mathfrak{eq}_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF}}\circ u_{\unicode[STIX]{x1D6FF}}\,=\,u$
the unit of
![]() $A$
. We continue then our computation
$A$
. We continue then our computation
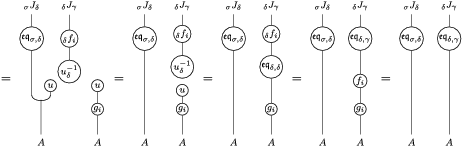
If
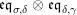 $\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE}}$
is a monomorphism, then we get
$\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE}}$
is a monomorphism, then we get
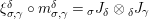 $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}\circ m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}=\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}}\otimes \text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FE}}$
, and so
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}\circ m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}=\text{}_{\unicode[STIX]{x1D70E}}J_{\unicode[STIX]{x1D6FF}}\otimes \text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FE}}$
, and so
![]() $m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}$
is an isomorphism.
$m_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}$
is an isomorphism.
The fact that
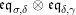 $\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE}}$
is a monomorphism is proved as follows. First, using Proposition 2.5 and that
$\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE}}$
is a monomorphism is proved as follows. First, using Proposition 2.5 and that
![]() $A_{\unicode[STIX]{x1D6FE}}|A_{\unicode[STIX]{x1D6FF}}$
, one shows that
$A_{\unicode[STIX]{x1D6FE}}|A_{\unicode[STIX]{x1D6FF}}$
, one shows that
 $(\text{}_{\unicode[STIX]{x1D6FE}}J_{\unicode[STIX]{x1D6FF}},\text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FE}},\overline{m}_{\unicode[STIX]{x1D6FF},\,\unicode[STIX]{x1D6FF}}^{\unicode[STIX]{x1D6FE}},\overline{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}})$
is a right dualizable datum between the monoids
$(\text{}_{\unicode[STIX]{x1D6FE}}J_{\unicode[STIX]{x1D6FF}},\text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FE}},\overline{m}_{\unicode[STIX]{x1D6FF},\,\unicode[STIX]{x1D6FF}}^{\unicode[STIX]{x1D6FE}},\overline{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}})$
is a right dualizable datum between the monoids
![]() $\text{}_{\unicode[STIX]{x1D6FE}}J_{\unicode[STIX]{x1D6FE}}$
and
$\text{}_{\unicode[STIX]{x1D6FE}}J_{\unicode[STIX]{x1D6FE}}$
and
![]() $\text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FF}}$
, where
$\text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FF}}$
, where
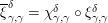 $\overline{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}\circ \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}$
is a splitting of
$\overline{\unicode[STIX]{x1D709}}_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}=\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}\circ \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}$
is a splitting of
![]() $\overline{m}_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}$
. Secondly, by Proposition 1.4, we obtain that
$\overline{m}_{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}}^{\unicode[STIX]{x1D6FF}}$
. Secondly, by Proposition 1.4, we obtain that
![]() $\text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FE}}$
is left flat as
$\text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FE}}$
is left flat as
![]() $\mathbb{I}\cong \text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FF}}$
. In this way, we deduce that
$\mathbb{I}\cong \text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FF}}$
. In this way, we deduce that
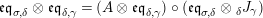 $\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE}}=(A\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE}})\circ (\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}\otimes \text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FE}})$
is a monomorphism since
$\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE}}=(A\otimes _{}\mathfrak{eq}_{\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FE}})\circ (\mathfrak{eq}_{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D6FF}}\otimes \text{}_{\unicode[STIX]{x1D6FF}}J_{\unicode[STIX]{x1D6FE}})$
is a monomorphism since
![]() $A$
is right flat.◻
$A$
is right flat.◻
As a consequence of Theorem 3.6, we have
Corollary 3.7. Let
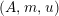 $(A,m,u)$
be a monoid such that
$(A,m,u)$
be a monoid such that
![]() $A$
is right flat and
$A$
is right flat and
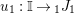 $u_{1}:\mathbb{I}\rightarrow \text{}_{1}J_{1}$
is an isomorphism. Take
$u_{1}:\mathbb{I}\rightarrow \text{}_{1}J_{1}$
is an isomorphism. Take
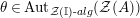 $\unicode[STIX]{x1D703}\in \text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-}alg}({\mathcal{Z}}(A))$
such that
$\unicode[STIX]{x1D703}\in \text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-}alg}({\mathcal{Z}}(A))$
such that
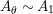 $A_{\unicode[STIX]{x1D703}}\sim A_{1}$
. Then
$A_{\unicode[STIX]{x1D703}}\sim A_{1}$
. Then
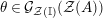 $\unicode[STIX]{x1D703}\in {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
the subgroup defined in (35).
$\unicode[STIX]{x1D703}\in {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
the subgroup defined in (35).
Under the assumptions of Corollary 3.7, we do not know if the invertibility of
![]() $\text{}_{\unicode[STIX]{x1D703}}J_{1}$
, for some
$\text{}_{\unicode[STIX]{x1D703}}J_{1}$
, for some
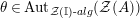 $\unicode[STIX]{x1D703}\in \text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-}alg}({\mathcal{Z}}(A))$
, is a sufficient condition to have that
$\unicode[STIX]{x1D703}\in \text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-}alg}({\mathcal{Z}}(A))$
, is a sufficient condition to have that
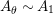 $A_{\unicode[STIX]{x1D703}}\sim A_{1}$
. This is why at this level of generality it is convenient to distinguish between the subset of elements
$A_{\unicode[STIX]{x1D703}}\sim A_{1}$
. This is why at this level of generality it is convenient to distinguish between the subset of elements
![]() $\unicode[STIX]{x1D703}$
for which
$\unicode[STIX]{x1D703}$
for which
![]() $\text{}_{\unicode[STIX]{x1D703}}J_{1}$
is invertible and those for which
$\text{}_{\unicode[STIX]{x1D703}}J_{1}$
is invertible and those for which
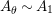 $A_{\unicode[STIX]{x1D703}}\sim A_{1}$
. However, as we will see below, for Azumaya monoids in
$A_{\unicode[STIX]{x1D703}}\sim A_{1}$
. However, as we will see below, for Azumaya monoids in
![]() ${\mathcal{M}}$
where
${\mathcal{M}}$
where
![]() ${\mathcal{Z}}$
is faithful, these two subsets coincide as subgroups of
${\mathcal{Z}}$
is faithful, these two subsets coincide as subgroups of
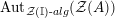 $\text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-}alg}({\mathcal{Z}}(A))$
. Thus, under these stronger assumptions one obtains the converse of the previous corollary, as in the classical case (see e.g., [Reference Miyashita23]).
$\text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-}alg}({\mathcal{Z}}(A))$
. Thus, under these stronger assumptions one obtains the converse of the previous corollary, as in the classical case (see e.g., [Reference Miyashita23]).
The following result collects useful properties of Definition 3.5.
Proposition 3.8. Let
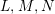 $L,M,N$
be
$L,M,N$
be
![]() $A$
-bimodules and let
$A$
-bimodules and let
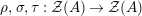 $\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}:{\mathcal{Z}}(A)\rightarrow {\mathcal{Z}}(A)$
be
$\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}:{\mathcal{Z}}(A)\rightarrow {\mathcal{Z}}(A)$
be
![]() ${\mathcal{Z}}(I)$
-linear maps. Then we have the following properties:
${\mathcal{Z}}(I)$
-linear maps. Then we have the following properties:
-
(1)
 $\text{Hom}_{A,A}\left(M,\,N\right)\subseteq {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(M_{\unicode[STIX]{x1D70E}},N_{\unicode[STIX]{x1D70E}})$
.
$\text{Hom}_{A,A}\left(M,\,N\right)\subseteq {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(M_{\unicode[STIX]{x1D70E}},N_{\unicode[STIX]{x1D70E}})$
. -
(2)
 $M|N$
implies
$M|N$
implies
 $M_{\unicode[STIX]{x1D70E}}|N_{\unicode[STIX]{x1D70E}}$
.
$M_{\unicode[STIX]{x1D70E}}|N_{\unicode[STIX]{x1D70E}}$
. -
(3)
 $M\cong N$
implies
$M\cong N$
implies
 $M_{\unicode[STIX]{x1D70E}}\sim N_{\unicode[STIX]{x1D70E}}$
.
$M_{\unicode[STIX]{x1D70E}}\sim N_{\unicode[STIX]{x1D70E}}$
. -
(4)
 $M|N$
implies
$M|N$
implies
 $M\otimes _{A}L|N\otimes _{A}L$
.
$M\otimes _{A}L|N\otimes _{A}L$
. -
(5)
 ${\mathcal{M}}_{A,{\mathcal{Z}}(A)}(M_{\unicode[STIX]{x1D70E}},N_{\unicode[STIX]{x1D70F}})\circ {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(L_{\unicode[STIX]{x1D70C}},M_{\unicode[STIX]{x1D70E}})\subseteq {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(L_{\unicode[STIX]{x1D70C}},N_{\unicode[STIX]{x1D70F}})$
, where
${\mathcal{M}}_{A,{\mathcal{Z}}(A)}(M_{\unicode[STIX]{x1D70E}},N_{\unicode[STIX]{x1D70F}})\circ {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(L_{\unicode[STIX]{x1D70C}},M_{\unicode[STIX]{x1D70E}})\subseteq {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(L_{\unicode[STIX]{x1D70C}},N_{\unicode[STIX]{x1D70F}})$
, where
 $\circ$
is the composition in
$\circ$
is the composition in
 $\text{}_{A}{\mathcal{M}}$
.
$\text{}_{A}{\mathcal{M}}$
. -
(6)
 $L_{\unicode[STIX]{x1D70C}}|M_{\unicode[STIX]{x1D70E}}$
and
$L_{\unicode[STIX]{x1D70C}}|M_{\unicode[STIX]{x1D70E}}$
and
 $M_{\unicode[STIX]{x1D70E}}|N_{\unicode[STIX]{x1D70F}}$
implies
$M_{\unicode[STIX]{x1D70E}}|N_{\unicode[STIX]{x1D70F}}$
implies
 $L_{\unicode[STIX]{x1D70C}}|N_{\unicode[STIX]{x1D70F}}$
.
$L_{\unicode[STIX]{x1D70C}}|N_{\unicode[STIX]{x1D70F}}$
. -
(7) If
 $M_{\unicode[STIX]{x1D70E}}|N_{\unicode[STIX]{x1D70F}}$
, then
$M_{\unicode[STIX]{x1D70E}}|N_{\unicode[STIX]{x1D70F}}$
, then
 $M_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70C}}|N_{\unicode[STIX]{x1D70F}\unicode[STIX]{x1D70C}}$
.
$M_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70C}}|N_{\unicode[STIX]{x1D70F}\unicode[STIX]{x1D70C}}$
.
Proof.
![]() $(1)$
Let
$(1)$
Let
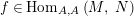 $f\in \text{Hom}_{A,A}\left(M,\,N\right)$
. Then
$f\in \text{Hom}_{A,A}\left(M,\,N\right)$
. Then
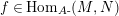 $f\in \text{Hom}_{A\text{-}}(M,N)$
and, for every
$f\in \text{Hom}_{A\text{-}}(M,N)$
and, for every
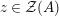 $z\in {\mathcal{Z}}(A)$
, we have
$z\in {\mathcal{Z}}(A)$
, we have
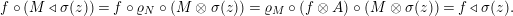 $$\begin{eqnarray}f\circ (M\lhd \unicode[STIX]{x1D70E}(z))=f\circ \unicode[STIX]{x1D71A}_{N}\circ (M\otimes \unicode[STIX]{x1D70E}(z))=\unicode[STIX]{x1D71A}_{M}\circ (f\otimes A)\circ (M\otimes \unicode[STIX]{x1D70E}(z))=f\lhd \unicode[STIX]{x1D70E}(z).\end{eqnarray}$$
$$\begin{eqnarray}f\circ (M\lhd \unicode[STIX]{x1D70E}(z))=f\circ \unicode[STIX]{x1D71A}_{N}\circ (M\otimes \unicode[STIX]{x1D70E}(z))=\unicode[STIX]{x1D71A}_{M}\circ (f\otimes A)\circ (M\otimes \unicode[STIX]{x1D70E}(z))=f\lhd \unicode[STIX]{x1D70E}(z).\end{eqnarray}$$
![]() $(2)$
It follows by
$(2)$
It follows by
![]() $(1)$
.
$(1)$
.
![]() $(3)$
Let
$(3)$
Let
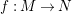 $f:M\rightarrow N$
be an isomorphism of
$f:M\rightarrow N$
be an isomorphism of
![]() $A$
-bimodules. Set
$A$
-bimodules. Set
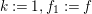 $k:=1,f_{1}:=f$
and
$k:=1,f_{1}:=f$
and
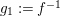 $g_{1}:=f^{-1}$
. Clearly
$g_{1}:=f^{-1}$
. Clearly
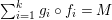 $\sum _{i=1}^{k}g_{i}\circ f_{i}=M$
so that, by
$\sum _{i=1}^{k}g_{i}\circ f_{i}=M$
so that, by
![]() $(2)$
, we get
$(2)$
, we get
![]() $M_{\unicode[STIX]{x1D70E}}|N_{\unicode[STIX]{x1D70E}}$
. If we interchange the roles of
$M_{\unicode[STIX]{x1D70E}}|N_{\unicode[STIX]{x1D70E}}$
. If we interchange the roles of
![]() $M$
and
$M$
and
![]() $N$
we get also
$N$
we get also
![]() $N_{\unicode[STIX]{x1D70E}}|M_{\unicode[STIX]{x1D70E}}$
.
$N_{\unicode[STIX]{x1D70E}}|M_{\unicode[STIX]{x1D70E}}$
.
![]() $(4)$
Let
$(4)$
Let
![]() $k\geqslant 1$
and let
$k\geqslant 1$
and let
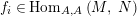 $f_{i}\in \text{Hom}_{A,A}\left(M,\,N\right)$
,
$f_{i}\in \text{Hom}_{A,A}\left(M,\,N\right)$
,
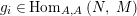 $g_{i}\in \text{Hom}_{A,A}\left(N,\,M\right)$
, for
$g_{i}\in \text{Hom}_{A,A}\left(N,\,M\right)$
, for
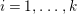 $i=1,\ldots ,k$
, such that
$i=1,\ldots ,k$
, such that
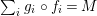 $\sum _{i}g_{i}\circ f_{i}=M$
. Then
$\sum _{i}g_{i}\circ f_{i}=M$
. Then
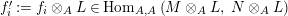 $f_{i}^{\prime }:=f_{i}\otimes _{A}L\in \text{Hom}_{A,A}\left(M\otimes _{A}L,\,N\otimes _{A}L\right)$
,
$f_{i}^{\prime }:=f_{i}\otimes _{A}L\in \text{Hom}_{A,A}\left(M\otimes _{A}L,\,N\otimes _{A}L\right)$
,
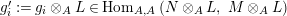 $g_{i}^{\prime }:=g_{i}\otimes _{A}L\in \text{Hom}_{A,A}\left(N\otimes _{A}L,\,M\otimes _{A}L\right)$
. Moreover,
$g_{i}^{\prime }:=g_{i}\otimes _{A}L\in \text{Hom}_{A,A}\left(N\otimes _{A}L,\,M\otimes _{A}L\right)$
. Moreover,
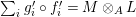 $\sum _{i}g_{i}^{\prime }\circ f_{i}^{\prime }=M\otimes _{A}L$
.
$\sum _{i}g_{i}^{\prime }\circ f_{i}^{\prime }=M\otimes _{A}L$
.
![]() $(5)$
Let
$(5)$
Let
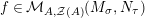 $f\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(M_{\unicode[STIX]{x1D70E}},N_{\unicode[STIX]{x1D70F}})$
and
$f\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(M_{\unicode[STIX]{x1D70E}},N_{\unicode[STIX]{x1D70F}})$
and
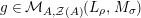 $g\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(L_{\unicode[STIX]{x1D70C}},M_{\unicode[STIX]{x1D70E}})$
. Then
$g\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(L_{\unicode[STIX]{x1D70C}},M_{\unicode[STIX]{x1D70E}})$
. Then
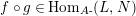 $f\circ g\in \text{Hom}_{A\text{-}}(L,N)$
. Moreover,
$f\circ g\in \text{Hom}_{A\text{-}}(L,N)$
. Moreover,
 $$\begin{eqnarray}\displaystyle f\circ g\circ (L\lhd \unicode[STIX]{x1D70C}(z)) & = & \displaystyle f\circ (g\lhd \unicode[STIX]{x1D70E}(z))=f\circ (M\lhd \unicode[STIX]{x1D70E}(z))\circ g\nonumber\\ \displaystyle & = & \displaystyle (f\lhd \unicode[STIX]{x1D70F}(z))\circ g=(f\circ g)\lhd \unicode[STIX]{x1D70F}(z).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f\circ g\circ (L\lhd \unicode[STIX]{x1D70C}(z)) & = & \displaystyle f\circ (g\lhd \unicode[STIX]{x1D70E}(z))=f\circ (M\lhd \unicode[STIX]{x1D70E}(z))\circ g\nonumber\\ \displaystyle & = & \displaystyle (f\lhd \unicode[STIX]{x1D70F}(z))\circ g=(f\circ g)\lhd \unicode[STIX]{x1D70F}(z).\nonumber\end{eqnarray}$$
![]() $(6)$
By assumption there is
$(6)$
By assumption there is
![]() $k\geqslant 1$
and morphisms
$k\geqslant 1$
and morphisms
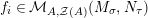 $f_{i}\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(M_{\unicode[STIX]{x1D70E}},N_{\unicode[STIX]{x1D70F}})$
,
$f_{i}\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(M_{\unicode[STIX]{x1D70E}},N_{\unicode[STIX]{x1D70F}})$
,
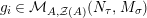 $g_{i}\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(N_{\unicode[STIX]{x1D70F}},M_{\unicode[STIX]{x1D70E}})$
, for
$g_{i}\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(N_{\unicode[STIX]{x1D70F}},M_{\unicode[STIX]{x1D70E}})$
, for
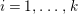 $i=1,\ldots ,k$
, such that
$i=1,\ldots ,k$
, such that
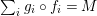 $\sum _{i}g_{i}\circ f_{i}=M$
. Moreover, there is
$\sum _{i}g_{i}\circ f_{i}=M$
. Moreover, there is
![]() $k^{\prime }\geqslant 1$
and morphisms
$k^{\prime }\geqslant 1$
and morphisms
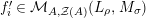 $f_{i}^{\prime }\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(L_{\unicode[STIX]{x1D70C}},M_{\unicode[STIX]{x1D70E}})$
,
$f_{i}^{\prime }\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(L_{\unicode[STIX]{x1D70C}},M_{\unicode[STIX]{x1D70E}})$
,
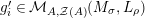 $g_{i}^{\prime }\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(M_{\unicode[STIX]{x1D70E}},L_{\unicode[STIX]{x1D70C}})$
, for
$g_{i}^{\prime }\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(M_{\unicode[STIX]{x1D70E}},L_{\unicode[STIX]{x1D70C}})$
, for
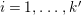 $i=1,\ldots ,k^{\prime }$
, such that
$i=1,\ldots ,k^{\prime }$
, such that
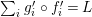 $\sum _{i}g_{i}^{\prime }\circ f_{i}^{\prime }=L$
. Set
$\sum _{i}g_{i}^{\prime }\circ f_{i}^{\prime }=L$
. Set
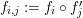 $f_{i,j}:=f_{i}\circ f_{j}^{\prime }$
and
$f_{i,j}:=f_{i}\circ f_{j}^{\prime }$
and
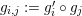 $g_{i,j}:=g_{i}^{\prime }\circ g_{j}$
. Then
$g_{i,j}:=g_{i}^{\prime }\circ g_{j}$
. Then
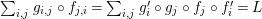 $\sum _{i,j}g_{i,j}\circ f_{j,i}=\sum _{i,j}g_{i}^{\prime }\circ g_{j}\circ f_{j}\circ f_{i}^{\prime }=L$
and, by
$\sum _{i,j}g_{i,j}\circ f_{j,i}=\sum _{i,j}g_{i}^{\prime }\circ g_{j}\circ f_{j}\circ f_{i}^{\prime }=L$
and, by
![]() $(5)$
, we have that
$(5)$
, we have that
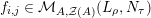 $f_{i,j}\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(L_{\unicode[STIX]{x1D70C}},N_{\unicode[STIX]{x1D70F}})$
and
$f_{i,j}\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(L_{\unicode[STIX]{x1D70C}},N_{\unicode[STIX]{x1D70F}})$
and
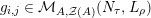 $g_{i,j}\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(N_{\unicode[STIX]{x1D70F}},L_{\unicode[STIX]{x1D70C}})$
.
$g_{i,j}\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(N_{\unicode[STIX]{x1D70F}},L_{\unicode[STIX]{x1D70C}})$
.
![]() $(7)$
It follows from the obvious inclusion
$(7)$
It follows from the obvious inclusion
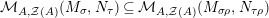 ${\mathcal{M}}_{A,{\mathcal{Z}}(A)}(M_{\unicode[STIX]{x1D70E}},N_{\unicode[STIX]{x1D70F}})\subseteq {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(M_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70C}},N_{\unicode[STIX]{x1D70F}\unicode[STIX]{x1D70C}})$
.◻
${\mathcal{M}}_{A,{\mathcal{Z}}(A)}(M_{\unicode[STIX]{x1D70E}},N_{\unicode[STIX]{x1D70F}})\subseteq {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(M_{\unicode[STIX]{x1D70E}\unicode[STIX]{x1D70C}},N_{\unicode[STIX]{x1D70F}\unicode[STIX]{x1D70C}})$
.◻
Take
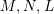 $M,N,L$
to be three
$M,N,L$
to be three
![]() $A$
-bimodules, and let
$A$
-bimodules, and let
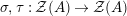 $\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}:{\mathcal{Z}}(A)\rightarrow {\mathcal{Z}}(A)$
be
$\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}:{\mathcal{Z}}(A)\rightarrow {\mathcal{Z}}(A)$
be
![]() ${\mathcal{Z}}(\mathbb{I})$
-linear maps. We define
${\mathcal{Z}}(\mathbb{I})$
-linear maps. We define
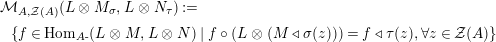 $$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(L\otimes _{}M_{\unicode[STIX]{x1D70E}},L\otimes _{}N_{\unicode[STIX]{x1D70F}}):=\nonumber\\ \displaystyle & & \displaystyle ~\left\{f\in \text{Hom}_{A\text{-}}(L\otimes _{}M,L\otimes _{}N)\,|\,f\circ (L\otimes _{}(M\lhd \unicode[STIX]{x1D70E}(z)))=f\lhd \unicode[STIX]{x1D70F}(z),\forall z\in {\mathcal{Z}}(A)\right\}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(L\otimes _{}M_{\unicode[STIX]{x1D70E}},L\otimes _{}N_{\unicode[STIX]{x1D70F}}):=\nonumber\\ \displaystyle & & \displaystyle ~\left\{f\in \text{Hom}_{A\text{-}}(L\otimes _{}M,L\otimes _{}N)\,|\,f\circ (L\otimes _{}(M\lhd \unicode[STIX]{x1D70E}(z)))=f\lhd \unicode[STIX]{x1D70F}(z),\forall z\in {\mathcal{Z}}(A)\right\}\nonumber\end{eqnarray}$$
where
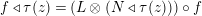 $f\lhd \unicode[STIX]{x1D70F}(z)=(L\otimes _{}(N\lhd \unicode[STIX]{x1D70F}(z)))\circ f$
as the right
$f\lhd \unicode[STIX]{x1D70F}(z)=(L\otimes _{}(N\lhd \unicode[STIX]{x1D70F}(z)))\circ f$
as the right
![]() $A$
-module structure of
$A$
-module structure of
![]() $L\otimes _{}N$
is the one coming from
$L\otimes _{}N$
is the one coming from
![]() $N$
. Using this set we define as in Definition 3.5, the relations
$N$
. Using this set we define as in Definition 3.5, the relations
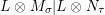 $L\otimes _{}M_{\unicode[STIX]{x1D70E}}|L\otimes _{}N_{\unicode[STIX]{x1D70F}}$
and
$L\otimes _{}M_{\unicode[STIX]{x1D70E}}|L\otimes _{}N_{\unicode[STIX]{x1D70F}}$
and
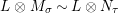 $L\otimes _{}M_{\unicode[STIX]{x1D70E}}\sim L\otimes _{}N_{\unicode[STIX]{x1D70F}}$
.
$L\otimes _{}M_{\unicode[STIX]{x1D70E}}\sim L\otimes _{}N_{\unicode[STIX]{x1D70F}}$
.
Proposition 3.9. Let
![]() $M$
be an
$M$
be an
![]() $A$
-bimodule and let
$A$
-bimodule and let
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
be two monoids automorphisms of
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
be two monoids automorphisms of
![]() $A$
. Set
$A$
. Set
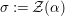 $\unicode[STIX]{x1D70E}:={\mathcal{Z}}(\unicode[STIX]{x1D6FC})$
and
$\unicode[STIX]{x1D70E}:={\mathcal{Z}}(\unicode[STIX]{x1D6FC})$
and
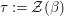 $\unicode[STIX]{x1D70F}:={\mathcal{Z}}(\unicode[STIX]{x1D6FD})$
. Then
$\unicode[STIX]{x1D70F}:={\mathcal{Z}}(\unicode[STIX]{x1D6FD})$
. Then
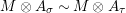 $M\otimes A_{\unicode[STIX]{x1D70E}}\sim M\otimes A_{\unicode[STIX]{x1D70F}}$
.
$M\otimes A_{\unicode[STIX]{x1D70E}}\sim M\otimes A_{\unicode[STIX]{x1D70F}}$
.
Proof. Set
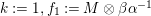 $k:=1,f_{1}:=M\otimes \unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}^{-1}$
and
$k:=1,f_{1}:=M\otimes \unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FC}^{-1}$
and
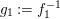 $g_{1}:=f_{1}^{-1}$
. Clearly
$g_{1}:=f_{1}^{-1}$
. Clearly
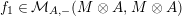 $f_{1}\in {\mathcal{M}}_{A,-}(M\otimes A,M\otimes A)$
. Moreover,
$f_{1}\in {\mathcal{M}}_{A,-}(M\otimes A,M\otimes A)$
. Moreover,
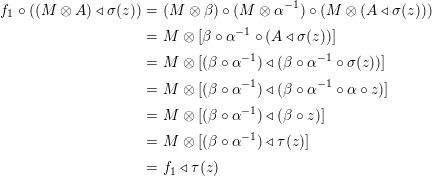 $$\begin{eqnarray}\displaystyle f_{1}\circ ((M\otimes A)\lhd \unicode[STIX]{x1D70E}(z)) & = & \displaystyle (M\otimes \unicode[STIX]{x1D6FD})\circ (M\otimes \unicode[STIX]{x1D6FC}^{-1})\circ (M\otimes (A\lhd \unicode[STIX]{x1D70E}(z)))\nonumber\\ \displaystyle & = & \displaystyle M\otimes [\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}^{-1}\circ (A\lhd \unicode[STIX]{x1D70E}(z))]\nonumber\\ \displaystyle & = & \displaystyle M\otimes [(\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}^{-1})\lhd (\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}^{-1}\circ \unicode[STIX]{x1D70E}(z))]\nonumber\\ \displaystyle & = & \displaystyle M\otimes [(\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}^{-1})\lhd (\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}^{-1}\circ \unicode[STIX]{x1D6FC}\circ z)]\nonumber\\ \displaystyle & = & \displaystyle M\otimes [(\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}^{-1})\lhd (\unicode[STIX]{x1D6FD}\circ z)]\nonumber\\ \displaystyle & = & \displaystyle M\otimes [(\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}^{-1})\lhd \unicode[STIX]{x1D70F}(z)]\nonumber\\ \displaystyle & = & \displaystyle f_{1}\lhd \unicode[STIX]{x1D70F}(z)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{1}\circ ((M\otimes A)\lhd \unicode[STIX]{x1D70E}(z)) & = & \displaystyle (M\otimes \unicode[STIX]{x1D6FD})\circ (M\otimes \unicode[STIX]{x1D6FC}^{-1})\circ (M\otimes (A\lhd \unicode[STIX]{x1D70E}(z)))\nonumber\\ \displaystyle & = & \displaystyle M\otimes [\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}^{-1}\circ (A\lhd \unicode[STIX]{x1D70E}(z))]\nonumber\\ \displaystyle & = & \displaystyle M\otimes [(\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}^{-1})\lhd (\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}^{-1}\circ \unicode[STIX]{x1D70E}(z))]\nonumber\\ \displaystyle & = & \displaystyle M\otimes [(\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}^{-1})\lhd (\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}^{-1}\circ \unicode[STIX]{x1D6FC}\circ z)]\nonumber\\ \displaystyle & = & \displaystyle M\otimes [(\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}^{-1})\lhd (\unicode[STIX]{x1D6FD}\circ z)]\nonumber\\ \displaystyle & = & \displaystyle M\otimes [(\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}^{-1})\lhd \unicode[STIX]{x1D70F}(z)]\nonumber\\ \displaystyle & = & \displaystyle f_{1}\lhd \unicode[STIX]{x1D70F}(z)\nonumber\end{eqnarray}$$
so that
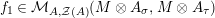 $f_{1}\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(M\otimes A_{\unicode[STIX]{x1D70E}},M\otimes A_{\unicode[STIX]{x1D70F}})$
. A similar argument shows that
$f_{1}\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(M\otimes A_{\unicode[STIX]{x1D70E}},M\otimes A_{\unicode[STIX]{x1D70F}})$
. A similar argument shows that
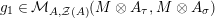 $g_{1}\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(M\otimes A_{\unicode[STIX]{x1D70F}},M\otimes A_{\unicode[STIX]{x1D70E}})$
. Since
$g_{1}\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(M\otimes A_{\unicode[STIX]{x1D70F}},M\otimes A_{\unicode[STIX]{x1D70E}})$
. Since
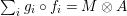 $\sum _{i}g_{i}\circ f_{i}=M\otimes A$
, we conclude that
$\sum _{i}g_{i}\circ f_{i}=M\otimes A$
, we conclude that
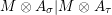 $M\otimes A_{\unicode[STIX]{x1D70E}}|M\otimes A_{\unicode[STIX]{x1D70F}}$
. If we interchange the roles of
$M\otimes A_{\unicode[STIX]{x1D70E}}|M\otimes A_{\unicode[STIX]{x1D70F}}$
. If we interchange the roles of
![]() $M$
and
$M$
and
![]() $N$
and the ones of
$N$
and the ones of
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D6FC}$
we get also
$\unicode[STIX]{x1D6FC}$
we get also
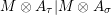 $M\otimes A_{\unicode[STIX]{x1D70F}}|M\otimes A_{\unicode[STIX]{x1D70E}}$
.◻
$M\otimes A_{\unicode[STIX]{x1D70F}}|M\otimes A_{\unicode[STIX]{x1D70E}}$
.◻
Theorem 3.10. Let
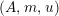 $(A,m,u)$
be a monoid in
$(A,m,u)$
be a monoid in
![]() ${\mathcal{M}}$
and assume that
${\mathcal{M}}$
and assume that
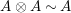 $A\otimes A\sim A$
. Let
$A\otimes A\sim A$
. Let
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
be two monoids automorphisms of
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
be two monoids automorphisms of
![]() $A$
and set
$A$
and set
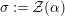 $\unicode[STIX]{x1D70E}:={\mathcal{Z}}(\unicode[STIX]{x1D6FC})$
and
$\unicode[STIX]{x1D70E}:={\mathcal{Z}}(\unicode[STIX]{x1D6FC})$
and
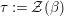 $\unicode[STIX]{x1D70F}:={\mathcal{Z}}(\unicode[STIX]{x1D6FD})$
. Then
$\unicode[STIX]{x1D70F}:={\mathcal{Z}}(\unicode[STIX]{x1D6FD})$
. Then
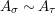 $A_{\unicode[STIX]{x1D70E}}\sim A_{\unicode[STIX]{x1D70F}}$
.
$A_{\unicode[STIX]{x1D70E}}\sim A_{\unicode[STIX]{x1D70F}}$
.
Proof. We split the proof in three steps.
(1) Since
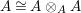 $A\cong A\otimes _{A}A$
, by Proposition 3.8(3), we get
$A\cong A\otimes _{A}A$
, by Proposition 3.8(3), we get
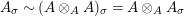 $A_{\unicode[STIX]{x1D70E}}\sim (A\otimes _{A}A)_{\unicode[STIX]{x1D70E}}=A\otimes _{A}A_{\unicode[STIX]{x1D70E}}$
.
$A_{\unicode[STIX]{x1D70E}}\sim (A\otimes _{A}A)_{\unicode[STIX]{x1D70E}}=A\otimes _{A}A_{\unicode[STIX]{x1D70E}}$
.
(2) Since
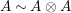 $A\sim A\otimes A$
, in view of Proposition 3.8(4), we have
$A\sim A\otimes A$
, in view of Proposition 3.8(4), we have
 $A\otimes _{A}A\sim A\otimes A\otimes _{A}A$
and hence
$A\otimes _{A}A\sim A\otimes A\otimes _{A}A$
and hence
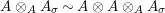 $A\otimes _{A}A_{\unicode[STIX]{x1D70E}}\sim A\otimes A\otimes _{A}A_{\unicode[STIX]{x1D70E}}$
, by Proposition 3.8(2).
$A\otimes _{A}A_{\unicode[STIX]{x1D70E}}\sim A\otimes A\otimes _{A}A_{\unicode[STIX]{x1D70E}}$
, by Proposition 3.8(2).
(3) Since
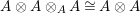 $A\otimes A\otimes _{A}A\cong A\otimes A$
, by Proposition 3.8(3), we get
$A\otimes A\otimes _{A}A\cong A\otimes A$
, by Proposition 3.8(3), we get
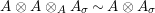 $A\otimes A\otimes _{A}A_{\unicode[STIX]{x1D70E}}\sim A\otimes A_{\unicode[STIX]{x1D70E}}$
.
$A\otimes A\otimes _{A}A_{\unicode[STIX]{x1D70E}}\sim A\otimes A_{\unicode[STIX]{x1D70E}}$
.
Now, if we glue together (1), (2) and (3) using Proposition 3.8(6), we obtain
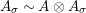 $A_{\unicode[STIX]{x1D70E}}\sim A\otimes A_{\unicode[STIX]{x1D70E}}$
. Similarly one gets
$A_{\unicode[STIX]{x1D70E}}\sim A\otimes A_{\unicode[STIX]{x1D70E}}$
. Similarly one gets
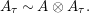 $A_{\unicode[STIX]{x1D70F}}\sim A\otimes A_{\unicode[STIX]{x1D70F}}.$
The conclusion follows by Propositions 3.9 and 3.8(6).◻
$A_{\unicode[STIX]{x1D70F}}\sim A\otimes A_{\unicode[STIX]{x1D70F}}.$
The conclusion follows by Propositions 3.9 and 3.8(6).◻
Corollary 3.11. Let
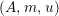 $(A,m,u)$
be a monoid in
$(A,m,u)$
be a monoid in
![]() ${\mathcal{M}}$
with a right flat underlying object
${\mathcal{M}}$
with a right flat underlying object
![]() $A$
. Assume that
$A$
. Assume that
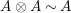 $A\otimes A\sim A$
and
$A\otimes A\sim A$
and
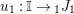 $u_{1}:\mathbb{I}\rightarrow \text{}_{1}J_{1}$
is an isomorphism. Let
$u_{1}:\mathbb{I}\rightarrow \text{}_{1}J_{1}$
is an isomorphism. Let
![]() $\unicode[STIX]{x1D6FC}$
be a monoid automorphism of
$\unicode[STIX]{x1D6FC}$
be a monoid automorphism of
![]() $A$
and set
$A$
and set
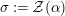 $\unicode[STIX]{x1D70E}:={\mathcal{Z}}(\unicode[STIX]{x1D6FC})$
. Then
$\unicode[STIX]{x1D70E}:={\mathcal{Z}}(\unicode[STIX]{x1D6FC})$
. Then
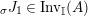 $\text{}_{\unicode[STIX]{x1D70E}}J_{1}\in \text{Inv}_{\mathbb{I}}(A)$
with inverse
$\text{}_{\unicode[STIX]{x1D70E}}J_{1}\in \text{Inv}_{\mathbb{I}}(A)$
with inverse
![]() $\text{}_{1}J_{\unicode[STIX]{x1D70E}}$
. Moreover,
$\text{}_{1}J_{\unicode[STIX]{x1D70E}}$
. Moreover,
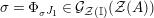 $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D6F7}_{\text{}_{\unicode[STIX]{x1D70E}}J_{1}}\in {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
, where
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D6F7}_{\text{}_{\unicode[STIX]{x1D70E}}J_{1}}\in {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
, where
![]() $\unicode[STIX]{x1D6F7}$
is the morphism of groups
$\unicode[STIX]{x1D6F7}$
is the morphism of groups
![]() $\unicode[STIX]{x1D6F7}^{\mathbb{I}}$
given in Proposition 2.3. In particular we have a group homomorphism
$\unicode[STIX]{x1D6F7}^{\mathbb{I}}$
given in Proposition 2.3. In particular we have a group homomorphism
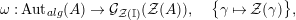 $$\begin{eqnarray}\unicode[STIX]{x1D714}:\text{Aut}_{alg}(A)\rightarrow {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A)),\quad \big\{\unicode[STIX]{x1D6FE}\mapsto {\mathcal{Z}}(\unicode[STIX]{x1D6FE})\big\},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}:\text{Aut}_{alg}(A)\rightarrow {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A)),\quad \big\{\unicode[STIX]{x1D6FE}\mapsto {\mathcal{Z}}(\unicode[STIX]{x1D6FE})\big\},\end{eqnarray}$$
where
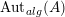 $\text{Aut}_{alg}(A)$
stands for the automorphisms group of the monoid
$\text{Aut}_{alg}(A)$
stands for the automorphisms group of the monoid
![]() $A$
inside
$A$
inside
![]() ${\mathcal{M}}$
.
${\mathcal{M}}$
.
Proof. By Theorem 3.10, we have that
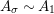 $A_{\unicode[STIX]{x1D70E}}\sim A_{1}$
. Henceforth, we apply Corollary 3.7 to obtain that
$A_{\unicode[STIX]{x1D70E}}\sim A_{1}$
. Henceforth, we apply Corollary 3.7 to obtain that
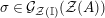 $\unicode[STIX]{x1D70E}\in {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
, which means that
$\unicode[STIX]{x1D70E}\in {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
, which means that
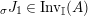 $\text{}_{\unicode[STIX]{x1D70E}}J_{1}\in \text{Inv}_{\mathbb{I}}(A)$
with inverse
$\text{}_{\unicode[STIX]{x1D70E}}J_{1}\in \text{Inv}_{\mathbb{I}}(A)$
with inverse
![]() $\text{}_{1}J_{\unicode[STIX]{x1D70E}}$
. By applying now Theorem 3.4, it is clear that
$\text{}_{1}J_{\unicode[STIX]{x1D70E}}$
. By applying now Theorem 3.4, it is clear that
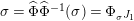 $\unicode[STIX]{x1D70E}=\widehat{\unicode[STIX]{x1D6F7}}\widehat{\unicode[STIX]{x1D6F7}}^{-1}(\unicode[STIX]{x1D70E})=\unicode[STIX]{x1D6F7}_{\text{}_{\unicode[STIX]{x1D70E}}J_{1}}$
. The particular statement is immediate.◻
$\unicode[STIX]{x1D70E}=\widehat{\unicode[STIX]{x1D6F7}}\widehat{\unicode[STIX]{x1D6F7}}^{-1}(\unicode[STIX]{x1D70E})=\unicode[STIX]{x1D6F7}_{\text{}_{\unicode[STIX]{x1D70E}}J_{1}}$
. The particular statement is immediate.◻
The following main result gives conditions under which the Miyashita action is bijective.
Theorem 3.12. Let
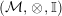 $({\mathcal{M}},\otimes _{},\mathbb{I})$
be a Penrose monoidal abelian, locally small and bicomplete category with right exact tensor products functors. Let
$({\mathcal{M}},\otimes _{},\mathbb{I})$
be a Penrose monoidal abelian, locally small and bicomplete category with right exact tensor products functors. Let
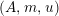 $(A,m,u)$
be a monoid in
$(A,m,u)$
be a monoid in
![]() ${\mathcal{M}}$
with a right flat underlying object
${\mathcal{M}}$
with a right flat underlying object
![]() $A$
. Assume that
$A$
. Assume that
 $A\otimes A\sim A$
and
$A\otimes A\sim A$
and
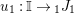 $u_{1}:\mathbb{I}\rightarrow \text{}_{1}J_{1}$
is an isomorphism. Consider the map
$u_{1}:\mathbb{I}\rightarrow \text{}_{1}J_{1}$
is an isomorphism. Consider the map
![]() $\unicode[STIX]{x1D714}$
as in Corollary 3.11 and
$\unicode[STIX]{x1D714}$
as in Corollary 3.11 and
![]() $\boldsymbol{\unicode[STIX]{x1D70D}},\unicode[STIX]{x1D6F7}$
as in Theorem 3.4.
$\boldsymbol{\unicode[STIX]{x1D70D}},\unicode[STIX]{x1D6F7}$
as in Theorem 3.4.
-
(1) If the map
 $\unicode[STIX]{x1D6FA}:\text{Aut}_{alg}(A)\rightarrow \text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-}alg}({\mathcal{Z}}(A)),\,\unicode[STIX]{x1D6FE}\mapsto {\mathcal{Z}}(\unicode[STIX]{x1D6FE})$
is surjective, then
$\unicode[STIX]{x1D6FA}:\text{Aut}_{alg}(A)\rightarrow \text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-}alg}({\mathcal{Z}}(A)),\,\unicode[STIX]{x1D6FE}\mapsto {\mathcal{Z}}(\unicode[STIX]{x1D6FE})$
is surjective, then
 $\boldsymbol{\unicode[STIX]{x1D70D}}$
and
$\boldsymbol{\unicode[STIX]{x1D70D}}$
and
 $\unicode[STIX]{x1D6F7}$
are bijective.
$\unicode[STIX]{x1D6F7}$
are bijective. -
(2) If
 $\unicode[STIX]{x1D6FA}$
is surjective and
$\unicode[STIX]{x1D6FA}$
is surjective and
 ${\mathcal{Z}}$
is faithful, then both
${\mathcal{Z}}$
is faithful, then both
 $\unicode[STIX]{x1D6FA}$
and
$\unicode[STIX]{x1D6FA}$
and
 $\unicode[STIX]{x1D714}$
are bijective. In this case, we obtain a chain of isomorphisms of groups:
$\unicode[STIX]{x1D714}$
are bijective. In this case, we obtain a chain of isomorphisms of groups:  $$\begin{eqnarray}\text{Inv}_{\mathbb{I}}(A)\cong \text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-}alg}({\mathcal{Z}}(A))\cong \text{Aut}_{alg}(A)\cong {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A)).\end{eqnarray}$$
$$\begin{eqnarray}\text{Inv}_{\mathbb{I}}(A)\cong \text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-}alg}({\mathcal{Z}}(A))\cong \text{Aut}_{alg}(A)\cong {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A)).\end{eqnarray}$$
Proof. (1) Since
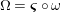 $\unicode[STIX]{x1D6FA}=\boldsymbol{\unicode[STIX]{x1D70D}}\circ \unicode[STIX]{x1D714}$
is surjective, it is clear that
$\unicode[STIX]{x1D6FA}=\boldsymbol{\unicode[STIX]{x1D70D}}\circ \unicode[STIX]{x1D714}$
is surjective, it is clear that
![]() $\boldsymbol{\unicode[STIX]{x1D70D}}$
is surjective, and so bijective as it is by construction injective. Therefore, by Theorem 3.4, this implies that
$\boldsymbol{\unicode[STIX]{x1D70D}}$
is surjective, and so bijective as it is by construction injective. Therefore, by Theorem 3.4, this implies that
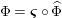 $\unicode[STIX]{x1D6F7}=\boldsymbol{\unicode[STIX]{x1D70D}}\circ \widehat{\unicode[STIX]{x1D6F7}}$
is bijective as well. (2) If
$\unicode[STIX]{x1D6F7}=\boldsymbol{\unicode[STIX]{x1D70D}}\circ \widehat{\unicode[STIX]{x1D6F7}}$
is bijective as well. (2) If
![]() ${\mathcal{Z}}$
is faithful, then clearly
${\mathcal{Z}}$
is faithful, then clearly
![]() $\unicode[STIX]{x1D6FA}$
is injective, hence it is also bijective. Thus
$\unicode[STIX]{x1D6FA}$
is injective, hence it is also bijective. Thus
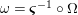 $\unicode[STIX]{x1D714}=\boldsymbol{\unicode[STIX]{x1D70D}}^{-1}\circ \unicode[STIX]{x1D6FA}$
is also bijective. The stated chain of isomorphisms of groups is now immediate.◻
$\unicode[STIX]{x1D714}=\boldsymbol{\unicode[STIX]{x1D70D}}^{-1}\circ \unicode[STIX]{x1D6FA}$
is also bijective. The stated chain of isomorphisms of groups is now immediate.◻
Remark 3.13. Under the assumptions made on
![]() $A$
in Theorem 3.12, if we further assume that
$A$
in Theorem 3.12, if we further assume that
![]() ${\mathcal{Z}}$
is full and faithful, then clearly we obtain the chain of isomorphisms stated there. As we will see below, part of those isomorphisms are also obtained in the special case of certain Azumaya monoids.
${\mathcal{Z}}$
is full and faithful, then clearly we obtain the chain of isomorphisms stated there. As we will see below, part of those isomorphisms are also obtained in the special case of certain Azumaya monoids.
4 Miyashita action: the Azumaya case
The main aim in this section is to apply the foregoing results to a certain class of Azumaya monoids (see Definition 4.3 below) when the base category in symmetric. The novelty here is the construction of a homomorphism of groups
![]() $\boldsymbol{\unicode[STIX]{x1D6E4}}$
from
$\boldsymbol{\unicode[STIX]{x1D6E4}}$
from
![]() $\text{Inv}_{\mathbb{I}}(A)$
to
$\text{Inv}_{\mathbb{I}}(A)$
to
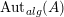 $\text{Aut}_{alg}(A)$
, which is shown to be bijective when
$\text{Aut}_{alg}(A)$
, which is shown to be bijective when
![]() $A$
is an Azumaya monoid (with a certain property) and
$A$
is an Azumaya monoid (with a certain property) and
![]() ${\mathcal{Z}}$
is faithful; see Corollary 4.9.
${\mathcal{Z}}$
is faithful; see Corollary 4.9.
In all this section
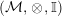 $({\mathcal{M}},\otimes _{},\mathbb{I})$
is symmetric monoidal abelian, locally small and bicomplete category with right exact tensor products functors. We denote by
$({\mathcal{M}},\otimes _{},\mathbb{I})$
is symmetric monoidal abelian, locally small and bicomplete category with right exact tensor products functors. We denote by
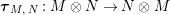 $\boldsymbol{\unicode[STIX]{x1D70F}}_{M,\,N}:M\otimes _{}N\rightarrow N\otimes _{}M$
the natural isomorphism defining the symmetry of
$\boldsymbol{\unicode[STIX]{x1D70F}}_{M,\,N}:M\otimes _{}N\rightarrow N\otimes _{}M$
the natural isomorphism defining the symmetry of
![]() ${\mathcal{M}}$
.
${\mathcal{M}}$
.
4.1 The map
 $\boldsymbol{\unicode[STIX]{x1D6E4}}$
$\boldsymbol{\unicode[STIX]{x1D6E4}}$
Let
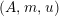 $(A,m,u)$
be a monoid in
$(A,m,u)$
be a monoid in
![]() ${\mathcal{M}}$
with
${\mathcal{M}}$
with
![]() $u$
a monomorphism. Consider
$u$
a monomorphism. Consider
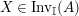 $X\in \text{Inv}_{\mathbb{I}}(A)$
with inverse
$X\in \text{Inv}_{\mathbb{I}}(A)$
with inverse
![]() $Y$
. Define the morphism
$Y$
. Define the morphism
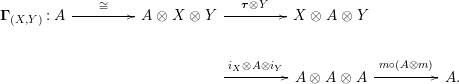
An argument analogue to the one used in Proposition 2.2 for
![]() $\boldsymbol{\unicode[STIX]{x1D70E}}_{X,Y}$
, shows that this morphism does not depend on the choice of
$\boldsymbol{\unicode[STIX]{x1D70E}}_{X,Y}$
, shows that this morphism does not depend on the choice of
![]() $Y$
(nor on a representing object of the equivalence class of
$Y$
(nor on a representing object of the equivalence class of
![]() $(X,i_{X})$
) so that we can also denote it by
$(X,i_{X})$
) so that we can also denote it by
![]() $\boldsymbol{\unicode[STIX]{x1D6E4}}_{X}$
. This, in fact, defines a map to the endomorphisms ring of
$\boldsymbol{\unicode[STIX]{x1D6E4}}_{X}$
. This, in fact, defines a map to the endomorphisms ring of
![]() $A$
with image in the automorphisms group as the following result shows. First we give the following diagrammatic expression of
$A$
with image in the automorphisms group as the following result shows. First we give the following diagrammatic expression of
![]() $\boldsymbol{\unicode[STIX]{x1D6E4}}_{X}$
$\boldsymbol{\unicode[STIX]{x1D6E4}}_{X}$
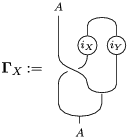
Proposition 4.1. The map
 $$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D6E4}}:\text{Inv}_{\mathbb{I}}(A)\longrightarrow \text{Aut}_{alg}(A),\qquad \big(X\longmapsto \unicode[STIX]{x1D6E4}_{X}\big)\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D6E4}}:\text{Inv}_{\mathbb{I}}(A)\longrightarrow \text{Aut}_{alg}(A),\qquad \big(X\longmapsto \unicode[STIX]{x1D6E4}_{X}\big)\end{eqnarray}$$
is a homomorphism of groups. In particular we have
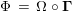 $\unicode[STIX]{x1D6F7}\,=\,\unicode[STIX]{x1D6FA}\circ \boldsymbol{\unicode[STIX]{x1D6E4}}$
, where
$\unicode[STIX]{x1D6F7}\,=\,\unicode[STIX]{x1D6FA}\circ \boldsymbol{\unicode[STIX]{x1D6E4}}$
, where
![]() $\unicode[STIX]{x1D6FA}$
is as in Theorem 3.12 and
$\unicode[STIX]{x1D6FA}$
is as in Theorem 3.12 and
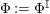 $\unicode[STIX]{x1D6F7}:=\unicode[STIX]{x1D6F7}^{\mathbb{I}}$
as in Proposition 2.3.
$\unicode[STIX]{x1D6F7}:=\unicode[STIX]{x1D6F7}^{\mathbb{I}}$
as in Proposition 2.3.
Proof. In view of Corollary 1.13 (here the assumption
![]() $u$
is monomorphism is used), it suffices to prove that we have a morphism of monoids
$u$
is monomorphism is used), it suffices to prove that we have a morphism of monoids
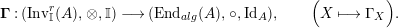 $$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D6E4}}:(\text{Inv}_{\mathbb{I}}^{r}(A),\otimes ,\mathbb{I})\longrightarrow (\text{End}_{alg}(A),\circ ,\text{Id}_{A}),\qquad \Big(X\longmapsto \unicode[STIX]{x1D6E4}_{X}\Big).\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D6E4}}:(\text{Inv}_{\mathbb{I}}^{r}(A),\otimes ,\mathbb{I})\longrightarrow (\text{End}_{alg}(A),\circ ,\text{Id}_{A}),\qquad \Big(X\longmapsto \unicode[STIX]{x1D6E4}_{X}\Big).\end{eqnarray}$$
First we have to check that this map is well defined, that is
![]() $\boldsymbol{\unicode[STIX]{x1D6E4}}_{X}$
is a monoid endomorphism of
$\boldsymbol{\unicode[STIX]{x1D6E4}}_{X}$
is a monoid endomorphism of
![]() $A$
. Let us check that
$A$
. Let us check that
![]() $\boldsymbol{\unicode[STIX]{x1D6E4}}_{X}$
is unitary
$\boldsymbol{\unicode[STIX]{x1D6E4}}_{X}$
is unitary
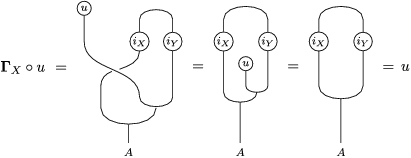
Let us check that
![]() $\boldsymbol{\unicode[STIX]{x1D6E4}}_{X}$
is multiplicative. We start by computing
$\boldsymbol{\unicode[STIX]{x1D6E4}}_{X}$
is multiplicative. We start by computing
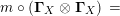 $m\circ (\boldsymbol{\unicode[STIX]{x1D6E4}}_{X}\otimes _{}\boldsymbol{\unicode[STIX]{x1D6E4}}_{X})\,=\,$
$m\circ (\boldsymbol{\unicode[STIX]{x1D6E4}}_{X}\otimes _{}\boldsymbol{\unicode[STIX]{x1D6E4}}_{X})\,=\,$
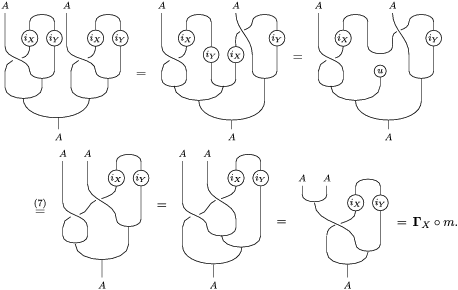
It is clear that
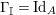 $\unicode[STIX]{x1D6E4}_{\mathbb{I}}=\text{Id}_{A}$
. Let now
$\unicode[STIX]{x1D6E4}_{\mathbb{I}}=\text{Id}_{A}$
. Let now
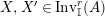 $X,X^{\prime }\in \text{Inv}_{\mathbb{I}}^{r}(A)$
have right inverses
$X,X^{\prime }\in \text{Inv}_{\mathbb{I}}^{r}(A)$
have right inverses
![]() $Y,Y^{\prime }$
respectively. Then, we compute
$Y,Y^{\prime }$
respectively. Then, we compute
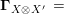 $\boldsymbol{\unicode[STIX]{x1D6E4}}_{X\otimes _{}X^{\prime }}\,=\,$
$\boldsymbol{\unicode[STIX]{x1D6E4}}_{X\otimes _{}X^{\prime }}\,=\,$
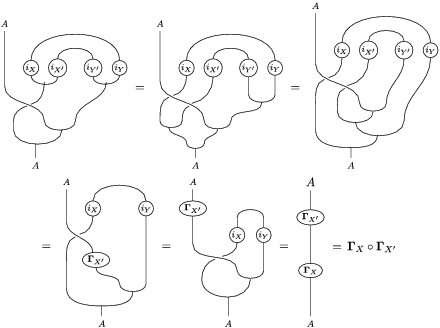
It is now clear that, for
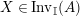 $X\in \text{Inv}_{\mathbb{I}}(A)$
with inverse
$X\in \text{Inv}_{\mathbb{I}}(A)$
with inverse
![]() $Y$
, one has
$Y$
, one has
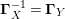 $\boldsymbol{\unicode[STIX]{x1D6E4}}_{X}^{-1}=\boldsymbol{\unicode[STIX]{x1D6E4}}_{Y}$
. The particular statement is clear, and this finishes the proof.◻
$\boldsymbol{\unicode[STIX]{x1D6E4}}_{X}^{-1}=\boldsymbol{\unicode[STIX]{x1D6E4}}_{Y}$
. The particular statement is clear, and this finishes the proof.◻
4.2 Central monoid with a left internal hom functor
Let
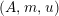 $(A,m,u)$
be a monoid in
$(A,m,u)$
be a monoid in
![]() ${\mathcal{M}}$
we denote by
${\mathcal{M}}$
we denote by
![]() $A^{e}$
the monoid
$A^{e}$
the monoid
![]() $A\otimes _{}A^{o}$
where
$A\otimes _{}A^{o}$
where
![]() $A^{o}$
is the opposite monoid (i.e.,
$A^{o}$
is the opposite monoid (i.e.,
![]() $A$
with the multiplication morphism twisted by the symmetry
$A$
with the multiplication morphism twisted by the symmetry
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}$
). Since our base category
$\boldsymbol{\unicode[STIX]{x1D70F}}$
). Since our base category
![]() ${\mathcal{M}}$
is symmetric, we can as in the classical case, identify the category of
${\mathcal{M}}$
is symmetric, we can as in the classical case, identify the category of
![]() $A$
-bimodules with the category of left (or right)
$A$
-bimodules with the category of left (or right)
![]() $A^{e}$
-modules. Assume that the functor
$A^{e}$
-modules. Assume that the functor
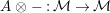 $A\otimes _{}-:{\mathcal{M}}\rightarrow {\mathcal{M}}$
has a right adjoint functor, which we denote by
$A\otimes _{}-:{\mathcal{M}}\rightarrow {\mathcal{M}}$
has a right adjoint functor, which we denote by
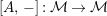 $[A,-]:{\mathcal{M}}\rightarrow {\mathcal{M}}$
. In this case, we say that
$[A,-]:{\mathcal{M}}\rightarrow {\mathcal{M}}$
. In this case, we say that
![]() $A$
has a left internal hom functor. Consider as in Appendix B the functor
$A$
has a left internal hom functor. Consider as in Appendix B the functor
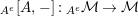 $\text{}_{A^{e}}[A,-]:\text{}_{A^{e}}{\mathcal{M}}\rightarrow {\mathcal{M}}$
which is the right adjoint of
$\text{}_{A^{e}}[A,-]:\text{}_{A^{e}}{\mathcal{M}}\rightarrow {\mathcal{M}}$
which is the right adjoint of
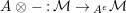 $A\otimes _{}-:{\mathcal{M}}\rightarrow \text{}_{A^{e}}{\mathcal{M}}$
with the canonical natural monomorphism
$A\otimes _{}-:{\mathcal{M}}\rightarrow \text{}_{A^{e}}{\mathcal{M}}$
with the canonical natural monomorphism
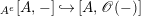 $\text{}_{A^{e}}[A,-]{\hookrightarrow}[A,\mathscr{O}(-)]$
, where
$\text{}_{A^{e}}[A,-]{\hookrightarrow}[A,\mathscr{O}(-)]$
, where
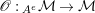 $\mathscr{O}:\text{}_{A^{e}}{\mathcal{M}}\rightarrow {\mathcal{M}}$
is the forgetful functor. On the other hand, notice that
$\mathscr{O}:\text{}_{A^{e}}{\mathcal{M}}\rightarrow {\mathcal{M}}$
is the forgetful functor. On the other hand, notice that
![]() $\mathscr{O}$
is faithful and exact.
$\mathscr{O}$
is faithful and exact.
The monoid
![]() $A$
is said to be central provided that the canonical map
$A$
is said to be central provided that the canonical map
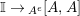 $\mathbb{I}\rightarrow \text{}_{A^{e}}[A,A]$
is an isomorphism (this is the counit at
$\mathbb{I}\rightarrow \text{}_{A^{e}}[A,A]$
is an isomorphism (this is the counit at
![]() $\mathbb{I}$
of the previous adjunction).
$\mathbb{I}$
of the previous adjunction).
Proposition 4.2. Let
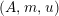 $(A,m,u)$
be a monoid in
$(A,m,u)$
be a monoid in
![]() ${\mathcal{M}}$
and consider the submonoid
${\mathcal{M}}$
and consider the submonoid
![]() $\text{}_{1}J_{1}$
of equation (23) with structure given by Proposition 2.5(iii). Assume that
$\text{}_{1}J_{1}$
of equation (23) with structure given by Proposition 2.5(iii). Assume that
![]() $A$
has a left internal hom functor. Then
$A$
has a left internal hom functor. Then
-
(i) there is a commutative diagram of monoids:

-
(ii) Assume that
 $\mathbb{I}\cong \text{}_{1}J_{1}$
via the unit given in (31) (thus
$\mathbb{I}\cong \text{}_{1}J_{1}$
via the unit given in (31) (thus
 $u$
is a monomorphism). Then
$u$
is a monomorphism). Then
 $\text{}_{A^{e}}[A,A]\cong \mathbb{I}$
and so
$\text{}_{A^{e}}[A,A]\cong \mathbb{I}$
and so
 $A$
is central.
$A$
is central. -
(iii) If
 $A$
is central and the functor
$A$
is central and the functor
 ${\mathcal{Z}}$
reflects isomorphisms, then
${\mathcal{Z}}$
reflects isomorphisms, then
 $\mathbb{I}\cong \text{}_{1}J_{1}$
via its unit.
$\mathbb{I}\cong \text{}_{1}J_{1}$
via its unit. -
(iv) When
 ${\mathcal{Z}}$
is faithful (i.e.,
${\mathcal{Z}}$
is faithful (i.e.,
 $\mathbb{I}$
is a generator), then
$\mathbb{I}$
is a generator), then
 $A$
is central if and only if
$A$
is central if and only if
 $\,\mathbb{I}\cong \text{}_{1}J_{1}$
.
$\,\mathbb{I}\cong \text{}_{1}J_{1}$
.
Proof. (i). By [Reference Femić10, Proposition 3.3.], we can identify
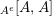 $\text{}_{A^{e}}[A,A]$
with the equalizer
$\text{}_{A^{e}}[A,A]$
with the equalizer
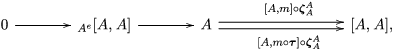
where
![]() $\boldsymbol{\unicode[STIX]{x1D701}}^{A}$
is the unit of the adjunction
$\boldsymbol{\unicode[STIX]{x1D701}}^{A}$
is the unit of the adjunction
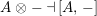 $A\otimes _{}-\dashv [A,-]$
. Now, using the universal property of
$A\otimes _{}-\dashv [A,-]$
. Now, using the universal property of
![]() $\text{}_{1}J_{1}$
given by equation (25), one shows the existence of the triangle. We leave to the reader to check that the stated diagram is in fact a triangle of monoids.
$\text{}_{1}J_{1}$
given by equation (25), one shows the existence of the triangle. We leave to the reader to check that the stated diagram is in fact a triangle of monoids.
(ii) It follows from the fact that the diagram in (i) commutes and that the morphisms involved are unitary.
(iii) The definition of the functor
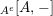 $\text{}_{A^{e}}[A,-]$
obviously implies the isomorphism
$\text{}_{A^{e}}[A,-]$
obviously implies the isomorphism
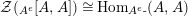 ${\mathcal{Z}}(\text{}_{A^{e}}[A,A])\cong \text{Hom}_{A^{e}\text{-}}(A,A)$
of
${\mathcal{Z}}(\text{}_{A^{e}}[A,A])\cong \text{Hom}_{A^{e}\text{-}}(A,A)$
of
![]() ${\mathcal{Z}}(\mathbb{I})$
-algebras. On the other hand, under the assumption made on the functor
${\mathcal{Z}}(\mathbb{I})$
-algebras. On the other hand, under the assumption made on the functor
![]() ${\mathcal{Z}}$
a tedious computation gives a chase to an isomorphism
${\mathcal{Z}}$
a tedious computation gives a chase to an isomorphism
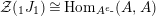 ${\mathcal{Z}}(\text{}_{1}J_{1})\cong \text{Hom}_{A^{e}\text{-}}(A,A)$
of
${\mathcal{Z}}(\text{}_{1}J_{1})\cong \text{Hom}_{A^{e}\text{-}}(A,A)$
of
![]() ${\mathcal{Z}}(\mathbb{I})$
-algebras. Combining these two isomorphisms shows that
${\mathcal{Z}}(\mathbb{I})$
-algebras. Combining these two isomorphisms shows that
![]() ${\mathcal{Z}}(\unicode[STIX]{x1D706})$
is an isomorphism. Therefore,
${\mathcal{Z}}(\unicode[STIX]{x1D706})$
is an isomorphism. Therefore,
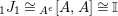 $\text{}_{1}J_{1}\cong \text{}_{A^{e}}[A,A]\cong \mathbb{I}$
, since
$\text{}_{1}J_{1}\cong \text{}_{A^{e}}[A,A]\cong \mathbb{I}$
, since
![]() $A$
is central.
$A$
is central.
(iv) We only need to check the direct implication since the converse follows by the second item. This implication clearly follows from part (iii), since a faithful functor, whose domain is an abelian category, reflects isomorphisms. ◻
4.3 The Azumaya case
The notion of Azumaya monoid in a monoidal category of modules over a commutative ring (see [Reference Knus and Ojanguren18, Théorème 5.1] for equivalent definitions), can be extended to any closed symmetric monoidal additive category; see for example [Reference Fisher-Palmquist11, Reference Vitale30]. However, one can droop the additivity and the closeness conditions on the base monoidal category, as was done in [Reference Pareigis26], and the definition of Azumaya monoid still makes sense in this context. In our setting
![]() ${\mathcal{M}}$
is a symmetric abelian category which is possibly not closed, so we can follow the ideas of [Reference Pareigis26, Reference Vitale30].
${\mathcal{M}}$
is a symmetric abelian category which is possibly not closed, so we can follow the ideas of [Reference Pareigis26, Reference Vitale30].
Definition 4.3. [Reference Fisher-Palmquist11, Reference Pareigis26, Reference Vitale30]
A monoid
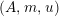 $(A,m,u)$
in the monoidal category
$(A,m,u)$
in the monoidal category
![]() ${\mathcal{M}}$
is called an Azumaya monoid if the functor
${\mathcal{M}}$
is called an Azumaya monoid if the functor
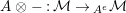 $A\otimes _{}-:{\mathcal{M}}\rightarrow \text{}_{A^{e}}{\mathcal{M}}$
establishes an equivalence of categories and the multiplication
$A\otimes _{}-:{\mathcal{M}}\rightarrow \text{}_{A^{e}}{\mathcal{M}}$
establishes an equivalence of categories and the multiplication
![]() $m$
splits as a morphism of
$m$
splits as a morphism of
![]() $A$
-bimodules (in other words
$A$
-bimodules (in other words
![]() $A$
is a separable monoid). This, in fact, is the notion of
$A$
is a separable monoid). This, in fact, is the notion of
![]() $2$
-Azumaya in the sense of [Reference Pareigis26].
$2$
-Azumaya in the sense of [Reference Pareigis26].
It is convenient to make some comments and remarks on the conditions of the previous definition.
Remarks 4.4. Consider an Azumaya monoid
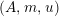 $(A,m,u)$
in
$(A,m,u)$
in
![]() ${\mathcal{M}}$
as in Definition 4.3.
${\mathcal{M}}$
as in Definition 4.3.
-
(i) It is noteworthy to mention that one cannot expect to have for free that
 $A$
is a dualizable object in
$A$
is a dualizable object in
 ${\mathcal{M}}$
, that is dualizable as in Definition 1.2 with the trivial structure of
${\mathcal{M}}$
, that is dualizable as in Definition 1.2 with the trivial structure of
 $(\mathbb{I},\mathbb{I})$
-bimodule. This perhaps happens when
$(\mathbb{I},\mathbb{I})$
-bimodule. This perhaps happens when
 $\mathbb{I}$
is a small generator in
$\mathbb{I}$
is a small generator in
 ${\mathcal{M}}$
. However, as was shown in [Reference Vitale30, Proposition 1.2],
${\mathcal{M}}$
. However, as was shown in [Reference Vitale30, Proposition 1.2],
 $A$
is in fact a dualizable object in a certain monoidal category of monoids whose dual object is exactly the opposite monoid
$A$
is in fact a dualizable object in a certain monoidal category of monoids whose dual object is exactly the opposite monoid
 $A^{o}$
. On the other hand, one can show as follows that
$A^{o}$
. On the other hand, one can show as follows that
 $A$
forms part of a two-sided dualizable datum in the sense of Definition 1.2 by taking
$A$
forms part of a two-sided dualizable datum in the sense of Definition 1.2 by taking
 $\mathbb{I}$
and
$\mathbb{I}$
and
 $A^{e}$
as base monoids. Following the proof of [Reference Vitale30, Proposition 1.2] since
$A^{e}$
as base monoids. Following the proof of [Reference Vitale30, Proposition 1.2] since
 $A$
can be considered either as an
$A$
can be considered either as an
 $(\mathbb{I},A^{e})$
-bimodule or as an
$(\mathbb{I},A^{e})$
-bimodule or as an
 $(A^{e},\mathbb{I})$
-bimodule,
$(A^{e},\mathbb{I})$
-bimodule,
 $A\otimes _{}-:{\mathcal{M}}\rightarrow \text{}_{A^{e}}{\mathcal{M}}$
is an equivalence of categories if and only if
$A\otimes _{}-:{\mathcal{M}}\rightarrow \text{}_{A^{e}}{\mathcal{M}}$
is an equivalence of categories if and only if
 $A\otimes _{A^{e}}-:\text{}_{A^{e}}{\mathcal{M}}\rightarrow {\mathcal{M}}$
is so. In this way, by applying twice [Reference Pareigis25, Proposition 5.1] or [Reference Vitale30, Proposition 1.3], we obtain the existence of two objects:
$A\otimes _{A^{e}}-:\text{}_{A^{e}}{\mathcal{M}}\rightarrow {\mathcal{M}}$
is so. In this way, by applying twice [Reference Pareigis25, Proposition 5.1] or [Reference Vitale30, Proposition 1.3], we obtain the existence of two objects:
 $[A,\mathbb{I}]$
and
$[A,\mathbb{I}]$
and
 $[A,A]$
together with the following natural isomorphisms
$[A,A]$
together with the following natural isomorphisms
 $\text{Hom}_{{\mathcal{M}}}\left(A\otimes _{}-,\,\mathbb{I}\right)\cong \text{Hom}_{{\mathcal{M}}}\left(-,\,[A,\mathbb{I}]\right)$
and
$\text{Hom}_{{\mathcal{M}}}\left(A\otimes _{}-,\,\mathbb{I}\right)\cong \text{Hom}_{{\mathcal{M}}}\left(-,\,[A,\mathbb{I}]\right)$
and
 $\text{Hom}_{{\mathcal{M}}}\left(A\otimes _{}-,\,A\right)\cong \text{Hom}_{{\mathcal{M}}}\left(-,\,[A,A]\right)$
. Furthermore, there are isomorphisms:
$\text{Hom}_{{\mathcal{M}}}\left(A\otimes _{}-,\,A\right)\cong \text{Hom}_{{\mathcal{M}}}\left(-,\,[A,A]\right)$
. Furthermore, there are isomorphisms:
 $[A,\mathbb{I}]\otimes _{}A\cong A^{e}$
of
$[A,\mathbb{I}]\otimes _{}A\cong A^{e}$
of
 $A^{e}$
-bimodules,
$A^{e}$
-bimodules,
 $\mathbb{I}\cong A\otimes _{A^{e}}[A,\mathbb{I}]$
of objects in
$\mathbb{I}\cong A\otimes _{A^{e}}[A,\mathbb{I}]$
of objects in
 ${\mathcal{M}}$
and
${\mathcal{M}}$
and
 $A^{e}=A\otimes _{}A^{o}\cong [A,A]$
of monoids. Thus, the pair
$A^{e}=A\otimes _{}A^{o}\cong [A,A]$
of monoids. Thus, the pair
 $(A,[A,\mathbb{I}])$
, within these two first isomorphisms, is a two-sided dualizable datum relating the monoids
$(A,[A,\mathbb{I}])$
, within these two first isomorphisms, is a two-sided dualizable datum relating the monoids
 $\mathbb{I}$
and
$\mathbb{I}$
and
 $A^{e}$
in the sense of Definition 1.2, as claimed above.
$A^{e}$
in the sense of Definition 1.2, as claimed above. -
(ii) Since
 $A\otimes _{}-:{\mathcal{M}}\rightarrow \text{}_{A^{e}}{\mathcal{M}}$
is an equivalence of categories, it has a right adjoint functor which, as in Appendix B, is denoted by
$A\otimes _{}-:{\mathcal{M}}\rightarrow \text{}_{A^{e}}{\mathcal{M}}$
is an equivalence of categories, it has a right adjoint functor which, as in Appendix B, is denoted by
 $\text{}_{A^{e}}[A,-]:\text{}_{A^{e}}{\mathcal{M}}\rightarrow {\mathcal{M}}$
. In contrast with Proposition B.1, here we only know that
$\text{}_{A^{e}}[A,-]:\text{}_{A^{e}}{\mathcal{M}}\rightarrow {\mathcal{M}}$
. In contrast with Proposition B.1, here we only know that
 $\text{}_{A^{e}}[A,-]$
exists and there are no indications about its construction. Indeed, at this level of generality, it is not clear whether
$\text{}_{A^{e}}[A,-]$
exists and there are no indications about its construction. Indeed, at this level of generality, it is not clear whether
 $A$
has a left internal hom functor in
$A$
has a left internal hom functor in
 ${\mathcal{M}}$
. Thus a very interesting class of Azumaya monoids consists of those for which the underlying object has this property. This is, of course, the case of the usual class of Azumaya algebras over commutative rings.
${\mathcal{M}}$
. Thus a very interesting class of Azumaya monoids consists of those for which the underlying object has this property. This is, of course, the case of the usual class of Azumaya algebras over commutative rings.
Remark 4.5. Let
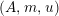 $(A,m,u)$
be a monoid in
$(A,m,u)$
be a monoid in
![]() ${\mathcal{M}}$
. In Definition 4.3 we cannot drop the separability condition in general as it happens in the classical case. This is due to the fact that
${\mathcal{M}}$
. In Definition 4.3 we cannot drop the separability condition in general as it happens in the classical case. This is due to the fact that
![]() $\mathbb{I}$
is not always projective in
$\mathbb{I}$
is not always projective in
![]() ${\mathcal{M}}$
. However, if we assume that
${\mathcal{M}}$
. However, if we assume that
![]() $\mathbb{I}$
is projective in
$\mathbb{I}$
is projective in
![]() ${\mathcal{M}}$
and
${\mathcal{M}}$
and
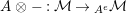 $A\otimes _{}-:{\mathcal{M}}\rightarrow \text{}_{A^{e}}{\mathcal{M}}$
is an equivalence, then
$A\otimes _{}-:{\mathcal{M}}\rightarrow \text{}_{A^{e}}{\mathcal{M}}$
is an equivalence, then
![]() $A$
must be an Azumaya monoid. Indeed, since
$A$
must be an Azumaya monoid. Indeed, since
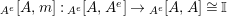 $\text{}_{A^{e}}[A,m]:\text{}_{A^{e}}[A,A^{e}]\rightarrow \text{}_{A^{e}}[A,A]\cong \mathbb{I}$
is an epimorphism being the image of
$\text{}_{A^{e}}[A,m]:\text{}_{A^{e}}[A,A^{e}]\rightarrow \text{}_{A^{e}}[A,A]\cong \mathbb{I}$
is an epimorphism being the image of
![]() $m$
by the equivalence
$m$
by the equivalence
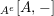 $\text{}_{A^{e}}[A,-]$
, then
$\text{}_{A^{e}}[A,-]$
, then
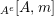 $\text{}_{A^{e}}[A,m]$
must split as
$\text{}_{A^{e}}[A,m]$
must split as
![]() $\mathbb{I}$
is projective. Therefore,
$\mathbb{I}$
is projective. Therefore,
![]() $m$
itself must split in
$m$
itself must split in
![]() $\text{}_{A^{e}}{\mathcal{M}}$
, that is,
$\text{}_{A^{e}}{\mathcal{M}}$
, that is,
![]() $A$
should be separable.
$A$
should be separable.
On the other hand, observe that
![]() $A$
is separable if and only if it is projective relatively to all morphisms in
$A$
is separable if and only if it is projective relatively to all morphisms in
![]() $_{A^{e}}{\mathcal{M}}$
which split as morphisms in
$_{A^{e}}{\mathcal{M}}$
which split as morphisms in
![]() ${\mathcal{M}}$
; see for example [Reference Ardizzoni, Menini and Ştefan1, Theorem 1.30 and equality (5)]. Since this does not mean that
${\mathcal{M}}$
; see for example [Reference Ardizzoni, Menini and Ştefan1, Theorem 1.30 and equality (5)]. Since this does not mean that
![]() $A$
is projective in
$A$
is projective in
![]() $_{A^{e}}{\mathcal{M}}$
, then
$_{A^{e}}{\mathcal{M}}$
, then
![]() $\mathbb{I}$
is not projective in
$\mathbb{I}$
is not projective in
![]() ${\mathcal{M}}$
provided that
${\mathcal{M}}$
provided that
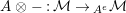 $A\otimes _{}-:{\mathcal{M}}\rightarrow \text{}_{A^{e}}{\mathcal{M}}$
is an equivalence. Hence if
$A\otimes _{}-:{\mathcal{M}}\rightarrow \text{}_{A^{e}}{\mathcal{M}}$
is an equivalence. Hence if
![]() $A$
is Azumaya, we cannot conclude that
$A$
is Azumaya, we cannot conclude that
![]() $\mathbb{I}$
is projective in
$\mathbb{I}$
is projective in
![]() ${\mathcal{M}}$
.
${\mathcal{M}}$
.
Before giving more consequences of Definition 4.3, we give here conditions under which
![]() ${\mathcal{Z}}(A)$
is an Azumaya
${\mathcal{Z}}(A)$
is an Azumaya
![]() ${\mathcal{Z}}(\mathbb{I})$
-algebra. Recall from [Reference Fausk, Lewis and May.9, Proposition 1.2] that an object
${\mathcal{Z}}(\mathbb{I})$
-algebra. Recall from [Reference Fausk, Lewis and May.9, Proposition 1.2] that an object
![]() $X$
in
$X$
in
![]() ${\mathcal{M}}$
is said to be a Künneth object if it is a direct summand of a finite product of copies of
${\mathcal{M}}$
is said to be a Künneth object if it is a direct summand of a finite product of copies of
![]() $\mathbb{I}$
. In the notation of Section 3.2 this means that
$\mathbb{I}$
. In the notation of Section 3.2 this means that
![]() $X|\mathbb{I}$
in
$X|\mathbb{I}$
in
![]() ${\mathcal{M}}$
. In case
${\mathcal{M}}$
. In case
![]() ${\mathcal{M}}$
is closed, any Künneth object is obviously a dualizable object cf. [Reference Fausk, Lewis and May.9].
${\mathcal{M}}$
is closed, any Künneth object is obviously a dualizable object cf. [Reference Fausk, Lewis and May.9].
Proposition 4.6. Let
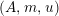 $(A,m,u)$
be an Azumaya monoid in
$(A,m,u)$
be an Azumaya monoid in
![]() ${\mathcal{M}}$
with underlying dualizable Künneth object
${\mathcal{M}}$
with underlying dualizable Künneth object
![]() $A$
. Then
$A$
. Then
![]() ${\mathcal{Z}}(A)$
is an Azumaya
${\mathcal{Z}}(A)$
is an Azumaya
![]() ${\mathcal{Z}}(\mathbb{I})$
-algebra in the classical sense.
${\mathcal{Z}}(\mathbb{I})$
-algebra in the classical sense.
Proof. It is clear that
![]() ${\mathcal{Z}}(A)$
is a finitely generated and projective
${\mathcal{Z}}(A)$
is a finitely generated and projective
![]() ${\mathcal{Z}}(\mathbb{I})$
-module. Using the characterization of Azumaya algebras (see for example [Reference DeMeyer and Ingraham7, Reference Kadison16]), we need to check that
${\mathcal{Z}}(\mathbb{I})$
-module. Using the characterization of Azumaya algebras (see for example [Reference DeMeyer and Ingraham7, Reference Kadison16]), we need to check that
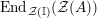 $\text{End}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
is isomorphic as a
$\text{End}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
is isomorphic as a
![]() ${\mathcal{Z}}(\mathbb{I})$
-algebra to
${\mathcal{Z}}(\mathbb{I})$
-algebra to
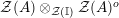 ${\mathcal{Z}}(A)\otimes _{{\mathcal{Z}}(\mathbb{I})}{\mathcal{Z}}(A)^{o}$
, which is proved as follows. Following the ideas of [Reference Fausk, Lewis and May.9, Proposition 1.2], for any object
${\mathcal{Z}}(A)\otimes _{{\mathcal{Z}}(\mathbb{I})}{\mathcal{Z}}(A)^{o}$
, which is proved as follows. Following the ideas of [Reference Fausk, Lewis and May.9, Proposition 1.2], for any object
![]() $X$
in
$X$
in
![]() ${\mathcal{M}}$
, we know that
${\mathcal{M}}$
, we know that
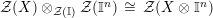 ${\mathcal{Z}}(X)\otimes _{{\mathcal{Z}}(\mathbb{I})}{\mathcal{Z}}(\mathbb{I}^{n})\,\cong \,{\mathcal{Z}}(X\otimes _{}\mathbb{I}^{n})$
. Thus, the same isomorphism is inherited by any direct summands of some
${\mathcal{Z}}(X)\otimes _{{\mathcal{Z}}(\mathbb{I})}{\mathcal{Z}}(\mathbb{I}^{n})\,\cong \,{\mathcal{Z}}(X\otimes _{}\mathbb{I}^{n})$
. Thus, the same isomorphism is inherited by any direct summands of some
![]() $\mathbb{I}^{n}$
. Therefore, we have an isomorphism
$\mathbb{I}^{n}$
. Therefore, we have an isomorphism
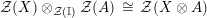 ${\mathcal{Z}}(X)\otimes _{{\mathcal{Z}}(\mathbb{I})}{\mathcal{Z}}(A)\,\cong \,{\mathcal{Z}}(X\otimes _{}A)$
and by symmetry
${\mathcal{Z}}(X)\otimes _{{\mathcal{Z}}(\mathbb{I})}{\mathcal{Z}}(A)\,\cong \,{\mathcal{Z}}(X\otimes _{}A)$
and by symmetry
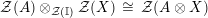 ${\mathcal{Z}}(A)\otimes _{{\mathcal{Z}}(\mathbb{I})}{\mathcal{Z}}(X)\,\cong \,{\mathcal{Z}}(A\otimes _{}X)$
, for any object
${\mathcal{Z}}(A)\otimes _{{\mathcal{Z}}(\mathbb{I})}{\mathcal{Z}}(X)\,\cong \,{\mathcal{Z}}(A\otimes _{}X)$
, for any object
![]() $X$
in
$X$
in
![]() ${\mathcal{M}}$
. In particular, we have
${\mathcal{M}}$
. In particular, we have
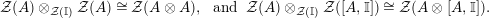 $$\begin{eqnarray}{\mathcal{Z}}(A)\otimes _{{\mathcal{Z}}(\mathbb{I})}{\mathcal{Z}}(A)\cong {\mathcal{Z}}(A\otimes _{}A),\,\text{ and }\,{\mathcal{Z}}(A)\otimes _{{\mathcal{Z}}(\mathbb{I})}{\mathcal{Z}}([A,\mathbb{I}])\cong {\mathcal{Z}}(A\otimes _{}[A,\mathbb{I}]).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Z}}(A)\otimes _{{\mathcal{Z}}(\mathbb{I})}{\mathcal{Z}}(A)\cong {\mathcal{Z}}(A\otimes _{}A),\,\text{ and }\,{\mathcal{Z}}(A)\otimes _{{\mathcal{Z}}(\mathbb{I})}{\mathcal{Z}}([A,\mathbb{I}])\cong {\mathcal{Z}}(A\otimes _{}[A,\mathbb{I}]).\end{eqnarray}$$
Therefore,
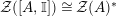 ${\mathcal{Z}}([A,\mathbb{I}])\cong {\mathcal{Z}}(A)^{\ast }$
as
${\mathcal{Z}}([A,\mathbb{I}])\cong {\mathcal{Z}}(A)^{\ast }$
as
![]() ${\mathcal{Z}}(\mathbb{I})$
-modules, where
${\mathcal{Z}}(\mathbb{I})$
-modules, where
![]() ${\mathcal{Z}}(A)^{\ast }$
is the
${\mathcal{Z}}(A)^{\ast }$
is the
![]() ${\mathcal{Z}}(\mathbb{I})$
-linear dual of
${\mathcal{Z}}(\mathbb{I})$
-linear dual of
![]() ${\mathcal{Z}}(A)$
, since
${\mathcal{Z}}(A)$
, since
![]() $[A,\mathbb{I}]$
is a dual object of
$[A,\mathbb{I}]$
is a dual object of
![]() $A$
in
$A$
in
![]() ${\mathcal{M}}$
. By Remark 4.4(i), we have a chain of isomorphisms
${\mathcal{M}}$
. By Remark 4.4(i), we have a chain of isomorphisms
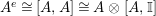 $A^{e}\cong [A,A]\cong A\otimes _{}[A,\mathbb{I}]$
, from which we deduce the following isomorphisms
$A^{e}\cong [A,A]\cong A\otimes _{}[A,\mathbb{I}]$
, from which we deduce the following isomorphisms
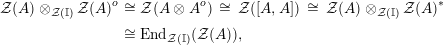 $$\begin{eqnarray}\displaystyle {\mathcal{Z}}(A)\otimes _{{\mathcal{Z}}(\mathbb{I})}{\mathcal{Z}}(A)^{o} & \cong & \displaystyle {\mathcal{Z}}(A\otimes _{}A^{o})\,\cong \,{\mathcal{Z}}([A,A])\,\cong \,{\mathcal{Z}}(A)\otimes _{{\mathcal{Z}}(\mathbb{I})}{\mathcal{Z}}(A)^{\ast }\nonumber\\ \displaystyle & \cong & \displaystyle \text{End}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A)),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{Z}}(A)\otimes _{{\mathcal{Z}}(\mathbb{I})}{\mathcal{Z}}(A)^{o} & \cong & \displaystyle {\mathcal{Z}}(A\otimes _{}A^{o})\,\cong \,{\mathcal{Z}}([A,A])\,\cong \,{\mathcal{Z}}(A)\otimes _{{\mathcal{Z}}(\mathbb{I})}{\mathcal{Z}}(A)^{\ast }\nonumber\\ \displaystyle & \cong & \displaystyle \text{End}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A)),\nonumber\end{eqnarray}$$
whose composition leads to the desired
![]() ${\mathcal{Z}}(\mathbb{I})$
-algebra isomorphism.◻
${\mathcal{Z}}(\mathbb{I})$
-algebra isomorphism.◻
In view of Remark 4.4(ii), in what follows we only consider an Azumaya monoid
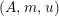 $(A,m,u)$
for which the underlying object
$(A,m,u)$
for which the underlying object
![]() $A$
has a left internal hom functor in
$A$
has a left internal hom functor in
![]() ${\mathcal{M}}$
. This is the case, for instance, when
${\mathcal{M}}$
. This is the case, for instance, when
![]() $A$
is a left dualizable object in
$A$
is a left dualizable object in
![]() ${\mathcal{M}}$
(in the sense of Definition 1.2 with
${\mathcal{M}}$
(in the sense of Definition 1.2 with
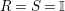 $R=S=\mathbb{I}$
). Obviously, the strong assumption of
$R=S=\mathbb{I}$
). Obviously, the strong assumption of
![]() ${\mathcal{M}}$
being left closed automatically guarantees the existence of left internal hom functor for any object; however, this is not the case of our interest.
${\mathcal{M}}$
being left closed automatically guarantees the existence of left internal hom functor for any object; however, this is not the case of our interest.
Corollary 4.7. Let
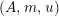 $(A,m,u)$
be an Azumaya monoid in
$(A,m,u)$
be an Azumaya monoid in
![]() ${\mathcal{M}}$
. Then
${\mathcal{M}}$
. Then
![]() $A$
is flat, central and the unit
$A$
is flat, central and the unit
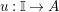 $u:\mathbb{I}\rightarrow A$
is a section in
$u:\mathbb{I}\rightarrow A$
is a section in
![]() ${\mathcal{M}}$
.
${\mathcal{M}}$
.
Proof. The functor
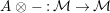 $A\otimes _{}-:{\mathcal{M}}\rightarrow {\mathcal{M}}$
is clearly the composition of the functor
$A\otimes _{}-:{\mathcal{M}}\rightarrow {\mathcal{M}}$
is clearly the composition of the functor
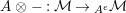 $A\otimes _{}-:{\mathcal{M}}\rightarrow \text{}_{A^{e}}{\mathcal{M}}$
with the forgetful functor
$A\otimes _{}-:{\mathcal{M}}\rightarrow \text{}_{A^{e}}{\mathcal{M}}$
with the forgetful functor
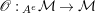 $\mathscr{O}:\text{}_{A^{e}}{\mathcal{M}}\rightarrow {\mathcal{M}}$
, so that it is left exact. Thus
$\mathscr{O}:\text{}_{A^{e}}{\mathcal{M}}\rightarrow {\mathcal{M}}$
, so that it is left exact. Thus
![]() $A$
is a flat object.
$A$
is a flat object.
We know that the unit and the counit
 $$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D700}}_{M}:A\otimes _{\,A^{e}}[A,M]\longrightarrow M,\qquad \boldsymbol{\unicode[STIX]{x1D701}}_{X}:X\longrightarrow _{A^{e}}[A,A\otimes _{}X],\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D700}}_{M}:A\otimes _{\,A^{e}}[A,M]\longrightarrow M,\qquad \boldsymbol{\unicode[STIX]{x1D701}}_{X}:X\longrightarrow _{A^{e}}[A,A\otimes _{}X],\end{eqnarray}$$
of the adjunction 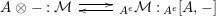 are natural isomorphisms, for every pair ofobjects
are natural isomorphisms, for every pair ofobjects
![]() $(X,M)$
in
$(X,M)$
in
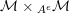 ${\mathcal{M}}\times _{A^{e}}{\mathcal{M}}$
. Thus,
${\mathcal{M}}\times _{A^{e}}{\mathcal{M}}$
. Thus,
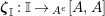 $\boldsymbol{\unicode[STIX]{x1D701}}_{\mathbb{I}}:\mathbb{I}\rightarrow _{A^{e}}[A,A]$
is an isomorphism, and so
$\boldsymbol{\unicode[STIX]{x1D701}}_{\mathbb{I}}:\mathbb{I}\rightarrow _{A^{e}}[A,A]$
is an isomorphism, and so
![]() $A$
is central. The retraction of
$A$
is central. The retraction of
![]() $u$
is given by the following dashed arrow
$u$
is given by the following dashed arrow
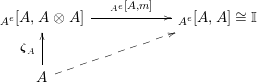
◻
Next we apply the results of Section 3, specially Theorem 3.12, to the case of Azumaya monoid. Most of the assumptions in that Theorem are in fact fulfilled for an Azumaya monoid
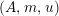 $(A,m,u)$
. Indeed, from the fact that
$(A,m,u)$
. Indeed, from the fact that
![]() $m$
splits in
$m$
splits in
![]() $\text{}_{A^{e}}{\mathcal{M}}$
, we have that
$\text{}_{A^{e}}{\mathcal{M}}$
, we have that
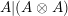 $A|(A\otimes _{}A)$
as in Definition 3.5(2). By Proposition 4.2 and Corollary 4.7, we know that
$A|(A\otimes _{}A)$
as in Definition 3.5(2). By Proposition 4.2 and Corollary 4.7, we know that
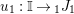 $u_{1}:\mathbb{I}\rightarrow \text{}_{1}J_{1}$
is an isomorphism and that
$u_{1}:\mathbb{I}\rightarrow \text{}_{1}J_{1}$
is an isomorphism and that
![]() $A$
is flat. Henceforth, the only condition on
$A$
is flat. Henceforth, the only condition on
![]() $A$
, which one needs to check is
$A$
, which one needs to check is
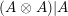 $(A\otimes _{}A)|A$
.
$(A\otimes _{}A)|A$
.
However, even under the assumption that
![]() ${\mathcal{Z}}$
is faithful, one can not expect to have for free this last condition, as was given in the classical case of modules over a commutative ring. In our setting, it seems that this condition depends heavily on the fact that
${\mathcal{Z}}$
is faithful, one can not expect to have for free this last condition, as was given in the classical case of modules over a commutative ring. In our setting, it seems that this condition depends heavily on the fact that
![]() $A$
and
$A$
and
![]() $A^{e}$
should be “progenerators” in the category of
$A^{e}$
should be “progenerators” in the category of
![]() $A^{e}$
-bimodules. To be more precise, as was argued in Remark 4.5, the projectivity of
$A^{e}$
-bimodules. To be more precise, as was argued in Remark 4.5, the projectivity of
![]() $A$
in
$A$
in
![]() $\text{}_{A^{e}}{\mathcal{M}}$
is, for instance, linked to that of
$\text{}_{A^{e}}{\mathcal{M}}$
is, for instance, linked to that of
![]() $\mathbb{I}$
in
$\mathbb{I}$
in
![]() ${\mathcal{M}}$
as the following natural isomorphism shows:
${\mathcal{M}}$
as the following natural isomorphism shows:
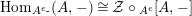 $\text{Hom}_{A^{e}\text{-}}(A,-)\cong {\mathcal{Z}}\circ \text{}_{A^{e}}[A,-]$
; see Appendix B.
$\text{Hom}_{A^{e}\text{-}}(A,-)\cong {\mathcal{Z}}\circ \text{}_{A^{e}}[A,-]$
; see Appendix B.
Recall from Proposition 1.6 that, for any element
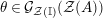 $\unicode[STIX]{x1D703}\in {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
the group defined in (35), there is, by Propositions 1.3 and 1.6, an isomorphism of left
$\unicode[STIX]{x1D703}\in {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
the group defined in (35), there is, by Propositions 1.3 and 1.6, an isomorphism of left
![]() $A$
-modules
$A$
-modules
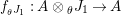 $f_{\text{}_{\unicode[STIX]{x1D703}}J_{1}}:A\otimes \text{}_{\unicode[STIX]{x1D703}}J_{1}\rightarrow A$
. Considering
$f_{\text{}_{\unicode[STIX]{x1D703}}J_{1}}:A\otimes \text{}_{\unicode[STIX]{x1D703}}J_{1}\rightarrow A$
. Considering
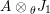 $A\otimes \text{}_{\unicode[STIX]{x1D703}}J_{1}$
as left
$A\otimes \text{}_{\unicode[STIX]{x1D703}}J_{1}$
as left
![]() $A^{e}$
-module, we also have
$A^{e}$
-module, we also have
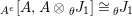 $\text{}_{A^{e}}[A,A\otimes \text{}_{\unicode[STIX]{x1D703}}J_{1}]\cong \text{}_{\unicode[STIX]{x1D703}}J_{1}$
via the unit
$\text{}_{A^{e}}[A,A\otimes \text{}_{\unicode[STIX]{x1D703}}J_{1}]\cong \text{}_{\unicode[STIX]{x1D703}}J_{1}$
via the unit
![]() $\boldsymbol{\unicode[STIX]{x1D701}}$
.
$\boldsymbol{\unicode[STIX]{x1D701}}$
.
For an element
![]() $\unicode[STIX]{x1D703}$
as above, we denote by
$\unicode[STIX]{x1D703}$
as above, we denote by
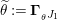 $\widetilde{\unicode[STIX]{x1D703}}:=\boldsymbol{\unicode[STIX]{x1D6E4}}_{\text{}_{\unicode[STIX]{x1D703}}J_{1}}$
the image of
$\widetilde{\unicode[STIX]{x1D703}}:=\boldsymbol{\unicode[STIX]{x1D6E4}}_{\text{}_{\unicode[STIX]{x1D703}}J_{1}}$
the image of
![]() $\text{}_{\unicode[STIX]{x1D703}}J_{1}$
by the morphism of groups
$\text{}_{\unicode[STIX]{x1D703}}J_{1}$
by the morphism of groups
![]() $\boldsymbol{\unicode[STIX]{x1D6E4}}$
stated in Proposition 4.1 (recall here that
$\boldsymbol{\unicode[STIX]{x1D6E4}}$
stated in Proposition 4.1 (recall here that
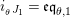 $i_{\text{}_{\unicode[STIX]{x1D703}}J_{1}}=\mathfrak{eq}_{\unicode[STIX]{x1D703},1}$
; see (24)). In this way, to each
$i_{\text{}_{\unicode[STIX]{x1D703}}J_{1}}=\mathfrak{eq}_{\unicode[STIX]{x1D703},1}$
; see (24)). In this way, to each
![]() $A$
-bimodule
$A$
-bimodule
![]() $M$
, we associate the
$M$
, we associate the
![]() $A$
-bimodule
$A$
-bimodule
![]() $M_{\widetilde{\unicode[STIX]{x1D703}}}$
whose underlying object is
$M_{\widetilde{\unicode[STIX]{x1D703}}}$
whose underlying object is
![]() $M$
where the left action is unchanged while the right action is twisted by
$M$
where the left action is unchanged while the right action is twisted by
![]() $\widetilde{\unicode[STIX]{x1D703}}$
. Precisely, we have
$\widetilde{\unicode[STIX]{x1D703}}$
. Precisely, we have
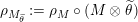 $\unicode[STIX]{x1D70C}_{M_{\widetilde{\unicode[STIX]{x1D703}}}}:=\unicode[STIX]{x1D70C}_{M}\circ (M\otimes _{}\widetilde{\unicode[STIX]{x1D703}})$
, where
$\unicode[STIX]{x1D70C}_{M_{\widetilde{\unicode[STIX]{x1D703}}}}:=\unicode[STIX]{x1D70C}_{M}\circ (M\otimes _{}\widetilde{\unicode[STIX]{x1D703}})$
, where
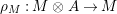 $\unicode[STIX]{x1D70C}_{M}:M\otimes _{}A\rightarrow M$
is the right structure morphism of
$\unicode[STIX]{x1D70C}_{M}:M\otimes _{}A\rightarrow M$
is the right structure morphism of
![]() $M$
.
$M$
.
Now, given another element
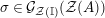 $\unicode[STIX]{x1D70E}\in {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
and another
$\unicode[STIX]{x1D70E}\in {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
and another
![]() $A$
-bimodule
$A$
-bimodule
![]() $N$
, we have two
$N$
, we have two
![]() ${\mathcal{Z}}(\mathbb{I})$
-modules under consideration. Namely, the first one is
${\mathcal{Z}}(\mathbb{I})$
-modules under consideration. Namely, the first one is
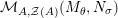 ${\mathcal{M}}_{A,{\mathcal{Z}}(A)}(M_{\unicode[STIX]{x1D703}},N_{\unicode[STIX]{x1D70E}})$
defined in the same way as in Section 3.2, and the other is the module of
${\mathcal{M}}_{A,{\mathcal{Z}}(A)}(M_{\unicode[STIX]{x1D703}},N_{\unicode[STIX]{x1D70E}})$
defined in the same way as in Section 3.2, and the other is the module of
![]() $A$
-bimodules morphisms
$A$
-bimodules morphisms
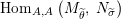 $\text{Hom}_{A,A}\left(M_{\widetilde{\unicode[STIX]{x1D703}}},\,N_{\widetilde{\unicode[STIX]{x1D70E}}}\right)$
.
$\text{Hom}_{A,A}\left(M_{\widetilde{\unicode[STIX]{x1D703}}},\,N_{\widetilde{\unicode[STIX]{x1D70E}}}\right)$
.
Proposition 4.8. Let
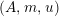 $(A,m,u)$
be an Azumaya monoid in
$(A,m,u)$
be an Azumaya monoid in
![]() ${\mathcal{M}}$
. Consider elements
${\mathcal{M}}$
. Consider elements
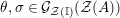 $\unicode[STIX]{x1D703},\unicode[STIX]{x1D70E}\in {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
and their respective associated images
$\unicode[STIX]{x1D703},\unicode[STIX]{x1D70E}\in {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
and their respective associated images
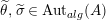 $\widetilde{\unicode[STIX]{x1D703}},\widetilde{\unicode[STIX]{x1D70E}}\in \text{Aut}_{alg}(A)$
. Assume that the functor
$\widetilde{\unicode[STIX]{x1D703}},\widetilde{\unicode[STIX]{x1D70E}}\in \text{Aut}_{alg}(A)$
. Assume that the functor
![]() ${\mathcal{Z}}$
is faithful. Then
${\mathcal{Z}}$
is faithful. Then
-
(i) For every
 $t\in {\mathcal{Z}}(A)$
, we have
$t\in {\mathcal{Z}}(A)$
, we have
 ${\mathcal{Z}}(\widetilde{\unicode[STIX]{x1D703}})(t)\,=\,\unicode[STIX]{x1D6F7}_{\text{}_{\unicode[STIX]{x1D703}}J_{1}}(t)\,=\,\unicode[STIX]{x1D703}(t)$
, that is,
${\mathcal{Z}}(\widetilde{\unicode[STIX]{x1D703}})(t)\,=\,\unicode[STIX]{x1D6F7}_{\text{}_{\unicode[STIX]{x1D703}}J_{1}}(t)\,=\,\unicode[STIX]{x1D703}(t)$
, that is,
 ${\mathcal{Z}}(\widetilde{\unicode[STIX]{x1D703}})\,=\,\unicode[STIX]{x1D703}$
.
${\mathcal{Z}}(\widetilde{\unicode[STIX]{x1D703}})\,=\,\unicode[STIX]{x1D703}$
. -
(ii) The homomorphism of groups
 $\unicode[STIX]{x1D714}$
stated in Corollary 3.11 is surjective.
$\unicode[STIX]{x1D714}$
stated in Corollary 3.11 is surjective. -
(iii) There is an equality
 $\text{Hom}_{A,A}\left(A_{\widetilde{\unicode[STIX]{x1D703}}},\,A_{\widetilde{\unicode[STIX]{x1D70E}}}\right)\,=\,{\mathcal{M}}_{A,{\mathcal{Z}}(A)}(A_{\unicode[STIX]{x1D703}},A_{\unicode[STIX]{x1D70E}})$
.
$\text{Hom}_{A,A}\left(A_{\widetilde{\unicode[STIX]{x1D703}}},\,A_{\widetilde{\unicode[STIX]{x1D70E}}}\right)\,=\,{\mathcal{M}}_{A,{\mathcal{Z}}(A)}(A_{\unicode[STIX]{x1D703}},A_{\unicode[STIX]{x1D70E}})$
.
Proof. By Corollary 4.7, we know that
![]() $A$
is central, hence
$A$
is central, hence
![]() $\mathbb{I}\cong \text{}_{1}J_{1}$
by Proposition 4.2(iv).
$\mathbb{I}\cong \text{}_{1}J_{1}$
by Proposition 4.2(iv).
(i) It is a direct consequence of Proposition 4.1 and Theorem 3.4 (see equation (36)).
(ii) It follows by item (i).
(iii) The direct inclusion follows as in Proposition 3.8(1). Conversely, take an element
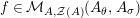 $f\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(A_{\unicode[STIX]{x1D703}},A_{\unicode[STIX]{x1D70E}})$
. This element belongs to
$f\in {\mathcal{M}}_{A,{\mathcal{Z}}(A)}(A_{\unicode[STIX]{x1D703}},A_{\unicode[STIX]{x1D70E}})$
. This element belongs to
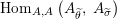 $\text{Hom}_{A,A}\left(A_{\widetilde{\unicode[STIX]{x1D703}}},\,A_{\widetilde{\unicode[STIX]{x1D70E}}}\right)$
if and only if
$\text{Hom}_{A,A}\left(A_{\widetilde{\unicode[STIX]{x1D703}}},\,A_{\widetilde{\unicode[STIX]{x1D70E}}}\right)$
if and only if
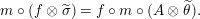 $$\begin{eqnarray}m\circ (f\otimes _{}\widetilde{\unicode[STIX]{x1D70E}})=f\circ m\circ (A\otimes _{}\widetilde{\unicode[STIX]{x1D703}}).\end{eqnarray}$$
$$\begin{eqnarray}m\circ (f\otimes _{}\widetilde{\unicode[STIX]{x1D70E}})=f\circ m\circ (A\otimes _{}\widetilde{\unicode[STIX]{x1D703}}).\end{eqnarray}$$
By the equalities
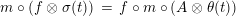 $m\circ (f\otimes _{}\unicode[STIX]{x1D70E}(t))\,=\,f\circ m\circ (A\otimes _{}\unicode[STIX]{x1D703}(t))$
,
$m\circ (f\otimes _{}\unicode[STIX]{x1D70E}(t))\,=\,f\circ m\circ (A\otimes _{}\unicode[STIX]{x1D703}(t))$
,
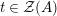 $t\in {\mathcal{Z}}(A)$
derived from the definition of
$t\in {\mathcal{Z}}(A)$
derived from the definition of
![]() $f$
, we have, using part (i), that
$f$
, we have, using part (i), that
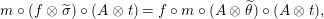 $$\begin{eqnarray}m\circ (f\otimes _{}\widetilde{\unicode[STIX]{x1D70E}})\circ (A\otimes _{}t)=f\circ m\circ (A\otimes _{}\widetilde{\unicode[STIX]{x1D703}})\circ (A\otimes _{}t),\end{eqnarray}$$
$$\begin{eqnarray}m\circ (f\otimes _{}\widetilde{\unicode[STIX]{x1D70E}})\circ (A\otimes _{}t)=f\circ m\circ (A\otimes _{}\widetilde{\unicode[STIX]{x1D703}})\circ (A\otimes _{}t),\end{eqnarray}$$
for every
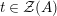 $t\in {\mathcal{Z}}(A)$
. Using these equalities and the fact that
$t\in {\mathcal{Z}}(A)$
. Using these equalities and the fact that
![]() $\mathbb{I}$
is a generator we are able to show that
$\mathbb{I}$
is a generator we are able to show that
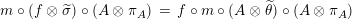 $m\circ (f\otimes _{}\widetilde{\unicode[STIX]{x1D70E}})\circ (A\otimes _{}\unicode[STIX]{x1D70B}_{A})\,=\,f\circ m\circ (A\otimes _{}\widetilde{\unicode[STIX]{x1D703}})\circ (A\otimes _{}\unicode[STIX]{x1D70B}_{A})$
, where
$m\circ (f\otimes _{}\widetilde{\unicode[STIX]{x1D70E}})\circ (A\otimes _{}\unicode[STIX]{x1D70B}_{A})\,=\,f\circ m\circ (A\otimes _{}\widetilde{\unicode[STIX]{x1D703}})\circ (A\otimes _{}\unicode[STIX]{x1D70B}_{A})$
, where
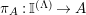 $\unicode[STIX]{x1D70B}_{A}:\mathbb{I}^{(\unicode[STIX]{x1D6EC})}\rightarrow A$
is the canonical epimorphism. Now, equality (44) follows since
$\unicode[STIX]{x1D70B}_{A}:\mathbb{I}^{(\unicode[STIX]{x1D6EC})}\rightarrow A$
is the canonical epimorphism. Now, equality (44) follows since
![]() $A\otimes _{}\unicode[STIX]{x1D70B}_{A}$
is an epimorphism, which completes the proof.◻
$A\otimes _{}\unicode[STIX]{x1D70B}_{A}$
is an epimorphism, which completes the proof.◻
Now, with notations as in Definition 3.5, we set
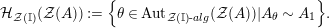 $$\begin{eqnarray}{\mathcal{H}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A)):=\Bigl\{\unicode[STIX]{x1D703}\in \text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-}alg}({\mathcal{Z}}(A))|A_{\unicode[STIX]{x1D703}}\sim A_{1}\Bigr\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A)):=\Bigl\{\unicode[STIX]{x1D703}\in \text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-}alg}({\mathcal{Z}}(A))|A_{\unicode[STIX]{x1D703}}\sim A_{1}\Bigr\}.\end{eqnarray}$$
Using Proposition 3.8(7), we easily check that this is a subgroup of
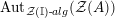 $\text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-}alg}({\mathcal{Z}}(A))$
. Now, it is clear from Corollary 3.7, that under the assumptions of
$\text{Aut}_{{\mathcal{Z}}(\mathbb{I})\text{-}alg}({\mathcal{Z}}(A))$
. Now, it is clear from Corollary 3.7, that under the assumptions of
![]() $A$
being Azumaya and
$A$
being Azumaya and
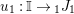 $u_{1}:\mathbb{I}\rightarrow \text{}_{1}J_{1}$
is an isomorphism, we have an inclusion
$u_{1}:\mathbb{I}\rightarrow \text{}_{1}J_{1}$
is an isomorphism, we have an inclusion
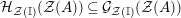 ${\mathcal{H}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))\subseteq {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
of groups.
${\mathcal{H}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))\subseteq {\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
of groups.
Corollary 4.9. Let
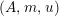 $(A,m,u)$
be an Azumaya monoid in
$(A,m,u)$
be an Azumaya monoid in
![]() ${\mathcal{M}}$
such that
${\mathcal{M}}$
such that
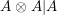 $A\otimes _{}A|A$
. Assume that the functor
$A\otimes _{}A|A$
. Assume that the functor
![]() ${\mathcal{Z}}$
is faithful. Then the maps
${\mathcal{Z}}$
is faithful. Then the maps
![]() $\unicode[STIX]{x1D714}$
and
$\unicode[STIX]{x1D714}$
and
![]() $\boldsymbol{\unicode[STIX]{x1D6E4}}$
are bijective so that we have the following commutative diagram
$\boldsymbol{\unicode[STIX]{x1D6E4}}$
are bijective so that we have the following commutative diagram
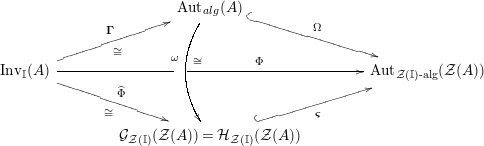
of homomorphisms of groups.
Proof. The map
![]() $\unicode[STIX]{x1D714}$
is bijective since by Proposition 4.8(ii) it is surjective and it is injective as
$\unicode[STIX]{x1D714}$
is bijective since by Proposition 4.8(ii) it is surjective and it is injective as
![]() ${\mathcal{Z}}$
is faithful. We know from Proposition 4.1, that
${\mathcal{Z}}$
is faithful. We know from Proposition 4.1, that
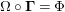 $\unicode[STIX]{x1D6FA}\circ \boldsymbol{\unicode[STIX]{x1D6E4}}=\unicode[STIX]{x1D6F7}$
. Therefore, Theorem 3.4 implies that
$\unicode[STIX]{x1D6FA}\circ \boldsymbol{\unicode[STIX]{x1D6E4}}=\unicode[STIX]{x1D6F7}$
. Therefore, Theorem 3.4 implies that
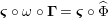 $\boldsymbol{\unicode[STIX]{x1D70D}}\circ \unicode[STIX]{x1D714}\circ \boldsymbol{\unicode[STIX]{x1D6E4}}=\boldsymbol{\unicode[STIX]{x1D70D}}\circ \widehat{\unicode[STIX]{x1D6F7}}$
, and so
$\boldsymbol{\unicode[STIX]{x1D70D}}\circ \unicode[STIX]{x1D714}\circ \boldsymbol{\unicode[STIX]{x1D6E4}}=\boldsymbol{\unicode[STIX]{x1D70D}}\circ \widehat{\unicode[STIX]{x1D6F7}}$
, and so
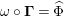 $\unicode[STIX]{x1D714}\circ \boldsymbol{\unicode[STIX]{x1D6E4}}=\widehat{\unicode[STIX]{x1D6F7}}$
which implies that
$\unicode[STIX]{x1D714}\circ \boldsymbol{\unicode[STIX]{x1D6E4}}=\widehat{\unicode[STIX]{x1D6F7}}$
which implies that
![]() $\boldsymbol{\unicode[STIX]{x1D6E4}}$
is bijective as well. Lastly, the inclusion
$\boldsymbol{\unicode[STIX]{x1D6E4}}$
is bijective as well. Lastly, the inclusion
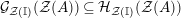 ${\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))\subseteq {\mathcal{H}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
is deduced from Proposition 4.8(i) in combination with Theorem 3.10.◻
${\mathcal{G}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))\subseteq {\mathcal{H}}_{{\mathcal{Z}}(\mathbb{I})}({\mathcal{Z}}(A))$
is deduced from Proposition 4.8(i) in combination with Theorem 3.10.◻
5 Application to the category of comodules over a flat Hopf algebroid
All Hopf algebroids which will be considered here are commutative and flat over the base ring, for the axiomatic definitions and basic properties, we refer the reader to [Reference Ravenel28, Appendix 1].
Let
![]() $(R,H)$
be a commutative Hopf algebroid with base ring
$(R,H)$
be a commutative Hopf algebroid with base ring
![]() $R$
and structure maps
$R$
and structure maps
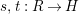 $s,t:R\rightarrow H$
,
$s,t:R\rightarrow H$
,
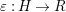 $\unicode[STIX]{x1D700}:H\rightarrow R$
,
$\unicode[STIX]{x1D700}:H\rightarrow R$
,
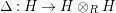 $\unicode[STIX]{x1D6E5}:H\rightarrow H\otimes _{R}H$
and
$\unicode[STIX]{x1D6E5}:H\rightarrow H\otimes _{R}H$
and
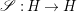 $\mathscr{S}:H\rightarrow H$
. An
$\mathscr{S}:H\rightarrow H$
. An
![]() $H$
-comodule stands for right
$H$
-comodule stands for right
![]() $H$
-comodule, we denote the category of
$H$
-comodule, we denote the category of
![]() $H$
-comodules by
$H$
-comodules by
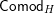 $\mathsf{Comod}\text{}_{H}$
. It is well-known, see for instance [Reference Bruguières5] or [Reference Hovey, Goerss and Priddy14], that any
$\mathsf{Comod}\text{}_{H}$
. It is well-known, see for instance [Reference Bruguières5] or [Reference Hovey, Goerss and Priddy14], that any
![]() $H$
-comodule
$H$
-comodule
![]() $P$
whose underlying
$P$
whose underlying
![]() $R$
-module is finitely generated and projective is a dualizable object in the monoidal category of comodules with dual the
$R$
-module is finitely generated and projective is a dualizable object in the monoidal category of comodules with dual the
![]() $R$
-module
$R$
-module
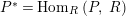 $P^{\ast }=\text{Hom}_{R}\left(P,\,R\right)$
. The comodule structure of
$P^{\ast }=\text{Hom}_{R}\left(P,\,R\right)$
. The comodule structure of
![]() $P^{\ast }$
is given by
$P^{\ast }$
is given by
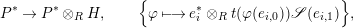 $$\begin{eqnarray}P^{\ast }\rightarrow P^{\ast }\otimes _{R}H,\qquad \Bigl\{\unicode[STIX]{x1D711}\longmapsto e_{i}^{\ast }\otimes _{R}t(\unicode[STIX]{x1D711}(e_{i,0}))\mathscr{S}(e_{i,1})\Bigr\},\end{eqnarray}$$
$$\begin{eqnarray}P^{\ast }\rightarrow P^{\ast }\otimes _{R}H,\qquad \Bigl\{\unicode[STIX]{x1D711}\longmapsto e_{i}^{\ast }\otimes _{R}t(\unicode[STIX]{x1D711}(e_{i,0}))\mathscr{S}(e_{i,1})\Bigr\},\end{eqnarray}$$
where
![]() $\{e_{i},e_{i}^{\ast }\}$
is a dual basis for
$\{e_{i},e_{i}^{\ast }\}$
is a dual basis for
![]() $P_{R}$
and
$P_{R}$
and
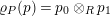 $\unicode[STIX]{x1D71A}_{P}(p)=p_{0}\otimes _{R}p_{1}$
is the
$\unicode[STIX]{x1D71A}_{P}(p)=p_{0}\otimes _{R}p_{1}$
is the
![]() $H$
-coaction of
$H$
-coaction of
![]() $P$
(the summation is understood). Notice that the converse also holds true which means that any dualizable object in
$P$
(the summation is understood). Notice that the converse also holds true which means that any dualizable object in
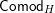 $\mathsf{Comod}\text{}_{H}$
is a finitely generated and projective
$\mathsf{Comod}\text{}_{H}$
is a finitely generated and projective
![]() $R$
-module. This is due to the fact that the forgetful functor
$R$
-module. This is due to the fact that the forgetful functor
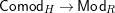 $\mathsf{Comod}\text{}_{H}\rightarrow \mathsf{Mod}_{R}$
is a strict monoidal functor and the unit object in
$\mathsf{Comod}\text{}_{H}\rightarrow \mathsf{Mod}_{R}$
is a strict monoidal functor and the unit object in
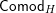 $\mathsf{Comod}\text{}_{H}$
is
$\mathsf{Comod}\text{}_{H}$
is
![]() $R[1]$
, that is
$R[1]$
, that is
![]() $R$
with structure of comodule given by the grouplike element
$R$
with structure of comodule given by the grouplike element
![]() $1_{H}$
, via the target map
$1_{H}$
, via the target map
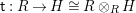 $\mathsf{t}:R\rightarrow H\cong R\otimes _{R}H$
.
$\mathsf{t}:R\rightarrow H\cong R\otimes _{R}H$
.
Next we want to apply the results of Section 4.3 to the category of comodules
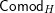 $\mathsf{Comod}\text{}_{H}$
. Observe that this category is a symmetric monoidal Grothendieck category with respect to the canonical flip over
$\mathsf{Comod}\text{}_{H}$
. Observe that this category is a symmetric monoidal Grothendieck category with respect to the canonical flip over
![]() $R$
, where the tensor product is right exact on both factors. Moreover, the forgetful functor
$R$
, where the tensor product is right exact on both factors. Moreover, the forgetful functor
 $\mathsf{Comod}\text{}_{H}\rightarrow \mathsf{Mod}_{R}$
is faithful and exact. So the category
$\mathsf{Comod}\text{}_{H}\rightarrow \mathsf{Mod}_{R}$
is faithful and exact. So the category
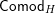 $\mathsf{Comod}\text{}_{H}$
fits in the context of that subsection.
$\mathsf{Comod}\text{}_{H}$
fits in the context of that subsection.
In the previous notations, the functor
![]() ${\mathcal{Z}}$
is identified with
${\mathcal{Z}}$
is identified with
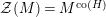 ${\mathcal{Z}}(M)=M^{\text{co}(H)}$
, for an
${\mathcal{Z}}(M)=M^{\text{co}(H)}$
, for an
![]() $H$
-comodule
$H$
-comodule
![]() $M$
, where
$M$
, where
 $$\begin{eqnarray}M^{\text{co}(H)}:=\{m\in M|\,\unicode[STIX]{x1D71A}_{M}(m)=m\otimes _{R}1\}\end{eqnarray}$$
$$\begin{eqnarray}M^{\text{co}(H)}:=\{m\in M|\,\unicode[STIX]{x1D71A}_{M}(m)=m\otimes _{R}1\}\end{eqnarray}$$
is the submodule of coinvariant elements. Therefore, the condition that
![]() $R[1]$
is a generator in
$R[1]$
is a generator in
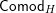 $\mathsf{Comod}\text{}_{H}$
, means that the sudmodule of coinvariant elements
$\mathsf{Comod}\text{}_{H}$
, means that the sudmodule of coinvariant elements
![]() $M^{\text{co}(H)}$
is not zero, for every right
$M^{\text{co}(H)}$
is not zero, for every right
![]() $H$
-comodule
$H$
-comodule
![]() $M$
. For simplicity we denote by
$M$
. For simplicity we denote by
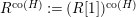 $R^{\text{co}(H)}:=(R[1])^{\text{co}(H)}$
the subalgebra of
$R^{\text{co}(H)}:=(R[1])^{\text{co}(H)}$
the subalgebra of
![]() $R$
of coinvariant elements, which is explicitly given by
$R$
of coinvariant elements, which is explicitly given by
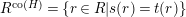 $R^{\text{co}(H)}=\{r\in R|s(r)=t(r)\}$
.
$R^{\text{co}(H)}=\{r\in R|s(r)=t(r)\}$
.
Lemma 5.1. Let
![]() $A$
be an
$A$
be an
![]() $H$
-comodule with coaction
$H$
-comodule with coaction
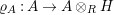 $\unicode[STIX]{x1D71A}_{A}:A\rightarrow A\otimes _{R}H$
. Then
$\unicode[STIX]{x1D71A}_{A}:A\rightarrow A\otimes _{R}H$
. Then
![]() $A$
admits a structure of monoid in
$A$
admits a structure of monoid in
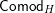 $\mathsf{Comod}\text{}_{H}$
if and only if
$\mathsf{Comod}\text{}_{H}$
if and only if
![]() $\unicode[STIX]{x1D71A}_{A}$
is a morphism of
$\unicode[STIX]{x1D71A}_{A}$
is a morphism of
![]() $R$
-algebras, where
$R$
-algebras, where
![]() $H$
is considered as an
$H$
is considered as an
![]() $R$
-algebra via its source map
$R$
-algebra via its source map
![]() $s$
.
$s$
.
Proof. Straightforward. ◻
We refer to such an object as an
![]() $H$
-comodule
$H$
-comodule
![]() $R$
-algebra.
$R$
-algebra.
Corollary 5.2. Let
![]() $A$
be an Azumaya
$A$
be an Azumaya
![]() $H$
-comodule
$H$
-comodule
![]() $R$
-algebra.
$R$
-algebra.
-
(i) If
 $A$
is finitely generated and projective
$A$
is finitely generated and projective
 $R$
-module, then
$R$
-module, then
 $A$
is an Azumaya
$A$
is an Azumaya
 $R$
-algebra.
$R$
-algebra. -
(ii) If the underlying comodule of
 $A$
is a direct summand of finite products of copies of
$A$
is a direct summand of finite products of copies of
 $R[1]$
, then
$R[1]$
, then
 $A^{\text{co}(H)}$
is an Azumaya
$A^{\text{co}(H)}$
is an Azumaya
 $R^{\text{co}(H)}$
-algebra.
$R^{\text{co}(H)}$
-algebra.
Proof. (i) Since
![]() $A$
is a dualizable
$A$
is a dualizable
![]() $H$
-comodule, the right adjoint of the functor
$H$
-comodule, the right adjoint of the functor
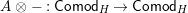 $A\otimes _{}-:\mathsf{Comod}\text{}_{H}\rightarrow \mathsf{Comod}\text{}_{H}$
is given by the functor
$A\otimes _{}-:\mathsf{Comod}\text{}_{H}\rightarrow \mathsf{Comod}\text{}_{H}$
is given by the functor
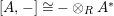 $[A,-]\cong -\otimes _{R}A^{\ast }$
defined using the tensor product of two
$[A,-]\cong -\otimes _{R}A^{\ast }$
defined using the tensor product of two
![]() $H$
-comodules. Using this adjunction and equation (41), we can show that the underlying
$H$
-comodules. Using this adjunction and equation (41), we can show that the underlying
![]() $R$
-algebra of the
$R$
-algebra of the
![]() $H$
-comodule algebra
$H$
-comodule algebra
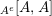 $\text{}_{A^{e}}[A,A]$
coincides with the centre of the underlying
$\text{}_{A^{e}}[A,A]$
coincides with the centre of the underlying
![]() $R$
-algebra of
$R$
-algebra of
![]() $A$
. Therefore, the centre of
$A$
. Therefore, the centre of
![]() $A$
coincides with
$A$
coincides with
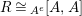 $R\cong \text{}_{A^{e}}[A,A]$
as
$R\cong \text{}_{A^{e}}[A,A]$
as
![]() $A$
is a central
$A$
is a central
![]() $H$
-comodule
$H$
-comodule
![]() $R$
-algebra. From this we conclude that
$R$
-algebra. From this we conclude that
![]() $A$
is a central separable
$A$
is a central separable
![]() $R$
-algebra, that is, an Azumaya
$R$
-algebra, that is, an Azumaya
![]() $R$
-algebra.
$R$
-algebra.
(ii) It follows directly from Proposition 4.6, since
![]() $A$
is a dualizable comodule.◻
$A$
is a dualizable comodule.◻
Example 5.3. Assume that
![]() $R[1]$
is a projective
$R[1]$
is a projective
![]() $H$
-comodule and take
$H$
-comodule and take
![]() $P$
an
$P$
an
![]() $H$
-comodule such that
$H$
-comodule such that
![]() $P_{R}$
is finitely generated and projective module. Consider in a canonical way
$P_{R}$
is finitely generated and projective module. Consider in a canonical way
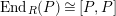 $\text{End}_{R}(P)\cong [P,P]$
as an
$\text{End}_{R}(P)\cong [P,P]$
as an
![]() $H$
-comodule
$H$
-comodule
![]() $R$
-algebra. Assume that the evaluation map
$R$
-algebra. Assume that the evaluation map
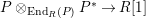 $P\otimes _{\text{End}_{R}(P)}P^{\ast }\rightarrow R[1]$
is an isomorphism of
$P\otimes _{\text{End}_{R}(P)}P^{\ast }\rightarrow R[1]$
is an isomorphism of
![]() $H$
-comodules. Since
$H$
-comodules. Since
![]() $R[1]$
is projective this isomorphism implies that
$R[1]$
is projective this isomorphism implies that
![]() $P$
is a progenerator in
$P$
is a progenerator in
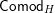 $\mathsf{Comod}\text{}_{H}$
in the sense of [Reference Pareigis26, page 113] whence, by [Reference Pareigis26, Theorem 14],
$\mathsf{Comod}\text{}_{H}$
in the sense of [Reference Pareigis26, page 113] whence, by [Reference Pareigis26, Theorem 14],
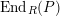 $\text{End}_{R}(P)$
is an Azumaya
$\text{End}_{R}(P)$
is an Azumaya
![]() $H$
-comodule
$H$
-comodule
![]() $R$
-algebra.
$R$
-algebra.
Example 5.4. Assume that
![]() $(R,H)$
is a split Hopf algebroid, that is
$(R,H)$
is a split Hopf algebroid, that is
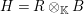 $H=R\otimes _{\mathbb{K}}B$
, where
$H=R\otimes _{\mathbb{K}}B$
, where
![]() $B$
is a flat commutative Hopf algebra over a ground commutative ring
$B$
is a flat commutative Hopf algebra over a ground commutative ring
![]() $\mathbb{K}$
and
$\mathbb{K}$
and
![]() $R$
is a (right)
$R$
is a (right)
![]() $B$
-comodule commutative
$B$
-comodule commutative
![]() $\mathbb{K}$
-algebra. Let
$\mathbb{K}$
-algebra. Let
![]() $A$
be an Azumaya
$A$
be an Azumaya
![]() $H$
-comodule
$H$
-comodule
![]() $R$
-algebra which finitely generated and projective as an
$R$
-algebra which finitely generated and projective as an
![]() $R$
-module. Then, by Corollary 5.2(i),
$R$
-module. Then, by Corollary 5.2(i),
![]() $A$
is an Azumaya
$A$
is an Azumaya
![]() $R$
-algebra. If
$R$
-algebra. If
![]() $R=\mathbb{K}$
, then
$R=\mathbb{K}$
, then
![]() $A$
is in particular an
$A$
is in particular an
![]() $B$
-comodule Azumaya algebra in the sense of [Reference Caenepeel6, page 328].
$B$
-comodule Azumaya algebra in the sense of [Reference Caenepeel6, page 328].
The fact that
![]() $A$
is an
$A$
is an
![]() $H$
-comodule
$H$
-comodule
![]() $R$
-algebra leads to different groups so far treated here. On the one hand, we have
$R$
-algebra leads to different groups so far treated here. On the one hand, we have
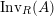 $\text{Inv}_{R}(A)$
and
$\text{Inv}_{R}(A)$
and
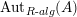 $\text{Aut}_{R\text{-}alg}(A)$
, where
$\text{Aut}_{R\text{-}alg}(A)$
, where
![]() $A$
is considered as an
$A$
is considered as an
![]() $R$
-algebra that is a monoid in the category of
$R$
-algebra that is a monoid in the category of
![]() $R$
-modules. On the other hand, we have
$R$
-modules. On the other hand, we have
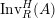 $\text{Inv}_{R}^{H}(A)$
and
$\text{Inv}_{R}^{H}(A)$
and
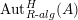 $\text{Aut}_{R\text{-}alg}^{H}(A)$
, where
$\text{Aut}_{R\text{-}alg}^{H}(A)$
, where
![]() $A$
is considered as a monoid in the category of
$A$
is considered as a monoid in the category of
![]() $H$
-comodules. Obviously we have the following inclusions of groups
$H$
-comodules. Obviously we have the following inclusions of groups
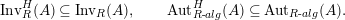 $$\begin{eqnarray}\text{Inv}_{R}^{H}(A)\subseteq \text{Inv}_{R}(A),\qquad \text{Aut}_{R\text{-}alg}^{H}(A)\subseteq \text{Aut}_{R\text{-}alg}(A).\end{eqnarray}$$
$$\begin{eqnarray}\text{Inv}_{R}^{H}(A)\subseteq \text{Inv}_{R}(A),\qquad \text{Aut}_{R\text{-}alg}^{H}(A)\subseteq \text{Aut}_{R\text{-}alg}(A).\end{eqnarray}$$
By a direct application of Corollary 4.9, we obtain the following.
Corollary 5.5. Let
![]() $A$
be an Azumaya
$A$
be an Azumaya
![]() $H$
-comodule
$H$
-comodule
![]() $R$
-algebra such that
$R$
-algebra such that
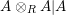 $A\otimes _{R}A|A$
simultaneously in the category of
$A\otimes _{R}A|A$
simultaneously in the category of
![]() $H$
-comodules and of
$H$
-comodules and of
![]() $A$
-bimodules. Assume that
$A$
-bimodules. Assume that
![]() $R[1]$
is a generator in
$R[1]$
is a generator in
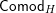 $\mathsf{Comod}\text{}_{H}$
. Then there is an isomorphism of groups
$\mathsf{Comod}\text{}_{H}$
. Then there is an isomorphism of groups
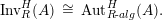 $$\begin{eqnarray}\text{Inv}_{R}^{H}(A)\,\cong \,\text{Aut}_{R\text{-}alg}^{H}(A).\end{eqnarray}$$
$$\begin{eqnarray}\text{Inv}_{R}^{H}(A)\,\cong \,\text{Aut}_{R\text{-}alg}^{H}(A).\end{eqnarray}$$
Remark 5.6. Consider an Azumaya
![]() $H$
-comodule
$H$
-comodule
![]() $R$
-algebra
$R$
-algebra
![]() $A$
which is finitely generated and projective as
$A$
which is finitely generated and projective as
![]() $R$
-module. One can expect to deduce Corollary 5.5 directly by using Corollary 5.2(i) in conjunction with [Reference Miyashita23, Corollary of Theorem 1.4]. This could be so simple if one succeeds to show, for instance, that the following diagram is commutative
$R$
-module. One can expect to deduce Corollary 5.5 directly by using Corollary 5.2(i) in conjunction with [Reference Miyashita23, Corollary of Theorem 1.4]. This could be so simple if one succeeds to show, for instance, that the following diagram is commutative
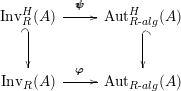
where the map
![]() $\pmb{\unicode[STIX]{x1D713}}$
is the isomorphism of Corollary 5.5 while
$\pmb{\unicode[STIX]{x1D713}}$
is the isomorphism of Corollary 5.5 while
![]() $\boldsymbol{\unicode[STIX]{x1D711}}$
is the isomorphism of [Reference Miyashita23, page 100] which for any element
$\boldsymbol{\unicode[STIX]{x1D711}}$
is the isomorphism of [Reference Miyashita23, page 100] which for any element
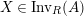 $X\in \text{Inv}_{R}(A)$
with inverse
$X\in \text{Inv}_{R}(A)$
with inverse
![]() $Y$
and decomposition of unit
$Y$
and decomposition of unit
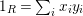 $1_{R}=\sum _{i}x_{i}y_{i}$
(
$1_{R}=\sum _{i}x_{i}y_{i}$
(
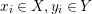 $x_{i}\in X,y_{i}\in Y$
), the associated automorphism is given by
$x_{i}\in X,y_{i}\in Y$
), the associated automorphism is given by
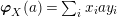 $\boldsymbol{\unicode[STIX]{x1D711}}_{X}(a)=\sum _{i}x_{i}ay_{i}$
, for any
$\boldsymbol{\unicode[STIX]{x1D711}}_{X}(a)=\sum _{i}x_{i}ay_{i}$
, for any
![]() $a\in A$
. That is, to show that the map
$a\in A$
. That is, to show that the map
![]() $\pmb{\unicode[STIX]{x1D713}}$
is the restriction of
$\pmb{\unicode[STIX]{x1D713}}$
is the restriction of
![]() $\boldsymbol{\unicode[STIX]{x1D711}}$
. However this is not clear at all. Or perhaps by showing that the map
$\boldsymbol{\unicode[STIX]{x1D711}}$
. However this is not clear at all. Or perhaps by showing that the map
![]() $\boldsymbol{\unicode[STIX]{x1D711}}_{X}$
is
$\boldsymbol{\unicode[STIX]{x1D711}}_{X}$
is
![]() $H$
-colinear whenever
$H$
-colinear whenever
![]() $X$
belongs to the subgroup
$X$
belongs to the subgroup
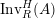 $\text{Inv}_{R}^{H}(A)$
. This is also not clear at all. In any case, both ways will only lead to the injectivity and one has to check the surjectivity which is perhaps much more complicated by using elementary methods.
$\text{Inv}_{R}^{H}(A)$
. This is also not clear at all. In any case, both ways will only lead to the injectivity and one has to check the surjectivity which is perhaps much more complicated by using elementary methods.
Acknowledgments
The authors would like to thank Claudia Menini for helpful discussions on a preliminary version of the paper. They are also grateful to the referee for carefully reading the manuscript and for several useful comments. L. El Kaoutit would like to thank all the members of the Department of Mathematics of University of Ferrara for a warm hospitality during his visit.
Appendix A. More results on invertible and dualizable bimodules
In all this appendix
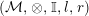 $({\mathcal{M}},\otimes _{},\mathbb{I},l,r)$
will be a Penrose monoidal abelian, locally small and bicomplete category, where tensor products are right exact on both factors. Let
$({\mathcal{M}},\otimes _{},\mathbb{I},l,r)$
will be a Penrose monoidal abelian, locally small and bicomplete category, where tensor products are right exact on both factors. Let
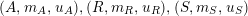 $(A,m_{A},u_{A}),(R,m_{R},u_{R}),(S,m_{S},u_{S})$
be monoids in
$(A,m_{A},u_{A}),(R,m_{R},u_{R}),(S,m_{S},u_{S})$
be monoids in
![]() ${\mathcal{M}}$
with two morphisms of monoids
${\mathcal{M}}$
with two morphisms of monoids
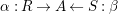 $\unicode[STIX]{x1D6FC}:R\rightarrow A\leftarrow S:\unicode[STIX]{x1D6FD}$
. In the sequel, we will use the notation of Section 1.
$\unicode[STIX]{x1D6FC}:R\rightarrow A\leftarrow S:\unicode[STIX]{x1D6FD}$
. In the sequel, we will use the notation of Section 1.
A.1 From right dualizable datum to right inverse
This subsection is devoted to discuss the converse of Proposition 1.3, that is, trying to give conditions under which a right invertible sub-bimodule can be extracted from a right dualizable datum in the sense of Definition 1.2.
The following corollary is complementary to Proposition 1.6.
Corollary A.1. If in Proposition 1.6, we assume
![]() $\text{ev}$
and
$\text{ev}$
and
![]() $\text{coev}$
are isomorphisms, then so are the following morphisms
$\text{coev}$
are isomorphisms, then so are the following morphisms
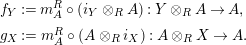 $$\begin{eqnarray}\displaystyle & f_{Y}:=m_{A}^{R}\circ \left(i_{Y}\otimes _{R}A\right):Y\otimes _{R}A\rightarrow A, & \displaystyle \nonumber\\ \displaystyle & g_{X}:=m_{A}^{R}\circ \left(A\otimes _{R}i_{X}\right):A\otimes _{R}X\rightarrow A. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & f_{Y}:=m_{A}^{R}\circ \left(i_{Y}\otimes _{R}A\right):Y\otimes _{R}A\rightarrow A, & \displaystyle \nonumber\\ \displaystyle & g_{X}:=m_{A}^{R}\circ \left(A\otimes _{R}i_{X}\right):A\otimes _{R}X\rightarrow A. & \displaystyle \nonumber\end{eqnarray}$$
Proof. Since
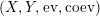 $\left(X,Y,\text{ev},\text{coev}\right)$
is a right dualizable datum then
$\left(X,Y,\text{ev},\text{coev}\right)$
is a right dualizable datum then
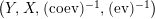 $\big(Y,X,(\text{coev})^{-1},(\text{ev})^{-1}\big)$
is a right dualizable datum. By Proposition 1.6, we get that
$\big(Y,X,(\text{coev})^{-1},(\text{ev})^{-1}\big)$
is a right dualizable datum. By Proposition 1.6, we get that
![]() $f_{Y}$
and
$f_{Y}$
and
![]() $g_{X}$
are isomorphisms too.◻
$g_{X}$
are isomorphisms too.◻
Proposition A.2. Consider a right dualizable datum
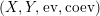 $\left(X,Y,\text{ev},\text{coev}\right)$
which satisfies equations (8) and (9). Assume that
$\left(X,Y,\text{ev},\text{coev}\right)$
which satisfies equations (8) and (9). Assume that
![]() $g_{X}$
is an isomorphism and the functor
$g_{X}$
is an isomorphism and the functor
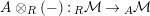 $A\otimes _{R}(-):\text{}_{R}{\mathcal{M}}\rightarrow \text{}_{A}{\mathcal{M}}$
is faithful. Then
$A\otimes _{R}(-):\text{}_{R}{\mathcal{M}}\rightarrow \text{}_{A}{\mathcal{M}}$
is faithful. Then
![]() $X$
is a two-sided invertible sub-bimodule.
$X$
is a two-sided invertible sub-bimodule.
Proof. By Proposition 1.6,
![]() $g_{Y}$
is an isomorphism with inverse
$g_{Y}$
is an isomorphism with inverse
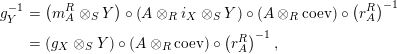 $$\begin{eqnarray}\displaystyle g_{Y}^{-1} & = & \displaystyle \left(m_{A}^{R}\otimes _{S}Y\right)\circ \left(A\otimes _{R}i_{X}\otimes _{S}Y\right)\circ \left(A\otimes _{R}\text{coev}\right)\circ \left(r_{A}^{R}\right)^{-1}\nonumber\\ \displaystyle & = & \displaystyle \left(g_{X}\otimes _{S}Y\right)\circ \left(A\otimes _{R}\text{coev}\right)\circ \left(r_{A}^{R}\right)^{-1},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle g_{Y}^{-1} & = & \displaystyle \left(m_{A}^{R}\otimes _{S}Y\right)\circ \left(A\otimes _{R}i_{X}\otimes _{S}Y\right)\circ \left(A\otimes _{R}\text{coev}\right)\circ \left(r_{A}^{R}\right)^{-1}\nonumber\\ \displaystyle & = & \displaystyle \left(g_{X}\otimes _{S}Y\right)\circ \left(A\otimes _{R}\text{coev}\right)\circ \left(r_{A}^{R}\right)^{-1},\nonumber\end{eqnarray}$$
Therefore, we get that
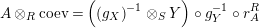 $$\begin{eqnarray}A\otimes _{R}\text{coev}=\left(\left(g_{X}\right)^{-1}\otimes _{S}Y\right)\circ g_{Y}^{-1}\circ r_{A}^{R}\end{eqnarray}$$
$$\begin{eqnarray}A\otimes _{R}\text{coev}=\left(\left(g_{X}\right)^{-1}\otimes _{S}Y\right)\circ g_{Y}^{-1}\circ r_{A}^{R}\end{eqnarray}$$
is an isomorphism. Hence, since the functor
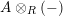 $A\otimes _{R}\left(-\right)$
is faithful, then
$A\otimes _{R}\left(-\right)$
is faithful, then
![]() $\text{coev}$
is an epimorphism as well as a monomorphism, so that it is an isomorphism. By (5), we have
$\text{coev}$
is an epimorphism as well as a monomorphism, so that it is an isomorphism. By (5), we have
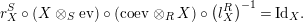 $$\begin{eqnarray}r_{X}^{S}\circ \left(X\otimes _{S}\text{ev}\right)\circ \left(\text{ coev}\otimes _{R}X\right)\circ \left(l_{X}^{R}\right)^{-1}=\text{Id}_{X}.\end{eqnarray}$$
$$\begin{eqnarray}r_{X}^{S}\circ \left(X\otimes _{S}\text{ev}\right)\circ \left(\text{ coev}\otimes _{R}X\right)\circ \left(l_{X}^{R}\right)^{-1}=\text{Id}_{X}.\end{eqnarray}$$
Since
![]() $\text{coev}$
is an isomorphism, we get that
$\text{coev}$
is an isomorphism, we get that
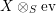 $X\otimes _{S}\text{ev}$
is an isomorphism too. Now, from the equality
$X\otimes _{S}\text{ev}$
is an isomorphism too. Now, from the equality
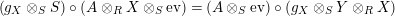 $$\begin{eqnarray}\left(g_{X}\otimes _{S}S\right)\circ \left(A\otimes _{R}X\otimes _{S}\text{ev}\right)=\left(A\otimes _{S}\text{ev}\right)\circ \left(g_{X}\otimes _{S}Y\otimes _{R}X\right)\end{eqnarray}$$
$$\begin{eqnarray}\left(g_{X}\otimes _{S}S\right)\circ \left(A\otimes _{R}X\otimes _{S}\text{ev}\right)=\left(A\otimes _{S}\text{ev}\right)\circ \left(g_{X}\otimes _{S}Y\otimes _{R}X\right)\end{eqnarray}$$
we deduce that
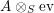 $A\otimes _{S}\text{ev}$
is an isomorphism. Therefore, we conclude as above that
$A\otimes _{S}\text{ev}$
is an isomorphism. Therefore, we conclude as above that
![]() $\text{ev}$
is an isomorphism.◻
$\text{ev}$
is an isomorphism.◻
A.2 Base change and dualizable datum
Keep the notation of Section 1, and assume that
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
are monomorphisms in
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
are monomorphisms in
![]() ${\mathcal{M}}$
. The main aim here is to prove that an
${\mathcal{M}}$
. The main aim here is to prove that an
![]() $(R,S)$
-bimodule
$(R,S)$
-bimodule
![]() $X$
such that
$X$
such that
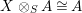 $X\otimes _{S}A\cong A$
and which fits into a right dualizable datum admits a right inverse if we change the ring
$X\otimes _{S}A\cong A$
and which fits into a right dualizable datum admits a right inverse if we change the ring
![]() $R$
by a suitable extension
$R$
by a suitable extension
![]() $R^{\prime }$
of it. First we need to prove the following technical result.
$R^{\prime }$
of it. First we need to prove the following technical result.
Proposition A.3. Let
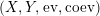 $(X,Y,\text{ev},\text{coev})$
be a right dualizable datum (Definition 1.2) such that
$(X,Y,\text{ev},\text{coev})$
be a right dualizable datum (Definition 1.2) such that
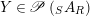 $Y\in \mathscr{P}\left(\text{}_{S}A_{R}\right)$
and
$Y\in \mathscr{P}\left(\text{}_{S}A_{R}\right)$
and
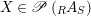 $X\in \mathscr{P}\left(\text{}_{R}A_{S}\right)$
. Assume that the morphism
$X\in \mathscr{P}\left(\text{}_{R}A_{S}\right)$
. Assume that the morphism
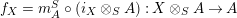 $f_{X}=m_{A}^{S}\circ \left(i_{X}\otimes _{S}A\right):X\otimes _{S}A\rightarrow A$
is an isomorphism. Define
$f_{X}=m_{A}^{S}\circ \left(i_{X}\otimes _{S}A\right):X\otimes _{S}A\rightarrow A$
is an isomorphism. Define
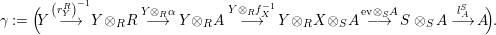 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}:=\Big(\!Y\overset{\left(r_{Y}^{R}\right)^{-1}}{\longrightarrow }\!Y\hspace{-2.0pt}\otimes _{R}\hspace{-2.0pt}R\overset{Y\otimes _{R}\unicode[STIX]{x1D6FC}}{\longrightarrow }Y\hspace{-2.0pt}\otimes _{R}\hspace{-2.0pt}A\overset{Y\otimes _{R}f_{X}^{-1}}{\longrightarrow }Y\hspace{-2.0pt}\otimes _{R}\hspace{-2.0pt}X\hspace{-2.0pt}\otimes _{S}\hspace{-2.0pt}A\overset{\text{ev}\otimes _{S}A}{\longrightarrow }S\otimes _{S}A\overset{l_{A}^{S}}{\longrightarrow }A\!\Big).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}:=\Big(\!Y\overset{\left(r_{Y}^{R}\right)^{-1}}{\longrightarrow }\!Y\hspace{-2.0pt}\otimes _{R}\hspace{-2.0pt}R\overset{Y\otimes _{R}\unicode[STIX]{x1D6FC}}{\longrightarrow }Y\hspace{-2.0pt}\otimes _{R}\hspace{-2.0pt}A\overset{Y\otimes _{R}f_{X}^{-1}}{\longrightarrow }Y\hspace{-2.0pt}\otimes _{R}\hspace{-2.0pt}X\hspace{-2.0pt}\otimes _{S}\hspace{-2.0pt}A\overset{\text{ev}\otimes _{S}A}{\longrightarrow }S\otimes _{S}A\overset{l_{A}^{S}}{\longrightarrow }A\!\Big).\end{eqnarray}$$
Then
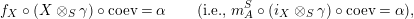 $$\begin{eqnarray}f_{X}\circ \left(X\otimes _{S}\unicode[STIX]{x1D6FE}\right)\circ \text{coev}=\unicode[STIX]{x1D6FC}\qquad \text{(i.e., }m_{A}^{S}\circ \left(i_{X}\otimes _{S}\unicode[STIX]{x1D6FE}\right)\circ \text{coev}=\unicode[STIX]{x1D6FC}\text{),}\end{eqnarray}$$
$$\begin{eqnarray}f_{X}\circ \left(X\otimes _{S}\unicode[STIX]{x1D6FE}\right)\circ \text{coev}=\unicode[STIX]{x1D6FC}\qquad \text{(i.e., }m_{A}^{S}\circ \left(i_{X}\otimes _{S}\unicode[STIX]{x1D6FE}\right)\circ \text{coev}=\unicode[STIX]{x1D6FC}\text{),}\end{eqnarray}$$
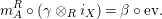 $$\begin{eqnarray}m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FE}\otimes _{R}i_{X}\right)=\unicode[STIX]{x1D6FD}\circ \text{ev }.\end{eqnarray}$$
$$\begin{eqnarray}m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FE}\otimes _{R}i_{X}\right)=\unicode[STIX]{x1D6FD}\circ \text{ev }.\end{eqnarray}$$
Proof. Using the diagrammatic convention of Section 1, we have
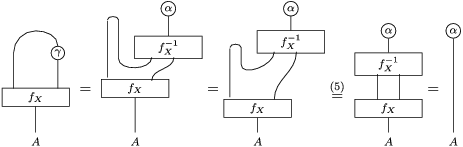
which gives equality (A1). On the other hand, we have

Using this equality and the fact that
![]() $f_{X}^{-1}$
is right
$f_{X}^{-1}$
is right
![]() $A$
-linear (being the inverse of a right
$A$
-linear (being the inverse of a right
![]() $A$
-linear morphism) we compute
$A$
-linear morphism) we compute

which gives the desired equality (A2).◻
Next result extends a result by Miyashita, see [Reference Miyashita23, Proposition 1.1, implication (ii) imlies (i)].
Theorem A.4. Keep the assumptions and notations of Proposition A.3. Let
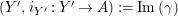 $\left(Y^{\prime },i_{Y^{\prime }}:Y^{\prime }\rightarrow A\right):=\text{Im}\left(\unicode[STIX]{x1D6FE}\right)$
be the image of
$\left(Y^{\prime },i_{Y^{\prime }}:Y^{\prime }\rightarrow A\right):=\text{Im}\left(\unicode[STIX]{x1D6FE}\right)$
be the image of
![]() $\unicode[STIX]{x1D6FE}$
in
$\unicode[STIX]{x1D6FE}$
in
![]() $\left(S,R\right)$
-bimodules, and let
$\left(S,R\right)$
-bimodules, and let
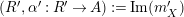 $\left(R^{\prime },\unicode[STIX]{x1D6FC}^{\prime }:R^{\prime }\rightarrow A\right):=\text{Im}(m_{X}^{\prime })$
be the image of
$\left(R^{\prime },\unicode[STIX]{x1D6FC}^{\prime }:R^{\prime }\rightarrow A\right):=\text{Im}(m_{X}^{\prime })$
be the image of
![]() $m_{X}^{\prime }$
in
$m_{X}^{\prime }$
in
![]() $\left(R,R\right)$
-bimodules, where
$\left(R,R\right)$
-bimodules, where
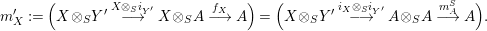 $$\begin{eqnarray}m_{X}^{\prime }:=\Big(X\hspace{-2.0pt}\otimes _{S}\hspace{-2.0pt}Y^{\prime }\overset{X\otimes _{S}i_{Y^{\prime }}}{\longrightarrow }X\hspace{-2.0pt}\otimes _{S}\hspace{-2.0pt}A\overset{f_{X}}{\longrightarrow }A\Big)=\Big(X\hspace{-2.0pt}\otimes _{S}\hspace{-2.0pt}Y^{\prime }\overset{i_{X}\otimes _{S}i_{Y^{\prime }}}{\longrightarrow }A\hspace{-2.0pt}\otimes _{S}\hspace{-2.0pt}A\overset{m_{A}^{S}}{\longrightarrow }A\Big).\end{eqnarray}$$
$$\begin{eqnarray}m_{X}^{\prime }:=\Big(X\hspace{-2.0pt}\otimes _{S}\hspace{-2.0pt}Y^{\prime }\overset{X\otimes _{S}i_{Y^{\prime }}}{\longrightarrow }X\hspace{-2.0pt}\otimes _{S}\hspace{-2.0pt}A\overset{f_{X}}{\longrightarrow }A\Big)=\Big(X\hspace{-2.0pt}\otimes _{S}\hspace{-2.0pt}Y^{\prime }\overset{i_{X}\otimes _{S}i_{Y^{\prime }}}{\longrightarrow }A\hspace{-2.0pt}\otimes _{S}\hspace{-2.0pt}A\overset{m_{A}^{S}}{\longrightarrow }A\Big).\end{eqnarray}$$
Denote by
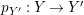 $p_{Y^{\prime }}:Y\rightarrow Y^{\prime }$
the canonical projection so that
$p_{Y^{\prime }}:Y\rightarrow Y^{\prime }$
the canonical projection so that
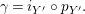 $\unicode[STIX]{x1D6FE}=i_{Y^{\prime }}\circ p_{Y^{\prime }}.$
Similarly denote by
$\unicode[STIX]{x1D6FE}=i_{Y^{\prime }}\circ p_{Y^{\prime }}.$
Similarly denote by
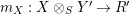 $m_{X}:X\otimes _{S}Y^{\prime }\rightarrow R^{\prime }$
the canonical projection such that
$m_{X}:X\otimes _{S}Y^{\prime }\rightarrow R^{\prime }$
the canonical projection such that
 $\unicode[STIX]{x1D6FC}^{\prime }\circ m_{X}=m_{X}^{\prime }$
. Then
$\unicode[STIX]{x1D6FC}^{\prime }\circ m_{X}=m_{X}^{\prime }$
. Then
-
(1)
 $R^{\prime }$
is a monoid in
$R^{\prime }$
is a monoid in
 $(R,R)$
-bimodules such that
$(R,R)$
-bimodules such that
 $\unicode[STIX]{x1D6FC}^{\prime }:R^{\prime }\rightarrow A$
is a morphism of monoids therein;
$\unicode[STIX]{x1D6FC}^{\prime }:R^{\prime }\rightarrow A$
is a morphism of monoids therein; -
(2)
 $X\in \mathscr{P}(\text{}_{R^{\prime }}A_{S})$
has a right inverse given by
$X\in \mathscr{P}(\text{}_{R^{\prime }}A_{S})$
has a right inverse given by
 $Y^{\prime }\in \mathscr{P}\left(\text{}_{S}A_{R^{\prime }}\right)$
.
$Y^{\prime }\in \mathscr{P}\left(\text{}_{S}A_{R^{\prime }}\right)$
.
Proof. Unfortunately it not possible to present here a smart proof using diagrammatic notation, since we are dealing with different type of multiplications
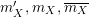 $m_{X}^{\prime },m_{X},\overline{m_{X}}$
and it could be difficult to distinguish them properly.
$m_{X}^{\prime },m_{X},\overline{m_{X}}$
and it could be difficult to distinguish them properly.
(1) Set
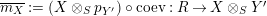 $\overline{m_{X}}:=\left(X\otimes _{S}p_{Y^{\prime }}\right)\circ \text{coev}:R\rightarrow X\otimes _{S}Y^{\prime }$
and
$\overline{m_{X}}:=\left(X\otimes _{S}p_{Y^{\prime }}\right)\circ \text{coev}:R\rightarrow X\otimes _{S}Y^{\prime }$
and
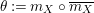 $\unicode[STIX]{x1D703}:=m_{X}\circ \overline{m_{X}}$
. Note that
$\unicode[STIX]{x1D703}:=m_{X}\circ \overline{m_{X}}$
. Note that
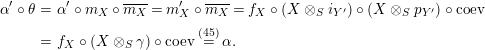 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}^{\prime }\circ \unicode[STIX]{x1D703} & = & \displaystyle \unicode[STIX]{x1D6FC}^{\prime }\circ m_{X}\circ \overline{m_{X}}=m_{X}^{\prime }\circ \overline{m_{X}}=f_{X}\circ \left(X\otimes _{S}i_{Y^{\prime }}\right)\circ \left(X\otimes _{S}p_{Y^{\prime }}\right)\circ \text{coev}\nonumber\\ \displaystyle & = & \displaystyle f_{X}\circ \left(X\otimes _{S}\unicode[STIX]{x1D6FE}\right)\circ \text{coev}\overset{(45)}{=}\unicode[STIX]{x1D6FC}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}^{\prime }\circ \unicode[STIX]{x1D703} & = & \displaystyle \unicode[STIX]{x1D6FC}^{\prime }\circ m_{X}\circ \overline{m_{X}}=m_{X}^{\prime }\circ \overline{m_{X}}=f_{X}\circ \left(X\otimes _{S}i_{Y^{\prime }}\right)\circ \left(X\otimes _{S}p_{Y^{\prime }}\right)\circ \text{coev}\nonumber\\ \displaystyle & = & \displaystyle f_{X}\circ \left(X\otimes _{S}\unicode[STIX]{x1D6FE}\right)\circ \text{coev}\overset{(45)}{=}\unicode[STIX]{x1D6FC}.\nonumber\end{eqnarray}$$
so that
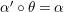 $\unicode[STIX]{x1D6FC}^{\prime }\circ \unicode[STIX]{x1D703}=\unicode[STIX]{x1D6FC}$
. Hence we have a commutative diagram
$\unicode[STIX]{x1D6FC}^{\prime }\circ \unicode[STIX]{x1D703}=\unicode[STIX]{x1D6FC}$
. Hence we have a commutative diagram
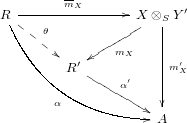
So the unit of
![]() $R^{\prime }$
is
$R^{\prime }$
is
![]() $\unicode[STIX]{x1D703}\circ u_{R}$
. The construction of the multiplication is more involved. Let
$\unicode[STIX]{x1D703}\circ u_{R}$
. The construction of the multiplication is more involved. Let
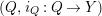 $\left(Q,i_{Q}:Q\rightarrow Y\right)$
be the kernel of
$\left(Q,i_{Q}:Q\rightarrow Y\right)$
be the kernel of
![]() $p_{Y^{\prime }}$
. Tensoring by
$p_{Y^{\prime }}$
. Tensoring by
![]() $X$
on the right we get the exact sequence
$X$
on the right we get the exact sequence
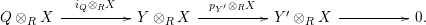
We then have
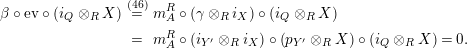 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FD}\circ \text{ev}\circ \left(i_{Q}\otimes _{R}X\right) & \overset{(46)}{=} & \displaystyle m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FE}\otimes _{R}i_{X}\right)\circ \left(i_{Q}\otimes _{R}X\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(i_{Y^{\prime }}\otimes _{R}i_{X}\right)\circ \left(p_{Y^{\prime }}\otimes _{R}X\right)\circ \left(i_{Q}\otimes _{R}X\right)=0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FD}\circ \text{ev}\circ \left(i_{Q}\otimes _{R}X\right) & \overset{(46)}{=} & \displaystyle m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FE}\otimes _{R}i_{X}\right)\circ \left(i_{Q}\otimes _{R}X\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(i_{Y^{\prime }}\otimes _{R}i_{X}\right)\circ \left(p_{Y^{\prime }}\otimes _{R}X\right)\circ \left(i_{Q}\otimes _{R}X\right)=0.\nonumber\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D6FD}$
is a monomorphism we get
$\unicode[STIX]{x1D6FD}$
is a monomorphism we get
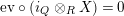 $\text{ev}\circ (i_{Q}\otimes _{R}X)=0$
so that there is a morphism of
$\text{ev}\circ (i_{Q}\otimes _{R}X)=0$
so that there is a morphism of
![]() $S$
-bimodules
$S$
-bimodules
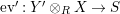 $\text{ev}^{\prime }:Y^{\prime }\otimes _{R}X\rightarrow S$
such that
$\text{ev}^{\prime }:Y^{\prime }\otimes _{R}X\rightarrow S$
such that
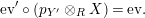 $$\begin{eqnarray}\text{ev}^{\prime }\circ (p_{Y^{\prime }}\otimes _{R}X)=\text{ev}.\end{eqnarray}$$
$$\begin{eqnarray}\text{ev}^{\prime }\circ (p_{Y^{\prime }}\otimes _{R}X)=\text{ev}.\end{eqnarray}$$
Let us check that there is a morphism
![]() $m_{R^{\prime }}^{R}$
which turns the following diagram commutative
$m_{R^{\prime }}^{R}$
which turns the following diagram commutative
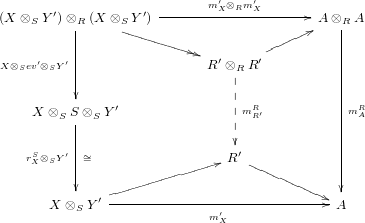
On the one hand we have
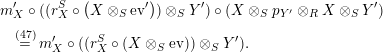 $$\begin{eqnarray}\displaystyle & & \displaystyle m_{X}^{\prime }\circ ((r_{X}^{S}\circ \left(X\otimes _{S}\text{ev}^{\prime }\right))\otimes _{S}Y^{\prime })\circ (X\otimes _{S}p_{Y^{\prime }}\otimes _{R}X\otimes _{S}Y^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad \overset{(47)}{=}m_{X}^{\prime }\circ ((r_{X}^{S}\circ \left(X\otimes _{S}\text{ev}\right))\otimes _{S}Y^{\prime }).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle m_{X}^{\prime }\circ ((r_{X}^{S}\circ \left(X\otimes _{S}\text{ev}^{\prime }\right))\otimes _{S}Y^{\prime })\circ (X\otimes _{S}p_{Y^{\prime }}\otimes _{R}X\otimes _{S}Y^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad \overset{(47)}{=}m_{X}^{\prime }\circ ((r_{X}^{S}\circ \left(X\otimes _{S}\text{ev}\right))\otimes _{S}Y^{\prime }).\nonumber\end{eqnarray}$$
Since
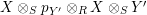 $X\otimes _{S}p_{Y^{\prime }}\otimes _{R}X\otimes _{S}Y^{\prime }$
is an epimorphism, it suffice to check that
$X\otimes _{S}p_{Y^{\prime }}\otimes _{R}X\otimes _{S}Y^{\prime }$
is an epimorphism, it suffice to check that
 $$\begin{eqnarray}\displaystyle & & \displaystyle m_{X}^{\prime }\circ ((r_{X}^{S}\circ \left(X\otimes _{S}\text{ev}\right))\otimes _{S}Y^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad =m_{A}^{R}\circ (m_{X}^{\prime }\otimes _{R}m_{X}^{\prime })\circ \left(X\otimes _{S}p_{Y^{\prime }}\otimes _{R}X\otimes _{S}Y^{\prime }\right)\!,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle m_{X}^{\prime }\circ ((r_{X}^{S}\circ \left(X\otimes _{S}\text{ev}\right))\otimes _{S}Y^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad =m_{A}^{R}\circ (m_{X}^{\prime }\otimes _{R}m_{X}^{\prime })\circ \left(X\otimes _{S}p_{Y^{\prime }}\otimes _{R}X\otimes _{S}Y^{\prime }\right)\!,\nonumber\end{eqnarray}$$
which follows from definitions by using equation (A2). From this, one proves that
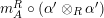 $m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\right)$
factors through a map
$m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\right)$
factors through a map
![]() $m_{R^{\prime }}^{R}$
(
$m_{R^{\prime }}^{R}$
(
![]() $R^{\prime }$
is a kernel) such that
$R^{\prime }$
is a kernel) such that
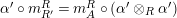 $\unicode[STIX]{x1D6FC}^{\prime }\circ m_{R^{\prime }}^{R}=m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\right)$
. We have
$\unicode[STIX]{x1D6FC}^{\prime }\circ m_{R^{\prime }}^{R}=m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\right)$
. We have
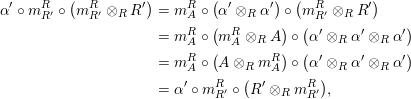 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}^{\prime }\circ m_{R^{\prime }}^{R}\circ \left(m_{R^{\prime }}^{R}\otimes _{R}R^{\prime }\right) & = & \displaystyle m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\right)\circ \left(m_{R^{\prime }}^{R}\otimes _{R}R^{\prime }\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(m_{A}^{R}\otimes _{R}A\right)\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(A\otimes _{R}m_{A}^{R}\right)\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\right)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FC}^{\prime }\circ m_{R^{\prime }}^{R}\circ \left(R^{\prime }\otimes _{R}m_{R^{\prime }}^{R}\right)\!,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}^{\prime }\circ m_{R^{\prime }}^{R}\circ \left(m_{R^{\prime }}^{R}\otimes _{R}R^{\prime }\right) & = & \displaystyle m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\right)\circ \left(m_{R^{\prime }}^{R}\otimes _{R}R^{\prime }\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(m_{A}^{R}\otimes _{R}A\right)\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(A\otimes _{R}m_{A}^{R}\right)\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\right)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FC}^{\prime }\circ m_{R^{\prime }}^{R}\circ \left(R^{\prime }\otimes _{R}m_{R^{\prime }}^{R}\right)\!,\nonumber\end{eqnarray}$$
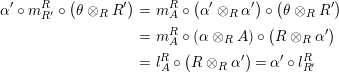 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}^{\prime }\circ m_{R^{\prime }}^{R}\circ \left(\unicode[STIX]{x1D703}\otimes _{R}R^{\prime }\right) & = & \displaystyle m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\right)\circ \left(\unicode[STIX]{x1D703}\otimes _{R}R^{\prime }\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FC}\otimes _{R}A\right)\circ \left(R\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\right)\nonumber\\ \displaystyle & = & \displaystyle l_{A}^{R}\circ \left(R\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\right)=\unicode[STIX]{x1D6FC}^{\prime }\circ l_{R^{\prime }}^{R}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC}^{\prime }\circ m_{R^{\prime }}^{R}\circ \left(\unicode[STIX]{x1D703}\otimes _{R}R^{\prime }\right) & = & \displaystyle m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\right)\circ \left(\unicode[STIX]{x1D703}\otimes _{R}R^{\prime }\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FC}\otimes _{R}A\right)\circ \left(R\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\right)\nonumber\\ \displaystyle & = & \displaystyle l_{A}^{R}\circ \left(R\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\right)=\unicode[STIX]{x1D6FC}^{\prime }\circ l_{R^{\prime }}^{R}\nonumber\end{eqnarray}$$
and hence
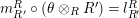 $m_{R^{\prime }}^{R}\circ \left(\unicode[STIX]{x1D703}\otimes _{R}R^{\prime }\right)=l_{R^{\prime }}^{R}$
. Similarly
$m_{R^{\prime }}^{R}\circ \left(\unicode[STIX]{x1D703}\otimes _{R}R^{\prime }\right)=l_{R^{\prime }}^{R}$
. Similarly
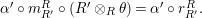 $\unicode[STIX]{x1D6FC}^{\prime }\circ m_{R^{\prime }}^{R}\circ \left(R^{\prime }\otimes _{R}\unicode[STIX]{x1D703}\right)=\unicode[STIX]{x1D6FC}^{\prime }\circ r_{R^{\prime }}^{R}.$
Since
$\unicode[STIX]{x1D6FC}^{\prime }\circ m_{R^{\prime }}^{R}\circ \left(R^{\prime }\otimes _{R}\unicode[STIX]{x1D703}\right)=\unicode[STIX]{x1D6FC}^{\prime }\circ r_{R^{\prime }}^{R}.$
Since
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
is a monomorphism we conclude that
$\unicode[STIX]{x1D6FC}^{\prime }$
is a monomorphism we conclude that
![]() $m_{R^{\prime }}^{R}$
is associative and unitary.
$m_{R^{\prime }}^{R}$
is associative and unitary.
(2) We have to prove that
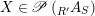 $X\in \mathscr{P}\left(\text{}_{R^{\prime }}A_{S}\right)$
. First, let
$X\in \mathscr{P}\left(\text{}_{R^{\prime }}A_{S}\right)$
. First, let
![]() $\left(K,i_{K}\right)$
be the kernel of
$\left(K,i_{K}\right)$
be the kernel of
![]() $m_{X}^{\prime }$
. By definition of
$m_{X}^{\prime }$
. By definition of
![]() $m_{X}$
we have the exact sequence
$m_{X}$
we have the exact sequence
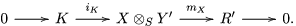
and hence
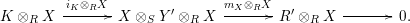
Now, using the unitality of
![]() $m_{A}^{S}$
, the definitions of the morphisms involved and equation (A2), we get
$m_{A}^{S}$
, the definitions of the morphisms involved and equation (A2), we get
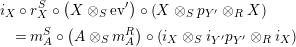 $$\begin{eqnarray}\displaystyle & & \displaystyle i_{X}\circ r_{X}^{S}\circ \left(X\otimes _{S}\text{ev}^{\prime }\right)\circ \left(X\otimes _{S}p_{Y^{\prime }}\otimes _{R}X\right)\nonumber\\ \displaystyle & & \displaystyle \quad =m_{A}^{S}\circ \left(A\otimes _{S}m_{A}^{R}\right)\circ \left(i_{X}\otimes _{S}i_{Y^{\prime }}p_{Y^{\prime }}\otimes _{R}i_{X}\right)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle i_{X}\circ r_{X}^{S}\circ \left(X\otimes _{S}\text{ev}^{\prime }\right)\circ \left(X\otimes _{S}p_{Y^{\prime }}\otimes _{R}X\right)\nonumber\\ \displaystyle & & \displaystyle \quad =m_{A}^{S}\circ \left(A\otimes _{S}m_{A}^{R}\right)\circ \left(i_{X}\otimes _{S}i_{Y^{\prime }}p_{Y^{\prime }}\otimes _{R}i_{X}\right)\nonumber\end{eqnarray}$$
so that
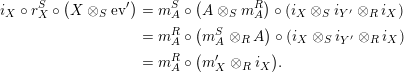 $$\begin{eqnarray}\displaystyle i_{X}\circ r_{X}^{S}\circ \left(X\otimes _{S}\text{ev}^{\prime }\right) & = & \displaystyle m_{A}^{S}\circ \left(A\otimes _{S}m_{A}^{R}\right)\circ \left(i_{X}\otimes _{S}i_{Y^{\prime }}\otimes _{R}i_{X}\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(m_{A}^{S}\otimes _{R}A\right)\circ \left(i_{X}\otimes _{S}i_{Y^{\prime }}\otimes _{R}i_{X}\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(m_{X}^{\prime }\otimes _{R}i_{X}\right)\!.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle i_{X}\circ r_{X}^{S}\circ \left(X\otimes _{S}\text{ev}^{\prime }\right) & = & \displaystyle m_{A}^{S}\circ \left(A\otimes _{S}m_{A}^{R}\right)\circ \left(i_{X}\otimes _{S}i_{Y^{\prime }}\otimes _{R}i_{X}\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(m_{A}^{S}\otimes _{R}A\right)\circ \left(i_{X}\otimes _{S}i_{Y^{\prime }}\otimes _{R}i_{X}\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(m_{X}^{\prime }\otimes _{R}i_{X}\right)\!.\nonumber\end{eqnarray}$$
Hence
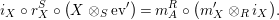 $$\begin{eqnarray}i_{X}\circ r_{X}^{S}\circ \left(X\otimes _{S}\text{ev}^{\prime }\right)=m_{A}^{R}\circ \left(m_{X}^{\prime }\otimes _{R}i_{X}\right)\!.\end{eqnarray}$$
$$\begin{eqnarray}i_{X}\circ r_{X}^{S}\circ \left(X\otimes _{S}\text{ev}^{\prime }\right)=m_{A}^{R}\circ \left(m_{X}^{\prime }\otimes _{R}i_{X}\right)\!.\end{eqnarray}$$
Therefore,
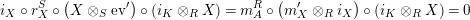 $$\begin{eqnarray}i_{X}\circ r_{X}^{S}\circ \left(X\otimes _{S}\text{ev}^{\prime }\right)\circ \left(i_{K}\otimes _{R}X\right)=m_{A}^{R}\circ \left(m_{X}^{\prime }\otimes _{R}i_{X}\right)\circ \left(i_{K}\otimes _{R}X\right)=0\end{eqnarray}$$
$$\begin{eqnarray}i_{X}\circ r_{X}^{S}\circ \left(X\otimes _{S}\text{ev}^{\prime }\right)\circ \left(i_{K}\otimes _{R}X\right)=m_{A}^{R}\circ \left(m_{X}^{\prime }\otimes _{R}i_{X}\right)\circ \left(i_{K}\otimes _{R}X\right)=0\end{eqnarray}$$
and so
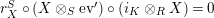 $r_{X}^{S}\circ \left(X\otimes _{S}\text{ev}^{\prime }\right)\circ \left(i_{K}\otimes _{R}X\right)=0$
. By exactness of the last sequence displayed above, there is a morphism
$r_{X}^{S}\circ \left(X\otimes _{S}\text{ev}^{\prime }\right)\circ \left(i_{K}\otimes _{R}X\right)=0$
. By exactness of the last sequence displayed above, there is a morphism
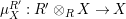 $\unicode[STIX]{x1D707}_{X}^{R^{\prime }}:R^{\prime }\otimes _{R}X\rightarrow X$
such that
$\unicode[STIX]{x1D707}_{X}^{R^{\prime }}:R^{\prime }\otimes _{R}X\rightarrow X$
such that
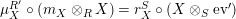 $\unicode[STIX]{x1D707}_{X}^{R^{\prime }}\circ \left(m_{X}\otimes _{R}X\right)=r_{X}^{S}\circ \left(X\otimes _{S}\text{ev}^{\prime }\right)$
. Let us check it is unitary. First, we have
$\unicode[STIX]{x1D707}_{X}^{R^{\prime }}\circ \left(m_{X}\otimes _{R}X\right)=r_{X}^{S}\circ \left(X\otimes _{S}\text{ev}^{\prime }\right)$
. Let us check it is unitary. First, we have
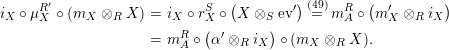 $$\begin{eqnarray}\displaystyle i_{X}\circ \unicode[STIX]{x1D707}_{X}^{R^{\prime }}\circ \left(m_{X}\otimes _{R}X\right) & = & \displaystyle i_{X}\circ r_{X}^{S}\circ \left(X\otimes _{S}\text{ev}^{\prime }\right)\overset{(49)}{=}m_{A}^{R}\circ \left(m_{X}^{\prime }\otimes _{R}i_{X}\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}i_{X}\right)\circ \left(m_{X}\otimes _{R}X\right)\!.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle i_{X}\circ \unicode[STIX]{x1D707}_{X}^{R^{\prime }}\circ \left(m_{X}\otimes _{R}X\right) & = & \displaystyle i_{X}\circ r_{X}^{S}\circ \left(X\otimes _{S}\text{ev}^{\prime }\right)\overset{(49)}{=}m_{A}^{R}\circ \left(m_{X}^{\prime }\otimes _{R}i_{X}\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}i_{X}\right)\circ \left(m_{X}\otimes _{R}X\right)\!.\nonumber\end{eqnarray}$$
Since
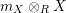 $m_{X}\otimes _{R}X$
is an epimorphism, we obtain
$m_{X}\otimes _{R}X$
is an epimorphism, we obtain
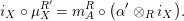 $$\begin{eqnarray}i_{X}\circ \unicode[STIX]{x1D707}_{X}^{R^{\prime }}=m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}i_{X}\right)\!.\end{eqnarray}$$
$$\begin{eqnarray}i_{X}\circ \unicode[STIX]{x1D707}_{X}^{R^{\prime }}=m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}i_{X}\right)\!.\end{eqnarray}$$
We get
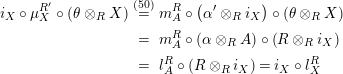 $$\begin{eqnarray}\displaystyle i_{X}\circ \unicode[STIX]{x1D707}_{X}^{R^{\prime }}\circ \left(\unicode[STIX]{x1D703}\otimes _{R}X\right) & \overset{(50)}{=} & \displaystyle m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}i_{X}\right)\circ \left(\unicode[STIX]{x1D703}\otimes _{R}X\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FC}\otimes _{R}A\right)\circ \left(R\otimes _{R}i_{X}\right)\nonumber\\ \displaystyle & = & \displaystyle l_{A}^{R}\circ \left(R\otimes _{R}i_{X}\right)=i_{X}\circ l_{X}^{R}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle i_{X}\circ \unicode[STIX]{x1D707}_{X}^{R^{\prime }}\circ \left(\unicode[STIX]{x1D703}\otimes _{R}X\right) & \overset{(50)}{=} & \displaystyle m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}i_{X}\right)\circ \left(\unicode[STIX]{x1D703}\otimes _{R}X\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FC}\otimes _{R}A\right)\circ \left(R\otimes _{R}i_{X}\right)\nonumber\\ \displaystyle & = & \displaystyle l_{A}^{R}\circ \left(R\otimes _{R}i_{X}\right)=i_{X}\circ l_{X}^{R}\nonumber\end{eqnarray}$$
and hence
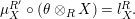 $\unicode[STIX]{x1D707}_{X}^{R^{\prime }}\circ \left(\unicode[STIX]{x1D703}\otimes _{R}X\right)=l_{X}^{R}.$
Let us check that
$\unicode[STIX]{x1D707}_{X}^{R^{\prime }}\circ \left(\unicode[STIX]{x1D703}\otimes _{R}X\right)=l_{X}^{R}.$
Let us check that
![]() $\unicode[STIX]{x1D707}_{X}^{R^{\prime }}$
is associative:
$\unicode[STIX]{x1D707}_{X}^{R^{\prime }}$
is associative:
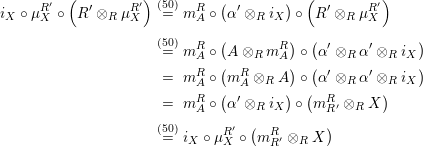 $$\begin{eqnarray}\displaystyle i_{X}\circ \unicode[STIX]{x1D707}_{X}^{R^{\prime }}\circ \left(R^{\prime }\otimes _{R}\unicode[STIX]{x1D707}_{X}^{R^{\prime }}\right) & \overset{(50)}{=} & \displaystyle m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}i_{X}\right)\circ \left(R^{\prime }\otimes _{R}\unicode[STIX]{x1D707}_{X}^{R^{\prime }}\right)\nonumber\\ \displaystyle & \overset{(50)}{=} & \displaystyle m_{A}^{R}\circ \left(A\otimes _{R}m_{A}^{R}\right)\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}i_{X}\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(m_{A}^{R}\otimes _{R}A\right)\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}i_{X}\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}i_{X}\right)\circ \left(m_{R^{\prime }}^{R}\otimes _{R}X\right)\nonumber\\ \displaystyle & \overset{(50)}{=} & \displaystyle i_{X}\circ \unicode[STIX]{x1D707}_{X}^{R^{\prime }}\circ \left(m_{R^{\prime }}^{R}\otimes _{R}X\right)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle i_{X}\circ \unicode[STIX]{x1D707}_{X}^{R^{\prime }}\circ \left(R^{\prime }\otimes _{R}\unicode[STIX]{x1D707}_{X}^{R^{\prime }}\right) & \overset{(50)}{=} & \displaystyle m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}i_{X}\right)\circ \left(R^{\prime }\otimes _{R}\unicode[STIX]{x1D707}_{X}^{R^{\prime }}\right)\nonumber\\ \displaystyle & \overset{(50)}{=} & \displaystyle m_{A}^{R}\circ \left(A\otimes _{R}m_{A}^{R}\right)\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}i_{X}\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(m_{A}^{R}\otimes _{R}A\right)\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}i_{X}\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FC}^{\prime }\otimes _{R}i_{X}\right)\circ \left(m_{R^{\prime }}^{R}\otimes _{R}X\right)\nonumber\\ \displaystyle & \overset{(50)}{=} & \displaystyle i_{X}\circ \unicode[STIX]{x1D707}_{X}^{R^{\prime }}\circ \left(m_{R^{\prime }}^{R}\otimes _{R}X\right)\nonumber\end{eqnarray}$$
so that
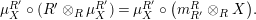 $\unicode[STIX]{x1D707}_{X}^{R^{\prime }}\circ (R^{\prime }\otimes _{R}\unicode[STIX]{x1D707}_{X}^{R^{\prime }})=\unicode[STIX]{x1D707}_{X}^{R^{\prime }}\circ \left(m_{R^{\prime }}^{R}\otimes _{R}X\right)\!.$
The properties we proved imply that
$\unicode[STIX]{x1D707}_{X}^{R^{\prime }}\circ (R^{\prime }\otimes _{R}\unicode[STIX]{x1D707}_{X}^{R^{\prime }})=\unicode[STIX]{x1D707}_{X}^{R^{\prime }}\circ \left(m_{R^{\prime }}^{R}\otimes _{R}X\right)\!.$
The properties we proved imply that
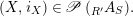 $\left(X,i_{X}\right)\in \mathscr{P}\left(\text{}_{R^{\prime }}A_{S}\right)\!.$
$\left(X,i_{X}\right)\in \mathscr{P}\left(\text{}_{R^{\prime }}A_{S}\right)\!.$
Next aim is to check that
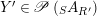 $Y^{\prime }\in \mathscr{P}\left(\text{}_{S}A_{R^{\prime }}\right)$
and it is a right inverse of
$Y^{\prime }\in \mathscr{P}\left(\text{}_{S}A_{R^{\prime }}\right)$
and it is a right inverse of
![]() $X$
. We need a morphism
$X$
. We need a morphism
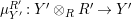 $\unicode[STIX]{x1D707}_{Y^{\prime }}^{R^{\prime }}:Y^{\prime }\otimes _{R}R^{\prime }\rightarrow Y^{\prime }$
. Consider again the exact sequence (A 4) and the induced one
$\unicode[STIX]{x1D707}_{Y^{\prime }}^{R^{\prime }}:Y^{\prime }\otimes _{R}R^{\prime }\rightarrow Y^{\prime }$
. Consider again the exact sequence (A 4) and the induced one
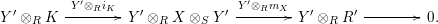
As before using the unitality of
![]() $m_{A}^{S}$
, the definitions of the morphisms involved and equation (A2), we get
$m_{A}^{S}$
, the definitions of the morphisms involved and equation (A2), we get
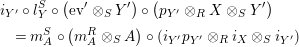 $$\begin{eqnarray}\displaystyle & & \displaystyle i_{Y^{\prime }}\circ l_{Y}^{S}\circ \left(\text{ev}^{\prime }\otimes _{S}Y^{\prime }\right)\circ \left(p_{Y^{\prime }}\otimes _{R}X\otimes _{S}Y^{\prime }\right)\nonumber\\ \displaystyle & & \displaystyle \quad =m_{A}^{S}\circ \left(m_{A}^{R}\otimes _{S}A\right)\circ \left(i_{Y^{\prime }}p_{Y^{\prime }}\otimes _{R}i_{X}\otimes _{S}i_{Y^{\prime }}\right)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle i_{Y^{\prime }}\circ l_{Y}^{S}\circ \left(\text{ev}^{\prime }\otimes _{S}Y^{\prime }\right)\circ \left(p_{Y^{\prime }}\otimes _{R}X\otimes _{S}Y^{\prime }\right)\nonumber\\ \displaystyle & & \displaystyle \quad =m_{A}^{S}\circ \left(m_{A}^{R}\otimes _{S}A\right)\circ \left(i_{Y^{\prime }}p_{Y^{\prime }}\otimes _{R}i_{X}\otimes _{S}i_{Y^{\prime }}\right)\nonumber\end{eqnarray}$$
and hence
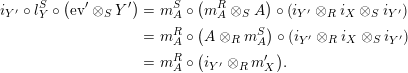 $$\begin{eqnarray}\displaystyle i_{Y^{\prime }}\circ l_{Y}^{S}\circ \left(\text{ev}^{\prime }\otimes _{S}Y^{\prime }\right) & = & \displaystyle m_{A}^{S}\circ \left(m_{A}^{R}\otimes _{S}A\right)\circ \left(i_{Y^{\prime }}\otimes _{R}i_{X}\otimes _{S}i_{Y^{\prime }}\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(A\otimes _{R}m_{A}^{S}\right)\circ \left(i_{Y^{\prime }}\otimes _{R}i_{X}\otimes _{S}i_{Y^{\prime }}\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(i_{Y^{\prime }}\otimes _{R}m_{X}^{\prime }\right)\!.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle i_{Y^{\prime }}\circ l_{Y}^{S}\circ \left(\text{ev}^{\prime }\otimes _{S}Y^{\prime }\right) & = & \displaystyle m_{A}^{S}\circ \left(m_{A}^{R}\otimes _{S}A\right)\circ \left(i_{Y^{\prime }}\otimes _{R}i_{X}\otimes _{S}i_{Y^{\prime }}\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(A\otimes _{R}m_{A}^{S}\right)\circ \left(i_{Y^{\prime }}\otimes _{R}i_{X}\otimes _{S}i_{Y^{\prime }}\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(i_{Y^{\prime }}\otimes _{R}m_{X}^{\prime }\right)\!.\nonumber\end{eqnarray}$$
Thus we get
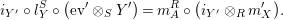 $$\begin{eqnarray}\displaystyle i_{Y^{\prime }}\circ l_{Y}^{S}\circ \left(\text{ev}^{\prime }\otimes _{S}Y^{\prime }\right)=m_{A}^{R}\circ \left(i_{Y^{\prime }}\otimes _{R}m_{X}^{\prime }\right)\!. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle i_{Y^{\prime }}\circ l_{Y}^{S}\circ \left(\text{ev}^{\prime }\otimes _{S}Y^{\prime }\right)=m_{A}^{R}\circ \left(i_{Y^{\prime }}\otimes _{R}m_{X}^{\prime }\right)\!. & & \displaystyle \nonumber\end{eqnarray}$$
Coming back to the exact sequence, we compute
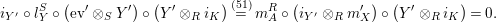 $$\begin{eqnarray}i_{Y^{\prime }}\circ l_{Y}^{S}\circ \left(\text{ev}^{\prime }\otimes _{S}Y^{\prime }\right)\circ \left(Y^{\prime }\otimes _{R}i_{K}\right)\overset{(51)}{=}m_{A}^{R}\circ \left(i_{Y^{\prime }}\otimes _{R}m_{X}^{\prime }\right)\circ \left(Y^{\prime }\otimes _{R}i_{K}\right)=0.\end{eqnarray}$$
$$\begin{eqnarray}i_{Y^{\prime }}\circ l_{Y}^{S}\circ \left(\text{ev}^{\prime }\otimes _{S}Y^{\prime }\right)\circ \left(Y^{\prime }\otimes _{R}i_{K}\right)\overset{(51)}{=}m_{A}^{R}\circ \left(i_{Y^{\prime }}\otimes _{R}m_{X}^{\prime }\right)\circ \left(Y^{\prime }\otimes _{R}i_{K}\right)=0.\end{eqnarray}$$
Therefore, there is a unique morphism
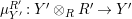 $\unicode[STIX]{x1D707}_{Y^{\prime }}^{R^{\prime }}:Y^{\prime }\otimes _{R}R^{\prime }\rightarrow Y^{\prime }$
such that
$\unicode[STIX]{x1D707}_{Y^{\prime }}^{R^{\prime }}:Y^{\prime }\otimes _{R}R^{\prime }\rightarrow Y^{\prime }$
such that
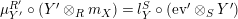 $\unicode[STIX]{x1D707}_{Y^{\prime }}^{R^{\prime }}\circ \left(Y^{\prime }\otimes _{R}m_{X}\right)=l_{Y}^{S}\circ \left(\text{ev}^{\prime }\otimes _{S}Y^{\prime }\right)$
. Using this equality we compute
$\unicode[STIX]{x1D707}_{Y^{\prime }}^{R^{\prime }}\circ \left(Y^{\prime }\otimes _{R}m_{X}\right)=l_{Y}^{S}\circ \left(\text{ev}^{\prime }\otimes _{S}Y^{\prime }\right)$
. Using this equality we compute
 $$\begin{eqnarray}\displaystyle i_{Y^{\prime }}\circ \unicode[STIX]{x1D707}_{Y^{\prime }}^{R^{\prime }}\circ \left(Y^{\prime }\otimes _{R}m_{X}\right) & = & \displaystyle i_{Y^{\prime }}\circ l_{Y}^{S}\circ \left(\text{ev}^{\prime }\otimes _{S}Y^{\prime }\right)\overset{(51)}{=}m_{A}^{R}\circ \left(i_{Y^{\prime }}\otimes _{R}m_{X}^{\prime }\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(i_{Y^{\prime }}\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\right)\circ \left(Y^{\prime }\otimes _{R}m_{X}\right)\!.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle i_{Y^{\prime }}\circ \unicode[STIX]{x1D707}_{Y^{\prime }}^{R^{\prime }}\circ \left(Y^{\prime }\otimes _{R}m_{X}\right) & = & \displaystyle i_{Y^{\prime }}\circ l_{Y}^{S}\circ \left(\text{ev}^{\prime }\otimes _{S}Y^{\prime }\right)\overset{(51)}{=}m_{A}^{R}\circ \left(i_{Y^{\prime }}\otimes _{R}m_{X}^{\prime }\right)\nonumber\\ \displaystyle & = & \displaystyle m_{A}^{R}\circ \left(i_{Y^{\prime }}\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\right)\circ \left(Y^{\prime }\otimes _{R}m_{X}\right)\!.\nonumber\end{eqnarray}$$
Since
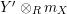 $Y^{\prime }\otimes _{R}m_{X}$
is an epimorphism, we obtain
$Y^{\prime }\otimes _{R}m_{X}$
is an epimorphism, we obtain
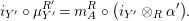 $$\begin{eqnarray}i_{Y^{\prime }}\circ \unicode[STIX]{x1D707}_{Y^{\prime }}^{R^{\prime }}=m_{A}^{R}\circ \left(i_{Y^{\prime }}\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\right)\!.\end{eqnarray}$$
$$\begin{eqnarray}i_{Y^{\prime }}\circ \unicode[STIX]{x1D707}_{Y^{\prime }}^{R^{\prime }}=m_{A}^{R}\circ \left(i_{Y^{\prime }}\otimes _{R}\unicode[STIX]{x1D6FC}^{\prime }\right)\!.\end{eqnarray}$$
Using this formula, as above, one proves that
![]() $\unicode[STIX]{x1D707}_{Y^{\prime }}^{R^{\prime }}$
is unitary and associative and hence
$\unicode[STIX]{x1D707}_{Y^{\prime }}^{R^{\prime }}$
is unitary and associative and hence
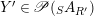 $Y^{\prime }\in \mathscr{P}(\text{}_{S}A_{R^{\prime }})$
.
$Y^{\prime }\in \mathscr{P}(\text{}_{S}A_{R^{\prime }})$
.
Let us check that
![]() $Y^{\prime }$
is a right inverse for
$Y^{\prime }$
is a right inverse for
![]() $X$
. Consider the coequalizer
$X$
. Consider the coequalizer
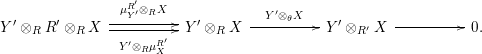
We have
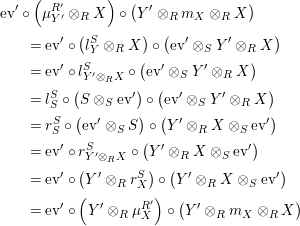 $$\begin{eqnarray}\displaystyle & & \displaystyle \text{ev}^{\prime }\circ \left(\unicode[STIX]{x1D707}_{Y^{\prime }}^{R^{\prime }}\otimes _{R}X\right)\circ \left(Y^{\prime }\otimes _{R}m_{X}\otimes _{R}X\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =\text{ev}^{\prime }\circ \left(l_{Y}^{S}\otimes _{R}X\right)\circ \left(\text{ev}^{\prime }\otimes _{S}Y^{\prime }\otimes _{R}X\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =\text{ev}^{\prime }\circ l_{Y^{\prime }\otimes _{R}X}^{S}\circ \left(\text{ev}^{\prime }\otimes _{S}Y^{\prime }\otimes _{R}X\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =l_{S}^{S}\circ \left(S\otimes _{S}\text{ev}^{\prime }\right)\circ \left(\text{ev}^{\prime }\otimes _{S}Y^{\prime }\otimes _{R}X\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =r_{S}^{S}\circ \left(\text{ev}^{\prime }\otimes _{S}S\right)\circ \left(Y^{\prime }\otimes _{R}X\otimes _{S}\text{ev}^{\prime }\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =\text{ev}^{\prime }\circ r_{Y^{\prime }\otimes _{R}X}^{S}\circ \left(Y^{\prime }\otimes _{R}X\otimes _{S}\text{ev}^{\prime }\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =\text{ev}^{\prime }\circ \left(Y^{\prime }\otimes _{R}r_{X}^{S}\right)\circ \left(Y^{\prime }\otimes _{R}X\otimes _{S}\text{ev}^{\prime }\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =\text{ev}^{\prime }\circ \left(Y^{\prime }\otimes _{R}\unicode[STIX]{x1D707}_{X}^{R^{\prime }}\right)\circ \left(Y^{\prime }\otimes _{R}m_{X}\otimes _{R}X\right)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{ev}^{\prime }\circ \left(\unicode[STIX]{x1D707}_{Y^{\prime }}^{R^{\prime }}\otimes _{R}X\right)\circ \left(Y^{\prime }\otimes _{R}m_{X}\otimes _{R}X\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =\text{ev}^{\prime }\circ \left(l_{Y}^{S}\otimes _{R}X\right)\circ \left(\text{ev}^{\prime }\otimes _{S}Y^{\prime }\otimes _{R}X\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =\text{ev}^{\prime }\circ l_{Y^{\prime }\otimes _{R}X}^{S}\circ \left(\text{ev}^{\prime }\otimes _{S}Y^{\prime }\otimes _{R}X\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =l_{S}^{S}\circ \left(S\otimes _{S}\text{ev}^{\prime }\right)\circ \left(\text{ev}^{\prime }\otimes _{S}Y^{\prime }\otimes _{R}X\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =r_{S}^{S}\circ \left(\text{ev}^{\prime }\otimes _{S}S\right)\circ \left(Y^{\prime }\otimes _{R}X\otimes _{S}\text{ev}^{\prime }\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =\text{ev}^{\prime }\circ r_{Y^{\prime }\otimes _{R}X}^{S}\circ \left(Y^{\prime }\otimes _{R}X\otimes _{S}\text{ev}^{\prime }\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =\text{ev}^{\prime }\circ \left(Y^{\prime }\otimes _{R}r_{X}^{S}\right)\circ \left(Y^{\prime }\otimes _{R}X\otimes _{S}\text{ev}^{\prime }\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =\text{ev}^{\prime }\circ \left(Y^{\prime }\otimes _{R}\unicode[STIX]{x1D707}_{X}^{R^{\prime }}\right)\circ \left(Y^{\prime }\otimes _{R}m_{X}\otimes _{R}X\right)\nonumber\end{eqnarray}$$
so that
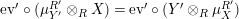 $\text{ev}^{\prime }\circ (\unicode[STIX]{x1D707}_{Y^{\prime }}^{R^{\prime }}\otimes _{R}X)=\text{ev}^{\prime }\circ (Y^{\prime }\otimes _{R}\unicode[STIX]{x1D707}_{X}^{R^{\prime }})$
and hence there exists
$\text{ev}^{\prime }\circ (\unicode[STIX]{x1D707}_{Y^{\prime }}^{R^{\prime }}\otimes _{R}X)=\text{ev}^{\prime }\circ (Y^{\prime }\otimes _{R}\unicode[STIX]{x1D707}_{X}^{R^{\prime }})$
and hence there exists
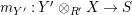 $m_{Y^{\prime }}:Y^{\prime }\otimes _{R^{\prime }}X\rightarrow S$
such that
$m_{Y^{\prime }}:Y^{\prime }\otimes _{R^{\prime }}X\rightarrow S$
such that
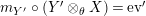 $m_{Y^{\prime }}\circ (Y^{\prime }\otimes _{\unicode[STIX]{x1D703}}X)=\text{ev}^{\prime }$
. Therefore,
$m_{Y^{\prime }}\circ (Y^{\prime }\otimes _{\unicode[STIX]{x1D703}}X)=\text{ev}^{\prime }$
. Therefore,
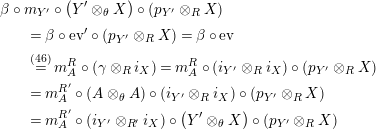 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FD}\circ m_{Y^{\prime }}\circ \left(Y^{\prime }\otimes _{\unicode[STIX]{x1D703}}X\right)\circ \left(p_{Y^{\prime }}\otimes _{R}X\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =\unicode[STIX]{x1D6FD}\circ \text{ev}^{\prime }\circ \left(p_{Y^{\prime }}\otimes _{R}X\right)=\unicode[STIX]{x1D6FD}\circ \text{ev}\nonumber\\ \displaystyle & & \displaystyle \qquad \overset{(46)}{=}m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FE}\otimes _{R}i_{X}\right)=m_{A}^{R}\circ \left(i_{Y^{\prime }}\otimes _{R}i_{X}\right)\circ \left(p_{Y^{\prime }}\otimes _{R}X\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =m_{A}^{R^{\prime }}\circ \left(A\otimes _{\unicode[STIX]{x1D703}}A\right)\circ \left(i_{Y^{\prime }}\otimes _{R}i_{X}\right)\circ \left(p_{Y^{\prime }}\otimes _{R}X\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =m_{A}^{R^{\prime }}\circ \left(i_{Y^{\prime }}\otimes _{R^{\prime }}i_{X}\right)\circ \left(Y^{\prime }\otimes _{\unicode[STIX]{x1D703}}X\right)\circ \left(p_{Y^{\prime }}\otimes _{R}X\right)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FD}\circ m_{Y^{\prime }}\circ \left(Y^{\prime }\otimes _{\unicode[STIX]{x1D703}}X\right)\circ \left(p_{Y^{\prime }}\otimes _{R}X\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =\unicode[STIX]{x1D6FD}\circ \text{ev}^{\prime }\circ \left(p_{Y^{\prime }}\otimes _{R}X\right)=\unicode[STIX]{x1D6FD}\circ \text{ev}\nonumber\\ \displaystyle & & \displaystyle \qquad \overset{(46)}{=}m_{A}^{R}\circ \left(\unicode[STIX]{x1D6FE}\otimes _{R}i_{X}\right)=m_{A}^{R}\circ \left(i_{Y^{\prime }}\otimes _{R}i_{X}\right)\circ \left(p_{Y^{\prime }}\otimes _{R}X\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =m_{A}^{R^{\prime }}\circ \left(A\otimes _{\unicode[STIX]{x1D703}}A\right)\circ \left(i_{Y^{\prime }}\otimes _{R}i_{X}\right)\circ \left(p_{Y^{\prime }}\otimes _{R}X\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =m_{A}^{R^{\prime }}\circ \left(i_{Y^{\prime }}\otimes _{R^{\prime }}i_{X}\right)\circ \left(Y^{\prime }\otimes _{\unicode[STIX]{x1D703}}X\right)\circ \left(p_{Y^{\prime }}\otimes _{R}X\right)\nonumber\end{eqnarray}$$
and hence
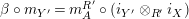 $\unicode[STIX]{x1D6FD}\circ m_{Y^{\prime }}=m_{A}^{R^{\prime }}\circ \left(i_{Y^{\prime }}\otimes _{R^{\prime }}i_{X}\right)$
. Moreover,
$\unicode[STIX]{x1D6FD}\circ m_{Y^{\prime }}=m_{A}^{R^{\prime }}\circ \left(i_{Y^{\prime }}\otimes _{R^{\prime }}i_{X}\right)$
. Moreover,
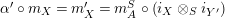 $\unicode[STIX]{x1D6FC}^{\prime }\circ m_{X}=m_{X}^{\prime }=m_{A}^{S}\circ \left(i_{X}\otimes _{S}i_{Y^{\prime }}\right)$
.
$\unicode[STIX]{x1D6FC}^{\prime }\circ m_{X}=m_{X}^{\prime }=m_{A}^{S}\circ \left(i_{X}\otimes _{S}i_{Y^{\prime }}\right)$
.
It remains to check that
![]() $m_{X}$
is an isomorphism. It is an epimorphism by construction. Since
$m_{X}$
is an isomorphism. It is an epimorphism by construction. Since
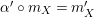 $\unicode[STIX]{x1D6FC}^{\prime }\circ m_{X}=m_{X}^{\prime }$
and
$\unicode[STIX]{x1D6FC}^{\prime }\circ m_{X}=m_{X}^{\prime }$
and
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
is a monomorphism by construction, we have that
$\unicode[STIX]{x1D6FC}^{\prime }$
is a monomorphism by construction, we have that
![]() $m_{X}$
is a monomorphism if and only if
$m_{X}$
is a monomorphism if and only if
![]() $m_{X}^{\prime }$
is. Now
$m_{X}^{\prime }$
is. Now
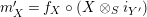 $m_{X}^{\prime }=f_{X}\circ \left(X\otimes _{S}i_{Y^{\prime }}\right)$
and
$m_{X}^{\prime }=f_{X}\circ \left(X\otimes _{S}i_{Y^{\prime }}\right)$
and
![]() $f_{X}$
is an isomorphism by assumption. Thus
$f_{X}$
is an isomorphism by assumption. Thus
![]() $m_{X}^{\prime }$
is a monomorphism if and only if
$m_{X}^{\prime }$
is a monomorphism if and only if
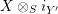 $X\otimes _{S}i_{Y^{\prime }}$
is a monomorphism. Since by Proposition 1.4, we know that the functor
$X\otimes _{S}i_{Y^{\prime }}$
is a monomorphism. Since by Proposition 1.4, we know that the functor
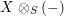 $X\otimes _{S}\left(-\right)$
is a right adjoint, hence
$X\otimes _{S}\left(-\right)$
is a right adjoint, hence
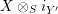 $X\otimes _{S}i_{Y^{\prime }}$
is a monomorphism. Thus
$X\otimes _{S}i_{Y^{\prime }}$
is a monomorphism. Thus
![]() $m_{X}$
is both an epimorphism and a monomorphism and hence it is an isomorphism, and this completes the proof.◻
$m_{X}$
is both an epimorphism and a monomorphism and hence it is an isomorphism, and this completes the proof.◻
Appendix B. Internals hom for modules and bimodules in monoidal categories
In this appendix we show the main steps to construct the internal homs functors which were implicitly used in Sections 4.2 and 4.3. To this aim, consider a symmetric monoidal abelian bicomplete category
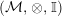 $({\mathcal{M}},\otimes _{},\mathbb{I})$
with right exact tensor products. Let
$({\mathcal{M}},\otimes _{},\mathbb{I})$
with right exact tensor products. Let
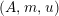 $(A,m,u)$
be a monoid in
$(A,m,u)$
be a monoid in
![]() ${\mathcal{M}}$
and denote by
${\mathcal{M}}$
and denote by
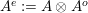 $A^{e}:=A\otimes _{}A^{o}$
its enveloping monoid, where
$A^{e}:=A\otimes _{}A^{o}$
its enveloping monoid, where
![]() $A^{o}$
is the opposite monoid. Assume that the functor
$A^{o}$
is the opposite monoid. Assume that the functor
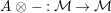 $A\otimes _{}-:{\mathcal{M}}\rightarrow {\mathcal{M}}$
has a right adjoint functor
$A\otimes _{}-:{\mathcal{M}}\rightarrow {\mathcal{M}}$
has a right adjoint functor
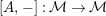 $[A,-]:{\mathcal{M}}\rightarrow {\mathcal{M}}$
with unit and counit
$[A,-]:{\mathcal{M}}\rightarrow {\mathcal{M}}$
with unit and counit
 $$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D700}}_{Y}^{A}:A\otimes _{}[A,Y]\longrightarrow Y\in {\mathcal{M}},\qquad \boldsymbol{\unicode[STIX]{x1D701}}_{X}^{A}:{\mathcal{M}}\ni X\longrightarrow [A,A\otimes _{}X].\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D700}}_{Y}^{A}:A\otimes _{}[A,Y]\longrightarrow Y\in {\mathcal{M}},\qquad \boldsymbol{\unicode[STIX]{x1D701}}_{X}^{A}:{\mathcal{M}}\ni X\longrightarrow [A,A\otimes _{}X].\end{eqnarray}$$
The functor
![]() $[A,-]$
is referred to as the left internal hom functor. It is clear that
$[A,-]$
is referred to as the left internal hom functor. It is clear that
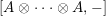 $[A\otimes _{}\cdots \otimes _{}A,-]$
also exists and so is in particular for
$[A\otimes _{}\cdots \otimes _{}A,-]$
also exists and so is in particular for
![]() $[A^{e},-]$
. We will use similar notation for the unit and counit of the corresponding adjunctions. Given any two objects
$[A^{e},-]$
. We will use similar notation for the unit and counit of the corresponding adjunctions. Given any two objects
![]() $X,Y$
in
$X,Y$
in
![]() ${\mathcal{M}}$
, one can define a morphism
${\mathcal{M}}$
, one can define a morphism
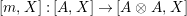 $[m,X]:[A,X]\rightarrow [A\otimes _{}A,X]$
which naturally turns commutative the following diagram:
$[m,X]:[A,X]\rightarrow [A\otimes _{}A,X]$
which naturally turns commutative the following diagram:
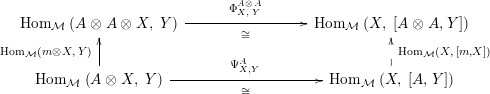
On the other hand, for any object
![]() $X$
in
$X$
in
![]() ${\mathcal{M}}$
we can define the following morphism:
${\mathcal{M}}$
we can define the following morphism:
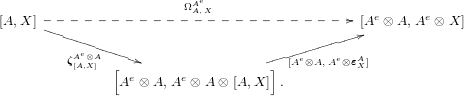
Clearly
![]() $\unicode[STIX]{x1D6FA}_{A,\,-}^{A^{e}}$
is a natural transformation as a composition of natural transformations.
$\unicode[STIX]{x1D6FA}_{A,\,-}^{A^{e}}$
is a natural transformation as a composition of natural transformations.
Now, for every left
![]() $A^{e}$
-module
$A^{e}$
-module
![]() $M$
(i.e., an
$M$
(i.e., an
![]() $A$
-bimodule) with action
$A$
-bimodule) with action
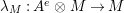 $\unicode[STIX]{x1D706}_{M}:A^{e}\otimes _{}M\rightarrow M$
we can consider the morphism
$\unicode[STIX]{x1D706}_{M}:A^{e}\otimes _{}M\rightarrow M$
we can consider the morphism
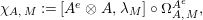 $\unicode[STIX]{x1D712}_{A,\,M}:=[A^{e}\otimes _{}A,\unicode[STIX]{x1D706}_{M}]\circ \unicode[STIX]{x1D6FA}_{A,\,M}^{A^{e}},$
and so the following equalizer:
$\unicode[STIX]{x1D712}_{A,\,M}:=[A^{e}\otimes _{}A,\unicode[STIX]{x1D706}_{M}]\circ \unicode[STIX]{x1D6FA}_{A,\,M}^{A^{e}},$
and so the following equalizer:
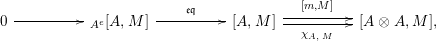
which leads to a natural monomorphism
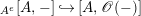 $\text{}_{A^{e}}[A,-]{\hookrightarrow}[A,\mathscr{O}(-)]$
, where
$\text{}_{A^{e}}[A,-]{\hookrightarrow}[A,\mathscr{O}(-)]$
, where
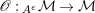 $\mathscr{O}:\text{}_{A^{e}}{\mathcal{M}}\rightarrow {\mathcal{M}}$
is the forgetful functor.
$\mathscr{O}:\text{}_{A^{e}}{\mathcal{M}}\rightarrow {\mathcal{M}}$
is the forgetful functor.
The following result whose proof is similar to that of [Reference Pareigis24, Proposition 3.10], summarize the relation between the functors constructed above. Indeed, its shows that, if the functor
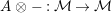 $A\otimes _{}-:{\mathcal{M}}\rightarrow {\mathcal{M}}$
has a right adjoint, then so is
$A\otimes _{}-:{\mathcal{M}}\rightarrow {\mathcal{M}}$
has a right adjoint, then so is
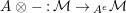 $A\otimes _{}-:{\mathcal{M}}\rightarrow \text{}_{A^{e}}{\mathcal{M}}$
.
$A\otimes _{}-:{\mathcal{M}}\rightarrow \text{}_{A^{e}}{\mathcal{M}}$
.
Proposition B.1. Let
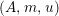 $(A,m,u)$
be a monoid in a symmetric monoidal abelian and bicomplete category
$(A,m,u)$
be a monoid in a symmetric monoidal abelian and bicomplete category
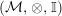 $({\mathcal{M}},\otimes _{},\mathbb{I})$
whose tensor products are right exact. Assume that there is an adjunction
$({\mathcal{M}},\otimes _{},\mathbb{I})$
whose tensor products are right exact. Assume that there is an adjunction
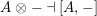 $A\otimes _{}-\dashv [A,-]$
, where
$A\otimes _{}-\dashv [A,-]$
, where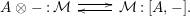 Then there is a commutative diagram of natural transformations:
Then there is a commutative diagram of natural transformations:

where the vertical arrows denote the canonical injections and
![]() $X\in {\mathcal{M}}$
,
$X\in {\mathcal{M}}$
,
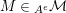 $M\in \text{}_{A^{e}}{\mathcal{M}}$
. That is, we have an adjunction
$M\in \text{}_{A^{e}}{\mathcal{M}}$
. That is, we have an adjunction
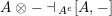 $A\otimes _{}-\dashv \text{}_{A^{e}}[A,-]$
, where
$A\otimes _{}-\dashv \text{}_{A^{e}}[A,-]$
, where