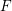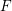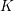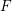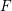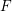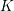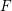1 Introduction
Throughout this manuscript we focus on
$F$
-pure standard graded algebras over a field
$K$
of positive characteristic
$p$
such that
$[K:K^{p}]<\infty$
. We say that
$R$
is
$F$
-pure if the Frobenius map
$F:R\rightarrow R$
splits. This property simplifies computations for cohomology groups and implies vanishing properties of these groups [Reference LyubeznikLyu06, Reference Singh and WaltherSW07, Reference MaMa13].
In this article, we show relations among three important classes of invariants that give information about the singularity of
$R$
: the
$a$
-invariants, the
$F$
-pure threshold, and the diagonal
$F$
-threshold.
We first consider the
$i$
th
$a$
-invariant of
$R,$
$a_{i}(R)$
, which is defined as the degree of the highest nonzero part of the
$i$
th local cohomology with support over
$\mathfrak{m}$
(see Section 2 for details). If
$d=\dim (R)$
, then
$a_{d}(R)$
is often just called the
$a$
-invariant of
$R$
, and it is a classical invariant, introduced by Goto and Watanabe [Reference Goto and WatanabeGW78]. For example, if
$R$
is Cohen–Macaulay,
$a_{d}(R)$
determines the highest shift in the resolution of
$R$
, and moreover the Hilbert function and the Hilbert polynomial of
$R$
coincide if and only if
$a_{d}(R)$
is negative.
We also consider the
$F$
-pure threshold with respect to
$\mathfrak{m}$
,
$\operatorname{fpt}(R)$
, which was introduced by Takagi and Watanabe [Reference Takagi and WatanabeTW04] (see Section 3 for details). This invariant is related to the log-canonical threshold and roughly speaking measures the asymptotic splitting order of
$\mathfrak{m}.$
Finally, we consider the diagonal
$F$
-threshold,
$c^{\mathfrak{m}}(R)$
. This invariant is, roughly speaking, the asymptotic Frobenius order of
$\mathfrak{m}$
, and it has several connections with tight closure theory [Reference Huneke, Mustaţă, Takagi and WatanabeHMTW08]. The
$F$
-threshold has also connections with the Hilbert–Samuel multiplicity [Reference Huneke, Mustaţă, Takagi and WatanabeHMTW08] and with the Hilbert Kunz multiplicity [Reference Núñez-Betancourt and SmirnovNBS14].
Hirose, Watanabe, and Yoshida [Reference Hirose, Watanabe and YoshidaHWY14] made the following conjecture that relates these invariants:
Conjecture A. [Reference Hirose, Watanabe and YoshidaHWY14]
Let
$R$
be a standard graded
$K$
-algebra with
$K$
an
$F$
-finite field and
$d=\dim (R)$
. Assume that
$R$
is strongly
$F$
-regular. Then,
-
(1)
$\operatorname{fpt}(R)\leqslant -a_{d}(R)\leqslant c^{\mathfrak{m}}(R)$
. -
(2)
$\operatorname{fpt}(R)=-a_{d}(R)$
if and only if
$R$
is Gorenstein.
This conjecture has been proved only for strongly
$F$
-regular Hibi rings [Reference Chiba and MatsudaCM12] and affine toric rings [Reference Hirose, Watanabe and YoshidaHWY14]. In addition,
$\operatorname{fpt}(R)=-a_{d}(R)$
for strongly
$F$
-regular standard graded Gorenstein rings [Reference Takagi and WatanabeTW04, Example 2.4(iv)]. In this paper we settle the first part of this conjecture and one direction of the second. Furthermore, we drop the restrictive hypotheses of strong
$F$
-regularity. We just assume that
$R$
is
$F$
-pure, which is needed to define
$\operatorname{fpt}(R)$
.
Theorem B. (See Theorems 4.3, 4.9, and 5.2)
Let
$R$
be a standard graded
$K$
-algebra which is
$F$
-finite and
$F$
-pure, and let
$d=\dim (R)$
. Then,
-
(1)
$\operatorname{fpt}(R)\leqslant -a_{i}(R)$
for every
$i\in \mathbb{N}$
. -
(2) If
$a_{i}(R)\neq -\infty ,$
then
$-a_{i}(R)\leqslant c^{\mathfrak{m}}(R)$
. -
(3) If
$R$
is Gorenstein, then
$\operatorname{fpt}(R)=-a_{d}(R).$
Theorem B(2) implies that
$-a_{d}(R)\leqslant c^{\mathfrak{m}}(R)$
for standard graded
$F$
-pure
$K$
-algebras. This inequality has been proven before for complete intersections without assuming strongly
$F$
-regularity or
$F$
-purity [Reference LiLi13, Proposition 2.3]. In Theorem 4.9, we prove
$-a_{d}(R)\leqslant c^{\mathfrak{m}}(R)$
for all
$F$
-finite standard graded
$K$
-algebras. In Example 5.3, we show that the converse of Theorem B(3) does not hold in general. This does not disprove Conjecture A(2), since the ring that we consider is not strongly
$F$
-regular.
We also prove the analogue of Conjecture A(1) in characteristic zero, and we show one direction of Conjecture A(2). These results are obtained by reduction to positive characteristic methods [Reference Hochster and HunekeHH99].
Theorem C. (See Theorem 6.8)
Let
$K$
be a field of characteristic zero, and let
$(R,\mathfrak{m},K)$
be a standard graded normal and
$\mathbb{Q}$
-Gorenstein
$K$
-algebra such that
$X=\operatorname{Spec}R$
is log-terminal. Let
$d=\dim (R)$
. Then,
-
(1)
$\operatorname{lct}(X)\leqslant -a_{d}(R)$
. -
(2) If
$R$
is Gorenstein, then
$\operatorname{lct}(X)=-a_{d}(R).$
Furthermore, we give a new interpretation of
$\operatorname{fpt}(R)$
for Gorenstein standard graded
$K$
-algebras in terms of regular sequences that preserve
$F$
-purity. We call such a sequence an
$F$
-pure regular sequence (see Definition 5.5).
Theorem D. (See Theorem 5.8)
Let
$(R,\mathfrak{m},K)$
be a Gorenstein standard graded
$K$
-algebra which is
$F$
-finite and
$F$
-pure over an infinite field. Let
$d=\dim (R)$
, and let
$s=\operatorname{fpt}(R)$
. Then, there exists a regular sequence consisting of
$s$
linear forms
$\ell _{1},\ldots ,\ell _{s}$
such that
$R/(\ell _{1},\ldots ,\ell _{j})$
is
$F$
-pure for every
$j=1,\ldots ,s$
.
Theorem 5.8 is in the spirit of Bertini type theorems and ladders on Fano varieties [Reference AmbroAmb99]. These theorems assert that ‘nice’ singularities are still ‘good’ after cutting by a general hyperplane. Among these nice singularities one encounters
$F$
-pure singularities of a projective variety [Reference Schwede and ZhangSZ13]. Theorem 5.8 gives a number of successive hyperplane cuts in
$\operatorname{Proj}(R)$
that preserve
$F$
-purity. Furthermore, the hyperplane cuts remain globally
$F$
-pure.
Finally, we give explicit bounds for the projective dimension and the Castelnuovo–Mumford regularity of
$R=S/I$
, where
$S=K[x_{1},\ldots ,x_{n}]$
is a polynomial ring over a field of positive characteristic, and
$I\subseteq S$
is a homogeneous ideal such that
$R$
is
$F$
-pure (see Theorem 7.3). In addition, we show that if an
$F$
-pure standard graded
$K$
-algebra
$R=S/I$
satisfies Serre’s
$S_{k}$
condition, for some
$k$
depending on the degrees of the generators of
$I$
, then
$R$
is in fact Cohen–Macaulay (see Proposition 7.6).
2 Background
Throughout this article,
$R$
denotes a commutative Noetherian ring with identity. A positively graded ring is a ring which admits a decomposition
$R=\bigoplus _{i\geqslant 0}R_{i}$
of abelian groups, with
$R_{i}\cdot R_{j}\subseteq R_{i+j}$
for all
$i$
and
$j$
. A standard graded ring is a positively graded ring such that
$R_{0}=K$
is a field,
$R=K[R_{1}]$
and
$\dim _{K}(R_{1})<\infty$
, that is,
$R$
is a finitely generated
$K$
-algebra, generated in degree one. We use the notation
$(R,\mathfrak{m},K)$
to denote a standard graded
$K$
-algebra, where
$\mathfrak{m}=\bigoplus _{i\geqslant 1}R_{i}$
is the irrelevant maximal ideal.
Suppose that
$R$
is a standard graded
$K$
-algebra. A graded module is an
$R$
-module
$M=\bigoplus _{n\in \mathbb{Z}}M_{n}$
such that
$R_{i}M_{j}\subseteq M_{i+j}$
. An
$R$
-homomorphism
$\unicode[STIX]{x1D711}:M\rightarrow N$
between graded
$R$
-modules is called homogeneous of degree
$c$
if
$\unicode[STIX]{x1D711}(M_{i})\subseteq N_{i+c}$
for all
$i\in \mathbb{Z}$
. The set of all graded homomorphisms
$M\rightarrow N$
of all degrees form a graded submodule of
$\operatorname{Hom}_{R}(M,N)$
. In general, these two modules are not the same, but they coincide when
$M$
is finitely generated [Reference Bruns and HerzogBH93]. Throughout this article,
$E_{R}(K)$
will denote the graded
$R$
-module
$\bigoplus _{i\in \mathbb{Z}}\operatorname{Hom}_{K}(R_{-i},K)$
.
Let
$I$
be a homogeneous ideal generated by the forms
$f_{1},\ldots ,f_{\ell }\in R$
. Consider the
$\check{\text{C}}$
ech complex,
$\check{\text{C}}^{\bullet }(\text{}\underline{f};R)$
:
$$\begin{eqnarray}0\rightarrow R\rightarrow \bigoplus _{i}R_{f_{i}}\rightarrow \bigoplus _{i,j}R_{f_{i}f_{j}}\rightarrow \cdots \rightarrow R_{f_{1}\cdots f_{\ell }}\rightarrow 0,\end{eqnarray}$$
where
$\check{\text{C}}^{i}(\text{}\underline{f};R)=\bigoplus _{1\leqslant j_{1}<\cdots <j_{i}\leqslant \ell }R_{f_{j_{1}}\cdots f_{j_{i}}}$
and the homomorphism in every summand is a localization map with an appropriate sign. Let
$M$
be a graded
$R$
-module. We define the
$i$
-th local cohomology of
$M$
with support in
$I$
by
$H_{I}^{i}(M):=H^{i}(\check{\text{C}}^{\bullet }(\text{}\underline{f};R)\otimes _{R}M)$
. The local cohomology module
$H_{I}^{i}(M)$
does not depend on the choice of generators,
$f_{1},\ldots ,f_{\ell }$
, of
$I$
. Moreover, it only depends on the radical of
$I$
. Since
$M$
is a graded
$R$
-module and
$I$
is homogeneous, the
$i$
th local cohomology
$H_{I}^{i}(M)$
is graded as well. Furthermore, if
$\unicode[STIX]{x1D711}:M\rightarrow N$
is a homogeneous
$R$
-module homomorphism of degree
$d$
, then the induced
$R$
-module map
$H_{I}^{i}(M)\rightarrow H_{I}^{i}(N)$
is homogeneous of degree
$d$
as well.
Assume that
$R$
has positive characteristic
$p$
. For
$e\in \mathbb{N}$
, let
$F^{e}:R\rightarrow R$
denote the
$e$
th iteration of the Frobenius endomorphism on
$R$
. If
$R$
is reduced,
$R^{1/p^{e}}$
denotes the ring of
$p^{e}$
th roots of
$R$
and we can identify
$F^{e}$
with the inclusion
$R\subseteq R^{1/p^{e}}$
. When
$R$
is standard graded, we view
$R^{1/p^{e}}$
as a
$1/p^{e}\mathbb{N}$
-graded module. In fact, if
$r^{1/p^{e}}\in R^{1/p^{e}}$
, then we write
$r\in R$
as
$r=r_{d_{1}}+\cdots +r_{d_{n}}$
, with
$r_{d_{j}}\in R_{d_{j}}$
. Then
$r^{1/p^{e}}=r_{d_{1}}^{1/p^{e}}+\cdots +r_{d_{n}}^{1/p^{e}}$
, and each
$r_{d_{j}}^{1/p^{e}}$
has degree
$d_{j}/p^{e}$
. Similarly, if
$M$
is a
$\mathbb{Z}$
-graded
$R$
-module, we have that
$M^{1/p^{e}}$
is a
$1/p^{e}\mathbb{Z}$
-graded
$R$
-module. Here
$M^{1/p^{e}}$
denotes the
$R$
-module which has the same additive structure as
$M$
, and multiplication defined by
$r\cdot m^{1/p^{e}}:=(r^{p^{e}}m)^{1/p^{e}}$
for all
$r\in R$
and
$m^{1/p^{e}}\in M^{1/p^{e}}$
.
Remark 2.1. When
$R$
is reduced, for any integer
$e\geqslant 1$
we have an inclusion
$R{\hookrightarrow}R^{1/p^{e}}$
. As a submodule of
$R^{1/p^{e}}$
,
$R$
inherits a natural
$1/p^{e}\mathbb{N}$
grading, which is compatible with the standard grading.
If
$\sqrt{I}=\mathfrak{m}$
and
$M$
is finitely generated, the modules
$H_{\mathfrak{m}}^{i}(M)$
are Artinian. Therefore, the following numbers are well defined.
Definition 2.2. Let
$M$
be a
$1/p^{e}\mathbb{N}$
-graded finitely generated
$R$
-module. For
$i\in \mathbb{N}$
, if
$H_{\mathfrak{m}}^{i}(M)\neq 0$
then the
$a_{i}$
-invariant of
$M$
is defined as
$$\begin{eqnarray}\displaystyle a_{i}(M):=\max \left\{\unicode[STIX]{x1D6FC}\in \frac{1}{p^{e}}\mathbb{Z}\mid H_{\mathfrak{m}}^{i}(M)_{\unicode[STIX]{x1D6FC}}\neq 0\right\}.\end{eqnarray}$$
If
$H_{\mathfrak{m}}^{i}(M)=0$
, we set
$a_{i}(M):=-\infty$
.
Remark 2.3. With the grading introduced above, for a finitely generated graded
$R$
-module,
$M$
, we have that
$a_{i}(M^{1/p^{e}})=a_{i}(M)/p^{e}$
for all
$i\in \mathbb{N}$
. In fact,
$H_{\mathfrak{m}}^{i}(M^{1/p^{e}})\cong H_{\mathfrak{m}}^{i}(M)^{1/p^{e}}$
since the functor
$(-)^{1/p^{e}}$
is exact.
Definition 2.4. Let
$R$
be a Noetherian ring of positive characteristic
$p$
. We say that
$R$
is
$F$
-finite if it is a finitely generated
$R$
-module via the action induced by the Frobenius endomorphism
$F:R\rightarrow R$
. When
$R$
is reduced, this is equivalent to say that
$R^{1/p}$
is a finitely generated
$R$
-module. If
$(R,\mathfrak{m},K)$
is a standard graded
$K$
-algebra, then
$R$
is
$F$
-finite if and only if
$K$
is
$F$
-finite, that is, if and only if
$[K:K^{p}]<\infty$
.
$R$
is called
$F$
-pure if
$F$
is a pure homomorphism, that is
$F\otimes 1:R\otimes _{R}M\rightarrow R\otimes _{R}M$
is injective for all
$R$
-modules
$M$
.
$R$
is called
$F$
-split if
$F$
is a split monomorphism.
Remark 2.5. Let
$(R,\mathfrak{m},K)$
be a standard graded
$F$
-pure
$K$
-algebra. Then necessarily
$a_{i}(R)\leqslant 0$
for all
$i\in \mathbb{Z}$
[Reference Hochster and RobertsHR76, Proposition 2.4].
Remark 2.6. If
$R$
is an
$F$
-pure ring,
$F$
itself is injective and
$R$
must be a reduced ring. We have that
$R$
is
$F$
-split if and only if
$R$
is a direct summand of
$R^{1/p}$
. If
$R$
is an
$F$
-finite ring,
$R$
is
$F$
-pure if and only
$R$
is
$F$
-split (see [Reference Hochster and RobertsHR76, Corollary
$5.3$
]). Since, throughout this article, we assume that
$R$
is
$F$
-finite, we use the word
$F$
-pure to refer to both.
Definition 2.7. An
$F$
-finite reduced ring
$R$
is strongly
$F$
-regular if for any element
$f\in R\setminus \{0\}$
, there exists
$e\in \mathbb{N}$
such that the inclusion
$f^{1/p^{e}}R\rightarrow R^{1/p^{e}}$
splits.
Definition 2.8. Let
$S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring over an
$F$
-finite field. The
$e$
-trace map,
$\unicode[STIX]{x1D6F7}_{e}:S^{1/p^{e}}\rightarrow S,$
is defined by
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6F7}_{e}(x_{1}^{\unicode[STIX]{x1D6FC}_{1}/p^{e}}\cdots x_{n}^{\unicode[STIX]{x1D6FC}_{n}/p^{e}})\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\begin{array}{@{}ll@{}}\displaystyle x_{1}^{(\unicode[STIX]{x1D6FC}_{1}-p^{e}+1)/p^{e}}\cdots x_{n}^{(\unicode[STIX]{x1D6FC}_{n}-p^{e}+1)/p^{e}}\quad & \displaystyle \unicode[STIX]{x1D6FC}_{1}\equiv \cdots \equiv \unicode[STIX]{x1D6FC}_{n}\equiv p^{e}-1\text{ mod }p^{e},\\ \displaystyle 0\quad & \displaystyle \text{otherwise}.\end{array}\right.\nonumber\end{eqnarray}$$
We note that
$\unicode[STIX]{x1D6F7}_{e^{\prime }}\circ \unicode[STIX]{x1D6F7}_{e}^{1/p^{e^{\prime }}}=\unicode[STIX]{x1D6F7}_{e^{\prime }+e}$
. Furthermore,
$\unicode[STIX]{x1D6F7}_{e}$
generates
$\operatorname{Hom}_{S}(S^{1/p^{e}},S)$
as an
$S^{1/p^{e}}$
-module.
Definition 2.9. [Reference SchwedeSch10]
Suppose that
$R$
is an
$F$
-pure ring. Let
$\unicode[STIX]{x1D719}:R^{1/p^{e}}\rightarrow R$
be an
$R$
-homomorphism and let
$J\subseteq R$
be an ideal. We say that
$J$
is
$\unicode[STIX]{x1D719}$
-compatible if
$\unicode[STIX]{x1D719}(J^{1/p^{e}})\subseteq J$
. An ideal
$J$
is said to be compatible if it is
$\unicode[STIX]{x1D719}$
-compatible for all
$R$
-linear maps
$\unicode[STIX]{x1D719}:R^{1/p^{e}}\rightarrow R$
and all
$e\in \mathbb{N}$
.
We end this section by recalling an explicit description of
$\operatorname{Hom}_{R}(R^{1/p^{e}},R)$
discovered by Fedder [Reference FedderFed83] that we use in the following sections.
Remark 2.10. [Reference FedderFed83, Corollary 1.5]
Let
$S$
be a polynomial ring over an
$F$
-finite field, and let
$\unicode[STIX]{x1D6F7}_{e}:S^{1/p^{e}}\rightarrow S$
be the trace map. Let
$I\subseteq S$
be a homogeneous ideal, and let
$R=S/I$
. We have a graded isomorphism
$$\begin{eqnarray}\frac{(IS^{1/p^{e}}:_{S^{1/p^{e}}}I^{1/p^{e}})}{IS^{1/p^{e}}}\cong \operatorname{Hom}_{R}(R^{1/p^{e}},R)\end{eqnarray}$$
given by the correspondence
$f^{1/p^{e}}\mapsto \unicode[STIX]{x1D711}_{f,e}$
, where
$\unicode[STIX]{x1D711}_{f,e}:R^{1/p^{e}}\rightarrow R$
is defined by
$\unicode[STIX]{x1D711}_{f,e}(\overline{r}^{1/p^{e}})=\overline{\unicode[STIX]{x1D6F7}_{e}(f^{1/p^{e}}r)}.$
Thanks to the correspondence in Remark 2.10, we can make the following observation.
Remark 2.11. Let
$S$
be a polynomial ring over an
$F$
-finite field. Let
$I\subseteq S$
be a homogeneous ideal, and let
$R=S/I$
. Let
$J\subseteq R$
be a homogeneous ideal, and let
$\widetilde{J}$
denote its pullback to
$S$
. We have that
$J$
is compatible if and only if
$(I^{[p^{e}]}:I)\subseteq (\widetilde{J}^{[p^{e}]}:\widetilde{J})$
for all
$e\geqslant 1$
.
3 Properties of
$F$
-thresholds
In this section we introduce basic definitions and properties for the diagonal
$F$
-threshold and the
$F$
-pure threshold.
Definition 3.1. [Reference Huneke, Mustaţă, Takagi and WatanabeHMTW08, Reference De Stefani, Núñez-Betancourt and PérezDSNBP16] Suppose that
$(R,\mathfrak{m},K)$
is a standard graded
$K$
-algebra. If
$\unicode[STIX]{x1D708}_{I}(p^{e})=\max \{r\in \mathbb{N}\mid I^{r}\not \subseteq \mathfrak{m}^{[p^{e}]}\}$
, the
$F$
-threshold of
$I$
with respect to
$\mathfrak{m}$
is defined by
$$\begin{eqnarray}\displaystyle c^{\mathfrak{m}}(I)=\lim _{e\rightarrow \infty }\frac{\unicode[STIX]{x1D708}_{I}(p^{e})}{p^{e}}.\end{eqnarray}$$
When
$I=\mathfrak{m}$
, we call
$c^{\mathfrak{m}}(\mathfrak{m})$
the diagonal
$F$
-threshold of
$R$
, and we denote it by
$c^{\mathfrak{m}}(R)$
.
$F$
-thresholds were introduced for rings that are not necessarily regular by Huneke, Mustaţǎ, Takagi and Watanabe [Reference Huneke, Mustaţă, Takagi and WatanabeHMTW08]. However, the existence of the limit in complete generality has been shown only recently [Reference De Stefani, Núñez-Betancourt and PérezDSNBP16].
Definition 3.2. [Reference Takagi and WatanabeTW04] Let
$(R,\mathfrak{m},K)$
be either a standard graded
$K$
-algebra or a local ring which is
$F$
-finite and
$F$
-pure, and let
$I\subseteq R$
be an ideal (homogeneous in the former case). For a real number
$\unicode[STIX]{x1D706}\geqslant 0$
, we say that
$(R,I^{\unicode[STIX]{x1D706}})$
is
$F$
-pure if for every
$e\gg 0$
, there exists an element
$f\in I^{\lfloor (p^{e}-1)\unicode[STIX]{x1D706}\rfloor }$
such that the inclusion of
$R$
-modules
$f^{1/p^{e}}R\subseteq R^{1/p^{e}}$
splits.
Remark 3.3. Note that
$(R,I^{0})=(R,R)$
being
$F$
-pure simply means that
$R$
is
$F$
-pure, according to Definition 2.4.
Definition 3.4. [Reference Takagi and WatanabeTW04] Let
$(R,\mathfrak{m},K)$
be either a standard graded
$K$
-algebra or a local ring which is
$F$
-finite and
$F$
-pure, and let
$I\subseteq R$
be an ideal (homogeneous in the former case). The
$F$
-pure threshold of
$I$
is defined by
$$\begin{eqnarray}\operatorname{fpt}(I)=\sup \{\unicode[STIX]{x1D706}\in \mathbb{R}_{{\geqslant}0}\mid (R,I^{\unicode[STIX]{x1D706}})\text{ is }F\text{-pure}\}.\end{eqnarray}$$
When
$I=\mathfrak{m}$
, we denote the
$F$
-pure threshold by
$\operatorname{fpt}(R)$
.
Definition 3.5. [Reference Aberbach and EnescuAE05] Let
$(R,\mathfrak{m},K)$
be either a standard graded
$K$
-algebra or a local ring which is
$F$
-finite and
$F$
-pure. We define
$$\begin{eqnarray}I_{e}(R):=\{r\in R\mid \unicode[STIX]{x1D711}(r^{1/\mathfrak{p}^{e}})\in \mathfrak{m}\quad \text{for every }\unicode[STIX]{x1D711}\in \operatorname{Hom}(R^{1/p^{e}},R)\}.\end{eqnarray}$$
In addition, we define the splitting prime of
$R$
as
${\mathcal{P}}(R):=\bigcap _{e}I_{e}(R)$
and the splitting dimension of
$R$
to be
$\operatorname{sdim}(R):=\dim (R/{\mathcal{P}}(R))$
.
Remark 3.6. We note that for a homogeneous element
$r$
,
$r\not \in I_{e}(R)$
if and only if there is a map
$\unicode[STIX]{x1D711}\in \operatorname{Hom}_{R}(R^{1/p^{e}},R)$
such that
$\unicode[STIX]{x1D711}(r^{1/p^{e}})=1$
.
The following proposition gives basic properties of the splitting prime for graded algebras. We include details of the proof in the graded case for sake of completeness.
Proposition 3.7. [Reference Aberbach and EnescuAE05]
Let
$(R,\mathfrak{m},K)$
be an
$F$
-finite
$F$
-pure standard graded
$K$
-algebra. Then
-
(1)
$I_{e}(R)$
and
${\mathcal{P}}(R)$
are homogeneous ideals. -
(2)
${\mathcal{P}}(R)$
is a prime ideal. -
(3)
${\mathcal{P}}(R)$
is the largest homogeneous compatible ideal of
$R$
, that is, the largest homogeneous ideal that is
$\unicode[STIX]{x1D711}$
-compatible for all
$\unicode[STIX]{x1D711}\in \operatorname{Hom}_{R}(R^{1/p^{e}},R)$
, and all
$e\in \mathbb{N}$
. -
(4)
$R/{\mathcal{P}}(R)$
is strongly
$F$
-regular. -
(5)
${\mathcal{P}}(R)_{\mathfrak{m}}={\mathcal{P}}(R_{\mathfrak{m}})$
.
Proof.
(1) Let
$e\geqslant 1$
. Since both
$R^{1/p^{e}}$
and
$R$
are graded, and
$R^{1/p^{e}}$
is a finitely generated
$R$
-module, we have that every homomorphism
$R^{1/p^{e}}\rightarrow R$
is a sum of graded homomorphisms. Therefore, in the definition of
$I_{e}(R)$
above, we can consider only graded homomorphisms. Let
$r=r_{0}+r_{1}+\cdots +r_{n}\in I_{e}(R)$
, with
$r_{i}$
of degree
$d_{i}$
. Let
$\unicode[STIX]{x1D711}\in \operatorname{Hom}_{R}(R^{1/p^{e}},R)$
be homogeneous of degree
$k$
. Then
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D711}(r^{1/p^{e}})=\unicode[STIX]{x1D711}(r_{0}^{1/p^{e}})+\cdots +\unicode[STIX]{x1D711}(r_{n}^{1/p^{e}})\in \mathfrak{m},\end{eqnarray}$$
and each
$\unicode[STIX]{x1D711}(r_{i}^{1/p^{e}})$
now has degree
$d_{i}+k$
. Since
$\mathfrak{m}$
is homogeneous, we get
$\unicode[STIX]{x1D711}(r_{i}^{1/p^{e}})\in \mathfrak{m}$
for all
$i=1,\ldots ,n$
, showing that
$r_{i}\in I_{e}(R)$
. Then
$I_{e}(R)$
is a homogeneous ideal. We have that
${\mathcal{P}}(R)$
is homogeneous is clear from its definition. The proofs of (2), (3) and (4) are completely analogous to the ones in [Reference Aberbach and EnescuAE05, Theorems 3.3, and 4.7] and [Reference SchwedeSch10, Remark 4.4] for local rings. For (5), we note that
$\unicode[STIX]{x1D711}({\mathcal{P}}(R)_{\mathfrak{m}}^{1/p^{e}})\subseteq {\mathcal{P}}(R)_{\mathfrak{m}}$
for every
$\unicode[STIX]{x1D711}\in \operatorname{Hom}(R_{\mathfrak{m}}^{1/p^{e}},R_{\mathfrak{m}})$
because
$R$
is
$F$
-finite. Since
$R_{\mathfrak{m}}/({\mathcal{P}}(R)_{\mathfrak{m}})$
is strongly
$F$
-regular by (4), we have that
${\mathcal{P}}(R)_{\mathfrak{m}}={\mathcal{P}}(R_{\mathfrak{m}}).$
◻
Definition 3.8. Let
$(R,\mathfrak{m},K)$
be an
$F$
-finite
$F$
-pure standard graded
$K$
-algebra. Let
$J\subseteq R$
be a homogeneous ideal. Then, we define
$$\begin{eqnarray}b_{J}(p^{e})=\max \{r\mid J^{r}\not \subseteq I_{e}(R)\}.\end{eqnarray}$$
Lemma 3.9. Let
$(R,\mathfrak{m},K)$
be a standard graded
$K$
-algebra which is
$F$
-finite and
$F$
-pure. Let
$J\subseteq R$
be a homogeneous ideal. Then,
$p\cdot b_{J}(p^{e})\leqslant b_{J}(p^{e+1})$
.
Proof. Let
$f\in J^{b_{J}(p^{e})}\smallsetminus I_{e}(R)$
be a homogeneous element. Then,
$Rf^{1/p^{e}}\rightarrow R^{1/p^{e}}$
splits as map of
$R$
-modules. Since
$R$
is
$F$
-pure, there is a splitting
$\unicode[STIX]{x1D6FC}:R^{1/p^{e+1}}\rightarrow R^{1/p^{e}}$
as
$R^{1/p^{e}}$
-modules. Then,
$$\begin{eqnarray}Rf^{1/p^{e}}\rightarrow R^{1/p^{e+1}}\stackrel{\unicode[STIX]{x1D6FC}}{\rightarrow }R^{1/p^{e}}\end{eqnarray}$$
splits as morphism of
$R$
-modules. Therefore,
$Rf^{p/p^{e+1}}\rightarrow R^{1/p^{e+1}}$
splits as a map of
$R$
-modules. Hence,
$f^{p}\in J^{p\cdot b_{J}(p^{e})}\smallsetminus I_{e+1}(R)$
, and so,
$p\cdot b_{J}(p^{e})\leqslant b_{J}(p^{e+1})$
.◻
We now present a characterization of the
$F$
-pure threshold that may be known to experts (see [Reference HernándezHer12, Key lemma] for principal ideals). However, we were not able to find it in the literature in the generality we need. We present the proof for the sake of completeness. This characterization is a key part for the proof of Theorem 4.3.
Proposition 3.10. Let
$(R,\mathfrak{m},K)$
be a standard graded
$K$
-algebra which is
$F$
-finite and
$F$
-pure. Let
$J\subseteq R$
be a homogeneous ideal. Then
$$\begin{eqnarray}\operatorname{fpt}(J)=\lim _{e\rightarrow \infty }\frac{b_{J}(p^{e})}{p^{e}}.\end{eqnarray}$$
Proof. By the definition of
$b_{J}(p^{e}),$
there exists
$f\in J^{b_{J}(p^{e})}\setminus I_{e}(R).$
Then, the map
$R\rightarrow R^{1/p^{e}}$
, defined by
$1\mapsto f^{1/p^{e}}$
splits by Remark 3.6. Thus,
$b_{J}(p^{e})/p^{e}\in \{\unicode[STIX]{x1D706}\in \mathbb{R}_{{\geqslant}0}\mid (R,J^{\unicode[STIX]{x1D706}})\text{ is }F\text{-pure}\}$
. Hence, for all
$e$
, we have
$b_{J}(p^{e})/p^{e}\leqslant \operatorname{fpt}(J)$
, and therefore
$\{b_{J}(p^{e})/p^{e}\}$
is a bounded sequence. By Lemma 3.9 we conclude that
$\lim _{e\rightarrow \infty }b_{J}(p^{e})/p^{e}$
exists, and that
$\lim _{e\rightarrow \infty }b_{J}(p^{e})/p^{e}\leqslant \operatorname{fpt}(J)$
.
Conversely, let
$\unicode[STIX]{x1D70E}\in \{\unicode[STIX]{x1D706}\in \mathbb{R}_{{\geqslant}0}\mid (R,J^{\unicode[STIX]{x1D706}})\text{ is }F\text{-pure}\}$
. For
$e\gg 0$
, we have that
$J^{\lfloor (p^{e}-1)\unicode[STIX]{x1D70E}\rfloor }\not \subseteq I_{e}(R)$
. Then,
$\lfloor (p^{e}-1)\unicode[STIX]{x1D70E}\rfloor /p^{e}\leqslant b_{J}(p^{e})/p^{e}$
and thus
$$\begin{eqnarray}\unicode[STIX]{x1D70E}=\sup \left\{\frac{\lfloor (p^{e}-1)\unicode[STIX]{x1D70E}\rfloor }{p^{e}}\right\}\leqslant \lim _{e\rightarrow \infty }\frac{b_{J}(p^{e})}{p^{e}}.\end{eqnarray}$$
Hence,
$$\begin{eqnarray}\hspace{115.00017pt}\operatorname{fpt}(J)\leqslant \lim _{e\rightarrow \infty }\frac{b_{J}(p^{e})}{p^{e}}.\hspace{95.00014pt}\square\end{eqnarray}$$
Remark 3.11. We note that analogous restatements of Proposition 3.10 for
$F$
-finite
$F$
-pure local rings is also true, and the proof is essentially the same.
4 F-thresholds and
$a$
-invariants
In this section, we prove the first part of our main theorem in positive characteristic. We start with a few preparation lemmas.
Lemma 4.1. Let
$(S,\mathfrak{n},K)$
be a standard graded
$F$
-finite regular ring. Let
$I\subseteq S$
be an ideal such that
$R=S/I$
is an
$F$
-pure ring. Let
$\mathfrak{m}=\mathfrak{n}R$
. Then,
${\mathcal{P}}(R)=\mathfrak{m}$
if and only if
$(I^{[p^{e}]}:I)\subseteq (\mathfrak{n}^{[p^{e}]}:\mathfrak{n})$
for all
$e\geqslant 0$
.
Proof. Let
$\unicode[STIX]{x1D6F7}_{e}:S^{1/p^{e}}\rightarrow S$
denote the
$e$
-trace map. If
$(I^{[p^{e}]}:I)\subseteq (\mathfrak{n}^{[p^{e}]}:\mathfrak{n})$
, then for every
$f\in (I^{[p^{e}]}:I)\smallsetminus \mathfrak{n}^{[p^{e}]}$
there exist a unit
$u\in S$
and an element
$g\in \mathfrak{n}^{[p^{e}]}$
such that
$f=ux_{1}^{p^{e}-1}\cdots x_{n}^{p^{e}-1}+g.$
Then,
$f\cdot \mathfrak{n}\subseteq \mathfrak{n}^{[p^{e}]}$
, and we get
$\unicode[STIX]{x1D6F7}_{e}(f^{1/p^{e}}\mathfrak{n}^{1/p^{e}})\subseteq \mathfrak{n}$
. Then by Remark 2.10, we have that
$\unicode[STIX]{x1D711}(\mathfrak{m}^{1/p^{e}})\subseteq \mathfrak{m}$
for every
$\unicode[STIX]{x1D711}:R^{1/p^{e}}\rightarrow R.$
Hence,
$I_{e}(R)=\mathfrak{m}$
for all
$e\geqslant 1$
and
${\mathcal{P}}(R)=\mathfrak{m}$
as well.
Conversely, if
$\mathfrak{m}={\mathcal{P}}(R)$
, then
$I_{e}(R)=\mathfrak{m}$
for all
$e\geqslant 1$
. This means that for every
$e\geqslant 1$
and every
$f\in (I^{[p^{e}]}:I)$
, we have
$\unicode[STIX]{x1D6F7}_{e}(f^{1/p^{e}}\mathfrak{n}^{1/p^{e}})\subseteq \mathfrak{n}$
by Remark 2.10. Thus,
$f\cdot \mathfrak{n}\subseteq \mathfrak{n}^{[p^{e}]},$
and hence
$f\in (\mathfrak{n}^{[p^{e}]}:\mathfrak{n})$
.◻
Lemma 4.2. Let
$S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring over an
$F$
-finite field
$K$
. Let
$\mathfrak{n}=(x_{1},\ldots ,x_{n})$
denote the maximal homogeneous ideal. Let
$I\subseteq S$
be a homogeneous ideal such that
$R:=S/I$
is an
$F$
-pure ring, and let
$\mathfrak{m}=\mathfrak{n}R$
. Then,
$$\begin{eqnarray}\min \left\{s\in \mathbb{N}~\bigg|\left[\frac{(I^{[p^{e}]}:I)+\mathfrak{n}^{[p^{e}]}}{\mathfrak{n}^{[p^{e}]}}\right]_{s}\neq 0\right\}=n(p^{e}-1)-b_{\mathfrak{ m}}(p^{e}).\end{eqnarray}$$
Proof. Let
$\unicode[STIX]{x1D6F7}_{e}:S^{1/p^{e}}\rightarrow S$
denote the
$e$
-trace map. Let
$$\begin{eqnarray}\displaystyle u:=\min \left\{s\in \mathbb{N}~\bigg|\left[\frac{(I^{[p^{e}]}:I)+\mathfrak{n}^{[p^{e}]}}{\mathfrak{n}^{[p^{e}]}}\right]_{s}\neq 0\right\}\end{eqnarray}$$
and
$b=b_{\mathfrak{m}}(p^{e})$
. By our definition of
$u$
, there exists
$f\in (I^{[p^{e}]}:I)\smallsetminus \mathfrak{n}^{[p^{e}]}$
, which is a homogeneous polynomial of degree
$u$
. Since
$f\not \in \mathfrak{n}^{[p^{e}]},$
there exists
$x^{\unicode[STIX]{x1D6FC}}\in \operatorname{Supp}\{f\}$
such that
$x^{\unicode[STIX]{x1D6FC}}\not \in \mathfrak{n}^{[p^{e}]}$
. We pick
$\unicode[STIX]{x1D6FD}=\mathbf{p}^{\mathbf{e}}-\mathbf{1}-\unicode[STIX]{x1D6FC}$
, so
$x^{\unicode[STIX]{x1D6FC}}x^{\unicode[STIX]{x1D6FD}}=x^{\mathbf{p}^{\mathbf{e}}-\mathbf{1}}$
, where
$\mathbf{p}^{\mathbf{e}}-\mathbf{1}$
denotes the multi-index
$(p^{e}-1,p^{e}-1,\ldots ,p^{e}-1)$
. We have that the map
$\unicode[STIX]{x1D711}:R^{1/p^{e}}\rightarrow R$
defined by
$\unicode[STIX]{x1D711}(\overline{r}^{1/p^{e}})=\overline{\unicode[STIX]{x1D6F7}_{e}(f^{1/p^{e}}r^{1/p^{e}})}$
is a splitting of the Frobenius map on
$R$
such that
$\unicode[STIX]{x1D711}((x^{\unicode[STIX]{x1D6FD}})^{1/p^{e}})=1$
. Hence,
$x^{\unicode[STIX]{x1D6FD}}\notin I_{e}(R)$
. Since
$|\unicode[STIX]{x1D6FD}|=(p^{e}-1)n-u,$
we have that
$(p^{e}-1)n-u\leqslant b$
; that is,
$u\geqslant n(p^{e}-1)-b$
.
For the other inequality, we pick a monomial
$g\in \mathfrak{n}$
of degree
$b$
such that
$\overline{g}\in \mathfrak{m}^{b}\smallsetminus I_{e}(R)$
. Then, there exists a map
$\unicode[STIX]{x1D711}:R^{1/p^{e}}\rightarrow R$
such that
$\unicode[STIX]{x1D711}(\overline{g}^{1/p^{e}})=1.$
Therefore, there exists an element
$f\in (I^{[q]}:I)\smallsetminus \mathfrak{n}^{[p^{e}]}$
such that
$\unicode[STIX]{x1D711}(\overline{r}^{1/p^{e}})=\overline{\unicode[STIX]{x1D6F7}_{e}(f^{1/p^{e}}r^{1/p^{e}})}$
for all
$\overline{r}^{1/p^{e}}\in R^{1/p^{e}}$
. By definition of
$\unicode[STIX]{x1D6F7}_{e},$
we have that
$x^{\mathbf{p}^{\mathbf{e}}-\mathbf{1}}\in \operatorname{Supp}(fg)$
. Let
$h$
be the homogeneous part of degree
$(p-1)n-b$
of
$f$
. We note that
$h\in (I^{[p^{e}]}:I)$
because
$I$
is homogeneous. In addition,
$h\notin \mathfrak{n}^{[p^{e}]}$
because
$x^{\mathbf{p}^{\mathbf{e}}-\mathbf{1}}\in \operatorname{Supp}(hg)$
. Then we get
$u\leqslant (p^{e}-1)n-b$
, as desired.◻
We are now ready to prove the first part of Theorem B.
Theorem 4.3. Let
$(R,\mathfrak{m},K)$
be a standard graded
$K$
-algebra which is
$F$
-finite and
$F$
-pure. Then
$\operatorname{fpt}(R)\leqslant -a_{i}(R)$
for every
$i\in \mathbb{N}$
.
Proof. If
$H_{\mathfrak{m}}^{i}(R)=0$
there is nothing to prove, since
$a_{i}(R)=-\infty$
. Let
$i\in \mathbb{N}$
be such that
$H_{\mathfrak{m}}^{i}(R)\neq 0$
. Let
$f\in \mathfrak{m}^{b_{\mathfrak{m}}(p^{e})}\setminus I_{e}(R)$
be a homogeneous element, and let
$\unicode[STIX]{x1D6FE}=b_{\mathfrak{m}}(p^{e})/p^{e}$
. By Remark 2.1 we can view
$R$
as a
$1/p^{e}\mathbb{N}$
-graded module. Then
splits, and the inclusion is homogeneous of degree zero. Applying the
$i$
th local cohomology, we get a homogeneous split inclusion
$H_{\mathfrak{m}}^{i}(R(-\unicode[STIX]{x1D6FE})){\hookrightarrow}H_{\mathfrak{m}}^{i}(R^{1/p^{e}})$
of degree zero. Let
$v\in H_{\mathfrak{m}}^{i}(R(-\unicode[STIX]{x1D6FE}))_{a_{i}(R)}$
be an element in the top graded part of
$H_{\mathfrak{m}}^{i}(R(-\unicode[STIX]{x1D6FE}))$
, which has degree
$a_{i}(R)+\unicode[STIX]{x1D6FE}$
. Under the inclusion above, this maps to a nonzero element of degree
$a_{i}(R)+\unicode[STIX]{x1D6FE}$
in
$H_{\mathfrak{m}}^{i}(R^{1/p^{e}})$
. Therefore,
$$\begin{eqnarray}\displaystyle a_{i}(R)+\frac{b_{\mathfrak{m}}(p^{e})}{p^{e}}\leqslant a_{i}(R^{1/p^{e}})=\frac{a_{i}(R)}{p^{e}},\end{eqnarray}$$
which is equivalent to
$$\begin{eqnarray}\displaystyle \frac{b_{\mathfrak{m}}(p^{e})}{p^{e}}\leqslant \frac{(1-p^{e})a_{i}(R)}{p^{e}}.\end{eqnarray}$$
Since this holds for all
$e\gg 1$
, we get
$$\begin{eqnarray}\displaystyle \operatorname{fpt}(R)=\lim _{e\rightarrow \infty }\frac{b_{\mathfrak{m}}(p^{e})}{p^{e}}\leqslant \lim _{e\rightarrow \infty }-\frac{(p^{e}-1)a_{i}(R)}{p^{e}}=-a_{i}(R)\end{eqnarray}$$
by Proposition 3.10. ◻
Corollary 4.4. Let
$(R,\mathfrak{m},K)$
be a standard graded
$K$
-algebra which is
$F$
-finite and
$F$
-pure. If
$a_{i}(R)=0$
for some
$i$
, then
$\operatorname{sdim}(R)=0$
.
Proof. If
$a_{i}(R)=0$
for some
$i$
, we have that
$\operatorname{fpt}(R)=0$
by Theorem 4.3. Then, we have that
$b_{e}=0$
for every
$e\in \mathbb{N}$
by Lemma 3.9 and Proposition 3.10. As a consequence,
$\mathfrak{m}\subseteq I_{e}$
for every
$e\in \mathbb{N}.$
Since
$I_{e}(R)\subseteq \mathfrak{m}$
holds true because
$R$
is
$F$
-pure, we have that
$\mathfrak{m}=I_{e}(R)$
for every
$e\in \mathbb{N}.$
Hence,
${\mathcal{P}}(R)=\mathfrak{m},$
and
$\operatorname{sdim}(R)=0.$
◻
We now review the definition of test ideal, which is closely related to the theory of tight closure. We refer the reader to [Reference Hochster and HunekeHH94] for definitions and details.
Definition 4.5. Let
$R$
be a Noetherian ring of positive characteristic
$p$
. The finitistic test ideal of
$R$
is defined as
$\unicode[STIX]{x1D70F}^{fg}(R):=\cap _{M}\operatorname{ann}(0_{M}^{\ast })$
, where
$M$
runs through all the finitely generated
$R$
-modules. We define the big test ideal of
$R$
to be
$\unicode[STIX]{x1D70F}(R)=\cap _{M}\operatorname{ann}(0_{M}^{\ast })$
, where
$M$
runs through all
$R$
-modules.
Remark 4.6. We point out that for
$F$
-finite rings,
$\unicode[STIX]{x1D70F}(R)$
is the smallest compatible ideal not contained in a minimal prime of
$R$
[Reference SchwedeSch10, Theorem 6.3]. In addition,
$\unicode[STIX]{x1D70F}^{fg}(R)$
is a compatible ideal [Reference VassilevVas98, Theorem 3.1]. One clearly has the inclusion
$\unicode[STIX]{x1D70F}(R)\subseteq \unicode[STIX]{x1D70F}^{fg}(R)$
. It is one of the most important open problems in tight closure theory whether these two ideals are the same. Equality is known to hold true in some cases. For instance, Lyubeznik and Smith proved that
$\unicode[STIX]{x1D70F}^{fg}(R)=\unicode[STIX]{x1D70F}(R)$
for finitely generated standard graded
$K$
-algebras [Reference Lyubeznik and SmithLS99, Corollary 3.4].
We use Proposition 3.10 to relate the
$F$
-pure threshold of the ring with its splitting dimension.
Theorem 4.7. Let
$(R,\mathfrak{m},K)$
be a standard graded
$K$
-algebra which is
$F$
-finite and
$F$
-pure, and let
$J\subseteq R$
be a compatible ideal. Then, we have
$$\begin{eqnarray}\operatorname{fpt}(R)\leqslant \operatorname{fpt}(R/J).\end{eqnarray}$$
In particular,
$$\begin{eqnarray}\operatorname{fpt}(R)\leqslant \operatorname{fpt}(R/\unicode[STIX]{x1D70F})\text{ and }\operatorname{fpt}(R)\leqslant \operatorname{fpt}(R/{\mathcal{P}})\leqslant \operatorname{sdim}(R),\end{eqnarray}$$
where
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}(R)$
denotes the test ideal of
$R$
, and
${\mathcal{P}}={\mathcal{P}}(R)$
is the splitting prime of
$R$
.
Proof. Let
$S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring such that there exists a surjection
$S\rightarrow R$
, and let
$\mathfrak{n}=(x_{1},\ldots ,x_{n})$
, so that
$\mathfrak{m}=\mathfrak{n}R$
. Let
$I$
denote the kernel of the surjection. Let
$\widetilde{J}\subseteq S$
be the pullback of
$J$
. We have that
$(I^{[p^{e}]}:I)\subseteq (\widetilde{J}^{[p^{e}]}:\widetilde{J})$
for every
$e\in \mathbb{N}$
by Remark 2.11. Then,
$$\begin{eqnarray}\displaystyle & & \displaystyle \min \left\{t\in \mathbb{N}~\bigg|\left[\frac{(\widetilde{J}^{[p^{e}]}:\widetilde{J})+\mathfrak{n}^{[p^{e}]}}{\mathfrak{n}^{[p^{e}]}}\right]_{t}\neq 0\right\}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \min \left\{t\in \mathbb{N}~\bigg|\left[\frac{(I^{[p^{e}]}:I)+\mathfrak{n}^{[p^{e}]}}{\mathfrak{n}^{[p^{e}]}}\right]_{t}\neq 0\right\}.\nonumber\end{eqnarray}$$
As a consequence, we get
$$\begin{eqnarray}\displaystyle b_{\mathfrak{m}}(p^{e}) & = & \displaystyle \max \{t\in \mathbb{N}\mid \mathfrak{m}^{t}\not \subseteq I_{e}(R)\}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \max \{t\in \mathbb{N}\mid \mathfrak{m}^{t}\not \subseteq I_{e}(R/J)\}=b_{\mathfrak{m}(R/J)}(p^{e})\nonumber\end{eqnarray}$$
by Proposition 3.10. Then,
$\operatorname{fpt}(R)\leqslant \operatorname{fpt}(R/J)$
. The last claim follows from the fact that the test ideal is compatible as noted in Remark 4.6, and the splitting prime is compatible by Proposition 3.7
(3). Finally,
$\operatorname{fpt}(R/{\mathcal{P}})\leqslant \dim (R/{\mathcal{P}})$
[Reference Takagi and WatanabeTW04, Proposition 2.6(1)].◻
We now focus on the diagonal
$F$
-threshold.
Remark 4.8. For any standard graded
$K$
-algebra
$(R,\mathfrak{m},K)$
, we have that
$$\begin{eqnarray}\max \left\{s\in \frac{1}{p^{e}}\cdot \mathbb{Z}~\bigg|\left[R^{1/p^{e}}/\mathfrak{m}R^{1/p^{e}}\right]_{s}\neq 0\right\}=\frac{\unicode[STIX]{x1D708}_{e}}{p^{e}}.\end{eqnarray}$$
We are now ready to prove the second part of Theorem B.
Theorem 4.9. Let
$R$
be an
$F$
-finite standard graded
$K$
-algebra, and let
$d=\dim (R)$
. Then,
$-a_{d}(R)\leqslant c^{\mathfrak{m}}(R)$
. Furthermore, if
$R$
is
$F$
-pure, then
$-a_{i}(R)\leqslant c^{\mathfrak{m}}(R)$
for every
$i$
such that
$H_{\mathfrak{m}}^{i}(R)\neq 0$
.
Proof. We fix
$i\in \mathbb{N}$
such that
$H_{\mathfrak{m}}^{i}(R)\neq 0$
. Let
$v_{1},\ldots ,v_{r}$
be a minimal system of homogeneous generators of
$R^{1/p^{e}}$
as an
$R$
-module, with degrees
$\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{r}\in 1/p^{e}\mathbb{N}$
. By Remark 2.1 we can view
$R$
as a
$1/p^{e}\mathbb{N}$
-graded module. We have a degree zero surjective map
$$\begin{eqnarray}\bigoplus _{j=0}^{r}R(-\unicode[STIX]{x1D6FE}_{j})\stackrel{\unicode[STIX]{x1D719}}{\longrightarrow }R^{1/p^{e}},\end{eqnarray}$$
where
$R(-\unicode[STIX]{x1D6FE}_{j})\rightarrow R^{1/p^{e}}$
maps
$1$
to
$v_{j}.$
This induces a degree zero homomorphism
$$\begin{eqnarray}\bigoplus _{i=0}^{j}H_{\mathfrak{ m}}^{i}(R(-\unicode[STIX]{x1D6FE}_{j}))\stackrel{\unicode[STIX]{x1D711}}{\longrightarrow }H_{\mathfrak{m}}^{i}(R^{1/p^{e}}).\end{eqnarray}$$
If
$i=d,$
$\unicode[STIX]{x1D711}$
is surjective. We now prove that
$\unicode[STIX]{x1D711}$
is also surjective for
$i\neq d$
, if
$R$
is
$F$
-pure. In this case, the natural inclusion
$R\rightarrow R^{1/p^{e}}$
induces an inclusion
$H_{\mathfrak{m}}^{i}(R)\rightarrow H_{\mathfrak{m}}^{i}(R^{1/p^{e}})$
. We have that the map
$\unicode[STIX]{x1D703}:H_{\mathfrak{m}}^{i}(R)\otimes _{R}R^{1/p^{e}}\rightarrow H_{\mathfrak{m}}^{i}(R^{1/p^{e}})$
induced by
$v\otimes f^{1/p^{e}}\mapsto f^{1/p^{e}}\unicode[STIX]{x1D6FC}(v)$
is surjective [Reference Singh and WaltherSW07, Lemma 2.5]. Then,
$$\begin{eqnarray}1\otimes \unicode[STIX]{x1D719}:H_{\mathfrak{m}}^{i}(R)\otimes _{R}\biggl(\bigoplus _{j=0}^{r}R(-\unicode[STIX]{x1D6FE}_{j})\biggr)\rightarrow H_{\mathfrak{m}}^{i}(R)\otimes _{R}R^{1/p^{e}}\end{eqnarray}$$
is surjective. Thus,
$\unicode[STIX]{x1D711}$
is surjective, because
$\unicode[STIX]{x1D711}=\unicode[STIX]{x1D703}\circ (1\otimes \unicode[STIX]{x1D719})$
.
We have now that
$\unicode[STIX]{x1D711}$
is surjective under the hypotheses assumed. Since
$$\begin{eqnarray}\unicode[STIX]{x1D708}_{\mathfrak{m}}(p^{e})/p^{e}=\max \{\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{j}\},\end{eqnarray}$$
we have that
$$\begin{eqnarray}\frac{a_{i}(R)}{p^{e}}=a_{i}(R^{1/p^{e}})\leqslant \max \{a_{d}(R(-\unicode[STIX]{x1D6FE}_{i}))\mid i=0,\ldots ,j\}=a_{i}(R)+\frac{\unicode[STIX]{x1D708}_{\mathfrak{m}}(p^{e})}{p^{e}}.\end{eqnarray}$$
Then,
$a_{i}(R)\leqslant p^{e}a_{d}(R)+\unicode[STIX]{x1D708}_{\mathfrak{m}}(p^{e}),$
and so
$(1-p^{e})a_{i}(R)\leqslant \unicode[STIX]{x1D708}_{\mathfrak{m}}(p^{e})$
. Hence,
$$\begin{eqnarray}\hspace{35.00005pt}-a_{i}(R)=\lim _{e\rightarrow \infty }\frac{(1-p^{e})a_{i}(R)}{p^{e}}\leqslant \lim _{e\rightarrow \infty }\frac{\unicode[STIX]{x1D708}_{\mathfrak{m}}(p^{e})}{p^{e}}=c^{\mathfrak{m}}(R).\hspace{35.00005pt}\square\end{eqnarray}$$
5 F-thresholds of graded Gorenstein rings
Suppose that
$(R,\mathfrak{m},K)$
is an
$F$
-finite standard graded Gorenstein
$K$
-algebra. Let
$S=K[x_{1},\ldots ,x_{n}]$
, and let
$I\subseteq S$
be a homogeneous ideal such that
$R\cong S/I$
as graded rings. Since
$\operatorname{Hom}_{R}(R^{1/p},R)$
is a cyclic
$R^{1/p}$
-module, we have that for all integers
$e\geqslant 1$
there exist homogeneous polynomials
$f_{e}\in S$
such that
$I^{[p^{e}]}:I=f_{e}S+I^{[p^{e}]}$
by Remark 2.10. In fact, if
$I^{[p]}:I=fS+I^{[p]}$
, then
$\displaystyle I^{[p^{e}]}:I=f^{(1+p+\cdots +p^{e-1})}S+I^{[p^{e}]}$
for all
$e\geqslant 2$
.
Remark 5.1. When
$R=S/I$
is
$F$
-pure, we have
$(I^{[p^{e}]}:I)\not \subseteq \mathfrak{n}^{[p^{e}]}$
by Fedder’s criterion. In the notation used above, if
$(I^{[p^{e}]}:_{S}I)=f_{e}S+I^{[p^{e}]}$
for some homogeneous polynomial
$f_{e}$
, we get that
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \min \left\{s\in \mathbb{N}~\bigg|\left[\frac{(I^{[p^{e}]}:I)+\mathfrak{n}^{[p^{e}]}}{\mathfrak{n}^{[p^{e}]}}\right]_{s}\neq 0\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\min \left\{s\in \mathbb{N}~\bigg|\left[\frac{f_{e}S+\mathfrak{n}^{[p^{e}]}}{\mathfrak{n}^{[p^{e}]}}\right]_{s}\neq 0\right\}=\deg (f_{e}).\nonumber\end{eqnarray}$$
We now prove the last part of Theorem B.
Theorem 5.2. Let
$(R,\mathfrak{m},K)$
be a Gorenstein standard graded
$K$
-algebra which is
$F$
-finite and
$F$
-pure, and let
$d=\dim (R)$
. Then,
$\operatorname{fpt}(R)=-a_{d}(R)$
.
Proof. Let
$S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring, and let
$I\subseteq S$
be a homogeneous ideal such that
$R\cong S/I$
as graded rings. Let
$\mathfrak{n}=(x_{1},\ldots ,x_{n})$
, so that
$\mathfrak{m}=\mathfrak{n}R$
. Let
$a=a_{d}(R)$
. Consider the natural map
$S/I^{[p]}\rightarrow S/I$
induced by the inclusion
$I^{[p]}\subseteq I$
. Then such a map extends to a map of complexes
$\unicode[STIX]{x1D713}_{\bullet }$
from a minimal free resolution of
$S/I^{[p]}$
to a minimal free resolution of
$S/I$
. Furthermore, such a map
$\unicode[STIX]{x1D713}_{\bullet }$
can be chosen graded of degree zero. We have that the last homomorphism in the map of complexes,
$S(p(-n-a))\rightarrow S(-n-a)$
is given by multiplication by a homogeneous polynomial
$f$
(see Remark 6.6). Furthermore,
$I^{[p]}:I=fS+I^{[p]}$
[Reference VraciuVra03, Lemma 1]. Since
$\unicode[STIX]{x1D713}_{\bullet }$
is homogeneous of degree zero, we have that
$\deg (f)=(p-1)(n+a)$
.
Recall that, for all
$e\geqslant 2$
, we have that
$(I^{[p^{e}]}:_{S}I)=f^{(1+p+\cdots +p^{e-1})}S+I^{[p^{e}]}$
. By Remark 5.1 and Lemma 4.2, we obtain that
$$\begin{eqnarray}\displaystyle \hspace{31.0001pt}\operatorname{fpt}(R) & = & \displaystyle \lim _{e\rightarrow \infty }\frac{n(p^{e}-1)-(\deg (f)\cdot (1+p+\cdots +p^{e-1}))}{p^{e}}\nonumber\\ \displaystyle & = & \displaystyle \lim _{e\rightarrow \infty }\frac{n(p^{e}-1)}{p^{e}}-\lim _{e\rightarrow \infty }\frac{\deg (f)\cdot (1+p+\cdots +p^{e-1})}{p^{e}}\nonumber\\ \displaystyle & = & \displaystyle n-\frac{\deg (f)}{p-1}\nonumber\\ \displaystyle & = & \displaystyle n-\frac{(p-1)(n+a)}{p-1}\nonumber\\ \displaystyle & = & \displaystyle -a.\hspace{211.00038pt}\square\nonumber\end{eqnarray}$$
We now give an example to show that an
$F$
-finite and
$F$
-pure standard graded
$K$
-algebra such that
$\operatorname{fpt}(R)=-a_{d}(R)$
is not necessarily Gorenstein. This is not a counterexample to Conjecture A(2), since the ring we consider is not strongly
$F$
-regular.
Example 5.3. Let
$S=K[x,y,z]$
with
$K$
a perfect field of characteristic
$p>0$
, and let
$\mathfrak{n}=(x,y,z)$
be its homogeneous maximal ideal.
$$\begin{eqnarray}\displaystyle I=(xy,xz,yz)=(x,y)\cap (x,z)\cap (y,z)\subseteq S.\end{eqnarray}$$
Let
$R=S/I$
, with maximal ideal
$\mathfrak{m}=\mathfrak{n}/I$
. Note that
$R$
is a one-dimensional Cohen–Macaulay
$F$
-pure ring. In addition,
${\mathcal{P}}(R)=(x,y,z)R$
; therefore,
$\operatorname{sdim}(R)=0$
and, by Theorem 4.7,
$\operatorname{fpt}(R)=0$
as well. On the other hand, from the short exact sequence
we get a long exact sequence of local cohomology modules
The maps in this sequence are homogeneous of degree zero. Thus,
$a_{1}(R)\geqslant 0$
, because
$K$
injects into
$H_{\mathfrak{m}}^{1}(R)$
. On the other hand, since
$R$
is
$F$
-pure, we have that
$a_{1}(R)\leqslant 0$
; therefore,
$\operatorname{fpt}(R)=a_{1}(R)=0$
. Although
$R$
is not Gorenstein, since the canonical module
$\unicode[STIX]{x1D714}_{R}\cong (x,y)/(xy,xz+yz)$
has two generators.
Sannai and Watanabe [Reference Sannai and WatanabeSW11, Theorem 4.2] showed that for an
$F$
-pure standard graded Gorenstein algebra,
$R$
, with an isolated singularity,
$\operatorname{sdim}(R)=0$
is equivalent to
$a_{d}(R)=0.$
The previous theorem recovers this result dropping the hypothesis of isolated singularity. This is because
$\operatorname{sdim}(R)=0$
is equivalent to
$\operatorname{fpt}(R)=0.$
In fact, for all
$F$
-pure rings, Corollary 4.4 shows that
$a_{d}(R)=0$
implies
$\operatorname{sdim}(R)=0.$
We now aim at an interpretation of the
$F$
-pure threshold of a standard graded Gorenstein
$K$
-algebra as the maximal length of a regular sequence that preserves
$F$
-purity.
Proposition 5.4. Let
$S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring over an
$F$
-finite infinite field
$K$
. Let
$\mathfrak{n}=(x_{1},\ldots ,x_{n})$
denote the maximal homogeneous ideal. Let
$I\subseteq S$
be a homogeneous ideal such that
$R=S/I$
is an
$F$
-pure ring, and let
$\mathfrak{m}=\mathfrak{n}R$
. Let
$f\in (I^{[p]}:I)\smallsetminus \mathfrak{n}^{[p]}$
. If
$\deg (f)\leqslant (p-1)(n-1)$
, then there exists a linear form
$\ell \in S$
such that:
-
(1)
$\ell ^{p-1}f\not \in \mathfrak{n}^{[p]}$
. -
(2) the class of
$\ell$
in
$R$
does not belong to
${\mathcal{P}}(R)$
. -
(3)
$\ell$
is a nonzero divisor in
$R$
. -
(4) The ring
$S/(I+(\ell ))$
is
$F$
-pure.
Proof. Let us pick
$c_{\unicode[STIX]{x1D6FC}}\in K$
such that
$f=\sum _{|\unicode[STIX]{x1D6FC}|=\deg (f)}c_{\unicode[STIX]{x1D6FC}}x^{\unicode[STIX]{x1D6FC}}$
. Let
$$\begin{eqnarray}\ell _{y}=y_{1}x_{1}+\cdots +y_{n}x_{n}\in S[y_{1},\ldots ,y_{n}]\end{eqnarray}$$
be a generic linear form. We note that
$$\begin{eqnarray}\left(\ell _{y}\right)^{p-1}=\mathop{\sum }_{|\unicode[STIX]{x1D703}|=p-1}g_{\unicode[STIX]{x1D703}}(y)x^{\unicode[STIX]{x1D703}},\end{eqnarray}$$
where
$g_{\unicode[STIX]{x1D703}}(y)=(p-1)!/\unicode[STIX]{x1D703}_{1}!\cdots \unicode[STIX]{x1D703}_{n}!y^{\unicode[STIX]{x1D703}}\in K[y_{1},\ldots ,y_{n}]$
.
Since
$f\not \in \mathfrak{n}^{[p]},$
there exists
$x^{\unicode[STIX]{x1D6FD}}\in \operatorname{Supp}\{f\}$
such that
$x^{\unicode[STIX]{x1D6FD}}\not \in \mathfrak{n}^{[p]}$
. Since
$|\unicode[STIX]{x1D6FD}|\leqslant (p-1)(n-1)$
and
$x^{\unicode[STIX]{x1D6FD}}\not \in \mathfrak{n}^{[p]}$
, there exists
$x^{\unicode[STIX]{x1D6FE}}\in \mathfrak{n}^{p-1}$
such that
$x^{\unicode[STIX]{x1D6FE}}x^{\unicode[STIX]{x1D6FD}}\not \in \mathfrak{n}^{[p]}$
by Pigeonhole principle. Let
$$\begin{eqnarray}h:=\mathop{\sum }_{\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FC}}c_{\unicode[STIX]{x1D6FC}}g_{\unicode[STIX]{x1D703}}(y)\in K[y_{1},\ldots ,y_{n}].\end{eqnarray}$$
We note that
$h\neq 0$
because
$c_{\unicode[STIX]{x1D6FD}}g_{\unicode[STIX]{x1D703}}\neq 0$
. In addition,
$h$
is the coefficient of
$x^{\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FE}}$
in
$\left(\ell _{y}\right)^{p-1}f$
. We note that
${\mathcal{P}}(R)\neq \mathfrak{m}$
by Lemma 4.1, and thus
${\mathcal{P}}(R)\cap \mathfrak{m}\neq \mathfrak{m}$
. Since
$K$
is an infinite field, we can pick a point
$v\in K^{n}$
such that
$h(v)\neq 0$
and the class of
$\ell _{y}(v)$
does not belong to
${\mathcal{P}}(R)$
. We set
$\ell =\ell _{y}(v).$
By our construction of
$\ell$
,
$x^{\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FE}}\in \operatorname{Supp}\{\ell ^{p-1}f\}$
and
$x^{\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FE}}\not \in \mathfrak{n}^{[p]}$
. In addition,
$\ell \notin {\mathcal{P}}(R).$
Since the pullback of
${\mathcal{P}}(R)$
to
$S$
contains every associated prime of
$R$
, we have that
$\ell$
is a nonzero divisor in
$R$
. To show the last claim we note that, setting
$I^{\prime }:=I+(\ell )$
, we have that
$\ell ^{p-1}f\in ({I^{\prime }}^{[p]}:I^{\prime })\smallsetminus \mathfrak{n}^{[p]}$
, and
$F$
-purity follows by Fedder’s criterion [Reference FedderFed83, Theorem 1.12].◻
As a consequence of these results, and of Theorem 5.2, we give an interpretation of the
$F$
-pure threshold, and the
$a$
-invariant, in terms of the maximal length of a regular sequence that preserves
$F$
-purity. We start by introducing the concept of
$F$
-pure regular sequence.
Definition 5.5. Let
$R$
be an
$F$
-finite
$F$
-pure ring. We say that a regular sequence
$f_{1},\ldots ,f_{r}$
is
$F$
-pure if
$R/(f_{1},\ldots ,f_{i})$
is an
$F$
-pure ring for all
$i=1,\ldots ,r.$
Lemma 5.6. Let
$(R,\mathfrak{m},K)$
be a standard graded
$K$
-algebra. If
$f$
is a regular element of degree
$d>0$
, then
$d+a_{i}(R)\leqslant a_{i-1}(R/(f))$
for all
$i\in \mathbb{N}$
such that
$H_{\mathfrak{m}}^{i}(R)\neq 0$
.
Proof. Suppose that
$H_{\mathfrak{m}}^{i}(R)\neq 0$
. Consider the homogeneous short exact sequence
For all
$j\in \mathbb{Z}$
, this gives rise to an exact sequence of
$K$
-vector spaces
Since
$d>0$
, for
$j=a_{i}(R)+d$
we have that
$H_{\mathfrak{m}}^{i}(R)_{j}=0$
. Then,
is a surjection. We note that
$H_{\mathfrak{m}}^{i}(R)_{a_{i}(R)}\neq 0$
, which yields
$$\begin{eqnarray}H_{\mathfrak{m}}^{i-1}(R/(f))_{a_{i}(R)+d}\neq 0,\end{eqnarray}$$
and hence
$a_{i-1}(R/(f))\geqslant a_{i}(R)+d$
.◻
Corollary 5.7. Let
$(R,\mathfrak{m},K)$
be a standard graded
$K$
-algebra which is
$F$
-finite and
$F$
-pure. If
$f_{1},\ldots ,f_{r}$
is a homogeneous
$F$
-pure regular sequence of degrees
$d_{1},\ldots ,d_{r}$
, then
$\sum _{j=1}^{r}d_{j}\leqslant \min \{-a_{i}(R)\mid i\in \mathbb{N}\}$
.
Proof. We proceed by induction on
$r\geqslant 1$
. Assume that
$r=1$
. If
$H_{\mathfrak{m}}^{i}(R)=0$
, we have that
$d_{1}\leqslant -a_{i}(R)=\infty$
, therefore there is nothing to prove in this case. If
$H_{\mathfrak{m}}^{i}(R)\neq 0$
, by Lemma 5.6 we have that
$a_{i}(R)+d_{1}\leqslant a_{i-1}(R/(f_{1}))$
. Since
$R/(f_{1})$
is
$F$
-pure, it follows from Remark 2.5 that
$a_{i-1}(R/(f))\leqslant 0$
, and hence
$d_{1}\leqslant -a_{i}(R)$
. Thus,
$d_{1}\leqslant -a_{i}(R)$
for all
$i\in \mathbb{N}$
, that is,
$d_{1}\leqslant \min \{-a_{i}(R)\mid i\in \mathbb{N}\}$
. This concludes the proof of the base case. For
$r>1$
, if
$H_{\mathfrak{m}}^{i}(R)=0$
we have that
$\sum _{i=1}^{r}d_{i}\leqslant -a_{i}(R)=\infty$
and, again, there is nothing to prove in this case. Assume that
$H_{\mathfrak{m}}^{i}(R)\neq 0$
. By induction, we get that
$\sum _{j=2}^{r}d_{j}\leqslant -a_{s}(R/(f_{1}))$
for all
$s\in \mathbb{N}$
. In particular, we have that
$\sum _{j=2}^{r}d_{j}\leqslant -a_{i-1}(R/(f_{1}))$
. By Lemma 5.6, we have that
$-a_{i-1}(R/(f_{1}))\geqslant -a_{i}(R)-d_{1}$
. Combining the two inequalities, and rearranging the terms in the sum, we obtain
$\sum _{j=1}^{r}d_{i}\leqslant -a_{i}(R)$
. Therefore, we obtain
$\sum _{j=1}^{r}d_{j}\leqslant \min \{-a_{i}(R)\mid i\in \mathbb{N}\}$
.◻
Theorem 5.8. Let
$(R,\mathfrak{m},K)$
be a Gorenstein standard graded
$K$
-algebra which is
$F$
-finite and
$F$
-pure, and let
$d=\dim (R)$
. If
$f_{1},\ldots ,f_{r}$
is an
$F$
-pure regular sequence, then
$r\leqslant \operatorname{fpt}(R)$
. Furthermore, if
$K$
is infinite, then there exists an
$F$
-pure regular sequence consisting of
$\operatorname{fpt}(R)$
linear forms.
Proof. By Theorem 5.2, we have that
$\operatorname{fpt}(R)=-a_{d}(R)$
. The first claim follows from Corollary 5.7. For the second claim, let
$S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring and let
$I\subseteq S$
be a homogeneous ideal such that
$R\cong S/I$
as graded rings. We proceed by induction on
$\operatorname{fpt}(R)$
. The case
$\operatorname{fpt}(R)=0$
is trivial. We now assume
$\operatorname{fpt}(R)>0$
. From the proof of Theorem 5.2, we have that
$(I^{[p]}:_{S}I)=fS+I^{[p]}$
for a homogeneous polynomial
$f\in (I^{[p]}:_{S}I)\smallsetminus \mathfrak{n}^{[p]}$
of degree
$\deg (f)\leqslant (p-1)(n+a_{d}(R))$
. Since
$a_{d}(R)=-\operatorname{fpt}(R)<0$
by assumption, there exists a linear nonzero divisor
$\ell _{1}\in R$
such that
$R/(\ell _{1})$
is
$F$
-pure by Proposition 5.4. Note that, from the homogeneous short exact sequence
it follows that
$a_{d-1}(R/(\ell _{1}))=a_{d}(R)+1$
. Since
$R/(\ell _{1})$
is Gorenstein, we have that
$\operatorname{fpt}(R/(\ell _{1}))=-a_{d-1}(R/(\ell _{1}))=-a_{d}(R)-1=\operatorname{fpt}(R)-1$
. The claim follows by induction.◻
6 Results in characteristic zero
In this section we present results in characteristic zero that are analogous to Theorem 4.3. These results are motivated by the relation between the log-canonical and the
$F$
-pure threshold.
We first fix the notation. Let
$K$
be a field of characteristic zero, and let
$(R,\mathfrak{m},K)$
be a
$\mathbb{Q}$
-Gorenstein normal standard graded
$K$
-algebra. Consider the closed subscheme
$V(\mathfrak{m})=Y\subseteq X=\operatorname{Spec}(R)$
, and let
$\mathfrak{a}$
be the corresponding ideal sheaf. We now use Hironaka’s resolution of singularities [Reference HironakaHir64]. Suppose that
$f:\widetilde{X}\rightarrow X$
is a log-resolution of the pair
$(X,Y)$
, that is,
$f$
is a proper birational morphism with
$\widetilde{X}$
nonsingular such that the ideal sheaf
$\mathfrak{a}{\mathcal{O}}_{\widetilde{X}}={\mathcal{O}}_{\widetilde{X}}(-F)$
is invertible, and
$\operatorname{Supp}(F)\cup \text{Exc}(f)$
is a simple normal crossing divisor. Let
$K_{X}$
and
$K_{\widetilde{X}}$
denote canonical divisors of X and
$\widetilde{X}$
, respectively.
Let
$\unicode[STIX]{x1D706}\geqslant 0$
be a real number. Then there are finitely many irreducible (not necessarily exceptional) divisors
$E_{i}$
on
$\widetilde{X}$
and real numbers
$a_{i}$
so that there exists an
$\mathbb{R}$
-linear equivalence of
$\mathbb{R}$
-divisors
$$\begin{eqnarray}\displaystyle K_{\widetilde{X}}\sim f^{\ast }K_{X}+\mathop{\sum }_{i}a_{i}E_{i}+\unicode[STIX]{x1D706}F.\end{eqnarray}$$
Definition 6.1. Continuing with the previous notation, we say that the pair
$(X,\unicode[STIX]{x1D706}Y)$
is log-canonical, or lc for short, if
$a_{i}\geqslant -1$
for all
$i$
. Define
$$\begin{eqnarray}\displaystyle \operatorname{lct}(X)=\sup \{\unicode[STIX]{x1D706}\in \mathbb{R}_{{\geqslant}0}\mid \text{the pair }(X,\unicode[STIX]{x1D706}Y)\text{ is lc}\}.\end{eqnarray}$$
We say that
$(X,\unicode[STIX]{x1D706}Y)$
is Kawamata log-terminal, or klt for short, if
$a_{i}>-1$
for all
$i.$
Remark 6.2. If
$X$
is log-terminal, we have that
$$\begin{eqnarray}\displaystyle \operatorname{lct}(X)=\sup \{\unicode[STIX]{x1D706}\in \mathbb{R}_{{\geqslant}0}\mid \text{the pair }(X,\unicode[STIX]{x1D706}Y)\text{ is klt}\}.\end{eqnarray}$$
Definition 6.3. Let
$K$
be a field of positive characteristic
$p$
, and let
$(R,\mathfrak{m},K)$
be a standard graded
$K$
-algebra which is
$F$
-finite and
$F$
-pure. Let
$I\subseteq R$
be a homogeneous ideal. For a real number
$\unicode[STIX]{x1D706}\geqslant 0$
, we say that
$(R,I^{\unicode[STIX]{x1D706}})$
is strongly
$F$
-regular if for every
$c\in R$
not in any minimal prime, there exists
$e\geqslant 0$
and an element
$f\in I^{\lceil p^{e}\unicode[STIX]{x1D706}\rceil }$
such that the inclusion of
$R$
-modules
$(cf)^{1/p^{e}}R\subseteq R^{1/p^{e}}$
splits.
Remark 6.4. Let
$(R,\mathfrak{m},K)$
be a standard graded
$K$
-algebra which is
$F$
-finite and strongly
$F$
-regular. Then, by [Reference Takagi and WatanabeTW04, Proposition 2.2(5)], we have
$$\begin{eqnarray}\operatorname{fpt}(R)=\sup \{\unicode[STIX]{x1D706}\in \mathbb{R}_{{\geqslant}0}\mid \text{the pair }(R,\mathfrak{m}^{\unicode[STIX]{x1D706}})\text{ is strongly }F\text{-regular}\}.\end{eqnarray}$$
Definition 6.5. Let
$R$
be a reduced algebra essentially of finite type over a field
$K$
of characteristic zero,
$\mathfrak{a}\subseteq R$
an ideal, and
$\unicode[STIX]{x1D706}>0$
a real number. The pair
$(R,\mathfrak{a}^{\unicode[STIX]{x1D706}})$
is said to be of dense
$F$
-pure type (respectively strongly
$F$
-regular type) if there exist a finitely generated
$\mathbb{Z}$
-subalgebra
$A$
of
$K$
and a reduced subalgebra
$R_{A}$
of
$R$
essentially of finite type over
$A$
which satisfy the following conditions:
-
(i)
$R_{A}$
is flat over
$A$
,
$R_{A}\otimes _{A}K\cong R$
, and
$\mathfrak{a}_{A}R=\mathfrak{a}$
, where
$\mathfrak{a}_{A}=\mathfrak{a}\cap R_{A}\subseteq R_{A}$
. -
(ii) The pair
$(R_{s},\mathfrak{a}_{s}^{\unicode[STIX]{x1D706}})$
is
$F$
-pure (respectively strongly
$F$
-regular) for every closed point
$s$
in a dense subset of
$\operatorname{Spec}(A)$
. Here, if
$\unicode[STIX]{x1D705}(s)$
denotes the residue field of
$s$
, we define
$R_{s}=R_{A}\otimes _{A}\unicode[STIX]{x1D705}(s)$
and
$\mathfrak{a}_{s}=\mathfrak{a}_{A}R_{s}\subseteq R_{s}$
.
Remark 6.6. Let
$S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring over a field
$K$
, and
$I\subseteq S$
be a homogeneous ideal. Let
$R=S/I$
, and consider a minimal graded free resolution of
$R$
over
$S$
If we write
$G_{n-d}=\bigoplus _{j}S(-j)^{\unicode[STIX]{x1D6FD}_{n-d,j}(R)}$
, where the positive integers
$\unicode[STIX]{x1D6FD}_{n-d,j}(R)$
are the
$(n-d)$
th graded Betti numbers of
$R$
over
$S$
, we have that
$\max \{j\mid \unicode[STIX]{x1D6FD}_{n-d,j}(R)\neq 0\}=-n-a_{d}(R)$
[Reference Bruns and HerzogBH93, Section 3.6]. Therefore, when
$R$
is Cohen–Macaulay,
$a_{d}(R)$
can be read from the graded Betti numbers of
$R$
over
$S$
.
Lemma 6.7. Let
$(R,\mathfrak{m},K)$
be a Cohen–Macaulay standard graded
$K$
-algebra of dimension
$d$
, with
$K$
a field of characteristic zero, and let
$A$
be a finitely generated
$\mathbb{Z}$
-subalgebra of
$K$
. Assume that
$R_{0}$
is a graded
$A$
-algebra such that
$R_{0}\otimes _{A}K\cong R$
as graded rings. For a closed point
$s\in \operatorname{Max}\operatorname{Spec}(A)$
, let
$R_{s}=R_{0}\otimes _{A}\unicode[STIX]{x1D705}(s)$
, where
$\unicode[STIX]{x1D705}(s)$
is the residue field of
$s\in \operatorname{Spec}(R)$
. Then, there exists a dense open subset
$U\subseteq \operatorname{Max}\operatorname{Spec}(A)$
such that
$a_{d}(R)=a_{d}(R_{s})$
for all
$s\in U$
.
Proof. Since
$R_{0}$
is a finitely generated graded
$A$
-algebra, we write
$R_{0}\cong B/J$
, for some homogeneous ideal
$J\subseteq B:=A[x_{1},\ldots ,x_{n}]$
. Let
$T=B\otimes _{A}K\cong K[x_{1},\ldots ,x_{n}]$
, and for
$s\in \operatorname{Max}\operatorname{Spec}(R)$
, let
$B_{s}=B\otimes _{A}\unicode[STIX]{x1D705}(s)\cong \unicode[STIX]{x1D705}(s)[x_{1},\ldots ,x_{n}]$
. By [Reference Hochster and HunekeHH99, Theorem 2.3.5 & Theorem 2.3.15], there exists a dense open subset
$U\subseteq \operatorname{Max}\operatorname{Spec}(R)$
such that, for all
$s\in U$
,
$R_{s}$
is Cohen–Macaulay of dimension
$d=\dim (R)$
. Furthermore, the graded Betti numbers of
$R$
over
$T$
are the same as the graded Betti numbers of
$R_{s}$
over
$B_{s}$
[Reference Hochster and HunekeHH99, Theorem 2.3.5(e)]. In particular, it follows from Remark 6.6 that
$a_{d}(R)=a_{d}(R_{s})$
for all
$s\in U$
.◻
Theorem 6.8. Let
$K$
be a field of characteristic zero, and let
$(R,\mathfrak{m},K)$
be a standard graded normal and
$\mathbb{Q}$
-Gorenstein
$K$
-algebra such that
$X=\operatorname{Spec}R$
is log-terminal. Let
$d=\dim (R)$
. Then,
-
(1)
$\operatorname{lct}(X)\leqslant -a_{d}(R)$
. -
(2) If
$R$
is Gorenstein, then
$\operatorname{lct}(X)=-a_{d}(R).$
Proof. We can write
$R=K[x_{1},\ldots ,x_{n}]/(f_{1},\ldots ,f_{\ell })$
for some integer
$n$
and some homogeneous polynomials
$f_{1},\ldots ,f_{\ell }\in S:=K[x_{1},\ldots ,x_{n}]$
. Let
$A$
be the finitely generated
$\mathbb{Z}$
-algebra generated by all the coefficients of
$f_{1},\ldots ,f_{\ell }$
. Define
$T:=A[x_{1},\ldots ,x_{n}]$
and notice that, if we set
$R_{0}:=T/(f_{1},\ldots ,f_{\ell })$
, we have that
$R_{0}\otimes _{A}K\cong R$
. Since
$X$
is log-terminal,
$R$
is a Cohen–Macaulay ring. For a closed point
$s\in \operatorname{Spec}(A)$
, set
$R_{s}:=R_{0}\otimes _{A}\unicode[STIX]{x1D705}(s)$
, and
$\mathfrak{m}_{s}:=(x_{1},\ldots ,x_{n})R_{s}$
. For
$m\in \mathbb{N}$
, let
$\unicode[STIX]{x1D706}_{m}=\operatorname{lct}(X)-1/m$
. Then, the pair
$(X,\unicode[STIX]{x1D706}_{m}Y)$
is klt by Remark 6.2. Thus,
$(X,\unicode[STIX]{x1D706}_{m}Y)$
is of dense strongly
$F$
-regular type [Reference Hara and YoshidaHY03, Theorem 6.8] [Reference TakagiTak04, Corollary 3.5]. It follows that
$(R_{s},\mathfrak{m}_{s}^{\unicode[STIX]{x1D706}_{m}})$
is strongly
$F$
-regular for each closed point
$s\in V$
, where
$V\subseteq \operatorname{Max}\operatorname{Spec}(A)$
is a dense set. By Remark 6.4, we have that
$\unicode[STIX]{x1D706}_{m}\leqslant \operatorname{fpt}(R_{s})$
for all
$m$
, and hence
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D706}_{m}\leqslant \operatorname{fpt}(R_{s})\leqslant -a_{d}(R_{s})\end{eqnarray}$$
by Theorem 4.3. By Lemma 6.7, there exists a dense open subset
$U\subseteq \operatorname{Max}\operatorname{Spec}(A)$
such that
$a_{d}(R_{s})=a_{d}(R)$
for all
$s\in U$
. Thus, for
$s$
in nonempty intersection
$U\cap V$
, we have
$$\begin{eqnarray}\displaystyle \operatorname{lct}(X)-\frac{1}{m}\leqslant -a_{d}(R_{s})=-a_{d}(R).\end{eqnarray}$$
After taking the limit as
$m\rightarrow \infty$
, we obtain that
$\operatorname{lct}(X)\leqslant -a_{d}(R)$
.
For the second result, we note that if
$R$
is a Gorenstein ring, then
$R_{s}$
is a Gorenstein ring for
$s$
in a dense open subset
$W\subseteq \operatorname{Max}\operatorname{Spec}(A)$
[Reference Hochster and HunekeHH99, Theorem 2.3.15]. Let
$U$
be as above. Then,
$\operatorname{fpt}(R_{s})=-a_{d}(R_{s})=-a_{d}(R)$
for
$s\in W\cap U$
, where
$W\cap U$
is a dense open subset of
$\operatorname{Max}\operatorname{Spec}(A)$
. Let
$\unicode[STIX]{x1D6FF}_{m}:=-a_{d}(R)-1/m$
. Because of the equality obtained above, we have that
$(R,\mathfrak{m}_{s}^{\unicode[STIX]{x1D6FF}_{m}})$
is
$F$
-pure for
$s\in W$
. Thus,
$\unicode[STIX]{x1D6FF}_{m}\leqslant \operatorname{lct}(X)$
for every
$m\in \mathbb{N}$
[Reference Takagi and WatanabeTW04, Proposition 3.2(1)], and hence
$-a_{d}(R)\leqslant \operatorname{lct}(X)$
. The desired equality now follows from the first part.◻
A key point in the proof of Theorem 6.8 is that, if
$X$
is log-terminal, then
$$\begin{eqnarray}\operatorname{lct}(X)=\sup \{\unicode[STIX]{x1D706}\in \mathbb{R}_{{\geqslant}0}\mid \text{the pair }(X,\unicode[STIX]{x1D706}Y)\text{ is klt}\},\end{eqnarray}$$
and a pair is klt if and only if the pair is of dense strongly
$F$
-regular type. In a private communication with Linquan Ma and Karl Schwede, we were informed that Theorem 6.8 holds, more generally, when
$X$
is a
$\mathbb{Q}$
-Gorenstein log-canonical normal scheme. The proof involves methods in characteristic zero. Our proof of Theorem 6.8, instead, relies on reduction to positive characteristic techniques. If we try to replace log-terminal by log-canonical in our proof, we face a very important and longstanding open problem in birational geometry, that is, whether a pair is log-canonical if and only if it is of dense
$F$
-pure type (see [Reference TakagiTak04, Reference Hara and WatanabeHW02, Reference Mustaţă and SrinivasMS11]). To the best of our knowledge, the characteristic zero analogue of Theorem 4.3 is open for non
$\mathbb{Q}$
-Gorenstein rings. We note that in this case one can still define log-canonical singularities by the work of De Fernex and Hacon [Reference de Fernex and HacondFH09]. Then, we ask the following question.
Question 6.9. Let
$(R,\mathfrak{m},K)$
be a standard graded normal algebra over a field,
$K$
, of characteristic zero. Let
$d=\dim (R)$
and let
$X=\operatorname{Spec}R$
. Suppose that
$X$
is log-canonical. Is
$\operatorname{lct}(X)\leqslant -a_{i}(R)$
for every
$i\in \mathbb{N}$
?
Ma also informed us that the analogue of Theorem 5.2 in characteristic zero is also true. This can be proved using geometric methods in characteristic zero, such as Bertini theorems, and his recent work on Du Bois singularities [Reference MaMa15].
7 Homological invariants of
$F$
-pure rings
Let
$K$
be a field and let
$S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring. Let
$I\subseteq S$
be a homogeneous ideal, and let
$R=S/I$
. Suppose that
$I=(f_{1},\ldots ,f_{j})$
is generated by forms of degree
$d_{i}=\deg (f_{i})$
. Let
$G_{\bullet }$
be the minimal graded free resolution of
$R$
. Each
$G_{i}$
can be written as a direct sum of copies of
$S$
with shifts:
$$\begin{eqnarray}G_{i}=\bigoplus _{j\in \mathbb{Z}}S(-j)^{\unicode[STIX]{x1D6FD}_{i,j}(R)},\end{eqnarray}$$
where
$S(-j)$
denotes a rank one free module where the generator has degree
$j$
. The exponents
$\unicode[STIX]{x1D6FD}_{i,j}(R)$
are called the graded Betti numbers of
$R$
. We define the projective dimension of
$R$
by
$$\begin{eqnarray}\displaystyle \operatorname{pd}_{S}(R)=\max \{i\mid \unicode[STIX]{x1D6FD}_{i,j}(R)\neq 0\text{ for some }j\}.\end{eqnarray}$$
The Castelnuovo–Mumford regularity of
$R=S/I$
is defined by
$$\begin{eqnarray}\displaystyle \operatorname{reg}_{S}(R)=\max \{j-i\mid \unicode[STIX]{x1D6FD}_{i,j}(R)\neq 0\text{ for some }i\}.\end{eqnarray}$$
Equivalently, if
$d=\dim (R)$
, it can be defined as
$$\begin{eqnarray}\displaystyle \operatorname{reg}_{S}(R)=\max \{a_{i}(R)+i\mid i=0,\ldots ,d\}.\end{eqnarray}$$
Suppose that
$R$
is an
$F$
-pure ring. In this section, we provide bounds for the projective dimension and Castelnuovo–Mumford regularity of
$R$
over
$S$
. This relates to an important question in commutative algebra asked by Stillman:
Question 7.1. [Reference Peeva and StillmanPS09, Problem 3.14]
Let
$S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring over a field
$K$
and fix a sequence of natural numbers
$d_{1},\ldots ,d_{j}$
. Does there exist a constant
$C=C(d_{1},\ldots ,d_{j})$
(independent of
$n$
) such that
$$\begin{eqnarray}\operatorname{pd}_{S}(S/J)\leqslant C\end{eqnarray}$$
for all homogeneous ideals
$J\subseteq S$
generated by homogeneous polynomials of degrees
$d_{1},\ldots ,d_{j}$
?
Recall that
$b_{\mathfrak{m}}(p^{e})=\max \{r\mid \mathfrak{m}^{r}\not \subseteq I_{e}(R)\}$
. Proposition 5.4 gives a relation between
$b_{\mathfrak{m}}(p)$
and
$\operatorname{depth}_{S}(R)$
, hence between
$b_{\mathfrak{m}}(p)$
and
$\operatorname{pd}_{S}(R)$
by the Auslander–Buchsbaum’s formula. For
$F$
-pure rings, the projective dimension and the Castelnuovo–Mumford regularity have explicit upper bounds. The bound for the projective dimension easily follows from a special case of a result of Lyubeznik.
Theorem 7.2. [Reference LyubeznikLyu06, Corollary 3.2]
Let
$S$
be regular local ring of positive characteristic
$p$
, and let
$I\subseteq S$
be an ideal. Let
$R=S/I$
, with maximal ideal
$\mathfrak{m}$
. Then, for
$i\in \mathbb{N}$
, we have
$H_{I}^{n-i}(S)=0$
if and only if
$F^{e}:H_{\mathfrak{m}}^{i}(R)\rightarrow H_{\mathfrak{m}}^{i}(R)$
is the zero map for some
$e\in \mathbb{N}$
.
We now exhibit some upper bounds for homological invariants of standard graded
$F$
-pure
$K$
-algebras. We note that the argument for projective dimension has already been used, essentially, in [Reference Singh and WaltherSW07, Theorem 4.1]. Moreover, the fact that
$\operatorname{pd}_{S}(S/I)=\operatorname{cd}(I,S)$
if
$S/I$
is
$F$
-pure was first pointed out in [Reference Dao, Huneke and SchweigDHS13]. However, the bound for the Castelnuovo–Mumford regularity follows from our results in this article, in particular, from Theorem B.
Theorem 7.3. Let
$S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring over a field of positive characteristic
$p$
. Let
$I\subseteq S$
be a homogeneous ideal such that
$R=S/I$
is
$F$
-pure. Then,
$$\begin{eqnarray}\operatorname{pd}_{S}(R)\leqslant \unicode[STIX]{x1D707}_{S}(I),\end{eqnarray}$$
where
$\unicode[STIX]{x1D707}_{S}(I)$
denotes the minimal number of generators of
$I$
in
$S$
. If
$K$
is
$F$
-finite, then
$$\begin{eqnarray}\operatorname{reg}_{S}(R)\leqslant \dim (R)-\operatorname{fpt}(R).\end{eqnarray}$$
Proof. Since
$R$
is an
$F$
-pure ring, so is the localization
$(R^{\prime },\mathfrak{m}^{\prime }):=(R_{\mathfrak{m}},\mathfrak{m}_{\mathfrak{m}})$
. In fact if
$R\subseteq R^{1/p}$
is pure, then so is
$R_{\mathfrak{m}}\subseteq (R^{1/p})_{\mathfrak{m}}=(R_{\mathfrak{m}})^{1/p}$
. Hence the Frobenius homomorphism acts injectively on the local cohomology modules of
$R^{\prime }$
. In particular, for any integer
$i$
and for any
$e\in \mathbb{N}$
, we have that
$F^{e}:H_{\mathfrak{m}^{\prime }}^{i}(R^{\prime })\rightarrow H_{\mathfrak{m}^{\prime }}^{i}(R^{\prime })$
is the zero map if and only if
$H_{\mathfrak{m}^{\prime }}^{i}(R^{\prime })=0$
. Let
$\mathfrak{n}=(x_{1},\ldots ,x_{n})$
. Since
$I$
is homogeneous, we have that
$H_{I}^{n-i}(S)=0$
if and only if
$H_{I_{\mathfrak{n}}}^{n-i}(S_{\mathfrak{n}})=0$
. By Theorem 7.2, it follows that
$H_{\mathfrak{m}^{\prime }}^{i}(R^{\prime })=0$
for all
$n-i>\operatorname{cd}(I,S)$
, and
$H_{\mathfrak{m}^{\prime }}^{n-\operatorname{cd}(I,S)}(R^{\prime })\neq 0$
. Therefore, by the Auslander–Buchsbaum’s formula, we get
$\operatorname{pd}_{S}(R)=n-\operatorname{depth}_{S_{\mathfrak{n}}}(R^{\prime })=\operatorname{cd}(I,S)$
. Since
$\operatorname{cd}(I,S)\leqslant \unicode[STIX]{x1D707}_{S}(I)$
, the first claim follows. For the second claim, let
$d=\dim (R)$
. Then we have that
$$\begin{eqnarray}\displaystyle \operatorname{reg}_{S}(R) & = & \displaystyle \max \{a_{i}(R)+i\mid i=0,\ldots ,d\}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \max \{i-\operatorname{fpt}(R)\mid i=0,\ldots ,d\}\nonumber\\ \displaystyle & = & \displaystyle d-\operatorname{fpt}(R),\nonumber\end{eqnarray}$$
where the second line follows from Theorem 4.3. ◻
Remark 7.4. In the notation introduced above, Caviglia proved that finding an upper bound
$C=C(d_{1},\ldots ,d_{j})$
for
$\operatorname{pd}_{S}(R)$
is equivalent to finding an upper bound
$B=B(d_{1},\ldots ,d_{j})$
for
$\operatorname{reg}_{S}(R)$
(see [Reference PeevaPee11, Theorem 29.5] and [Reference McCullough and SeceleanuMS13, Theorem 2.4]). The bound for
$\operatorname{reg}_{S}(R)$
that we give in Theorem 7.3, a priori, does not give an answer to Stillman’s question. However, the inequality
$\operatorname{pd}_{S}(R)\leqslant \unicode[STIX]{x1D707}_{S}(I)$
for the projective dimension shows that Stillman’s question has positive answer for
$F$
-pure rings. In particular, there also exists
$B=B(d_{1},\ldots ,d_{j})$
such that
$\operatorname{reg}_{S}(R)\leqslant B$
.
Motivated by the results in the previous theorem, we ask the following question.
Question 7.5. Let
$S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring over a field,
$K$
, of characteristic zero, and let
$I$
be a homogeneous ideal. Suppose that
$R=S/I$
is a normal, and that
$X=\operatorname{Spec}R$
is log-canonical. Is it true that
$$\begin{eqnarray}\operatorname{pd}_{S}(R)\leqslant \unicode[STIX]{x1D707}_{S}(I)\quad \text{and}\quad \operatorname{reg}_{S}(R)\leqslant \dim (R)-\operatorname{lct}(X)?^{1}\end{eqnarray}$$
We end this section by exhibiting an
$S_{k}$
condition that forces an
$F$
-pure ring to be Cohen–Macaulay.
Proposition 7.6. Let
$S=K[x_{1},\ldots ,x_{n}]$
be a polynomial ring over a field of positive characteristic
$p$
. Let
$I$
be a homogeneous ideal generated by forms
$f_{1},\ldots ,f_{\ell }.$
Let
$D=\deg (f_{1})+\cdots +\deg (f_{\ell }).$
Suppose that
$R=S/I$
is
$F$
-pure. If
$R_{Q}$
is Cohen–Macaulay for every prime ideal such
$\dim (R_{Q})\leqslant D$
, then
$R$
is Cohen–Macaulay.
Proof. Our proof will be by contradiction. Suppose that
$R$
is not Cohen–Macaulay. Then,
$\operatorname{depth}(R)<\dim (R).$
Let
$c=\operatorname{cd}(I,S)$
and
$r=\operatorname{depth}_{I}(S).$
We have that
$$\begin{eqnarray}r=n-\dim (R)<n-\operatorname{depth}(R)=\operatorname{pd}_{S}(R)=c\end{eqnarray}$$
by Theorem 7.3. Let
$Q\in \operatorname{Ass}_{S}H_{I}^{c}(S)$
. Note that
$H_{I}^{c}(S_{Q})\neq 0$
by our choice of
$Q$
, and then
$c=\operatorname{cd}(IS_{Q},S_{Q})$
. In addition,
$H_{I}^{r}(S_{Q})\neq 0$
because
$I\subseteq Q$
. Thus,
$r=\operatorname{depth}_{I}(S_{Q})$
. It follows that
$$\begin{eqnarray}r=\dim (S_{Q})-\dim (R_{Q})<\dim (S_{Q})-\operatorname{depth}(R)=\operatorname{pd}_{S_{Q}}(R_{Q})=c\end{eqnarray}$$
by Theorem 7.3. Thus,
$\dim (R_{Q})\neq \operatorname{depth}(R_{Q})$
, and so
$R_{Q}$
is not Cohen–Macaulay.
We have that
$\dim S/Q\geqslant n-D$
[Reference ZhangZha11, Theorem 1], therefore
$\dim S_{Q}\leqslant D$
, because regular rings satisfy the dimension formula. In particular,
$\dim (R_{Q})\leqslant D$
. Since we are assuming that
$R$
is
$S_{D}$
, we have that
$R_{Q}$
must be Cohen–Macaulay, and we reach a contradiction.◻
Acknowledgments
We thank Craig Huneke for very helpful discussions. In particular, we thank him for suggesting a shorter and more elegant proof of Theorem 5.2. We thank Karl Schwede for discussions about geometric interpretations of Theorem 5.8, and Linquan Ma for helpful comments about Section 6. We also thank Andrew Bydlon for reading a preliminary version of this article, and for useful feedback and comments. We thank the referee for carefully reading the article, and for suggesting improvements to the exposition.
