Hostname: page-component-848d4c4894-hfldf Total loading time: 0 Render date: 2024-06-12T13:09:53.037Z Has data issue: false hasContentIssue false
  • English
  • Français

The Heisenberg covering of the Fermat curve

Part of: Discontinuous groups and automorphic forms Arithmetic algebraic geometry

Published online by Cambridge University Press:  10 May 2024

Debargha Banerjee  and
Loïc Merel
Debargha Banerjee*
Affiliation:
Department of Mathematics, Indian Institute of Science Education and Research, Pune, India
Loïc Merel
Affiliation:
Department of Mathematics, Université Paris Cité and Sorbonne Université, CNRS, IMJ-PRG, F-75013 Paris, France e-mail: loic.merel@imj-prg.fr
*
e-mail: debargha.banerjee@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

For N integer 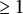$\ge 1$, K. Murty and D. Ramakrishnan defined the Nth Heisenberg curve, as the compactified quotient 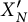$X^{\prime }_N$ of the upper half-plane by a certain non-congruence subgroup of the modular group. They ask whether the Manin–Drinfeld principle holds, namely, if the divisors supported on the cusps of those curves are torsion in the Jacobian. We give a model over 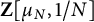$\mathbf {Z}[\mu _N,1/N]$ of the Nth Heisenberg curve as covering of the Nth Fermat curve. We show that the Manin–Drinfeld principle holds for 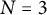$N=3$, but not for 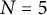$N=5$. We show that the description by generator and relations due to Rohrlich of the cuspidal subgroup of the Fermat curve is explained by the Heisenberg covering, together with a higher covering of a similar nature. The curves 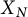$X_N$ and the classical modular curves 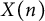$X(n)$, for n even integer, both dominate 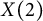$X(2)$, which produces a morphism between Jacobians 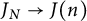$J_N\rightarrow J(n)$. We prove that the latter has image 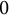$0$ or an elliptic curve of j-invariant 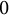$0$. In passing, we give a description of the homology of 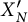$X^{\prime }_{N}$.

Keywords

Fermat’s curvesmodular symbolsHeisenberg curves

MSC classification

Secondary: 11F11: Holomorphic modular forms of integral weight 11G05: Elliptic curves over global fields 11G30: Curves of arbitrary genus or genus $ne 1$ over global fields
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 27
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author was partially supported by the SERB grant MTR/2017/000357 and CRG/2020/000223. The first named author is deeply indebted to Professor Yuri Manin for several stimulating conversation at the MPIM. The authors are deeply indebted to the anonymous referees for careful reading of the paper. We are sincerely grateful to the anonymous referee for drawing our attention to [1].

References

Anderson, G. and Ihara, Y., Pro- $l$ branched coverings of P1 and higher circular $l$ -units. Ann. of Math. (2) 128(1988), no. 2, 271–293.CrossRefGoogle Scholar
Banerjee, D. and Merel, L., The Eisenstein cycles and Manin–Drinfeld properties . Forum Math. 36(2024), 305–325.CrossRefGoogle Scholar
Curilla, C., Regular models of Fermat’s curves and applications to Arakelov theory, ProQuest LLC, Ann Arbor, MI, 2010. Thesis (Ph.D.), Yale University.Google Scholar
Deligne, P., Le groupe fondamental de la droite projective moins trois points . In: Ihara, Y., Ribet, K., and Serre, J. P. (eds.), Galois groups over Q (Berkeley, CA, 1987), Mathematical Sciences Research Institute Publications, 16, Springer, New York, 1989, pp. 79–297.CrossRefGoogle Scholar
Ejder, O., Modular symbols for Fermat curves . Proc. Amer. Math. Soc. 147(2019), no. 6, 2305–2319.CrossRefGoogle Scholar
Hall, M. Jr., The theory of groups, The MacMillan Company, New York, 1959.Google Scholar
Lang, S., Introduction to algebraic and abelian functions, Graduate Texts in Mathematics, 89, Springer-Verlag, New York, 2nd ed., 1982.CrossRefGoogle Scholar
Liu, Q., Algebraic geometry and arithmetic curves, Oxford Graduate Texts in Mathematics, 6, Oxford University Press, Oxford, 2002. Translated from the French by Reinie Erné, Oxford Science Publications.CrossRefGoogle Scholar
Manin, J. I., Parabolic points and zeta functions of modular curves . Izv. Akad. Nauk SSSR Ser. Mat. 36(1972), 19–66.Google Scholar
Mazur, B., Modular curves and the Eisenstein ideal . Inst. Hautes Études Sci. Publ. Math. 47(1977), 33–186.CrossRefGoogle Scholar
Mazur, B., Rational isogenies of prime degree (with an appendix by D. Goldfeld) . Invent. Math. 44(1978), no. 2, 129–162.CrossRefGoogle Scholar
Merel, L., L’accouplement de Weil entre le sous-groupe de Shimura et le sous-groupe cuspidal de ${J}_0(p)$ , J. Reine Angew. Math. 477(1996), 71–115.Google Scholar
Murty, V. K. and Ramakrishnan, D., The Manin–Drinfeld theorem and Ramanujan sums . Proc. Indian Acad. Sci. Math. Sci. 97(1987), no. 1-3, 251–262.CrossRefGoogle Scholar
Phillips, R. and Sarnak, P., The spectrum of Fermat curves . Geom. Funct. Anal. 1(1991), no. 1, 80–146.CrossRefGoogle Scholar
Posingies, A. E., Belyi pairs and scattering constants. Ph.D. thesis, Humboldt-University Berlin, Berlin, 2010.Google Scholar
Rohrlich, D. E., Modular functions and the Fermat’s curves, ProQuest LLC, Ann Arbor, MI, 1976. Thesis (Ph.D.), Yale University.Google Scholar
Rohrlich, D. E., Points at infinity on the Fermat curves . Invent. Math. 39(1977), no. 2, 95–127.CrossRefGoogle Scholar
Vélu, J., Le groupe cuspidal des courbes de Fermat . In: Séminaire Delange-Pisot-Poitou, 20e année: 1978/1979, Théorie des nombres, Fasc. 2 (French), Exp. No. 28, 11, Secrétariat Math., Paris, 1980.Google Scholar