1 Introduction
We fix integers
$n>0,d$
and
$g\geqslant 0$
. Let
$\unicode[STIX]{x1D6F4}$
be a smooth complex projective curve of genus
$g$
. The nonabelian Hodge theory of
$\unicode[STIX]{x1D6F4}$
gives the equivalence of categories related to the following three moduli spaces: the moduli space of semistable Higgs bundles of rank
$n$
and of degree
$0$
on
$\unicode[STIX]{x1D6F4}$
(denoted by
${\mathcal{M}}_{\text{Dol}}(\unicode[STIX]{x1D6F4})$
); the moduli space of holomorphic connections of rank
$n$
and of degree
$0$
on
$\unicode[STIX]{x1D6F4}$
(denoted by
${\mathcal{M}}_{\text{DR}}(\unicode[STIX]{x1D6F4})$
); and the character variety
$\text{Hom}(\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D6F4}),\text{GL}(n,\mathbb{C}))/\!/\text{GL}(n,\mathbb{C})$
, which is a universal categorical quotient (denoted by
${\mathcal{M}}_{\text{B}}(\unicode[STIX]{x1D6F4})$
). The closed points of the character variety parametrize certain equivalence classes of representations of the fundamental group
$\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D6F4})$
into
$\text{GL}(n,\mathbb{C})$
(see [Reference Simpson14, Proposition 6.1]). These moduli spaces are related to each other in the following way. First, the moduli space
${\mathcal{M}}_{\text{Hod}}(\unicode[STIX]{x1D6F4})$
of
$\unicode[STIX]{x1D706}$
-connections (which are semistable with degree 0 in the case
$\unicode[STIX]{x1D706}=0$
) gives the relationship between
${\mathcal{M}}_{\text{Dol}}(\unicode[STIX]{x1D6F4})$
and
${\mathcal{M}}_{\text{DR}}(\unicode[STIX]{x1D6F4})$
. Here, we call
$(E,\unicode[STIX]{x1D6FB})$
a
$\unicode[STIX]{x1D706}$
-connection if
$E$
is a vector bundle on
$\unicode[STIX]{x1D6F4}$
and
$\unicode[STIX]{x1D6FB}:E\rightarrow E\otimes \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6F4}}^{1}$
is a homomorphism of sheaves satisfying
$\unicode[STIX]{x1D6FB}(ae)=a\unicode[STIX]{x1D6FB}(e)+\unicode[STIX]{x1D706}d(a)\otimes e$
where
$\unicode[STIX]{x1D706}\in \mathbb{C}$
,
$a\in {\mathcal{O}}_{\unicode[STIX]{x1D6F4}}$
and
$e\in E$
. Then we have the natural map
$\unicode[STIX]{x1D706}:{\mathcal{M}}_{\text{Hod}}(\unicode[STIX]{x1D6F4})\rightarrow \mathbb{C}^{1}$
such that
$\unicode[STIX]{x1D706}^{-1}(0)={\mathcal{M}}_{\text{Dol}}(\unicode[STIX]{x1D6F4})$
and
$\unicode[STIX]{x1D706}^{-1}(1)={\mathcal{M}}_{\text{DR}}(\unicode[STIX]{x1D6F4})$
(e.g., see [Reference Simpson15, Theorem 14]). Finally, the Riemann–Hilbert correspondence gives an isomorphism between the associated complex analytic spaces
${\mathcal{M}}_{\text{DR}}^{\text{an}}(\unicode[STIX]{x1D6F4})$
and
${\mathcal{M}}_{B}^{\text{an}}(\unicode[STIX]{x1D6F4})$
(e.g., see [Reference Simpson15, Proposition 9]).
In this paper, we consider variants of those moduli spaces in the case of punctured curves. We fix an integer
$k>0$
and a
$k$
-tuple
$\boldsymbol{\unicode[STIX]{x1D707}}=(\unicode[STIX]{x1D707}^{1},\ldots ,\unicode[STIX]{x1D707}^{k})$
of partitions of
$n$
, that is,
$\unicode[STIX]{x1D707}^{i}=(\unicode[STIX]{x1D707}_{1}^{i},\ldots ,\unicode[STIX]{x1D707}_{r_{i}}^{i})$
satisfies
$\unicode[STIX]{x1D707}_{1}^{i}\geqslant \unicode[STIX]{x1D707}_{2}^{i}\geqslant \cdots \,$
and
$\unicode[STIX]{x1D707}_{1}^{i}+\cdots +\unicode[STIX]{x1D707}_{r_{i}}^{i}=n$
for
$i=1,\ldots ,k$
. We take
$k$
-distinct points
$p_{1},\ldots ,p_{k}$
on
$\unicode[STIX]{x1D6F4}$
, and define a divisor by
$D:=p_{1}+\cdots +p_{k}$
.
Definition 1.1. (Parabolic Higgs bundles)
We call
$(E,\unicode[STIX]{x1D6F7},\{l_{\ast }^{(i)}\}_{1\leqslant i\leqslant k})$
a parabolic Higgs bundle of rank
$n$
, of degree
$d$
, and of type
$\boldsymbol{\unicode[STIX]{x1D707}}$
if:
-
(1)
$E$
is an algebraic vector bundle on
$\unicode[STIX]{x1D6F4}$
of rank
$n$
and of degree
$d$
; -
(2)
$\unicode[STIX]{x1D6F7}:E\rightarrow E\otimes \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6F4}}^{1}(D)$
is an
${\mathcal{O}}_{\unicode[STIX]{x1D6F4}}$
-homomorphism; and -
(3) for each
$p_{i}$
,
$l_{\ast }^{(i)}$
is a filtration
$E|_{p_{i}}=l_{1}^{(i)}\supset l_{2}^{(i)}\supset \cdots \supset l_{r_{i}}^{(i)}\supset l_{r_{i}+1}^{(i)}=0$
such that
$\dim (l_{j}^{(i)}/l_{j+1}^{(i)})=\unicode[STIX]{x1D707}_{j}^{i}$
and
$\unicode[STIX]{x1D6F7}|_{p_{i}}(l_{j}^{(i)})\subset l_{j+1}^{(i)}\otimes \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6F4}}^{1}(D)|_{p_{i}}$
for
$j=1,\ldots ,r_{i}$
.
The
${\mathcal{O}}_{\unicode[STIX]{x1D6F4}}$
-homomorphism
$\unicode[STIX]{x1D6F7}$
is called a Higgs field.
Definition 1.2. (Parabolic connections)
We call
$(E,\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\}_{1\leqslant i\leqslant k})$
a (regular singular)
$\boldsymbol{\unicode[STIX]{x1D709}}$
-parabolic connection of rank
$n$
, of degree
$d$
, and of type
$\boldsymbol{\unicode[STIX]{x1D707}}$
if:
-
(1)
$E$
is an algebraic vector bundle on
$\unicode[STIX]{x1D6F4}$
of rank
$n$
and of degree
$d$
; -
(2)
$\unicode[STIX]{x1D6FB}:E\rightarrow E\otimes \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6F4}}^{1}(D)$
is a connection; and -
(3) for each
$p_{i}$
,
$l_{\ast }^{(i)}$
is a filtration
$E|_{p_{i}}=l_{1}^{(i)}\supset l_{2}^{(i)}\supset \cdots \supset l_{r_{i}}^{(i)}\supset l_{r_{i}+1}^{(i)}=0$
such that
$\dim (l_{j}^{(i)}/l_{j+1}^{(i)})=\unicode[STIX]{x1D707}_{j}^{i}$
and
$(\text{Res}_{p_{i}}(\unicode[STIX]{x1D6FB})-\unicode[STIX]{x1D709}_{j}^{i}\text{id}_{E|_{p_{i}}})(l_{j}^{(i)})\subset l_{j+1}^{(i)}$
for
$j=1,\ldots ,r_{i}$
.
Here, we put
$r:=\sum \!r_{i}$
and
$\boldsymbol{\unicode[STIX]{x1D709}}:=(\unicode[STIX]{x1D709}_{j}^{i})_{1\leqslant j\leqslant r_{i}}^{1\leqslant i\leqslant k}\in \mathbb{C}^{r}\!$
satisfying
$d+\sum _{i,j}\!\unicode[STIX]{x1D707}_{j}^{i}\unicode[STIX]{x1D709}_{j}^{i}=0$
(see Remark 3.2).
The filtrations
$\{l_{\ast }^{(i)}\}_{1\leqslant i\leqslant k}$
in Definitions 1.1 and 1.2 are said to be parabolic structures of the vector bundles
$E$
.
We take rational numbers
$$\begin{eqnarray}0<\unicode[STIX]{x1D6FC}_{1}^{(i)}<\unicode[STIX]{x1D6FC}_{2}^{(i)}<\cdots <\unicode[STIX]{x1D6FC}_{r_{i}}^{(i)}<1\end{eqnarray}$$
for
$i=1,\ldots ,k$
satisfying
$\unicode[STIX]{x1D6FC}_{j}^{(i)}\neq \unicode[STIX]{x1D6FC}_{j^{\prime }}^{(i^{\prime })}$
for
$(i,j)\neq (i^{\prime },j^{\prime })$
. For the tuple
$\boldsymbol{\unicode[STIX]{x1D6FC}}=(\unicode[STIX]{x1D6FC}_{j}^{(i)})$
, we define the parabolic degree and parabolic slope of a vector bundle with filtrations
$(E,\{l_{\ast }^{(i)}\}_{1\leqslant i\leqslant k})$
by
$$\begin{eqnarray}\displaystyle \text{pardeg}(E) & := & \displaystyle \deg (E)+\mathop{\sum }_{i=1}^{k}\mathop{\sum }_{j=1}^{r_{i}}\unicode[STIX]{x1D6FC}_{j}^{(i)}\dim (l_{j}^{(i)}/l_{j+1}^{(i)}),\nonumber\\ \displaystyle \text{par}\unicode[STIX]{x1D707}(E) & := & \displaystyle \frac{\text{pardeg}(E)}{\text{rk}(E)}.\nonumber\end{eqnarray}$$
Definition 1.3. A parabolic Higgs bundle
$(E,\unicode[STIX]{x1D6F7},\{l_{\ast }^{(i)}\}_{1\leqslant i\leqslant k})$
is
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
-stable (resp.
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
-semistable) if for any proper nonzero subbundle
$F\subset E$
satisfying
$\unicode[STIX]{x1D6F7}(F)\subset F\otimes \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6F4}}^{1}(D)$
, the inequality
$\text{par}\unicode[STIX]{x1D707}(F)<\text{par}\unicode[STIX]{x1D707}(E)$
(resp.
${\leqslant}$
) holds.
Definition 1.4. A
$\boldsymbol{\unicode[STIX]{x1D709}}$
-parabolic connection
$(E,\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\}_{1\leqslant i\leqslant k})$
is
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
-stable (resp.
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
-semistable) if for any proper nonzero subbundle
$F\subset E$
satisfying
$\unicode[STIX]{x1D6FB}(F)\subset F\otimes \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6F4}}^{1}(D)$
, the inequality
$\text{par}\unicode[STIX]{x1D707}(F)<\text{par}\unicode[STIX]{x1D707}(E)$
(resp.
${\leqslant}$
) holds.
We take
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
sufficiently generic. Then we have the equivalence of the notions of
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
-semistable and
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
-stable for parabolic Higgs bundles and
$\boldsymbol{\unicode[STIX]{x1D709}}$
-parabolic connections. We consider the following three moduli spaces: the moduli space of
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
-stable parabolic Higgs bundles on
$\unicode[STIX]{x1D6F4}$
of rank
$n$
, of degree
$d$
, and of type
$\boldsymbol{\unicode[STIX]{x1D707}}$
; the moduli space of
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
-stable
$\boldsymbol{\unicode[STIX]{x1D709}}$
-parabolic connections on
$\unicode[STIX]{x1D6F4}$
of rank
$n$
, of degree
$d$
, and of type
$\boldsymbol{\unicode[STIX]{x1D707}}$
; and the (generic)
$\text{GL}(n,\mathbb{C})$
-character variety, whose points parametrize representations of the fundamental group of
$\unicode[STIX]{x1D6F4}\setminus D$
into
$\text{GL}(n,\mathbb{C})$
where the images of simple loops at the punctures associated to
$p_{1},\ldots ,p_{k}$
are contained in
${\mathcal{C}}_{1},\ldots ,{\mathcal{C}}_{k}$
, respectively. Here,
$({\mathcal{C}}_{1},\ldots ,{\mathcal{C}}_{k})$
is a generic
$k$
-tuple of semisimple conjugacy classes of
$\text{GL}(n,\mathbb{C})$
such that, for each
$i=1,\ldots ,k$
,
$\{\unicode[STIX]{x1D707}_{1}^{i},\unicode[STIX]{x1D707}_{2}^{i},\ldots \}$
is the set of the multiplicities of the eigenvalues of any matrix in
${\mathcal{C}}_{i}$
. These moduli spaces are connected nonsingular algebraic varieties of dimension
$$\begin{eqnarray}n^{2}(2g-2+k)-\mathop{\sum }_{i,j}(\unicode[STIX]{x1D707}_{j}^{i})^{2}+2\end{eqnarray}$$
(see [Reference Hausel, Letellier and Rodriguez-Villegas5], [Reference Hausel, Letellier and Rodriguez-Villegas6], [Reference Inaba8], [Reference Inaba and Saito9] and [Reference Konno11]). Note that, for any
$\boldsymbol{\unicode[STIX]{x1D709}}$
, the moduli space of
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
-stable
$\boldsymbol{\unicode[STIX]{x1D709}}$
-parabolic connections on
$\unicode[STIX]{x1D6F4}$
is nonsingular by the parabolic structures and the stability. On the other hand, only for generic
$({\mathcal{C}}_{1},\ldots ,{\mathcal{C}}_{k})$
, the character variety is nonsingular. We denote the three moduli spaces by
${\mathcal{M}}_{Dol}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\mathbf{0})$
,
${\mathcal{M}}_{DR}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D709}})$
, and
${\mathcal{M}}_{B}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D708}})$
, respectively. Here,
$\boldsymbol{\unicode[STIX]{x1D708}}$
denotes the eigenvalues of any matrix of each conjugacy class in
$({\mathcal{C}}_{1},\ldots ,{\mathcal{C}}_{k})$
and
$\mathbf{0}$
means that Higgs fields have nilpotent residues at each puncture.
For the case of the punctured curve
$\unicode[STIX]{x1D6F4}\setminus D$
, we study relationships between those moduli spaces. We put
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}:=\left\{\left(\unicode[STIX]{x1D706},(\unicode[STIX]{x1D709}_{j}^{i})_{1\leqslant j\leqslant r_{i}}^{1\leqslant i\leqslant k}\right)\in \mathbb{C}\times \mathbb{C}^{r}\,\left|\,\unicode[STIX]{x1D706}d+\mathop{\sum }_{i,j}\unicode[STIX]{x1D707}_{j}^{i}\unicode[STIX]{x1D709}_{j}^{i}=0\right.\right\}.\end{eqnarray}$$
Definition 1.5. (Parabolic
$\unicode[STIX]{x1D706}$
-connections)
For
$(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}})\in \unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
, we call
$(\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\}_{1\leqslant i\leqslant k})$
a
$\boldsymbol{\unicode[STIX]{x1D709}}$
-parabolic
$\unicode[STIX]{x1D706}$
-connection of rank
$n$
, of degree
$d$
, and of type
$\boldsymbol{\unicode[STIX]{x1D707}}$
if:
-
(1)
$E$
is an algebraic vector bundle on
$\unicode[STIX]{x1D6F4}$
of rank
$n$
and of degree
$d$
; -
(2)
$\unicode[STIX]{x1D6FB}:E\rightarrow E\otimes \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6F4}}^{1}(D)$
is a
$\unicode[STIX]{x1D706}$
-connection, that is,
$\unicode[STIX]{x1D6FB}$
is a homomorphism of sheaves of
$\mathbb{C}$
vector spaces satisfying
$\unicode[STIX]{x1D6FB}(fa)=\unicode[STIX]{x1D706}a\otimes df+f\unicode[STIX]{x1D6FB}(a)$
for
$f\in {\mathcal{O}}_{\unicode[STIX]{x1D6F4}}$
and
$a\in E$
; and -
(3) for each
$p_{i}$
,
$l_{\ast }^{(i)}$
is a filtration
$E|_{p_{i}}=l_{1}^{(i)}\supset l_{2}^{(i)}\supset \cdots \supset l_{r_{i}}^{(i)}\supset l_{r_{i}+1}^{(i)}=0$
such that
$\dim (l_{j}^{(i)}/l_{j+1}^{(i)})=\unicode[STIX]{x1D707}_{j}^{i}$
and
$(\text{Res}_{p_{i}}(\unicode[STIX]{x1D6FB})-\unicode[STIX]{x1D709}_{j}^{i}\text{id}_{E|_{p_{i}}})(l_{j}^{(i)})\subset l_{j+1}^{(i)}$
for
$j=1,\ldots ,r_{i}$
.
Definition 1.6. A parabolic
$\unicode[STIX]{x1D706}$
-connection
$(\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\}_{1\leqslant i\leqslant k})$
is
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
-stable (resp.
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
-semistable) if for any proper nonzero subbundle
$F\subset E$
satisfying
$\unicode[STIX]{x1D6FB}(F)\subset F\otimes \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6F4}}^{1}(D)$
, the inequality
$\text{par}\unicode[STIX]{x1D707}(F)<\text{par}\unicode[STIX]{x1D707}(E)$
(resp.
${\leqslant}$
) holds.
If we chose
$\boldsymbol{\unicode[STIX]{x1D6FC}}=(\unicode[STIX]{x1D6FC}_{j}^{(i)})$
sufficiently generic, then a parabolic
$\unicode[STIX]{x1D706}$
-connection
$(\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\})$
is
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
-stable if and only if
$(\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\})$
is
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
-semistable.
We take
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
sufficiently generic. We construct the moduli space of
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
-stable parabolic
$\unicode[STIX]{x1D706}$
-connections over
$\unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
as a subscheme of the coarse moduli scheme of semistable parabolic
$\unicode[STIX]{x1D6EC}_{D}^{1}$
-tuples constructed in [Reference Inaba, Iwasaki and Saito10], denoted by
$$\begin{eqnarray}\unicode[STIX]{x1D70B}:{\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}\longrightarrow \unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}.\end{eqnarray}$$
We have
$\unicode[STIX]{x1D70B}^{-1}(1,\boldsymbol{\unicode[STIX]{x1D709}})={\mathcal{M}}_{\text{DR}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D709}})$
and
$\unicode[STIX]{x1D70B}^{-1}(0,\mathbf{0})={\mathcal{M}}_{\text{Dol}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\mathbf{0})$
. On the other hand, by the moduli theoretic description of the Riemann–Hilbert correspondence (see [Reference Inaba, Iwasaki and Saito10], [Reference Inaba8] and [Reference Inaba and Saito9]), we obtain the analytic isomorphism
${\mathcal{M}}_{\text{DR}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D709}})\cong {\mathcal{M}}_{\text{B}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D708}})$
where
$\boldsymbol{\unicode[STIX]{x1D708}}=rh_{d}(\boldsymbol{\unicode[STIX]{x1D709}})$
and
$\boldsymbol{\unicode[STIX]{x1D708}}$
is generic. Here,
$rh_{d}$
is the map defined by
$\unicode[STIX]{x1D709}_{j}^{i}\mapsto \text{exp}(-2\unicode[STIX]{x1D70B}\sqrt{-1}\unicode[STIX]{x1D709}_{j}^{i})$
for
$i=1,\ldots ,k$
and
$j=1,\ldots ,r_{i}$
.
For smooth projective varieties, one can define the Hodge structure on the cohomology groups of the smooth projective varieties. Deligne generalized the Hodge structure to any complex algebraic varieties, not necessarily smooth or projective, that is, one can define the mixed Hodge structure on the cohomology groups of the varieties ([Reference Deligne3], [Reference Deligne4]). The moduli spaces
${\mathcal{M}}_{Dol}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\mathbf{0})$
,
${\mathcal{M}}_{DR}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D709}})$
, and
${\mathcal{M}}_{B}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D708}})$
are smooth. However, these moduli spaces are not projective. The purpose of this paper is to study the mixed Hodge structures of
${\mathcal{M}}_{Dol}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\mathbf{0})$
,
${\mathcal{M}}_{DR}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D709}})$
.
The main theorem is the following
Theorem 1.7. (Theorems 3.13 and 4.13)
-
(1) The ordinary rational cohomology groups of the fibers of
$\unicode[STIX]{x1D70B}:{\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}\rightarrow \unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
are isomorphic. Moreover, the isomorphism preserves the mixed Hodge structures on the cohomology groups of the fibers. -
(2) In particular, we have an isomorphism
which preserves the mixed Hodge structures.
$$\begin{eqnarray}H^{k}({\mathcal{M}}_{\text{DR}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D709}}),\mathbb{Q})\cong H^{k}({\mathcal{M}}_{\text{Dol}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\mathbf{0}),\mathbb{Q})\end{eqnarray}$$
-
(3) The mixed Hodge structure of
$H^{k}({\mathcal{M}}_{\text{Dol}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\mathbf{0}),\mathbb{Q})$
is pure of weight
$k$
, and the mixed Hodge structure on
$H^{k}({\mathcal{M}}_{\text{DR}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D709}}),\mathbb{Q})$
is pure of weight
$k$
. -
(4) The Poincaré polynomials of character varieties
${\mathcal{M}}_{B}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D708}})$
are independent of the choice of generic eigenvalues.
These assertions hold for the rational cohomology groups with compact support.
The main idea of the proof of this theorem is as follows. First, we show that the map
$\unicode[STIX]{x1D70B}:{\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}\rightarrow \unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
is smooth in the same way as in [Reference Arinkin1, Lemma 4], [Reference Inaba8, Theorem 2.1], [Reference Inaba and Saito9] and [Reference Simpson17, Lemma 6.1]. Second, there is a natural
$\mathbb{C}^{\times }$
-action on
${\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}$
. We check that some conditions are fulfilled for this
$\mathbb{C}^{\times }$
-action (Lemma 3.12). The conditions are the assumptions of [Reference Hausel, Letellier and Rodriguez-Villegas5, Theorem B.1] in Appendix B. By the application of [Reference Hausel, Letellier and Rodriguez-Villegas5, Theorem B.1] for the map
$\unicode[STIX]{x1D70B}$
, we obtain the assertions (1), (2) and (3). Third, we consider the moduli theoretic description of the Riemann–Hilbert correspondence, which induces an analytic isomorphism between
${\mathcal{M}}_{\text{DR}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D709}})$
and
${\mathcal{M}}_{\text{B}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D708}})$
in general case. It is shown in [Reference Inaba and Saito9] that the Riemann–Hilbert correspondence induces this analytic isomorphism. In the general case, the proof in [Reference Inaba and Saito9] is same as in the proof of [Reference Inaba8, Theorem 2.2]. By this analytic isomorphism and the assertion (1), we obtain the assertion (4).
The organization of this paper is as follows. In Section 2, we recall Deligne’s mixed Hodge structure. In Section 3, we construct the moduli space of semistable parabolic
$\unicode[STIX]{x1D706}$
-connection
$\unicode[STIX]{x1D70B}:{\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}\rightarrow \unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
and we show that the map
$\unicode[STIX]{x1D70B}:{\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}\rightarrow \unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
is smooth. In Section 3.3, we prove the assertions (1), (2) and (3) of Theorem 1.7. In Section 4, we recall the Riemann–Hilbert correspondence, and we show that the Poincaré polynomials of character varieties
${\mathcal{M}}_{B}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D708}})$
are independent of the choice of generic eigenvalues by the correspondence.
2 Preliminaries
In this section, we recall the definition of the mixed Hodge structures and a basic property of the mixed Hodge structures.
2.1 Mixed Hodge structure
Definition 2.1. A mixed Hodge structure consists of:
-
(1) a finitely generated free
$\mathbb{Z}$
-module
$H^{\mathbb{Z}}$
; -
(2) an increasing filtration
$W_{k}\subset W_{k+1}$
of
$H^{\mathbb{Q}}=H^{\mathbb{Z}}\otimes \mathbb{Q}$
; -
(3) a decreasing filtration
$F^{p}\supset F^{p+1}$
of
$H^{\mathbb{C}}$
such that the filtration induced by
$F^{\bullet }$
on the complexified graded pieces of the filtration
$W_{\bullet }$
endows every graded piece
$\text{Gr}^{k}W_{\bullet }:=W_{k}/W_{k-1}$
with a pure Hodge structure of weight
$k$
, that is, for any
$0\leqslant p\leqslant k$
we have
$$\begin{eqnarray}\text{Gr}^{k}W_{\bullet }^{\mathbb{C}}=F^{p}\text{Gr}^{k}W_{\bullet }^{\mathbb{C}}\oplus \overline{F^{k-p+1}\text{Gr}^{k}W_{\bullet }^{\mathbb{C}}}.\end{eqnarray}$$
The increasing filtration
$W_{\bullet }$
is called the weight filtration, and the decreasing filtration
$F^{\bullet }$
is called the Hodge filtration.
Deligne in [Reference Deligne3] and [Reference Deligne4] proved the existence of mixed Hodge structures on the cohomology of a complex algebraic variety.
Theorem 2.2. ([Reference Deligne3], [Reference Deligne4])
Let
$X$
be a complex algebraic variety. Then there exists a mixed Hodge structure on
$H^{j}(X,\mathbb{C})$
. Moreover, the weight filtration satisfies
$$\begin{eqnarray}0=W_{-1}\subseteq W_{0}\subseteq \cdots \subseteq W_{2j}=H^{j}(X,\mathbb{Q})\end{eqnarray}$$
and the Hodge filtration satisfies
$$\begin{eqnarray}H^{j}(X,\mathbb{C})=F^{0}\supseteq F^{1}\supseteq \cdots \supseteq F^{j}\supseteq F^{j+1}=0.\end{eqnarray}$$
One can define a mixed Hodge structure on the compactly supported cohomology
$H_{c}^{\ast }(X,\mathbb{Q})$
. The following theorem is basic property of mixed Hodge structures (for a proof, e.g., see [Reference Peters and Steenbrink13]).
Theorem 2.3. (Poincaré duality)
For a smooth connected
$X$
, we have that Poincaré duality
$$\begin{eqnarray}H^{k}(X,\mathbb{Q})\times H_{c}^{2d-k}(X,\mathbb{Q})\longrightarrow H_{c}^{2d}(X)\cong \mathbb{Q}(-d)\end{eqnarray}$$
is compatible with mixed Hodge structures, where
$\mathbb{Q}(-d)$
is the pure mixed Hodge structure on
$\mathbb{Q}$
with weight
$2d$
and Hodge filtration
$F^{d}=\mathbb{Q}$
and
$F^{d+1}=0$
.
3 Nonabelian Hodge theory
3.1
$\unicode[STIX]{x1D706}$
-connection
We fix integers
$g\geqslant 0,k>0$
and
$n>0$
. We also fix a
$k$
-tuple of partition of
$n$
, denoted by
$\boldsymbol{\unicode[STIX]{x1D707}}=(\unicode[STIX]{x1D707}^{1},\ldots ,\unicode[STIX]{x1D707}^{k})$
, that is,
$\unicode[STIX]{x1D707}^{i}=(\unicode[STIX]{x1D707}_{1}^{i},\ldots ,\unicode[STIX]{x1D707}_{r_{i}}^{i})$
such that
$\unicode[STIX]{x1D707}_{1}^{i}\geqslant \unicode[STIX]{x1D707}_{2}^{i}\geqslant \cdots \,$
are nonnegative integers and
$\sum _{j}\unicode[STIX]{x1D707}_{j}^{i}=n$
. Let
$\unicode[STIX]{x1D6F4}$
be a smooth complex projective curve of genus
$g$
. We fix
$k$
-distinct points
$p_{1},\ldots ,p_{k}$
in
$\unicode[STIX]{x1D6F4}$
and we define a divisor by
$D:=p_{1}+\cdots +p_{k}$
. We put
$\unicode[STIX]{x1D6F4}_{0}=\unicode[STIX]{x1D6F4}\setminus D$
. For integer
$d$
, we put
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}:=\left\{\left(\unicode[STIX]{x1D706},(\unicode[STIX]{x1D709}_{j}^{i})_{1\leqslant j\leqslant r_{i}}^{1\leqslant i\leqslant k}\right)\in \mathbb{C}\times \mathbb{C}^{r}\,\left|\,\unicode[STIX]{x1D706}d+\mathop{\sum }_{i,j}\unicode[STIX]{x1D707}_{j}^{i}\unicode[STIX]{x1D709}_{j}^{i}=0\right.\right\}\end{eqnarray}$$
where
$r:=\sum r_{i}$
. We take
$(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}})\in \unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
where
$\boldsymbol{\unicode[STIX]{x1D709}}=(\unicode[STIX]{x1D709}_{j}^{i})_{1\leqslant j\leqslant r_{i}}^{1\leqslant i\leqslant k}$
.
Definition 3.1. For
$(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}})\in \unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
, we call
$(\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\}_{1\leqslant i\leqslant k})$
a
$\boldsymbol{\unicode[STIX]{x1D709}}$
-parabolic
$\unicode[STIX]{x1D706}$
-connection of rank
$n$
, of degree
$d$
, and of type
$\boldsymbol{\unicode[STIX]{x1D707}}$
if:
-
(1)
$E$
is an algebraic vector bundle on
$\unicode[STIX]{x1D6F4}$
of rank
$n$
and of degree
$d$
; -
(2)
$\unicode[STIX]{x1D6FB}:E\rightarrow E\otimes \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6F4}}^{1}(D)$
is a
$\unicode[STIX]{x1D706}$
-connection, that is,
$\unicode[STIX]{x1D6FB}$
is a homomorphism of sheaves of
$\mathbb{C}$
vector spaces satisfying
$\unicode[STIX]{x1D6FB}(fa)=\unicode[STIX]{x1D706}a\otimes df+f\unicode[STIX]{x1D6FB}(a)$
for
$f\in {\mathcal{O}}_{\unicode[STIX]{x1D6F4}}$
and
$a\in E$
; and -
(3) for each
$p_{i}$
,
$l_{\ast }^{(i)}$
is a filtration
$E|_{p_{i}}=l_{1}^{(i)}\supset l_{2}^{(i)}\supset \cdots \supset l_{r_{i}}^{(i)}\supset l_{r_{i}+1}^{(i)}=0$
such that
$\dim (l_{j}^{(i)}/l_{j+1}^{(i)})=\unicode[STIX]{x1D707}_{j}^{i}$
and
$(\text{Res}_{p_{i}}(\unicode[STIX]{x1D6FB})-\unicode[STIX]{x1D709}_{j}^{i}\text{id}_{E|_{p_{i}}})(l_{j}^{(i)})\subset l_{j+1}^{(i)}$
for
$j=1,\ldots ,r_{i}$
.
For
$\unicode[STIX]{x1D706}=1$
, this is a regular singular
$\boldsymbol{\unicode[STIX]{x1D709}}$
-parabolic connection of spectral type
$\boldsymbol{\unicode[STIX]{x1D707}}$
(Definition 1.2). For
$\unicode[STIX]{x1D706}=0$
and
$\boldsymbol{\unicode[STIX]{x1D709}}=0$
, this is a parabolic Higgs bundle (Definition 1.1).
Remark 3.2. For
$\unicode[STIX]{x1D706}\neq 0$
, we have
$$\begin{eqnarray}\deg E=\deg (\det (E))=-\mathop{\sum }_{i=1}^{k}\text{tr}\left(\text{Res}_{p_{i}}((\unicode[STIX]{x1D706}^{-1}\unicode[STIX]{x1D6FB}))\right)=-\mathop{\sum }_{i=1}^{k}\mathop{\sum }_{j=1}^{r_{i}}\frac{\unicode[STIX]{x1D707}_{j}^{i}\unicode[STIX]{x1D709}_{j}^{i}}{\unicode[STIX]{x1D706}}=d.\end{eqnarray}$$
We take rational numbers
$$\begin{eqnarray}0<\unicode[STIX]{x1D6FC}_{1}^{(i)}<\unicode[STIX]{x1D6FC}_{2}^{(i)}<\cdots <\unicode[STIX]{x1D6FC}_{r_{i}}^{(i)}<1\end{eqnarray}$$
for
$i=1,\ldots ,k$
satisfying
$\unicode[STIX]{x1D6FC}_{j}^{(i)}\neq \unicode[STIX]{x1D6FC}_{j^{\prime }}^{(i^{\prime })}$
for
$(i,j)\neq (i^{\prime },j^{\prime })$
. We choose
$\boldsymbol{\unicode[STIX]{x1D6FC}}=(\unicode[STIX]{x1D6FC}_{j}^{(i)})$
sufficiently generic.
Definition 3.3. A parabolic
$\unicode[STIX]{x1D706}$
-connection
$(\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\}_{1\leqslant i\leqslant k})$
is
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
-stable (resp.
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
-semistable) if for any proper nonzero subbundle
$F\subset E$
satisfying
$\unicode[STIX]{x1D6FB}(F)\subset F\otimes \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6F4}}^{1}(D)$
, the inequality
$$\begin{eqnarray}\text{par}\,\unicode[STIX]{x1D707}(F)<\text{par}\,\unicode[STIX]{x1D707}(E)\quad (\text{resp. }\leqslant )\end{eqnarray}$$
holds. Here, the induced parabolic structure on a subbundle
$F\subset E$
is the filtrations
$F|_{p_{i}}=F|_{p_{i}}\cap l_{1}^{(i)}\supset F|_{p_{i}}\cap l_{2}^{(i)}\supset \cdots \supset F|_{p_{i}}\cap l_{r_{i}}^{(i)}\supset F|_{p_{i}}\cap l_{r_{i}+1}^{(i)}=0$
for each
$p_{i}$
.
Remark 3.4. [Reference Inaba8, Remark 2.2]
We chose
$\boldsymbol{\unicode[STIX]{x1D6FC}}=(\unicode[STIX]{x1D6FC}_{j}^{(i)})$
sufficiently generic. Then a parabolic
$\unicode[STIX]{x1D706}$
-connection
$(\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\})$
is
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
-stable if and only if
$(\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\})$
is
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
-semistable.
3.2 Construction of the moduli space
The argument in this subsection is almost same as in [Reference Inaba8]. The difference from [Reference Inaba8] is that we fix the
$k$
-distinct points
$\{p_{1},\ldots ,p_{k}\}$
, the flag
$\{l_{\ast }^{(i)}\}$
is not necessarily full flag, and we construct the moduli space of
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
-semistable parabolic
$\unicode[STIX]{x1D706}$
-connections instead of
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
-semistable parabolic connections.
We recall the definition of a parabolic
$\unicode[STIX]{x1D6EC}_{D}^{1}$
-triple defined in [Reference Inaba, Iwasaki and Saito10]. Let
$D$
be an effective divisor on a nonsingular curve
$\unicode[STIX]{x1D6F4}$
. We define
$\unicode[STIX]{x1D6EC}_{D}^{1}$
as
${\mathcal{O}}_{\unicode[STIX]{x1D6F4}}\oplus \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6F4}}^{1}(D)^{\vee }$
with the bimodule structure given by
$$\begin{eqnarray}\displaystyle & \displaystyle f(a,v)=(fa,fv)\quad (f,a\in {\mathcal{O}}_{\unicode[STIX]{x1D6F4}},~v\in \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6F4}}^{1}(D)^{\vee }), & \displaystyle \nonumber\\ \displaystyle & \displaystyle (a,v)f=(fa+v(f),fv)\quad (f,a\in {\mathcal{O}}_{\unicode[STIX]{x1D6F4}},~v\in \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6F4}}^{1}(D)^{\vee }). & \displaystyle \nonumber\end{eqnarray}$$
Definition 3.5. We say
$(E_{1},E_{2},\unicode[STIX]{x1D6F7},F_{\ast }(E_{1}))$
a parabolic
$\unicode[STIX]{x1D6EC}_{D}^{1}$
-triple on
$\unicode[STIX]{x1D6F4}$
of rank
$n$
and of degree
$d$
if:
-
(1)
$E_{1}$
and
$E_{2}$
are vector bundles on
$\unicode[STIX]{x1D6F4}$
of rank
$n$
and of degree
$d$
; -
(2)
$\unicode[STIX]{x1D6F7}:\unicode[STIX]{x1D6EC}_{D}^{1}\otimes E_{1}\rightarrow E_{2}$
is a left
${\mathcal{O}}_{\unicode[STIX]{x1D6F4}}$
-homomorphism; and -
(3)
$E_{1}=F_{1}(E_{1})\supset F_{2}(E_{1})\supset \cdots \supset F_{l}(E_{1})\supset F_{l+1}(E_{1})=E_{1}(-D)$
is a filtration by coherent subsheaves.
Note that to give a left
${\mathcal{O}}_{\unicode[STIX]{x1D6F4}}$
-homomorphism
$\unicode[STIX]{x1D6F7}:\unicode[STIX]{x1D6EC}_{D}^{1}\otimes E_{1}\rightarrow E_{2}$
is equivalent to give an
${\mathcal{O}}_{\unicode[STIX]{x1D6F4}}$
-homomorphism
$\unicode[STIX]{x1D719}:E_{1}\rightarrow E_{2}$
and a morphism
$\unicode[STIX]{x1D6FB}:E_{1}\rightarrow E_{2}\otimes \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6F4}}^{1}(D)$
such that
$\unicode[STIX]{x1D6FB}(fa)=\unicode[STIX]{x1D719}(a)\otimes df+f\unicode[STIX]{x1D6FB}(a)$
for
$f\in {\mathcal{O}}_{\unicode[STIX]{x1D6F4}}$
and
$a\in E_{1}$
. We also denote the parabolic
$\unicode[STIX]{x1D6EC}_{D}^{1}$
-triple
$(E_{1},E_{2},\unicode[STIX]{x1D6F7},F_{\ast }(E_{1}))$
by
$(E_{1},E_{2},\unicode[STIX]{x1D719},\unicode[STIX]{x1D6FB},F_{\ast }(E_{1}))$
.
We take positive integers
$\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2},\unicode[STIX]{x1D6FE}$
and rational numbers
$0<\unicode[STIX]{x1D6FC}_{1}^{\prime }<\cdots <\unicode[STIX]{x1D6FC}_{l}^{\prime }<1$
. We assume
$\unicode[STIX]{x1D6FE}\gg 0$
.
Definition 3.6. A parabolic
$\unicode[STIX]{x1D6EC}_{D}^{1}$
-triple
$(E_{1},E_{2},\unicode[STIX]{x1D719},\unicode[STIX]{x1D6FB},F_{\ast }(E_{1}))$
is
$(\boldsymbol{\unicode[STIX]{x1D6FC}}^{\prime },\boldsymbol{\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D6FE})$
-stable (resp.
$(\boldsymbol{\unicode[STIX]{x1D6FC}}^{\prime },\boldsymbol{\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D6FE})$
-semistable) if for any subbundle
$(F_{1},F_{2})\subset (E_{1},E_{2})$
satisfying
$(0,0)\neq (F_{1},F_{2})\neq (E_{1},E_{2})$
and
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D6EC}_{D}^{1}\otimes F_{1})\subset F_{2}$
, the inequality
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D6FD}_{1}\deg F_{1}(-D)+\unicode[STIX]{x1D6FD}_{2}(\deg F_{2}-\unicode[STIX]{x1D6FE}\,\text{rank}\,F_{2})+\unicode[STIX]{x1D6FD}_{1}\mathop{\sum }_{j=1}^{l}\unicode[STIX]{x1D6FC}_{j}^{\prime }\text{length}(F_{j}(E_{1})\cap F_{1}/(F_{j+1}(E_{1})\cap F_{1}))}{\unicode[STIX]{x1D6FD}_{1}\,\text{rank}\,F_{1}+\unicode[STIX]{x1D6FD}_{2}\,\text{rank}\,F_{2}} & & \displaystyle \nonumber\\ \displaystyle \underset{(\text{resp.}~\leqslant )}{{<}}\frac{\unicode[STIX]{x1D6FD}_{1}\deg E_{1}(-D)+\unicode[STIX]{x1D6FD}_{2}(\deg E_{2}-\unicode[STIX]{x1D6FE}\,\text{rank}\,E_{2})+\unicode[STIX]{x1D6FD}_{1}\mathop{\sum }_{j=1}^{l}\unicode[STIX]{x1D6FC}_{j}^{\prime }\text{length}((F_{j}(E_{1}))/(F_{j+1}(E_{1})))}{\unicode[STIX]{x1D6FD}_{1}\,\text{rank}\,E_{1}+\unicode[STIX]{x1D6FD}_{2}\,\text{rank}\,E_{2}} & & \displaystyle \nonumber\end{eqnarray}$$
holds.
Theorem 3.7. [Reference Inaba, Iwasaki and Saito10, Theorem 5.1]
Fix integers
$g\geqslant 0$
,
$k>0$
,
$n>0$
,
$l>0$
,
$d$
and a tuple of positive integers
$\{d_{i}\}_{1\leqslant i\leqslant l}$
where
$0<d_{1}\leqslant d_{2}\leqslant \cdots \leqslant d_{l}=kn$
. Let
$S$
be an algebraic scheme over
$\mathbb{C}$
,
${\mathcal{C}}$
be a flat family of smooth projective curves of genus
$g$
and
${\mathcal{D}}$
be an effective Cartier divisor on
${\mathcal{C}}$
flat over
$S$
. Then, there exists the coarse moduli scheme
$\overline{{\mathcal{M}}_{n,d,\{d_{i}\}}^{\boldsymbol{\unicode[STIX]{x1D6FC}}^{\prime },\boldsymbol{\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D6FE}}}({\mathcal{C}}/S,{\mathcal{D}})$
of
$(\boldsymbol{\unicode[STIX]{x1D6FC}}^{\prime },\boldsymbol{\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D6FE})$
-stable parabolic
$\unicode[STIX]{x1D6EC}_{D}^{1}$
-triples
$(E_{1},E_{2},\unicode[STIX]{x1D719},\unicode[STIX]{x1D6FB},F_{\ast }(E_{1}))$
on
${\mathcal{C}}$
over
$S$
such that
$n=\text{rank}\,E_{1}=\text{rank}\,E_{2}$
,
$d=\deg E_{1}=\deg E_{2}$
and
$d_{i}=\text{length}(E_{1}/F_{i+1}(E_{1}))$
. If
$\boldsymbol{\unicode[STIX]{x1D6FC}}^{\prime }$
is generic, then it is projective over
$S$
.
Definition 3.8. We put
${\mathcal{C}}=\unicode[STIX]{x1D6F4}\times \unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
,
$S=\unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
,
$\tilde{p}_{i}=p_{i}\times \unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
(for
$i=1,\ldots ,k$
) and
${\mathcal{D}}=\tilde{p}_{1}+\cdots +\tilde{p}_{k}$
. We define a functor
${\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D707}},d}({\mathcal{C}}/S,{\mathcal{D}})$
of the category of locally Noetherian schemes over
$S$
to the category of sets by
$$\begin{eqnarray}{\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D707}},d}({\mathcal{C}}/S,{\mathcal{D}})(T):=\left\{(\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\}_{1\leqslant i\leqslant k})\right\}/\sim ,\end{eqnarray}$$
for a locally Noetherian scheme
$T$
over
$S$
where:
-
(1)
$E$
is a vector bundle on
${\mathcal{C}}_{T}$
of rank
$n$
; -
(2)
$\unicode[STIX]{x1D706}:E\rightarrow E$
is the
${\mathcal{O}}_{{\mathcal{C}}_{T}}$
-homomorphism defined by
$a(x)\mapsto \unicode[STIX]{x1D706}(x)\cdot a(x)$
where
$\unicode[STIX]{x1D706}(x)$
is the image of
$x\in {\mathcal{C}}_{T}$
by the composition
${\mathcal{C}}_{T}\rightarrow S\rightarrow \mathbb{C}$
of the natural morphism and the projection; -
(3)
$\unicode[STIX]{x1D6FB}:E\rightarrow E\otimes \unicode[STIX]{x1D6FA}_{{\mathcal{C}}_{T}}^{1}(({\mathcal{D}}_{T}))$
is a relative
$\unicode[STIX]{x1D706}_{T/S}$
-connection; -
(4)
$E|_{(\tilde{p}_{i})_{T}}=l_{1}^{(i)}\supset l_{2}^{(i)}\supset \cdots \supset l_{r_{i}}^{(i)}\supset l_{r_{i}+1}^{(i)}=0$
is a filtration by subbundles such that
$(\text{Res}_{(\tilde{p}_{i})_{T}}(\unicode[STIX]{x1D6FB})-(\unicode[STIX]{x1D709}_{j}^{i})_{T})\subset l_{j+1}^{(i)}$
for
$j=1,\ldots ,r_{i}$
,
$i=1,\ldots ,k$
; -
(5) for any geometric point
$t\in T$
,
$\dim (l_{j}^{i}/l_{j+1}^{i})\otimes k(t)=\unicode[STIX]{x1D707}_{j}^{i}$
for any
$i,j$
and
$(\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\})\otimes k(t)$
is
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
-stable.
The following proposition is shown by the same way as in the proof [Reference Inaba8, Theorem 2.1].
Proposition 3.9. There exists a relative coarse moduli scheme
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}:{\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}} & \longrightarrow & \displaystyle \unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}\nonumber\\ \displaystyle (\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\}_{1\leqslant i\leqslant r_{i}}) & \longmapsto & \displaystyle (\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}})\nonumber\end{eqnarray}$$
of
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
-stable parabolic
$\unicode[STIX]{x1D706}$
-connections of rank
$n$
, of degree
$d$
, and of type
$\boldsymbol{\unicode[STIX]{x1D707}}$
. For simplicity, we drop
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
and
$d$
from the notation of the moduli space.
If
$n$
and
$d$
are coprime, then
${\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}$
is a relative fine moduli scheme, that is, there is a universal family over
${\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}$
.
Proof. Fix a weight
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
which determines the stability of parabolic
$\unicode[STIX]{x1D706}$
-connections. We take positive integers
$\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2},\unicode[STIX]{x1D6FE}$
and rational numbers
$0<\tilde{\unicode[STIX]{x1D6FC}}_{1}^{(i)}<\cdots <\tilde{\unicode[STIX]{x1D6FC}}_{r_{i}}^{(i)}<1$
satisfying
$(\unicode[STIX]{x1D6FD}_{1}+\unicode[STIX]{x1D6FD}_{2})\unicode[STIX]{x1D6FC}_{j}^{(i)}=\unicode[STIX]{x1D6FD}_{1}\tilde{\unicode[STIX]{x1D6FC}}_{j}^{(i)}$
for any
$i,j$
. We assume
$\unicode[STIX]{x1D6FE}\gg 0$
. We take an increasing sequence
$0<\unicode[STIX]{x1D6FC}_{1}^{\prime }<\cdots <\unicode[STIX]{x1D6FC}_{l}^{\prime }<1$
such that
$$\begin{eqnarray}\{\unicode[STIX]{x1D6FC}_{i}^{\prime }\mid 1\leqslant i\leqslant l\}=\{\tilde{\unicode[STIX]{x1D6FC}}_{j}^{(i)}\mid 1\leqslant i\leqslant k,1\leqslant j\leqslant r_{i}\}\end{eqnarray}$$
where we put
$l=\sum _{i=1}^{k}r_{i}$
. We take any member
$(\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\}_{1\leqslant i\leqslant k})\in {\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D707}},d}({\mathcal{C}}/S,{\mathcal{D}})(T)$
. For each
$1\leqslant p\leqslant l$
, there exist
$i,j$
satisfying
$\tilde{\unicode[STIX]{x1D6FC}}_{j}^{(i)}=\unicode[STIX]{x1D6FC}_{p}^{\prime }$
. We put
$F_{1}(E):=E$
and define inductively
$$\begin{eqnarray}F_{p}(E):=\text{Ker}(F_{p-1}(E)\longrightarrow E|_{(\tilde{p}_{i})_{T}}/l_{p})\end{eqnarray}$$
for
$p=1,\ldots ,l$
. Here, we put
$l_{p}:=l_{j}^{(i)}$
for the unique
$(i,j)$
for which
$\tilde{\unicode[STIX]{x1D6FC}}_{j}^{(i)}=\unicode[STIX]{x1D6FC}_{p}^{\prime }$
. We also put
$d_{p}:=\text{length}((E/F_{p+1}(E))\otimes k(t))$
for
$p=1,\ldots ,l$
and
$t\in T$
. Then
$(\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\})\mapsto (E,E,\unicode[STIX]{x1D706}\text{id},\unicode[STIX]{x1D6FB},F_{\ast }(E))$
determines the morphism
$$\begin{eqnarray}\unicode[STIX]{x1D704}:{\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D707}},d}({\mathcal{C}}/S,{\mathcal{D}})\longrightarrow \overline{{\mathcal{M}}_{n,d,\{d_{i}\}}^{\boldsymbol{\unicode[STIX]{x1D6FC}}^{\prime },\boldsymbol{\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D6FE}}}({\mathcal{C}}/S,{\mathcal{D}})\end{eqnarray}$$
where
$\overline{{\mathcal{M}}_{n,d,\{d_{i}\}}^{\boldsymbol{\unicode[STIX]{x1D6FC}}^{\prime },\boldsymbol{\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D6FE}}}({\mathcal{C}}/S,{\mathcal{D}})$
is the moduli functor of
$(\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D6FE})$
-stable
$\unicode[STIX]{x1D6EC}_{D}^{1}$
-triples whose coarse moduli scheme exists by Theorem 3.7. Then we have that a certain subscheme
${\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}$
of
$\overline{{\mathcal{M}}_{n,d,\{d_{i}\}}^{\boldsymbol{\unicode[STIX]{x1D6FC}}^{\prime },\boldsymbol{\unicode[STIX]{x1D6FD}},\unicode[STIX]{x1D6FE}}}({\mathcal{C}}/S,{\mathcal{D}})$
is just the coarse moduli scheme of
${\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D6FC}},\boldsymbol{\unicode[STIX]{x1D707}},d}({\mathcal{C}}/S,{\mathcal{D}})$
in the same way as in [Reference Inaba, Iwasaki and Saito10, Theorem 2.1] and [Reference Inaba8, Theorem 2.1].
If
$n$
and
$d$
are coprime, then there is a universal family on
${\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}\times \unicode[STIX]{x1D6F4}$
(see [Reference Huybrechts and Lehn7, Theorem 4.6.5] and the proof of [Reference Inaba8, Theorem 2.1]).◻
We denote the fibers of
${\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}$
over
$\unicode[STIX]{x1D706}=0$
and
$\unicode[STIX]{x1D706}=1$
by
${\mathcal{M}}_{\text{Dol}}^{\boldsymbol{\unicode[STIX]{x1D707}}}$
and
${\mathcal{M}}_{\text{DR}}^{\boldsymbol{\unicode[STIX]{x1D707}}}$
, respectively. Let
${\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}})$
be the fiber of
$(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}})$
. Let
${\mathcal{M}}_{\text{DR}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D709}})$
and
${\mathcal{M}}_{\text{Dol}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\mathbf{0})$
be the fibers of
$(1,\boldsymbol{\unicode[STIX]{x1D709}})$
and
$(0,\mathbf{0})$
, respectively. The fiber
${\mathcal{M}}_{\text{DR}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D709}})$
is the moduli space of
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
-stable regular singular
$\boldsymbol{\unicode[STIX]{x1D709}}$
-parabolic connections of spectral type
$\boldsymbol{\unicode[STIX]{x1D707}}$
(constructed in [Reference Inaba and Saito9]), and the fiber
${\mathcal{M}}_{\text{Dol}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\mathbf{0})$
is the moduli space of
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
-stable parabolic Higgs bundles of rank
$n$
and of degree
$d$
(constructed as a hyperkähler quotient using gauge theory in [Reference Konno11] or as a closed subvariety of the moduli space of parabolic Higgs sheaves constructed in [Reference Yokogawa19]).
The following proposition is shown by the same way as in the proofs [Reference Arinkin1, Lemma 4], [Reference Inaba8, Theorem 2.1], [Reference Inaba and Saito9] and [Reference Simpson17, Lemma 6.1].
Proposition 3.10. The morphism
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}:{\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}} & \longrightarrow & \displaystyle \unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}\nonumber\\ \displaystyle (\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\}_{1\leqslant i\leqslant r_{i}}) & \longmapsto & \displaystyle (\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}})\nonumber\end{eqnarray}$$
is smooth. Moreover,
${\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}$
is nonsingular.
Proof. At first, we prove that
$\unicode[STIX]{x1D70B}:{\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}\rightarrow \unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
is smooth. Let
${\mathcal{M}}_{\text{Hod}}^{1}$
be the moduli space of tuples
$(\unicode[STIX]{x1D706},L,\unicode[STIX]{x1D6FB}_{L})$
where
$L$
is a line bundle of degree
$d$
on
$\unicode[STIX]{x1D6F4}$
and
$\unicode[STIX]{x1D6FB}_{L}:L\rightarrow L\otimes \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6F4}}^{1}(D)$
is a
$\unicode[STIX]{x1D706}$
-connection. We put
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}^{k,d}:=\left\{(\unicode[STIX]{x1D706},(\unicode[STIX]{x1D709}^{i}))\in \mathbb{C}\times \mathbb{C}^{k}\,\left|\,\unicode[STIX]{x1D706}d+\mathop{\sum }_{i=1}^{k}\unicode[STIX]{x1D709}^{i}=0\right.\right\}.\end{eqnarray}$$
Let
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D706}=1}^{k,d}$
be the subset of
$\unicode[STIX]{x1D6EF}^{k,d}$
where
$\unicode[STIX]{x1D706}=1$
and let
${\mathcal{M}}_{\text{DR}}^{1}$
be the inverse image of the subset
$\unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D706}=1}^{k,d}$
. Since
${\mathcal{M}}_{\text{DR}}^{1}\rightarrow \unicode[STIX]{x1D6EF}_{\unicode[STIX]{x1D706}=1}^{k,d}$
is smooth (see [Reference Inaba8] and [Reference Inaba and Saito9]),
${\mathcal{M}}_{\text{Hod}}^{1}\rightarrow \unicode[STIX]{x1D6EF}^{k,d}$
is smooth (see [Reference Simpson17, Lemma 6.1]). We consider the morphism
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{det}:{\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}\longrightarrow {\mathcal{M}}_{\text{Hod}}^{1}\times _{\unicode[STIX]{x1D6EF}^{k,d}}\unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}\nonumber\\ \displaystyle & & \displaystyle (\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{j}^{(i)}\})\longmapsto ((\unicode[STIX]{x1D706},\text{det}(E),\text{det}(\unicode[STIX]{x1D6FB})),\unicode[STIX]{x1D70B}(\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{j}^{(i)}\})).\nonumber\end{eqnarray}$$
It is sufficient to show that the morphism
$\text{det}$
is smooth. Let
$A$
be an Artinian local ring over
${\mathcal{M}}_{\text{Hod}}^{1}\times _{\unicode[STIX]{x1D6EF}^{k,d}}\unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
with the maximal ideal
$m$
and
$I$
be an ideal of
$A$
such that
$mI=0$
. Let
$(\unicode[STIX]{x1D706},L,\unicode[STIX]{x1D6FB})\in {\mathcal{M}}_{\text{Hod}}^{1}(A)$
and
$(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}})\in \unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}(A)$
be the elements corresponding to the morphism
$$\begin{eqnarray}\text{Spec}\,A\longrightarrow {\mathcal{M}}_{\text{Hod}}^{1}\times _{\unicode[STIX]{x1D6EF}^{k,d}}\unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}.\end{eqnarray}$$
We take any member
$(\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{j}^{(i)}\})\in {\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(A/I)$
such that
$$\begin{eqnarray}\det (\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{j}^{(i)}\})\cong ((\unicode[STIX]{x1D706},L,\unicode[STIX]{x1D6FB}),(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}}))\otimes A/I.\end{eqnarray}$$
It is sufficient to show that
$(\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{j}^{(i)}\})$
may be lifted to a flat family
$(\tilde{\unicode[STIX]{x1D706}},\tilde{E},\tilde{\unicode[STIX]{x1D6FB}},\{\tilde{l}_{j}^{(i)}\})$
over
$A$
such that
$\det (\tilde{\unicode[STIX]{x1D706}},\tilde{E},\tilde{\unicode[STIX]{x1D6FB}},\{\tilde{l}_{j}^{(i)}\})\cong ((\unicode[STIX]{x1D706},L,\unicode[STIX]{x1D6FB}),(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}}))$
. The obstructions lie in the hypercohomology
$\mathbb{H}^{2}(\unicode[STIX]{x1D6F4},{\mathcal{F}}_{0}^{\bullet }\otimes I)$
. Here,
${\mathcal{F}}_{0}^{\bullet }$
is the complex of sheaves defined by
${\mathcal{F}}_{0}^{i}=0$
for
$i\neq 0,1$
,
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{F}}_{0}^{0}:=\left\{s\in {\mathcal{E}}nd(E\otimes A/m)\,\left|\,\begin{array}{@{}l@{}}\text{Tr}(s)=0\text{ and }\\ s_{|_{p_{i}\otimes A/m}}(l_{j}^{i})_{A/m}\subset (l_{j}^{i})_{A/m}~\text{for any}~i,j\end{array}\right.\right\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle {\mathcal{F}}_{0}^{1}:=\left\{s\in {\mathcal{E}}nd(E\otimes A/m)\otimes \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6F4}}^{1}(D)\,\left|\,\begin{array}{@{}l@{}}\text{Tr}(s)=0\text{ and }\\ \text{Res}_{p_{i}\otimes A/m}(s)(l_{j}^{i})_{A/m}\\ \quad \subset (l_{j+1}^{i})_{A/m}~\text{for any}~i,j\end{array}\right.\right\}, & \displaystyle \nonumber\end{eqnarray}$$
and
$d:{\mathcal{F}}_{0}^{0}\rightarrow {\mathcal{F}}_{0}^{1}$
maps
$s$
to
$\unicode[STIX]{x1D6FB}\circ s-s\circ \unicode[STIX]{x1D6FB}$
. From the spectral sequence
$H^{q}({\mathcal{F}}_{0}^{p})\Rightarrow \mathbb{H}^{p+q}({\mathcal{F}}_{0}^{\bullet })$
, there is an isomorphism
$$\begin{eqnarray}\mathbb{H}^{2}({\mathcal{F}}_{0}^{\bullet })\cong \text{Coker}\left(H^{1}({\mathcal{F}}_{0}^{0})\xrightarrow[]{\{}H^{1}({\mathcal{F}}_{0}^{1})\right).\end{eqnarray}$$
Since
$({\mathcal{F}}_{0}^{0})^{\vee }\otimes \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6F4}}^{1}\cong {\mathcal{F}}_{0}^{1}$
and
$({\mathcal{F}}_{0}^{1})^{\vee }\otimes \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6F4}}^{1}\cong {\mathcal{F}}_{0}^{0}$
, we have
$$\begin{eqnarray}\displaystyle \mathbb{H}^{2}({\mathcal{F}}_{0}^{\bullet }) & \cong & \displaystyle \text{Coker}\left(H^{1}({\mathcal{F}}_{0}^{0})\xrightarrow[]{\{}H^{1}({\mathcal{F}}_{0}^{1})\right)\nonumber\\ \displaystyle & \cong & \displaystyle \text{Ker}\left(H^{1}({\mathcal{F}}_{0}^{1})^{\vee }\xrightarrow[]{\{}H^{1}({\mathcal{F}}_{0}^{0})^{\vee }\right)^{\vee }\nonumber\\ \displaystyle & \cong & \displaystyle \text{Ker}\left(H^{0}(({\mathcal{F}}_{0}^{1})^{\vee }\otimes \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6F4}}^{1})\xrightarrow[]{\{}H^{0}(({\mathcal{F}}_{0}^{0})^{\vee }\otimes \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6F4}}^{1})\right)^{\vee }\nonumber\\ \displaystyle & \cong & \displaystyle \text{Ker}\left(H^{0}({\mathcal{F}}_{0}^{0})\xrightarrow[]{\{}H^{0}({\mathcal{F}}_{0}^{1})\right)^{\vee }.\nonumber\end{eqnarray}$$
We take any element
$s\in \text{Ker}(H^{0}({\mathcal{F}}_{0}^{0})\xrightarrow[]{\{}H^{0}({\mathcal{F}}_{0}^{1}))$
, which may be regarded as an element of
$\text{End}((\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{j}^{(i)}\}))$
. Since
$(\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{j}^{(i)}\})$
is
$\boldsymbol{\unicode[STIX]{x1D6FC}}$
-stable, the endomorphism
$s$
is a scalar multiplication. By
$\text{Tr}(s)=0$
, we have
$s=0$
. Hence,
$\mathbb{H}^{2}({\mathcal{F}}_{0}^{\bullet })=0$
.
Secondly, we prove that
${\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}$
is nonsingular (see [Reference Inaba, Iwasaki and Saito10, Remark 6.1]). It is enough to show
$\unicode[STIX]{x1D706}:{\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}\rightarrow \mathbb{C}$
given by
$(\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\})\mapsto \unicode[STIX]{x1D706}$
is smooth. In this case, the obstructions of the extensions lie in the hypercohomology
$\mathbb{H}^{2}(\unicode[STIX]{x1D6F4},{\mathcal{F}}_{0}^{\bullet ,+}\otimes I)$
. Here,
${\mathcal{F}}_{0}^{\bullet ,+}$
is the complexes of sheaves defined by
${\mathcal{F}}_{0}^{i,+}=0$
for
$i\neq 0,1$
,
${\mathcal{F}}_{0}^{0,+}:={\mathcal{F}}_{0}^{0}$
,
$$\begin{eqnarray}{\mathcal{F}}_{0}^{1,+}:=\left\{s\in {\mathcal{E}}nd(E\otimes A/m)\otimes \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6F4}}^{1}(D)\,\left|\,\begin{array}{@{}l@{}}\text{Tr}(s)=0,\\ \text{Res}_{p_{i}(s)\otimes A/m}(l_{j}^{(i)})_{A/m}\\ \subset (l_{j}^{(i)})_{A/m}\text{ for any}\\ i,j\text{ and the element of }\\ \text{End}((l_{j}^{(i)})_{A/m}/(l_{j+1}^{(i)})_{A/m})~\\ \text{induced by }\text{Res}_{p_{i}(s)\otimes A/m}~\\ \text{is a scalar}.\end{array}\right.\right\},\end{eqnarray}$$
and
$d^{+}:{\mathcal{F}}_{0}^{0,+}\rightarrow {\mathcal{F}}_{0}^{1,+}$
maps
$s$
to
$\unicode[STIX]{x1D6FB}\circ s-s\circ \unicode[STIX]{x1D6FB}$
. We put
${\mathcal{T}}_{0}^{1}={\mathcal{F}}_{0}^{1.+}/{\mathcal{F}}_{0}^{1}$
and
${\mathcal{T}}_{0}^{\bullet }=[0\rightarrow {\mathcal{T}}_{0}^{1}]$
. Then, we have the following exact sequence of the complex on
$\unicode[STIX]{x1D6F4}$
:
Note that
${\mathcal{T}}_{0}^{1}$
is a skyscraper sheaf. We consider the long exact sequence. Since
$\mathbb{H}^{2}({\mathcal{F}}_{0}^{\bullet })=\mathbb{H}^{2}({\mathcal{T}}_{0}^{\bullet })=0$
, we obtain
$\mathbb{H}^{2}({\mathcal{F}}_{0}^{\bullet ,+})=0$
.◻
The following proposition is shown by the same way as in the proofs [Reference Inaba8, Theorem 2.1] and [Reference Inaba and Saito9].
Proposition 3.11. For any
$(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}})\in \unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
, the fiber
${\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}})$
is of equidimensional of
$d_{\boldsymbol{\unicode[STIX]{x1D707}}}:=n^{2}(2g-2+k)-\sum _{i,j}(\unicode[STIX]{x1D707}_{j}^{i})^{2}+2$
, that is, it is the disjoint union of its irreducible components which are smooth of same dimension
$d_{\boldsymbol{\unicode[STIX]{x1D707}}}$
.
Proof. Since the fiber
${\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}})$
is smooth, we show that the tangent space
$\unicode[STIX]{x1D6E9}_{{\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}})}(y)$
at
$y=(\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\}_{1\leqslant i\leqslant k})\in {\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}})$
is of dimension
$n^{2}(2g-2+k)-\sum _{i,j}(\unicode[STIX]{x1D707}_{j}^{i})^{2}+2$
. Put
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{F}}^{0}:=\left\{s\in {\mathcal{E}}nd(E)\,\left|\,s_{|_{p_{i}}}(l_{j}^{i})\subset (l_{j}^{i})~\text{for any}~i,j\right.\right\} & \displaystyle \nonumber\\ \displaystyle & \displaystyle {\mathcal{F}}^{1}:=\left\{s\in {\mathcal{E}}nd(E)\otimes \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6F4}}^{1}(D)\,\left|\,\text{Res}_{p_{i}}(s)(l_{j}^{i})\subset (l_{j+1}^{i})~\text{for any}~i,j\right.\right\} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6FB}^{\dagger }:{\mathcal{F}}^{0}\ni s\mapsto \unicode[STIX]{x1D6FB}\circ s-s\circ \unicode[STIX]{x1D6FB}\in {\mathcal{F}}^{1}. & \displaystyle \nonumber\end{eqnarray}$$
Then we have an isomorphism
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{{\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}})}(y)\cong \mathbb{H}^{1}({\mathcal{F}}^{\bullet }).\end{eqnarray}$$
By the same computation as in the proof of [Reference Inaba8, Theorem 2.1], we have
$$\begin{eqnarray}\dim \mathbb{H}^{1}({\mathcal{F}}^{\bullet })=n^{2}(2g-2+k)-\mathop{\sum }_{i,j}(\unicode[STIX]{x1D707}_{j}^{i})^{2}+2.\square\end{eqnarray}$$
3.3 Mixed Hodge structures of the moduli space
${\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}})$
We consider the natural
$\mathbb{C}^{\times }$
-action on
${\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}$
$$\begin{eqnarray}\displaystyle \mathbb{C}^{\times }\times {\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}} & \longrightarrow & \displaystyle {\mathcal{M}}_{Hod}^{\boldsymbol{\unicode[STIX]{x1D707}}}\nonumber\\ \displaystyle (t,(\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\})) & \longmapsto & \displaystyle (t\unicode[STIX]{x1D706},E,t\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\}).\nonumber\end{eqnarray}$$
Since the relation between
$\unicode[STIX]{x1D706}$
and
$\boldsymbol{\unicode[STIX]{x1D709}}$
is
$\unicode[STIX]{x1D706}d+\sum \unicode[STIX]{x1D707}_{j}^{i}\unicode[STIX]{x1D709}_{j}^{i}=0$
, the following
$\mathbb{C}^{\times }$
action on
$\unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
is well defined,
$$\begin{eqnarray}\displaystyle \mathbb{C}^{\times }\times \unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d} & \longrightarrow & \displaystyle \unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}\nonumber\\ \displaystyle (t,(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}})) & \longmapsto & \displaystyle (t\unicode[STIX]{x1D706},t\boldsymbol{\unicode[STIX]{x1D709}}).\nonumber\end{eqnarray}$$
Clearly,
$\unicode[STIX]{x1D70B}:{\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}\rightarrow \unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
is a
$\mathbb{C}^{\times }$
-equivariant morphism.
Lemma 3.12. The fixed point set
$({\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}})^{\mathbb{C}^{\times }}$
is proper over
$\unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
, and for any
$(\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\})$
the limit
$\lim _{t\rightarrow 0}t\cdot (\unicode[STIX]{x1D706},E,\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\})$
exists in
$({\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}})^{\mathbb{C}^{\times }}$
.
Proof. The fixed point set lies over the origin
$(0,\mathbf{0})\in \unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
. Therefore, this fixed point set is just the fixed point set of the moduli space of semistable parabolic Higgs bundles, which is a closed subvariety of the moduli space of parabolic Higgs sheaves (see [Reference Yokogawa19]). Then, the fixed point set is proper by [Reference Yokogawa19, Theorem 5.12].
The second part follows from Langton type theorem [Reference Inaba, Iwasaki and Saito10, Proposition 5.5] in the same way as in [Reference Simpson16, Corollary 10.2]. (Also see [Reference Simpson18, Lemma 4.1] and [Reference Loray, Saito and Simpson12, Proposition 4.1].) ◻
For any pairs
$(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}})\in \unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
where the fiber
${\mathcal{M}}_{Hod}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}})$
is nonempty, we consider the following subset of
$\unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}_{(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}})}:=\{(t\unicode[STIX]{x1D706},t\boldsymbol{\unicode[STIX]{x1D709}})\mid t\in \mathbb{C}\}\cong \mathbb{C}.\end{eqnarray}$$
Let
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}})}:{\mathcal{M}}_{\unicode[STIX]{x1D6EF}_{(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}})}}\longrightarrow \unicode[STIX]{x1D6EF}_{(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}})}\end{eqnarray}$$
be the base change of
${\mathcal{M}}_{Hod}^{\boldsymbol{\unicode[STIX]{x1D707}}}\rightarrow \unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
via
$\unicode[STIX]{x1D6EF}_{(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}})}{\hookrightarrow}\unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
. By the smoothness of the map
$\unicode[STIX]{x1D70B}_{(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}})}$
, Lemma 3.12, and [Reference Hausel, Letellier and Rodriguez-Villegas5, Theorem B.1], there are isomorphisms
$$\begin{eqnarray}H^{\bullet }({\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}}),\mathbb{Q})\cong H^{\bullet }({\mathcal{M}}_{\text{Dol}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\mathbf{0}),\mathbb{Q})\end{eqnarray}$$
which preserve the mixed Hodge structures and the mixed Hodge structures of
$H^{\bullet }({\mathcal{M}}_{\text{Hod}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\unicode[STIX]{x1D706},\boldsymbol{\unicode[STIX]{x1D709}}),\mathbb{Q})$
are pure. Therefore, we obtain the following theorem:
Theorem 3.13. There are isomorphisms between ordinary rational cohomology groups of fibers of
$\unicode[STIX]{x1D70B}:{\mathcal{M}}_{Hod}^{\boldsymbol{\unicode[STIX]{x1D707}}}\rightarrow \unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
which preserve the mixed Hodge structures. The mixed Hodge structures on these cohomology groups of the fibers are pure. These assertions hold for the rational cohomology groups with compact support by the Poincaré duality (Theorem 2.3).
Here, note that the Poincaré duality is applied for each connected components of fibers of
$\unicode[STIX]{x1D70B}:{\mathcal{M}}_{Hod}^{\boldsymbol{\unicode[STIX]{x1D707}}}\rightarrow \unicode[STIX]{x1D6EF}_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
, which have same dimension (Proposition 3.11).
4 Riemann–Hilbert correspondence
4.1 Character varieties
We fix integers
$g\geqslant 0,k>0$
and
$n>0$
. We also fix a
$k$
-tuple of partition of
$n$
, denoted by
$\boldsymbol{\unicode[STIX]{x1D707}}=(\unicode[STIX]{x1D707}^{1},\ldots ,\unicode[STIX]{x1D707}^{k})$
, that is,
$\unicode[STIX]{x1D707}^{i}=(\unicode[STIX]{x1D707}_{1}^{i},\ldots ,\unicode[STIX]{x1D707}_{r_{i}}^{i})$
such that
$\unicode[STIX]{x1D707}_{1}^{i}\geqslant \unicode[STIX]{x1D707}_{2}^{i}\geqslant \cdots \,$
are nonnegative integers and
$\sum _{j}\unicode[STIX]{x1D707}_{j}^{i}=n$
. Let
$\unicode[STIX]{x1D6F4}$
be a smooth complex projective curve of genus
$g$
. We fix
$k$
-distinct points
$p_{1},\ldots ,p_{k}$
in
$\unicode[STIX]{x1D6F4}$
and we define a divisor by
$D:=p_{1}+\cdots +p_{k}$
. We put
$\unicode[STIX]{x1D6F4}_{0}=\unicode[STIX]{x1D6F4}\setminus D$
.
We now construct a variety, called a character variety, whose points parametrize representation of the fundamental group of
$\unicode[STIX]{x1D6F4}_{0}$
into
$\text{GL}(n,\mathbb{C})$
where the images of simple loops at the punctures associated to
$p_{1},\ldots ,p_{k}$
are contained in semisimple conjugacy classes
${\mathcal{C}}_{1},\ldots ,{\mathcal{C}}_{k}$
, respectively. Assume that
$$\begin{eqnarray}\mathop{\prod }_{i=1}^{k}\det {\mathcal{C}}_{i}=1\end{eqnarray}$$
and that
$({\mathcal{C}}_{1},\ldots ,{\mathcal{C}}_{k})$
has type
$\boldsymbol{\unicode[STIX]{x1D707}}=(\unicode[STIX]{x1D707}^{1},\ldots ,\unicode[STIX]{x1D707}^{k})$
; that is,
${\mathcal{C}}_{i}$
has type
$\unicode[STIX]{x1D707}^{i}$
for each
$i=1,\ldots ,k$
, where the type of the semisimple conjugacy class
${\mathcal{C}}_{i}\subset \text{GL}(n,\mathbb{C})$
is defined as the partition
$\unicode[STIX]{x1D707}^{i}=(\unicode[STIX]{x1D707}_{1}^{i},\ldots ,\unicode[STIX]{x1D707}_{r_{i}}^{i})$
describing the multiplicities of the eigenvalues of any matrix in
${\mathcal{C}}_{i}$
. Let
$\unicode[STIX]{x1D708}^{i}=(\unicode[STIX]{x1D708}_{1}^{i},\ldots ,\unicode[STIX]{x1D708}_{r_{i}}^{i})\in (\mathbb{C}^{\times })^{r_{i}}$
be the eigenvalues of
${\mathcal{C}}_{i}$
. We denote the
$k$
-tuple
$(\unicode[STIX]{x1D708}^{1},\ldots ,\unicode[STIX]{x1D708}^{k})$
by
$\boldsymbol{\unicode[STIX]{x1D708}}$
.
Definition 4.1. The
$k$
-tuple
$({\mathcal{C}}_{1},\ldots ,{\mathcal{C}}_{k})$
is generic if the following holds. If
$V\subset \mathbb{C}^{n}$
is a subset which is stable by some
$X_{i}\in {\mathcal{C}}_{i}$
for each
$i$
such that
$$\begin{eqnarray}\mathop{\prod }_{i=1}^{k}\det (X_{i}|_{V})=1,\end{eqnarray}$$
then either
$V=0$
or
$V=\mathbb{C}^{n}$
.
Lemma 4.2. [Reference Hausel, Letellier and Rodriguez-Villegas5, Lemma 2.1.2]
For any
$\boldsymbol{\unicode[STIX]{x1D707}}$
, there exists a generic
$k$
-tuple of semisimple conjugacy classes
$({\mathcal{C}}_{1},\ldots ,{\mathcal{C}}_{k})$
of type
$\boldsymbol{\unicode[STIX]{x1D707}}$
over
$\mathbb{C}$
.
Definition 4.3. For a
$k$
-tuple of generic semisimple conjugacy classes
$({\mathcal{C}}_{1},\ldots ,{\mathcal{C}}_{k})$
of type
$\boldsymbol{\unicode[STIX]{x1D707}}$
, we define a subvariety of
$\text{GL}(n,\mathbb{C})^{2g+n}$
by
$$\begin{eqnarray}\displaystyle {\mathcal{U}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D708}}) & := & \displaystyle \big\{(A_{1},B_{1},\ldots ,A_{g},B_{g};X_{1},\ldots ,X_{k})\in \text{GL}(n,\mathbb{C})^{2g}\times {\mathcal{C}}_{1}\times \cdots \times {\mathcal{C}}_{k}\nonumber\\ \displaystyle & & \displaystyle \quad \mid (A_{1},B_{1})\cdots (A_{g},B_{g})X_{1}\cdots X_{k}=I_{n}\big\},\nonumber\end{eqnarray}$$
where
$(A,B):=ABA^{-1}B^{-1}$
. The group
$\text{GL}(n,\mathbb{C})$
acts by conjugation on
$\text{GL}(n,\mathbb{C})^{2g+n}$
. As the center acts trivially, the action induces that of
$\text{PGL}(n,\mathbb{C})$
. The action induces that of
$\text{PGL}(n,\mathbb{C})$
on
${\mathcal{U}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D708}})$
. We call the affine GIT quotient
$$\begin{eqnarray}{\mathcal{M}}_{\text{B}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D708}}):={\mathcal{U}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D708}})/\!/\text{PGL}(n,\mathbb{C})\end{eqnarray}$$
a generic character variety of type
$\boldsymbol{\unicode[STIX]{x1D707}}$
. We denote by
$\unicode[STIX]{x1D70B}_{\boldsymbol{\unicode[STIX]{x1D707}}}$
the quotient morphism
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\boldsymbol{\unicode[STIX]{x1D707}}}:{\mathcal{U}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D708}})\longrightarrow {\mathcal{M}}_{\text{B}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D708}}).\end{eqnarray}$$
Proposition 4.4. [Reference Hausel, Letellier and Rodriguez-Villegas5, Proposition 2.1.4]
If
$({\mathcal{C}}_{1},\ldots ,{\mathcal{C}}_{k})$
is generic of type
$\boldsymbol{\unicode[STIX]{x1D707}}$
, then the group
$\text{PGL}(n,\mathbb{C})$
acts set-theoretically freely on
${\mathcal{U}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D708}})$
and every point of
${\mathcal{U}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D708}})$
corresponds to an irreducible representation of
$\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D6F4}_{0})$
.
Theorem 4.5. [Reference Hausel, Letellier and Rodriguez-Villegas5, Theorem 2.1.5]
If
$({\mathcal{C}}_{1},\ldots ,{\mathcal{C}}_{k})$
is a generic type
$\boldsymbol{\unicode[STIX]{x1D707}}$
, then the quotient
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\boldsymbol{\unicode[STIX]{x1D707}}}:{\mathcal{U}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D708}})\longrightarrow {\mathcal{M}}_{\text{B}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D708}})\end{eqnarray}$$
is a geometric quotient and a principal
$\text{PGL}(n,\mathbb{C})$
-bundle.
Theorem 4.6. [Reference Hausel, Letellier and Rodriguez-Villegas6, Theorem 1.1.1]
If nonempty, the generic character variety
${\mathcal{M}}_{B}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D708}})$
is a connected nonsingular variety of dimension
$$\begin{eqnarray}n^{2}(2g-2+k)-\mathop{\sum }_{i,j}(\unicode[STIX]{x1D707}_{j}^{i})^{2}+2.\end{eqnarray}$$
4.2 Riemann–Hilbert correspondence
First, we define a generic tuple of the eigenvalues of the residue matrixes of a parabolic connection corresponding to Definition 4.1 for character varieties cases. We put
$$\begin{eqnarray}\text{g.c.d.}(\boldsymbol{\unicode[STIX]{x1D707}}):=\text{g.c.d.}(\unicode[STIX]{x1D707}_{1}^{1},\ldots ,\unicode[STIX]{x1D707}_{j}^{i},\ldots ,\unicode[STIX]{x1D707}_{r_{k}}^{k}),\end{eqnarray}$$
where
$r_{i}$
implies the number of the distinct eigenvalues of the residue matrix at
$p_{i}$
of a parabolic connection. For an integer
$d$
, we put
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}_{n,\unicode[STIX]{x1D706}=1}^{\boldsymbol{\unicode[STIX]{x1D707}},d}:=\left\{\boldsymbol{\unicode[STIX]{x1D709}}=(\unicode[STIX]{x1D709}_{j}^{i})_{1\leqslant j\leqslant r_{i}}^{1\leqslant i\leqslant k}\in \mathbb{C}^{r}\,\left|\,d+\mathop{\sum }_{i,j}\unicode[STIX]{x1D707}_{j}^{i}\unicode[STIX]{x1D709}_{j}^{i}=0\right.\right\}\end{eqnarray}$$
where
$r:=\sum r_{i}$
.
Definition 4.7. Take an element
$\boldsymbol{\unicode[STIX]{x1D709}}\in \unicode[STIX]{x1D6EF}_{n,\unicode[STIX]{x1D706}=1}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
. We call
$\boldsymbol{\unicode[STIX]{x1D709}}$
generic if:
-
(1)
$\unicode[STIX]{x1D709}_{j}^{i}-\unicode[STIX]{x1D709}_{k}^{i}\not \in \mathbb{Z}$
for any
$i$
and
$j\neq k$
; and -
(2) there exist no integer
$s$
with
$0<s<n$
, integers
$s_{i}$
with
$1\leqslant s_{i}\leqslant r_{i}$
, and subsets
$\{j_{1}^{i},\ldots ,j_{s_{i}}^{i}\}\subset \{1,\ldots ,r_{i}\}$
for each
$1\leqslant i\leqslant k$
such that for any tuple of integer
$$\begin{eqnarray}\mathop{\sum }_{i=1}^{k}\mathop{\sum }_{l=1}^{s_{i}}\unicode[STIX]{x1D710}_{j_{l}^{i}}^{i}\unicode[STIX]{x1D709}_{j_{l}^{i}}^{i}\not \in \mathbb{Z},\end{eqnarray}$$
$\boldsymbol{\unicode[STIX]{x1D710}}=(\unicode[STIX]{x1D710}_{j}^{i})$
with
$0\leqslant \unicode[STIX]{x1D710}_{j}^{i}\leqslant \unicode[STIX]{x1D707}_{j}^{i}$
where
$\unicode[STIX]{x1D710}_{j_{1}^{i}}^{i}+\cdots +\unicode[STIX]{x1D710}_{j_{s_{i}}^{i}}^{i}=s$
for
$i=1,\ldots ,k$
.
Let
$\unicode[STIX]{x1D6EF}_{n,\unicode[STIX]{x1D706}=1}^{\boldsymbol{\unicode[STIX]{x1D707}},d,irr}$
be the locus of generic elements in
$\unicode[STIX]{x1D6EF}_{n,\unicode[STIX]{x1D706}=1}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
, and let
${\mathcal{M}}_{DR}^{\boldsymbol{\unicode[STIX]{x1D707}},irr}$
be the inverse image of
$\unicode[STIX]{x1D6EF}_{n,\unicode[STIX]{x1D706}=1}^{\boldsymbol{\unicode[STIX]{x1D707}},d,irr}$
via
${\mathcal{M}}_{DR}^{\boldsymbol{\unicode[STIX]{x1D707}}}\rightarrow \unicode[STIX]{x1D6EF}_{n,\unicode[STIX]{x1D706}=1}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
.
Remark 4.8. If
$d$
and
$\text{g.c.d.}(\boldsymbol{\unicode[STIX]{x1D707}})$
have the greatest common divisor
$r^{\prime }\neq 1$
, then
$\unicode[STIX]{x1D6EF}_{n,\unicode[STIX]{x1D706}=1}^{\boldsymbol{\unicode[STIX]{x1D707}},d,irr}=\emptyset$
, since
$$\begin{eqnarray}\mathop{\sum }_{i,j}\frac{\unicode[STIX]{x1D707}_{j}^{i}}{r^{\prime }}\unicode[STIX]{x1D709}_{j}^{i}=-\frac{d}{r^{\prime }}\in \mathbb{Z}\end{eqnarray}$$
for any
$\boldsymbol{\unicode[STIX]{x1D709}}\in \unicode[STIX]{x1D6EF}_{n,\unicode[STIX]{x1D706}=1}^{\boldsymbol{\unicode[STIX]{x1D707}},d}$
.
Conversely, if
$d$
and
$\text{g.c.d.}(\boldsymbol{\unicode[STIX]{x1D707}})$
are coprime, then
$\unicode[STIX]{x1D6EF}_{n,\unicode[STIX]{x1D706}=1}^{\boldsymbol{\unicode[STIX]{x1D707}},d,irr}$
is nonempty. (See Remark 4.10 as below and the proof of [Reference Hausel, Letellier and Rodriguez-Villegas5, Lemma 2.1.2].)
Remark 4.9. See [Reference Inaba8, Section 2]
For generic
$\boldsymbol{\unicode[STIX]{x1D709}}$
, any regular singular
$\boldsymbol{\unicode[STIX]{x1D709}}$
-parabolic connection
$(E,\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\})$
is irreducible. Here, we call
$(E,\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\})$
reducible if there is a nontrivial subbundle
$0\neq F\subsetneq E$
such that
$\unicode[STIX]{x1D6FB}(F)\subset F\otimes \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6F4}}^{1}(D)$
. We call
$(E,\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\})$
irreducible if it is not reducible. In particular, for generic
$\boldsymbol{\unicode[STIX]{x1D709}}$
, any
$(E,\unicode[STIX]{x1D6FB},\{l_{\ast }^{(i)}\})$
is semistable.
Next, we construct a family of all generic character varieties of type
$\boldsymbol{\unicode[STIX]{x1D707}}$
. We put
$r:=\sum r_{i}$
and
$$\begin{eqnarray}N_{n}^{\boldsymbol{\unicode[STIX]{x1D707}}}:=\left\{\boldsymbol{\unicode[STIX]{x1D708}}=(\unicode[STIX]{x1D708}_{j}^{i})_{1\leqslant j\leqslant r_{i}}^{1\leqslant i\leqslant k}\in \mathbb{C}^{r}\,\left|\,\mathop{\prod }_{i,j}{\unicode[STIX]{x1D708}_{j}^{i}}^{\unicode[STIX]{x1D707}_{j}^{i}}=1\right.\right\},\end{eqnarray}$$
which is the set of eigenvalues of
$k$
-tuple of semisimple conjugacy classes
$({\mathcal{C}}_{1},\ldots ,{\mathcal{C}}_{k})$
. We denote by
${\mathcal{U}}^{\boldsymbol{\unicode[STIX]{x1D707}}}$
the following subvariety of
$N_{n}^{\boldsymbol{\unicode[STIX]{x1D707}}}\times \text{GL}(n,\mathbb{C})^{2g+n}$
$$\begin{eqnarray}\left\{(\boldsymbol{\unicode[STIX]{x1D708}},A_{1},B_{1},\ldots ,A_{g},B_{g},X_{1},\ldots ,X_{k})\,\left|\,\begin{array}{@{}l@{}}(1)~(A_{1},B_{1})\cdots (A_{g},B_{g})X_{1}\\ \qquad \cdots X_{k}=I_{n},\\ (2)~\text{For each}~i,\text{there is a filtration}\\ \quad ~~\mathbb{C}^{n}=W_{1}^{i}\supset W_{2}^{i}\supset \cdots \supset W_{r_{i}+1}^{i}\\ \quad ~~=0~\text{such that }\\ \quad ~~\dim W_{j}^{i}/W_{j+1}^{i}=\unicode[STIX]{x1D707}_{j}^{i}\text{ and }\\ \quad ~~(X_{i}-\unicode[STIX]{x1D708}_{j}^{i}\text{id})(W_{j}^{i})\subset W_{j+1}^{i}\\ \quad ~~\text{for any }i,j\end{array}\right.\right\}\end{eqnarray}$$
where
$(\boldsymbol{\unicode[STIX]{x1D708}},A_{1},B_{1},\ldots ,A_{g},B_{g},X_{1},\ldots ,X_{k})\in N_{n}^{\boldsymbol{\unicode[STIX]{x1D707}}}\times \text{GL}(n,\mathbb{C})^{2g+n}$
. The group
$\text{PGL}(n,\mathbb{C})$
acts on
$N_{n}^{\boldsymbol{\unicode[STIX]{x1D707}}}\times \text{GL}(n,\mathbb{C})^{2g+n}$
which is trivial on
$N_{n}^{\boldsymbol{\unicode[STIX]{x1D707}}}$
and conjugation on
$\text{GL}(n,\mathbb{C})^{2g+n}$
. We take the categorical quotient of
${\mathcal{U}}^{\boldsymbol{\unicode[STIX]{x1D707}}}$
by the
$\text{PGL}(n,\mathbb{C})$
-action;
$$\begin{eqnarray}\displaystyle {\mathcal{M}}_{B}^{\boldsymbol{\unicode[STIX]{x1D707}}} & := & \displaystyle {\mathcal{U}}^{\boldsymbol{\unicode[STIX]{x1D707}}}/\!/\text{PGL}(n,\mathbb{C})\nonumber\\ \displaystyle & = & \displaystyle \text{Spec}(\mathbb{C}[{\mathcal{U}}^{\boldsymbol{\unicode[STIX]{x1D707}}}]^{\text{PGL}(n,\mathbb{C})}).\nonumber\end{eqnarray}$$
The map
$$\begin{eqnarray}\displaystyle {\mathcal{M}}_{B}^{\boldsymbol{\unicode[STIX]{x1D707}}} & \longrightarrow & \displaystyle N_{n}^{\boldsymbol{\unicode[STIX]{x1D707}}}\nonumber\\ \displaystyle [(\boldsymbol{\unicode[STIX]{x1D708}},A_{1},B_{1},\ldots ,A_{g},B_{g},X_{1},\ldots ,X_{k})] & \longmapsto & \displaystyle \boldsymbol{\unicode[STIX]{x1D708}}\nonumber\end{eqnarray}$$
is well defined. Let
$N_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},irr}\subset N_{n}^{\boldsymbol{\unicode[STIX]{x1D707}}}$
be the set of generic eigenvalues in the sense of Definition 4.1. Then we take the base change of
${\mathcal{M}}_{B}^{\boldsymbol{\unicode[STIX]{x1D707}}}\rightarrow N_{n}^{\boldsymbol{\unicode[STIX]{x1D707}}}$
via the inclusion map
$N_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},irr}{\hookrightarrow}N_{n}^{\boldsymbol{\unicode[STIX]{x1D707}}}$
, denoted by
$$\begin{eqnarray}{\mathcal{M}}_{B}^{\boldsymbol{\unicode[STIX]{x1D707}},irr}\longrightarrow N_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},irr},\end{eqnarray}$$
which is a family of any generic character varieties of type
$\boldsymbol{\unicode[STIX]{x1D707}}$
. Observe that the fiber over
$\boldsymbol{\unicode[STIX]{x1D708}}$
is precisely the space
${\mathcal{M}}_{B}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D708}})$
introduced in Definition 4.3.
We define the morphism
$$\begin{eqnarray}rh_{d}:\unicode[STIX]{x1D6EF}_{n,\unicode[STIX]{x1D706}=1}^{\boldsymbol{\unicode[STIX]{x1D707}},d}\ni \boldsymbol{\unicode[STIX]{x1D709}}\longmapsto \boldsymbol{\unicode[STIX]{x1D708}}\in N_{n}^{\boldsymbol{\unicode[STIX]{x1D707}}}\end{eqnarray}$$
by
$\unicode[STIX]{x1D708}_{j}^{i}=\text{exp}(-2\unicode[STIX]{x1D70B}\sqrt{-1}\unicode[STIX]{x1D709}_{j}^{i})$
for any
$i,j$
.
Remark 4.10. (See the proof of [Reference Hausel, Letellier and Rodriguez-Villegas5, Lemma 2.1.2])
Let
$({\mathcal{C}}_{1},\ldots ,{\mathcal{C}}_{k})$
be a
$k$
-tuple of semisimple conjugacy classes such that the eigenvalue of any matrix in
${\mathcal{C}}_{i}$
is
$(\text{exp}(-2\unicode[STIX]{x1D70B}\sqrt{-1}\unicode[STIX]{x1D709}_{1}^{i}),\ldots ,\text{exp}(-2\unicode[STIX]{x1D70B}\sqrt{-1}\unicode[STIX]{x1D709}_{r_{i}}^{i}))$
where the multiplicity of
$\text{exp}(-2\unicode[STIX]{x1D70B}\sqrt{-1}\unicode[STIX]{x1D709}_{j}^{i})$
is
$\unicode[STIX]{x1D707}_{j}^{i}$
. If
$\boldsymbol{\unicode[STIX]{x1D709}}$
is generic, then
$({\mathcal{C}}_{1},\ldots ,{\mathcal{C}}_{k})$
is generic in the sense of Definition 4.1.
Remark 4.11. For any
$\boldsymbol{\unicode[STIX]{x1D708}}\in N_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},irr}$
, there exist integers
$d$
with
$0\leqslant d<\text{g.c.d.}(\boldsymbol{\unicode[STIX]{x1D707}})$
such that
$\boldsymbol{\unicode[STIX]{x1D708}}$
is contained in the images of the morphisms
$$\begin{eqnarray}rh_{d}:\unicode[STIX]{x1D6EF}_{n,\unicode[STIX]{x1D706}=1}^{\boldsymbol{\unicode[STIX]{x1D707}},d,irr}\longrightarrow N_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},irr},\end{eqnarray}$$
that is,
$\boldsymbol{\unicode[STIX]{x1D708}}\in \text{Im}(rh_{d})$
for some
$d$
(
$0\leqslant d<\text{g.c.d.}(\boldsymbol{\unicode[STIX]{x1D707}})$
).
For each member
$(E,\unicode[STIX]{x1D6FB},\{l_{j}^{i}\})\in {\mathcal{M}}_{DR}^{\boldsymbol{\unicode[STIX]{x1D707}},irr}$
,
$\text{Ker}(\unicode[STIX]{x1D6FB}^{an}|_{\unicode[STIX]{x1D6F4}_{0}})$
becomes a local system on
$\unicode[STIX]{x1D6F4}_{0}$
, where
$\unicode[STIX]{x1D6FB}^{an}$
means the analytic connection corresponding to
$\unicode[STIX]{x1D6FB}$
. The local system
$\text{Ker}(\unicode[STIX]{x1D6FB}^{an}|_{\unicode[STIX]{x1D6F4}_{0}})$
corresponds to a representation of
$\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D6F4}_{0})$
. Let
$\unicode[STIX]{x1D6FE}_{i}$
be a loop around
$p_{i}$
. The representation of
$\unicode[STIX]{x1D6FE}_{i}$
is semisimple for
$i=1,\ldots ,k$
, and the eigenvalues of the representation of
$\unicode[STIX]{x1D6FE}_{i}$
are
$$\begin{eqnarray}\text{exp}(-2\unicode[STIX]{x1D70B}\sqrt{-1}\unicode[STIX]{x1D709}_{1}^{i}),\ldots ,\text{exp}(-2\unicode[STIX]{x1D70B}\sqrt{-1}\unicode[STIX]{x1D709}_{r_{i}}^{i})\end{eqnarray}$$
where the multiplicities are
$\unicode[STIX]{x1D707}_{1}^{i},\ldots ,\unicode[STIX]{x1D707}_{r_{i}}^{i}$
, respectively. Then we can define the morphism
$$\begin{eqnarray}\mathbf{RH}_{\boldsymbol{\unicode[STIX]{x1D709}}}:{\mathcal{M}}_{\text{DR}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D709}})\longrightarrow {\mathcal{M}}_{\text{B}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D708}})\end{eqnarray}$$
where
$\boldsymbol{\unicode[STIX]{x1D708}}=rh_{d}(\boldsymbol{\unicode[STIX]{x1D709}})$
. Then
$\{\mathbf{RH}_{\boldsymbol{\unicode[STIX]{x1D709}}}\}$
induces the morphism
$$\begin{eqnarray}\mathbf{RH}:{\mathcal{M}}_{\text{DR}}^{\boldsymbol{\unicode[STIX]{x1D707}},irr}\longrightarrow {\mathcal{M}}_{\text{B}}^{\boldsymbol{\unicode[STIX]{x1D707}},irr},\end{eqnarray}$$
which gives the commutative diagram
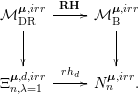
The following theorem follows from the result of Inaba [Reference Inaba8, Theorem 2.2] and Inaba–Saito [Reference Inaba and Saito9].
Theorem 4.12. (See [Reference Inaba8, Theorem 2.2] and [Reference Inaba and Saito9])
The morphism
$$\begin{eqnarray}\mathbf{RH}_{\boldsymbol{\unicode[STIX]{x1D709}}}:{\mathcal{M}}_{\text{DR}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D709}})\longrightarrow {\mathcal{M}}_{\text{B}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(rh_{d}(\boldsymbol{\unicode[STIX]{x1D709}}))\end{eqnarray}$$
is an analytic isomorphism for any
$\boldsymbol{\unicode[STIX]{x1D709}}\in \unicode[STIX]{x1D6EF}_{n,\unicode[STIX]{x1D706}=1}^{\boldsymbol{\unicode[STIX]{x1D707}},d,irr}$
.
Proof. We take any point
$\unicode[STIX]{x1D70C}\in {\mathcal{M}}_{\text{B}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(rh_{d}(\boldsymbol{\unicode[STIX]{x1D709}}))$
where
$\boldsymbol{\unicode[STIX]{x1D709}}$
is generic. By [Reference Inaba8, Proposition 3.1], we obtain the following isomorphism,
$$\begin{eqnarray}{\mathcal{M}}_{\text{DR}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D709}})\cong {\mathcal{M}}_{\text{DR}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D709}}^{\prime })\end{eqnarray}$$
where
$0\leqslant \text{Re}(\unicode[STIX]{x1D709}_{j}^{\prime i})<1$
for any
$i,j$
. Hence, we assume that
$\boldsymbol{\unicode[STIX]{x1D709}}$
satisfy
$0\leqslant \text{Re}(\unicode[STIX]{x1D709}_{j}^{i})<1$
for any
$i,j$
. By [Reference Deligne2, II, Proposition 5.4], there is a unique pair
$(E,\unicode[STIX]{x1D6FB}_{E})$
where
$E$
is a vector bundle on
$\unicode[STIX]{x1D6F4}$
and
$\unicode[STIX]{x1D6FB}_{E}:E\rightarrow E\otimes \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6F4}}^{1}(D)$
is a logarithmic connection, such that the local system
$\text{Ker}(\unicode[STIX]{x1D6FB}_{E}^{an})|_{\unicode[STIX]{x1D6F4}\setminus \{p_{1},\ldots ,p_{k}\}}$
corresponds to the representation
$\unicode[STIX]{x1D70C}$
and all the eigenvalue of
$\text{Res}_{p_{i}}(\unicode[STIX]{x1D6FB}_{E})$
lie in
$\{z\in \mathbb{C}\mid 0\leqslant \text{Re}(z)<1\}$
. Since
$\boldsymbol{\unicode[STIX]{x1D709}}$
is generic, we can define a parabolic structure of
$(E,\unicode[STIX]{x1D6FB}_{E})$
, uniquely. Therefore,
$\mathbf{RH}_{\boldsymbol{\unicode[STIX]{x1D709}}}$
gives a one to one correspondence between the points of
${\mathcal{M}}_{DR}^{\boldsymbol{\unicode[STIX]{x1D707}},irr}(\boldsymbol{\unicode[STIX]{x1D709}})$
and the points of
${\mathcal{M}}_{B}^{\boldsymbol{\unicode[STIX]{x1D707}},irr}(rh_{d}(\boldsymbol{\unicode[STIX]{x1D709}}))$
. We can define this correspondence between flat families. Hence,
$$\begin{eqnarray}\mathbf{RH}_{\boldsymbol{\unicode[STIX]{x1D709}}}:{\mathcal{M}}_{\text{DR}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D709}})\longrightarrow {\mathcal{M}}_{\text{B}}^{\boldsymbol{\unicode[STIX]{x1D707}}}(rh_{d}(\boldsymbol{\unicode[STIX]{x1D709}}))\end{eqnarray}$$
is an analytic isomorphism. ◻
Theorem 4.13. The Poincaré polynomials of character varieties
${\mathcal{M}}_{B}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D708}})$
are independent of the choice of generic eigenvalues.
Proof. We put
$$\begin{eqnarray}N_{d}:=\text{Im}(\unicode[STIX]{x1D6EF}_{n,\unicode[STIX]{x1D706}=1}^{\boldsymbol{\unicode[STIX]{x1D707}},d,irr})\subset N_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},irr}.\end{eqnarray}$$
We can describe
$N_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},irr}$
as follows:
$$\begin{eqnarray}N_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},irr}=N_{0}\cup N_{1}\cup \cdots \cup N_{\text{g.c.d.}(\boldsymbol{\unicode[STIX]{x1D707}})-1}\end{eqnarray}$$
(see Remark 4.11).
By Theorems 3.13 and 4.12, for any
$\boldsymbol{\unicode[STIX]{x1D708}}_{1},\boldsymbol{\unicode[STIX]{x1D708}}_{2}\in N_{d}\;(d=1,\ldots ,\text{g.c.d.}(\boldsymbol{\unicode[STIX]{x1D707}})-1)$
the Poincaré polynomials of the character varieties
${\mathcal{M}}_{B}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D708}}_{\mathbf{1}})$
and
${\mathcal{M}}_{B}^{\boldsymbol{\unicode[STIX]{x1D707}}}(\boldsymbol{\unicode[STIX]{x1D708}}_{\mathbf{2}})$
are same. On the other hand, there is a dense subset in the analytic topology of
$N_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},irr}$
such that the Poincaré polynomial is constant [Reference Hausel, Letellier and Rodriguez-Villegas5, Theorem 5.1.1]. Then the Poincaré polynomials is constant in
$N_{n}^{\boldsymbol{\unicode[STIX]{x1D707}},irr}$
.◻
Acknowledgments
The author would like to thank Professor Masa-Hiko Saito and Professor Kentaro Mitsui for many comments and discussions. He thanks Professor Masa-Hiko Saito for warm encouragement. The author is also grateful to the referee for reading the paper carefully and giving many valuable suggestion.
