Hostname: page-component-7479d7b7d-qlrfm Total loading time: 0 Render date: 2024-07-15T22:37:58.008Z Has data issue: false hasContentIssue false
  • English
  • Français

Approach to Stationarity of the Bernoulli–Laplace Diffusion Model

Part of: Markov processes Probability theory on algebraic and topological structures

Published online by Cambridge University Press:  01 July 2016

Peter Donnelly ,
Peter Lloyd  and
Aidan Sudbury
Peter Donnelly*
Affiliation:
Queen Mary and Westfield College, London
Peter Lloyd*
Affiliation:
Monash University
Aidan Sudbury*
Affiliation:
Monash University
*
* Postal address: School of Mathematical Sciences, Queen Mary and Westfield College, University of London, Mile End Road, London El 4NS, UK.
** Postal address: Department of Physics and Mathematics, Monash University, Clayton, VIC 3168, Australia.
** Postal address: Department of Physics and Mathematics, Monash University, Clayton, VIC 3168, Australia.
Get access Rights & Permissions [Opens in a new window]

Abstract

Two urns initially contain r red balls and n – r black balls respectively. At each time epoch a ball is chosen randomly from each urn and the balls are switched. Effectively the same process arises in many other contexts, notably for a symmetric exclusion process and random walk on the Johnson graph. If Y(·) counts the number of black balls in the first urn then we give a direct asymptotic analysis of its transition probabilities to show that (when run at rate (n – r)/n in continuous time) for 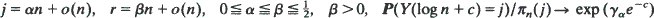as n →∞, where π n denotes the equilibrium distribution of Y(·) and γ α = 1 – α /β (1 – β). Thus for large n the transient probabilities approach their equilibrium values at time log n + log|γ α | (≦log n) in a particularly sharp manner. The same is true of the separation distance between the transient distribution and the equilibrium distribution. This is an explicit analysis of the so-called cut-off phenomenon associated with a wide variety of Markov chains.

Keywords

RANDOM WALKEXCLUSION PROCESSSEPARATION DISTANCEDISTANCE TRANSITIVE GRAPHJOHNSON GRAPHEBERLEIN POLYNOMIALS

MSC classification

Primary: 60B15: Probability measures on groups or semigroups, Fourier transforms, factorization
Secondary: 60J20: Applications of Markov chains and discrete-time Markov processes on general state spaces (social mobility, learning theory, industrial processes, etc.)
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 26 , Issue 3 , September 1994 , pp. 715 - 727
Copyright
Copyright © Applied Probability Trust 1994 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aldous, D. and Diaconis, P. (1987) Strong uniform times and finite random walks. Adv. Appl. Math. 8, 69–97.Google Scholar
Askey, R. (1975) Orthogonal Polynomials and Special Functions. SIAM, Philadelphia.Google Scholar
Bannai, E. and Ito, T. (1984). Algebraic Combinatorics I. Benjamin/Cummings, London.Google Scholar
Bayer, D. and Diaconis, P. (1992) Trailing the dovetail shuffle to its lair. Ann. Appl. Prob. 2, 294–313.Google Scholar
Biggs, N. (1974) Algebraic Graph Theory. Cambridge University Press.Google Scholar
Bingham, N. H. (1991) Fluctuation theory for the Ehrenfest urn. Adv. Appl. Prob. 23, 598–611.Google Scholar
Devroye, L. and Sbihi, A. (1990) Random walks on highly symmetric graphs. J. Theoret. Prob. 3, 497–514.Google Scholar
Diaconis, P. (1988) Group Representations in Probability and Statistics. IMS, Hayward, CA.Google Scholar
Diaconis, P. and Fill, J. A. (1990) Strong stationary times via a new form of duality. Ann. Prob. 18, 1483–1522.CrossRefGoogle Scholar
Diaconis, P. and Shahshahani, M. (1987) Time to reach stationarity in the Bernoulli-Laplace diffusion model. SIAM J. Math. Anal. 18, 208–218.Google Scholar
Diaconis, P. and Stroock, D. (1991). Geometric bounds for eigenvalues of Markov chains. Ann. Appl. Prob. 1, 36–62.CrossRefGoogle Scholar
Diaconis, P., Graham, R. L. and Morrison, J. A. (1990) Asymptotic analysis of a random walk on a hypercube with many dimensions. Random Structures and Algorithms 1, 51–72.CrossRefGoogle Scholar
Donnelly, P. J. (1984) The transient behaviour of the Moran model in population genetics. Math. Proc. Camb. Phil. Soc. 95, 349–358.Google Scholar
Donnelly, P. J. and Welsh, D. J. A. (1984) The anti-voter problem: random 2-colourings of graphs. In Graph Theory and Combinatorics, ed. Bollobás, B. Academic Press, London.Google Scholar
Ewens, W. J. (1979) Mathematical Population Genetics. Springer-Verlag, New York.Google Scholar
Feller, W. (1968). An Introduction to Probability Theory and its Applications, Vol. I, 3rd edn. Wiley, New York.Google Scholar
Fill, J. A. (1991a). Eigenvalue bounds on convergence to stationarity for non-reversible Markov chains with an application to the exclusion process. Ann. Appl. Prob. 1, 62–88.Google Scholar
Fill, J. A. (1991b). Time to stationarity for a continuous-time Markov chain. Prob. Eng. Inf. Sci. 5, 61–76.Google Scholar
Fill, J. A. (1992). Strong stationary duality for continuous-time Markov chains I: theory. J. Theoret. Prob. 5, 45–70.Google Scholar
Karlin, S. and Mcgregor, J. (1957) The differential equations of birth and death processes and the Stieltjes moment problem. Trans. Amer. Math. Soc. 85, 489–546.Google Scholar
Karlin, S. and Mcgregor, J. (1962) On a genetics model of Moran. Proc. Camb. Phil. Soc. 58, 299–311.Google Scholar
Karlin, S. and Rinott, Y. (1980) Classes of orderings of measures and related correlation inequalities. I. Multivariate totally positive distributions. J. Multivar. Anal. 10, 467–498.Google Scholar
Liggett, T. (1985) Interacting Particle Systems. Springer-Verlag, New York.Google Scholar
Moran, P. A. P. (1958) Random processes in genetics. Proc. Camb. Phil. Soc. 54, 60–71.Google Scholar
Piaget, J. and Inhelder, B. (1975) The Origin of the Idea of Chance in Children. Norton, New York.Google Scholar
Sloane, N. J. A. (1975) An introduction to association schemes and coding theory. In Theory and Applications of Special Functions, ed. Askey, R. Academic Press, New York.Google Scholar