Hostname: page-component-5c6d5d7d68-vt8vv Total loading time: 0.001 Render date: 2024-08-17T06:05:16.800Z Has data issue: false hasContentIssue false
  • English
  • Français

Convergence theorems for empirical Lorenz curves and their inverses

Published online by Cambridge University Press:  01 July 2016

Charles M. Goldie
Charles M. Goldie*
Affiliation:
University of Sussex
Get access Rights & Permissions [Opens in a new window]

Abstract

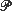The Lorenz curve of the distribution of ‘wealth’ is a graph of cumulative proportion of total ‘wealth’ owned, against cumulative proportion of the population owning it. This paper uses Gastwirth's definition of the Lorenz curve which applies to a general probability distribution on (0, ∞) having finite mean; thus it applies both to a ‘population’ distribution and to empirical distributions obtained on sampling. The Lorenz curves of the latter are proved to converge, with probability 1, uniformly to the former, and similarly for their inverses. Modified Lorenz curves are also defined, which treat atoms of 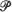differently, and these and their inverses are proved strongly consistent. Functional central limit theorems are then proved for empirical Lorenz curves and their inverses, under condition that 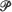be continuous and have finite variance. A mild variation condition is also needed in some circumstances. If the support of 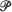is connected, the weak convergence is relative to C[0, 1] with uniform topology, otherwise to D[0, 1] with M1 topology. Selected applications are discussed, one being to the Gini coefficient.

Keywords

ALMOST-SURELY CONVERGENT CONSTRUCTIONSCONCENTRATION CURVESCONSISTENCYDOMINATED VARIATIONFUNCTIONS OF A BROWNIAN BRIDGEFUNCTION SPACES D AND CGINI COEFFICIENTINVERSE LORENZ CURVESLORENZ CURVESMEAN DIFFERENCEM1 TOPOLOGYPYKE-SHORACK METRICSWEAK CONVERGENCE
Type
Research Article
Information
Advances in Applied Probability , Volume 9 , Issue 4 , December 1977 , pp. 765 - 791
Copyright
Copyright © Applied Probability Trust 1977 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

References

Allison, P. D., de Solla Price, D., Griffith, B. C., Moravcsik, M. J., and Stewart, J. A. (1976) Lotka's Law: a problem in its interpretation and application. Social Studies of Science 6, 269–276.CrossRefGoogle Scholar
Billingsley, P. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
Chung, K. L. (1968) A Course in Probability Theory. Harcourt, Brace and World, New York.Google Scholar
Dugué, D. (1958) Traité de Statistique Théorique et Appliquée. Masson, Paris.Google Scholar
Feller, W. (1969) One-sided analogues of Karamata's regular variation. Enseignement Math. 15, 107–121.Google Scholar
Gastwirth, J. L. (1972) The estimation of the Lorenz curve and Gini index. Rev. Econom. Statist. 54, 306–316.CrossRefGoogle Scholar
Hart, P. E. (1971) Entropy and other measures of concentration. J. R. Statist. Soc. A 134, 73–85.Google Scholar
Hart, P. E. (1975) Moment distributions in economics: an exposition. J. R. Statist. Soc. A 138, 423–434.Google Scholar
House of Commons (1975) Second Report on Scientific Research in British Universities (First Report from the Select Committee on Science & Technology. Session 1975–76). Cmnd. 504. Her Majesty's Stationery Office, London.Google Scholar
Iglehart, D. L. (1974) Weak convergence in applied probability. Stoch. Proc. Appl. 2, 211–241.Google Scholar
Kakwani, N. C. and Podder, N. (1973) On the estimation of Lorenz curves from grouped observations. Internat. Econom. Rev. 14, 278–292.CrossRefGoogle Scholar
Kakwani, N. C. and Podder, N. (1976) Efficient estimation of the Lorenz curve and associated inequality measures from grouped observations. Econometrica 44, 137–148.Google Scholar
Kendall, M. G. and Stuart, A. (1977) The Advanced Theory of Statistics, Vol. 1, 4th ed. Griffin, London.Google Scholar
Kingman, J. F. C. and Taylor, S. J. (1966) Introduction to Measure and Probability. Cambridge University Press, London.Google Scholar
Leimkuhler, F. F. (1967) The Bradford distribution. J. Documentation 23, 197–207.Google Scholar
Lindvall, T. (1973) Weak convergence of probability measures and random functions in the function space D[0, ∞). J. Appl. Prob. 10, 109–121.CrossRefGoogle Scholar
Matuszewska, W. (1962) Regularly increasing functions in connection with the theory of L Φ-spaces. Studia Math. 21, 317–344.CrossRefGoogle Scholar
O'Reilly, N. E. (1974) On the weak convergence of empirical processes in sup-norm metrics. Ann. Prob. 2, 642–651.CrossRefGoogle Scholar
Pomarède, J. L. (1976a) A Unified Approach via Graphs to Skorokhod's Topologies on the Function Space D. Ph. D. Thesis, Yale University.Google Scholar
Pomarède, J. L. (1976b) On Skorokhod's Topologies on D. Preprint, Université de Sherbrooke, Québec.Google Scholar
Pyke, R. (1965) Spacings. J. R. Statist. Soc. B 27, 395–449.Google Scholar
Pyke, R. (1969) Applications of almost surely convergent constructions of weakly convergent processes. In Probability and Information Theory, Proceedings of the International Symposium at McMaster University, 1968, ed. Behara, M., Krickeberg, K. and Wolfowitz, J., Lecture Notes no. 89, Springer-Verlag, Berlin.Google Scholar
Pyke, R. and Shorack, G. R. (1968) Weak convergence of a two-sample empirical process and a new approach to Chernoff-Savage theorems. Ann. Math. Statist. 39, 755–771.CrossRefGoogle Scholar
Rudin, W. (1964) Principles of Mathematical Analysis, 2nd edn. McGraw-Hill, New York.Google Scholar
Seneta, E. (1976) Regularly Varying Functions. Lecture Notes no. 508, Springer-Verlag, Berlin.Google Scholar
Shorack, G. R. (1972) Functions of order statistics. Ann. Math. Statist. 43, 412–427.Google Scholar
Skorokhod, A. V. (1956) Limit theorems for stochastic processes. Theor. Prob. Appl. 1, 261–290.Google Scholar
Stigler, S. M. (1974) Linear functions of order statistics with smooth weight functions. Ann. Statist. 2, 676–693.Google Scholar
Taguchi, T. (1968) Concentration-curve methods and structures of skew populations. Ann. Inst. Statist. Math. 20, 107–141.Google Scholar
Whitt, W. (1977) Continuity of several functions on the function space D. Ann. Prob. Google Scholar
Wold, H. (1935) A study on the mean difference, concentration curves and concentration ratio. Metron XII No. 2, 39–58.Google Scholar

References added in proof

Alker, H. R. Jr. (1965) Mathematics and Politics. Macmillan, New York.Google Scholar
Gastwirth, J. L. (1971) A general definition of the Lorentz curve. Econometrica 39, 1037–1039.Google Scholar
Thompson, W. A. Jr. (1976) Fisherman's luck. Biometrics 32, 265–271.Google Scholar
Whitt, W. (1973) Representation and convergence of point processes on the line. Preprint, Yale University.Google Scholar