Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-06-01T16:26:55.376Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimally Stopping at a Given Distance from the Ultimate Supremum of a Spectrally Negative Lévy Process

Part of: Stochastic processes Inference from stochastic processes

Published online by Cambridge University Press:  17 March 2021

Mónica B. Carvajal Pinto  and
Kees van Schaik Open the ORCID record for Kees van Schaik [Opens in a new window]
Mónica B. Carvajal Pinto*
Affiliation:
University of Manchester
Kees van Schaik*
Affiliation:
University of Manchester
*
*Postal address: Department of Mathematics, University of Manchester, Manchester, M13 9PL, UK. Email address: kees.vanschaik@manchester.ac.uk
*Postal address: Department of Mathematics, University of Manchester, Manchester, M13 9PL, UK. Email address: kees.vanschaik@manchester.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the optimal prediction problem of stopping a spectrally negative Lévy process as close as possible to a given distance 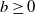$b \geq 0$ from its ultimate supremum, under a squared-error penalty function. Under some mild conditions, the solution is fully and explicitly characterised in terms of scale functions. We find that the solution has an interesting non-trivial structure: if b is larger than a certain threshold then it is optimal to stop as soon as the difference between the running supremum and the position of the process exceeds a certain level (less than b), while if b is smaller than this threshold then it is optimal to stop immediately (independent of the running supremum and position of the process). We also present some examples.

Keywords

Spectrally negative Lévy processoptimal predictionoptimal stoppingscale functions

MSC classification

Primary: 60G40: Stopping times; optimal stopping problems; gambling theory
Secondary: 62M20: Prediction
Type
Original Article
Information
Advances in Applied Probability , Volume 53 , Issue 1 , March 2021 , pp. 279 - 299
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allaart, P. (2010). A general ‘bang-bang’ principle for predicting the maximum of a random walk. J. Appl. Prob. 47, 1072–1083.CrossRefGoogle Scholar
Alili, L. and Kyprianou, A. E. (2005). Some remarks on first passage of Lévy processes, the American put and pasting principles. Ann. Appl. Prob. 15, 2062–2080.CrossRefGoogle Scholar
Asmussen, S. and Albrecher, H. (2010). Ruin Probabilities. World Scientific, Singapore.CrossRefGoogle Scholar
Baurdoux, E. J. and van Schaik, K. (2014). Predicting the time at which a Lévy process attains its ultimate supremum. Acta Appl. Math. 134, 21–44.CrossRefGoogle Scholar
Baurdoux, E. J., Kyprianou, A. E. and Ott, C. (2016). Optimal prediction for positive self-similar Markov processes. Electron. J. Prob. 21.Google Scholar
Bernyk, V., Dalang, R. C. and Peskir, G. (2011). Predicting the ultimate supremum of a stable Lévy process with no negative jumps. Ann. Prob. 39, 2385–2423.CrossRefGoogle Scholar
Bertoin, J. (1996). Lévy Processes. Cambridge University Press.Google Scholar
Bichteler, K. (2002). Stochastic Integration with Jumps. Cambridge University Press.CrossRefGoogle Scholar
Cohen, A. (2010). Examples of optimal prediction in the infinite horizon case. Statist. Prob. Lett. 80, 950–957.CrossRefGoogle Scholar
Du Toit, J. and Peskir, G. (2007). The trap of complacency in predicting the maximum. Ann. Prob. 35, 340–365.CrossRefGoogle Scholar
Du Toit, J. and Peskir, G. (2008). Predicting the time of the ultimate maximum for Brownian motion with drift. In Mathematical Control Theory and Finance, Springer, Berlin, pp. 95–112.CrossRefGoogle Scholar
Du Toit, J. and Peskir, G. (2009). Selling a stock at the ultimate maximum. Ann. Appl. Prob. 19, 983–1014.CrossRefGoogle Scholar
Espinosa, G.-E. and Touzi, N. (2012). Detecting the maximum of a mean-reverting scalar diffusion. SIAM J. Control Optimization 50, 2543–2572.CrossRefGoogle Scholar
Graversen, S. E., Peskir, G. and Shiryaev, A. N. (2001). Stopping Brownian motion without anticipation as close as possible to its ultimate maximum. Theory Prob. Appl. 45, 125–136.CrossRefGoogle Scholar
Hubalek, F. and Kyprianou, A. E. (2010). Old and new examples of scale functions for spectrally negative Lévy processes. In Seminar on Stochastic Analysis, Random Fields and Applications VI, Springer, Basel, pp. 119–145.Google Scholar
Kuznetsov, A., Kyprianou, A. E. and Rivero, V. (2012). The theory of scale functions for spectrally negative Lévy processes. In Lévy Matters II, Springer, Berlin, pp. 97–186.CrossRefGoogle Scholar
Kyprianou, A. E. (2013). Gerber–Shiu Risk Theory. Springer, Cham.CrossRefGoogle Scholar
Kyprianou, A. E. (2014). Fluctuations of Lévy Processes with Applications: Introductory Lectures. Springer, Berlin, Heidelberg.CrossRefGoogle Scholar
Peskir, G. and Shiryaev, A. N. (2006). Optimal Stopping and Free-Boundary Problems. Birkhäuser, Basel.Google Scholar
Sato, K. (1999). Lévy Processes and Infinitely Divisible Distributions. Cambridge University Press.Google Scholar
Schoutens, W. (2003). Lévy Processes in Finance: Pricing Financial Derivatives. John Wiley, New York.CrossRefGoogle Scholar
Shiryaev, A. N. (2008). Optimal Stopping Rules. Springer, Berlin.Google Scholar
Tankov, P. (2003). Financial Modelling with Jump Processes. CRC Press, Boca Raton.CrossRefGoogle Scholar
Williams, D. (1991). Probability with Martingales. Cambridge University Press.CrossRefGoogle Scholar