We investigate random minimal factorizations of the n-cycle, that is, factorizations of the permutation 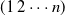$(1 \, 2 \cdots n)$ into a product of cycles 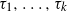$\tau_1, \ldots, \tau_k$ whose lengths 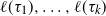$\ell(\tau_1), \ldots, \ell(\tau_k)$ satisfy the minimality condition $\sum_{i=1}^k(\ell(\tau_i)-1)=n-1$ . By associating to a cycle of the factorization a black polygon inscribed in the unit disk, and reading the cycles one after another, we code a minimal factorization by a process of colored laminations of the disk. These new objects are compact subsets made of red noncrossing chords delimiting faces that are either black or white. Our main result is the convergence of this process as 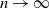$n \rightarrow \infty$ , when the factorization is randomly chosen according to Boltzmann weights in the domain of attraction of an $\alpha$ -stable law, for some $\alpha \in (1,2]$ . The limiting process interpolates between the unit circle and a colored version of Kortchemski’s $\alpha$ -stable lamination. Our principal tool in the study of this process is a new bijection between minimal factorizations and a model of size-conditioned labeled random trees whose vertices are colored black or white, as well as the investigation of the asymptotic properties of these trees.