2.1. DC funds

In the economics literature (e.g. Von Neumann & Morgenstern, Reference Von Neumann and Morgenstern1947; Savage, Reference Savage1954; Samuelson, Reference Samuelson1969) expected-utility theory is developed as a basis for decision-making by individual agents. The argument of the utility function is the consumption of the decision-maker, discounted at a rate equal to the subjective discount rate (Merton, Reference Merton1969), which reflects the decision-maker’s liquidity preference.

Some actuarial authors – particularly in addressing the asset-allocation problem of a member of a DC retirement fund during the accumulation phase (e.g. Merton, Reference Merton1993; Gerber & Shiu, Reference Gerber and Shiu2000 – cf. Cairns et al., Reference Cairns, Blake and Dowd2000; Nielsen, Reference Nielsen2006; Deelstra et al., Reference Deelstra, Grasselli and Koehl1999) – define utility functions in terms of terminal wealth, i.e. the lump-sum benefit on retirement. The problem with this definition is that it does not take cognisance of the post-retirement income that can be purchased from the benefit on retirement. (Here a “member” includes a contributing member, a deferred pensioner and a pensioner.)

Cairns et al. (Reference Cairns, Blake and Dowd2000) use the pension purchased at retirement. The problem with this approach is that it treats members with large current balances as having greater expected utilities at retirement. Whilst this definition may be useful for a member, it does not solve the trustees’ problem of designing a default asset allocation (i.e. of determining the asset allocation in the default investment channel) for all members of a certain attained age.

Vigna & Haberman (Reference Vigna and Haberman2001), Levitan & Thomson (Reference Levitan and Thomson2009) and Levitan (Reference Levitan2006) use the net replacement ratio as the argument of the utility function for the asset-allocation problem facing a member of a DC retirement fund. The use of a net replacement ratio may be justified for the purposes of investment-channel choice by an individual member. However, it still does not address the trustees’ problem of designing a default asset allocation for all members of a certain age. For a group of members of a particular attained age it would be possible to use an aggregate net replacement ratio for the whole group, but this would again place greater weight on those with large current balances than on those with small balances.

The above critique suggests that the argument of the utility function should be a ratio of the post-retirement income to a reference income. As we are using expected-utility theory to determine the optimal exposure to risky assets, we should use as our reference income a risk-free post-retirement income based on a member’s current balance. Furthermore, in order to ensure that we can conveniently and fairly assign members to groups so that the same asset allocation will apply to each member of a group, our argument should satisfy the requirement that, for each member of a particular group, the argument is the same.

For a member of a certain group, the argument of the utility function may be taken as the ratio of her/his post-retirement income to an inflation-protected deferred annuity notionally purchased from her/his current balance, expressed as

(2) $$z_{T} \,{\equals}\,{{\left( {{{A_{T} } \over {a_{T} }}} \right)} \over {\left( {{{A_{0} } \over {{}_{T}a_{0} }}} \right)}}$$

where A _T is the member’s accumulated balance at time T, being the outstanding term to her/his retirement date; a _T the value per unit at time T of an inflation-protected immediate annuity; A ₀ the member’s current balance at time 0; and _T a ₀ the value per unit of an inflation-protected deferred annuity payable with effect from retirement date, notionally purchased at time 0.

Equation (2) thus expresses the argument of the utility function as the ratio of an outcome to a benchmark outcome, both of which relate to the objectives of a DC fund.

As z _T is the same for all members of a particular attained age, with a particular retirement age and with particular annuity terms, the same ratio – and therefore the same asset allocation – may be used for all such members. Within each such group of members it also avoids placing greater emphasis on members with large current balances than on members with small balances. It therefore solves the trustees’ problem of designing a default asset allocation: the same asset allocation may be used for every member in the group. This ratio is referred to below as the “DC benefit ratio”.

The above definition presupposes that the benefit on retirement will be payable as a lump sum. In effect, however, it is assumed either that the fund will purchase an annuity for a retiring member or that she/he will do so. Longevity risks will therefore not be borne by the fund. Because preferences must ultimately be expressed in terms of goods and services rather than money, z _T is defined in terms of inflation-protected annuities. However, if and to the extent that the benefit on retirement is payable in the form of an annuity, the terms and conditions of that annuity (i.e. its frequency, its provision for a term certain or a survivor’s annuity and whether it is inflation-protected) should be applied in the determination both of _T a ₀ and of a _T .

Both A _T and a _T are stochastic. Allowance will have to be made for correlation between a _T and the returns on the various investment channels as these correlations will affect the variance of the distribution of z _T .

If the fund buys annuities from a life office, the value of a _T will have to be modelled accordingly. If a member has options between alternative annuities, or the option to defer annuitisation – or not to annuitise – then the trustees will need to decide on a default annuity option. This option may be applied before retirement, unless and until the member makes an option, for the purposes of simulating equation (2) during the accumulation phase. It may be appropriate to allow for a combination of alternative annuities, optimising between them by maximising the expected utility of real post-retirement income. For this purpose, the bequest motive may be disregarded, because the trustees’ fiduciary duties are to the members and stated dependants, not to other legatees. As shown by Samuelson (Reference Samuelson1969), though, the consumption–saving problem will not necessarily be separable, except for constant relative risk aversion. In general, the simultaneous maximisation of expected utility for annuitisation (and for asset allocation during deferment of annuitisation) and for post-retirement consumption year by year will therefore be complicated. In practice, it would be preferable to assume no savings or dissavings – i.e. to assume that the accumulated savings will be immediately annuitised on attainment of the retirement age and that all post-retirement income will be required for consumption year by year. For this purpose, a level inflation-protected annuity would need to be assumed for the default option. Even if most members select an annuity that is constant in nominal terms, the requirement of type-2 prudence suggests that the default should be expressed in real terms. There may be some room for compromise if allowance is made for life-cycle expenses varying by age, but this would also need to be expressed in real terms. The features of the default option – including frequency of payment and the provision of annuities to surviving spouses and dependants – would need to be reflected in the determination of a _T . There may be grounds for arguing that some capital may be required on retirement, either for paying off debts or for investment in income-generating activities. The counter-argument to this is that such arrangements are preferable only if and to the extent that they improve post-retirement income. The latter should therefore be used as the default argument.

As mentioned above, the value of _T a ₀ is intended to be notional; it need not be based on the prices of deferred annuities available in the market. As markets for such annuities are generally illiquid, it would be better to determine the value internally. It should, however, be consistent with the basis used for determining a _T so that

$$\mathop{{\lim }}\limits_{{T\to0}} \left( {_{T} a_{0} } \right)\,{\equals}\,a_{0} .$$

In principle, A _t should include not only the retirement savings in the fund, but also those outside of the fund. If it is assumed that the retirement savings outside of the fund will be invested (and taxed) similarly to the asset allocation in the fund, the DC benefit ratio is unaffected. However, the trustees have no responsibility for members’ retirement savings outside of the fund.

As shown in equation (2), the time horizon for a particular member is the date of attainment of the retirement age. However, as explained above, it should be recognised that it will be possible to re-determine the default asset allocation at regular intervals during the accumulation phase. This necessitates dynamic asset allocation, as explained in section 4.2 below.

For the purposes of dynamic asset allocation, some authors (e.g. Cairns, Reference Cairns2000) use continuous time. As explained by Cairns (Reference Cairns2000), this may be useful for the purposes of analysis of the sensitivity of asset allocations to various parameters. However, for practical applications the utility function and the models of risky assets may be too complex to permit solutions in closed form. In principle, as argued elsewhere by one of the authors (Thomson, Reference Thomson2011), the time interval to be used for dynamic asset allocation should be the same as the decision interval. Thus, if the trustees review the mandates of investment managers annually, if they reconsider their model of risky assets and the parameters of their utility function annually, and if members are grouped into annual age intervals for the purposes of determining default allocations, it would be appropriate to use an annual interval for dynamic modelling. Dynamic modelling is further considered in section 4.2 below.

2.2. DB funds

Some authors (e.g. Sherris, Reference Sherris1993; Boulier et al., Reference Boulier, Trussant and Florens1995; Siegmann & Lucas, Reference Siegmann and Lucas1999) treat the sponsoring employer as the beneficiary of the pension fund. Others (e.g. Sharpe & Tint, Reference Sharpe and Tint1990; Cairns, Reference Cairns2000; Cairns et al., Reference Cairns, Blake and Dowd2000; Haberman et al., Reference Haberman, Day, Fogarty, Khorasanee, McWhirter, Nash, Ngwira, Wright and Yakoubov2003; Cardinale et al., Reference Cardinale, Katz, Kumar and Orszag2006; McCarthy & Miles, Reference McCarthy and Miles2013) attempt to reflect a compromise between the interests of the sponsoring employer and the obligations of the trustees to members.

Whilst for an individual the argument of the utility function may be defined in terms of her/his post-retirement income, it must be recognised that this is not necessarily appropriate for the trustees of a retirement fund. In the case of a DB fund, the argument of the utility function must take cognisance not only of the assets of the fund but also of its liabilities. An individual has choices with regard to the liabilities that she/he may incur from time to time, but with the possible exceptions of increases to pensions, the trustees have no such choices. The risks faced by the trustees of a retirement fund cannot be defined without reference to its liabilities.

For a DB fund, it would be natural to take “wealth” to mean the excess of the assets over the liabilities; i.e. the surplus at a time horizon (as does Sherris (Reference Sherris1992) in the single-period case). However, this would mean that the trustees would prefer a large fund to a small fund with the same funding ratio. That would clearly be wrong; the size of a fund does not determine its financial soundness, and it is the latter, not the former, for which the trustees are responsible. For example, the amalgamation of a well-funded scheme with a scheme with a relatively low funding ratio should not be accepted by the trustees of the former without arrangements to safeguard the interests of its members and its sponsoring employer. This suggests that the funding ratio itself would be more appropriate. The funding ratio also has more meaning with regard to the security of the prospective beneficiaries. The numerator of the funding ratio can also be adjusted to allow for the sponsor’s solvency and share of surpluses and shortfalls (e.g. McCarthy & Miles, Reference McCarthy and Miles2013).

A problem with the use of the funding ratio is that, if the argument of the utility function is required at the date of expiry of the liabilities, the denominator of the ratio is 0. Also – and more importantly – whilst in the absence of a sponsoring employer’s guarantee and insurance against its failure a high funding ratio gives greater security to members, it does not relate to the benefits actually payable to members.

The above critique suggests that the argument of the utility function should be expressed in terms of the benefits payable up to the time horizon, together with the assets available to pay subsequent benefits. (The inclusion of the sponsor covenant is dealt with below.) As for the DC benefit ratio, the argument should be relative to a standard value. In contrast to the DC case, however, a DB fund creates rights to benefits that are unrelated to the contributions paid by and in respect of members. The standard value should therefore be expressed in terms of benefits payable up to the time horizon, together with liabilities for subsequent benefits.

The argument may be taken as

(3) $$z_{t} \,{\equals}\,{{A_{t} {\plus}P_{t} } \over {L_{t} {\plus}P_{t} }}$$

where A _t is the value of the assets of the fund available at time t for subsequent benefits; L _t the value of the liabilities of the fund at time t for subsequent benefits in respect of service to time 0; and P _t the value of benefits payable during the period [0, t], accumulated to time t with interest at the beneficiary’s risk-free rate from time to time.

In particular

(4) $$z_{0} \,{\equals}\,{{A_{0} } \over {L_{0} }}{\rm\ \ \ and}$$

(5) $$z_{T} \,{\equals}\,{{A_{T} {\plus}P_{T} } \over {P_{T} }}$$

where T is the date of expiry of the liabilities.

The numerator of equation (3) represents the value of benefits payable to members up to and beyond time t, together with surplus assets available. (P _t represents the benefits payable up to time t, whilst A _t represents the assets required to cover subsequent benefits, and any surplus assets available for possible improvements.) The denominator represents the value of benefits payable up to and beyond time t. We refer to the ratio as the “DB benefit ratio”. Equation (3) thus expresses the argument of the utility function as the ratio of an outcome to a benchmark outcome, both of which relate to the objectives of a DB fund.

It may be questioned why P _t should be accumulated with interest at the beneficiary’s risk-free rate. The reason for this is that the benefits cannot be assumed to have been invested in risky assets after they have been paid; it is the trustees who are accountable for investment in risky assets. In effect, the beneficiary’s risk-free rate is assumed to represent the liquidity preference of the beneficiary.

It may also be questioned whether the choice of T as the date of expiry of the liabilities is prejudicial to pensioners as at time 0, whose pensions will cease long before T. For a DC fund the definition of z _T is specific to a member whose retirement date is T, so there is no issue; the optimal exposure to risky assets applies to that member. But for a DB fund the question is material: if there was only one member in the fund the optimal exposure to risky assets would generally be very different from the optimal exposure for a diverse range of members. From the point of view of a particular member, the proposed choice of T is arbitrary. This matter is dealt with in section 4.2 below.

As noted above, consideration also needs to be given to the sponsor covenant. In principle, the argument of the utility function should take cognisance of the objectives both of the members and of the sponsoring employer. Whilst the trustees’ prime concern is not the minimisation of employers’ contributions, they do have an indirect responsibility to avoid precipitating the default of the sponsoring employer, particularly while the fund is in shortfall. In fact, the suggested DB benefit ratio in equation (3) addresses not only the objectives of the members but also those of the sponsoring employer. The pension fund is a mechanism for assisting the negotiation between sponsor and beneficiaries with regard to future benefits. By focussing on the fund’s capacity to pay benefits, such negotiations become integrative rather than distributive bargaining.

It would, however, be possible to analyse the difference between the interests of the members and those of the sponsoring employer. This could be done by analysing the assets A _t as those available for members less the shortfall (if any) payable by the employer. Thus

(6) $$A_{t} \,{\equals}\,A_{t}^{{\rm M}} {\plus}A_{t}^{{\rm E}} $$

where $$A_{t}^{{\rm M}} \,{\equals}\,L_{t} {\plus}jS_{t} $$ constitutes the funds available to members; $$A_{t}^{{\rm E}} \,{\equals}\,(1\,{\minus}\,j)S_{t} $$ constitutes the funds available to the employer; and j∈[0, 1] is the proportion of the surplus available to members. The value of j will depend on the rules of the fund and the regulatory requirements regarding the funding of shortfalls and the transfer of surplus to employers, as well as the probability of default by the sponsoring employer and the arrangements regarding insurance against that contingency. It will typically depend on whether the surplus is positive and it may itself depend on the funding ratio.

Now suppose that we wish to apply a weighting l∈[0, 1] to the employer relative to members, so that

$$A'_{t} \,{\equals}\,A_{t}^{{\rm M}} {\plus}lA_{t}^{{\rm E}} $$

i.e.

$$\eqalignno{ A'_{t} &\,{\equals}\,\left\{ {L_{t} {\plus}jS_{t} } \right\}{\plus}l\left\{ {\left( {1\,{\minus}\,j} \right)S_{t} } \right\} \cr & \,{\equals}\,\left\{ {L_{t} {\plus}S_{t} } \right\}\,{\minus}\,\left( {1\,{\minus}\,j} \right)S_{t} {\plus}l\left\{ {\left( {1\,{\minus}\,j} \right)S_{t} } \right\} \cr & \,{\equals}\,A_{t} \,{\minus}\,\left\{ {\left( {1\,{\minus}\,l} \right)\left( {1\,{\minus}\,j} \right)S_{t} } \right\} $$

Equation (3) can then be adjusted as

(7) $$z_{t}^{{\rm M}} \,{\equals}\,{{A_{t}^{{\rm M}} \,{\minus}\,kS_{t}^{{\rm E}} {\plus}P_{t} } \over {L_{t} {\plus}P_{t} }}$$

where

$$k\,{\equals}\,(1\,{\minus}\,j)(1\,{\minus}\,l).$$

When k=0 (either because j=1 or l=1), equation (7) reduces to equation (3), which gives neutral weighting. When k=1 (because j=0 and l=0), the numerator of equation (7) ignores the surplus. The optimal asset allocation can then be found for various values of k and the decision can be made by distributive bargaining.

It may be argued that members’ concerns are confined to shortfalls, whilst employers have an interest both in surpluses and in shortfalls. This can be accommodated by adjusting k accordingly. However, it is questionable whether members’ interests are in fact confined to the downside; the greater the surplus at time t the lower the probability of a shortfall at time t+1.

The above discussion relates only to past-service benefits, i.e. to benefits for service up to time 0. The optimal portfolio based on the maximisation of the expected utility of that argument relates to the assets of the fund at time 0. The argument for service currently accruing may be similarly determined. The optimal portfolio based on the maximisation of the expected utility of the latter argument relates to the investment of contributions to the fund during the period [0, 1) or the annual rate of contributions at time 0. (Although dynamic asset allocation is used to determine future optimal asset allocations as described in section 4.2 below, the object of that exercise is to find the optimum asset allocation for current contributions. The whole exercise will be repeated at the start of the next year, which will then be defined as time 0.) This approach would correspond to the use of the projected-unit-credit method of valuation, which would be appropriate for an open fund. The optimal asset allocation of contributions can be determined accordingly. For a closed fund it would be appropriate to allow for all future service, which would correspond to an aggregate-funding method.

As for DC funds, it should be recognised that it will be possible to re-determine the asset allocation at regular intervals. This necessitates dynamic asset allocation. Again, the time interval to be used for dynamic asset allocation should be the same as the decision interval. Thus, if the trustees review the mandates of investment managers annually, if they reconsider their model of risky assets and the parameters of their utility function annually, and if the fund is valued annually, it would be appropriate to use an annual interval for dynamic modelling.

3.1. The functional form of the utility function: a review

Numerous empirical tests of the descriptive validity of various utility functions have been made. For example, Levy (Reference Levy2005) finds, in an experiment involving an actual monetary gain or loss indexed to the participant’s investment performance, that “[decreasing absolute risk aversion] is strongly supported, but [increasing relative risk aversion] is rejected”. Friend (Reference Friend1973) and Cohn et al. (Reference Cohn, Lewellen, Lease and Schlarbaum1975) provide empirical evidence of decreasing relative risk aversion. Some evidence of decreasing relative risk aversion is also found by Bossons (Reference Bossons1973) and Projector & Weiss (Reference Projector and Weiss1966). In principle, the functional form of the utility function for a DC fund should be the same as for a DB fund; it is only the argument of the functions that differ.

The shapes of the utility functions of individual decision-makers may be quite variable. Levitan & Thomson (Reference Levitan and Thomson2009) show those elicited from a sample of members of a South African retirement fund. In that sample, there are examples of individuals who show aspiration levels – i.e. points below which risk aversion is negative and above which it is positive. The preferences implied by such utility functions would not be appropriate for fiduciaries as they constitute aspirational behaviour (Diecidue & Van de Ven, Reference Diecidue and Van de Ven2008). Prudence requires, inter alia, that trustees should not take higher risks when the fund is in shortfall than when it is in surplus. Indeed, any utility function that exhibits negative risk aversion over any part of its range would constitute aspirational behaviour. Thus, the value function defined in prospect theory would typically be inappropriate. Furthermore, it may be argued that any utility function that exhibits increasing absolute or relative risk aversion (depending on which of these measures is adopted) over any part of its range would constitute aspirational behaviour; it would suggest that lower risk aversion may be acceptable at lower values of the benefit ratio than at higher values. Also, the elicitation of a utility function may be affected by the problems associated with the descriptive application of expected-utility theory. These matters are considered further below.

For most purposes, the hyperbolic absolute risk aversion (HARA) class of utility functions has been considered to be sufficiently flexible and its mathematical tractability has established its popularity in the literature. As the name suggests, this class satisfies the requirement (Mossin, Reference Mossin1968) that, for a utility function u(∙), the absolute risk aversion is

(8) $$r(x)\,{\equals}\,\,{\minus}\,{{u''(x)} \over {u'(x)}}\,{\equals}\,{1 \over {ax{\plus}b}}.$$

For a>0, b>0, this establishes decreasing absolute risk aversion. Defining “absolute risk tolerance” as

(9) $$t(x)\,{\equals}\,{1 \over {r(x)}}$$

we obtain the result that absolute risk tolerance is linear. As shown by Merton (Reference Merton1971), the utility function for this class is

(10) $$u(x)\,{\equals}\,\left\{ \matrix{ {\gamma \over {1\,{\minus}\,\gamma }}\left( {{{\alpha x} \over \gamma }{\plus}\beta } \right)^{{1\,{\minus}\,\gamma }} \,{\rm\ \ for}\,a\,\ne\,0,\,\gamma \,\ne\,1 \hfill \cr {\rm ln}(x{\plus}\beta )\,{\rm for}\,a\,\ne\,0,\,\gamma \,{\equals}\,1 \hfill \cr \,{\minus}\,{\rm exp}\left( {\alpha x} \right)\,{\rm for}\,a\,{\equals}\,0 \hfill \cr} \right.$$

These forms are referred to as “generalised power utility”, “generalised logarithmic utility” and “exponential utility”, respectively. This class includes

1. − quadratic utility, with γ=−1;

2. − constant absolute risk aversion, with a=0; and

3. − constant relative risk aversion with a≠0, β=0.

HARA utility functions show decreasing relative risk aversion only if β<0. This is generally problematic for small values of x. The problems with quadratic utility functions are well documented (e.g. Pratt, Reference Pratt1964; Booth, Reference Booth1995) and are not further discussed here.

The utility function

(11) $$u(x)\,{\equals}\,\left\{ \matrix{ {{x^{{1\,{\minus}\,\gamma }} \,{\minus}\,1} \over {1\,{\minus}\,\gamma }}\,{\rm for}\,\gamma \,\ne\,1 \hfill \cr {\rm ln}(x)\,{\rm for}\,\gamma \,{\equals}\,1 \hfill \cr} \right.$$

is referred to by Samuelson (Reference Samuelson1969) as the “isoelastic” utility function. The use of this expression is explained by Gerber & Shiu (Reference Gerber and Shiu2000). Isoelastic utility implies (and is implied by) constant relative risk aversion:

(12) $$\eqalignno{\gamma (x)&#x0026;\,{\equals}\,\,{\minus}\,x{{u''(x)} \over {u'(x)}} \cr &#x0026;\,{\equals}\,\gamma $$

The use of a discontinuous utility function such as those used by Booth (Reference Booth1995) and Khorasanee & Smith (Reference Khorasanee and Smith1997) are inappropriate as they imply infinite relative risk aversion (generally negative below the point of discontinuity and positive above it). Similar problems arise with kinked utility functions (i.e. with utility functions exhibiting discontinuities in marginal utility).

For the purposes of determining the form of the utility function, it would be possible to elicit the utility functions of at least a sample of members. The functional form so elicited may be parametric or non-parametric. Whilst such utility functions might be informative, they could not be used in any mechanical way to construct a utility function for use by the trustees. In the first place, the trustees are required to be prudent, and second, if such a method had been contemplated, it would not have been necessary to appoint them. The way in which the utility functions of a sample of members may be used to inform the development of a utility function for use by the trustees is illustrated in sections 3.2 and 4.1.

We first consider the HARA class. From equations (Reference Cardinale, Katz, Kumar and Orszag8) and (Reference Diecidue and Van de Ven12) it follows that the relative risk aversion for HARA utility is

(13) $$\gamma (z)\,{\equals}\,\,{\minus}\,z{{u''(z)} \over {u'(z)}}\,{\equals}\,{z \over {az{\plus}b}}.$$

The derivative of this is

(14) $${d \over {dz}}\left( {\gamma (z)} \right)\,{\equals}\,{b \over {\left( {az{\plus}b} \right)^{2} }}$$

For our purposes we require a≥0; otherwise risk aversion becomes negative for large z. We also require that b≥0 or that the range of z must be restricted to $$z\,\gt\,{{\,{\minus}\,b} \over a}$$ ; otherwise there is a discontinuity at $$z\,\gt\,{{\,{\minus}\,b} \over a}$$ . The range of z cannot be so restricted. This means that, unless b=0 (in which case relative risk aversion is constant), relative risk aversion is increasing. This applies both to generalised power utility and to generalised logarithmic utility. The latter has been advanced by Rubinstein (Reference Rubinstein1976), but neither of these forms is possible with an argument z∈(0,∞).

The findings of Projector & Weiss (Reference Projector and Weiss1966), Bossons (Reference Bossons1973), Friend (Reference Friend1973), Cohn et al. (Reference Cohn, Lewellen, Lease and Schlarbaum1975) and Levy (Reference Levy2005) that, even amongst individual decision-makers, non-increasing relative risk aversion is supported suggests that constant relative risk aversion is not generally appropriate for trustees. Instead, non-increasing relative risk aversion should be used. It would be aspirational for trustees to take more risk when funding ratios are low than when they are high. As relative risk aversion is the measure to be used, this means that increasing relative risk aversion (and therefore constant absolute risk aversion) would be aspirational.

Another advantage of the use of relative risk aversion over that of absolute risk aversion is that the former is dimensionless. The dimension of absolute risk tolerance is that of the argument of the utility function. This means that the dimension of absolute risk aversion is the inverse of that of the argument of the utility function. The advantage of a dimensionless measure is that it applies regardless of the size of the fund. If, as in equation (3), the argument is itself dimensionless, it appears at first sight that the problem falls away. However, it must be borne in mind that, for given values of future benefits, the proposed argument is effectively expressed in terms of currency. The use of relative risk aversion ensures that the problem is truly dimensionless even for given values of the denominator of equation (3).

In the light of the above arguments, apart from the case of constant relative risk aversion, the HARA class is inappropriate.

The fitting of utility functions as contemplated by Thomson (2003 Reference Thomsonb ) and Levitan & Thomson (Reference Levitan and Thomson2009) allows for degrees of risk tolerance that, whilst they might be acceptable for individual members, would not be appropriate for the purposes of decision-making by trustees as contemplated in this paper.

Because of the requirements of type-2 prudence, the relative risk aversion will invariably be greater than 1; this is discussed further in section 3.2 below. The case of constant relative risk aversion may be acceptable to the trustees, and there is no intrinsic reason why it should not be. However, if the trustees require decreasing relative risk aversion, or if they wish to effect a compromise between different levels of relative risk aversion amongst themselves, then another class of utility functions is necessary. That is considered in sections 3.2 and 3.3 below.

3.2. Levels of risk aversion and the requirements of prudence

The legislative and regulatory requirements of many jurisdictions explicitly or implicitly require fiduciary duties including prudence, and common law in this regard is well established. We now turn to the relationship between risk appetite and type-2 prudence. In terms of expected-utility theory, risk appetite is measured in terms of risk aversion. As we have accepted expected-utility theory as normatively valid, we shall consider the relationship between risk aversion and type-2 prudence.

Biasca (Reference Biasca2009) uses illustrative levels of constant relative risk aversion of 10–30. These levels are selected without justification. Cardinale et al. (Reference Cardinale, Katz, Kumar and Orszag2006) use illustrative levels of constant relative risk aversion of 0–7. McCarthy & Miles (Reference McCarthy and Miles2013) use constant relative risk aversion of 5. Examples of widely differing levels of constant absolute risk aversion are given by Pézier & Scheller (Reference Pézier and Scheller2011).

If the trustees are to make a reasonable decision about the level of relative risk aversion they should adopt, it would arguably be appropriate for them to be informed by the levels of relative risk aversion exhibited by members of the fund. In doing so, they need to recognise that not all members will be prudent. Nevertheless, such information could at least be used as a check on their own utility functions, so as to establish how they as trustees compare with members. For this purpose, the trustees may elicit the utility functions of a sample of members.

This approach may be illustrated with reference to the sample of members of a retirement fund that was used in Levitan & Thomson (Reference Levitan and Thomson2009). More details of that sample, and of the research conducted on it, are contained in Levitan (Reference Levitan2006). In those works, for each respondent m, an average relative risk aversion was found as

(15) $$\bar{\gamma }_{m} \,{\equals}\,{1 \over {x_{\omega } \,{\minus}\,x_{\alpha } }}\mathop{\int}\limits_{x_{\alpha } }^{x_{\omega } } {\gamma _{m} (x)dx} $$

where x is the member’s net replacement ratio at retirement and γ _m (x) the relative risk aversion of the member as a function of the net replacement ratio x. Whilst the net replacement ratio differs from the benefit ratios used in this paper, the elicitation could be framed in terms of benefit ratios. The range of integration [x _α , x _ω ] was the range of net replacement ratios over which the member’s utility function was elicited. For the purpose of calculating γ _m (x), the member’s utility function was elicited using the equally likely certainty equivalent (ELCE) method (Anderson et al., Reference Anderson, Dillon and Hardaker1977; Farquhar, Reference Farquhar1984; Thomson, 2003 Reference Thomsonb ) at discrete values of x over the range. The values of the utility function for intermediate values of x were found by interpolation, using an interpolation method suggested in Thomson (2003 Reference Thomsonb ).

The cumulative distribution of the average relative risk aversion of members in this sample is shown in Figure 1. As discussed in Levitan & Thomson (Reference Levitan and Thomson2009), two outliers have been ignored. The median was 2.90 and the upper extreme was 7.06.

Figure 1 Cumulative sample distribution of average relative risk aversion.

Because the trustees need to be more prudent than most members, the relative risk aversion to be adopted by the trustees should be at least the median. Clearly, though, one would not expect them to adopt the upper extreme. The relative risk aversion must therefore be between 2.90 and 7.06.

However, the requirement of type-2 prudence does not only relate to risk aversion; it also relates to the levels of risk aversion exhibited over the range of possible outcomes. Analogously to the Pratt–Arrow definitions of absolute and relative risk aversion, Kimball (Reference Kimball1990) defines a “coefficient of absolute prudence”

(16) $$p(x)\,{\equals}\,\,{\minus}\,{{u'''(x)} \over {u''(x)}}$$

and a “coefficient of relative prudence”

(17) $$\pi (x)\,{\equals}\,\,{\minus}\,x{{u'''(x)} \over {u''(x)}}$$

He motivates these coefficients by a definition of “prudence” as “the sensitivity of the optimal choice of a decision variable” (e.g. the amount to be invested in the fund’s risk-free asset) to risk. He suggests that, if p(x)>0 or π(x)>0 then the decision-maker exhibits absolute or relative prudence, respectively.

In the context of the obligations of trustees, it seems that Kimball’s (Reference Kimball1990) definition is insufficient. If, for example, an isoelastic utility function is adopted by the trustees, then Kimball’s coefficient of relative prudence will be

(18) $$\pi (z)\,{\equals}\,\,{\minus}\,z{{u'''(z)} \over {u''(z)}}\,{\equals}\,\gamma (z){\plus}1$$

This will be positive (implying “prudence”) even for −1<γ<0. In that range a decision-maker would not even be risk-averse (and in fact not even unsatiated), let alone “prudent” in the sense intended in the context of trustees’ obligations.

In our context, it is clearly intended that type-2 prudence relates to risk aversion. First, it requires greater risk aversion than that of the median member, and certainly greater risk aversion than 1. Second, the requirement of type-2 prudence would be incompatible with increasing relative risk aversion, let alone increasing absolute risk aversion. As discussed in section 3.1 above, it would not be prudent for a trustee to adopt lower risk aversion when the fund is in shortfall than when it is in surplus. (Some literature shows that, on certain assumptions, the adoption of this principle produces results suggesting the contrary. That paradox is considered in section 5 below.) By the same token, as also indicated in that section, there should not be a discontinuity in marginal utility. Third, for any given level of the argument of the utility function (the DC benefit ratio in the case of a DC fund or the DB benefit ratio in the case of a DB fund) the trustees’ level of prudence should be greater than or equal to the level of prudence that would be exhibited by an agent with constant relative risk aversion equal to the trustees’ relative risk aversion at that level of the argument.

3.3. Criteria required for type-2 prudence

In the light of the discussion in sections 3.1 and 3.2 it follows that, in order to satisfy the requirements of type-2 prudence, the trustees’ utility function u(∙) should conform to the following criteria:

1. 1. The range criterion: it should map the open interval (0, +∞) into the open interval (−∞, +∞) or into a subset of that interval.

2. 2. The continuity criterion: it should be thrice differentiable.

3. 3. The unsatiation criterion: the trustees should be unsatiated, so that, for all z, u′(z)>0.

4. 4. The relative risk-aversion criterion: for all z there exists a γ* such that γ(z)≥γ*>1.

5. 5. The non-increasing relative risk aversion criterion: for any z* and for all z<z*, γ(z)≥γ(z*).

In condition 4, following from the preceding discussion, the value of γ* needs to be set high enough to establish the trustees’ level of risk aversion as adequately prudent. On the other hand, the value of γ* should not be unreasonably high.

We refer to a utility function satisfying these criteria as a “prudent utility function”.

3.4. The WARRA class

If, as observed above, the trustees require decreasing relative risk aversion, or if they wish to effect a compromise between different levels of relative risk aversion amongst themselves, then another class of utility functions is necessary. In this section, such a class is defined. As before, the same principles apply to DC funds as to DB funds.

We define the WARRA class by a generalisation of the isoelastic utility function as follows:

(19) $$u(z)\,{\equals}\,{{u_{0} (z){\plus}cu_{\infty} (z)} \over {1{\plus}c}}$$

where

(20) $$u_{0} (z)\,{\equals}\,{{z^{{1\,{\minus}\,\gamma _{0} }} \,{\minus}\,1} \over {1\,{\minus}\,\gamma _{0} }}$$

(21) $$\eqalignno{u_{\infty} (z)&#x0026;\,{\equals}\,{{z^{{1\,{\minus}\,\gamma _{\infty} }} \,{\minus}\,1} \over {1\,{\minus}\,\gamma _{\infty} }}; $$

$$\eqalignno{&#x0026;c\,\gt\,0 \ \ \ {\rm and} \cr &#x0026; {\gamma _{0} \geq \gamma _{\infty} \,\gt\,1}.$$

The rationale behind the subscripts becomes clear below.

The relative risk aversion of this utility function is

(22) $$\eqalignno{ \gamma (z)&#x0026;\,{\equals}\,\,{\minus}\,z{{u''(z)} \over {u'(z)}} \cr &#x0026;\,{\equals}\,{{\gamma _{0} z^{{\,{\minus}\,\gamma _{0} }} {\plus}c\gamma _{\infty} z^{{\,{\minus}\,\gamma _{\infty} }} } \over {z^{{\,{\minus}\,\gamma _{0} }} {\plus}cz^{{\,{\minus}\,\gamma _{\infty} }} }} \cr &#x0026;\,{\equals}\,{{\gamma _{0} {\plus}c\gamma _{\infty} z^{\lambda } } \over {1{\plus}cz^{\lambda } }} $$

where

$$\lambda \,{\equals}\,\gamma _{0} \,{\minus}\,\gamma _{\infty} $$

The relative risk aversion of the WARRA class is thus a weighted average of those of a more risk-averse decision-maker and a less risk-averse decision-maker, the weighting increasing to the latter as the argument increases.

Figure 2 shows the relative risk aversion of a WARRA-class utility function as a function of the argument z. In that figure the following parameters have been used

$$\eqalignno {\gamma _{0} \,{\equals}\,5 \!\!\!\cr \gamma _{\infty} \, {\equals}\,3 \, {\rm \,and } \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\cr c\,{\equals}\,1$$

Figure 2 Relative risk aversion of a WARRA-class utility function.

From equation (22) it may be shown that

(23) $$\,\,\,\,\,\,\,\mathop{{{\rm lim}}}\limits_{{z\to0}} \left( {\gamma (z)} \right)\,{\equals}\,\gamma _{0} \,{\rm and}$$

(24) $$\mathop{{{\rm lim}}}\limits_{{z\to\infty}} \left( {\gamma (z)} \right)\,{\equals}\,\gamma _{\infty} .$$

This means that, if WARRA is adopted as a compromise between the most risk-averse trustee A, with constant relative risk aversion of γ ₀, and the least risk-averse trustee B, with relative risk aversion of γ _∞, then, as shown in Figure 2, the relative risk aversion of trustee A is accommodated when benefit ratios are very low, and that of trustee B is accommodated when benefit ratios are very high. This provides a suitable basis for compromise, as trustee A is likely to be more concerned about the risk at low levels, whilst trustee B is likely to be more concerned about excessive risk aversion at higher levels.

It may also be shown that

(25) $${d \over {dz}}\left( {\gamma (z)} \right)\leq 0$$

thus establishing non-increasing risk aversion over the whole range, as shown in Figure 2. This shows that WARRA may be adopted not only for the purpose of effecting a compromise between different trustees, but also for the purpose of deliberately achieving decreasing relative risk aversion.

For suitable values of the parameters, the WARRA class satisfies the requirements of type-2 prudence as set out in section 3.2. This class does not uniquely satisfy those requirements, but it provides a simple formulation of a utility function that does satisfy them, with sufficient flexibility for most purposes.

Finally, it follows from equation (22) that

(26) $$\gamma (1)\,{\equals}\,{{\gamma _{0} {\plus}c\gamma _{\infty} } \over {1{\plus}c}}$$

so that, as shown in Figure 2, when the benefits are equal to their benchmarks, the weighting given to trustee B’s risk aversion relative to trustee A’s is equal to the weighting given to trustee B’s utility function relative to trustee A’s.

4.1. The determination of the parameters

If the WARRA class is adopted for the purpose of deliberately achieving decreasing relative risk aversion (as opposed to a compromise between less risk-averse and more risk-averse trustees) then the trustees must reach consensus as to the relative risk aversion at extremely low funding levels (γ ₀), at extremely high funding levels (γ _∞) and when the assets are equal to the liabilities, so that, from equation (26)

(27) $$c\,{\equals}\,{{\gamma _{0} \,{\minus}\,\gamma (1)} \over {\gamma (1)\,{\minus}\,\gamma _{\infty} }}.$$

For this purpose, the trustees’ utility functions at these levels need to be elicited. This may be done using the ELCE method (Anderson et al., Reference Anderson, Dillon and Hardaker1977; Farquhar, Reference Farquhar1984; Thomson, 2003 Reference Thomsonb ). This method addresses some of the problems raised above. If the trustees find it difficult to respond to the elicitation process with reference to extreme levels, a more reasonable range of levels may be used. Suppose the levels elicited are

$$z_{i} \,{\rm for}\,i{\rm \,{\equals}\,1,}\,\ldots\,{\rm ,}\,{\rm 5}$$

and that the corresponding values of the utility function are

$$u_{i} \,{\rm for}\,i\,{\equals}\,1,\,\ldots\,,\,5.$$

Without loss of generality we may assume that the utility function is shifted and scaled by the factors θ and ϕ, so that

(28) $$u_{i} \,{\equals}\,\theta {\plus}\phi v_{i} $$

where v _i is the utility function before shifting and scaling, i.e.

(29) $$v_{i} \,{\equals}\,{1 \over {1{\plus}c}}\left( {{{z_{i}^{{1\,{\minus}\,\gamma _{0} }} \,{\minus}\,1} \over {1\,{\minus}\,\gamma _{0} }}{\plus}c{{z_{i}^{{1\,{\minus}\,\gamma _{\infty} }} \,{\minus}\,1} \over {1\,{\minus}\,\gamma _{\infty} }}} \right).$$

Let

(30) $$w_{i} \,{\equals}\,\theta {\plus}\phi v_{i} \,{\minus}\,u_{i} .$$

Then we require

$$w_{i} \,{\equals}\,0.$$

We may then express the relationships between the five given values of z _i and u _i in terms of the simultaneous equations

(31) $$w_{i} \,{\equals}\,\theta {\plus}{\phi \over {1{\plus}c}}\left( {{{z_{i}^{{1\,{\minus}\,\gamma _{0} }} \,{\minus}\,1} \over {1\,{\minus}\,\gamma _{0} }}{\plus}c{{z_{i}^{{1\,{\minus}\,\gamma _{\infty} }} \,{\minus}\,1} \over {1\,{\minus}\,\gamma _{\infty} }}} \right)\,{\minus}\,u_{i} \,{\rm for}\,i\,{\equals}\,{\rm 1,\,\ldots\,,}\,{\rm 5}.$$

In order to solve these equations we may apply Newton’s method as follows. Using the subscript n to denote the nth estimate of the respective parameters we have

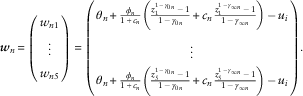(32) $${\mib w}_{n} \,{\equals}\,\left( {\matrix{ {w_{{n1}} } \cr \vdots \cr {w_{{n5}} } \cr } } \right)\,{\equals}\,\left( {\matrix{ {\theta _{n} {\plus}{{\phi _{n} } \over {1{\plus}c_{n} }}\left( {{{z_{1}^{{1\,{\minus}\,\gamma _{{0n}} }} \,{\minus}\,1} \over {1\,{\minus}\,\gamma _{{0n}} }}{\plus}c_{n} {{z_{1}^{{1\,{\minus}\,\gamma _{{\infty n}} }} \,{\minus}\,1} \over {1\,{\minus}\,\gamma _{{\infty n}} }}} \right)\,{\minus}\,u_{i} } \cr \vdots \cr {\theta _{n} {\plus}{{\phi _{n} } \over {1{\plus}c_{n} }}\left( {{{z_{5}^{{1\,{\minus}\,\gamma _{{0n}} }} \,{\minus}\,1} \over {1\,{\minus}\,\gamma _{{0n}} }}{\plus}c_{n} {{z_{5}^{{1\,{\minus}\,\gamma _{{\infty n}} }} \,{\minus}\,1} \over {1\,{\minus}\,\gamma _{{\infty n}} }}} \right)\,{\minus}\,u_{i} } \cr } } \right).$$

The Jacobian matrix of this equation is

(33) $${\mib J}_{n} \,{\equals}\,\left( {\matrix{ {{{\partial w_{{n1}} } \over {\partial \theta _{n} }}} &#x0026; {{{\partial w_{{n1}} } \over {\partial \phi _{n} }}} &#x0026; {{{\partial w_{{n1}} } \over {\partial \gamma _{{0n}} }}} &#x0026; {{{\partial w_{{n1}} } \over {\partial \gamma _{{\infty n}} }}} &#x0026; {{{\partial w_{{n1}} } \over {\partial c_{n} }}} \cr \vdots &#x0026; \vdots &#x0026; \vdots &#x0026; \vdots &#x0026; \vdots \cr {{{\partial w_{{n5}} } \over {\partial \theta _{n} }}} &#x0026; {{{\partial w_{{n5}} } \over {\partial \phi _{n} }}} &#x0026; {{{\partial w_{{n5}} } \over {\partial \gamma _{{0n}} }}} &#x0026; {{{\partial w_{{n5}} } \over {\partial \gamma _{{\infty n}} }}} &#x0026; {{{\partial w_{{n5}} } \over {\partial c_{n} }}} \cr } } \right).$$

where

(34) $${{\partial w_{{ni}} } \over {\partial \theta _{n} }}\,{\equals}\,1$$

(35) $${{\partial w_{{ni}} } \over {\partial \phi _{n} }}\,{\equals}\,{1 \over {1{\plus}c_{n} }}\left( {{{z_{i}^{{1\,{\minus}\,\gamma _{{0n}} }} \,{\minus}\,1} \over {1\,{\minus}\,\gamma _{{0n}} }}{\plus}c_{n} {{z_{i}^{{1\,{\minus}\,\gamma _{{\infty n}} }} \,{\minus}\,1} \over {1\,{\minus}\,\gamma _{{\infty n}} }}} \right)$$

(36) $${{\partial w_{{ni}} } \over {\partial \gamma _{{0n}} }}\,{\equals}\,{{\phi _{n} \left[ {z_{i}^{{1\,{\minus}\,\gamma _{{0n}} }} \left\{ {1\,{\minus}\,\left( {1\,{\minus}\,\gamma _{{0n}} } \right){\rm ln}\ z_{i} } \right\}\,{\minus}\,1} \right]} \over {\left( {1{\plus}c_{n} } \right)\left( {1\,{\minus}\,\gamma _{{0n}} } \right)^{2} }}$$

(37) $${{\partial w_{{ni}} } \over {\partial \gamma _{{\infty n}} }}\,{\equals}\,{{\phi _{n} c_{n} \left[ {z_{i}^{{1\,{\minus}\,\gamma _{{\infty n}} }} \left\{ {1\,{\minus}\,\left( {1\,{\minus}\,\gamma _{{\infty n}} } \right){\rm ln}\ z_{i} } \right\}\,{\minus}\,1} \right]} \over {\left( {1{\plus}c_{n} } \right)\left( {1\,{\minus}\,\gamma _{{\infty n}} } \right)^{2} }}\,{\rm and}$$

(38) $${{\partial w_{{ni}} } \over {\partial c_{n} }}\,{\equals}\,{{\phi _{n} } \over {\left( {1{\plus}c_{n} } \right)^{2} }}\left( {{{z_{i} ^{{1\,{\minus}\,\gamma _{{\infty n}} }} \,{\minus}\,1} \over {1\,{\minus}\,\gamma _{{\infty n}} }}\,{\minus}\,{{z_{i} ^{{1\,{\minus}\,\gamma _{{0n}} }} \,{\minus}\,1} \over {1\,{\minus}\,\gamma _{0\,n} }}} \right).$$

Let

(39) $${\bf &#x03C7;}{}_{n} \,{\equals}\,\left( {\matrix{ {\theta _{n} } \cr {\phi _{n} } \cr {\gamma _{{0n}} } \cr {\gamma _{{\infty n}} } \cr {c_{n} } \cr } } \right).$$

Applying Newton’s method we may, in principle, solve the equation iteratively using the updating equation

(40) $${\bf &#x03C7;}_{{n{\plus}1}} \,{\equals}\,{\bf &#x03C7;}_{n} \,{\minus}\,{\mib J}_{n}^{{\,{\minus}\,1}} {\mib w}_{n} .$$

A problem arises with this approach: however, in general the Jacobian matrix is almost singular, so that Newton’s method fails to converge. If we assume that the parameter c is known, then the above method may be applied, omitting that parameter. For that purpose, we use only four given values, we omit the last column and the bottom row of the Jacobian and the last component of w _n and χ _n . This procedure may be accessed by another function optimising c so as to approach a fifth observation as closely as possible. If c is allowed to become large, the higher risk aversion at lower levels of γ ₀ would be undermined. In optimising c, it would therefore be appropriate to apply a maximum.

Algorithms and R code for the determination of the parameters of the utility function are available from the authors free of charge.

Multiple solutions are possible. For this reason it may be necessary to use a range of starting values $${\bf \mathord{\buildrel{\lower3pt\hbox{&#x0024;\scriptscriptstyle\smile&#x0024;}}\over \gamma } }_{1} $$ . It is also possible that no solution exists. If this is the case, it would be necessary to question the appropriateness of the trustees’ attitudes to risk. If constant relative risk aversion is required the determination of the parameters of the utility function may be simplified accordingly.

The approach suggested in this section presupposes two postulates: first, that the trustees accept the axioms of expected-utility theory as normative, and second, that the elicitation process does not introduce any bias into the measurement of trustees’ risk aversion. As argued in Thomson (2003 Reference Thomsona ), whilst the use of expected-utility theory is not uniquely rational, it is rational. There is therefore no reason why it should not be accepted for normative purposes.

The second postulate, whilst problematic in principle, need not necessarily be regarded as problematic in practice. In the first place, the method of elicitation avoids – or at least reduces – the problems of framing, continuity, the common ratio condition, probability weighting, biases in subjective probabilities and the reference effect. Second, problems such as the Allais problem, preference reversal, inconsistent orderings, ambiguity and violations of the independence axiom may be reduced by education. Details of these problems have been described in Thomson (2003 Reference Thomsona ). Other problems raised in the literature have also been addressed in that paper.

It should, nevertheless, be recognised that there may be some remaining bias, and the risk aversions determined should not be regarded as accurate; they should rather be interpreted as reasonably indicative.

4.2. Dynamic asset allocation

As explained by Jarvis et al. (Reference Jarvis, Lawrence and Miao2009), the use of a long-term time horizon without allowance for dynamic asset allocation at shorter intervals is generally sub-optimal. This applies both to DC funds and to DB funds. An exception may occur if it is assumed that the trustees adopt constant relative risk aversion. However, as discussed in section 3 above, that assumption is too restrictive and cannot be made in this paper. Because the trustees of a retirement fund may revisit their asset-allocation decision regularly, dynamic modelling is required. In this section, the use of dynamic asset allocation is discussed.

As discussed in sections 2.1 and 2.2, the time interval to be used for dynamic programming will depend on the decision interval, both for DC funds and for DB funds. Without loss of generality it is assumed in this section that the decision interval is a year.

As shown by Mossin (Reference Mossin1968), we may allow for annual optimisation by dynamic programming as follows. Let X _it denote the ith simulation of a vector representing the state of the world at time t for i=1, … , I and t=1, … , T. The components of that vector comprise the variables needed to determine the values of z _T from X _iT at time T (namely A _T and a _T in equation (2) for a DC fund or A _T and P _T in equation (5) for a DB fund) as well as any other variables on which the value of X _i,t+1 will depend (e.g. L _t in equation (3) yield curves at time t and cumulative improvements in mortality to that time). We refer to these simulations as “primary simulations”. From each primary simulation i we select, for t=1, … , T−1, the 10th, 30th, 50th, 70th and 90th percentiles of z _it , and the corresponding values of its components, which we refer to as $$\tilde{z}_{{it}} $$ and $$ \tilde{\mib {X}}_{{it}} $$ , respectively, for i=1, … , 5.

For selected primary simulation i at time t=T−1 we may optimise for the final year before retirement by determining the maximum expected utility at that time, namely

(41) $$u_{{T\,{\minus}\,1}}^{{\asterisk}} \left( {\tilde{z}_{{iT}} } \right)\,{\equals}\,\mathop{{{\rm max}}}\limits_{{{\bf g}_{{i,T\,{\minus}\,1}} }} \left[ {E\left\{ {u\left( {\tilde{z}_{{iT}} } \right)\!\mid\!\tilde{\mib {X}}_{{i,T\,{\minus}\,1}} ,{\mib g}_{{i,T\,{\minus}\,1}} } \right\}} \right]$$

where

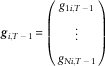$${\mib g}_{{i,T\,{\minus}\,1}} \,{\equals}\,\left( {\matrix{ {g_{{1i,T\,{\minus}\,1}} } \cr \vdots \cr {g_{{Ni,T\,{\minus}\,1}} } \cr } } \right)$$ is a vector representing the portfolio – i.e. the proportion invested in each investment channel available – at time T−1, such that

(42) $$\mathop{\sum}\limits_{n\,{\equals}\,1}^N {g_{{ni,T\,{\minus}\,1}} } \,{\equals}\,1.$$

The function $$u_{{T\,{\minus}\,1}}^{{\asterisk}} \left( {\bullet} \right)$$ represents what Mossin (Reference Mossin1968) refers to as an “indirect” or “derived” utility function at time T−1. For each selected primary simulation i the estimation of the value of that function requires a set of “secondary simulations” j=1, … , J of $$\tilde{\mib {X}}_{{iT}} $$ (say $$\tilde{\mib {X}}_{{ijT}} $$ ), so that g _i,T−1 may be calculated as the portfolio that maximises

(43) $$E_{{i,T\,{\minus}\,1}}^{{\asterisk}} \,{\equals}\,\hat{E}_{{T\,{\minus}\,1}} \left\{ {u\left( {\tilde{z}_{{iT}} } \right)\!\mid\!\tilde{\mib {X}}_{{i,T\,{\minus}\,1}} ,{\mib g}_{{i,T\,{\minus}\,1}} } \right\}\,{\equals}\,{1 \over J}\mathop{\sum}\limits_{j\,{\equals}\,1}^J {u\left( {\tilde{z}_{{ijT}} } \right)} $$

where $$\tilde{z}_{{ijT}} $$ is calculated by updating $$\tilde{\mib {X}}_{{i,T\,{\minus}\,1}} $$ to $$\tilde{\mib {X}}_{{i,T} $$ for trial values of g _i,T−1 until convergence to a maximum is obtained. That maximum then constitutes an estimate of $$u_{{i,T\,{\minus}\,1}}^{{\asterisk}} \left( {\tilde{z}_{{iT}} } \right)$$ for the purposes of equation (41).

At time t=T−2, T−3, … , 0, as explained by Mossin (Reference Mossin1968) we may obtain the indirect utility function as

(44) $$u_{{t\,{\minus}\,1}}^{{\asterisk}} \left( {\tilde{z}_{{it}} } \right)\,{\equals}\,\mathop{{{\rm max}}}\limits_{{{\mib g}_{{i,t\,{\minus}\,1}} }} \left[ {E\left\{ {u_{t}^{{\asterisk}} \left( {\tilde{z}_{{it}} } \right)\!\mid\!\tilde{\mib {X}}_{{i,t\,{\minus}\,1}} ,{\mib g}_{{i,t\,{\minus}\,1}} } \right\}} \right]$$

As before, for that purpose we require secondary simulations. Here we need to calculate

(45) $$E_{{i,t\,{\minus}\,1}}^{{\asterisk}} \,{\equals}\,\hat{E}\left\{ {u_{t}^{{\asterisk}} \left( {\tilde{z}_{{it}} } \right)\!\mid\!\tilde{\mib {X}}_{{i,t\,{\minus}\,1}} ,{\mib g}_{{i,t\,{\minus}\,1}} } \right\}\,{\equals}\,{1 \over J}\mathop{\sum}\limits_{j\,{\equals}\,1}^J {u_{t}^{{\asterisk}} \left( {\tilde{z}_{{ijt}} } \right)} $$

For this purpose, we need values of the function $$u_{{it}}^{{\asterisk}} \left( {\mib X} \right)$$ for all $${\mib X}\in\left( {{\mib X}_{{i1t}} ,\,\ldots\,,\,{\mib X}_{{iJt}} } \right)$$ . But we only have those values that have been simulated during the primary simulation, i.e. X ∈( X _1t , … , X _It ). The required values must be determined by fitting an indirect utility function to the selected values X ∈( X _1t , … , X _5t ).

For this purpose, we need to use prudent utility functions for the maximisation of indirect expected utilities at the beginning of each year. This is because type-2 prudence must be applied not only to the asset allocation decision at the time horizon, but also to those at the beginning of each prior year. We therefore obtain a prudent utility function from the selected simulations. This is done in the same manner as for the elicitation of such a utility function from trustees or members, as explained in section 4.1 above, using J 1-year-ahead secondary simulations for each of the five selected values $$\tilde{z}_{{ijt}} $$ and the corresponding values of $$E_{{it}}^{{\asterisk}} $$ to determine the parameters of the indirect utility function $$u_{t}^{{\asterisk}} ({\bullet})$$ and hence, for each of the five selected simulations, the optimal asset allocation $${\mib g}_{{i,t\,{\minus}\,1}} $$ and $$E_{{i,t\,{\minus}\,1}}^{{\asterisk}} $$ as in equation (45).

Although the utility function is expressed in terms of the outcome at the time horizon, the indirect utility function is expressed from year to year in terms of the outcome over the following year; it reflects what the trustees’ 1-year-ahead utility functions will be. This means that the shape – and therefore the parameters – of the latter may differ from that of the former. Nevertheless, it must still conform to the requirements of prudence.

From the maximisation for t=0 we obtain an estimate of the value of g that represents the optimal asset allocation during the period [0, 1]. The method is the same as for t=T−2, … , 1, except that $$\tilde{\mib {X}}_{{i,t\,{\minus}\,1}} \,{\equals}\,{\mib X}_{0} $$ is known. Here we need to determine the portfolio g ₀ that maximises

(46) $$E_{0}^{{\asterisk}} \,{\equals}\,\hat{E}\left\{ {u_{1}^{{\asterisk}} \left( {z_{1} } \right)\!\mid\!{\mib X}_{0} ,{\mib g}_{0} } \right\}\,{\equals}\,{1 \over J}\mathop{\sum}\limits_{j\,{\equals}\,1}^J {u_{1}^{{\asterisk}} \left( {z_{{j1}} } \right)} .$$

As noted in section 2.2, it may be questioned whether the choice of T as the date of expiry of the liabilities is prejudicial to those members and pensioners as at time 0 whose pensions will cease long before T. However, the use of dynamic asset allocation addresses this issue by defining utility functions along the whole path from time 0 to time T; all that is required at time 0 is that the trustees find an optimal allocation during the period [0, 1]. The utility function used for that purpose is an indirect utility function, so that for a fund with young members it will differ from that for a fund with pensioners only. Nevertheless, minimum and maximum constraints may be applied to the parameters of the indirect utility function, so as to avoid unrealistic indirect utility functions. It may also be questioned whether the accumulation of the assets to time T is preferable to discounting to time 0. In fact this is immaterial; if the numerator and the denominator were both discounted from time T to time 0 then the value of the ratio would be unaffected.

The values of I and J must be determined so that the process converges to a satisfactorily stable result.

5.1. Counter-intuitive results

As argued in section 3.1, it would not be prudent for a trustee to adopt lower risk aversion when a DB fund is in shortfall than when it is in surplus. If a person takes more risk when his/her assets fall short of his requirements than when they exceed his requirements, he may well be acting rationally, but in terms of neo-classical economics, his preferences would generally be described as aspirational (Diecidue & Van de Ven, Reference Diecidue and Van de Ven2008). For example, trustees may prefer to lock in surpluses by investing more conservatively when the fund is in surplus. In itself such a policy would not be imprudent. But if, when the fund is in shortfall, the trustees go for broke by adopting a deliberately riskier policy than they would when the fund is in surplus, then they may justifiably be accused of attempting to save their own reputations in conflict with the requirements of prudence. As shown in the behavioural-finance literature, members may well exhibit aspirational preferences. However, trustees should not. Though aspirational behaviour may be intuitively appropriate to a member, it cannot be treated as intuitively appropriate to a trustee. We therefore refer to findings that support aspirational behaviour by trustees as “counter-intuitive”.

One would expect that, if the trustees’ utility function shows higher relative risk aversion when the fund is in shortfall, then their exposure to the risky asset should be lower. In general, the literature finds that, in a DB fund, for certain arguments and forms of the utility function, the asset allocation is counter-intuitive: at lower levels of funding, optimal investment allocations require greater exposure to risky assets when the fund is in shortfall than when it is in surplus (Boulier et al., Reference Boulier, Trussant and Florens1995; Siegmann & Lucas, Reference Siegmann and Lucas1999; Cairns, Reference Cairns2000; Haberman et al., Reference Haberman, Day, Fogarty, Khorasanee, McWhirter, Nash, Ngwira, Wright and Yakoubov2003; McCarthy & Miles, Reference McCarthy and Miles2013). In this section, the implications of these findings for the application of type-2 prudence are explored.

A problem with some of the approaches in the literature is that they treat the minimisation of contributions as the objective. But that is not a concern to members. In fact high contributions from the sponsoring employer are advantageous to the security of members’ benefits. Whilst it is appropriate to take cognisance of the interests of the sponsoring employer, it is not appropriate to disregard those of members. The DB benefit ratio such as that proposed in section 2.2 effectively embraces both the interests of members and those of the employer and the proposed adjustments allow the trustees to take the interests of both parties into account. The emergence of asset allocations that are counter-intuitive in terms of members’ interests is therefore not surprising.

More importantly, though, the objective functions used in the literature do not generally conform to the requirement of type-2 prudence.

Because of the problems outlined above, it cannot be concluded that the dynamic use of a prudent utility function of the DB benefit ratio would necessarily produce counter-intuitive investment allocations. However, the circumstances (if any) in which type-2 prudence would produce such results must be considered.

5.2. Formulation of the model

Suppose for the purposes of illustration that there are two assets available: an asset matching the fund’s liabilities for members’ benefits and a risky asset. From the point of view of the trustees the former may be regarded as risk-free: if the assets comprised just enough of the matching asset to match the liabilities, then the fund itself would be risk-free. The value of those assets and the payments from those assets will at all times be equal to the corresponding value and payments in respect of the liabilities. (In practice, such an asset will not generally be available; practical applications will require the modelling of all the assets available. But such a model here would have complicated the analysis unnecessarily.) Let δ _t denote the expected force of growth of the value of the liabilities (and therefore the expected force of return on the matching asset) during year t (where t=1 denotes the forthcoming year). Let p _t denote the amount of the benefits payable during year t, allowing for expected future increases in salaries and pensions and for future mortality on the basis of specified assumptions. Let ξ _t denote the actual increase in the benefits payable during that year in excess of the expected increase. That excess may be positive or negative. We assume that the expected value of ξ _t is 0 and that these increases follow a Markov process. Let h _t be the force of return on the risky asset in year t in excess of that on the matching asset. This means that the force of return on the fund’s risk-free asset is δ _t +ξ _t and the force of return on the risky asset is δ _t +h _t .

Then the amount of benefits payable during year t, before allowance for increases during that year, is

(47) $$\tilde{p}_{t} \,{\equals}\,p_{t} S_{t} $$

where

(48) $$S_{t} \,{\equals}\,\left\{ \matrix{ {\rm 1}\,{\rm for}\,t\,{\equals}\,1 \hfill \cr {\rm exp}\left( {\mathop{\sum}\limits_{s\,{\equals}\,1}^{t\,{\minus}\,1} {\xi _{s} } } \right)\,{\rm for}\,t\,\gt\,1. \hfill \cr} \right.$$

Suppose for convenience that the benefits paid during that year comprise the amount of $${\textstyle{1 \over 2}}\tilde{p}_{t} $$ at the beginning of the year and the amount of $${\textstyle{1 \over 2}}\tilde{p}_{t} \,{\rm exp}\,\left( {\xi _{t} } \right)$$ at the end.

For simplicity of illustration, suppose that j=1 (so that all the surplus is available to members) and that l=0 (so that no weighting is applied to the sponsoring employer). This means that k=0 and we may use equation (3) instead of equation (7).

From equation (3), the value of the DB benefit ratio at the end of year t will be

(49) $$z_{t} \,{\equals}\,{{A_{t} {\plus}P_{t} } \over {L_{t} {\plus}P_{t} }}$$

where

(50) $$\eqalignno{ A_{t} &#x0026;\,{\equals}\,\left( {A_{{t\,{\minus}\,1}} \,{\minus}\,{1 \over 2}\tilde{p}_{t} } \right){\rm exp}\left\{ {\delta _{t} {\plus}\left( {1\,{\minus}\,\alpha _{t} } \right)\xi _{t} {\plus}\alpha _{t} h_{t} } \right\}\,{\minus}\,{1 \over 2}\tilde{p}_{t} {\rm exp}\left( {\xi _{t} } \right)\,{\rm for}\,t\,\gt\,0 \cr &#x0026;\,{\equals}\,A_{0} \,{\rm for}\,t\,{\equals}\,0 $$

is the value of the assets at the end of year t;

(51) $$\eqalignno{ P_{t} &#x0026;\,{\equals}\,\left\{ {P_{{t\,{\minus}\,1}} {\rm exp}\left( {\delta _{t} } \right){\rm {\plus}}{1 \over 2}\tilde{p}_{t} \left( {1{\plus}{\rm exp}\left( {\delta _{t} } \right)} \right)} \right\}{\rm exp}\left( {\xi _{t} } \right)\,{\rm for}\,t\,\gt\,0 \cr &#x0026;\,{\equals}\,0\,{\rm for}\,t\,{\equals}\,0 $$

the value at the end of year t of the benefits paid from year 1 up to and including year t;

(52) $$\eqalignno{ L_{t} &#x0026;\,{\equals}\,\left\{ {L_{{t\,{\minus}\,1}} {\rm exp}\left( {\delta _{t} } \right)\,{\minus}\,{1 \over 2}\tilde{p}_{t} \left( {1{\plus}{\rm exp}\left( {\delta _{t} } \right)} \right)} \right\}{\rm exp}\left( {\xi _{t} } \right)\,{\rm for}\,t\,\gt\,0 \cr &#x0026;\,{\equals}\,L_{0} \,{\rm for}\,t\,{\equals}\,0 $$

the value at the end of year t of the liabilities in respect of benefits payable after that year; α _t the proportion of the fund’s assets invested in the risky asset; A ₀ the value of the assets at the end of year 0; L ₀ the value of the liabilities at the end of year 0, i.e. the price of the matching asset; and T the year of expiry of the liabilities; i.e. the year for which p _t =0 for t>T.

In the definition of P _t it is assumed for convenience that the beneficiary’s risk-free rate during year t is equal to the fund’s expected risk-free rate during that year.

Thus

(53) $$\eqalignno{ z_{t} &#x0026;\,{\equals}\,{{A_{t} {\plus}P_{t} } \over {L_{t} {\plus}P_{t} }} \cr &#x0026;\,{\equals}\,{{\left( {A_{{t\,{\minus}\,1}} \,{\minus}\,{1 \over 2}\tilde{p}_{t} } \right){\rm exp}\left( {\delta _{t} {\plus}\left( {1\,{\minus}\,\alpha _{t} } \right)\xi _{t} {\plus}\alpha _{t} h_{t} } \right){\plus}\left( {P_{{t\,{\minus}\,1}} {\plus}{1 \over 2}\tilde{p}_{t} } \right){\rm exp}\left( {\delta _{t} {\plus}\xi _{t} } \right)} \over {\left( {L_{{t\,{\minus}\,1}} \,{\minus}\,{1 \over 2}\tilde{p}_{t} } \right){\rm exp}\left( {\delta _{t} } \right){\plus}\left( {P_{{t\,{\minus}\,1}} {\plus}{1 \over 2}\tilde{p}_{t} } \right){\rm exp}\left( {\delta _{t} } \right)}} \cr &#x0026;\,{\equals}\,{{\left( {A_{{t\,{\minus}\,1}} \,{\minus}\,{1 \over 2}\tilde{p}_{t} } \right){\rm exp}\left( {\left( {1\,{\minus}\,\alpha _{t} } \right)\xi _{t} {\plus}\alpha _{t} h_{t} } \right){\plus}\left( {P_{{t\,{\minus}\,1}} {\plus}{1 \over 2}\tilde{p}_{t} } \right){\rm exp}\left( {\xi _{t} } \right)} \over {L_{{t\,{\minus}\,1}} {\plus}P_{{t\,{\minus}\,1}} }}\,{\rm for}\,t\,\gt\,0 \cr &#x0026;\,{\equals}\,{{A_{0} } \over {L_{0} }}\,{\rm for}\,t\,{\equals}\,0. $$

In particular

(54) $$z_{T} \,{\equals}\,1{\plus}{{A_{T} } \over {P_{T} }}.$$

The accumulation in the numerator of equations (Reference Booth3) and (49) is the same as in the denominator, so, as noted in section 4.2, the ratio is independent of δ _t . This means that, for the purposes of optimisation, we may redefine A _t , P _t and L _t so that δ _t =δ is a constant. From equation (52) it follows that δ is such that

$$L_{{t\,{\minus}\,1}} \,{\equals}\,\left\{ {L_{t} {\plus}{\textstyle{1 \over 2}}\tilde{p}_{t} {\rm exp}\left( {\xi _{t} } \right)} \right\}{\rm exp}\left( {\,{\minus}\,\delta \,{\minus}\,\xi _{t} } \right){\plus}{1 \over 2}\tilde{p}_{t} $$

i.e.

(55) $$L_{0} \,{\equals}\,\mathop{\sum}\limits_{t\,{\equals}\,1}^T {{1 \over 2}\tilde{p}_{t} \left\{ {{\rm exp}\left( {\delta {\plus}\xi _{t} } \right){\plus}{\rm exp}\left( {\xi _{t} } \right)} \right\}} {\rm exp}\left\{ {\,{\minus}\,\mathop{\sum}\limits_{r\,{\equals}\,1}^t {\left( {\delta {\plus}\xi _{r} } \right)} } \right\}$$

where L ₀ is the value of the liabilities (i.e. the price of the matching asset) at time 0. Alternatively, δ may be defined by the user and L ₀ calculated from equation (55). This feature constitutes a further advantage of the proposed DB benefit ratio: because at the beginning of a year the expected return on the fund’s risk-free asset is known, it should not affect the optimum asset allocation for that year. The proposed benefit ratio satisfies that criterion.

Equations (50), (51) and (52) may then be used to determine A _t , P _t and L _t for t=1, … , T. By definition we shall have L _T =0.

The value of α ₁ that gives the greatest indirect utility at the beginning of year 1 may be found by dynamic programming as explained in section 4.2. In this application, for a given value of z _T−1 we may determine the value of α _T (say $$\alpha _{T}^{{\asterisk}} $$ ) that maximises the expected utility at the end of year T. The expected utility for that value (say $$E_{{T\,{\minus}\,1}}^{{\asterisk}} $$ ) then constitutes the indirect utility for that value of z _T−1. We may determine such values for a range of values of A _T−1 to give indirect utility function values $$E_{T}^{{\asterisk}} (z)$$ . These values may then be used to solve for a WARRA-class utility function. This procedure may be continued for t from T to 1. For t=0 the known value A ₀ of the assets may be used. It may happen that the resulting parameters will give lower relative risk aversion than the utility function used for year T. Whilst it may be acceptable to reduce the risk-aversion parameters of the indirect utility functions below those of the terminal values γ _0T and γ _∞T , minimum values should be applied. The risk-aversion parameters are therefore subject to minima of γ _0min and γ _∞min, respectively. Also, the weighting parameter c is subject to a minimum of 0 and a selected maximum c _max. An algorithm for the determination of $$\alpha _{1}^{{\asterisk}} $$ and R code are available from the authors free of charge.

5.3. Parameters used

Suppose that the variables ξ _t and h _t are normally distributed with means μ _ξ and μ _h and standard deviations σ _ξ and σ _h , respectively. As p _t is the expected value of the benefits during year t before increases in salaries and pensions during that year and ξ _t is the excess of the benefit increase during year t over the expected increase, μ _ξ must be taken to be 0. For illustrative purposes, the algorithm was used to determine the parameters of the indirect utility function and the optimum values $$\alpha _{0}^{{\asterisk}} $$ for the following parameters

(56) $${\mib p}\,{\equals}\,\left( {\matrix{ {p_{1} } \cr {p_{2} } \cr \vdots \cr {p_{{20}} } \cr } } \right)\,{\equals}\,\left( {\matrix{ {{{40} \over {20{\times}21}}} \cr {{{38} \over {20{\times}21}}} \cr \vdots \cr {{2 \over {20{\times}21}}} \cr } } \right)$$

so that

(57) $$P_{{20}} \,{\equals}\,\mathop{\sum}\limits_{t\,{\equals}\,1}^{20} {p_{t} } \,{\equals}\,1$$

and p _t decreases linearly.

This set of assumptions is referred to below as the “standard” set.

A ₀ is thus equal to the value of the liabilities for future payments, i.e. the value of those payments before allowance for growth, discounted at the expected risk-free rate δ or, alternatively, the value of those payments including allowance for growth, discounted at the fund’s risk-free rate δ+ξ _t from time to time. The values of γ _0T , γ _∞T , γ _0min and γ _∞min are informed by the values found in section 3.2.

Stopping conditions were used that generally produced reasonable convergence. It was found, however, that better convergence could be obtained by rerunning the program numerous times and averaging the results. For positive values of σ _ξ – i.e. where future increases in benefits are uncertain – it was found that convergence was relatively slow. This is because the dimensionality of the problem is effectively increased: at each node of the primary simulations the state of the world depends not only on the excess returns earned on the risky asset but also on the increases in salaries and pensions.

6.1. Summary

In this paper, a distinction is drawn between “type-1 prudence” and “type-2 prudence”: the former relates to the adoption of deliberately conservative assumptions for the valuation of a retirement fund, whereas the latter, on which the paper focuses, relates to the risk aversion of the fund’s trustees. It is argued that, to satisfy the requirements of type-2 prudence, expected-utility theory may be used as a normative theory for the purposes of asset allocation by the trustees of retirement funds.

For that purpose, definitions of the arguments of the utility function for DC funds and for DB funds are proposed. These are referred to as the “DC benefit ratio” and the “DB benefit ratio”, respectively.

In order to place greater or less weight on the sponsoring employer’s interests relative to those of members, a method of modifying the DB benefit ratio is proposed.

It is found that the utility functions generally used for retirement-fund decision-making are problematic. Furthermore, there is little consensus in the literature about the levels of risk aversion that are appropriate for the trustees of a retirement fund. In order to address these problems, and in particular to satisfy the requirements of type-2 prudence, it is proposed that the trustees’ utility function u(∙) should conform to five criteria. A class of utility functions (the “WARRA” class) that meets these requirements is introduced and its properties are discussed and shown to be satisfactory in terms of the above criteria. This class includes constant relative risk aversion as a special case.

Methods of determining the risk-aversion parameters of a WARRA-class utility function are described with reference to values elicited from the trustees of a retirement fund. In particular, it is shown how, for a particular fund, they may be determined with reference to the utility functions elicited from a sample of members of the fund.

In practice, spurious accuracy in the determination of the parameters of the trustees’ utility function should be avoided. Sensitivity tests may be made so as to establish the extent to which marginal changes in those parameters will affect the decisions to be made. This may reduce the difficulties that trustees might experience in reaching consensus or a compromise with regard to the adoption of a utility function.

In order to apply the WARRA class of utility functions to retirement-fund asset-allocation decision-making, dynamic asset allocation is required. A method of implementing dynamic programming for this purpose is outlined.

Results were obtained from an illustrative formulation of the model for a DB fund with illustrative parameter values. The sensitivity of those results to changes in the parameter values were analysed.

Counter-intuitive results found by other authors suggest that the trustees of a DB retirement fund should invest more in risky assets when the fund is in shortfall and less when it is in surplus.

For initial funding ratios below 1, the optimal exposure on the standard assumptions increases as the initial funding ratio increases. This is intuitive. But for initial funding ratios above 1 it remains almost constant. The latter effect, like the effects found in the literature, is counter-intuitive. However, unlike the findings in the literature, the exposure to risky assets does not decrease; it merely stays constant. This is because the counter-intuitive effect is offset by the reduction in relative risk aversion as the funding ratio increases.

However, when higher levels of prudence are considered, relative risk aversion decreases at a higher rate as the initial funding ratio increases. The result is intuitive: it suggests that the higher the funding level, the higher the optimal exposure to risky asset becomes. This effect becomes stronger than the counter-intuitive effect in the standard case. Ultimately, at initial funding ratios above 1.1, the level of relative risk aversion under the high-prudence assumptions becomes so low that the exposure to risky assets exceeds that under the standard assumptions. This resolves the paradox in the findings of the articles referred to above.

The findings obtained from the illustrative examples in this paper cannot be regarded as generalised results. Whilst they serve to illustrate the effects of variations in the parameters on the asset-allocation decision in a DB fund, they do not show the effects of combinations of variations. Practitioners are therefore advised to apply their own sensitivity tests. For that purpose the algorithms and R code available from the authors may be useful. The algorithms and R code for a DC fund are similar.

6.2. Suggestions for further research

Further research on levels of relative risk aversion both amongst members of retirement funds and amongst trustees would be helpful, particularly research on explanatory variables that might be used to inform or predict the parameters of WARRA-class utility functions for use by trustees.

Further analysis of the implications of the proposed method for asset allocation by the trustees of retirement funds is also a matter for further research.

The application of WARRA-class utility functions to the pricing of the unhedgeable components of the liabilities of a DB retirement fund in an incomplete market could be explored. For this purpose, certainty equivalents could be used, which could be based on the trustees’ utility function.

In this research, a simple model of returns on risky assets was used. In practice, more complex models may be used. The modelling of contributions by the sponsoring employer to fund shortfalls from time to time would also result in greater complexity, especially the allowance for correlation between the financial condition of the sponsoring employer and that of the fund. Such models require further research.

Whilst the focus of this research was on the form of the utility function rather than on the model of returns on risky assets, it has been noted that the findings of Jones et al. (Reference Jones, Allen, Silver, Cameron, Howarth and Caldecott2013) with regard to the effects of resource constraints on future returns on risky assets would have a substantial effect both on the parameters of such models and on the optimal exposures to risky assets. At present there are no models of such effects. The development of such models is a matter of urgency.