No CrossRef data available.
Article contents
AN ITERATIVE MODEL ORDER REDUCTION METHOD FOR LARGE-SCALE DYNAMICAL SYSTEMS
Published online by Cambridge University Press: 05 April 2017
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We present a new iterative model order reduction method for large-scale linear time-invariant dynamical systems, based on a combined singular value decomposition–adaptive-order rational Arnoldi (SVD-AORA) approach. This method is an extension of the SVD-rational Krylov method. It is based on two-sided projections: the SVD side depends on the observability Gramian by the resolution of the Lyapunov equation, and the Krylov side is generated by the adaptive-order rational Arnoldi based on moment matching. The use of the SVD provides stability for the reduced system, and the use of the AORA method provides numerical efficiency and a relative lower computation complexity. The reduced model obtained is asymptotically stable and minimizes the error (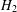
$H_{2}$ and 
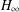$H_{\infty }$) between the original and the reduced system. Two examples are given to study the performance of the proposed approach.
- Type
- Research Article
- Information
- Copyright
- © 2017 Australian Mathematical Society
References
Antoulas, A. C., Approximation of large-scale dynamical systems (Society for Industrial and Applied Mathematics, Philadelphia).Google Scholar
Chahlaoui, Y. and Dooren, P. V., “A collection of benchmark examples for model reduction of linear time invariant dynamical systems”, Niconet (2002)http://www.icm.tu-bs.de/NICONET/benchmodred.html.Google Scholar
Chahlaoui, Y. and Dooren, P. V., “Benchmark examples for model reduction of linear time-invariant dynamical systems”, Dimens. Reduction of Large-Scale Systems
45 (2005) 379–392;doi:10.1007/3-540-27909-1_24.Google Scholar
Chu, C. C., Lai, M. H. and Feng, W. S., “Model-order reductions for MIMO systems using global Krylov subspace methods”, Math. Comput. Simulation
79 (2008) 1153–1164;doi:10.1016/j.matcom.2007.09.007.Google Scholar
Druskin, V. and Simoncini, V., “Adaptive rational Krylov subspaces for large-scale dynamical systems”, Systems Control Lett.
60 (2011) 546–560; doi:10.1016/j.sysconle.2011.04.013.CrossRefGoogle Scholar
Frangos, M. and Jaimoukha, I. M., “Adaptive rational interpolation: Arnoldi and Lanczos-like equations”, Eur. J. Control
14 (2008) 342–354; doi:10.3166/ejc.14.342-354.Google Scholar
Gallivan, K., Grimme, E. and Dooren, P. V., “A rational Lanczos algorithm for model reduction”, Numer. Algorithms
12 (1996) 33–63; doi:10.1007/BF02141740.CrossRefGoogle Scholar
Grimme, E. J., Sorensen, D. C. and Dooren, P. V., “Model reduction of state space systems via an implicitly restarted Lanczos method”, Numer. Algorithms
12 (1995) 1–31;doi:10.1007/BF02141739.CrossRefGoogle Scholar
Gugercin, S., “An iterative SVD-Krylov based method for model reduction of large-scale dynamical systems”, Linear Algebra Appl.
428 (2008) 1964–1986; doi:10.1016/j.laa.2007.10.041.Google Scholar
Gugercin, S., Sorensen, D. C. and Antoulas, A. C., “A modified low-rank Smith method for large-scale Lyapunov equations”, Numer. Algorithms
32 (2003) 27–55; doi:10.1023/A:1022205420182.CrossRefGoogle Scholar
Hashimoto, Y. and Nodera, T., “Inexact shift-invert Arnoldi method for evolution equations”, ANZIAM J.
58 (2016) E1–E27; doi:10.21914/anziamj.v58i0.10766.Google Scholar
Lee, H. J., Chu, C. C. and Feng, W. S., “An adaptive-order rational Arnoldi method for model-order reductions of linear time-invariant systems”, Linear Algebra Appl.
415 (2006) 235–261;doi:10.1016/j.laa.2004.10.011.Google Scholar
Mohamed, K., Mehdi, A. and Abdelkader, M., “Arnoldi model reduction for switched linear systems”, in: 5th International Conference Modeling, Simulation and Applied Optimization (Hammamet, Tunisia) (IEEE, Piscataway, NJ, 2013) 1–6; doi:10.1109/ICMSAO.2013.6552568.Google Scholar
Mohamed, K., Mehdi, A. and Abdelkader, M., “A survey of linear invariant time model reduction”, ICIC Express Letters, An International Journal of Research and Surveys
7 (2013) 909–916;http://www.ijicic.org/el-7(3)b.htm.Google Scholar
Mohamed, K., Mehdi, A. and Abdelkader, M., “Rational Arnoldi & adaptive order rational Arnoldi for switched linear systems”, Neural Parallel Sci. Comput.
22 (2014) 75–88;http://cat.inist.fr/?aModele=afficheN&cpsidt=28604453.Google Scholar
Mohamed, K., Mehdi, A. and Abdelkader, M., “Iterative dual rational Krylov and iterative SVD-dual rational Krylov model reduction for switched linear systems”, in: Complex system modelling and control through intelligent soft computations,
Studies in Fuzziness and Soft Computing, Volume 319
(eds Zhu, Q. and Azar, A. T.), (Springer International Publishing, Switzerland, 2015) 407–435.Google Scholar
Mohamed, K., Mehdi, A. and Abdelkader, M., “SVD-AORA method for dynamic linear time invariant model order reduction”, IFAC-PapersOnLine
48(1) (2015) 695–696;doi:10.1016/j.ifacol.2015.05.175.CrossRefGoogle Scholar
Mohamed, K., Mehdi, A. and Abdelkader, M., “Arnoldi model reduction for switched linear systems”, Int. J. Oper. Res.
27 (2016) 85–112; doi:10.1504/IJOR.2016.078456.Google Scholar
You have
Access