Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-19T16:56:11.107Z Has data issue: false hasContentIssue false
  • English
  • Français

From “Metabelian ℚ-Vector Spaces” to New ω-Stable Groups

Published online by Cambridge University Press:  15 January 2014

Olivier Chapuis
Olivier Chapuis*
Affiliation:
Institut Girard Desargues, CNRS - Université Lyon I, Mathématiques, Bât. 101, 43, Bd Du 11 Novembre 1918, 69622 Villeurbanne Cedex, France.E-mail: chapuis@jonas.univ-lyon1.fr
Get access Rights & Permissions [Opens in a new window]

Extract

The aim of this paper is to describe (without proofs) an analogue of the theory of nontrivial torsion-free divisible abelian groups for metabelian groups. We obtain illustrations for “old-fashioned” model theoretic algebra and “new” examples in the theory of stable groups. We begin this paper with general considerations about model theory. In the second section we present our results and we give the structure of the rest of the paper. Most parts of this paper use only basic concepts from model theory and group theory (see [14] and especially Chapters IV, V, VI and VIII for model theory, and see for example [23] and especially Chapters II and V for group theory). However, in Section 5, we need some somewhat elaborate notions from stability theory. One can find the beginnings of this theory in [14], and we refer the reader to [16] or [21] for stability theory and to [22] for stable groups.

§1. Some model theoretic considerations. Denote by 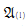the theory of torsion-free abelian groups in the language of groups ℒgp. A finitely generated group G satisfies 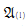iff G is isomorphic to a finite direct power of ℤ. It follows that 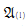axiomatizes the universal theory of free abelian groups and that the theory of nontrivial torsion-free abelian groups is complete for the universal sentences. Denote by 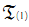the theory of nontrivial divisible torsion-free abelian groups.

Type
Research Article
Information
Bulletin of Symbolic Logic , Volume 2 , Issue 1 , March 1996 , pp. 84 - 93
Copyright
Copyright © Association for Symbolic Logic 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Baudisch, A., Decidability and stability of free nilpotent lie algebras and free nilpotent p-groups of finite exponent, Annals of Mathematical Logic, vol. 23 (1982), pp. 1–25.Google Scholar
[2] Baudisch, A., On Lascar rank in non-multidimensional theories, Logic colloquium '85 (The Paris Logic group, editors), North-Holland, Amsterdam, 1987, pp. 33–51.Google Scholar
[3] Baudisch, A. and Wilson, J. S., Stable actions of torsion groups and stable soluble groups, Journal of Algebra, vol. 153 (1992), pp. 453–457.Google Scholar
[4] Berline, Ch., Superstable groups; a partial answer to a conjecture of Cherlin and Zil'ber, Annals of Pure and Applied Logic, vol. 30 (1986), pp. 44–61.CrossRefGoogle Scholar
[5] Berline, Ch. and Lascar, D., Superstable groups, Annals of Mathematical Logic, vol. 30 (1986), pp. 1–43.Google Scholar
[6] Borovik, A. and Nesin, A., Groups of finite Morley rank, Oxford Science Publication, Oxford, 1994.Google Scholar
[7] Chapuis, O., ∀-free metabelian groups, The Journal of Symbolic Logic, to appear.Google Scholar
[8] Chapuis, O., On the theories of free solvable groups, submitted for publication.Google Scholar
[9] Chapuis, O., Universal theory of certain solvable groups andbounded Ore group-rings, Journal of Algebra, vol. 176 (1995), pp. 368–391.CrossRefGoogle Scholar
[10] Cherlin, G., Groups of finite Morley rank, Annals of Mathematical Logic, vol. 17 (1979), pp. 1–28.Google Scholar
[11] Grünenwald, C. and Haug, F., On stable groups in some soluble group classes, Proceedings of the 10th easter conference on model theory (Weese, , Martin, , et al., editors), Wendisch Rietz, 1993, pp. 169–176.Google Scholar
[12] Hirschfeld, J. and Wheeler, W., Forcing, arithmetic, and division rings, Lecture Notes in Mathematics, vol. 454, Springer-Verlag, Berlin, 1975, pp. 169–176.Google Scholar
[13] Hodges, W., Building models by games, London Mathematical Society, Cambridge, 1985.Google Scholar
[14] Hodges, W., Model theory, Cambridge University Press, Cambridge, 1993.Google Scholar
[15] Hrushovski, H., Locally modular regular types, Classification theory (Baldwin, J., editor), Lecture Notes in Mathematics, vol. 1292, Springer-Verlag, Berlin, 1985, pp. 132–164.Google Scholar
[16] Lascar, D., Stability in model theory, Longmann, Avon, 1987.Google Scholar
[17] Malcev, A.I., On free solvable groups, Soviet Mathematics Dolkady, vol. 1 (1960), pp. 65–68.Google Scholar
[18] Nesin, A., On sharply n-transitive superstable groups, Annals of Pure and Applied Algebra, vol. 69 (1990), pp. 73–88.Google Scholar
[19] Passman, D., The algebraic structure of group-rings, Kriger, Malabar, 1977.Google Scholar
[20] Pillay, A., The model-theoretic content of Lang's conjecture, preprint.Google Scholar
[21] Poizat, B., Cours de théorie des modèles, Nur al'Mantiq wal-Ma'rifah, Villeurbanne, 1985.Google Scholar
[22] Poizat, B., Groupes stables, Nur al'Mantiq wal-Ma'rifah, Villeurbanne, 1987.Google Scholar
[23] Robinson, D. J., A course in the theory of groups, Springer-Verlag, New York, 1982.CrossRefGoogle Scholar
[24] Roman'kov, V. A., Equation in free metabelian group, Siberian Mathematical Journal, vol. 20 (1979), pp. 469–471.Google Scholar
[25] Sabbagh, G., Sous-modules purs, existentiellement clos et élémentaires, Compte Rendu de l'Académie des Sciences Paris Serie I, vol. 272 (1971), pp. 1289–1292.Google Scholar
[26] Simonetta, P., Equivalence élémentaire et decidabilité pour des structures du type groupe agissant sur un groupe abélien, preprint.Google Scholar
[27] Simonetta, P., Décidabilité et interpretabilité dans les corps et les groupes non commutatifs, Doctoral thesis , University Paris VII, 1994.Google Scholar
[28] Zil'ber, B., ω-stability of the field of complex numbers with a predicate distinguishing the roots of unity, Manuscript, Kermerovo, 1993.Google Scholar
[29] Zil'ber, B., Groups and rings whose theory is categorical, American Mathematical Society Translation, vol. 149 (1991), pp. 1–16.Google Scholar