Hostname: page-component-7479d7b7d-wxhwt Total loading time: 0 Render date: 2024-07-11T05:18:37.218Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE PROBLEM OF NON-BERWALDIAN LANDSBERG SPACES

Part of: Infinite-dimensional manifolds Local differential geometry

Published online by Cambridge University Press:  08 January 2020

S. G. ELGENDI Open the ORCID record for S. G. ELGENDI [Opens in a new window]
S. G. ELGENDI*
Affiliation:
Department of Mathematics, Faculty of Science, Benha University, Egypt email salah.ali@fsci.bu.edu.eg, salahelgendi@yahoo.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the long-standing problem of the existence of non-Berwaldian Landsberg spaces from the perspective of conformal transformations. We calculate the Berwald and Landsberg tensors in terms of the T-tensor and show that there are Landsberg spaces with nonvanishing T-tensor. We give a necessary condition for a Landsberg space to be Berwaldian. We find conditions under which the Landsberg spaces cannot be Berwaldian and give examples of (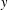$y$-local) non-Berwaldian Landsberg spaces.

Keywords

T-tensorLandsberg spaceBerwald spaceconformal transformationS3 -like spaceC2 -like spaceC-reducible space

MSC classification

Primary: 58B20: Riemannian, Finsler and other geometric structures
Secondary: 53B40: Finsler spaces and generalizations (areal metrics)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 102 , Issue 2 , October 2020 , pp. 331 - 341
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asanov, G. S., ‘Finsleroid–Finsler spaces of positive-definite and relativistic types’, Rep. Math. Phys. 58 (2006), 275–300.CrossRefGoogle Scholar
Asanov, G. S. and Kirnasov, E. G., ‘On Finsler spaces satisfying the T-condition’, Aequationes Math. 24 (1982), 66–73.CrossRefGoogle Scholar
Bácsó, S., Cheng, X. and Shen, Z., ‘Curvature properties of (𝛼, 𝛽)-metrics’, Adv. Stud. Pure Math. 48 (2007), 73–110.CrossRefGoogle Scholar
Bao, D., ‘On two curvature-driven problems in Riemann–Finsler geometry’, Adv. Stud. Pure Math. 48 (2007), 19–71.CrossRefGoogle Scholar
Bao, D., Chern, S. S. and Shen, Z., An Introduction to Riemann–Finsler Geometry (Springer, Berlin, 2000).CrossRefGoogle Scholar
Chern, S. S., ‘Finsler geometry is just Riemannian geometry without the quadratic equation’, Notices Amer. Math. Soc. 43(9) (1996), 959–963.Google Scholar
Hashiguchi, M., ‘On conformal transformations of Finsler metrics’, J. Math. Kyoto Univ. 16 (1976), 25–50.CrossRefGoogle Scholar
Landsberg, G., ‘Über die Totalkrümmung’, Jahresber. Dtsch. Math.-Ver. 16 (1907), 36–46.Google Scholar
Landsberg, G., ‘Über die Krümmungstheorie und Variationsrechnung’, Jahresber. Dtsch. Math.-Ver. 16 (1907), 547–557.Google Scholar
Landsberg, G., ‘Über die Krümmung in der Variationsrechnung’, Math. Ann. 65 (1908), 313–349.CrossRefGoogle Scholar
Matsumoto, M., ‘V-transformations of Finsler spaces. I. Definition, infinitesimal transformations and isometries’, J. Math. Kyoto Univ. 12 (1972), 479–512.CrossRefGoogle Scholar
Matsumoto, M., ‘Finsler geometry in the 20th century’, in: Handbook of Finsler Geometry II (ed. Antonelli, P. L.) (Kluwer Academic, Dordrecht, 2003).Google Scholar
Shen, Z., ‘On a class of Landsberg metrics in Finsler geometry’, Canad. J. Math. 61 (2009), 1357–1374.CrossRefGoogle Scholar
Szabo, Z., ‘Positive definite Finsler spaces satisfying the T-condition are Riemannian’, Tensor (N.S.) 35 (1981), 247–248.Google Scholar
Youssef, N. L. and Elgendi, S. G., ‘New Finsler package’, Comput. Phys. Commun. 185 (2014), 986–997.CrossRefGoogle Scholar