Hostname: page-component-7bb8b95d7b-nptnm Total loading time: 0 Render date: 2024-09-06T04:25:58.622Z Has data issue: false hasContentIssue false
  • English
  • Français

An Euler-type volume identity

Published online by Cambridge University Press:  17 April 2009

Kevin Callahan  and
Kathy Hann
Kevin Callahan
Affiliation:
Department of Mathematics and Computer ScienceCalifornia State UniversityHayward CA 94542, United States of America e-mail: callahan@csuhayward.edu
Kathy Hann
Affiliation:
Department of Mathematics and Computer ScienceCalifornia State UniversityHayward CA 94542, United States of America e-mail: khann@csuhayward.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we present an elementary proof of a congruence by subtraction relation. In order to prove congruence by subtraction, we produce a dissection relating equal sub-polytopes. An immediate consequence of this relation is an Euler-type volume identity in ℝ3 which appeared in the Unsolved Problems section of the December 1996 MAA Monthly.

This Euler-type volume identity relates the volumes of subsets of a polytope called wedges that correspond to its faces, edges, and vertices. A wedge consists of the inward normal chords of the polytope emanating from a face, vertex, or edge. This identity is stated in the theorem below.

Euler Volume Theorem. For any three dimensional convex polytope P

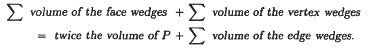
This identity follows immediately from

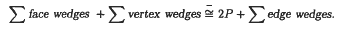
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 59 , Issue 3 , June 1999 , pp. 495 - 508
Copyright
Copyright © Australian Mathematical Society 1999

References

[1]Eves, H., A survey of geometry (Allyn and Bacon, Inc., Boston, 1972).Google Scholar
[2]Hann, K., ‘What's the bound on the average number of normals’, Amer. Math. Monthly 103 (1996), 897–900.CrossRefGoogle Scholar
[3]Hann, K., ‘The average number of normals through a point in a convex body and a related Euler-type identity’, Geom. Dedicata 48 (1993), 27–55.CrossRefGoogle Scholar
[4]Hug, D., ‘On the mean number of normals through a point in the interior of a convex body’, Geom. Dedicata 55 (1995), 319–340.CrossRefGoogle Scholar