Hostname: page-component-84b7d79bbc-2l2gl Total loading time: 0 Render date: 2024-07-27T23:59:17.841Z Has data issue: false hasContentIssue false
  • English
  • Français

GROUPS OF FINITE NORMAL LENGTH

Part of: Special aspects of infinite or finite groups Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  01 February 2018

FRANCESCO DE GIOVANNI Open the ORCID record for FRANCESCO DE GIOVANNI [Opens in a new window]  and
ALESSIO RUSSO
FRANCESCO DE GIOVANNI*
Affiliation:
Dipartimento di Matematica e Applicazioni, Università di Napoli Federico II, Complesso Universitario Monte S. Angelo, Via Cintia, Napoli, Italy email degiovan@unina.it
ALESSIO RUSSO
Affiliation:
Dipartimento di Matematica e Fisica, Università della Campania “L. Vanvitelli”, via Lincoln 5, Caserta, Italy email alessio.russo@unicampania.it
*
✉degiovan@unina.it
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 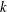$k$ be a nonnegative integer. A subgroup 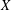$X$ of a group 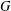$G$ has normal length 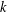$k$ in 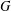$G$ if all chains between 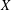$X$ and its normal closure 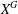$X^{G}$ have length at most 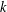$k$, and 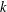$k$ is the length of at least one of these chains. The group 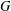$G$ is said to have finite normal length if there is a finite upper bound for the normal lengths of its subgroups. The aim of this paper is to study groups of finite normal length. Among other results, it is proved that if all subgroups of a locally (soluble-by-finite) group 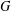$G$ have finite normal length in 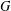$G$, then the commutator subgroup 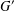$G^{\prime }$ is finite and so 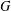$G$ has finite normal length. Special attention is given to the structure of groups of normal length 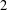$2$. In particular, it is shown that finite groups with this property admit a Sylow tower.

Keywords

normal lengthSylow tower

MSC classification

Primary: 20E15: Chains and lattices of subgroups, subnormal subgroups
Secondary: 20F24: FC-groups and their generalizations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 2 , April 2018 , pp. 229 - 239
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The authors are members of GNSAGA (INdAM) and work within the ADV-AGTA project.

References

Catino, F. and de Giovanni, F., Some Topics in the Theory of Groups with Finite Conjugacy Classes (Aracne, Roma, 2015).Google Scholar
Hawkes, T., ‘Groups whose subnormal subgroups have bounded defect’, Arch. Math. (Basel) 43 (1984), 289–294.CrossRefGoogle Scholar
Herzog, M., Longobardi, P., Maj, M. and Mann, A., ‘On generalized Dedekind groups and Tarski super monsters’, J. Algebra 226 (2000), 690–713.CrossRefGoogle Scholar
Mahdavianary, S. K., ‘A special class of three-Engel groups’, Arch. Math. (Basel) 40 (1983), 193–199.Google Scholar
Neumann, B. H., ‘Groups with finite classes of conjugate subgroups’, Math. Z. 63 (1955), 76–96.CrossRefGoogle Scholar
Ol’shanskiĭ, A. Y., ‘Infinite groups with cyclic subgroups’, Dokl. Akad. Nauk SSSR 245 (1979), 785–787.Google Scholar
Ol’shanskiĭ, A. Y., Geometry of Defining Relations in Groups (Kluwer, Dordrecht, 1991).CrossRefGoogle Scholar
Robinson, D. J. S., Finiteness Conditions and Generalized Soluble Groups (Springer, Berlin, 1972).Google Scholar
Robinson, D. J. S., A Course in the Theory of Groups, 2nd edn (Springer, Berlin, 1996).Google Scholar
Tomkinson, M. J., FC-Groups (Pitman, Boston, MA, 1984).Google Scholar
Zappa, G., ‘Sui gruppi di Hirsch supersolubili’, Rend. Semin. Mat. Univ. Padova 12 (1941), 1–11.Google Scholar