Hostname: page-component-77c89778f8-n9wrp Total loading time: 0 Render date: 2024-07-17T19:31:54.187Z Has data issue: false hasContentIssue false
  • English
  • Français

Iterative solution of nonlinear equations of the monotone type in Banach spaces

Published online by Cambridge University Press:  17 April 2009

C.E. Chidume
C.E. Chidume
Affiliation:
Department of Mathematics, University of Nigeria Nsukka, Nigeria
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

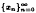Let E be a real Banach space with a uniformly convex dual, and let K be a nonempty closed convex and bounded subset of E. Suppose T: K → K is a continuous monotone map. Define S: K → K by Sx = f – Tx for each x in K and define the sequence iteratively by x0 ∈ K, xn+1 = (1 – Cn)xn + CnSxn, n ≥ 0, where 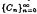is a real sequence satisfying appropriate conditions. Then, for any given f in K, the sequence 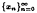converges strongly to a solution of x + Tx = f in K. Explicit error estimates are also computed. A related result deals with iterative solution of nonlinear equations of the dissipative type.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 42 , Issue 1 , August 1990 , pp. 21 - 31
Copyright
Copyright © Australian Mathematical Society 1990

References

[1]Browder, F.E., ‘Nonlinear elliptic boundary value problems’, Bull. Amer. Math. Soc. 69 (1967), 862–874.Google Scholar
[2]Browder, F.E, ‘Nonlinear mappings of nonexpansive and accretive type in Banach spaces’, Bull. Amer. Math. Soc. 73 (1967), 875–882.Google Scholar
[3]Browder, F.E., ‘Nonlinear monotone and accretive operators in Banach spaces’, Proc. Nat. Acad. Sci. U.S.A. 61 (1968), 388–393.Google Scholar
[4]Bruck, R.E. Jr., ‘The iterative solution of the equation y ∈ x + Tx for a monotone operator T in Hilbert space’, Bull. Amer. Math. Soc. 79 (1973), 1258–1262.Google Scholar
[5]Caristi, J., ‘Fixed point theorems for mappings satisfying inwardness conditions’, Trans. Amer. Math. Soc. 215 (1976), 241–251.CrossRefGoogle Scholar
[6]Chidume, C.E., ‘An approximation method for monotone Lipschitzian operators in Hilbert space’, J. Austral. Math. Soc. (series A) 41 (1986), 59–63.CrossRefGoogle Scholar
[7]Chidume, C.E., ‘The iterative solution of the equation f ∈ x + Tx for a monotone operator T in L p spaces’, J. Math. Anal. Appl. 116 (1986), 531–537.Google Scholar
[8]Chidume, C.E., ‘Iterative solution of nonlinear equations of the monotone and dissipative types’, Appl. Anal. 33 (1989), 79–86.CrossRefGoogle Scholar
[9]Dotson, W.G., ‘an iterative process for nonlinear monotonic nonexpansive operators in Hilbert space’, Math. Camp. 32 (1978), 223–225.xsGoogle Scholar
[10]Kato, T., ‘Nonlinear semigroups and evolution equations’, J. Math. Soc. Japan 19 (1967), 508–520.Google Scholar
[11]Kirk, W.A., ‘A fixed point theorem for mappings which do not increase distance’, Amer. Math. Monthly 72 (1965), 1004–1006.Google Scholar
[12]Mann, W.R., ‘Mean value methods in iteration’, Proc. Amer. Math. Soc. 4 (1953), 506–510.Google Scholar
[13]Martin, R.H. Jr., ‘A global existence theorem for autonomous differential equations in Banach spaces’, Proc. Amer. Math. Soc. 26 (1970), 307–314.CrossRefGoogle Scholar
[14]Minty, G.J., ‘Monotone (nonlinear) operators in Hilbert spaces’, Duke Math. J. 29 (1962), 541–546.Google Scholar
[15]Petryshyn, W.V., ‘On the extension and solution of nonlinear operator equations’, Illinois J. Math. 10 (1966), 255–274.CrossRefGoogle Scholar
[16]Ray, W.O., ‘An elementary proof of surjectivity for a class of accretive operators’, Proc. Amer. Math. Soc. 75 (1979), 255–258.CrossRefGoogle Scholar
[17]Nevanlinna, O. and Reich, S., ‘Strong convergence of contraction semigroups and of iterative methods for accretive operators in Banach spaces’, Israel J. Math. 32 (1979), 44–58.CrossRefGoogle Scholar
[18]Reich, S., ‘Constructive techniques for accretive and monotone operators’, Applied Nonlinear Analysis (1979), 335–345.Google Scholar
[19]Reich, S., ‘Constructing zeros of accretive operators II’, Applicable Analysis 9 (1979), 159–163.CrossRefGoogle Scholar
[20]Reich, S., ‘Strong convergence theorems for resolvents of accretive operators in Banach spaces’, J. Math. Anal. Appl. 75 (1980), 287–292.Google Scholar
[21]Reich, S., ‘An iterative procedure for constructing zeros of accretive sets in Banach spaces’, Nonlinear Anal. 2 (1978), 85–92.Google Scholar
[22]Smul'Yan, V.L., ‘On the derivation of the norm in a Banach space’, Dokl. Akad. Nauk SSSR 27 (1940), 255–258.Google Scholar
[23]Vainberg, M.M., ‘On the convergence of the method of steepest descent for nonlinear equations’, Sibirsk. Math. Zh. Z. 2 (1961), 201–220.Google Scholar
[24]Zarantonello, E.H., ‘Solving functional equations by contractive averaging’, in Technical Report No.160 (U.S. Army Math. Res. Centre, Madison, Wisconsin, 1960).Google Scholar