Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-06-09T00:02:38.689Z Has data issue: false hasContentIssue false
  • English
  • Français

LANDAU’S THEOREM FOR SOLUTIONS OF THE 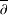$\overline{\unicode[STIX]{x2202}}$-EQUATION IN DIRICHLET-TYPE SPACES

Part of: Two-dimensional theory Other generalizations Spaces and algebras of analytic functions

Published online by Cambridge University Press:  28 September 2017

SHAOLIN CHEN  and
SAMINATHAN PONNUSAMY Open the ORCID record for SAMINATHAN PONNUSAMY [Opens in a new window]
SHAOLIN CHEN
Affiliation:
Department of Mathematics, Soochow University, Suzhou, Jiangsu 215006, PR China College of Mathematics and Statistics, Hengyang Normal University, Hengyang, Hunan 421008, PR China email mathechen@126.com
SAMINATHAN PONNUSAMY*
Affiliation:
Stat-Math Unit, Indian Statistical Institute (ISI), Chennai Centre, 110, Nelson Manickam Road, Aminjikarai, Chennai, 600 029, India email samy@isichennai.res.in, samy@iitm.ac.in
*
✉samy@isichennai.res.in
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The main aim of this article is to establish analogues of Landau’s theorem for solutions to the 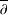$\overline{\unicode[STIX]{x2202}}$-equation in Dirichlet-type spaces.

Keywords

Landau’s theorem∂ -equationDirichlet-type space

MSC classification

Primary: 30H10: Hardy spaces
Secondary: 30H30: Bloch spaces 31A05: Harmonic, subharmonic, superharmonic functions 31C05: Harmonic, subharmonic, superharmonic functions 31C25: Dirichlet spaces
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 1 , February 2018 , pp. 80 - 87
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

This research was partly supported by the National Natural Science Foundation of China (nos 11571216 and 11401184), the Hunan Province Natural Science Foundation of China (no. 2015JJ3025), China’s Fifty-ninth Batch of Postdoctoral Foundation (no. 2016M590492), the Jiangsu Province Postdoctoral Foundation of China (no. 7131710516), the Science and Technology Plan Project of Hunan Province (no. 2016TP1020) and the Construct Program of the Key Discipline in Hunan Province. The second author is on leave from IIT Madras.

References

Baernstein, A. II and Kovalev, L. V., ‘On Hölder regularity for elliptic equations of non-divergence type in the plane’, Ann. Sc. Norm. Super. Pisa Cl. Sci. 4 (2005), 295–317.Google Scholar
Bonk, M., ‘On Bloch’s constant’, Proc. Amer. Math. Soc. 378 (1990), 889–894.Google Scholar
Brody, R., ‘Compact manifolds and hyperbolicity’, Trans. Amer. Math. Soc. 235 (1978), 213–219.Google Scholar
Chen, H., Gauthier, P. M. and Hengartner, W., ‘Bloch constants for planar harmonic mappings’, Proc. Amer. Math. Soc. 128 (2000), 3231–3240.Google Scholar
Chen, S. L., Mateljević, M., Ponnusamy, S. and Wang, X., ‘Lipschitz type spaces and Landau–Bloch type theorems for harmonic functions’, Acta Math. Sinica (Chin. Ser.) 60 (2017), 1–12.Google Scholar
Chen, S. L., Ponnusamy, S. and Wang, X., ‘On planar harmonic Lipschitz and planar harmonic Hardy classes’, Ann. Acad. Sci. Fenn. Math. 36 (2011), 567–576.Google Scholar
Chen, S. L., Ponnusamy, S. and Wang, X., ‘Stable geometric properties of pluriharmonic and biholomorphic mappings, and Landau–Bloch’s theorem’, Monatsh. Math. 177 (2015), 33–51.CrossRefGoogle Scholar
Chen, S. L., Rasila, A. and Vuorinen, M., ‘Characterizations of Hardy-type, Bergman-type and Dirichlet-type spaces on certain classes of complex-valued functions’, Preprint, 2014, arXiv:1410.8283.Google Scholar
Chen, S. L., Rasila, A. and Wang, X., ‘Radial growth, Lipschitz and Dirichlet spaces on solutions to the non-homogenous Yukawa equation’, Israel J. Math. 204 (2014), 261–282.CrossRefGoogle Scholar
Gray, J. and Morris, S., ‘When is a function that satisfies the Cauchy–Riemann equations analytic?’, Amer. Math. Monthly 85 (1978), 246–256.CrossRefGoogle Scholar
Hedenmalm, H., ‘On Hörmander’s solution of the ∂ -equation. I’, Math. Z. 281 (2015), 349–355.Google Scholar
Hörmander, L., Notions of Convexity, Progress in Mathematics, 127 (Birkhäuser Boston Inc, Boston, 1994).Google Scholar
Landau, E., ‘Über die Bloch’sche Konstante und zweiverwandte Weltkonstanten’, Math. Z. 30 (1929), 608–634.Google Scholar
Liu, X. Y. and Minda, C. D., ‘Distortion theorems for Bloch functions’, Trans. Amer. Math. Soc. 333 (1992), 325–338.Google Scholar
Pavlović, M., ‘On Dyakonov’s paper “Equivalent norms on Lipschitz-type spaces of holomorphic functions”’, Acta Math. 183 (1999), 141–143.CrossRefGoogle Scholar
Rado, T. and Reichelderfer, P. V., Continuous Transformations in Analysis, Die Grundlehren der math. Wissenschaften, LXXV, Springer, Berlin, 1955.CrossRefGoogle Scholar
Vuorinen, M., Conformal Geometry and Quasiregular Mapings, Lecture Notes in Mathematics, 1319 (Springer, Berlin, 1988).CrossRefGoogle Scholar
Wu, H., ‘Normal families of holomorphic mappings’, Acta Math. 119 (1967), 193–233.Google Scholar
Yamashita, S., ‘Dirichlet-finite functions and harmonic majorants’, Illinois J. Math 25 (1981), 626–631.CrossRefGoogle Scholar
Zalcman, L., ‘Normal families: new perspectives’, Bull. Amer. Math. Soc. (N.S.) 35 (1998), 215–230.Google Scholar