Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-05-17T22:11:10.032Z Has data issue: false hasContentIssue false
  • English
  • Français

NEW OPTIMAL LINEAR CODES OVER 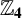$\ \boldsymbol {\mathbb {Z}_{4}}$

Part of: Theory of error-correcting codes and error-detecting codes

Published online by Cambridge University Press:  03 June 2022

HOPEIN CHRISTOFEN TANG Open the ORCID record for HOPEIN CHRISTOFEN TANG [Opens in a new window]  and
DJOKO SUPRIJANTO Open the ORCID record for DJOKO SUPRIJANTO [Opens in a new window]
HOPEIN CHRISTOFEN TANG
Affiliation:
Combinatorial Mathematics Research Group, Faculty of Mathematics and Natural Sciences, Institut Teknologi Bandung, Jl. Ganesha 10, Bandung 40132, Indonesia e-mail: hopeinct@students.itb.ac.id
DJOKO SUPRIJANTO*
Affiliation:
Combinatorial Mathematics Research Group, Faculty of Mathematics and Natural Sciences, Institut Teknologi Bandung, Jl. Ganesha 10, Bandung 40132, Indonesia
*
e-mail: djoko.suprijanto@itb.ac.id
Get access Rights & Permissions [Opens in a new window]

Abstract

We present novel approaches for constructing linear codes over 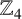$\mathbb {Z}_{4}$ from the known ones. We obtain new linear codes, many of which are optimal. In particular, we find all optimal codes of type 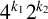$4^{k_{1}}2^{k_{2}}$ for 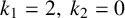$k_{1}=2,~k_{2}=0$ and many optimal codes for 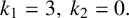$k_{1}=3,~k_{2}=0.$

Keywords

ℤ 4-linear codesPlotkin boundoptimal codes

MSC classification

Primary: 94B05: Linear codes, general
Secondary: 94B65: Bounds on codes
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 107 , Issue 1 , February 2023 , pp. 158 - 169
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research is supported by Institut Teknologi Bandung (ITB) and the Ministry of Education, Culture, Research and Technology (Kementerian Pendidikan, Kebudayaan, Riset dan Teknologi (Kemdikbud-ristek)), Republic of Indonesia.

References

Abualrub, T. and Oehmke, R. H., ‘Cyclic codes of length ${2}^e$ over ${\mathbb{Z}}_4$ ’, Discrete Appl. Math. 128(1) (2003), 3–9.CrossRefGoogle Scholar
Aydin, N. and Asamov, T., ‘A database of ${\mathbb{Z}}_4$ codes’, J. Comb. Inf. Syst. Sci. 34(1–4) (2009), 1–12.Google Scholar
Aydin, N. and Asamov, T., ‘Online database of ${\mathbb{Z}}_4$ codes’. Available at http://quantumcodes.info/Z4 (accessed February 5, 2022).Google Scholar
Berlekamp, E. R., Algebraic Coding Theory, revised edition (World Scientific,Singapore, 2015).CrossRefGoogle Scholar
Blackford, T., ‘Cyclic codes over ${\mathbb{Z}}_4$ of oddly even length’, Discrete Appl. Math. 128(1) (2003), 27–46.CrossRefGoogle Scholar
Blackford, T., ‘Negacyclic codes over ${\mathbb{Z}}_4$ of even length’, IEEE Trans. Inform. Theory 49(6) (2003), 1417–1424.10.1109/TIT.2003.811915CrossRefGoogle Scholar
Blake, I. F., ‘Codes over certain rings’, Inf. Control 20 (1972), 396–404.10.1016/S0019-9958(72)90223-9CrossRefGoogle Scholar
Blake, I. F., ‘Codes over integer residue rings’, Inf. Control 29 (1975), 295–300.CrossRefGoogle Scholar
Bonnecaze, A. and Duursma, I., ‘Translate of linear codes over ${\mathbb{Z}}_4$ ’, IEEE Trans. Inform. Theory 43(4) (1997), 1218–1230.CrossRefGoogle Scholar
Bustomi, , Santika, A. P. and Suprijanto, D., ‘Linear codes over the ring ${\mathbb{Z}}_4+u{\mathbb{Z}}_4+v{\mathbb{Z}}_4+w{\mathbb{Z}}_4+\mathrm{uv}{\mathbb{Z}}_4+\mathrm{uw}{\mathbb{Z}}_4+\mathrm{vw}{\mathbb{Z}}_4+\mathrm{uv}\mathrm{w}{\mathbb{Z}}_4$ ’, IAENG Int. J. Comput. Sci. 43(8) (2021), 11 pages.Google Scholar
Byrne, E., Greferath, M., Pernas, J. and Zumbrägel, J., ‘Algebraic decoding of negacyclic codes over ${\mathbb{Z}}_4$ ’, Des. Codes Cryptogr. 66(1–3) (2013), 3–16.CrossRefGoogle Scholar
Dinh, H. Q., Singh, A. K., Kumar, N. and Sriboonchitta, S., ‘On constacyclic codes over ${\mathbb{Z}}_4\left[v\right]/ \langle {v}^2-v\rangle$ and their Gray images’, IEEE Comm. Lett. 22(9) (2018), 1758–1762.CrossRefGoogle Scholar
Dougherty, S. T., Gulliver, T. A., Park, Y. H. and Wong, J. N. C., ‘Optimal linear codes over ${\mathbb{Z}}_m$ ’, J. Korean Math. Soc. 44(5) (2007), 1139–1162.CrossRefGoogle Scholar
Dougherty, S. T. and Shiromoto, K., ‘Maximum distance codes over rings of order $4$ ’, IEEE Trans. Inform. Theory 47(1) (2001), 400–404.CrossRefGoogle Scholar
Gulliver, T. A. and Wong, J. N. C., ‘Classification of optimal linear ${\mathbb{Z}}_4$ rate $1/ 2$ codes of length $\ge 8$ ’, Ars Combin. 85 (2007), 287–306.Google Scholar
Hammons, A. R., Kumar, P. V., Calderbank, A. R., Sloane, N. J. A. and Solé, P., ‘The ${\mathbb{Z}}_4$ -linearity of Kerdock, Preparata, Goethals and related codes’, IEEE Trans. Inform. Theory 40(2) (1994), 301–319.10.1109/18.312154CrossRefGoogle Scholar
Huffman, W. C., ‘On the classification and enumeration of self-dual codes’, Finite Fields Appl. 11(3) (2005), 451–490.10.1016/j.ffa.2005.05.012CrossRefGoogle Scholar
Huffman, W. C. and Pless, V., Fundamentals of Error Correcting Codes (Cambridge University Press,Cambridge, 2003).CrossRefGoogle Scholar
Kløve, T., ‘Support weight distribution of linear codes’, Discrete Math. 106–107 (1992), 311–316.10.1016/0012-365X(92)90559-XCrossRefGoogle Scholar
Magma Calculator . Available at http://magma.maths.usyd.edu.au/calc/.Google Scholar
Pless, V. S. and Qiang, Z., ‘Cyclic codes and quadratic residue codes over ${\mathbb{Z}}_4$ ’, IEEE Trans. Inform. Theory 42(5) (1996), 1594–1600.CrossRefGoogle Scholar
Rains, E. M., ‘Optimal self-dual codes over ${\mathbb{Z}}_4$ ’, Discrete Math. 203(1–3) (1999), 215–228.CrossRefGoogle Scholar
Shi, M., Qian, L., Sok, L., Aydin, N. and Solé, P., ‘On constacyclic codes over ${\mathbb{Z}}_4\left[u\right]/ \langle {u}^2-1\rangle$ and their Gray images’, Finite Fields Appl. 45 (2017), 86–95.CrossRefGoogle Scholar
Spiegel, E., ‘Codes over ${\mathbb{Z}}_m$ ’, Inf. Control 35 (1977), 48–51.CrossRefGoogle Scholar
Spiegel, E., ‘Codes over ${\mathbb{Z}}_m,$ revisited’, Inf. Control 37 (1978), 100–104.CrossRefGoogle Scholar
Wan, Z., Quaternary Codes (World Scientific,Singapore, 1997).10.1142/3603CrossRefGoogle Scholar
Wyner, A. D. and Graham, R. L., ‘An upper bound on minimum distance for a $k$ -ary code’, Inf. Control 13(1) (1968), 46–52.10.1016/S0019-9958(68)90779-1CrossRefGoogle Scholar
Zinoviev, V. A. and Zinoviev, D. V., ‘On the generalized concatenated construction for codes in ${L}_1$ and Lee metrics’, Probl. Inf. Transm. 57(1) (2021), 70–83.CrossRefGoogle Scholar