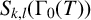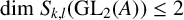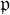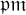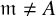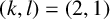1 Introduction
The theory of oldforms and newforms is a well-understood area in the theory of classical modular forms. Certain properties of modular forms depend heavily on whether they are oldforms or newforms. For example, the space of newforms has a basis consisting of normalised eigenforms for all the Hecke operators and the Fourier coefficients of these normalised eigenforms generate a number field. The analogous theory of oldforms and newforms is much less developed for Drinfeld modular forms.
Bandini and Valentino [Reference Bandini and Valentino3–Reference Bandini and Valentino5, Reference Valentino19]) defined
$\mathfrak {p}$
-oldforms and
$\mathfrak {p}$
-newforms, and studied some of their properties. In [Reference Bandini and Valentino3], they defined T-oldforms
$S_{k,l}^{T\text {-}\mathrm {old}}(\Gamma _0(T))$
and T-newforms
$S_{k,l}^{T\text {-}\mathrm {new}}(\Gamma _0(T))$
for
$\mathfrak {p} = (T)$
. In [Reference Bandini and Valentino4], they made the following conjecture.
Conjecture 1.1 ([Reference Bandini and Valentino4, Conjecture 1.1] for
$\Gamma _0(T)$
).
-
(i)
$\ker (T_T)=0$
where
$T_T$
is acting on
$S_{k,l}(\mathrm {GL}_2(A))$
; -
(ii)
$S_{k,l}(\Gamma _0(T))=S_{k,l}^{T\text {-}\mathrm {old}}(\Gamma _0(T))\oplus S_{k,l}^{T\text {-}\mathrm {new}}(\Gamma _0(T))$
; -
(iii) for odd characteristic,
$U_T$
is diagonalisable on
$S_{k,l}(\Gamma _0(T))$
.
For even characteristic, Conjecture 1.1(iii) is not true [Reference Bandini and Valentino2]. Assuming that the characteristic p is odd, Conjecture 1.1 is proved in [Reference Bandini and Valentino4, Reference Bandini and Valentino6] in some special cases, using harmonic cocycles, the trace maps
$\mathrm {Tr}$
and
$\mathrm {Tr}^\prime $
, and the linear algebra interpretation of the Hecke operators
$T_{\mathfrak {p}}$
and
$U_{\mathfrak {p}}$
. By studying the action of the
$T_T$
-operators on the Fourier coefficients of Drinfeld modular forms, we prove the following result.
Theorem 1.2 (Theorems 4.8 and 4.9).
If
$\dim S_{k,l}(\mathrm {GL}_2(A))\leq 1$
, then Conjecture 1.1 is true for
$S_{k,l}(\Gamma _0(T))$
. Furthermore, if
$\dim S_{k,l}(\mathrm {GL}_2(A))=2$
, then
$S_{k,l}(\Gamma _0(T))=S_{k,l}^{T\text {-}\mathrm {old}}(\Gamma _0(T))\oplus S_{k,l}^{T\text {-}\mathrm {new}}(\Gamma _0(T))$
.
Our methods are completely different from those of [Reference Bandini and Valentino4, Reference Bandini and Valentino6]. We are very optimistic that our methods can be used when
$\dim S_{k,l}(\mathrm {GL}_2(A)) \geq 3$
.
In [Reference Bandini and Valentino5], Bandini and Valentino extended the definition of
$\mathfrak {p}$
-oldforms and
$\mathfrak {p}$
-newforms from level
$\mathfrak {p}$
to level
$\mathfrak {p}\mathfrak {m}$
with
$\mathfrak {p}\nmid \mathfrak {m}$
. We frame Conjecture 1.1 for level
$\mathfrak {p}\mathfrak {m}$
with
$\mathfrak {p}\nmid \mathfrak {m}$
as a question (Question 4.3) and provide some evidence in favour of it.
First, we generalise the results of [Reference Bandini and Valentino4] for
$\mathfrak {p}=(T)$
to an arbitrary prime ideal
$\mathfrak {p}$
(Proposition 4.10). This implies that Question 4.3 has an affirmative answer in these cases. Then, we exhibit some cases where Question 4.3 for the level
$\mathfrak {p}\mathfrak {m}$
is true (Proposition 4.11). If
$\mathfrak {m}\ne A$
, we show that the direct sum decomposition in Question 4.3(2) may fail when
$l=1$
(Proposition 4.13, Remark 4.14). More precisely, we exhibit nonzero Drinfeld cusp forms which are both
$\mathfrak {p}$
-oldforms and
$\mathfrak {p}$
-newforms. We believe that this is the only case where it may fail.
For classical modular forms, it is well known that the space of newforms can be characterised in terms of kernels of the Trace and twisted Trace operators [Reference Li15, Reference Serre, Kuijk and Serre18]. In the final section, we consider the extent that this is valid for Drinfeld modular forms.
Notation. Throughout the article, we use the following notation. For an odd prime number p and
$q=p^r$
for some
$r \in \mathbb {N}$
,
$\mathbb {F}_q$
is the finite field of order q. For
$k\in \mathbb {N}$
and
${l\in \mathbb {Z}/(q-1)\mathbb {Z}}$
such that
$k\equiv 2l \pmod {q-1}$
, let
$l \ (0 \leq l \leq q-2)$
be a lift of
${l \in \mathbb {Z}/(q-1)\mathbb {Z}}$
. By abuse of notation, we write l for the integer as well as its class.
Set
$A :=\mathbb {F}_q[T]$
,
$K :=\mathbb {F}_q(T)$
. For
$f \in A$
,
$g\in A \setminus \{0\}$
, the norm of
${f}/{g}$
is defined as
$|{f}/{g}| := q^{\deg (f)-\deg (g)}$
(with respect to the
${1}/{T}$
-adic valuation).
Let
$K_\infty =\mathbb {F}_q(({1}/{T}))$
be the completion of K with respect to the infinite place
$\infty $
(corresponding to the
${1}/{T}$
-adic valuation) and
$C:= {\widehat {\overline {K}}}_\infty $
, the completion of an algebraic closure of
$K_\infty $
. Let
$\mathfrak {p} = (P)$
denote a prime ideal of A with a monic irreducible polynomial P.
2 Basic theory of Drinfeld modular forms
In this section, we recall some basic theory of Drinfeld modular forms (see [Reference Gekeler10–Reference Goss13] for more details).
Let
$L=\tilde {\pi }A \subseteq C$
be the A-lattice of rank
$1$
corresponding to the rank
$1$
Drinfeld module (also called a Carlitz module)
$\rho _T=TX+X^q$
, where
$\tilde {\pi }\in K_\infty (\!\!\sqrt [q-1]{-T})$
is defined up to a
$(q-1)$
th root of unity. The Drinfeld upper half-plane
$\Omega = C-K_\infty $
, which is analogous to the complex upper half-plane, has a rigid analytic structure. The group
$\mathrm {GL}_2(K_\infty )$
acts on
$\Omega $
via fractional linear transformations.
Definition 2.1. Let
$k\in \mathbb {N}$
,
$l \in \mathbb {Z}/(q-1)\mathbb {Z}$
and
$f:\Omega \rightarrow C$
be a rigid holomorphic function on
$\Omega $
. For
$\gamma =( \begin {smallmatrix} a & b \\ c & d \!\end {smallmatrix})\in \mathrm {GL}_2(K_{\infty })$
, we define the slash operator
$|_{k,l} \gamma $
on f by
$$ \begin{align*} f|_{k,l} \gamma := (\det \gamma)^{l}(cz+d)^{-k}f(\gamma z). \end{align*} $$
Define the congruence subgroup
$\Gamma _0(\mathfrak {n}) = \{( \begin {smallmatrix} a & b \\ c & d \!\end {smallmatrix})\in \mathrm {GL}_2(A): c\in \mathfrak {n} \}$
, where
$\mathfrak {n} \subseteq A$
is an ideal. Next, we define a Drinfeld modular form of weight k and type l for
$\Gamma _0(\mathfrak {n})$
.
Definition 2.2. A rigid holomorphic function
$f:\Omega \rightarrow C$
is a Drinfeld modular form of weight k, type l for
$\Gamma _0(\mathfrak {n})$
if:
-
(1)
$f|_{k,l}\gamma = f$
for all
$\gamma \in \Gamma _0(\mathfrak {n})$
; -
(2) f is holomorphic at the cusps of
$\Gamma _0(\mathfrak {n})$
.
The space of Drinfeld modular forms of weight k, type l for
$\Gamma _0(\mathfrak {n})$
is denoted by
$M_{k,l}(\Gamma _0(\mathfrak {n})).$
If f vanishes at the cusps of
$\Gamma _0(\mathfrak {n})$
, then we say f is a Drinfeld cusp form of weight k, type l for
$\Gamma _0(\mathfrak {n})$
and the space of such forms is denoted by
$S_{k,l}(\Gamma _0(\mathfrak {n}))$
.
If
$k\not \equiv 2l \pmod {q-1}$
, then
$M_{k,l}(\Gamma _0(\mathfrak {n}))=\{0\}$
. So, without loss of generality, we can assume that
$k\equiv 2l \pmod {q-1}$
. Let
$u(z) := {1}/{e_L(\tilde {\pi }z)}$
, where
$e_L(z):= z{\prod _{\substack {0 \ne \lambda \in L }}}(1-{z}/{\lambda }) $
is the exponential function attached to the lattice L. Then, each Drinfeld modular form
$f\in M_{k,l}(\Gamma _0(\mathfrak {n}))$
has a unique u-series expansion at
$\infty $
given by
$f=\sum _{i=0}^\infty a_f(i)u^i$
. Since
$( \begin {smallmatrix} \zeta & 0 \\ 0 & 1 \!\end {smallmatrix}) \in \Gamma _0(\mathfrak {n})$
for
$\zeta \in \mathbb {F}_q^\times $
, Definition 2.2(1) implies
$a_f(i)=0$
if
$i\not \equiv l \pmod {q-1}$
. Hence, the u-series expansion of f at
$\infty $
can be written as
$\sum _{0 \leq i \equiv l\ \mod (q-1)} a_f(i)u^{i}.$
Any Drinfeld modular form of type
$l \neq 0$
is a cusp form, that is,
$M_{k,l}(\Gamma _0(\mathfrak {n}))=S_{k,l}(\Gamma _0(\mathfrak {n}))$
.
2.1 Examples
We now give some examples of Drinfeld modular forms.
Example 2.3 [Reference Gekeler10, Reference Goss12].
Let
$d\in \mathbb {N}$
. For
$z\in \Omega $
, the function
$$ \begin{align*} g_d(z) := (-1)^{d+1}\tilde{\pi}^{1-q^d}L_d \sum_{\substack{a,b\in \mathbb{F}_q[T] \\ (a,b)\ne (0,0)}} \frac{1}{(az+b)^{q^d-1}} \end{align*} $$
is a Drinfeld modular form of weight
$q^d-1$
, type
$0$
for
$\mathrm {GL}_2(A)$
, where
$\tilde {\pi }$
is the Carlitz period and
$L_d:=(T^q-T)\cdots (T^{q^d}-T)$
is the least common multiple of all monic polynomials of degree d. We refer to
$g_d$
as an Eisenstein series and it does not vanish at
$\infty $
.
Example 2.4 [Reference Gekeler10, Reference Goss13].
For
$z\in \Omega $
, the function
$$ \begin{align*} \Delta(z) := (T-T^{q^2})\tilde{\pi}^{1-q^2}E_{q^2-1} + (T^q-T)^q\tilde{\pi}^{1-q^2}(E_{q-1})^{q+1} \end{align*} $$
is a Drinfeld cusp form of weight
$q^2-1$
, type
$0$
for
$\mathrm {GL}_2(A)$
, where
$E_k(z)= \sum _{\substack {(0,0)\ne (a,b)\in A^2}} (az+b)^{-k}.$
Example 2.5 [Reference Gekeler10].
For
$z \in \Omega $
, the function
$$ \begin{align*} h(z) := \sum_{\gamma = ( \begin{smallmatrix} a & b \\ c & d \!\end{smallmatrix}) \in H \backslash \mathrm{GL}_2(A)} \frac{\det \gamma}{(cz+d)^{q+1}} u(\gamma z), \end{align*} $$
where
$H=\{( \begin {smallmatrix} * & * \\ 0 & 1 \!\end {smallmatrix})\in \mathrm {GL}_2(A)\}$
, is a Drinfeld cusp form of weight
$q+1$
, type
$1$
for
$\mathrm {GL}_2(A)$
.
We end this section by introducing an important function E, which is not modular. In [Reference Gekeler10], Gekeler defined the function
$E(z):= {1}/{\tilde {\pi }} \sum _{a\in \mathbb {F}_q[T],\,a \ \mathrm {monic}} ( \sum _{b\in \mathbb {F}_q[T]} {a}/{(az+b)}),$
which is analogous to the Eisenstein series of weight
$2$
over
$\mathbb {Q}$
. For any prime ideal
$\mathfrak {p}=(P)$
, using E, we can construct the Drinfeld modular form
$$ \begin{align*} E_P(z) := E(z)- PE(Pz) \in S_{2,1}(\Gamma_0(\mathfrak{p})) \end{align*} $$
(see [Reference Dalal and Kumar9, Proposition 3.3] for a detailed discussion of
$E_P$
).
3 Certain important operators
3.1 Atkin–Lehner operators
Let
$\mathfrak {r}$
,
$\mathfrak {n}$
be two ideals of A generated by monic polynomials r, n, respectively, with
$\mathfrak {r} \mid \mathfrak {n}$
.
Definition 3.1 [Reference Schweizer, Gekeler, van der Put, Reversat and Van Geel17, page 331].
For
$\mathfrak {r}||\mathfrak {n}$
(that is,
$\mathfrak {r}|\mathfrak {n}$
with
$(\mathfrak {r}, {\mathfrak {n}}/{\mathfrak {r}})=1$
), the (partial) Atkin–Lehner operator
$W_{\mathfrak {r}}^{(\mathfrak {n})}$
is defined by the action of the matrix
$( \begin {smallmatrix} ar & b \\ cn & dr \!\end {smallmatrix})$
on
$M_{k,l}(\Gamma _0(\mathfrak {n}))$
, where
$a,b, c,d\in A$
such that
$adr^2-bcn=\zeta \cdot r$
for some
$\zeta \in \mathbb {F}_q^\times $
.
By [Reference Dalal and Kumar9, Proposition 3.2], the action of
$W_{\mathfrak {r}}^{(\mathfrak {n})}$
on
$M_{k,l}(\Gamma _0(\mathfrak {n}))$
is well defined (here the action of the slash operator is different from the one in [Reference Dalal and Kumar9]). Assume that
$\mathfrak {p}^\alpha ||\mathfrak {n}$
with
$\alpha \in \mathbb {N}$
. Write
$n=Pm$
and
$\mathfrak {m}=(m)$
. We now fix some representatives for the (partial) Atkin–Lehner operators
$W_{\mathfrak {p}^\alpha }^{(\mathfrak {n})}$
and
$W_{\mathfrak {p}^{\alpha -1}}^{(\mathfrak {m})}$
.
Definition 3.2. For
$f\in S_{k,l}(\Gamma _0(\mathfrak {n}))$
, we write
$f|_{k,l}{W_{\mathfrak {p}^\alpha }^{(\mathfrak {n})}} := f|_{k,l} ( \begin {smallmatrix} P^\alpha & b \\ n & P^\alpha d \!\end {smallmatrix}),$
where
$b,d\in A$
such that
$P^{2\alpha }d-nb= P^\alpha .$
Since
$(P^\alpha , {n}/{P^\alpha })=1$
, such
$b,d \in A$
exist.
When
$\alpha \geq 2$
, we can take
$(\! \begin {smallmatrix} P^{\alpha -1} & b \\ m & P^\alpha d \!\end {smallmatrix})$
as a representative for the (partial) Atkin–Lehner operator
$W_{\mathfrak {p}^{\alpha -1}}^{(\mathfrak {m})}$
.
Lemma 3.3. The operator
$|_{k,l} W_{\mathfrak {p}^\alpha }^{(\mathfrak {n})}$
on
$S_{k,l}(\Gamma _0(\mathfrak {n}))$
defines an endomorphism and for all
$f\in S_{k,l}(\Gamma _0(\mathfrak {n}))$
, we have
$(f|_{k,l}{W_{\mathfrak {p}^\alpha }^{(\mathfrak {n})}})|_{k,l}{W_{\mathfrak {p}^\alpha }^{(\mathfrak {n})}} = P^{\alpha (2l-k)}f$
.
Proof. Since
$W_{\mathfrak {p}^\alpha }^{(\mathfrak {n})} \cdot W_{\mathfrak {p}^\alpha }^{(\mathfrak {n})} = ( \begin {smallmatrix} P^{\alpha } & 0 \\ 0 & P^\alpha \!\end {smallmatrix})\gamma $
for some
$\gamma \in \Gamma _0(\mathfrak {n})$
, the lemma follows.
Lemma 3.4. For
$i=1,2$
, let
$\mathfrak {p}_i$
be two distinct prime ideals of A such that
$\mathfrak {p}_i^{\alpha _i}||\mathfrak {n}$
for some
$\alpha _i\in \mathbb {N}.$
Then
$W_{\mathfrak {p}_1^{\alpha _1}}^{(\mathfrak {n})}W_{\mathfrak {p}_2^{\alpha _2}}^{(\mathfrak {n})}=W_{\mathfrak {p}_2^{\alpha _2}}^{(\mathfrak {n})}W_{\mathfrak {p}_1^{\alpha _1}}^{(\mathfrak {n})}.$
Proof. The lemma follows from
$W_{\mathfrak {p}_1^{\alpha _1}}^{(\mathfrak {n})}W_{\mathfrak {p}_2^{\alpha _2}}^{(\mathfrak {n})}\,{=}\,W_{\mathfrak {p}_1^{\alpha _1}\mathfrak {p}_2^{\alpha _2}}^{(\mathfrak {n})}\,{=}\,W_{\mathfrak {p}_2^{\alpha _2}}^{(\mathfrak {n})}W_{\mathfrak {p}_1^{\alpha _1}}^{(\mathfrak {n})}$
.
3.2 Hecke operators
We now recall the definitions of
$T_{\mathfrak {p}}$
and
$U_{\mathfrak {p}}$
-operators.
Definition 3.5. For
$f \in S_{k,l}(\Gamma _0(\mathfrak {n}))$
, we define
$$ \begin{align*} T_{\mathfrak{p}}(f) &:= P^{k-l} \sum_{\substack{Q\in A\\ \deg Q<\deg P}}f|_{k,l}( \begin{smallmatrix} 1 & Q \\ 0 & P \!\end{smallmatrix}) + P^{k-l}f|_{k,l}( \begin{smallmatrix} P & 0 \\ 0 & 1 \!\end{smallmatrix}) \quad \mathrm{if} \ \mathfrak{p}\nmid \mathfrak{n},\\ U_{\mathfrak{p}}(f) &:= P^{k-l} \sum_{\substack{Q\in A\\ \deg Q < \deg P}}f|_{k,l}( \begin{smallmatrix} 1 & Q \\ 0 & P \!\end{smallmatrix}) \quad \mathrm{if} \ \mathfrak{p}\mid \mathfrak{n}. \end{align*} $$
The commutativity of the
$T_{\mathfrak {p}}$
and
$U_{\mathfrak {p}}$
-operators follows from the next proposition.
Proposition 3.6. Let
$\mathfrak {n}$
be an ideal of A and
$\mathfrak {p}_1,\mathfrak {p}_2$
be two distinct prime ideals of A generated by monic irreducible polynomials
$P_1,P_2$
, respectively. Suppose that
$\mathfrak {p}_1\mid \mathfrak {n}$
. Then,
$U_{\mathfrak {p}_1}$
commutes with
$U_{\mathfrak {p}_2}$
if
${\mathfrak {p}_2} \mid \mathfrak {n}$
and with
$T_{\mathfrak {p}_2}$
if
${\mathfrak {p}_2} \nmid \mathfrak {n}$
, as operators on
$S_{k,l}(\Gamma _0(\mathfrak {n}))$
.
Proof. Since
$P_1$
and
$P_2$
are distinct primes, for any
$b\in A$
with
$\deg b<\deg P_1$
, there exists a unique
$b^\prime \in A$
with
$\deg b^\prime < \deg P_1$
such that
$P_1|(b- b^\prime P_2)$
. Thus,
$( \begin {smallmatrix} 1 & {(b-b^\prime P_2)}/{P_1} \\ 0 & 1 \!\!\end {smallmatrix})\in \Gamma _0(\mathfrak {n})$
and
$( \begin {smallmatrix} 1 & b \\ 0 & P_1 \!\!\end {smallmatrix})( \begin {smallmatrix} P_2 & 0 \\ 0 & 1 \!\end {smallmatrix}) = ( \begin {smallmatrix} 1 & {(b-b^\prime P_2)}/{P_1} \\ 0 & 1 \!\!\end {smallmatrix}) ( \begin {smallmatrix} P_2 & 0 \\ 0 & 1 \!\end {smallmatrix})( \begin {smallmatrix} 1 & b^\prime \\ 0 & P_1 \!\end {smallmatrix}).$
Now the result follows from Definition 3.5 and the equality
$$ \begin{align*} \small \displaystyle \sum_{\substack{b\in A\\ \deg b<\deg P_1}}\sum_{\substack{d\in A\\ \deg d<\deg P_2}} ( \begin{smallmatrix} 1 & b+dP_1 \\ 0 & P_1P_2 \!\end{smallmatrix})=\sum_{\substack{c\in A \\ \deg c<\deg P_1 + \deg P_2}} ( \begin{smallmatrix} 1 & c \\ 0 & P_1P_2 \!\end{smallmatrix})=\sum_{\substack{d^\prime\in A\\ \deg d^\prime<\deg P_2}} \sum_{\substack{b^\prime\in A\\ \deg b^\prime<\deg P_1}} ( \begin{smallmatrix} 1 & d^\prime+b^\prime P_2 \\ 0 & P_1P_2 \!\end{smallmatrix}). \\[-53pt]\end{align*} $$
3.3 The trace operators
We define the trace operators and mention their prop erties.
Definition 3.7. For any ideal
$\mathfrak {r}|\mathfrak {n}$
, the trace operator
$\mathrm {Tr}_{\mathfrak {r}}^{\mathfrak {n}} : M_{k,l}(\Gamma _0(\mathfrak {n})) \longrightarrow M_{k,l}(\Gamma _0(\mathfrak {r}))$
is defined by
$\mathrm {Tr}_{\mathfrak {r}}^{\mathfrak {n}}(f) = \sum _{\gamma \in \Gamma _0(\mathfrak {n})\backslash \Gamma _0(\mathfrak {r})} f|_{k,l}\gamma. $
The next proposition gives the action of the trace operator in terms of the (partial) Atkin–Lehner operators and the Hecke operators.
Proposition 3.8. Let
$\mathfrak {m},\mathfrak {n}$
be two ideals of A generated by monic polynomials
$m, n$
, respectively, such that
$n=Pm$
. Let
$\alpha \in \mathbb {N}$
such that
$P^\alpha ||n$
. If
$f\in S_{k,l}(\Gamma _0(\mathfrak {n})),$
then
$$ \begin{align*}\mathrm{Tr}^{\mathfrak{n}}_{\mathfrak{m}}(f)= \begin{cases} f+ P^{-l}U_{\mathfrak{p}}(f|W_{\mathfrak{p}}^{(\mathfrak{n})}) & \mathrm{if} \ \alpha=1,\\ P^{-l-(\alpha-1)(2l-k)}U_{\mathfrak{p}}(f|W^{(\mathfrak{n})}_{\mathfrak{p}^\alpha})|_{k,l}W^{(\mathfrak{m})}_{\mathfrak{p}^{\alpha-1}} & \mathrm{if} \ \alpha\geq 2. \end{cases} \end{align*} $$
Proof. If
$\alpha =1$
, this proposition is [Reference Dalal and Kumar9, Proposition
$3.6$
]. When
$\mathfrak {n}$
is a prime ideal, it coincides with [Reference Vincent20, Proposition 3.8] (but note that the action of the slash operator here is different). Now, we let
$\alpha \geq 2$
. By definition,
$$ \begin{align*} U_P(f|W^{(\mathfrak{n})}_{\mathfrak{p}^\alpha}) &= P^{k-l} \sum\limits_{\deg Q<\deg P}f|_{k,l}( \begin{smallmatrix} P^\alpha & b \\ n & P^\alpha d \!\end{smallmatrix})( \begin{smallmatrix} 1 & Q \\ 0 & P \!\end{smallmatrix}) = P^{k-l} \sum\limits_{\deg Q<\deg P}f|_{k,l} ( \begin{smallmatrix} P^\alpha & P^\alpha Q+bP \\ n & nQ+P^{\alpha+1}d \!\end{smallmatrix})\\ &= P^{k-l} \sum\limits_{\deg Q<\deg P}f|_{k,l}( \begin{smallmatrix} P & 0 \\ 0 & P \!\end{smallmatrix})( \begin{smallmatrix} P^{\alpha-1} & P^{\alpha-1} Q+b \\ m & mQ+P^{\alpha}d \!\end{smallmatrix}) = P^{l} \sum\limits_{\deg Q<\deg P}f|_{k,l}( \begin{smallmatrix} P^{\alpha-1} & P^{\alpha-1} Q+b \\ m & mQ+P^{\alpha}d \!\end{smallmatrix})\\ &= P^{l} \sum\limits_{\deg Q<\deg P}f|_{k,l} ( \begin{smallmatrix} 1-mQ & P^{\alpha-1} Q \\ -({m^2}/{P^{\alpha-1})}Q & 1+mQ \!\end{smallmatrix}) ( \begin{smallmatrix} P^{\alpha-1} & b \\ m & P^\alpha d \!\end{smallmatrix}). \end{align*} $$
We now show that
$\{( \begin {smallmatrix} 1-mQ & P^{\alpha -1} Q \\ -({m^2}/{P^{\alpha -1})}Q & 1+mQ \!\end {smallmatrix}) : \deg Q<\deg P\}$
is a set of representatives for
$\Gamma _0(\mathfrak {n})\backslash \Gamma _0(\mathfrak {m})$
. Let
$( \begin {smallmatrix} s & t \\ mx & y \!\end {smallmatrix})\in \Gamma _0(\mathfrak {m}),$
where
$s,t,x,y \in A$
satisfy
$sy-tmx=\zeta \in \mathbb {F}_q^\times $
. Let
$-\zeta ^{-1}sx \equiv Q_1 \pmod P$
, where
$Q_1\in A$
is such that
$\deg Q_1< \deg P.$
Since
$P^{\alpha -1}||m$
, there exists a unique
$Q_2\in A$
with
$\deg Q_2< \deg P$
such that
$({m}/{P^{\alpha -1}})Q_2\equiv 1 \pmod P.$
Since
$P|m$
, the choice of
$Q_1$
and
$sy-tmx=\zeta \in \mathbb {F}_q^\times $
implies that
$x+yQ_1\equiv 0 \pmod P.$
Let
$Q\in A$
with
$\deg Q< \deg P$
such that
$Q_1Q_2\equiv Q\pmod P$
. Then
$x+({m}/{P^{\alpha -1}})Qy \equiv 0 \pmod P$
. Hence, the equation
$$ \begin{align*}( \begin{smallmatrix} s & t \\ mx & y \!\end{smallmatrix})=( \begin{smallmatrix} s(1+mQ)+t({m^2}/{P^{\alpha-1}})Q & t(1-mQ)-sP^{\alpha-1}Q \\ mx(1+mQ)+y({m^2}/{P^{\alpha-1}})Q & y(1-mQ)-mxP^{\alpha-1}Q \!\end{smallmatrix})( \begin{smallmatrix} 1-mQ & P^{\alpha-1} Q \\ -({m^2}/{P^{\alpha-1}})Q & 1+mQ \!\end{smallmatrix})\end{align*} $$
shows that
$\{( \begin {smallmatrix} 1-mQ & P^{\alpha -1} Q \\ -({m^2}/{P^{\alpha -1}})Q & 1+mQ \!\end {smallmatrix}) : \deg Q<\deg P\}$
forms a complete set of representatives for
$\Gamma _0(\mathfrak {n})\backslash \Gamma _0(\mathfrak {m})$
. Therefore,
$$ \begin{align*} U_P(f|W^{(\mathfrak{n})}_{\mathfrak{p}^\alpha})=P^{l} \sum\limits_{\deg Q<\deg P}f|_{k,l} ( \begin{smallmatrix} 1-mQ & P^{\alpha-1} Q \\ -({m^2}/{P^{\alpha-1}})Q & 1+mQ \!\end{smallmatrix}) ( \begin{smallmatrix} P^{\alpha-1} & b \\ m & P^\alpha d \!\end{smallmatrix}) = P^{l}(\mathrm{Tr}^{\mathfrak{n}}_{\mathfrak{m}} f)|_{k,l}W^{(\mathfrak{m})}_{\mathfrak{p}^{\alpha-1}}. \end{align*} $$
Apply the
$W^{(\mathfrak {m})}_{\mathfrak {p}^{\alpha -1}}$
operator on both sides. The proposition follows from Lemma 3.3.
Corollary 3.9. If
$\mathfrak {p},\mathfrak {m}$
satisfy
$(\mathfrak {p},\mathfrak {m})=1$
and
$f\in S_{k,l}(\Gamma _0(\mathfrak {p}))$
, then
$\mathrm {Tr}^{\mathfrak {p}\mathfrak {m}}_{\mathfrak {m}}(f)= \mathrm {Tr}^{\mathfrak {p}}_{1}(f).$
Proof. Since
$f|W^{(\mathfrak {p}\mathfrak {m})}_{\mathfrak {p}}=f|W^{(\mathfrak {p})}_{\mathfrak {p}}$
, the result follows from Proposition 3.8.
4
$\mathfrak {p}$
-oldforms and
$\mathfrak {p}$
-newforms for level
$\mathfrak {p}\mathfrak {m}$
Let
$\mathfrak {p}$
be a prime ideal of A. Throughout this section, we consider
$\mathfrak {m}$
an ideal of A generated by a monic polynomial m such that
$\mathfrak {p}\nmid \mathfrak {m}$
. We first recall the definitions of
$\mathfrak {p}$
-oldforms and
$\mathfrak {p}$
-newforms (see [Reference Bandini and Valentino5, Reference Valentino19]). Consider the map
$$ \begin{align*} (\delta_1, \delta_P): (S_{k,l}(\Gamma_0(\mathfrak{m})))^2 \longrightarrow S_{k,l}(\Gamma_0(\mathfrak{p}\mathfrak{m}))\quad \mathrm{defined \ by}\ (f,g) \longrightarrow \delta_1f + \delta_P g, \end{align*} $$
with
$\delta _1$
,
$\delta _P : S_{k,l}(\Gamma _0(\mathfrak {m})) \rightarrow S_{k,l}(\Gamma _0(\mathfrak {p}\mathfrak {m}))$
given by
$\delta _1(f)=f$
and
$\delta _P(f)= f|_{k,l}( \begin {smallmatrix} P & 0 \\ 0 & 1 \!\end {smallmatrix}).$
Definition 4.1. The space of
$\mathfrak {p}$
-oldforms
$S_{k,l}^{\mathfrak {p}\text {-}\mathrm {old}}(\Gamma _0(\mathfrak {p}\mathfrak {m}))$
of level
$\mathfrak {p}\mathfrak {m}$
is the subspace of
$S_{k,l}(\Gamma _0(\mathfrak {p}\mathfrak {m}))$
generated by the image of
$(\delta _1, \delta _P)$
.
Definition 4.2. The space of
$\mathfrak {p}$
-newforms
$S_{k,l}^{\mathfrak {p}\text {-}\mathrm {new}}(\Gamma _0(\mathfrak {p}\mathfrak {m}))$
of level
$\mathfrak {p}\mathfrak {m}$
is
$$ \begin{align*}S_{k,l}^{\mathfrak{p}\text{-}\mathrm{new}}(\Gamma_0(\mathfrak{p}\mathfrak{m})):= \mathrm{Ker}(\mathrm{Tr}^{\mathfrak{p}\mathfrak{m}}_{\mathfrak{m}})\cap \mathrm{Ker}(\mathrm{Tr^\prime}^{\mathfrak{p}\mathfrak{m}}_{\mathfrak{m}}) \quad \mathrm{where\ } \mathrm{Tr^\prime}^{\mathfrak{p}\mathfrak{m}}_{\mathfrak{m}} f : = \mathrm{Tr}^{\mathfrak{p}\mathfrak{m}}_{\mathfrak{m}}(f|W_{\mathfrak{p}}^{(\mathfrak{p}\mathfrak{m})}).\end{align*} $$
We formulate Conjecture 1.1 for primes
$\mathfrak {p}$
and higher levels
$\mathfrak {p}\mathfrak {m}$
as the following question and provide some evidence in favour of it.
Question 4.3 (For level
$\mathfrak {p}\mathfrak {m}$
).
Suppose
$\mathfrak {m}$
is an ideal of A such that
$\mathfrak {p} \nmid \mathfrak {m}\!:$
-
(1)
$\ker (T_{\mathfrak {p}})=0$
, where
$T_{\mathfrak {p}} \in \mathrm {End}(S_{k,l}(\Gamma _0(\mathfrak {m})));$
-
(2)
$ \label {direct sum decomposition level pm in corollary} S_{k,l}(\Gamma _0(\mathfrak {p}\mathfrak {m}))=S_{k,l}^{\mathfrak {p}\text {-}\mathrm {old}}(\Gamma _0(\mathfrak {p}\mathfrak {m}))\oplus S_{k,l}^{\mathfrak {p}\text {-}\mathrm {new}}(\Gamma _0(\mathfrak {p}\mathfrak {m}))$
; -
(3) the
$U_{\mathfrak {p}}$
-operator is diagonalisable on
$S_{k,l}(\Gamma _0(\mathfrak {p}\mathfrak {m})).$
When we say that ‘Question 4.3 is true for level
$\mathfrak {p}\mathfrak {m}$
’, we mean all the statements of Question 4.3 are true. We first show that if
$\mathfrak {m}=A, \mathfrak {p} = (P)$
with
$\deg P=1$
, then Question 4.3 is true for level
$\mathfrak {p}$
if
$\dim \ S_{k,l}(\mathrm {GL}_2(A))\leq 1$
. In particular, Conjecture 1.1 is true for
$S_{k,l}(\Gamma _0(T))$
when
$\dim \ S_{k,l}(\mathrm {GL}_2(A))\leq 1$
. Furthermore, we show the direct sum decomposition in Question 4.3(2) holds for
$S_{k,l}(\Gamma _0(\mathfrak {p}))$
if
$\dim S_{k,l}(\mathrm {GL}_2(A))\leq 2$
. Finally, we give some evidence to support Question 4.3 for level
$\mathfrak {p}\mathfrak {m}$
.
4.1 Question 4.3 when
$\mathbf {dim}\ S_{k,l}(\mathrm {GL}_2(A))\leq 2$
If Question 4.3(2) is true, then the diagonalisability of the
$U_{\mathfrak {p}}$
-operator on
$S_{k,l}(\Gamma _0(\mathfrak {p}\mathfrak {m}))$
depends on that of the
$U_{\mathfrak {p}}$
-operators on
$S_{k,l}^{\mathfrak {p}\text {-}\mathrm {old}}(\Gamma _0(\mathfrak {p}\mathfrak {m}))$
,
$S_{k,l}^{\mathfrak {p}\text {-}\mathrm {new}}(\Gamma _0(\mathfrak {p}\mathfrak {m})).$
By [Reference Bandini and Valentino5, Remark 2.17], the
$U_{\mathfrak {p}}$
-operator is diagonalisable on
$S_{k,l}^{\mathfrak {p}\text {-}\mathrm {new}}(\Gamma _0(\mathfrak {p}\mathfrak {m}))$
. However, the
$U_{\mathfrak {p}}$
-operator is diagonalisable on
$S_{k,l}^{\mathfrak {p}\text {-}\mathrm {old}}(\Gamma _0(\mathfrak {p}\mathfrak {m}))$
if and only if the
$T_{\mathfrak {p}}$
-operator is diagonalisable on
$S_{k,l}(\Gamma _0(\mathfrak {m}))$
and is injective (see [Reference Bandini and Valentino5, Remark 2.4]). Therefore, if Questions 4.3(1) and 4.3(2) are true, then Question 4.3(3) is equivalent to checking the diagonalisability of the
$T_{\mathfrak {p}}$
-operator on
$S_{k,l}(\Gamma _0(\mathfrak {m})).$
4.1.1 Reformulation of Question 4.3(2)
In [Reference Valentino19], Valentino gave a necessary and sufficient condition for Question 4.3(2) to hold.
Theorem 4.4 [Reference Valentino19, Theorem 3.15].
The map
$\mathrm {Id}- P^{k-2l}(\mathrm {Tr^\prime }^{\mathfrak {p}\mathfrak {m}}_{\mathfrak {m}})^2$
is bijective on
$S_{k,l}(\Gamma _0(\mathfrak {p}\mathfrak {m}))$
if and only if Question 4.3(2) holds.
We now rephrase Theorem 4.4 in terms of the eigenvalues of the
$T_{\mathfrak {p}}$
-operator.
Proposition 4.5. The
$T_{\mathfrak {p}}$
-operator has no eigenform on
$S_{k,l}(\Gamma _0(\mathfrak {m}))$
with eigenvalues
$\pm P^{{k}/{2}}$
if and only if Question 4.3(2) holds.
The proof of Proposition 4.5 depends on the following observations. For any
${\varphi \in S_{k,l}(\Gamma _0(\mathfrak {m}))}$
,
$$ \begin{align} \begin{aligned} \varphi|_{k,l} W_{\mathfrak{p}}^{(\mathfrak{p}\mathfrak{m})} &= \varphi|_{k,l}( \begin{smallmatrix} 1 & b \\ m & dP \!\end{smallmatrix})( \begin{smallmatrix} P & 0 \\ 0 & 1 \!\end{smallmatrix}) = \varphi|_{k,l}( \begin{smallmatrix} P & 0 \\ 0 & 1 \!\end{smallmatrix})= \delta_P\varphi, \\ (\delta_P\varphi)|_{k,l} W_{\mathfrak{p}}^{(\mathfrak{p}\mathfrak{m})} &= \varphi|_{k,l}( \begin{smallmatrix} P & 0 \\ 0 & 1 \!\end{smallmatrix})( \begin{smallmatrix} P & b \\ Pm & dP \!\end{smallmatrix})= P^{2l-k}\varphi. \end{aligned} \end{align} $$
Combining Proposition 3.8 with (4.1),
$$ \begin{align} \mathrm{Tr}^{\prime \mathfrak{p}\mathfrak{m}}_{\mathfrak{m}} (\delta_1(\varphi))=\varphi |_{k,l}W_{\mathfrak{p}}^{(\mathfrak{p}\mathfrak{m})}+P^{l-k}(U_{\mathfrak{p}}(\delta_1(\varphi)))=\delta_P \varphi+P^{l-k}(U_{\mathfrak{p}}(\delta_1(\varphi)))= P^{l-k}T_{\mathfrak{p}}\varphi, \end{align} $$
where
$W_{\mathfrak {p}}^{(\mathfrak {p}\mathfrak {m})}:=( \begin {smallmatrix} P & b \\ Pm & d P \!\end {smallmatrix})$
for some
$b,d\in A$
with
$dP^2-bPm=P.$
Proof of Proposition 4.5.
If
$f\in \ker (\mathrm {Id} - P^{k-2l}(\mathrm {Tr^\prime }^{\mathfrak {p}\mathfrak {m}}_{\mathfrak {m}})^2)$
, then
$f\in \mathrm {Im}(\delta _1)$
(from the proof of Theorem 4.4), so
$\ker (\mathrm {Id} - P^{k-2l}(\mathrm {Tr^\prime }^{\mathfrak {p}\mathfrak {m}}_{\mathfrak {m}})^2) \subseteq S_{k,l}(\Gamma _0(\mathfrak {m})).$
Therefore,
${\mathrm {Id} - P^{k-2l}(\mathrm {Tr^\prime }^{\mathfrak {p}\mathfrak {m}}_{\mathfrak {m}})^2}$
is bijective on
$S_{k,l}(\Gamma _0(\mathfrak {p}\mathfrak {m}))$
if and only if it is bijective on
$S_{k,l}(\Gamma _0(\mathfrak {m}))$
.
For any
$f\in S_{k,l}(\Gamma _0(\mathfrak {m}))$
, (4.2) implies
$\mathrm {Tr^\prime }^{\mathfrak {p}\mathfrak {m}}_{\mathfrak {m}}(\mathrm {Tr^\prime }^{\mathfrak {p}\mathfrak {m}}_{\mathfrak {m}}(f)) = P^{l-k}\mathrm {Tr^\prime }^{\mathfrak {p}\mathfrak {m}}_{\mathfrak {m}}(T_{\mathfrak {p}}(f))= P^{2l-2k}T_{\mathfrak {p}}(T_{\mathfrak {p}}(f))$
. Thus,
$\mathrm {Id} - P^{k-2l}(\mathrm {Tr^\prime }^{\mathfrak {p}\mathfrak {m}}_{\mathfrak {m}})^2 = \mathrm {Id} - P^{-k}T_{\mathfrak {p}}^2$
on
$S_{k,l}(\Gamma _0(\mathfrak {m}))$
. The map
$\mathrm {Id} - P^{-k}T_{\mathfrak {p}}^2$
is bijective on
$S_{k,l}(\Gamma _0(\mathfrak {m}))$
if and only if the
$T_{\mathfrak {p}}$
-operator has no eigenform on
$S_{k,l}(\Gamma _0(\mathfrak {m}))$
with eigenvalues
$\pm P^{{k}/{2}}$
. The result follows from Theorem 4.4.
We now discuss the validity of Question 4.3. We need a proposition, which is a generalisation of a result of Gekeler [Reference Gekeler10, Corollary 7.6], where
$T_{\mathfrak {p}} h = Ph$
for any prime ideal
$\mathfrak {p}=(P)$
. We show that this continues to hold for
$f\in M_{k,1}(\Gamma _0(\mathfrak {m}))$
with
$a_f(1)\ne 0$
.
Proposition 4.6. Suppose the u-series expansion of
$f\in M_{k,1}(\Gamma _0(\mathfrak {m}))$
at
$\infty $
is given by
$\sum _{j=0}^\infty a_f(\,j(q-1)+1)u^{\,j(q-1)+1}$
with
$a_f(1)\ne 0$
. If
$T_{\mathfrak {p}} f = \lambda f$
for some
$\lambda \in C$
, then
$\lambda =P.$
In particular,
$T_{\mathfrak {p}} f = P^{{k}/{2}} f$
can happen only when
$k=2$
.
Proof. Let
$G_{i,P}(X)$
denote the ith Goss polynomial corresponding to the lattice
${\Lambda _P= \ker (\kern1.5pt\rho _P)=\{x\in C \mid \rho _P(x)=0\}}$
, where
$\rho _P$
is the Carlitz module with value at P. By [Reference Armana1, Proposition 5.2] (the normalisation here is different),
$$ \begin{align} T_{\mathfrak{p}} f = P^k\sum_{j\geq 0}a_f(\,j(q-1)+1)(u_{\mathfrak{p}})^{\,j(q-1)+1} + \sum_{j\geq 0}a_f(\,j(q-1)+1)G_{j(q-1)+1,P}(P u), \end{align} $$
where
$u_{\mathfrak {p}}(z)=u(Pz)=u^{q^d}+\cdots .$
To determine
$\lambda $
, we compute the coefficient of u in the u-series expansion of
$T_{\mathfrak {p}} f$
. In (4.3), the term involving
$u_{\mathfrak {p}}$
does not contribute to the coefficient of u. By [Reference Gekeler10, Proposition 3.4(ii)],
$$ \begin{align*} G_{i,P}(X)=X(G_{i-1,P}(X)+\alpha_1 G_{i-q,P}(X)+\cdots + \alpha_j G_{i-q^{\,j},P}(X)+\cdots).\end{align*} $$
In
$G_{i,P}(Pu)$
, the coefficient of u in
$G_{j(q-1)+1,P}(P u)$
is
$0$
for
$j>0$
. Since
$G_{1,P}(X)=X$
(see [Reference Gekeler10, Proposition 3.4(v)]),
$T_{\mathfrak {p}} f= Pa_f(1)u+ \mathrm {higher\ terms}.$
Comparing the coefficient of u on both sides gives
$\lambda =P$
.
Remark 4.7. The Goss polynomials, which occur as the coefficients of
$T_{\mathfrak {p}} f$
, are very difficult to handle if
$l \neq 1$
(see (4.3) and [Reference Armana1, Proposition 5.2]). So, we have restricted ourselves to
$l=1$
in the last proposition.
We now prove that Conjecture 1.1 is true for
$S_{k,l}(\Gamma _0(T))$
when
$\dim \ S_{k,l}(\mathrm {GL}_2(A))\leq 1$
.
Theorem 4.8. For
$\mathfrak {m} =A$
,
$\deg P =1$
, Question 4.3 is true for
$S_{k,l}(\Gamma _0(P))$
when
$\dim S_{k,l}(\mathrm {GL}_2(A))\leq 1$
. In particular, Conjecture 1.1 is true for
$S_{k,l}(\Gamma _0(T))$
when
$\dim S_{k,l}(\mathrm {GL}_2(A))\leq 1$
.
Proof. Recall that
$\dim M_{k,l}(\mathrm {GL}_2(A)) \kern1.3pt{=}\kern1.3pt [{(k\kern1.3pt{-}\kern1.3ptl(q\kern1.3pt{+}\kern1.3pt1))}/{(q^2\kern1.3pt{-}\kern1.3pt 1)}] \kern1.3pt{+}\kern1.3pt1$
(see [Reference Cornelissen, Gekeler, van der Put, Reversat and Van Geel7, Proposition 4.3]). By [Reference Gekeler10, Theorem 5.13], the graded algebra
$\oplus _{k,l}M_{k,l}(\mathrm {GL}_2(A))$
is generated by
$g_1,h$
.
Suppose
$\dim S_{k,l}(\mathrm {GL}_2(A))=0$
. Then Question 4.3(1) is trivially true. Questions 4.3(2) and 4.3(3) are true by Proposition 4.5 and by the diagonalisability of the
$T_{\mathfrak {p}}$
-operator on
$S_{k,l}(\mathrm {GL}_2(A))$
.
Now, suppose
$\dim S_{k,l}(\mathrm {GL}_2(A))=1$
. Clearly, the
$T_{\mathfrak {p}}$
-operator is diagonalisable on
$S_{k,l}(\mathrm {GL}_2(A)).$
Therefore, combining Proposition 4.5 with the discussions in Section 4.1, Question 4.3 for the level
$(P) $
is true if we show that
$\ker (T_{\mathfrak {p}})=0$
and the
$T_{\mathfrak {p}}$
-operator has no eigenform on
$S_{k,l}(\mathrm {GL}_2(A))$
with eigenvalues
$\pm P^{{k}/{2}}$
. Without loss of generality, we assume that
$\mathfrak {p}=(T)$
.
We first consider the case
$l \neq 0$
. In this case,
$S_{k,l}(\mathrm {GL}_2(A))=\langle g_1^x h^l\rangle $
for some
${x\in \{0, \ldots , q\}}$
such that
$k=x(q-1)+l(q+1)$
. The u-series expansions of
$g_1, h$
are given by
$$ \begin{align*} g_1&=1- (T^q-T)u^{q-1}- (T^q-T) u^{(q-1)(q^2-q+1)}+\cdots\in A[[u]],\\ h&=-u-u^{1+(q-1)^2}+(T^q-T)u^{1+q(q-1)}-u^{1+(2q-2)(q-1)}+\cdots \in A[[u]]. \end{align*} $$
Therefore,
$g_1^xh^l= (-1)^l\sum _{i=0}^x (-1)^i( \begin {smallmatrix} x \\ i \!\end {smallmatrix})(T^q-T)^iu^{i(q-1)+l} + O(u^{(q-1)^2+l})\in A[[u]].$
Let
$T_{\mathfrak {p}} (g_1^xh^l)=\sum _{j=0}^\infty a_{T_{\mathfrak {p}}(g_1^xh^l)}(\,j(q-1)+l)u^{\,j(q-1)+l}$
. By [Reference Gekeler10, Example 7.4],
$$ \begin{align*} a_{T_{\mathfrak{p}}(g_1^xh^l)}(l)= \sum_{0\leq j < l} ( \begin{smallmatrix} l-1 \\ j \!\end{smallmatrix})T^{l-j} a_{g_1^xh^l}(\,j(q-1)+l)\in A.\end{align*} $$
Define
$x_0:=\min \{x,l-1\}$
. Then,
$ a_{T_{\mathfrak {p}}(g_1^xh^l)}(l)= \sum _{0\leq j \leq x_0} ( \begin {smallmatrix} l-1 \\ j \!\end {smallmatrix}) T^{l-j} (-1)^{l+j} ( \begin {smallmatrix} x \\ j \!\end {smallmatrix})(T^q-T)^{\,j}.$
Clearly, the set
$\{0\leq j \leq x_0\mid ( \begin {smallmatrix} l-1 \\ j \!\end {smallmatrix})( \begin {smallmatrix} x \\ j \!\end {smallmatrix}) \neq 0\}$
is nonempty; let
$j_{\max }$
be its maximum. Since
$\deg (T^{l-j}(T^q-T)^{\,j})<\deg (T^{l-(\,j+1)}(T^q-T)^{\,j+1})$
,
$$ \begin{align*} 0<\deg (a_{T_{\mathfrak{p}}(g_1^xh^l)}(l))= l+j_{\max} (q-1)\leq l+x_0 (q-1) < \frac{x(q-1)+l(q+1)}{2}. \end{align*} $$
Hence,
$$ \begin{align} 1< |a_{T_{\mathfrak{p}}(g_1^xh^l)}(l)| < q^{({x(q-1)+l(q+1))}/{2}}. \end{align} $$
The first inequality in (4.4) shows that
$\ker (T_{\mathfrak {p}})=0.$
From (4.4),
$T_{\mathfrak {p}}(g_1^xh^l)$
cannot be equal to
$\pm T^{{(x(q-1)+l(q+1))}/{2}}g_1^xh^l$
. In particular, the
$T_{\mathfrak {p}}$
-operator has no eigenform on
$S_{k,l}(\mathrm {GL}_2(A))$
with eigenvalues
$\pm T^{{k}/{2}}$
.
We now consider the case
$l=0$
. In this case,
$S_{k,0}(\mathrm {GL}_2(A)) =\langle g_1^x\Delta \rangle $
for some
$x{\in \{0,\ldots , q\}}$
such that
$k=x(q-1)+(q^2-1)$
. Since
$\Delta =-h^{q-1}$
, we can argue as before replacing l with
$q-1$
. We briefly sketch the proof. Recall that
$$ \begin{align*}g_1^x\Delta= \sum_{i=0}^x ( \begin{smallmatrix} x \\ i \!\end{smallmatrix})(-1)^{i+1}(T^q-T)^iu^{(i+1)(q-1)} + O(u^{q(q-1)})\in A[[u]].\end{align*} $$
Since
$a_{g_1^x\Delta }(0)=0$
, we have
$a_{T_{\mathfrak {p}}(g_1^x\Delta )}(q-1)= \sum _{0\leq j < q-1} ( \begin {smallmatrix} q-2 \\ j \!\end {smallmatrix}) T^{q-1-j} a_{g_1^x\Delta }((\,j\kern1.2pt{+}\kern1.2pt1)(q\kern1.2pt{-}\kern1.2pt1))$
(see [Reference Gekeler10, Example 7.4]). Set
$y_0 \kern1.2pt{:=}\kern1.2pt\min \{x, q\kern1.2pt{-}\kern1.2pt 2\}$
. Then,
$$ \begin{align*}a_{T_{\mathfrak{p}}(g_1^x\Delta)}(q-1)=\sum_{0\leq j \leq y_0} ( \begin{smallmatrix} q-2 \\ j \!\end{smallmatrix})T^{q-1-j} (-1)^{\,j+1} ( \begin{smallmatrix} x \\ j \!\end{smallmatrix}) (T^q-T)^{\,j}.\end{align*} $$
As in the previous case,
$1< |a_{T_{\mathfrak {p}}(g_1^x\Delta )}(q-1)|< q^{{(x(q-1)+(q^2-1))}/{2}}$
, which shows that
$\ker (T_{\mathfrak {p}})=0$
and the
$T_{\mathfrak {p}}$
-operator has no eigenform on
$S_{k,l}(\mathrm {GL}_2(A))$
with eigenvalues
$\pm T^{{k}/{2}}$
. This completes the proof of the proposition.
We show part of Conjecture 1.1 is true for
$S_{k,l}(\Gamma _0(T))$
when
$\dim \ S_{k,l}(\mathrm {GL}_2(A)) = 2$
.
Theorem 4.9. Let
$\mathfrak {m}=A$
and
$\deg P=1$
. If
$\dim S_{k,l}(\mathrm {GL}_2(A)) = 2$
, then the direct sum decomposition in Question 4.3(2) is true for
$S_{k,l}(\Gamma _0(\mathfrak {p}))$
.
Proof. By Proposition 4.5, it is enough to show the
$T_{\mathfrak {p}}$
-operator has no eigenform on
$S_{k,l}(\mathrm {GL}_2(A))$
with eigenvalues
$\pm P^{k/2}$
. Without loss of generality, we assume that
$\mathfrak {p}=(T)$
. We give a complete proof only for
$l\neq 0$
. The proof is similar when
$l=0$
.
Assume
$l \neq 0$
. Since
$\dim S_{k,l}(\mathrm {GL}_2(A))=2$
,
$S_{k,l}(\mathrm {GL}_2(A))=\langle g_1^yh^l, g_1^{x}\Delta h^l\rangle $
for some
$y\in \{q+1, \ldots , 2q+1\}$
such that
$k=y(q-1)+l(q+1)$
and where
$x := y-(q+1)$
.
There are three cases to be considered. We first assume that
$l\ne 1$
. Recall the following u-expansions:
$$ \begin{align} \phantom{\hspace{-20pt}}g_1^y &= \begin{cases} \displaystyle \sum_{i=0}^{y} ( \begin{smallmatrix} y \\ i \!\end{smallmatrix})(-1)^{i}(T^q-T)^iu^{i(q-1)} + O(u^{(l+q)(q-1)}) \qquad & \mathrm{if} \ y<l+(q-1),\\ \displaystyle \sum_{i=0}^{l+(q-1)} ( \begin{smallmatrix} y \\ i \!\end{smallmatrix})(-1)^{i}(T^q-T)^iu^{i(q-1)} + O(u^{(l+q)(q-1)}) & \mathrm{if} \ y\geq l+(q-1), \end{cases} \notag \\ \phantom{\hspace{-9pt}}g_1^x &= \sum_{i=0}^x ( \begin{smallmatrix} x \\ i \!\end{smallmatrix})(-1)^i(T^q-T)^iu^{i(q-1)} + O(u^{(q-1)(q^2-q+1)}),\qquad\qquad \qquad \qquad \end{align} $$
$$ \begin{align} h^l & = (-1)^lu^l + (-1)^l l u^{(q-1)^2+l} +(-1)^{l-1}l (T^q-T) u^{q(q-1)+l} + O(u^{(l+q)(q-1)+l}), \end{align} $$
$$ \begin{align} &\hspace{-17pt}\Delta = -u^{q-1}+u^{q(q-1)} -(T^q-T)u^{(q+1)(q-1)} +O(u^{(q^2-q+1)(q-1)}),\quad \notag \\[2.5pt] &\hspace{-25pt}\Delta h^l = (-1)^{l+1}u^{q-1+l} +(-1)^l (1-l)u^{q(q-1)+l}+ (-1)^l (l-1) (T^q-T)u^{(q^2-1)+l} \quad\notag \\[2.5pt]&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\ + O(u^{(l+q)(q-1)+l}), \end{align} $$
from which we obtain
$$ \begin{align*} g_1^{x}\Delta h^l & = \begin{cases} \displaystyle (-1)^{l+1}\sum_{i=1}^{x+1}( \begin{smallmatrix} x \\ i-1 \!\end{smallmatrix})(-1)^{i-1}(T^q-T)^{i-1}u^{i(q-1)+l} + O(u^{l(q-1)+l}) \quad \mathrm{if} \ x+1<l, \\ \displaystyle (-1)^{l+1}\sum_{i=1}^{l-1}( \begin{smallmatrix} x \\ i-1 \!\end{smallmatrix})(-1)^{i-1}(T^q-T)^{i-1}u^{i(q-1)+l} + O(u^{l(q-1)+l}) \quad \mathrm{if} \ x+1\geq l, \end{cases} \\[5pt] g_1^yh^l & = (-1)^l\sum_{i=0}^{l-1} ( \begin{smallmatrix} y \\ i \!\end{smallmatrix})(-1)^{i}(T^q-T)^iu^{i(q-1)+l} + O(u^{l(q-1)+l}). \end{align*} $$
We first show that
$T_{\mathfrak {p}}(g_1^x\Delta h^l)\ne \pm T^{{(x(q-1)+(q^2-1)+l(q+1))}/{2}}g_1^x\Delta h^l.$
From [Reference Gekeler10, Example 7.4], the
$(l+(q-1))$
th coefficient of
$T_{\mathfrak {p}}(g_1^x\Delta h^l)$
is given by
$$ \begin{align} a_{T_{\mathfrak{p}}(g_1^x\Delta h^l)}(l+(q-1))= \sum_{0\leq i < l+q-1} ( \begin{smallmatrix} l+q-2 \\ i \!\end{smallmatrix}) T^{l+q-1-i} a_{g_1^x\Delta h^l}(l+(i+1)(q-1)). \end{align} $$
Taking the norm,
$$ \begin{align*} |a_{T_{\mathfrak{p}}(g_1^x\Delta h^l)}(l+(q-1))| &\leq \max_{\substack{1\leq i \leq l+q-1}}\{|T^{l+q-i} a_{g_1^x\Delta h^l}(l+i(q-1))|\}\\ &= \max_{\substack{1\leq i \leq l+q-1}}\bigg\{\bigg|T^{l+q-i}\sum_{\substack{\alpha\in \mathbb{N} \cup \{0\}, \beta \in \mathbb{N}\\ \alpha + \beta =i}} a_{g_1^x}(\alpha(q-1))\cdot a_{\Delta h^l}(\,\beta(q-1)+l)\bigg|\bigg\}. \end{align*} $$
By (4.5) and (4.7),
$a_{g_1^x}(i(q-1))=0$
for
$x<i\leq l+q-1$
and
$a_{\Delta h^l}(\,\beta (q-1)+l)=0$
for
$1\leq \beta \leq l+q-1$
with
$\beta \notin \{1, q, q+1\}.$
Therefore, the maximum above is
$$ \begin{align*} &\leq \max_{\beta\in \{1, q, q+1\}} \Big\{ \max_{\substack{1\leq i \leq l+q-1, \\ 0\leq i-\beta \leq x}} \{|T^{l+q-i} a_{g_1^x}((i-\beta)(q-1)) a_{\Delta h^l}(\,\beta(q-1)+l)|\}\Big\}\\ &{=} \max \Big\{\max_{\substack{1\leq i \leq l+q-1\\ 0\leq i-1\leq x}}\{q^{i(q-1)+l}\}, \max_{\substack{1\leq i \leq l+q-1\\ 0\leq i-q\leq x}}\{q^{(i-q)(q-1)+l} \}, \max_{\substack{1\leq i \leq l+q-1\\ 0\leq i-q-1\leq x}}\{q^{(i-q)(q-1)+l}\} \Big\}\\ &\leq \max \{q^{(x+1)(q-1)+l}, q^{x(q-1)+l}, q^{(x+1)(q-1)+l} \}= q^{(x+1)(q-1)+l}. \end{align*} $$
Hence,
$$ \begin{align} |a_{T_{\mathfrak{p}}(g_1^x\Delta h^l)}(l+(q-1))| \leq q^{(x+1)(q-1)+l}. \end{align} $$
The assumption
$l\ne 1$
implies
$(x+1)(q-1)+l< {(x(q-1)+(q^2-1)+l(q+1))}/{2}.$
Since
$a_{g_1^x\Delta h^l}(l+(q-1))= (-1)^{l+1}$
, combining the last inequality with (4.9), we get
$T_{\mathfrak {p}}(g_1^x\Delta h^l)\ne \pm T^{{(x(q-1)+(q^2-1)+l(q+1))}/{2}}g_1^x\Delta h^l$
. By the same technique, we give an upper bound on the coefficient
$a_{T_{\mathfrak {p}}(g_1^yh^l)}(l+(q-1)).$
Recall that
$$ \begin{align} a_{T_{\mathfrak{p}}(g_1^yh^l)}(l+(q-1))= \sum_{0\leq i < l+(q-1)} ( \begin{smallmatrix} l+q-2 \\ i \!\end{smallmatrix}) T^{l+q-1-i} a_{g_1^yh^l}(l+(i+1)(q-1)). \end{align} $$
Taking the norm,
$$ \begin{align*} |a_{T_{\mathfrak{p}}(g_1^yh^l)}(l+(q-1))| &\leq \max_{\substack{1\leq i \leq l+q-1}}\{|T^{l+q-i} a_{g_1^yh^l}(l+i(q-1))|\}\\ &= \max_{\substack{1\leq i \leq l+q-1}}\bigg\{\bigg|T^{l+q-i}\sum_{\substack{\alpha, \beta\in \mathbb{N} \cup \{0\}\\ \alpha + \beta =i}} a_{g_1^y}(\alpha(q-1))\cdot a_{h^l}(\,\beta(q-1)+l)\bigg|\bigg\}. \end{align*} $$
By (4.6),
$a_{h^l}(\,\beta (q-1)+l)=0$
for
$0\leq \beta \leq l+q-1$
with
$\beta \notin \{0, q-1, q\}.$
When
${y<l+q-1}$
, we have
$a_{g_1^y}(i(q-1))=0$
for
$y< i\leq l+q-1$
, and when
$y\geq l+(q-1)$
, we have
$a_{g_1^y}(i(q-1))=0$
for
$l+q-1 \leq i \leq y$
. Computing the maximum in each case as before,
$$ \begin{align} |a_{T_{\mathfrak{p}}(g_1^yh^l)}(l+(q-1))| \leq \begin{cases} q^{y(q-1)+l+q} & \mathrm{if} \ y< l+(q-1),\\ q^{(l+(q-1))(q-1)+l+q} & \mathrm{if} \ y\geq l+(q-1). \end{cases} \end{align} $$
Since
$T_{\mathfrak {p}}(g_1^x\Delta h^l)\ne \pm T^{{(x(q-1)+(q^2-1)+l(q+1))}/{2}}g_1^x\Delta h^l$
, it is now enough to show that there does not exist any
$c\in C$
such that
$$ \begin{align} T_{\mathfrak{p}}(g_1^y h^l + c g_1^{x} \Delta h^l)= \pm T^{{(y(q-1)+l(q+1))}/{2}}(g_1^y h^l + c g_1^{x}\Delta h^l). \end{align} $$
In contrast, suppose there is an element
$c\in C$
such that (4.12) holds with the ‘
$+$
’ sign. A similar argument works with ‘
$-$
’. The lth coefficients of
$T_{\mathfrak {p}}(g_1^yh^l)$
and
$T_{\mathfrak {p}}(g_1^x\Delta h^l)$
are given by (see [Reference Gekeler10, Example 7.4])
$$ \begin{align*} a_{T_{\mathfrak{p}}(g_1^yh^l)}(l) = (-1)^l \sum_{0\leq j < l} ( \begin{smallmatrix} l-1 \\ j \!\end{smallmatrix})T^{l-j} ( \begin{smallmatrix} y \\ j \!\end{smallmatrix})(-1)^{\,j}(T^q-T)^{\,j}, \end{align*} $$
$$ \begin{align*} a_{T_{\mathfrak{p}}(g_1^x\Delta h^l)}(l)= \begin{cases} \displaystyle (-1)^{l+1}\sum_{j=1}^{x+1}( \begin{smallmatrix} l-1 \\ j \!\end{smallmatrix})T^{l-j}( \begin{smallmatrix} x \\ j-1 \!\end{smallmatrix})(-1)^{\,j-1}(T^q-T)^{\,j-1} \quad \mathrm{if} \ x+1< l,\\ \displaystyle (-1)^{l+1}\sum_{j=1}^{l-1}( \begin{smallmatrix} l-1 \\ j \!\end{smallmatrix})T^{l-j}( \begin{smallmatrix} x \\ j-1 \!\end{smallmatrix})(-1)^{\,j-1}(T^q-T)^{\,j-1} \quad \mathrm{if} \ x+1\geq l. \end{cases} \end{align*} $$
Comparing the lth coefficients on both sides of (4.12) gives
$$ \begin{align} \small \sum_{0\leq j < l} \!( \begin{smallmatrix} l-1 \\ j \!\end{smallmatrix})T^{l-j} ( \begin{smallmatrix} y \\ j \!\end{smallmatrix})(-1)^{\,j}(T^q-T)^{\,j} \kern1.2pt{-}\kern1.2pt c\!\sum_{j=1}^{x_0}( \begin{smallmatrix} l-1 \\ j \!\end{smallmatrix})T^{l-j}( \begin{smallmatrix} x \\ j-1 \!\end{smallmatrix})(-1)^{\,j-1}(T^q-T)^{\,j-1}\kern1.2pt{=}\kern1.2pt T^{{(y(q-1)+l(q+1))}/{2}}\kern-1pt, \end{align} $$
where
$x_0:= \mathrm \min \{ x,l-2\}+1$
. Here,
$c\sum _{j=1}^{x_0}( \begin {smallmatrix} l-1 \\ j \!\end {smallmatrix})T^{l-j}( \begin {smallmatrix} x \\ j-1 \!\end {smallmatrix})(-1)^{\,j-1}(T^q-T)^{\,j-1} \ne 0$
. Otherwise, the inequality
$lq<{(y(q-1)+l(q+1))}/{2}$
would imply that the two sides of (4.13) have different degrees. Let
$j_{\max }:= \max \{1\leq j \leq x_0 \mid ( \begin {smallmatrix} l-1 \\ j \!\end {smallmatrix})( \begin {smallmatrix} x \\ j-1 \!\end {smallmatrix})\neq 0\}.$
Then,
$|\sum _{j=1}^{x_0}( \begin {smallmatrix} l-1 \\ j \!\end {smallmatrix})T^{l-j}( \begin {smallmatrix} x \\ j-1 \!\end {smallmatrix})(-1)^{\,j-1}(T^q-T)^{\,j-1}|=q^{\,j_{\max }(q-1)+l-q}.$
Again, since
$lq<(y(q-1)+ l(q+1))/{2}$
, it follows that
$$ \begin{align*}|T^{{(y(q-1)+l(q+1))}/{2}}- \sum_{0\leq j < l} ( \begin{smallmatrix} l-1 \\ j \!\end{smallmatrix})T^{l-j} ( \begin{smallmatrix} y \\ j \!\end{smallmatrix})(-1)^{\,j}(T^q-T)^{\,j}|=q^{(y(q-1)+l(q+1))/{2}}.\end{align*} $$
Therefore, (4.13) gives
$$ \begin{align} c= -\frac{T^{{(y(q-1)+l(q+1))}/{2}}- \sum_{0\leq j < l} ( \begin{smallmatrix} l-1 \\ j \!\end{smallmatrix})T^{l-j} ( \begin{smallmatrix} y \\ j \!\end{smallmatrix})(-1)^{\,j}(T^q-T)^{\,j}}{\sum_{j=1}^{\,j_{\max}}( \begin{smallmatrix} l-1 \\ j \!\end{smallmatrix})T^{l-j}( \begin{smallmatrix} x \\ j-1 \!\end{smallmatrix})(-1)^{\,j-1}(T^q-T)^{\,j-1}}\in K \end{align} $$
and
$ |c|= q^{{(y(q-1)+l(q+1))}/{2}-(\,j_{\max }(q-1)+l-q)}.$
Since
$lq<{(y(q-1)+l(q+1))}/{2}$
, from (4.14),
$$ \begin{align} |a_{(g_1^y h^l + c g_1^{x} \Delta h^l)}((q-1)+l)| &= |(-1)^{l+1}y(T^q-T)+(-1)^{l+1} c|\nonumber\\&= q^{(y(q-1)+l(q+1))/2-(\,j_{\max}(q-1)+l-q)}. \end{align} $$
Comparing the
$((q-1)+l)$
th coefficients on both sides of (4.12),
$$ \begin{align} |a_{T_{\mathfrak{p}}(g_1^y h^l + c g_1^{x} \Delta h^l)}((q-1)+l)| = q^{y(q-1)+l(q+1)-(\,j_{\max}(q-1)+l-q)}. \end{align} $$
However, from (4.11),
$$ \begin{align*} |a_{T_{\mathfrak{p}}(g_1^y h^l + c g_1^{x} \Delta h^l)}((q-1)+l)| &\leq \max \{|a_{T_{\mathfrak{p}}(g_1^y h^l)}((q-1)+l)|, |c| \, | a_{T_{\mathfrak{p}}(g_1^{x} \Delta h^l)}((q-1)+l)|\}\\ &\leq \max\{q^{y_0(q-1)+l+q}, q^{{(y(q-1)+l(q+1))}/{2}-(\,j_{\max}(q-1)+l-q)} q^{(x+1)(q-1)+l} \}, \end{align*} $$
where
$y_0:= \mathrm \min \{y, l+(q-1) \}.$
Since
$0\leq j_{\max } <l$
, an easy verification shows that
$q^{y_0(q-1)+l+q}{\kern-1.5pt}<{\kern-1.5pt}q^{y(q-1)+l(q+1)-(\,j_{\max }(q-1)+l-q)}. $
Moreover,
$(x{\kern-1.5pt}+{\kern-1.5pt}1)(q{\kern-1.5pt}-{\kern-1.5pt}1){\kern-1.5pt}+{\kern-1.5pt}l{\kern-1.5pt}<{\kern-1.5pt}(x (q{\kern-1.5pt}-{\kern-1.5pt}1){\kern-1.5pt}+{\kern-1.5pt}(q^2{\kern-1.5pt}-{\kern-1.5pt}1){\kern-1.5pt}+ l(q{\kern-1.5pt}+{\kern-1.5pt}1))/{2}$
implies
$q^{{(y(q-1)+l(q+1))}/{2}-(\,j_{\max }(q-1)+l-q)}{\kern-1pt}\cdot{\kern-1pt} q^{(x+1)(q-1)+l}{\kern-1.2pt}<{\kern-1.2pt} q^{y(q-1)+l(q+1)-(\,j_{\max }(q-1)+l-q)}.$
Therefore, we can conclude
$$ \begin{align*}|a_{T_{\mathfrak{p}}(g_1^y h^l + c g_1^{x} \Delta h^l)}((q-1)+l)|<q^{y(q-1)+l(q+1)-(\,j_{\max}(q-1)+l-q)},\end{align*} $$
which contradicts (4.16). Hence, the
$T_{\mathfrak {p}}$
-operator has no eigenform on
$S_{k,l}(\mathrm {GL}_2(A))$
with eigenvalue
$\pm T^{k/2}$
, and the result now follows from Proposition 4.5.
We now consider the case when
$l=1$
and
$y\ne 2q+1$
. Since
$a_{g_1^x\Delta h}(1)=0$
and
$(x+1)(q-1)+1< {(x(q-1)+(q^2-1)+(q+1))}/{2}$
, a similar argument shows that
$T_{\mathfrak {p}}(g_1^x\Delta h)\ne \pm T^{{(x(q-1)+(q^2-1)+(q+1))}/{2}}g_1^x\Delta h$
(see (4.9)). However, since
$a_{c_1 g_1^x\Delta h + c_2 g_1^yh}(1)\ne 0$
for
$c_2\in C\setminus \{0\}$
and
$x(q-1)+(q^2-1)+(q+1)>2$
, Proposition 4.6 implies that
$T_{\mathfrak {p}}(c_1g_1^x\Delta h+c_2 g_1^y h)\ne \pm T^{{(x(q-1)+(q^2-1)+(q+1))}/{2}}(c_1g_1^x\Delta h+c_2 g_1^y h)$
.
We now consider the the case
$(y,l)=(2q+1,1)$
. By the u-series expansion,
$a_{T_{\mathfrak {p}}(g_1^{2q+1}h)}(1)=-T, a_{T_{\mathfrak {p}}(g_1^q\Delta h)}(1)=0$
and
$a_{T_{\mathfrak {p}}(g_1^q\Delta h)}(q)=T^q$
. This implies that for any
$(c_1,c_2) \in C^2 \setminus \{ (0,0)\}$
,
$T_{\mathfrak {p}}(c_1 g_1^{2q+1}h+c_2 g_1^q\Delta h)\ne T^{q^2}(c_1 g_1^{2q+1}h+c_2 g_1^q\Delta h)$
. This can be checked by comparing the qth coefficients if
$c_1=0$
and by Proposition 4.6 if
$c_1\ne 0$
. Now, we are done by Proposition 4.5.
We now consider the last case
$l=0$
. Here, the proof is similar to
$l\neq 0$
, except that we need to consider the
$(q-1)$
th,
$2(q-1)$
th coefficients and use the inequality
$(x+2)(q-1)<{(x(q-1)+2(q^2-1))}/{2}$
.
4.2 Evidence for Question 4.3 for prime ideals
$\mathfrak {p}$
We now give some instances where Question 4.3 for prime ideals
$\mathfrak {p}$
has an affirmative answer.
Proposition 4.10. For any prime ideal
$\mathfrak {p}$
, Question 4.3 is true for level
$\mathfrak {p}$
in the following cases:
-
(1)
-
(a)
$1\leq l \leq q-2$
and
$k=2l+\alpha (q-1)$
, where
$\alpha \in \{0,\ldots , l\}$
; -
(b)
$l=0$
and
$k=\beta (q-1)$
, where
$\beta \in \{1, \ldots , q+1\}$
; -
(c)
$l=1$
and
$k=\alpha (q-1)+(q+1)$
, where
$\alpha \in \{0,\ldots , q\}$
;
-
-
(2)
$k\leq 3q.$
Proof. In all of these cases,
$\dim S_{k,l}(\mathrm {GL}_2(A))\leq 1.$
Hence, the
$T_{\mathfrak {p}}$
-operator is diagonalisable on
$S_{k,l}(\mathrm {GL}_2(A)).$
As in our earlier discussion, Question 4.3 has an affirmative answer for
$\mathfrak {p}$
if we show that
$\ker (T_{\mathfrak {p}})=0$
and the
$T_{\mathfrak {p}}$
-operator has no eigenform on
$S_{k,l}(\mathrm {GL}_2(A))$
with eigenvalues
$\pm P^{{k}/{2}}$
. We prove these statements in all cases.
(1a). Since
$l>0$
,
$M_{k,l}(\mathrm {GL}_2(A))=S_{k,l}(\mathrm {GL}_2(A))$
. If
$\alpha \in \{0,\ldots , l-1\}$
, then
$\dim S_{2l+\alpha (q-1),l}(\mathrm {GL}_2(A))=0$
and the result follows trivially. If
$\alpha =l$
, then
$\dim S_{2l+\alpha (q-1),l} (\mathrm {GL}_2(A))=1$
and
$S_{2l+\alpha (q-1),l}(\mathrm {GL}_2(A))= \langle h^l\rangle $
. By [Reference Joshi and Petrov14, (9)] (or by [Reference Petrov16, Theorem 3.17]), the
$T_{\mathfrak {p}}$
-operator acts on
$h^i$
by
$P^i$
for
$1\leq i\leq q-2.$
Since
$P^l\ne \pm P^{{l(q+1)}/{2}}$
for
$1\leq l \leq q-2$
, the result follows.
(1b). When
$l=0$
, we prove the required claim in two steps. For
$\beta \in \{1, \ldots , q\}$
,
$M_{\beta (q-1),0}(\mathrm {GL}_2(A))=\langle g_1^{\kern1pt\beta} \rangle $
. Therefore,
$S_{\beta (q-1),0}(\mathrm {GL}_2(A))=\{0\}$
and the result follows. If
$\beta = q+1$
,
$S_{q^2-1,0}(\mathrm {GL}_2(A))=\langle \Delta \rangle .$
By [Reference Gekeler10, Corollary 7.5],
$T_{\mathfrak {p}}(\Delta )= P^{q-1}\Delta $
. Since
$P^{q-1}\ne \pm P^{{q^2-1}/{2}}$
, the result follows.
(1c). If
$\alpha \in \{0,\ldots , q\} $
,
$S_{k,1}(\mathrm {GL}_2(A)) = \langle g_1^\alpha h \rangle $
. Since
$a_{g_1^\alpha h}(1)\ne 0$
, by Proposition 4.6,
$T_{\mathfrak {p}}(g_1^\alpha h)= P g_1^\alpha h$
and the result follows.
(2). This part can be deduced from the earlier known cases as follows. Let
$0\leq l \leq q-2.$
If
$k\not \equiv 2l \pmod {q-1}$
, then
$M_{k,l}(\mathrm {GL}_2(A))=\{0\}$
and Question 4.3 is trivially true. So, we only consider the cases
$k \equiv 2l \pmod {q-1}$
, that is,
$k=2l+x(q-1)$
for some
$x\in \mathbb {N}\cup \{0\}$
. The condition
$k \leq 3q$
implies
$x\leq 4$
.
If
$x<l$
, then
$\dim M_{k,l}(\mathrm {GL}_2(A))=0$
and the result follows. If
$x=l$
, then
${k=l(q+1)}$
. If
$l \neq 0$
, then
$S_{l(q+1), l}(\mathrm {GL}_2(A))=\langle h^l \rangle $
. So, we are back to case 1(a). If
$l=0$
, then
${S_{0,0}=\{0\}}$
and the result follows. Therefore, the remaining cases of interest are
${l < x \leq 4}$
. If
$l\geq 2$
, the inequality
$k\leq 3q$
forces
$x\leq 2$
and we are back to the case
$x\leq l$
. So, it is enough to consider
$l\in \{0,1\}$
with
$ l < x \leq 4$
.
For
$l=0$
: if
$(q,x)\ne (3,4)$
, then
$M_{x(q-1),0}(\mathrm {GL}_2(A)) = \langle g_1^x \rangle $
,
$S_{x(q-1),0}(\mathrm {GL}_2(A))=\{0\}$
and the result follows; if
$(q,x)=(3,4)$
, then
$k=(q+1)(q-1)$
and we are back to case 1(b). For
$l=1$
, we have
$k=(x-1)(q-1)+(q+1)$
where
$1<x\leq 3.$
Since
$q\geq 3$
, we are back to case 1(c). This completes the proof of the proposition.
We remark that our Proposition 4.10 is similar to [Reference Bandini and Valentino4, Theorem 5.8, Corollary 5.11 and Theorem 5.14] for the
$\mathfrak {p}= (T)$
-case. In a contrast to Proposition 4.10, we have the following proposition.
Proposition 4.11. For
$\deg m=1$
and
$\mathfrak {p}\nmid \mathfrak {m}$
, Question 4.3 is true for level
$\mathfrak {p}\mathfrak {m}$
when:
-
(i)
$l> {(q-1)}/{2}$
and
$k=2l-(q-1)$
; or -
(ii)
$l=1$
and
$k=q+1$
.
Proof. We may assume that
$\mathfrak {m}=(T)$
, since a similar calculation works for any ideal
$\mathfrak {m}$
with
$\deg m=1$
. We now follow the strategy in the proof of the Proposition 4.10.
(i). In this case,
$S_{k,l}(\Gamma _0(T))=\{0\}$
by [Reference Dalal and Kumar8, Proposition 4.1] and the result follows trivially.
(ii) First, we show that the operator
$T_{\mathfrak {p}}-P$
is zero on
$S_{q+1,1}(\Gamma _0(T))$
. Recall that
$\Delta _T(z) {\kern-1.5pt}:={\kern-1.3pt} {(g_1(Tz){\kern-1.3pt}-{\kern-1.3pt}g_1(z))}/{(T^q{\kern-1.5pt}-{\kern-1.3pt}T)}, \Delta _W(z) {\kern-1.3pt}:={\kern-1.3pt} {(T^qg_1(Tz){\kern-1.3pt}-{\kern-1.3pt}Tg_1(z))}/{(T^q{\kern-1.3pt}-{\kern-1.3pt}T)}{\kern-1.5pt}\in{\kern-1.3pt} M_{q-1,0} (\Gamma _0(T){\kern-1pt})$
.
By [Reference Dalal and Kumar8, Proposition 4.3(3)],
$\dim _C\ S_{q+1,1}(\Gamma _0(T)) = 2$
with basis
$\{\Delta _T E_T$
,
$\Delta _W E_T\}$
. By [Reference Dalal and Kumar8, Proposition 4.3(8)]),
$h= -\Delta _W E_T$
. Since
$T_{\mathfrak {p}} h= Ph$
, we obtain
$T_{\mathfrak {p}}(\Delta _W E_T)= P\Delta _W E_T$
. Note that
$\Delta _T = -T^{-1}\Delta _W|_{q-1,0}W_T^{(T)}$
and
$T_{\mathfrak {p}} W_T^{(T)}=W_T^{(T)} T_{\mathfrak {p}}$
by [Reference Valentino19, Theorem 1.1]. Using
$E_T|_{2,1}W_T^{(T)}=-E_T$
[Reference Dalal and Kumar9, Proposition 3.3],
$$ \begin{align*} T_{\mathfrak{p}}(\Delta_T E_T) & = T_{\mathfrak{p}}((T^{-1}\Delta_W E_T)|_{q+1,1}W_T^{(T)}) = (T_{\mathfrak{p}}(T^{-1}\Delta_W E_T))|_{q+1,1}W_T^{(T)} \\ & = T^{-1} ( P\Delta_W E_T)|_{q+1,1}W_T^{(T)}=P\cdot T^{-1}\Delta_W|_{q-1,0}W_T^{(T)}\cdot E_T|_{2,1}W_T^{(T)} = P\Delta_TE_T. \end{align*} $$
Thus,
$T_{\mathfrak {p}} \equiv P$
on
$S_{q+1,1}(\Gamma _0(T))$
. So, the
$T_{\mathfrak {p}}$
-operator is injective and diagonalisable on
$S_{q+1,1}(\Gamma _0(T))$
, which proves Question 4.3(1). Question 4.3(2) follows from Proposition 4.5. Finally, Question 4.3(3) follows from the diagonalisability of the
$T_{\mathfrak {p}}$
-operator on
$S_{q+1, 1}(\Gamma _0(T))$
.
4.3 Counterexample to question in Question 4.3(2)
In this section, we show that the direct sum decomposition in Question 4.3(2) does not hold if
$\mathfrak {m}\ne A$
and
${(k,l)=(2,1)}$
because there are nonzero Drinfeld cusp forms which are both
$\mathfrak {p}$
-oldforms and
$\mathfrak {p}$
-newforms. We first prove a result which is of independent interest.
Lemma 4.12. Let
$\mathfrak {p}_1, \mathfrak {p}_2$
be two distinct prime ideals of A generated by monic irreducible polynomials
$P_1, P_2$
, respectively. Then,
$T_{\mathfrak {p}_1} E_{P_2}= P_1E_{P_2}.$
Proof. By [Reference Gekeler10, (8.2)], the function
$E(z)=\sum _{a\in A_+}au(az)$
, where
$A_+$
denotes the set of all monic polynomials in
$A.$
Hence,
$ E_{P_2}(z) = \sum _{a\in A_+}au(az)- P_2\sum _{a\in A_+}au(P_2az) = \sum _{a\in A_+,\ P_2\nmid a} au(az).$
We now use an argument in the proof of [Reference Petrov16, Theorem 2.3] to get
$$ \begin{align*} T_{\mathfrak{p}_1} E_{P_2} &= \sum_{\substack{Q\in A\\ \deg Q<\deg P_1}}E_{P_2} \bigg(\frac{z+Q}{P_1}\bigg) +P_1^2 E_{P_2}(P_1z)\\ &= \sum_{\substack{Q\in A\\ \deg Q<\deg P_1}} \sum_{\substack{a\in A_+\\ P_2\nmid a}} au\bigg(a\frac{z+Q}{P_1}\bigg) + P_1^2 \sum_{\substack{a\in A_+\\ P_2\nmid a}} au(P_1az)\\ &= \frac{1}{\tilde{\pi}} \sum_{\substack{Q\in A\\ \deg Q<\deg P_1}} \sum_{\substack{a\in A_+\\ P_2\nmid a}} \sum_{b\in A} \frac{aP_1}{az+aQ+P_1b} + P_1 \sum_{\substack{a\in A_+\\ P_2\nmid a}} P_1a u(P_1az)\\ &= \frac{1}{\tilde{\pi}} \sum_{\substack{a\in A_+\\ P_2\nmid a}} aP_1 \sum_{b\in A} \sum_{\substack{Q\in A\\ \deg Q<\deg P_1}} \frac{1}{az+aQ+P_1b} + P_1 \sum_{\substack{a\in A_+\\ P_2\nmid a}} P_1a u(P_1az)\\ &= P_1\sum_{\substack{a\in A_+\\ P_1P_2\nmid a}}au(az) + P_1\sum_{\substack{a\in A_+\\ P_2\nmid a}}P_1au(P_1 az) = P_1 \sum_{\substack{a\in A_+\\ P_2\nmid a}} au(az)= P_1 E_{P_2}. \end{align*} $$
This completes the proof of the Lemma.
Proposition 4.13. Suppose
$\mathfrak {m}\ne A$
. For any prime ideal
$\mathfrak {p} \nmid \mathfrak {m}$
,
$$ \begin{align*}S_{2,1}^{\mathfrak{p}\text{-}\mathrm{old}}(\Gamma_0(\mathfrak{p}\mathfrak{m}))\cap S_{2,1}^{\mathfrak{p}\text{-}\mathrm{new}}(\Gamma_0(\mathfrak{p}\mathfrak{m}))\ne\{0\}.\end{align*} $$
Proof. Let
$\mathfrak {p}_2$
be a prime divisor of
$\mathfrak {m}$
generated by a monic irreducible polynomial
$P_2.$
Clearly,
$0 \neq E_{P_2}-\delta _P E_{P_2} \in S_{2,1}(\Gamma _0(\mathfrak {p}\mathfrak {m})).$
We show that
$E_{P_2}-\delta _P E_{P_2} \in S_{2,1}^{\mathfrak {p}\text {-}\mathrm {old}}(\Gamma _0(\mathfrak {p} \mathfrak {m}))\cap S_{2,1}^{\mathfrak {p}\text {-}\mathrm {new}}(\Gamma _0(\mathfrak {p} \mathfrak {m})).$
By definition,
$E_{P_2}-\delta _P E_{P_2} \in S_{2,1}^{\mathfrak {p}\text {-}\mathrm {old}}(\Gamma _0(\mathfrak {p} \mathfrak {m}))$
. Combining (4.2), (4.1) and Lemma 4.12,
$$ \begin{align} \mathrm{Tr}_{\mathfrak{m}}^{\mathfrak{p} \mathfrak{m}}(E_{P_2}-\delta_P E_{P_2}) =E_{P_2}-P^{-1}T_{\mathfrak{p}}(E_{P_2}) = E_{P_2}-E_{P_2} =0. \end{align} $$
By (4.1),
$$ \begin{align*} \mathrm{Tr}_{\mathfrak{m}}^{\mathfrak{p} \mathfrak{m}}((E_{P_2}-\delta_P E_{P_2})|W_{\mathfrak{p}}^{(\mathfrak{p} \mathfrak{m})}) &= \mathrm{Tr}_{\mathfrak{m}}^{\mathfrak{p} \mathfrak{m}}(E_{P_2}|W_{\mathfrak{p}}^{(\mathfrak{p} \mathfrak{m})}-(\delta_{P}E_{P_2})|W_{\mathfrak{p}}^{(\mathfrak{p} \mathfrak{m})})\\ &= \mathrm{Tr}_{\mathfrak{m}}^{\mathfrak{p} \mathfrak{m}}(\delta_{P}E_{P_2} -E_{P_2})=0. \end{align*} $$
This proves that
$E_{P_2}-\delta _P E_{P_2} \in S_{2,1}^{\mathfrak {p}\text {-}\mathrm {new}}(\Gamma _0(\mathfrak {p} \mathfrak {m}))$
. The result follows.
Remark 4.14. For
$f\in S_{k,l}(\Gamma _0(\mathfrak {n}))$
,
$T_{\mathfrak {p}}(f^{q^n})=(T_{\mathfrak {p}}(f))^{q^n}$
for any
$n \in \mathbb {N}$
. An argument similar to Proposition 4.13 gives
$$ \begin{align} 0\ne E_{P_2}^{q^n}-{P^{q^n-1}} \delta_P E_{P_2}^{q^n} \in S_{2{q^n},1}^{\mathfrak{p}-\mathrm{old}}(\Gamma_0(\mathfrak{p} \mathfrak{m}))\cap S_{2{q^n},1}^{\mathfrak{p}-\mathrm{new}}(\Gamma_0(\mathfrak{p} \mathfrak{m})). \end{align} $$
Since E behaves like a classical weight
$2$
Eisenstein series, we believe that the phenomenon in (4.18) may not happen for
$l\ne 1$
.
Proposition 4.13 and Remark 4.14 imply that either one needs to reformulate the definition of
$\mathfrak {p}$
-newforms for level
$\mathfrak {p}\mathfrak {m}$
or exclude the cases above in formulating Question 4.3 for level
$\mathfrak {p}\mathfrak {m}$
.
5 Oldforms and newforms for square-free level
$\mathfrak {n}$
For classical modular forms, it is well known that the space of newforms can be characterised in terms of kernels of the Trace and twisted Trace operators [Reference Li15, Reference Serre, Kuijk and Serre18]. In this section, we examine the extent that this is valid for Drinfeld modular forms.
Throughout this section, we assume that
$\mathfrak {n}$
is a square-free ideal of A generated by a (square-free) monic polynomial
$n\in A$
. Let
$\mathfrak {p}, \mathfrak {p}_1$
be two prime ideals of A generated by monic irreducible polynomials
$P,P_1\in A$
, respectively.
Definition 5.1 (Oldforms).
The space of oldforms of weight k, type l and square-free level
$\mathfrak {n}$
is defined as
$$ \begin{align*} S_{k,l}^{\mathrm{old}}(\Gamma_0(\mathfrak{n})):= \sum\limits_{\mathfrak{p}|\mathfrak{n}}(\delta_1,\delta_P)((S_{k,l}(\Gamma_0(\mathfrak{n}/\mathfrak{p})))^2). \end{align*} $$
Definition 5.2 (Newforms).
The space of newforms of weight k, type l and square-free level
$\mathfrak {n}$
is defined as
$$ \begin{align*}S_{k,l}^{\mathrm{new}}(\Gamma_0(\mathfrak{n})):= \bigcap\limits_{\mathfrak{p}|\mathfrak{n}} (\mathrm{Ker}(\mathrm{Tr}_{{\mathfrak{n}}/{\mathfrak{p}}}^{\mathfrak{n}})\cap \mathrm{Ker}({\mathrm{Tr}^\prime}_{{\mathfrak{n}}/{\mathfrak{p}}}^{\mathfrak{n}})), \quad \mathrm{where} \ {\mathrm{Tr}^\prime}_{{\mathfrak{n}}/{\mathfrak{p}}}^{\mathfrak{n}}f= {\mathrm{Tr}}_{{\mathfrak{n}}/{\mathfrak{p}}}^{\mathfrak{n}}(f|_{k,l}W^{(\mathfrak{n})}_{\mathfrak{p}}).\end{align*} $$
The action of Hecke operators on
$S_{k,l}^{\mathrm {old}}(\Gamma _0(\mathfrak {n}))$
,
$S_{k,l}^{\mathrm {new}}(\Gamma _0(\mathfrak {n}))$
depends on the commutativity of the (partial) Atkin–Lehner operators with the
$T_{\mathfrak {p}}$
and
$U_{\mathfrak {p}}$
-operators.
Theorem 5.3 [Reference Valentino19, Theorem 1.1].
Let
$\mathfrak {n},\mathfrak {p} \subseteq A$
be ideals such that
$\mathfrak {p} \nmid \mathfrak {n}$
and
$\mathfrak {p}$
is prime. For any ideal
$\mathfrak {d}$
of A such that
$\mathfrak {d}||\mathfrak {n}$
, the actions of
$T_{\mathfrak {p}}W_{\mathfrak {d}}^{(\mathfrak {n})}$
and
$W_{\mathfrak {d}}^{(\mathfrak {n})}T_{\mathfrak {p}}$
on
$S_{k,l}(\Gamma _0(\mathfrak {n}))$
are equal.
The following result can be thought of as a generalisation of Theorem 5.3 to the
$U_{\mathfrak {p}}$
-operator. Note that Theorem 5.4 holds for any integral ideal
$\mathfrak {n}$
.
Theorem 5.4. Assume that
$\mathfrak {p}^\alpha || \mathfrak {n}$
for some
$\alpha \in \mathbb {N}$
. For all prime divisors
$\mathfrak {p}_1$
of
$\mathfrak {n}$
with
$\mathfrak {p}_1 \neq \mathfrak {p}$
, the actions of
$U_{\mathfrak {p}_1}W_{\mathfrak {p}^\alpha }^{(\mathfrak {n})}$
and
$W_{\mathfrak {p}^\alpha }^{(\mathfrak {n})}U_{\mathfrak {p}_1}$
on
$S_{k,l}(\Gamma _0(\mathfrak {n})) $
are equal.
Proof. By definition,
$$ \begin{align*} P_1^{l-k}U_{\mathfrak{p}_1}W_{\mathfrak{p}^\alpha}^{(\mathfrak{n})} = \sum_{\substack{Q\in A\\ \deg Q < \deg P_1}}( \begin{smallmatrix} P^\alpha & b \\ n & P^\alpha d \!\end{smallmatrix})( \begin{smallmatrix} 1 & Q \\ 0 & P_1 \!\end{smallmatrix})= \sum_{\substack{Q\in A\\ \deg Q < \deg P_1}} ( \begin{smallmatrix} P^\alpha & P^\alpha Q+bP_1 \\ n & nQ+P^\alpha P_1d \!\end{smallmatrix}), \end{align*} $$
$$ \begin{align*} P_1^{l-k}W_{\mathfrak{p}^\alpha}^{(\mathfrak{n})}U_{\mathfrak{p}_1} = \sum_{\substack{Q\in A\\ \deg Q < \deg P_1}}( \begin{smallmatrix} 1 & Q \\ 0 & P_1 \!\end{smallmatrix})( \begin{smallmatrix} P^\alpha & b \\ n & P^\alpha d \!\end{smallmatrix})= \sum_{\substack{Q\in A\\ \deg Q < \deg P_1}} ( \begin{smallmatrix} P^\alpha+Q n & b+P^\alpha Q d \\ nP_1 & P^\alpha P_1d \!\end{smallmatrix}). \end{align*} $$
To prove the proposition, it suffices to show that for any
$Q\in A$
with
$\deg Q<\deg P_1$
, there exists a unique
$Q^\prime \in A$
with
$\deg Q^\prime <\deg P_1$
such that
$$ \begin{align} ( \begin{smallmatrix} P^\alpha+Q n & b+P^\alpha Q d \\ nP_1 & P^\alpha P_1d \!\end{smallmatrix})= ( \begin{smallmatrix} x & y \\ z & w \!\end{smallmatrix})( \begin{smallmatrix} P^\alpha & P^\alpha Q^\prime+bP_1 \\ n & nQ^\prime+P^\alpha P_1d \!\end{smallmatrix}) \end{align} $$
for some
$( \begin {smallmatrix} x & y \\ z & w \!\end {smallmatrix})\in \Gamma _0(\mathfrak {n})$
. For any
$Q,Q^\prime \in A$
, (5.1) implies
$x,w\in A$
,
$z\in \mathfrak {n}$
and
$$ \begin{align*} -P_1 y= P^{\alpha}Q^\prime -P^{\alpha}Qd -b + \bigg(n Q Q^\prime+bP_1 + \frac{n}{P^\alpha} bP_1 Q\bigg). \end{align*} $$
Thus, we are reduced to show that for any
$Q\in A$
with
$\deg Q<\deg P_1$
, there exists a unique
$Q^\prime \in A$
with
$\deg Q^\prime <\deg P_1$
such that
$y\in A$
.
Since
$P_1 \mid n$
, we have
$P_1|(n Q Q^\prime +bP_1 + ({n}/{P^\alpha }) bP_1 Q)$
. Now it is enough to show that there exists a unique
$Q^\prime \in A$
with
$\deg Q^\prime <\deg P_1$
such that
$P_1\mid P^\alpha (Q^\prime - Qd)-b$
.
Recall that
$P^\alpha d-b{n}/{P^\alpha }=1$
. Since
$P_1$
divides
${n}/{P^{\alpha }}$
, we get
$QP^\alpha d \equiv Q \pmod {P_1}$
for any
$Q \in A.$
So, it is enough to show that there exists a unique
$Q^\prime \in A$
such that
$P_1\mid P^\alpha Q^\prime - (Q+b)$
. Since
$(P^\alpha ,P_1)=1$
, the congruence
$P^\alpha f(X) \equiv (Q+b) \pmod {P_1}$
has a unique solution in A with
$\deg (f(X))<\deg P_1$
.
Theorem 5.5. The spaces
$S_{k,l}^{\mathrm {old}}(\Gamma _0(\mathfrak {n}))$
,
$S_{k,l}^{\mathrm {new}}(\Gamma _0(\mathfrak {n}))$
are invariant under the action of the Hecke operators
$T_{\mathfrak {p}}$
for
$\mathfrak {p} \nmid \mathfrak {n}$
and
$U_{\mathfrak {p}}$
for
$\mathfrak {p}\mid \mathfrak {n}$
.
Proof. Let
$\mathfrak {p}$
be a prime ideal of A such that
$\mathfrak {p}\mid \mathfrak {n}$
. We first show that the space
$S_{k,l}^{\mathrm {new}}(\Gamma _0(\mathfrak {n}))$
is stable under the
$U_{\mathfrak {p}}$
-operator. Let
$\mathfrak {p}_1 \ne \mathfrak {p}$
be a prime divisor of
$\mathfrak {n}$
and
$f\in S_{k,l}^{\mathfrak {p}_1\text {-}\mathrm {new}}(\Gamma _0(\mathfrak {n}))$
. By Theorem 5.4 and Proposition 3.6, the
$U_{\mathfrak {p}}$
-operator commutes with the
$W_{\mathfrak {p}_1}^{(\mathfrak {n})}$
-operator and the
$U_{\mathfrak {p}_1}$
-operator. Since
$f\in S_{k,l}^{\mathfrak {p}_1\text {-}\mathrm {new}}(\Gamma _0(\mathfrak {n}))$
, from Proposition 3.8,
$$ \begin{align*}\mathrm{Tr}_{{\mathfrak{n}}/{\mathfrak{p}_1}}^{\mathfrak{n}}(U_{\mathfrak{p}}(f)) = U_{\mathfrak{p}}(f)+ P_1^{-l}U_{\mathfrak{p}_1}(U_{\mathfrak{p}}(f)|W_{\mathfrak{p}}^{(\mathfrak{n})}) =U_{\mathfrak{p}}(\mathrm{Tr}_{{\mathfrak{n}}/{\mathfrak{p}_1}}^{\mathfrak{n}}(f))=0.\end{align*} $$
A similar argument shows that
${\mathrm {Tr}^\prime }_{{\mathfrak {n}}/{\mathfrak {p}_1}}^{\mathfrak {n}}(U_{\mathfrak {p}}(f))=0$
. Thus,
$S_{k,l}^{\mathfrak {p}_1\text {-}\mathrm {new}}(\Gamma _0(\mathfrak {n}))$
is stable under the
$U_{\mathfrak {p}}$
-operator. Since the space
$S_{k,l}^{\mathfrak {p}\text {-}\mathrm {new}}(\Gamma _0(\mathfrak {n}))$
is stable under the action of the
$U_{\mathfrak {p}}$
-operator by [Reference Bandini and Valentino5, Proposition 2.15], the space
$S_{k,l}^{\mathrm {new}}(\Gamma _0(\mathfrak {n}))$
is stable under the action of the
$U_{\mathfrak {p}}$
-operator.
Next, we show that the space
$S_{k,l}^{\mathrm {old}}(\Gamma _0(\mathfrak {n}))$
is stable under the action of the
$U_{\mathfrak {p}}$
-operator. Let
$\mathfrak {p}_1 \ne \mathfrak {p}$
be a prime divisor of
$\mathfrak {n}$
. Let
$\psi , \varphi \in S_{k,l}(\Gamma _0({{\mathfrak {n}}/{\mathfrak {p}_1}}))$
. Since
$\mathfrak {p} \mid ({\mathfrak {n}}/{\mathfrak {p}_1})$
, we have
$U_{\mathfrak {p}}(\psi ), U_{\mathfrak {p}}(\varphi )\in S_{k,l}(\Gamma _0({\mathfrak {n}}/{\mathfrak {p}_1}))$
. Moreover, (4.1) and Theorem 5.4 yield
$$ \begin{align*}U_{\mathfrak{p}}(\delta_{P_1} \varphi) = U_{\mathfrak{p}}(\varphi|W_{P_1}^{(\mathfrak{n})}) = (U_{\mathfrak{p}}(\varphi))|W_{P_1}^{(\mathfrak{n})} = \delta_{P_1}(U_{\mathfrak{p}}(\varphi)).\end{align*} $$
Hence, for all
$\mathfrak {p}_1\mid \mathfrak {n}$
with
$\mathfrak {p}_1\ne \mathfrak {p}$
, we have
$U_{\mathfrak {p}}(\psi +\delta _{P_1}\varphi )= U_{\mathfrak {p}}(\psi ) + \delta _{P_1} U_{\mathfrak {p}}(\varphi )$
with
$ U_{\mathfrak {p}}(\psi ), U_{\mathfrak {p}}(\varphi ) \in S_{k,l}(\Gamma _0({\mathfrak {n}}/{\mathfrak {p}_1})).$
Since the space
$S_{k,l}^{\mathfrak {p}\text {-}\mathrm {old}}(\Gamma _0(\mathfrak {n}))$
is stable under the action of the
$U_{\mathfrak {p}}$
-operator by [Reference Bandini and Valentino5, Proposition 2.15], the space
$S_{k,l}^{\mathrm {old}}(\Gamma _0(\mathfrak {n}))$
is stable under the action of the
$U_{\mathfrak {p}}$
-operator.
By a similar argument, the spaces
$S_{k,l}^{\mathrm {new}}(\Gamma _0(\mathfrak {n}))$
and
$S_{k,l}^{\mathrm {old}}(\Gamma _0(\mathfrak {n}))$
are stable under the
$T_{\mathfrak {p}}$
-operator for
$\mathfrak {p}\nmid \mathfrak {n}$
.
Corollary 5.6. The set of
$U_{\mathfrak {p}}$
-operators (for
$\mathfrak {p} \mid \mathfrak {n}$
) are simultaneously diagonalisable on
$S_{k,l}^{\mathrm {new}}(\Gamma _0(\mathfrak {n}))$
.
Proof. Let
$\mathfrak {p}$
be a prime ideal of A such that
$\mathfrak {p} \mid \mathfrak {n}$
. By [Reference Bandini and Valentino5, Remark 2.17], the
$U_{\mathfrak {p}}$
-operator is diagonalisable on
$S_{k,l}^{\mathfrak {p}\text {-}\mathrm {new}}(\Gamma _0(\mathfrak {n}))$
. By Theorem 5.5, the space
$S_{k,l}^{\mathrm {new}}(\Gamma _0(\mathfrak {n}))$
is a
$U_{\mathfrak {p}}$
-invariant subspace of
$S_{k,l}^{\mathfrak {p}\text {-}\mathrm {new}}(\Gamma _0(\mathfrak {n}))$
; hence, the
$U_{\mathfrak {p}}$
-operator is also diagonalisable on
$S_{k,l}^{\mathrm {new}}(\Gamma _0(\mathfrak {n}))$
. Now, the corollary follows from Proposition 3.6 and the fact that a commuting set of diagonalisable operators on a finite dimensional vector space are simultaneously diagonalisable.
Finally, we remark that
$S_{k,l}^{\mathrm {old}}(\Gamma _0(\mathfrak {n}))\cap S_{k,l}^{\mathrm {new}}(\Gamma _0(\mathfrak {n})) =\{ 0 \}$
may happen only for
$l\ne 1$
.
Lemma 5.7. For any two distinct prime ideals
$\mathfrak {p}, \mathfrak {q}$
generated by monic irreducible polynomials
$P, Q$
, respectively, the intersection
$S_{2{q^n},1}^{\mathrm {old}}(\Gamma _0(\mathfrak {p} \mathfrak {q}))\cap S_{2{q^n},1}^{\mathrm {new}}(\Gamma _0(\mathfrak {p} \mathfrak {q}))\ne \{0\}$
for any
$n\in \mathbb {N}$
.
Proof. By an argument similar to that in the proof of Proposition 4.13, it follows that
$0\ne E_{Q}^{q^n}-{{P}^{q^n-1}} \delta _{P} E_{Q}^{q^n} \in S_{2{q^n},1}^{\mathrm {old}}(\Gamma _0(\mathfrak {p} \mathfrak {q}))\cap S_{2{q^n},1}^{\mathrm {new}}(\Gamma _0(\mathfrak {p} \mathfrak {q}))$
.
Acknowledgements
The authors would like to thank Professor Andrea Bandini for his encouragement to check the validity of Conjecture 1.1, when
$\mathrm {dim}\ S_{k,l}(\mathrm {GL}_2(A))=2$
. We would also like to thank Professor Francesc Bars for his valuable comments on an earlier version of this article. We thank the anonymous referee for comments which improved our article, especially suggestions in the proof of Theorem 4.9.
