Hostname: page-component-5c6d5d7d68-thh2z Total loading time: 0 Render date: 2024-08-25T11:20:03.175Z Has data issue: false hasContentIssue false
  • English
  • Français

On the existence and uniqueness of solutions of parabolic equations

Published online by Cambridge University Press:  17 April 2009

K.L. Teo
K.L. Teo
Affiliation:
School of Mathematics, University of New South Wales, Kensington, New South Wales.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Recently, Eklund (Proc. Amer. Math. Soc. 47 (1975), 137–142) has shown that to each continuous function F on ∂pQ −⊲ {∂Ω × [0, T]} ∪ {Ω × (0)} there is a unique solution to the boundary value problem

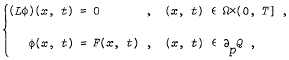
where L is a linear second order parabolic operator in divergence form, Ω ⊂ Rn is a bounded domain with compact closure and ∂Ω denotes its boundary. In this note, it is shown that the existence theorem of Eklund remains valid for the following boundary problem

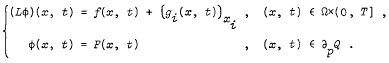
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 13 , Issue 3 , December 1975 , pp. 451 - 456
Copyright
Copyright © Australian Mathematical Society 1975

References

[1]Aronson, D.G., “Non-negative solutions of linear parabolic equations”, Ann. Sauola Norm. Sup. Pisa 22 (1968), 607–694.Google Scholar
[2]Aronson, D.G. and Serrin, James, “Local behavior of solutions of quasilinear parabolic equations”, Arch. Rational Mech. Anal. 25 (1967), 81–122.CrossRefGoogle Scholar
[3]Eklund, Neil A., “Existence and representation of solutions of parabolic equations”, Proc. Amer. Math. Soc. 47 (1975), 137–142.CrossRefGoogle Scholar
[4]Friedman, Avner, Partial differential equations of parabolic type (Prentice-Hall, Englewood Cliffs, New Jersey, 1964).Google Scholar
[5]Ladyženskaja, O.A., Solonnikov, V.A., Ural'ceva, N.N., Linear and quasilinear equations of parabolic type (Translations of Mathematical Monographs, 23. Amer. Math. Soc., Providence, Rhode Island, 1968).CrossRefGoogle Scholar