Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-06-03T07:23:56.623Z Has data issue: false hasContentIssue false
  • English
  • Français

PRIMES IN ARITHMETIC PROGRESSIONS AND NONPRIMITIVE ROOTS

Part of: Multiplicative number theory

Published online by Cambridge University Press:  24 May 2019

PIETER MOREE Open the ORCID record for PIETER MOREE [Opens in a new window]  and
MIN SHA Open the ORCID record for MIN SHA [Opens in a new window]
PIETER MOREE
Affiliation:
Max-Planck-Institut für Mathematik, Vivatsgasse 7, D-53111 Bonn, Germany email moree@mpim-bonn.mpg.de
MIN SHA*
Affiliation:
Department of Computing, Macquarie University, Sydney, NSW 2109, Australia email shamin2010@gmail.com
*
✉shamin2010@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 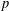$p$ be a prime. If an integer 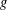$g$ generates a subgroup of index $t$ in 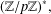$(\mathbb{Z}/p\mathbb{Z})^{\ast },$ then we say that 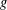$g$ is a $t$-near primitive root modulo 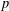$p$. We point out the easy result that each coprime residue class contains a subset of primes 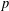$p$ of positive natural density which do not have 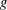$g$ as a $t$-near primitive root and we prove a more difficult variant.

Keywords

primitive rootnear-primitive rootArtin’s primitive root conjecturearithmetic progression

MSC classification

Primary: 11N13: Primes in progressions
Secondary: 11N69: Distribution of integers in special residue classes
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 3 , December 2019 , pp. 388 - 394
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

On-line encyclopedia of integer sequences, ‘Genocchi irregular primes’, sequence A321217, available at https://oeis.org.Google Scholar
Gupta, R. and Murty, M. R., ‘A remark on Artin’s conjecture’, Invent. Math. 78 (1984), 127–130.10.1007/BF01388719Google Scholar
Heath-Brown, D. R., ‘Artin’s conjecture for primitive roots’, Q. J. Math. (2) 37 (1986), 27–38.10.1093/qmath/37.1.27Google Scholar
Hooley, C., ‘On Artin’s conjecture’, J. reine angew. Math 225 (1967), 209–220.Google Scholar
Hu, S. and Kim, M.-S., ‘The (S, {2})-Iwasawa theory’, J. Number Theory 158 (2016), 73–89.10.1016/j.jnt.2015.06.013Google Scholar
Hu, S., Kim, M.-S., Moree, P. and Sha, M., ‘Irregular primes with respect to Genocchi numbers and Artin’s primitive root conjecture’, J. Number Theory (to appear), arXiv:1809.08431.Google Scholar
Lenstra, H. W. Jr., ‘On Artin’s conjecture and Euclid’s algorithm in global fields’, Invent. Math. 42 (1977), 202–224.10.1007/BF01389788Google Scholar
Lenstra, H. W. Jr., Moree, P. and Stevenhagen, P., ‘Character sums for primitive root densities’, Math. Proc. Cambridge Philos. Soc. 157 (2014), 489–511.10.1017/S0305004114000450Google Scholar
Moree, P., ‘On primes in arithmetic progression having a prescribed primitive root’, J. Number Theory 78 (1999), 85–98.Google Scholar
Moree, P., ‘On the distribution of the order and index of g (mod p) over residue classes I’, J. Number Theory 114 (2005), 238–271.10.1016/j.jnt.2004.09.004Google Scholar
Moree, P., ‘On primes in arithmetic progression having a prescribed primitive root II’, Funct. Approx. Comment. Math. 39 (2008), 133–144.10.7169/facm/1229696559Google Scholar
Moree, P., ‘Artin’s primitive root conjecture—a survey’, Integers 12A (2012), Article ID A13, 100 pages.Google Scholar
Moree, P., ‘Near-primitive roots’, Funct. Approx. Comment. Math. 48 (2013), 133–145.10.7169/facm/2013.48.1.11Google Scholar
Serre, J.-P., ‘Quelques applications du théorème de densité de Chebotarev’, Publ. Math. Inst. Hautes Études Sci. 54 (1981), 323–401.Google Scholar
Wagstaff, S. S. Jr., ‘Pseudoprimes and a generalization of Artin’s conjecture’, Acta Arith. 41 (1982), 141–150.10.4064/aa-41-2-141-150Google Scholar