Hostname: page-component-77c89778f8-swr86 Total loading time: 0 Render date: 2024-07-17T12:36:01.315Z Has data issue: false hasContentIssue false
  • English
  • Français

Ramanujan's remarkable summation formula and an interesting convolution identity

Published online by Cambridge University Press:  17 April 2009

S. Bhargava Chandrashekar Adiga  and
D.D. Somashekara
S. Bhargava Chandrashekar Adiga
Affiliation:
Department of Mathematics, University of Mysore, Manasagangotri Mysore 570 006, India
D.D. Somashekara
Affiliation:
Department of Mathematics, Yuvaraja's College University of Mysore, Mysore 570 005, India
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note we obtain a convolution identity for the coefficients Bn(α, θ, q) defined by

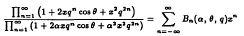
using Ramanujan's 1Ψ1 summation. The identity contains as special cases convolution identities of Kung-Wei Yang and a few more interesting analogue.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 47 , Issue 1 , February 1993 , pp. 155 - 162
Copyright
Copyright © Australian Mathematical Society 1993

References

[1]Adiga, C., Berndt, B.C., Bhargava, S. and Watson, G.N., ‘Chapter 16 of Ramanujan's second notebook: Theta-functions and q–series’, Mem. Amer. Math. Soc. 53 (1985), 315.Google Scholar
[2]Andrews, G.E., ‘On Ramanujan's summation of 1 Ψ 1(a;b;z)’, Proc. Amer. Math. Soc. 22 (1969), 552–553.Google Scholar
[3]Andrews, G.E., ‘On a transformation of bilateral series with applications’, Proc. Amer. Math. Soc. 25 (1970), 554–558.CrossRefGoogle Scholar
[4]Andrews, G.E., The theory of partitions, Encyclopedia of Math, and its Applications 2 (Addison-Wesley, Reading, 1976).Google Scholar
[5]Andrews, G.E., ‘Generalized Frobenius partitions’, Mem. Amer. Math. Soc. 49 (1984), 301.Google Scholar
[6]Andrews, G.E. and Askey, R., ‘A simple proof of Ramanujan's summation of the 1 Ψ 1’, Aequationes Math. 18 (1978), 333–337.CrossRefGoogle Scholar
[7]Askey, R., ‘Ramanujan's extensions of the gamma and beta functions’, Amer. Math. Monthly 87 (1980), 346–357.CrossRefGoogle Scholar
[8]Askey, R., ‘The number of representations of an integer as the sum of two squares’, Indian. J. Math. 2, 32 (1990), 187–192.Google Scholar
[9]Berndt, B.C., Ramanujan's notebooks, Part III (Springer-Verlag, Berlin, Heidelberg, New York, 1991).CrossRefGoogle Scholar
[10]Bhargava, S., Adiga, Chandrashekar and Somashekara, D.D., ‘Ramanujan's 1 Ψ 1 summation and an interesting generalization of an identity of Jacobi’, (submitted).Google Scholar
[11]Bhargava, S., Adiga, Chandrashekar and Somashekara, D.D., ‘On the representations of an integer as a sum of a square and thrice a square’, (submitted).Google Scholar
[12]Exton, H., q-hypergeometric functions and applications, Ellis Horwood series in Mathematics and its applications (Chichester, 1983).Google Scholar
[13]Hahn, W., ‘Beitrage zur theorie der Heineschen reihen’, Math. Nachr. 2 (1949), 340–379.CrossRefGoogle Scholar
[14]Ismail, M.E.H., ‘A simple proof of Ramanujan's 1 Ψ 1 sum’, Proc. Amer. Math. Soc. 63 (1977), 185–186.Google Scholar
[15]Jackson, M., ‘On Lerch's transcendent and the basic bilateral hypergeometric series 2 Ψ 2’, J. London Math. Soc. 25 (1950), 189–196.CrossRefGoogle Scholar
[16]Jacobi, C.G.J., Fundamenta Nova theoriae functionum ellipticarum (Gesammelte Werke, Erster Band, G. Reimer, Berlin, 1981), pp. 49–239.Google Scholar
[17]Ramanujan, S., Notebooks (Vol II) (Tata Institute of Fundamental Research, Bombay, 1957).Google Scholar
[18]Rothe, H.A., Systametiches Lehrbuch der arithmetik (Barth, Leipzig, 1811).Google Scholar
[19]Venkatachaliengar, K., Development of elliptic functions according to Ramanujan, Madurai Kamaraj University, Technical Report-2.CrossRefGoogle Scholar
[20]Yang, K.W., ‘On the product (1 + q nx + q 2nx 2)’, J. Austral. Math. Soc. Ser. A 48 (1990), 148–151.CrossRefGoogle Scholar