Hostname: page-component-7dd5485656-wjfd9 Total loading time: 0 Render date: 2025-10-30T11:12:44.576Z Has data issue: false hasContentIssue false
  • English
  • Français

SHARP BOUNDS OF SOME COEFFICIENT FUNCTIONALS OVER THE CLASS OF FUNCTIONS CONVEX IN THE DIRECTION OF THE IMAGINARY AXIS

Part of: Geometric function theory

Published online by Cambridge University Press:  29 January 2019

NAK EUN CHO Open the ORCID record for NAK EUN CHO [Opens in a new window] ,
BOGUMIŁA KOWALCZYK Open the ORCID record for BOGUMIŁA KOWALCZYK [Opens in a new window]  and
ADAM LECKO Open the ORCID record for ADAM LECKO [Opens in a new window]
NAK EUN CHO
Affiliation:
Department of Applied Mathematics, Pukyong National University, Busan 48513, Korea email necho@pknu.ac.kr
BOGUMIŁA KOWALCZYK
Affiliation:
Department of Complex Analysis, Faculty of Mathematics and Computer Science, University of Warmia and Mazury in Olsztyn, ul. Słoneczna 54, 10-710 Olsztyn, Poland email b.kowalczyk@matman.uwm.edu.pl
ADAM LECKO*
Affiliation:
Department of Complex Analysis, Faculty of Mathematics and Computer Science, University of Warmia and Mazury in Olsztyn, ul. Słoneczna 54, 10-710 Olsztyn, Poland email alecko@matman.uwm.edu.pl
*
✉alecko@matman.uwm.edu.pl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

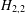We apply the Schwarz lemma to find general formulas for the third coefficient of Carathéodory functions dependent on a parameter in the closed unit polydisk. Next we find sharp estimates of the Hankel determinant $H_{2,2}$ and Zalcman functional 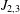$J_{2,3}$ over the class 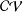${\mathcal{C}}{\mathcal{V}}$ of analytic functions 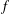$f$ normalised such that 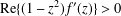$\text{Re}\{(1-z^{2})f^{\prime }(z)\}>0$ for 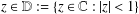$z\in \mathbb{D}:=\{z\in \mathbb{C}:|z|<1\}$, that is, the subclass of the class of functions convex in the direction of the imaginary axis.

Keywords

univalent functionsfunctions convex in the direction of the imaginary axisHankel determinantZalcman functionalcoefficientsCarathéodory class

MSC classification

Primary: 30C45: Special classes of univalent and multivalent functions (starlike, convex, bounded rotation, etc.)

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 1 , August 2019 , pp. 86 - 96
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

The first-named author was supported by the Basic Science Research Program through the National Research Foundation of the Republic of Korea (NRF) funded by the Ministry of Education, Science and Technology (No. 2016R1D1A1A09916450).

References

Babalola, K. O., ‘On H 3(1) Hankel determinant for some classes of univalent functions’, in: Inequality Theory and Applications, Vol. 6 (Nova Science Publishers, Hauppauge, NY, 2010), 1–7.Google Scholar
Bansal, D., Maharana, S. and Prajpapat, J. K., ‘Third order Hankel determinant for certain univalent functions’, J. Korean Math. Soc. 52(6) (2015), 1139–1148.10.4134/JKMS.2015.52.6.1139Google Scholar
Carathéodory, C., ‘Über den Variabilitatsbereich der Koeffizienten von Potenzreihen, die gegebene Werte nicht annehmen’, Math. Ann. 64 (1907), 95–115.10.1007/BF01449883Google Scholar
Cho, N. E., Kowalczyk, B., Kwon, O. S., Lecko, A. and Sim, Y. J., ‘Some coefficient inequalities related to the Hankel determinant for strongly starlike functions of order alpha’, J. Math. Inequal. 11(2) (2017), 429–439.10.7153/jmi-11-36Google Scholar
Cho, N. E., Kowalczyk, B., Kwon, O. S., Lecko, A. and Sim, Y. J., ‘The bounds of some determinants for starlike functions of order alpha’, Bull. Malays. Math. Sci. Soc. 41(1) (2018), 523–535.10.1007/s40840-017-0476-xGoogle Scholar
Duren, P. T., Univalent Functions (Springer, NY, 1983).Google Scholar
Goodman, A. W., Univalent Functions (Mariner, Tampa, FL, 1983).Google Scholar
Grenander, U. and Szegö, G., Toeplitz Forms and their Applications (University of California Press, Berkeley and Los Angeles, CA, 1958).10.1063/1.3062237Google Scholar
Hengartner, W. and Schober, G., ‘On Schlicht mappings to domains convex in one direction’, Comment. Math. Helv. 45 (1970), 303–314.10.1007/BF02567334Google Scholar
Janteng, A., Halim, S. A. and Darus, M., ‘Hankel determinant for starlike and convex functions’, Int. J. Math. Anal. 1(13) (2007), 619–625.Google Scholar
Kowalczyk, B., Kwon, O. S., Lecko, A. and Sim, Y. J., ‘The bounds of some determinants for functions of bounded turning of order alpha’, Bull. Soc. Sci. Lett. Łódź Sér. Rech. Déform. 67(1) (2017), 107–118.Google Scholar
Kowalczyk, B. and Lecko, A., ‘Polynomial close-to-convex functions I. Preliminaries and the univalence problem’, Bull. Soc. Sci. Lett. Łódź Sér. Rech. Déform. 63(3) (2013), 49–62.Google Scholar
Kowalczyk, B. and Lecko, A., ‘Polynomial close-to-convex functions II. Inclusion relation and coefficient formulae’, Bull. Soc. Sci. Lett. Łódź Sér. Rech. Déform. 63(3) (2013), 63–75.Google Scholar
Krishna, D. V., Venkateswarlu, B. and Ramreddy, T., ‘Third Hankel determinant for bounded turning functions of order alpha’, J. Nigerian Math. Soc. 34(2) (2015), 121–127.10.1016/j.jnnms.2015.03.001Google Scholar
Lecko, A., ‘Some subclasses of close-to-convex functions’, Ann. Polon. Math. 58(1) (1993), 53–64.10.4064/ap-58-1-53-64Google Scholar
Lecko, A., ‘A generalization of analytic condition for convexity in one direction’, Demonstratio Math. 30(1) (1997), 155–170.Google Scholar
Lee, S. K., Ravichandran, V. and Supramanian, S., ‘Bound for the second Hankel determinant of certain univalent functions’, J. Inequal. Appl. 2013 (2013), Article ID 281, 17 pages.Google Scholar
Libera, R. J. and Zlotkiewicz, E. J., ‘Early coefficients of the inverse of a regular convex function’, Proc. Amer. Math. Soc. 85(2) (1982), 225–230.10.1090/S0002-9939-1982-0652447-5Google Scholar
Libera, R. J. and Zlotkiewicz, E. J., ‘Coefficient bounds for the inverse of a function with derivatives in O’, Proc. Amer. Math. Soc. 87(2) (1983), 251–257.Google Scholar
Ma, W., ‘Generalized Zalcman conjecture for starlike and typically real functions’, J. Math. Anal. Appl. 234(1) (1999), 328–339.Google Scholar
Mishra, A. K. and Gochhayat, P., ‘Second Hankel determinant for a class of analytic functions defined by fractional derivative’, Int. J. Math. Math. Sci. 2008 (2008), Article ID 153280, 10 pages.Google Scholar
Pommerenke, C., Univalent Functions (Vandenhoeck & Ruprecht, Göttingen, 1975).Google Scholar
Ravichandran, V. and Verma, S., ‘Generalized Zalcman conjecture for some classes of analytic functions’, J. Math. Anal. Appl. 450(1) (2017), 592–605.10.1016/j.jmaa.2017.01.053Google Scholar
Robertson, M. S., ‘On the theory of univalent functions’, Ann. of Math. (2) 37 (1936), 374–408.Google Scholar
Royster, W. C. and Ziegler, M., ‘Univalent functions convex in one direction’, Publ. Math. Debrecen 23(3–4) (1976), 339–345.Google Scholar