No CrossRef data available.
Article contents
A SHARP UPPER BOUND FOR THE SUM OF RECIPROCALS OF LEAST COMMON MULTIPLES II
Published online by Cambridge University Press: 09 June 2022
Abstract
Let n and k be positive integers with
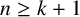$n\ge k+1$
and let
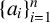$\{a_i\}_{i=1}^n$
be a strictly increasing sequence of positive integers. Let
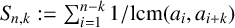$S_{n, k}:=\sum _{i=1}^{n-k} {1}/{\mathrm {lcm}(a_{i},a_{i+k})}$
. In 1978, Borwein [‘A sum of reciprocals of least common multiples’, Canad. Math. Bull. 20 (1978), 117–118] confirmed a conjecture of Erdős by showing that
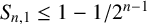$S_{n,1}\le 1-{1}/{2^{n-1}}$
. Hong [‘A sharp upper bound for the sum of reciprocals of least common multiples’, Acta Math. Hungar. 160 (2020), 360–375] improved Borwein’s upper bound to
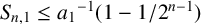$S_{n,1}\le {a_{1}}^{-1}(1-{1}/{2^{n-1}})$
and derived optimal upper bounds for
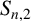$S_{n,2}$
and
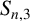$S_{n,3}$
. In this paper, we present a sharp upper bound for
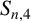$S_{n,4}$
and characterise the sequences
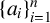$\{a_i\}_{i=1}^n$
for which the upper bound is attained.
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 107 , Issue 1 , February 2023 , pp. 10 - 21
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
This work was supported in part by research grants from the Natural Sciences and Engineering Research Council of Canada (Grant No. DDG-2019-04206 and RGPIN 2017-03903).
References
Bateman, P., Kalb, J. and Stenger, A., ‘A limit involving least common multiples’, Amer. Math. Monthly 109 (2002), 393–394.CrossRefGoogle Scholar
Behrend, F. A., ‘Generalization of an inequality of Heilbronn and Rohrbach,’ Bull. Amer. Math. Soc. (N.S.) 54 (1948), 681–684.CrossRefGoogle Scholar
Borwein, D., ‘A sum of reciprocals of least common multiples’, Canad. Math. Bull. 20 (1978), 117–118.CrossRefGoogle Scholar
Chebyshev, P. L., ‘Memoire sur les nombres premiers’, J. Math. Pures Appl. (9) 17 (1852), 366–390.Google Scholar
Erdős, P. and Selfridge, J., ‘The product of consecutive integers is never a power’, Illinois J. Math. 19 (1975), 292–301.CrossRefGoogle Scholar
Farhi, B., ‘Nontrivial lower bounds for the least common multiple of some finite sequences of integers’, J. Number Theory 125 (2007), 393–411.CrossRefGoogle Scholar
Goutziers, C. J., ‘On the least common multiple of a set of integers not exceeding
$N$
’, Indag. Math. (N.S.) 42 (1980), 163–169.CrossRefGoogle Scholar
$N$
’, Indag. Math. (N.S.) 42 (1980), 163–169.CrossRefGoogle ScholarHanson, D., ‘On the product of the primes’, Canad. Math. Bull. 15 (1972), 33–37.CrossRefGoogle Scholar
Heilbronn, H. A., ‘On an inequality in the elementary theory of numbers’, Math. Proc. Cambridge Philos. Soc. 33 (1937), 207–209.CrossRefGoogle Scholar
Hong, S. A., ‘A sharp upper bound for the sum of reciprocals of least common multiples’, Acta Math. Hungar. 160 (2020), 360–375.CrossRefGoogle Scholar
Hong, S. F., Luo, Y. Y., Qian, G. Y. and Wang, C. L., ‘Uniform lower bound for the least common multiple of a polynomial sequence’, C. R. Math. Acad. Sci. Paris Ser. I 351 (2013), 781–785.CrossRefGoogle Scholar
Hong, S. F., Qian, G. Y. and Tan, Q. R., ‘The least common multiple of a sequence of products of linear polynomials’, Acta Math. Hungar. 135 (2012), 160–167.CrossRefGoogle Scholar
Ireland, K. and Rosen, M., A Classical Introduction to Modern Number Theory, Graduate Texts in Mathematics, 84 (Springer-Verlag, New York, 1990).CrossRefGoogle Scholar
Nair, M., ‘On Chebyshev-type inequalities for primes’, Amer. Math. Monthly 89 (1982), 126–129.CrossRefGoogle Scholar
Rohrbach, H., ‘Beweis einer zahlentheoretischen Ungleichung’, J. reine angew. Math. 177 (1937), 193–196.CrossRefGoogle Scholar