Hostname: page-component-848d4c4894-2pzkn Total loading time: 0 Render date: 2024-05-17T02:45:34.278Z Has data issue: false hasContentIssue false
  • English
  • Français

THE SUMMED PAPERFOLDING SEQUENCE

Part of: Sequences and sets

Published online by Cambridge University Press:  25 March 2024

MARTIN BUNDER ,
BRUCE BATES  and
STEPHEN ARNOLD
MARTIN BUNDER
Affiliation:
School of Mathematics and Applied Statistics, University of Wollongong, Wollongong NSW 2522, Australia e-mail: mbunder@uow.edu.au
BRUCE BATES*
Affiliation:
School of Mathematics and Applied Statistics, University of Wollongong, Wollongong NSW 2522, Australia
STEPHEN ARNOLD
Affiliation:
Compass Learning Technologies, Swansea NSW 2281, Australia e-mail: steve@compasstech.com.au
*
e-mail: bbates@uow.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

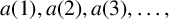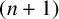The sequence $a( 1) ,a( 2) ,a( 3) ,\ldots, $ labelled A088431 in the Online Encyclopedia of Integer Sequences, is defined by: $a( n) $ is half of the $( n+1) $th component, that is, the 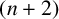$( n+2) $th term, of the continued fraction expansion of

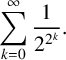$$ \begin{align*} \sum_{k=0}^{\infty }\frac{1}{2^{2^{k}}}. \end{align*} $$

Dimitri Hendriks has suggested that it is the sequence of run lengths of the paperfolding sequence, A014577. This paper proves several results for this summed paperfolding sequence and confirms Hendriks’s conjecture.

Keywords

paperfoldingsequence A088431sequence A014577

MSC classification

Primary: 11B83: Special sequences and polynomials
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 10
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allouche, J.-P. and Shallit, J., Automatic Sequences. Theory, Applications, Generalizations (Cambridge University Press, Cambridge, 2003).CrossRefGoogle Scholar
Bates, B. P., Bunder, M. W. and Tognetti, K. P., ‘Mirroring and interleaving in the paperfolding sequence’, Appl. Anal. Discrete Math. 4 (2010), 96–118.CrossRefGoogle Scholar
Bates, B. P., Bunder, M. W. and Tognetti, K. P., ‘Self-matching bands in the paperfolding sequence’ Appl. Anal. Discrete Math. 5 (2011), 46–54.CrossRefGoogle Scholar
Ben-Abraham, S. I., Quandt, A. and Shapira, D., ‘Multidimensional paperfolding systems’, Acta Cryst. A 69(2) (2013), 123–130.CrossRefGoogle ScholarPubMed
Davis, C. and Knuth, D. E., ‘Number representations and dragon curves’, J. Recreat. Math. 3 (1970), Part 1: 66–81, Part 2: 133–149.Google Scholar
Dekking, F. M., Mendes France, M. and van der Poorten, A. J., ‘Folds!’, Math. Intelligencer 4 (1982), 130–138, II: ibid. 173–181, III: ibid. 190–195.CrossRefGoogle Scholar
Gardner, M., ‘Mathematical games’, Sci. Amer. 216(3) (March 1967), 124–125; 216(4) (April 1967), 118–120; 217(7) (July 1967), 115.CrossRefGoogle Scholar
Mendès France, M. and Shallit, J. O., ‘Wire bending’, J. Combin. Theory Ser. A 50 (1989), 1–23.CrossRefGoogle Scholar
Mendès France, M. and van der Poorten, A. J., ‘Arithmetic and analytical properties of paper folding sequences’, Bull. Aust. Math. Soc. 24 (1981), 123–131.CrossRefGoogle Scholar
Pethö, A., ‘Simple continued fractions for the Fredholm numbers’, J. Number Theory 14 (1982), 232–236.CrossRefGoogle Scholar
Shallit, J. O., ‘Simple continued fractions for some irrational numbers’, J. Number Theory 11 (1979), 209–217.CrossRefGoogle Scholar
Shallit, J. O., ‘What is Walnut?’. Available at https://cs.uwaterloo.ca/~shallit/walnut.html.Google Scholar
Sloane, N. J. A., Online Encyclopedia of Integer Sequences. Available at https://oeis.org/A088431.Google Scholar