Hostname: page-component-848d4c4894-cjp7w Total loading time: 0 Render date: 2024-06-28T15:51:35.212Z Has data issue: false hasContentIssue false
  • English
  • Français

The uniform central limit theorem for the Kaplan-Meier integral process

Published online by Cambridge University Press:  17 April 2009

Jongsig Bae  and
Sungyeun Kim
Jongsig Bae
Affiliation:
Department of Mathematics and Institute of Basic Science, SungKyunKwan University, Suwon 440–746, Korea, e-mail: jsbae@yurim.skku.ac.kr, coke@math.skku.ac.kr
Sungyeun Kim
Affiliation:
Department of Mathematics and Institute of Basic Science, SungKyunKwan University, Suwon 440–746, Korea, e-mail: jsbae@yurim.skku.ac.kr, coke@math.skku.ac.kr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 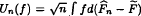be the Kaplan-Meier integral process constructed from the random censorship model. We prove a uniform central limit theorem for {Un} under the bracketing entropy condition and mild conditions due to the censoring effects. We also prove a sequential version of the uniform central limit theorem that will give a functional law of the iterated logarithm of Strassen type.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 67 , Issue 3 , June 2003 , pp. 467 - 480
Copyright
Copyright © Australian Mathematical Society 2003

References

[1]Dudley, R.M. and Philipp, W., ‘Invariance principles for sums of Banach space valued random elements and empirical processes’, Z. Wahrsch. Verw. Gebitete 62 (1983), 509–552.CrossRefGoogle Scholar
[2]Hoffmann-Jørgensen, J., Stochastic processes on Polish spaces (Aahus Universite, Matematisk Institut, Aarhus, 1991).Google Scholar
[3]Kaplan, E.L. and Meier, P., ‘Nonparametric estimation from incomplete observations’, J. Amer. Statist. Assoc. 53 (1958), 457–481.CrossRefGoogle Scholar
[4]Kuelbs, J. and Dudley, R.M., ‘Long log law for Empirical measures’, Ann. Probab. 8 (1980), 405–418.Google Scholar
[5]Ossiander, M., ‘A central limit theorem under metric entropy with L 2 bracketing’, Ann. Probab. 15 (1987), 897–919.CrossRefGoogle Scholar
[6]Pollard, D., Empirical processes: theory and applications, Regional conference series in Probability and Statistics 2 (Inst. Math. Statist, Hayward CA, 1990).CrossRefGoogle Scholar
[7]Stute, W., ‘The central limit theorem under random censorship’, Ann. Statist. 23 (1995), 422–439.CrossRefGoogle Scholar
[8]Van der Vaart, A. W. and Wellner, J.A., Weak convergence and empirical processes with applications to statistics, Springer series in Statistics (Springer-Verlag, New York, 1996).CrossRefGoogle Scholar