Hostname: page-component-5c6d5d7d68-lvtdw Total loading time: 0 Render date: 2024-08-30T05:23:33.287Z Has data issue: false hasContentIssue false
  • English
  • Français

Unimodal expanding maps of the interval

Published online by Cambridge University Press:  17 April 2009

Bau-Sen Du
Bau-Sen Du
Affiliation:
Institute of Mathematics, Academia Sinica Nankang Taipei, Taiwan, 11529, Republic of China
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let I = [0, 1] and let f be an unimodal expanding map in C0(I, I). If f has an expanding constant 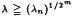for some integers m ≧ 0 and n ≧ 1, where λn is the unique positive zero of the polynomial x2n+1 − 2x2n−1 −1, then we show that f has a periodic point of period 2m(2n + 1). The converse of the above result is trivially false. The condition 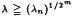in the above result is the best possible in the sense that we cannot have the same conclusion if the number λn is replaced by any smaller positive number and the generalisation of the above result to arbitrary piecewise monotonic expanding maps in C0(I, I) is not possible.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 38 , Issue 1 , August 1988 , pp. 125 - 130
Copyright
Copyright © Australian Mathematical Society 1988

References

[1]Adler, R., Konheim, A. and McAndrew, M., ‘Topological entropy’, Trans. Amer. Math. Soc. 114 (1965), 309–319.CrossRefGoogle Scholar
[2]Block, L., Guckenheimer, J., Misiurewicz, M. and Young, L.-S., ‘Periodic points and topological entropy of one dimensional maps’, in Global theory of dynamical systems 819: Lecture Notes in Math (Springer-Verlag, New York, 1980).Google Scholar
[3]Burkart, U., ‘Interval mapping graphs and periodic points of continuous functions’, J. Combin Theory Ser B 32 (1982), 57–68.CrossRefGoogle Scholar
[4]Byers, B., ‘Periodic points and chaos for expanding maps of the interval’, Bull. Austral. Math. Soc. 24 (1981), 79–83.CrossRefGoogle Scholar
[5]Du, B.-S., ‘The minimal number of periodic orbits of periods guaranteed in Sharkovskii's theorem’, Bull. Austral. Math. Soc. 31 (1985), 89–103.CrossRefGoogle Scholar
[6]Du, B.-S., ‘A note on periodic points of expanding maps of the interval’, Bull. Austral. Math. Soc. 33 (1986), 435–447.CrossRefGoogle Scholar
[7]Du, B.-S., ‘An example of a bifurcation from fixed points to period 3 points’, Nonlinear Anal 10 (1986), 639–641.CrossRefGoogle Scholar
[8]Du, B.-S., ‘Examples of expanding maps with some special properties’, Bull. Austral. Math. Soc. 36 (1987), 469–474.CrossRefGoogle Scholar
[9]Ho, C.-W. and Morris, C., ‘A graph theoretic proof of Sharkovsky's theorem on the periodic points of continuous functions’, Pacific J. Math. 96 (1981), 361–370.CrossRefGoogle Scholar
[10]Ito, S., Tanaka, S. and Nakada, H., ‘On unimodal linear transformations and chaos I’, Tokyo J. Math. 2 (1979), 221–239.Google Scholar
[11]Li, T.-Y., Misiurewicz, M., Pianigiani, G. and Yorke, J.A., ‘Odd chaos’, Phys. Lett. A 87 (1982), 271–273.CrossRefGoogle Scholar
[12]Li, T.-Y., Misiurewicz, M., Pianigiani, G. and Yorke, J.A., ‘No division implies chaos’, Trans. Amer. Math. Soc. 273 (1982), 191–199.CrossRefGoogle Scholar
[13]Osikawa, M. and Oono, Y., ‘Chaos in C 0-endomorphism of interval’, Publ. Res. Inst. Math. Sci. Kyoto Univ. 17 (1981), 165–177.CrossRefGoogle Scholar
[14]Sharkovskii, A.N., ‘Coexistence of cycles of a continuous map of the line into itself’, Ukain. Mat. Zh 61 (1964), 61–71. (Russian)Google Scholar
[15]Stefan, P., ‘A theorem of Sharkovsky on the existence of periodic orbits of continuous endomorphisms of the real line’, Comm. Math. Phys. 54 (1977), 237–248.CrossRefGoogle Scholar
[16]Straffin, P.D. Jr, ‘Periodic points of continuous functions’, Math. Mag. 51 (1978), 99–105.CrossRefGoogle Scholar
[17]Zhang, Z.-H., ‘Periodic points and chaos for expanding self-maps of the interval’, Bull. Austral. Math. Soc. 31 (1985), 439–443.Google Scholar