No CrossRef data available.
Article contents
UNIQUENESS OF EXTENDABLE TEMPERATURES
Published online by Cambridge University Press: 02 October 2020
Abstract
Let E and D be open subsets of
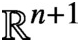$\mathbb {R}^{n+1}$
such that
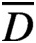$\overline {D}$
is a compact subset of E, and let v be a supertemperature on E. A temperature u on D is called extendable by v if there is a supertemperature w on E such that
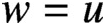$w=u$
on D and
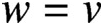$w=v$
on
$E\backslash \overline D$
. From earlier work of N. A. Watson, [‘Extendable temperatures’, Bull. Aust. Math. Soc.100 (2019), 297–303], either there is a unique temperature extendable by v, or there are infinitely many; a necessary condition for uniqueness is that the generalised solution of the Dirichlet problem on D corresponding to the restriction of v to
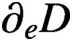$\partial _eD$
is equal to the greatest thermic minorant of v on D. In this paper we first give a condition for nonuniqueness and an example to show that this necessary condition is not sufficient. We then give a uniqueness theorem involving the thermal and cothermal fine topologies and deduce a corollary involving only parabolic and coparabolic tusks.
MSC classification
Primary:
35K05: Heat equation
- Type
- Research Article
- Information
- Copyright
- © 2020 Australian Mathematical Publishing Association Inc.
References
Armitage, D. H. and Gardiner, S. J., Classical Potential Theory (Springer-Verlag,
London, 2001).CrossRefGoogle Scholar
Bauer, H.,
Harmonische Räume und ihre Potentialtheorie
, Lecture Notes in Mathematics, 22 (Springer-Verlag,
Berlin, 1966).CrossRefGoogle Scholar
Bliedtner, J. and Hansen, W., Potential Theory: An Analytic and Probabilistic Approach to Balayage (Springer-Verlag,
Berlin, 1986).CrossRefGoogle Scholar
Doob, J. L.,
Classical Potential Theory and its Probabilistic Counterpart
, Grundlehren der mathematischen Wissenschaften, 262 (Springer-Verlag,
New York, 1984).CrossRefGoogle Scholar
Effros, E. G. and Kazdan, J. L., ‘On the Dirichlet problem for the heat equation’, Indiana Univ. Math. J. 20 (1970–1), 683–693.CrossRefGoogle Scholar
Kaufman, R. and Wu, J., ‘Parabolic potential theory’, J. Differential Equations 43 (1982), 204–234.CrossRefGoogle Scholar
Watson, N. A., ‘Green functions, potentials, and the Dirichlet problem for the heat equation’, Proc. London Math. Soc. 33 (1976), 251–298.CrossRefGoogle Scholar
Watson, N. A., ‘Mean values of subtemperatures over level surfaces of Green functions’, Ark. Mat. 30 (1992), 165–185.CrossRefGoogle Scholar
Watson, N. A., ‘Caloric measure for arbitrary open sets’, J. Aust. Math. Soc. 92 (2012), 391–407.CrossRefGoogle Scholar
Watson, N. A.,
Introduction to Heat Potential Theory
, Mathematical Surveys and Monographs, 182 (American Mathematical Society,
Providence, RI, 2012).Google Scholar
Watson, N. A., ‘Thermic minorants and reductions of supertemperatures’, J. Aust. Math. Soc. 99 (2015), 128–144.CrossRefGoogle Scholar
Watson, N. A., ‘Extensions of Green functions and the representation of greatest thermic minorants’, New Zealand J. Math. 47 (2017), 97–110.Google Scholar
Watson, N. A., ‘Extendable temperatures’, Bull. Aust. Math. Soc. 100 (2019), 297–303.CrossRefGoogle Scholar