Hostname: page-component-6d856f89d9-72csx Total loading time: 0 Render date: 2024-07-16T03:22:06.376Z Has data issue: false hasContentIssue false
  • English
  • Français

2-row Springer Fibres and KhovanovDiagram Algebras for Type D

Published online by Cambridge University Press:  20 November 2018

Michael Ehrig  and
Catharina Stroppel
Michael Ehrig
Affiliation:
Department of Mathematics, University of Bonn, 53115 Bonn, Germany e-mail: mehrig@math.uni-bonn.de, stroppel@math.uni-bonn.de
Catharina Stroppel
Affiliation:
Department of Mathematics, University of Bonn, 53115 Bonn, Germany e-mail: mehrig@math.uni-bonn.de, stroppel@math.uni-bonn.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

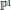We study in detail two row Springer fibres of even orthogonal type from an algebraic as well as a topological point of view. We show that the irreducible components and their pairwise intersections are iterated ${{\mathbb{P}}^{1}}$-bundles. Using results of Kumar and Procesi we compute the cohomology ring with its action of the Weyl group. The main tool is a type 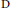$\text{D}$ diagram calculus labelling the irreducible components in a convenient way that relates to a diagrammatical algebra describing the category of perverse sheaves on isotropic Grassmannians based on work of Braden. The diagram calculus generalizes Khovanov's arc algebra to the type 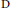$\text{D}$ setting and should be seen as setting the framework for generalizing well-known connections of these algebras in type $\text{A}$ to other types.

Keywords

17-11Springer fibersKhovanov homologyWeyl group type D
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 68 , Issue 6 , 01 December 2016 , pp. 1285 - 1333
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Brown, J. S. and Goodwin, S. M., Finite dimensional irreducible representations of finite W-algebras associated to even multiplicity nilpotent orbits in classical Lie algebras. Math. Z. 273(y), no. 1-2, 123–160.http://dx.doi.Org/10.1007/s00209-012-0998-8 Google Scholar
[2] Brundan, J. and Goodwin, S. M., Good gradingpolytopes. Proc. Lond. Math. Soc. (3) 94(2007), no. 1, 155–180.http://dx.doi.Org/10.1112/plms/pdlOO9 http://dx.doi.Org/10.1112/plms/pdlOO9 Google Scholar
[3] Brundan, J. and Kleshchev, A., Schur-Weyl duality for higher levels. Selecta Math. (N.S.) 14(2008), no. 1, 1–57. http://dx.doi.org/10.1007/s00029-008-0059-7 Google Scholar
[4] Braden, T., Perverse sheaves on Grassmannians. Canad. J. Math. 54(2002), no. 3, 493–532.http://dx.doi.Org/10.4153/CJM-2OO2-O17-6 http://dx.doi.Org/10.4153/CJM-2OO2-O17-6 Google Scholar
[5] Brown, J., Representation theory of rectangular finite W -algebras. J. Algebra 340(2011), 114–150.http://dx.doi.Org/10.1016/j.jalgebra.2011.05.014 http://dx.doi.Org/10.1016/j.jalgebra.2011.05.014 Google Scholar
[6] Brundan, J. and Stroppel, C., Highest weight categories arising from Khovanov's diagram algebra I:cellularity. Mosc. Math. J. 11(2011), 685–722.Google Scholar
[7] Brundan, J. and Stroppel, C., Gradings on walled Brauer algebras and Khovanov's arc algebra. Adv. Math. 231(2012), no. 2, 709–773. http://dx.doi.Org/10.1016/j.aim.2O12.05.016 http://dx.doi.Org/10.1016/j.aim.2012.05.016 Google Scholar
[8] Cox, A. and Visscher, M. De, Diagrammatic Kazhdan-Lusztig theory for the (walled) Brauer algebra. J. Algebra 340,151–181.http://dx.doi.Org/10.1016/j.jalgebra.2O11.05.024 http://dx.doi.Org/10.1016/j.jalgebra.2O11.05.024 Google Scholar
[9] Carré, C. and Leclerc, B., Splitting the square of a Schur function into its symmetric and antisymmetric parts. J. Algebraic Combin. 4(1995), no. 3, 201–231. doi=10.1023/A:1022475927626 http://dx.doi.Org/10.1023/A:1022475927626 Google Scholar
[10] Ehrig, M. and Stroppel, C., Diagrammatic description for the categories of perverse sheaves onisotropic Grassmannians. Selecta Math. (N.S.) 22(2016), no. 3,1455–1536. http://dx.doi.Org/10.1007/s00029-015-0215-9 Google Scholar
[11] Ehrig, M., Nazarov-Wenzl algebras, coideal subalgebras and categorified skew Howe duality. arxiv:1310.1972 Google Scholar
[12] Ehrig, M., Koszul gradings on Brauer algebras. Int. Math. Res. Notices 13(2016), 3970–4011. http://dx.doi.org/10.1093/imrn/rnv267 Google Scholar
[13] Presse, L. and Melnikov, A., On the singularity of the irreducible components of a Springer fiber in sln. Selecta Math. (N.S.) 16(2010), no. 3, 393–418.http://dx.doi.org/10.1007/s00029-010-0025-z http://dx.doi.org/10.1007/s00029-010-0025-z Google Scholar
[14] Presse, L., Singular components of Springer fibers in the two-column case. Ann. Inst. Fourier (Grenoble) 59(2009), no. 6, 2429–2444. http://dx.doi.Org/10.5802/aif.2495 Google Scholar
[15] Frenkel, I., Stroppel, C., and Sussan, J.. Categorifying fractional Euler characteristics, Jones-Wenzl projectors and 3j-symbols. Quantum Topol. 3(2012), 181–253.http://dx.doi.Org/10.4171/QT/28 http://dx.doi.Org/10.4171/QT/28 Google Scholar
[16] Fung, F. Y. C., On the topology of components of some Springer fibers and their relation to Kazhdan-Lusztig theory. Adv. Math. 178(2003), no. 2, 244–276.http://dx.doi.Org/10.1016/S0001-8708(02)00072-5 http://dx.doi.Org/10.1016/S0001-8708(02)00072-5 Google Scholar
[17] Garfinkle, D., On the classification of primitive ideals for complex classical Lie algebras. I. Compositio Math. 75(1990), no. 2,135–169.Google Scholar
[18] Gerstenhaber, M., Dominance over the classical groups. Ann. of Math. (2) 74(1961).http://dx.doi.Org/10.2307/1970297 Google Scholar
[19] Goresky, M., Kottwitz, R., and MacPherson, R.. Equivariant cohomology, Koszul duality, and the localization theorem. Invent. Math. 131(1998), no. 1, 25–83. http://dx.doi.Org/10.1OO7/sOO222OO5O197 http://dx.doi.Org/10.1OO7/sOO222OO5O197 Google Scholar
[20] Henderson, A. and Licata, A., Diagram automorphisms of quiver varieties. Adv. Math. 267(2014), 225–276. http://dx.doi.Org/10.1016/j.aim.2O14.08.007 http://dx.doi.Org/10.1016/j.aim.2O14.08.007 Google Scholar
[21] Hotta, R. and Springer, T. A., A specialization theorem for certain Weyl group representations and an application to the Green polynomials of unitary groups. Invent. Math. 41(1977), no. 2,113–127. http://dx.doi.Org/10.1007/BF01418371 Google Scholar
[22] Khovanov, M., A categorification of the Jones polynomial. Duke Math. J. 101(2000), no. 3, 359–426. http://dx.doi.org/10.1215/S0012-7094-00-10131-7 http://dx.doi.org/10.1215/S0012-7094-00-10131-7 Google Scholar
[23] Khovanov, M., Crossingless matchings and the cohomology of(n, n) Springer varieties. Commun. Contemp. Math. 6(2004), no. 4, 561–577.http://dx.doi.Org/10.1142/S0219199704001471 http://dx.doi.Org/10.1142/S0219199704001471 Google Scholar
[24] Kumar, S. and Procesi, C., An algebro-geometric realization of equivariant cohomology of some Springer fibers. J. Algebra 368(2012), 70–74.http://dx.doi.Org/10.1016/j.jalgebra.2O12.06.019 http://dx.doi.Org/10.1016/j.jalgebra.2O12.06.019 Google Scholar
[25] Losev, I. and Ostrik, V., Classification of finite-dimensional irreducible modules over Vf-algebras. Compos. Math. 150(2014), no. 6, 1024–1076.http://dx.doi.Org/10.1112/S0010437X13007604 http://dx.doi.Org/10.1112/S0010437X13007604 Google Scholar
[26] Losev, I., Finite W'-algebras. Proceedings of the International Congress of Mathematicians Volume III, Hindustan Book Agency, New Delhi, 2010, pp. 1281–1307.Google Scholar
[27] Losev, I., Dimensions of irreducible modules over W-algebras and Goldie ranks. arxiv:1209.1083 Google Scholar
[28] Lejczykand, T. Stroppel, C., A graphical description of(Dn,An-i)Kazhdan-Lusztigpolynomails. Glasg. Math. J. 55(2013). http://dx.doi.Org/10.1017/S0017089512000547 http://dx.doi.org/10.1017/S0017089512000547 Google Scholar
[29] Lusztig, G., An induction theorem for Springer's representations. In: Representation theory of algebraic groups and quantum groups, Adv. Stud. Pure Math., 40, Math. Soc. Japan, Tokyo, 2004,pp. 253–259.Google Scholar
[30] Macdonald, I. G., Symmetric functions and Hall polynomials. Oxford Mathematical Monographs,Oxford Science Publications, The Clarendon Press, Oxford University Press, New York, 1995.Google Scholar
[31] McGovern, W. M., On the Spaltenstein-Steinberg map for classical Lie algebras. Comm. Algebra 27(1999), no. 6, 2979–2993. http://dx.doi.org/10.1080/00927879908826605 http://dx.doi.org/10.1080/00927879908826605 Google Scholar
[32] Naruse, H., Representation theory of Weyl group of type Cn. Tokyo J. Math. 8(1985), 177–190. http://dx.doi.Org/10.3836/tjm/1270151578 Google Scholar
[33] Naruse, H., On an isomorphism between Specht module and left cell ofSn. Tokyo J. Math. 12(1989), 247–267. http://dx.doi.org/10.3836/tjm/1270133181 http://dx.doi.org/10.3836/tjm/1270133181 Google Scholar
[34] Pietraho, T., Components of the Springer fiber and domino tableaux. J. Algebra 272(2004), 711–729. http://dx.doi.Org/10.1016/SOO21-8693(03)00434-4 http://dx.doi.Org/10.1016/SOO21-8693(03)00434-4 Google Scholar
[35] Pietraho, T., A relation for domino Robinson-Schensted algorithms. Ann. Comb. 13(2010), 519–532. http://dx.doi.org/10.1007/s00026-009-0034-9 http://dx.doi.org/10.1007/s00026-009-0034-9 Google Scholar
[36] Premet, A., Special transverse slices and their enveloping algebras. Adv. Math. 170(2002), 1–55. http://dx.doi.Org/10.1OO6/aima.2OO1.2063 http://dx.doi.Org/10.1OO6/aima.2OO1.2063 Google Scholar
[37] Rouquier, R., q-Schur algebras and complex reflection groups. Mosc. Math. J. 8(2008), no. 1, 119–158. Google Scholar
[38] Russell, H. M. and Tymoczko, J. S., Springer representations on the Khovanov Springer varieties. Math. Proc. Cambridge Philos. Soc. 151(2011), no. 1, 59-81. http://dx.doi.Org/10.1017/S0305004111000132 http://dx.doi.Org/10.1017/S0305004111000132 Google Scholar
[39] Russell, H. M., A topological construction for all two-row Springer varieties. Pacific J. Math. 253 (2011), no. 1, 221–255. http://dx.doi.org/10.2140/pjm.2011.253.221 http://dx.doi.org/10.2140/pjm.2011.253.221 Google Scholar
[40] Schâfer, G., A graphical calculus for 2-block Spaltenstein varieties. GMJ 54(2012), no. 2, 449–477. http://dx.doi.Org/10.1017/S0017089512000110 http://dx.doi.Org/10.1017/S0017089512000110 Google Scholar
[41] Serre, J.-P., Linear representations of finite groups. Graduate Texts in Mathematics, 42, Springer-Verlag, New York, 1977.Google Scholar
[42] Slodowy, P., Platonic solids, Kleinian singularities, and Lie groups. In: Algebraic geometry (Ann Arbor, Mich., 1981), Lecture Notes in Math., 1008, Springer, Berlin, 1983 pp. 102–138. http://dx.doi.org/10.1007/BFb0065703 Google Scholar
[43] Spaltenstein, N., The fixed point set of a unipotent transformation on the flag manifold. Nederl.Akad. Wetensch. Proc. Ser. A 79 Indag. Math. 38(1976), no. 5, 452–456. http://dx.doi.Org/10.1016/S1385-7258(76)80008-X Google Scholar
[44] Spaltenstein, N., On the fixed point set of a unipotent element on the variety ofBorel subgroups. Topology 16(1977), no. 2, 203–204. http://dx.doi.Org/10.1016/0040-9383(77)90022-2 Google Scholar
[45] Spaltenstein, N., Classes unipotentes et sous-groupes de Borel. Lecture Notes in Mathematics, 946, Springer-Verlag, Berlin, 1982.Google Scholar
[46] Springer, T. A. and Steinberg, R., Conjugacy classes. Lecture Notes in Mathematics, 131, Springer, Berlin, 1970, pp. 167–266.Google Scholar
[47] Stanley, R. P., Enumerative combinatorics. Vol. 2. Cambridge Studies in Advanced Mathematics, 62, Cambridge University Press, Cambridge, 1999. http://dx.doi.Org/10.1017/CBO9780511609589 Google Scholar
[48] Stroppel, C., Category O: quivers and endomorphism rings of projectives. Represent. Theory 7(2003), 322–345. http://dx.doi.Org/10.1090/S1088-4165-03-00152-3 http://dx.doi.Org/10.1090/S1088-4165-03-00152-3 Google Scholar
[49] Stroppel, C., Parabolic category O, perverse sheaves on Grassmannians, Springer fibres and Khovanov homology. Compos. Math. 145(2009), no. 4, 954–992. http://dx.doi.Org/10.1112/S0010437X09004035 http://dx.doi.Org/10.1112/S0010437X09004035 Google Scholar
[50] Stanton, D. W. and White, D. E., A Schensted algorithm for rim hook tableaux. J. Combin. Theory Ser. A 40(1985), no. 2, 211–247.http://dx.doi.Org/10.1016/0097-3165(85)90088-3 http://dx.doi.Org/10.1016/0097-3165(85)90088-3 Google Scholar
[51] Stroppel, C. and Webster, B.,2-block Springer fibers: convolution algebras and coherent sheaves. Comment. Math. Helv. 87(2012), no. 2, 477–520. http://dx.doi.Org/10.4171/CMH/261 http://dx.doi.Org/10.4171/CMH/261 Google Scholar
[52] Vargas, J. A., Fixed points under the action of unipotent elements of SLn in the flag variety. Bol. Soc. Mat. Mexicana (2) 24(1979), no. (1), 1–14.Google Scholar
[53] van Leeuwen, M., A Robinson-Schensted algorithm in the geometry of flags for classical groups. PhD thesis, Rijksuniversiteit Utrecht, 1989.Google Scholar
[54] Williamson, J., The conjunctive equivalence of pencils ofHermitian and anti-Hermitian matrices. Amer. J. Math. 59(1937), no. 2, 399–413. http://dx.doi.Org/10.2307/2371425 http://dx.doi.org/10.2307/2371425 Google Scholar