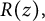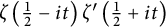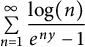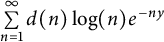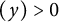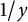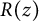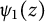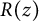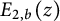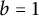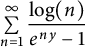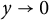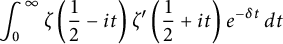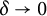1 Introduction
Eisenstein series are the building blocks of modular forms and thus lie at the heart of the theory. In the case of the full modular group
$\text {SL}_{2}\left (\mathbb {Z}\right )$
, the Eisenstein series of even integral weight
$k\geq 2$
are given by
$$ \begin{align} E_k(z):=1-\frac{2k}{B_k}\sum_{n=1}^{\infty}\frac{n^{k-1}q^n}{1-q^n}, \end{align} $$
where
$q=e^{2\pi iz}$
with
$z\in \mathbb {H}$
(the upper-half plane) and
$B_k$
are the Bernoulli numbers. They satisfy the modular transformations
$$ \begin{align} E_k(z+1)&=E_k(z)\hspace{5mm}(k\geq 2),\nonumber\\ E_{k}\left(\frac{-1}{z}\right)&=z^kE_{k}(z)\hspace{2mm}(k>2), \hspace{5mm} E_{2}\left(\frac{-1}{z}\right)=z^2E_{2}(z)+\frac{6z}{\pi i}. \end{align} $$
The series on the right-hand side of (1.1) is an example of what is known as a Lambert series whose general form is
$$ \begin{align} \sum_{n=1}^{\infty}\frac{a(n)q^{n}}{1-q^n}=\sum_{n=1}^{\infty}\frac{a(n)}{e^{ny}-1}=\sum_{n=1}^{\infty}(1*a)(n)e^{-ny}, \end{align} $$
where
$q=e^{-y}$
with Re
$(y)>0$
, and
$a(n)$
is an arithmetic function with
$(1*a)(n)=\sum _{d|n}a(d)$
as the Dirichlet convolution.
For Re
$(s)>1$
, the Riemann zeta function is defined by
$\zeta (s)=\sum _{n=1}^{\infty }n^{-s}$
. Ramanujan [Reference Berndt9, pp. 275–276], [Reference Ramanujan52, pp. 319–320, Formula (28)], [Reference Ramanujan53, p. 173, Chapter 14, Entry 21(i)] derived a beautiful transformation involving the Lambert series associated with
$a(n)=n^{-2m-1}, m\in \mathbb {Z}\backslash \{0\}$
, and the odd zeta value
$\zeta (2m+1)$
, namely, for Re
$(\alpha ), \text {Re}(\beta )>0$
with
$\alpha \beta =\pi ^2$
,
$$ \begin{align} \alpha^{-m}\left\{\frac{1}{2}\zeta(2m+1)+\sum_{n=1}^{\infty}\frac{n^{-2m-1}}{e^{2\alpha n}-1}\right\}&=(-\beta)^{-m}\left\{\frac{1}{2}\zeta(2m+1)+\sum_{n=1}^{\infty}\frac{n^{-2m-1}}{e^{2\beta n}-1}\right\}\nonumber\\ &\quad-2^{2m}\sum_{j=0}^{m+1}\frac{(-1)^jB_{2j}B_{2m+2-2j}}{(2j)!(2m+2-2j)!}\alpha^{m+1-j}\beta^j. \end{align} $$
Along with the transformations of the Eisenstein series in (1.2), this formula also encapsulates the transformations of the corresponding Eichler integrals of the Eisenstein series as well as the transformation property of the Dedekind eta-function. The literature on this topic is vast with many generalizations and analogs for other L-functions, for example, [Reference Banerjee and Kumar4, Reference Berndt6, Reference Berndt7, Reference Bradley12, Reference Dixit and Gupta20–Reference Dixit and Maji24, Reference Gupta and Maji32, Reference Kanemitsu, Tanigawa, Yoshimoto, Kanemitsu and Jia41, Reference Katayama42, Reference Komori, Matsumoto and Tsumura44]. See also the recent survey article [Reference Berndt, Straub, Montgomery, Nikeghbali and Rassias10].
Recently, Kesarwani, Kumar, and the second author [Reference Dixit, Kesarwani and Kumar23, Theorem 2.4] obtained a new generalization of (1.4), namely, for
$\text {Re}(y)>0$
and any complex a such that
$\text {Re}(a)>-1$
,
$$ \begin{align} &\sum_{n=1}^\infty \sigma_a(n)e^{-ny}+\frac{1}{2}\left(\left(\frac{2\pi}{y}\right)^{1+a}\mathrm{cosec}\left(\frac{\pi a}{2}\right)+1\right)\zeta(-a)-\frac{1}{y}\zeta(1-a)\nonumber\\ &=\frac{2\pi}{y\sin\left(\frac{\pi a}{2}\right)}\sum_{n=1}^\infty \sigma_{a}(n)\Bigg(\frac{(2\pi n)^{-a}}{\Gamma(1-a)} {}_1F_2\left(1;\frac{1-a}{2},1-\frac{a}{2};\frac{4\pi^4n^2}{y^2} \right) -\left(\frac{2\pi}{y}\right)^{a}\cosh\left(\frac{4\pi^2n}{y}\right)\Bigg), \end{align} $$
where
${}_1F_{2}(a;b, c;z)$
is the generalized hypergeometric function
$$ \begin{align*} {}_1F_2(a;b, c; z):=\sum_{n=0}^{\infty}\frac{(a)_n}{(b)_n(c)_n}\frac{z^n}{n!}, \end{align*} $$
where
$z\in \mathbb {C}$
and
$(a)_n=a(a+1)\ldots (a+n-1)$
. They [Reference Dixit, Kesarwani and Kumar23, Theorem 2.5] also analytically continued this result to Re
$(a)>-2m-3$
,
$m\in \mathbb {N}\cup \{0\}$
, and in this way, they were able to get as corollaries not only Ramanujan’s formula (1.4) and the transformation formula for the Dedekind eta-function but also new transformations when a is an even integer. Moreover, they showed [Reference Dixit, Kesarwani and Kumar23, Equation (2.19)] that letting
$a\to 0$
in (1.5) gives the following transformation of Wigert [Reference Wigert63, p. 203, Equation (A)]:
$$ \begin{align} \sum_{n=1}^{\infty}\frac{1}{e^{ny}-1}=\frac{1}{4}+\frac{\gamma-\log(y)}{y}+\frac{2}{y}\sum_{n=1}^{\infty}\left\{\log\left(\frac{2\pi n}{y}\right)-\frac{1}{2}\left(\psi\left(\frac{2\pi in}{y}\right)+\psi\left(-\frac{2\pi in}{y}\right)\right)\right\}, \end{align} $$
where
$\psi (z):=\Gamma '(z)/\Gamma (z)$
is the logarithmic derivative of the gamma function commonly known as the digamma function. Wigert [Reference Wigert63, p. 203] called this transformation “la formule importante” (an important formula). Indeed, it is important, for, if we let
$y\to 0$
in any angle
$|\arg (y)|\leq \lambda $
, where
$\lambda <\pi /2$
, it gives the complete asymptotic expansion upon using (3.13), that is,
$$ \begin{align} \sum_{n=1}^{\infty} d(n)e^{-ny}\sim\frac{1}{4}+\frac{(\gamma-\log (y))}{y}-\sum_{n=1}^{\infty}\frac{B_{2n}^2y^{2n-1}}{(2n)(2n)!}, \end{align} $$
where
$\gamma $
is Euler’s constant, which, in turn, readily implies [Reference Titchmarsh59, p. 163, Theorem 7.15]
$$ \begin{align} \sum_{n=1}^{\infty} d(n)e^{-ny}=\frac{1}{4}+\frac{\gamma-\log y}{y}-\sum_{n=0}^{N-1}\frac{B_{2n+2}^2}{(2n+2)(2n+2)!} y^{2n+1}+O(|y|^{2N}). \end{align} $$
The study of the moments
$$ \begin{align} M_{k}(T):=\int_{0}^{T}\left|\zeta\left(\frac{1}{2}+it\right)\right|{}^{2k}\, dt \end{align} $$
is of fundamental importance in the theory of the Riemann zeta function. It is conjectured that
$M_{k}(T)\sim C_k T\log ^{k^2}(T)$
as
$T\to \infty $
for positive constants
$C_k$
although for
$k=1$
and
$2$
, this has been proved by Hardy and Littlewood [Reference Hardy and Littlewood33] and Ingham [Reference Ingham35], respectively. Such results are known as mean value theorems for the zeta function. The importance of the study of moments lies, for example, in the fact that the estimate
$M_k(T)=O_{k,\epsilon }(T^{1+\epsilon })$
for every natural number k is equivalent to the Lindelöf hypothesis [Reference Soundararajan57] (see also [Reference Hardy and Littlewood34]).
Another set of mean value theorems which plays an important role in the theory is the one concerning the asymptotic behavior of the smoothly weighted moments, namely,
$$ \begin{align} \int_{0}^{\infty}\left|\zeta\left(\frac{1}{2}+it\right)\right|{}^{2k}e^{-\delta t}\, dt \end{align} $$
as
$\delta \to 0$
. The relation between the two types of moments in (1.9) and (1.10) is given by a result [Reference Titchmarsh59, p. 159] which states that if
$f(t)\geq 0$
for all t and for a given positive m,
$$ \begin{align*} \int_{0}^{\infty}f(t)e^{-\delta t}\, dt\sim\frac{1}{\delta}\log^{m}\left(\frac{1}{\delta}\right) \end{align*} $$
as
$\delta \to 0$
, then
$$ \begin{align*} \int_{0}^{T}f(t)\, dt\sim T\log^{m}(T) \end{align*} $$
as
$T\to \infty $
. For an excellent survey on the moments, we refer the reader to [Reference Ivić38].
The asymptotic expansion of
$\sum _{n=1}^{\infty } d(n)e^{-ny}$
as
$y\to 0$
in (1.8) allows us to obtain the asymptotic estimate for the smoothly weighted second moment, namely, as
$\delta \to 0$
, for every natural number N, we have [Reference Titchmarsh59, p. 164, Theorem 7.15(A)]
$$ \begin{align} \int_{0}^{\infty}\left|\zeta\left(\frac{1}{2}+it\right)\right|{}^{2}e^{-\delta t}\, dt=\frac{\gamma-\log(2\pi\delta)}{2\sin(\delta/2)}+\sum_{n=0}^{N}c_n\delta^n+O(\delta^{N+1}), \end{align} $$
where the
$c_n$
are constants and the constant implied by the big-O depends on N. A simple proof of (1.11) was given by Atkinson [Reference Atkinson3]. In fact, (1.7) gives the complete asymptotic expansion for this moment.
The primary goal of this paper is to give a nontrivial application of (1.5). Note that the complex variable a in (1.5) enables differentiation of (1.5) with respect to a, which is not possible in (1.4) or other such known results. Indeed, it is an easy affair to check that differentiating the series on the left-hand side of (1.5) with respect to a and then letting
$a=0$
gives
$\sum \limits _{n=1}^{\infty }\displaystyle \frac {\log (n)}{e^{ny}-1}$
, which, in view of (1.3), satisfies
$$ \begin{align*} \sum_{n=1}^{\infty}\frac{\log(n) }{e^{ny}-1} =\sum_{n=1}^{\infty}\log\big(\prod_{d|n}d\big)e^{-ny} =\frac{1}{2}\sum_{n=1}^{\infty}d(n)\log(n)e^{-ny}. \end{align*} $$
Here, in the last step, we used an elementary result
$\prod _{d|n}d=n^{d(n)/2}$
(see, for example, [Reference Apostol2, Exercise 10, p. 47]).
What is surprising though is, differentiating the right-hand side of (1.5) with respect to a and then letting
$a=0$
leads to an explicit and interesting series involving a well-known special function. This special function deserves a separate mention and hence after its brief introduction here, the literature on it is discussed in detail in Section 3.
In a beautiful paper [Reference Deninger17], Deninger comprehensively studied the function
$R:\mathbb {R}^{+}\to \mathbb {R}$
uniquely defined by the difference equation
$$ \begin{align*} R(x+1)-R(x)=\log^{2}(x)\hspace{8mm}(R(1)=-\zeta"(0)), \end{align*} $$
and with the requirement that R be convex in some interval
$(A, \infty ), A>0$
.
The function
$R(x)$
is an analog of
$\log (\Gamma (x))$
in view of the fact that the latter satisfies the difference equation
$f(x+1)-f(x)=\log (x)$
with the initial condition
$f(1)=0$
. As noted in [Reference Deninger17, Remark 2.4], R can be analytically continued to
$$ \begin{align*} \mathbb{D}:=\mathbb{C}\backslash\{x\in\mathbb{R}|\ x\leq0\}. \end{align*} $$
The special function which appears in our main theorem, that is, in Theorem 1.1, is
$\psi _1(z)$
, which is essentially the derivative of Deninger’s function
$R(z)$
(see (3.5)). For
$z\in \mathbb {D}$
, it is given by
$$ \begin{align} \psi_1(z)=-\gamma_1-\frac{\log(z)}{z}-\sum_{n=1}^{\infty}\left(\frac{\log(n+z)}{n+z}-\frac{\log(n)}{n}\right), \end{align} $$
where
$\gamma _1$
is the first Stieltjes constant.
We are now ready to state the main result of our paper which transforms the Lambert series of logarithm into an infinite series consisting of
$\psi _1(z)$
.
Theorem 1.1 Let
$\psi _1(z)$
be given in (1.12). Then, for
$\text {Re}(y)>0$
,
$$ \begin{align} \sum_{n=1}^{\infty}\frac{\log(n) }{e^{ny}-1}&=-\frac{1}{4}\log(2\pi)+\frac{1}{2y}\log^{2}(y)-\frac{\gamma^2}{2y}+\frac{\pi^2}{12y}\nonumber\\ &\quad-\frac{2}{y}(\gamma+\log(y))\sum_{n=1}^{\infty}\left\{\log\left(\frac{2\pi n}{y}\right)-\frac{1}{2}\left(\psi\left(\frac{2\pi in}{y}\right)+\psi\left(-\frac{2\pi in}{y}\right)\right)\right\}\nonumber\\ &\quad+\frac{1}{y}\sum_{n=1}^{\infty}\left\{\psi_1\left(\frac{2\pi in}{y}\right)+\psi_1\left(-\frac{2\pi in}{y}\right)-\frac{1}{2}\left(\log^{2}\left(\frac{2\pi in}{y}\right)+\log^{2}\left(-\frac{2\pi in}{y}\right)\right)+\frac{y}{4n}\right\}. \end{align} $$
Equivalently,
$$ \begin{align} &y\sum_{n=1}^{\infty}\frac{\gamma+\log(ny) }{e^{ny}-1}-\frac{1}{4}y\log(y)+y\left(\frac{1}{4}\log(2\pi)-\frac{\gamma}{4}\right)+\frac{1}{2}\log^2 (y)-\frac{\gamma^2}{2}-\frac{\pi^2}{12}\nonumber\\ &=\sum_{n=1}^{\infty}\left\{\psi_1\left(\frac{2\pi in}{y}\right)+\psi_1\left(-\frac{2\pi in}{y}\right)-\frac{1}{2}\left(\log^{2}\left(\frac{2\pi in}{y}\right)+\log^{2}\left(-\frac{2\pi in}{y}\right)\right)+\frac{y}{4n}\right\}. \end{align} $$
Remark 1.1 That the series
$$ \begin{align*} \sum_{n=1}^{\infty}\left\{\psi_1\left(\frac{2\pi in}{y}\right)+\psi_1\left(-\frac{2\pi in}{y}\right)-\frac{1}{2}\left(\log^{2}\left(\frac{2\pi in}{y}\right)+\log^{2}\left(-\frac{2\pi in}{y}\right)\right)+\frac{y}{4n}\right\} \end{align*} $$
converges absolutely is clear from (5.13).
The exact transformation in (1.13) is an analog of Wigert’s result (1.6). This is evident from the fact that
$$ \begin{align*} \log\left(\tfrac{2\pi n}{y}\right)-\tfrac{1}{2}\left(\psi\left(\tfrac{2\pi in}{y}\right)+\psi\left(-\tfrac{2\pi in}{y}\right)\right)=-\tfrac{1}{2}\left\{\psi\left(\tfrac{2\pi in}{y}\right)+\psi\left(-\tfrac{2\pi in}{y}\right)-\left(\log\left(\tfrac{2\pi i n}{y}\right)+\log\left(\tfrac{-2\pi i n}{y}\right)\right)\right\}, \end{align*} $$
which should be compared with the summand of the second series on the right-hand side of (1.13).
Thus, (1.13) allows us to transform
$\sum _{n=1}^{\infty }d(n)\log (n)e^{-ny}$
into series having a constant times
$1/y$
in the arguments of the functions in their summands. This “modular” behavior has an instant application: it gives the complete asymptotic expansion of
$\sum _{n=1}^{\infty }d(n)\log (n)e^{-ny}$
as
$y\to 0$
, which is given in the following result.
Theorem 1.2 Let A denote the Glaisher–Kinkelin constant defined by [Reference Glaisher27, Reference Glaisher28, Reference Kinkelin43] and [Reference Voros61, p. 461, Equation (A.7)]
$$ \begin{align*} \log(A):=\lim_{n\to\infty}\left\{\sum_{k=1}^{n}k\log(k)-\left(\frac{n^2}{2}+\frac{n}{2}+\frac{1}{12}\right)\log(n)+\frac{n^2}{4}\right\}. \end{align*} $$
As
$y\to 0$
in
$|\arg (y)|<\pi /2$
,
$$ \begin{align} \sum_{n=1}^{\infty}\frac{\log(n) }{e^{ny}-1}&\sim\frac{1}{2y}\log^{2}(y) + \frac{1}{y}\left(\frac{\pi^2}{12} - \frac{\gamma^2}{2} \right)-\frac{1}{4}\log(2\pi) +\frac{y}{12}\left(\log A - \frac{1}{12} \right) \nonumber\\ &\quad +\sum_{k=2}^{\infty} \frac{B_{2k} y^{2k-1}}{k}\left\{\frac{B_{2k}}{2(2k)!}\left(\gamma - \sum_{j=1}^{2k-1}\frac{1}{j}+\log (2\pi)\right)+ \frac{(-1)^k \zeta'(2k)}{(2\pi)^{2k}}\right\}. \end{align} $$
As seen earlier, Wigert’s result (1.8) is useful in getting the asymptotic estimate for the smoothly weighted second moment of the zeta function on the critical line given in (1.11). It is now natural to ask whether our result in Theorem 1.2 has an application in the theory of moments. Indeed, (1.15) implies the following result.
Theorem 1.3 As
$\delta \to 0, |\arg (\delta )|<\pi /2$
,
$$ \begin{align} \int_{0}^{\infty}\zeta\left(\frac{1}{2}-it\right)\zeta'\left(\frac{1}{2}+it\right)e^{-\delta t}\, dt &=-{1\over 4\sin\left({\delta}\over 2\right)}\left( \log^{2}(2\pi{\delta})+ {\pi^2\over 6}-{\gamma^2 }\right) +\sum_{k=0}^{2m-2}(d_k+d_k'\log(\delta))\delta^k\nonumber\\ &\quad+O\left(\delta^{2m-1}\log(\delta)\right), \end{align} $$
where
$d_k$
and
$d_k'$
are effectively computable constants and the constant implied by the big-O depends on m.
In fact, one can obtain the complete asymptotic expansion of the left-hand side of (1.16) using (1.15).
Mean value theorems involving the derivatives of the Riemann zeta function have been well-studied. For example, Ingham [Reference Ingham35] (see also Gonek [Reference Gonek29, Equation (2)]Footnote 1 ) showed that
$$ \begin{align*} \int_{0}^{T}\zeta^{(\mu)}\left(\frac{1}{2}+it\right)\zeta^{(\nu)}\left(\frac{1}{2}-it\right)\, dt\sim\frac{(-1)^{\mu+\nu}\hspace{1mm}T}{\mu+\nu+1}\log^{\mu+\nu+1}(T) \end{align*} $$
as
$T\to \infty $
, where
$\mu , \nu \in \mathbb {N}\cup \{0\}$
(see also [Reference Turnage-Butterbaugh60, p. 102]). In particular, for
$\mu =1$
and
$\nu =0$
, we have
$$ \begin{align*} \int_{0}^{T}\zeta\left(\frac{1}{2}-it\right)\zeta'\left(\frac{1}{2}+it\right)\, dt\sim \frac{-T}{2}\log^{2}(T) \end{align*} $$
as
$T\to \infty $
.
The proof of Theorem 1.1 is quite involved and first requires establishing several new results that may seem quite unexpected at first glance. These results are important in themselves and may have applications in other areas. Hence, this paper is organized as follows.
We collect frequently used results in the next section. In Section 3, we first prove Theorem 3.2 which gives an asymptotic expansion of
$\psi _1(z)$
followed by Theorem 3.3, a Kloosterman-type result for
$\psi _1(z)$
. Theorem 3.4 is the highlight of this section and is an analog of (2.2) established in [Reference Dixit, Gupta, Kumar and Maji22, Theorem 2.2]. Section 4 is devoted to obtaining a new representation for the second derivative of the two-variable Mittag-Leffler function
$E_{2, b}(z)$
at
$b=1$
. In Section 5, we prove our main results, that is, Theorems 1.1–1.3. Finally, we conclude the paper with some remarks and directions for future research.
2 Preliminaries
Stirling’s formula in a vertical strip
$\alpha \leq \sigma \leq \beta $
,
$s=\sigma +it$
states that [Reference Copson16, p. 224]
$$ \begin{align} |\Gamma(s)|=(2\pi)^{\tfrac{1}{2}}|t|^{\sigma-\tfrac{1}{2}}e^{-\tfrac{1}{2}\pi |t|}\left(1+O\left(\frac{1}{|t|}\right)\right) \end{align} $$
uniformly as
$|t|\to \infty $
.
We will also need the following result established in [Reference Dixit, Gupta, Kumar and Maji22, Theorem 2.2] which is valid for
$\text {Re}(w)>0$
:
$$ \begin{align} \sum_{n=1}^\infty\int_0^\infty\frac{t\cos(t)}{t^2+n^2w^2}\ dt=\frac{1}{2}\left\{\log\left(\frac{w}{2\pi}\right)-\frac{1}{2}\left(\psi\left(\frac{iw}{2\pi}\right)+\psi\left(-\frac{iw}{2\pi}\right)\right)\right\}. \end{align} $$
Watson’s lemma is a very useful result in the asymptotic theory of Laplace integrals
$\displaystyle \int _{0}^{\infty }e^{-zt}f(t)\, dt$
. This result typically holds for
$|\arg (z)|<\pi /2$
. However, with additional restrictions on f, Watson’s lemma is known to hold for extended sectors. For the sake of completeness, we include it here in the form given in [Reference Temme58, p. 14, Theorem 2.2].
Theorem 2.1 Let f be analytic inside a sector
$D: \alpha <\arg (t)<\beta $
, where
$\alpha <0$
and
$\beta>0$
. For each
$\delta \in \left (0, \frac {1}{2}\beta -\frac {1}{2}\alpha \right )$
, as
$t\to 0$
in the sector
$D_{\delta }: \alpha +\delta <\arg (t)<\beta -\delta $
, we have
$$ \begin{align*} f(t)\sim t^{\lambda-1}\sum_{n=0}^{\infty}a_nt^n, \end{align*} $$
where
$\text {Re}(\lambda )>0$
. Suppose there exists a real number
$\sigma $
such that
$f(t)=O\left (e^{\sigma |t|}\right )$
as
$t\to \infty $
in
$D_{\delta }$
. Then the integral
$$ \begin{align} F_{\lambda}(z):=\int_{0}^{\infty}e^{-zt}f(t)\, dt \end{align} $$
or its analytic continuation, has the asymptotic expansion
$$ \begin{align*} F_{\lambda}(z)\sim\sum_{n=0}^{\infty}a_n\frac{\Gamma(n+\lambda)}{z^{n+\lambda}} \end{align*} $$
as
$|z|\to \infty $
in the sector
$$ \begin{align*} -\beta-\frac{\pi}{2}+\delta<\arg(z)<-\alpha+\frac{\pi}{2}-\delta. \end{align*} $$
The many-valued functions
$t^{\lambda -1}$
and
$z^{n+\lambda }$
have their principal values on the positive real axis and are defined by continuity elsewhere.
Actually, we will be using an analog of the above theorem where the integrand in (2.3) has a logarithmic factor.
We next give Dirichlet’s test for uniform convergence of definite integrals [Reference Rogers55, p. 261] which will be used in the course of proving Theorem 4.4.
Theorem 2.2 If
$g(x, y)$
is continuous on
$\{(x, y)|c\leq x, m\leq y\leq n\}$
and
$|\int _{c}^{X}g(x, y)\, dx|<K$
for all
$X\geq c$
and all y on
$[m, n]$
, if
$f(x, y)$
is a decreasing function of x for
$x\geq c$
and each fixed y on
$[m, n]$
, and if
$f(x, y)$
tends to zero uniformly in y as
$x\to \infty $
, then
$\int _{c}^{\infty }f(x, y)g(x, y)\, dx$
converges uniformly on
$m\leq y\leq n$
.
Another result which will be needed in the sequel is the following [Reference Rogers55, p. 260].
Theorem 2.3 Let
$\frac {\partial }{\partial y}h(x, y)$
and
$h(x, y)$
are continuous on
$[c, \infty )\times [m, n]$
, if
$\int _{c}^{\infty }h(x, y)\, dx$
converges for at least one
$y_0$
in
$[m, n]$
, and if
$\int _{c}^{\infty }\frac {\partial }{\partial y}h(x, y)\, dx$
converges uniformly on
$[m, n]$
, then
$\int _{c}^{\infty }h(x, y)\, dx$
converges uniformly on
$[m, n]$
, and
$$ \begin{align} \frac{d}{dy}\int_{c}^{\infty}h(x, y)\, dx=\int_{c}^{\infty}\frac{\partial}{\partial y}h(x, y)\, dx. \end{align} $$
We will also be using Parseval’s theorem given next. Let
$\mathfrak {F}(s)=M[f;s]$
and
$\mathfrak {G}(s)=M[g;s]$
denote the Mellin transforms of functions
$f(x)$
and
$g(x),$
respectively, and let
$c=\text {Re}(s)$
. If
$M[f;1-c-it]\in L(-\infty , \infty )$
and
$x^{c-1}g(x)\in L[0,\infty )$
, then Parseval’s formula [Reference Paris and Kaminski49, p. 83] is given by
$$ \begin{align} \int_{0}^{\infty} f(x) g(x) dx = \frac{1}{2 \pi i } \int_{(c)}\mathfrak{F}(1-s)\mathfrak{G}(s)\, ds, \end{align} $$
where the vertical line Re
$(s) = c$
lies in the common strip of analyticity of the Mellin transforms
$\mathfrak {F}(1-s)$
and
$\mathfrak {G}(s)$
, and, here and throughout the sequel, we employ the notation
$\int _{(c)}$
to denote the line integral
$\int _{c-i\infty }^{c+i\infty }$
.
3 New results on
$\psi _1(z)$
In [Reference Dilcher19], Dilcher studied in detail, the generalized gamma function
$\Gamma _k(z)$
which relates to the Stieltjes constant
$\gamma _k, k\geq 0$
, defined byFootnote
2
$$ \begin{align} \gamma_k:=\lim_{n\to\infty}\left(\sum_{j=1}^{n}\frac{\log^{k}(j)}{j}-\frac{\log^{k+1}(n)}{k+1}\right), \end{align} $$
in a similar way as the Euler gamma function
$\Gamma (z)$
relates to the Euler constant
$\gamma =\gamma _0$
. Using [Reference Dilcher19, Equation (2.1)] and [Reference Deninger17, Equation (2.3.1)], we see that Dilcher’s
$\Gamma _1(z)$
is related to Deninger’s
$R(z)$
byFootnote
3
$$ \begin{align} \log(\Gamma_1(z))=\frac{1}{2}(R(z)+\zeta"(0)). \end{align} $$
As mentioned by Deninger in [Reference Deninger17, Remark 2.4], contrary to Euler’s
$\Gamma $
, the function
$\exp (R(x))$
, or equivalently
$\Gamma _1(x)$
, where
$x>0,$
cannot be meromorphically continued to the whole complex plane. But
$\Gamma _1(z)$
is analytic in
$z\in \mathbb {D}$
. It is this
$\exp (R(x))$
that Languasco and Righi [Reference Languasco and Righi45] call as the Ramanujan–Deninger gamma function. They have also given a fast algorithm to compute it.
Dilcher also defined the generalized digamma function
$\psi _k(z)$
as the logarithmic derivative of
$\Gamma _k(z)$
. His Proposition 10 from [Reference Dilcher19] implies that for
$z\in \mathbb {D}$
,
$$ \begin{align} \psi_k(z)=-\gamma_k-\frac{\log^{k}(z)}{z}-\sum_{n=1}^{\infty}\left(\frac{\log^{k}(n+z)}{n+z}-\frac{\log^{k}(n)}{n}\right), \end{align} $$
where
$k\in \mathbb {N}\cup \{0\}$
. Its special case
$k=1$
has already been given in (1.12). The function
$\psi _k(z)$
occurs in Entry 22 of Chapter 8 in Ramanujan’s second notebook, see [Reference Berndt8]. It is also used by Ishibashi [Reference Ishibashi36] to construct the kth order Herglotz function which, in turn, plays an important role in his evaluation of the Laurent series coefficients of a zeta function associated with an indefinite quadratic form. As noted by Ishibashi and Kanemitsu [Reference Ishibashi and Kanemitsu37, p. 78],
$$ \begin{align*} \psi_k(z)=\frac{1}{k+1}R_{k+1}'(z), \end{align*} $$
where
$R_k(z)$
is defined by [Reference Deninger17, p. 173]
$$ \begin{align} R_k(z)=(-1)^{k+1}\left(\frac{\partial^{k}}{\partial s^k}\zeta(0, z)-\zeta^{(k)}(0)\right), \end{align} $$
and
$R_2(z)=R(z)$
of Deninger. Thus,
$$ \begin{align} \psi_1(z)=\frac{1}{2}R'(z), \end{align} $$
which is also implied by (3.2). The function
$\psi _k(z)$
is related to the Laurent series coefficients
$\gamma _k(z)$
of the Hurwitz zeta function
$\zeta (s, z)$
known as the generalized Stieltjes constants. To see this, from [Reference Berndt5, Theorem 1], note that if
$$ \begin{align} \zeta(s, z)=\frac{1}{s-1}+\sum_{k=0}^{\infty}\frac{(-1)^k\gamma_k(z)}{k!}(s-1)^k, \end{align} $$
thenFootnote 4
$$ \begin{align} \gamma_k(z)=\lim_{n\to\infty}\left(\sum_{j=0}^{n}\frac{\log^{k}(j+z)}{j+z}-\frac{\log^{k+1}(n+z)}{k+1}\right) \end{align} $$
so that
$\gamma _k(1)=\gamma _k$
. Then from (3.1), (3.3), (3.7) and the fact [Reference Dilcher19, Lemma 1] that
$$ \begin{align*} \lim_{n\to\infty}\left(\log^{k+1}(n+z)-\log^{k+1}(n)\right)=0 \hspace{6mm} (z\in\mathbb{D}), \end{align*} $$
it is not difficult to see that
$$ \begin{align} \psi_k(z)=-\gamma_k(z), \end{align} $$
which was also shown by Shirasaka [Reference Shirasaka56, p. 136]. Further properties and applications of
$\psi _k(z)$
are derived in [Reference Dilcher18].
We thus see that the literature on
$R(z)$
, that is,
$R_2(z)$
, and, in general, on
$R_k(z)$
, is growing fast. In the words of Ishibashi [Reference Ishibashi36, p. 61], “Deninger proved several analytic properties of
$R_2(x)$
in order to familiarize and assimilate it as one of the most commonly used number-theoretic special functions,….” Languasco and Righi [Reference Languasco and Righi45] have also given a fast algorithm to compute
$\psi _1(x), x>0$
. The papers of Berndt [Reference Berndt5], Blagouchine [Reference Blagouchine11], Coffey [Reference Coffey15], Chatterjee and Khurana [Reference Chatterjee and Khurana14] (and also the references therein) on the generalized Stieltjes constants, which, in view of (3.8), are nothing but
$-\psi _k(z)$
, are also vast sources of information on them. However, none of the studies prior to our current work is devoted to applications of these constants in obtaining a “modular” transformation for the Lambert series of logarithm and its application in the theory of the moments of the Riemann zeta function given in Theorems 1.1 and 1.3, respectively.
Our first result of this section gives the asymptotic expansion of
$\psi _1(z)$
for
$z\in \mathbb {D}$
. To accomplish it, we require a generalization of Watson’s lemma which allows for a logarithmic factor in the integrand. Such an expansion seems to have been first obtained by Jones [Reference Jones40, p. 439] (see also [Reference Wong and Wyman65, Equations (4.14) and (4.15)]). Though we will be using the same expansion, it is useful to rigorously derive it as a special case of a more general result due to Wong and Wyman [Reference Wong and Wyman65, Theorem 4.1] given in the following theorem. We note in passing that Riekstins [Reference Riekstins54] has also obtained asymptotic expansions of integrals involving logarithmic factors.
Theorem 3.1 For
$\gamma \in \mathbb {R}$
, define a function
$$ \begin{align*} F(z):=\int_{0}^{\infty e^{i\gamma}}f(t)e^{-zt}dt. \end{align*} $$
Assume that
$F(z)$
exists for some
$z=z_0$
. If:
-
(1) For each integer
$N\in \mathbb {N}\cup \{0\},$
as
$$ \begin{align*} f(t)=\sum_{n=0}^{N}a_nt^{\lambda_n-1}P_n(\log t)+o(t^{\lambda_N-1}(\log t)^{m(N)}), \end{align*} $$
$t\to 0$
along
$\arg (t)=\gamma $
.
-
(2)
$P_n(\omega )$
is a polynomial of degree
$m=m(n)$
. -
(3)
$\{\lambda _n\}$
is a sequence of complex numbers, with
$\Re (\lambda _{n+1})>\Re ( \lambda _{n}), \Re (\lambda _{0})>0,$
for all n such that n and
$n+1$
are in
$\mathbb {N}\cup \{0\}$
. -
(4)
$\{a_n\}$
is a sequence of complex numbers.
Then as
$z\to \infty $
in
$S(\Delta )$
$$ \begin{align*} F(z)\sim \sum_{n=0}^{N} a_nP_n(D_n)[\Gamma(\lambda_n)z^{-\lambda_n}]+o\left(z^{-\lambda_N}(\log z)^{m(N)}\right), \end{align*} $$
where
$S(\Delta ): |\arg (ze^{i\gamma })|\leqq {\pi \over 2}-\Delta $
, and
$D_n$
is the operator
$D_n:={d\over d\lambda _n}$
. This result is uniform in the approach of
$z\to \infty $
in
$S(\Delta )$
.
Theorem 3.2 Fix any
$\Delta>0$
. Then as
$z\to \infty $
with
$|\arg (z)|\leq \pi -\Delta $
,
$$ \begin{align} \psi_1(z)\sim{1\over 2}\log^2(z)-{1 \over 2z}\log z+\sum_{k=1}^{\infty}{B_{2k}\over 2kz^{2k}} \left(\sum_{j=1}^{2k-2}{1\over j}+{1\over 2k-1}-\log z \right). \end{align} $$
Proof We first prove the result for
$|\arg (z)|<\pi /2$
and then extend it to
$|\arg (z)|\leq \pi -\Delta $
. To that end, we begin with the analog for
$R(z)$
of Plana’s integral for
$\log (\Gamma (z))$
, namely, for
$\text {Re}(z)>0$
, we have [Reference Deninger17, Equation (2.12)]
$$ \begin{align} R(z)=-\zeta"(0)-2\int_{0}^{\infty}\left((z-1)e^{-t}+\frac{e^{-zt}-e^{-t}}{1-e^{-t}}\right)\frac{\gamma+\log(t)}{t}\, dt. \end{align} $$
Differentiating (3.10) under the integral sign with respect to z and using (3.5), we see that
$$ \begin{align} \psi_1(z)&=-\int_{0}^{\infty}\left(e^{-t}-\frac{te^{-zt}}{1-e^{-t}} \right) \frac{(\gamma+\log( t))}{t}dt \nonumber \\ & =-\int_{0}^{\infty}\left(e^{-t}-e^{-zt}\right){(\gamma+\log (t))}{ dt \over t} -\int_{0}^{\infty}e^{-zt}\left({1\over t}-\frac{1}{1-e^{-t}} \right) {(\gamma+\log( t))}dt\nonumber \\ &={1\over 2} \log ^2(z) -\int_{0}^{\infty}e^{-zt}\left({1\over t}-\frac{1}{1-e^{-t}} \right) {(\gamma+\log( t))}dt, \end{align} $$
where we used the fact that for Re
$(z)>0$
,
$$ \begin{align*} \int_{0}^{\infty}(e^{-t}-e^{-zt})(\gamma+\log(t))\frac{dt}{t}=-\frac{1}{2}\log^{2}(z), \end{align*} $$
which follows from [Reference Deninger17, Equation (2.13)]Footnote 5
$$ \begin{align*} \int_{0}^{\infty}(e^{-\beta t}-e^{-\alpha t})(\gamma+\log(t))\frac{dt}{t}=\frac{1}{2}\left(\log^{2}(\beta)-\log^{2}(\alpha)\right). \end{align*} $$
Thus
$$ \begin{align} \psi_1(z)&={1\over 2} \log ^2(z)-\gamma(\psi(z)-\log(z))-\int_{0}^{\infty}e^{-zt}\left({1\over t}-\frac{1}{1-e^{-t}} \right){\log(t)}\, dt, \end{align} $$
where we employed the well-known result [Reference Gradshteyn and Ryzhik31, p. 903, Formula 8.361.8] that for Re
$(z)>0$
,
$$ \begin{align*} \psi(z)=\log(z)+\int_{0}^{\infty}e^{-zt}\left(\frac{1}{t}-\frac{1}{1-e^{-t}}\right)\, dt. \end{align*} $$
We now find the asymptotic expansion of the integral on the right-hand side of (3.12), that is, of
$$ \begin{align*} I:=\int_{0}^{\infty}e^{-zt}f(t)\, dt, \end{align*} $$
where
$$ \begin{align*} f(t):=\left({1\over t}-\frac{1}{1-e^{-t}} \right) \log(t), \end{align*} $$
by applying Theorem 3.1. To that end, observe that for
$|t|<2\pi $
,
$$ \begin{align*} f(t)& = \log(t)\left({1\over t}-\frac{1}{1-e^{-t}} \right) \nonumber \\ &=-{\log(t)\over t} \left(\frac{te^t}{e^{t}-1}-1 \right) \nonumber \\ &=-{\log(t)\over t} \left(\sum_{n=0}^{\infty }{B_n(1)t^n\over n!}-1 \right) \nonumber \\ &={\log(t)} \sum_{n=0}^{\infty }{(-1)^nB_{n+1}t^n\over (n+1)!}, \end{align*} $$
where
$B_n(x)$
are Bernoulli polynomials. Thus, with
$P_n(x)=x$
,
$\lambda _n=n+1$
,
$a_n={(-1)^nB_{n+1}\over (n+1)!}$
,
$n\geq 0$
, all of the hypotheses of Theorem 3.1 are satisfied, and hence
$$ \begin{align*} I&\sim\sum_{n=0}^{\infty}\frac{(-1)^nB_{n+1}}{(n+1)z^{n+1}} \left(\psi(n+1)-\log(z)\right) \nonumber\\ &= \sum_{n=1}^{\infty}{(-1)^{n-1}B_{n}\over nz^{n}} \left(-\gamma+\sum_{k=1}^{n-1}{1\over k}-\log(z) \right) , \end{align*} $$
where we used the elementary fact
$\psi (n)=-\gamma +\sum _{k=1}^{n-1}\frac {1}{k}$
. Inserting this asymptotic expansion of I in (3.12) along with that of
$\psi (z)$
, namely, for
$|\arg z|\leq \pi -\Delta $
, (with
$\Delta>0$
),
$$ \begin{align} \psi(z) &\sim\log(z)-\frac{1}{2z}-\sum_{n=1}^{\infty}\frac{B_{2n}}{2nz^{2n}}, \end{align} $$
as
$z\to \infty $
, we arrive at
$$ \begin{align*} \psi_1(z)&\sim{1\over 2} \log ^2(z)-\gamma\left(-\frac{1}{2z}-\sum_{n=1}^{\infty}\frac{B_{2n}}{2nz^{2n}}\right)+\sum_{n=1}^{\infty}{(-1)^{n}B_{n}\over nz^{n}} \left(-\gamma+\sum_{j=1}^{n-1}{1\over j}-\log(z) \right) \nonumber\\ &={1\over 2} \log ^2(z)+\sum_{n=1}^{\infty}{(-1)^{n}B_{n}\over nz^{n}} \left(\sum_{j=1}^{n-1}{1\over j}-\log(z) \right)\nonumber\\ &={1\over 2}\log^2(z)-{1 \over 2z}\log z+\sum_{n=1}^{\infty}{B_{2n}\over 2nz^{2n}} \left(\sum_{j=1}^{2n-2}{1\over j}+{1\over 2n-1}-\log(z) \right) \end{align*} $$
using the well-known facts
$B_1=-1/2$
and
$B_{2n-1}=0, n>1$
. This proves (3.9) for
$|\arg (z)|\leq \pi /2-\Delta $
, where
$\Delta>0$
.
To extend it to
$|\arg (z)|\leq \pi -\Delta $
, we use the analog of Theorem 2.1 containing a logarithmic factor in the integrand of the concerned integral, which practically changes none of the hypotheses in the statement of Theorem 2.1 and its proofFootnote
6
since
$\log (t)=O\left (t^{\epsilon }\right )$
as
$t\to \infty $
for any
$\epsilon>0$
. We apply it with
$\alpha =-\pi /2$
and
$\beta =\pi /2$
. It shows that the expansion in (3.9) holds for
$|\arg (z)|\leq \pi -\Delta $
.
Remark 3.1 The result in the above theorem is not new. In fact, in [Reference Coffey15, Proposition 3], this has been done for
$\psi _k(z)$
for all
$k\in \mathbb {N}$
in view of (3.8). We derive the asymptotic expansion for
$\psi _1(z)$
right from scratch only to make this paper self-contained. Also, it is to be noted that in [Reference Coffey15], the result has been proved only for
$|\arg (z)|<\pi /2$
whereas we crucially require the result to hold for
$|\arg (z)|\leq \pi -\Delta $
for
$\Delta>0$
. We also note that one could also obtain this asymptotic behavior beginning with the Euler–Maclaurin summation formula.
Our next result is a new analog of Kloosterman’s result for
$\psi (x)$
[Reference Titchmarsh59, pp. 24–25].
Theorem 3.3 Let
$|\arg (z)|<\pi $
. Let
$\psi _1$
be defined in (1.12). For
$0<c=\text {Re}(s)<1$
,
$$ \begin{align} \psi_1(z+1)-\frac{1}{2}\log^{2}(z)=\frac{1}{2\pi i}\int_{(c)}\frac{\pi\zeta(1-s)}{\sin(\pi s)}\left(\gamma-\log(z)+\psi(s)\right)z^{-s}\, ds. \end{align} $$
Proof We first prove the result for
$z>0$
and later extend it to
$|\arg (z)|<\pi $
by analytic continuation. Using (3.11), we have
$$ \begin{align} \psi_1(z)-\frac{1}{2}\log^{2}(z) &=\int_{0}^{\infty}e^{-zt}\left(\gamma+\log(t)\right)\, dt+\int_{0}^{\infty}\left(\frac{1}{e^{t}-1}-\frac{1}{t}\right)e^{-zt}\left(\gamma+\log(t)\right)\, dt\nonumber\\ &=-\frac{\log(z)}{z}+\int_{0}^{\infty}\left(\frac{1}{e^{t}-1}-\frac{1}{t}\right)e^{-zt}\left(\gamma+\log(t)\right)\, dt, \end{align} $$
where in the last step, we employed [Reference Gradshteyn and Ryzhik31, p. 573, Formula 4.352.1]
$$ \begin{align} \int_{0}^{\infty}t^{s-1}e^{-zt}\left(\gamma+\log(t)\right)\, dt=\frac{\Gamma(s)}{z^{s}}\left(\gamma-\log(z)+\psi(s)\right)\hspace{10mm}(\text{Re}(s)>0) \end{align} $$
with
$s=1$
and the fact that
$\psi (1)=-\gamma $
. We now evaluate the integral on the right-hand side of (3.15) by means of Parseval’s formula for Mellin transforms [Reference Paris and Kaminski49, p. 83, Equation (3.1.13)]. For
$0<\text {Re}(s)<1$
, we have [Reference Titchmarsh59, p. 23, Equation (2.7.1)]
$$ \begin{align} \int_{0}^{\infty}t^{s-1}\left(\frac{1}{e^{t}-1}-\frac{1}{t}\right)\, dt=\Gamma(s)\zeta(s). \end{align} $$
Therefore, along with (3.16) and the equation given above, for
$0<c=\text {Re}(s)<1$
, Parseval’s formula (2.5) implies
$$ \begin{align} \int_{0}^{\infty}\left(\frac{1}{e^{t}-1}-\frac{1}{t}\right)e^{-zt}\left(\gamma+\log(t)\right)\, dt &=\frac{1}{2\pi i}\int_{(c)}\Gamma(s)\zeta(s)\frac{\Gamma(1-s)}{z^{1-s}}\left(\gamma-\log(z)+\psi(1-s)\right)\, ds\nonumber\\ &=\frac{1}{2\pi iz}\int_{(c)}\frac{\pi\zeta(s)}{\sin(\pi s)}\left(\gamma-\log(z)+\psi(1-s)\right)z^{s}\, ds\nonumber\\ &=\frac{1}{2\pi i}\int_{(c')}\frac{\pi\zeta(1-s)}{\sin(\pi s)}\left(\gamma-\log(z)+\psi(s)\right)z^{-s}\, ds, \end{align} $$
where
$0<c'<1$
. In the second step, we used the reflection formula
$\Gamma (s)\Gamma (1-s)=\pi /\sin (\pi s),s\notin \mathbb {Z}$
, and in the last step, we replaced s by
$1-s$
.
Now, (3.14) follows by substituting (3.18) in (3.15) and using the fact [Reference Dilcher19, Equation (8.3)]
$$ \begin{align} \psi_1(z)=\psi_1(z+1)-\frac{\log(z)}{z}. \end{align} $$
This proves (3.14) for
$z>0$
. The result is easily seen to be true for any complex z such that
$|\arg (z)|<\pi $
by analytic continuation with the help of (1.12), elementary bounds on the Riemann zeta function, Stirling’s formula (2.1) and the corresponding estimate for
$\psi (s)$
.
In the next theorem, we give a closed-form evaluation of an infinite series of integrals in terms of the digamma function and
$\psi _1(z)$
. This theorem is an analog of (2.2) and will play a fundamental role in the proof of Theorem 1.1.
Theorem 3.4 For
$\text {Re}(w)>0$
, we have
$$ \begin{align} 4\sum_{m=1}^{\infty}\int_{0}^{\infty}\frac{u\cos(u)\log(u/w)}{u^2+(2\pi mw)^2}\, du &=\psi_1(iw)-\frac{1}{2}\log^{2}(iw)+\psi_1(-iw)-\frac{1}{2}\log^{2}(-iw)+\frac{\pi}{2w}\nonumber\\ &\quad+\gamma\left(\psi(iw)+\psi(-iw)-2\log(w)\right). \end{align} $$
Proof Using Theorem 3.3, once with
$z=iw$
, and again with
$z=-iw$
and adding the respective sides, for
$0<c=\text {Re}(s)<1$
, we obtain
$$ \begin{align} &\psi_1(iw+1)-\frac{1}{2}\log^{2}(iw)+\psi_1(-iw+1)-\frac{1}{2}\log^{2}(-iw)\nonumber\\ &=\frac{1}{2\pi i}\int\limits_{(c)}\frac{\pi\zeta(1-s)}{\sin(\pi s)}\left(\gamma-\log(iw)+\psi(s)\right)(iw)^{-s}ds\nonumber\\ &\quad +\frac{1}{2\pi i}\int\limits_{(c)}\frac{\pi\zeta(1-s)}{\sin(\pi s)}\left(\gamma-\log(-iw)+\psi(s)\right)(-iw)^{-s}ds\nonumber\\ &=\frac{1}{2\pi i}\int\limits_{(c)}\frac{2\pi\zeta(1-s)}{\sin(\pi s)}\left(\gamma+\psi(s)\right)\cos\left(\frac{\pi s}{2}\right)w^{-s}\, ds-I_2, \end{align} $$
where
$$ \begin{align} I_2:=\frac{1}{2\pi i}\int_{(c)}\frac{\pi\zeta(1-s)}{\sin(\pi s)}\left(e^{-\frac{i\pi s}{2}}\log(iw)+e^{\frac{i\pi s}{2}}\log(-iw)\right)w^{-s}\, ds. \end{align} $$
Next, using the series expansions of the exponential functions
$e^{\frac {i\pi s}{2}}$
and
$e^{-\frac {i\pi s}{2}}$
and splitting them according to n even and n odd, it is easily seen that
$$ \begin{align} e^{-\frac{i\pi s}{2}}\log(iw)+e^{\frac{i\pi s}{2}}\log(-iw)=2\log(w)\cos\left(\frac{\pi s}{2}\right)+\pi\sin\left(\frac{\pi s}{2}\right). \end{align} $$
Hence, from (3.21)–(3.23), we see that
$$ \begin{align} \psi_1(iw+1)-\frac{1}{2}\log^{2}(iw)+\psi_1(-iw+1)-\frac{1}{2}\log^{2}(-iw)=:J_1-J_2, \end{align} $$
where
$$ \begin{align*} J_1&:=\frac{1}{2\pi i}\int_{(c)}\frac{\pi\zeta(1-s)}{\sin\left(\frac{\pi s}{2}\right)}\left(\gamma+\psi(s)-\log(w)\right)w^{-s}\, ds,\\ J_2&:=\frac{1}{2\pi i}\int_{(c)}\frac{\pi^2\zeta(1-s)}{2\cos\left(\frac{\pi s}{2}\right)}w^{-s}\, ds. \end{align*} $$
Using the functional equation of
$\zeta (s)$
[Reference Titchmarsh59, p. 13, Equation (2.1.1)]
$$ \begin{align} \zeta(s) = 2^s \pi^{s-1} \Gamma(1-s) \zeta(1-s) \sin\left( \frac{1}{2}\pi s \right), \end{align} $$
with s replaced by
$1-s$
, we have
$$ \begin{align} J_2=\frac{\pi^2}{2\pi i}\int_{(c)}\Gamma(s)\zeta(s)(2\pi w)^{-s}\, ds =\pi^{2}\left(\frac{1}{e^{2\pi w}-1}-\frac{1}{2\pi w}\right), \end{align} $$
where the last step follows from (3.17). Again using (3.25) with s replaced by
$1-s$
, we observe that
$$ \begin{align*} J_1=\frac{1}{2\pi i}\int_{(c)}2\pi\Gamma(s)\zeta(s)\cot\left(\frac{\pi s}{2}\right)\left(\gamma+\psi(s)-\log(w)\right)(2\pi w)^{-s}\, ds. \end{align*} $$
Now, it is important to observe that shifting the line of integration from Re
$(s)=c$
,
$0<c<1$
to Re
$(s)=d,\ 1<d<2$
does not introduce any pole of the integrand. So consider the rectangular contour
$[c-iT, d-iT], [d-iT, d+iT], [d+iT, c+iT],$
and
$[c+iT, c-iT]$
. By Cauchy’s residue theorem and the fact that the integral along the horizontal segments of the contour tend to zero as
$T\to \infty $
, as can be seen from (2.1), elementary bounds of the zeta function and the fact [Reference Gonek29, Equation (15)]
$\psi (s)=\log (s)+O(1/|s|)$
, it is seen that
$$ \begin{align} J_1&=\frac{1}{2\pi i}\int_{(d)}2\pi\Gamma(s)\zeta(s)\cot\left(\frac{\pi s}{2}\right)\left(\gamma+\psi(s)-\log(w)\right)(2\pi w)^{-s}\, ds\nonumber\\ &=\sum_{m=1}^{\infty}\frac{1}{2\pi i}\int_{(d)}2\pi\Gamma(s)\cot\left(\frac{\pi s}{2}\right)\left(\gamma+\psi(s)-\log(w)\right)(2\pi mw)^{-s}\, ds\nonumber\\ &=2\pi\sum_{m=1}^{\infty}\left\{\frac{\left(\gamma-\log(w)\right)}{2\pi i}\int_{(d)}\Gamma(s)\cot\left(\frac{\pi s}{2}\right)(2\pi mw)^{-s}\, ds\right.\nonumber\\ &\quad \left.+\frac{1}{2\pi i}\int_{(d)}\Gamma(s)\psi(s)\cot\left(\frac{\pi s}{2}\right)(2\pi mw)^{-s}\, ds\right\}, \end{align} $$
where in the first step, we used the series representation for
$\zeta (s)$
and then interchanged the order of summation and integration which is valid because of absolute and uniform convergence. We now find convenient representations for the two line integrals.
For
$0<\text {Re}(s)=(c_1)<2$
and Re
$(z)>0$
, we show that
$$ \begin{align} \frac{1}{2\pi i}\int_{(c_1)}\Gamma(s)\cot\left(\frac{\pi s}{2}\right)z^{-s}\, ds=\frac{2}{\pi}\int_{0}^{\infty}\frac{u\cos(u)}{u^2+z^2}\, du. \end{align} $$
We first prove this result for
$z>0$
and then extend it by analytic continuation. We also first prove the result for
$0<\text {Re}(s)=c_1<1$
. To that end, using the double angle formulas for sine and cosine, we have
$$ \begin{align} \frac{1}{2\pi i}\int_{(c_1)}\Gamma(s)\cot\left(\frac{\pi s}{2}\right)z^{-s}\, ds&=\frac{1}{2\pi i}\int_{(c_1)}\Gamma(s)\frac{(1+\cos\left(\pi s\right))}{\sin(\pi s)}z^{-s}\, ds\nonumber\\ &=\frac{1}{2\pi i}\int_{(c_1)}\Gamma(s)\text{cosec}(\pi s)z^{-s}\, ds\nonumber\\ &\quad +\frac{1}{2\pi i}\int_{(c_1)}\Gamma(s)\cot(\pi s)z^{-s}\, ds\nonumber\\ &=-\frac{1}{\pi}e^{z}\text{Ei}(-z)-\frac{1}{\pi}e^{-z}\text{Ei}(z), \end{align} $$
where in the last step we used [Reference Brychkov, Marichev and Savischenko13, p. 102, Formula 3.3.2.1], and where
$\text {Ei}(x)$
is the exponential integral defined [Reference Prudnikov, Brychkov and Marichev51, p. 788] for
$z>0$
by
$\text {Ei}(z):=\int _{-\infty }^{z}e^{t}/t\, dt,$
or, as is seen from [Reference Jahnke and Emde39, p. 1], by
$\text {Ei}(-z):=-\int _{z}^{\infty }e^{-t}/t\, dt$
. Equation (3.28) now follows upon using [Reference Prudnikov, Brychkov and Marichev50, p. 395, Formula 2.5.9.12]
$$ \begin{align} e^{-z}\text{Ei}(z)+e^{z}\text{Ei}(-z)=-2\int_{0}^{\infty}\frac{u\cos(u)}{u^2+z^2}\, du. \end{align} $$
Since both sides are analytic for Re
$(z)>0$
, the result now follows by analytic continuation for Re
$(z)>0$
.
Next, observe that shifting the line of integration from Re
$(s)=c_1$
to Re
$(s)=d$
, where
$1<d<2$
, and using Cauchy’s residue theorem does not change the evaluation of the integral on the left-hand side of (3.28). Hence, invoking (3.28) with
$z=2\pi mw$
, we find that
$$ \begin{align} \sum_{m=1}^{\infty}\frac{1}{2\pi i}\int_{(d)}\Gamma(s)\cot\left(\frac{\pi s}{2}\right)(2\pi mw)^{-s}\, ds&=\frac{2}{\pi}\sum_{m=1}^{\infty}\int_{0}^{\infty}\frac{u\cos(u)}{u^2+(2\pi mw)^2}\, du\nonumber\\ &=\frac{1}{\pi}\left(\log(w)-\frac{1}{2}\left(\psi(iw)+\psi(-iw)\right)\right), \end{align} $$
where in the last step, we employed (2.2).
Here, it is important to note that the series representation of
$J_1$
in (3.27) and the convergence of the series in (3.31) together imply that the series
$$ \begin{align*} \sum_{m=1}^{\infty}\frac{1}{2\pi i}\int_{(d)}\Gamma(s)\psi(s)\cot\left(\frac{\pi s}{2}\right)(2\pi mw)^{-s}\, ds \end{align*} $$
converges too. We now suitably transform the line integral in the above equation into an integral of a real variable by proving that for
$0<\text {Re}(s)=c<1$
and Re
$(z)>0$
, we have
$$ \begin{align} \frac{1}{2\pi i}\int_{(c)}\Gamma(s)\psi(s)\cot\left(\frac{\pi s}{2}\right)z^{-s}\, ds=\frac{2}{\pi}\int_{0}^{\infty}\frac{u\cos(u)\log(u)}{u^2+z^2}\, du+\frac{\pi}{2}e^{-z}. \end{align} $$
Again, we first prove this result for
$z>0$
and later extend it by analytic continuation to Re
$(z)>0$
. Note that from [Reference Oberhettinger46, p. 201, Equation (5.68)], for
$0<\text {Re}(s)=c<1$
and
$x>0$
,
$$ \begin{align} \frac{1}{2\pi i}\int_{(c)}\Gamma(s)\psi(s)\cos\left(\frac{\pi s}{2}\right)(xz)^{-s}\, ds=\cos(xz)\log(xz)+\frac{\pi}{2}\sin(xz). \end{align} $$
Multiply both sides by
$\frac {x}{1+x^2}$
and integrate with respect to x from
$0$
to
$\infty $
thereby obtaining
$$ \begin{align} \int_{0}^{\infty}\frac{x}{1+x^2}\frac{1}{2\pi i}\int_{(c)}\Gamma(s)\psi(s)\cos\left(\frac{\pi s}{2}\right)(xz)^{-s}\, ds\, dx=\int_{0}^{\infty}\left(\cos(xz)\log(xz)+\frac{\pi}{2}\sin(xz)\right)\frac{x\, dx}{1+x^2}. \end{align} $$
On the left-hand side, an application of Fubini’s theorem allows us to interchange the order of integration. On the right-hand side, we employ the change of variable
$x=u/z$
. Doing this and then using the well-known evaluation
$$ \begin{align*} \int_{0}^{\infty}\frac{x^{1-s}}{1+x^2}\, dx=\frac{\pi}{2\sin\left(\frac{\pi s}{2}\right)}, \end{align*} $$
we get
$$ \begin{align} \frac{\pi}{2}\frac{1}{2\pi i}\int_{(c)}\Gamma(s)\psi(s)\cot\left(\frac{\pi s}{2}\right)z^{-s}\, ds=\int_{0}^{\infty}\frac{u\cos(u)\log(u)}{u^2+z^2}\, du+\frac{\pi}{2}\int_{0}^{\infty}\frac{u\sin(u)}{u^2+z^2}\, du. \end{align} $$
From [Reference Erdélyi, Magnus, Oberhettinger and Tricomi26, p. 65, Formula (15)],
$$ \begin{align} \int_{0}^{\infty}\frac{u\sin(u)}{u^2+z^2}\, du=\frac{\pi}{2}e^{-z}. \end{align} $$
Substituting (3.36) in (3.35) and multiplying both sides by
$2/\pi $
, we arrive at (3.32). The identity also holds, by analytic continuation, for Re
$(z)>0,$
since both sides are analytic in this region.
Now again, shifting the line of integration from Re
$(s)=c$
to Re
$(s)=d, 1<d<2$
, noting that there is no pole of the integrand, applying Cauchy’s residue theorem and making use of the fact that the integrals along the horizontal segments tend to zero as the height of the contour tends to
$\infty $
, we see that for Re
$(w)>0$
,
$$ \begin{align*} \frac{1}{2\pi i}\int_{(c)}\Gamma(s)\psi(s)\cot\left(\frac{\pi s}{2}\right)(2\pi mw)^{-s}\, ds= \frac{1}{2\pi i}\int_{(d)}\Gamma(s)\psi(s)\cot\left(\frac{\pi s}{2}\right)(2\pi mw)^{-s}\, ds. \end{align*} $$
Hence, from (3.32) with
$z=2\pi mw$
,
$$ \begin{align} \sum_{m=1}^{\infty}\frac{1}{2\pi i}\int_{(d)}\Gamma(s)\psi(s)\cot\left(\frac{\pi s}{2}\right)(2\pi mw)^{-s}\, ds=\sum_{m=1}^{\infty}\left\{\frac{2}{\pi}\int_{0}^{\infty}\frac{u\cos(u)\log(u)}{u^2+(2\pi mw)^2}\, du+\frac{\pi}{2}e^{-2\pi mw}\right\}. \end{align} $$
Therefore, substituting (3.37) and (3.31) in (3.27), we get
$$ \begin{align} J_1&=2\pi\Bigg[\frac{\left(\gamma-\log(w)\right)}{2\pi}\left(2\log(w)-\left(\psi(iw)+\psi(-iw)\right)\right)+\sum_{m=1}^{\infty}\Bigg\{\frac{2}{\pi}\int_{0}^{\infty}\frac{u\cos(u)\log(u)}{u^2+(2\pi mw)^2}\, du+\frac{\pi}{2}e^{-2\pi mw}\Bigg\}\Bigg]\nonumber\\ &=2(\gamma-\log(w))\left(\log(w)-\frac{1}{2}\left(\psi(iw)+\psi(-iw)\right)\right)+4\sum_{m=1}^{\infty}\int_{0}^{\infty}\frac{u\cos(u)\log(u)}{u^2+(2\pi mw)^2}\, du+\frac{\pi^2}{e^{2\pi w}-1}. \end{align} $$
Now, from (3.24), (3.26), and (3.38), we have
$$ \begin{align*} &\psi_1(iw+1)-\frac{1}{2}\log^{2}(iw)+\psi_1(-iw+1)-\frac{1}{2}\log^{2}(-iw)\nonumber\\ &=2(\gamma-\log(w))\left(\log(w)-\frac{1}{2}\left(\psi(iw)+\psi(-iw)\right)\right)+4\sum_{m=1}^{\infty}\int_{0}^{\infty}\frac{u\cos(u)\log(u)}{u^2+(2\pi mw)^2}\, du+\frac{\pi^2}{e^{2\pi w}-1}\nonumber\\ &\quad-\pi^{2}\left(\frac{1}{e^{2\pi w}-1}-\frac{1}{2\pi w}\right). \end{align*} $$
Now, using (3.19) twice and using the elementary fact
$\log (iw)-\log (-iw)=\pi i$
for Re
$(w)>0$
, we are led to
$$ \begin{align} 4\sum_{m=1}^{\infty}\int_{0}^{\infty}\frac{u\cos(u)\log(u)}{u^2+(2\pi mw)^2}\, du &=\psi_1(iw)-\frac{1}{2}\log^{2}(iw)+\psi_1(-iw)-\frac{1}{2}\log^{2}(-iw)+\frac{\pi}{2w}\nonumber\\ &\quad+\left(\gamma-\log(w)\right)\left(\psi(iw)+\psi(-iw)-2\log(w)\right). \end{align} $$
Lastly, employing (2.2) again with w replaced by
$2\pi w$
, we see that
$$ \begin{align} -4\log(w)\sum_{m=1}^{\infty}\int_{0}^{\infty}\frac{u\cos(u)}{u^2+(2\pi mw)^2}\, du=\log(w)\left(\psi(iw)+\psi(-iw)-2\log(w)\right). \end{align} $$
Finally, adding the respective sides of (3.39) and (3.40), we are led to (3.20). This completes the proof.
4 A new representation for
$\left .\frac {\partial ^2}{\partial b^2}E_{2, b}(z)\right |{}_{b=1}$
The two-variable Mittag-Leffler function
$E_{\alpha , \beta }(z)$
, introduced by Wiman [Reference Wiman64], is defined by
$$ \begin{align} E_{\alpha, \beta}(z):=\sum_{k=0}^{\infty}\frac{z^k}{\Gamma(\alpha k+\beta)}\hspace{10mm}(\text{Re}(\alpha)>0, \text{Re}(\beta)>0). \end{align} $$
There is an extensive literature on these Mittag-Leffler functions (see, for example, [Reference Gorenflo, Kilbas, Mainardi and Rogosin30] and the references therein). Yet, closed-form expressions exist only for the first derivatives of
$E_{\alpha , \beta }(z)$
with respect to the parameters
$\alpha $
and
$\beta $
. The reader is referred to a recent paper of Apelblat [Reference Apelblat1] for a collection of such evaluations most of which involve the
$\text {Shi}(z)$
and
$\text {Chi}(z)$
functions defined in (4.3).
From (4.1), it is easy to see that [Reference Apelblat1, Equation (98)]
$$ \begin{align} \frac{\partial^2}{\partial\beta^2}E_{\alpha, \beta}(t)=\sum_{k=0}^{\infty}\frac{\psi^{2}(\alpha k+\beta)-\psi'(\alpha k+\beta)}{\Gamma(\alpha k+\beta)}t^k. \end{align} $$
However, there are no closed-form evaluations known for the above series. In what follows, we establish a new result which transforms
$\left .\frac {\partial ^2}{\partial \beta ^2}E_{2, \beta }(t)\right |{}_{\beta =1}$
into a suitable integral which is absolutely essential in proving Theorem 1.1. Before we embark upon the proof though, we need a few lemmas concerning the hyperbolic sine and cosine integrals
$\text {Shi}(z)$
and
$\text {Chi}(z)$
defined by [Reference Olver, Lozier, Boisvert and Clark48, p. 150, Equations (6.2.15) and (6.2.16)]
$$ \begin{align} \mathrm{Shi}(z):=\int_0^z\frac{\sinh(t)}{t}\ dt,\hspace{3mm} \mathrm{Chi}(z):=\gamma+\log(z)+\int_0^z\frac{\cosh(t)-1}{t}\ dt. \end{align} $$
The first lemma involving these functions was established in [Reference Dixit, Kesarwani and Kumar23, Lemma 9.1]. Here, and throughout the sequel, we use the following notation for brevity.
$$ \begin{align*} \left(\sinh\operatorname{Shi}-\cosh\operatorname{Chi}\right)(w):=\sinh(w) \operatorname{Shi} (w)- \cosh(w) \operatorname{Chi} (w). \end{align*} $$
Lemma 4.1 Let
$\mathrm {Re}(w)>0$
. Then
$$ \begin{align*} \int_{0}^{\infty}\frac{t\cos t\, dt}{t^2+w^2}=\left(\sinh\operatorname{Shi}-\cosh\operatorname{Chi}\right)(w). \end{align*} $$
We require another result from [Reference Dixit, Gupta, Kumar and Maji22, Lemma 3.2].
Lemma 4.2 For Re
$(w)>0$
,
$$ \begin{align*} \sum_{k=0}^\infty\frac{\psi(2k+1)}{\Gamma\left(2k+1\right)}w^{2k}&=\left(\sinh\operatorname{Shi}-\cosh\operatorname{Chi}\right)(w)+\log(w)\cosh(w). \end{align*} $$
We also need the following integral representation for the Mittag-Leffler function
$E_{2,b}(z)$
which was obtained by Dzhrbashyan [Reference Dzhrbashyan25, p. 130, Equation (2.12)]. Since Dzhrbashyan’s book [Reference Dzhrbashyan25] is not easily accessible and we could not find this result in any contemporary texts on these functions, for example, [Reference Gorenflo, Kilbas, Mainardi and Rogosin30], we briefly sketch his proof of it.
Lemma 4.3 Let the two-variable Mittag-Leffler function
$E_{\alpha , \beta }(z)$
be defined in (4.1). For
$0<\text {Re}(b)<3$
, and
$0\leq \arg (z)<\pi $
or
$-\pi <\arg (z)\leq 0$
, one hasFootnote
7
$$ \begin{align} E_{2,b}(z)=\frac{1}{2}z^{\frac{1}{2}(1-b)}\left\{e^{\sqrt{z}}+e^{\mp i\pi(1-b)-\sqrt{z}}\right\}+\frac{\sin(\pi b)}{2\pi}\int_{0}^{\infty}\frac{e^{\pm i\left(\sqrt{t}-\frac{\pi}{2}(1-b)\right)}}{t+z}t^{\frac{1}{2}(1-b)}\, dt, \end{align} $$
where the upper or lower signs are taken, respectively, for
$0\leq \arg (z)<\pi $
or
$-\pi <\arg (z)\leq 0$
.
Proof For
$\text {Re}(\eta )>0$
, Hankel’s representation for the reciprocal of
$\Gamma (\eta )$
is given by [Reference Dzhrbashyan25, Equation (2.7’)]
$$ \begin{align} \frac{1}{\Gamma(\eta)}=\frac{1}{4\pi i}\int_{\gamma(\epsilon; \pi)}e^{s^{1/2}}s^{-(\eta+1)/2}\, ds, \end{align} $$
where
$\gamma (\epsilon; \pi )$
represents the Hankel contour which runs from
$-\infty , \arg (s)=-\pi $
, encircles the origin in the form a circle with infinitesimal radius
$\epsilon>0$
in the counter-clockwise direction and then terminates at
$-\infty $
, but now with
$\arg (s)=+\pi $
. This contour divides the complex plane into two unbounded regions
$G^{(-)}(\epsilon; \pi )$
and
$G^{(+)}(\epsilon; \pi )$
, where
$G^{(-)}(\epsilon; \pi )=\{s: |\arg (s)|<\pi , |s|<\epsilon \}$
and
$G^{(+)}(\epsilon; \pi )=\{s: |\arg (s)|<\pi , |s|>\epsilon \}$
.
Let
$|\arg (z)|<\pi $
and Re
$(b)>0$
. Using (4.5) in the definition (4.1) of
$E_{2, b}(z)$
, after some simplification, we find that for
$z\in G^{(-)}(\epsilon; \pi )$
, we have [Reference Dzhrbashyan25, Equation (2.4)],
$$ \begin{align*} E_{2, b}(z)=\frac{1}{4\pi i}\int_{\gamma(\epsilon; \pi)}\frac{e^{s^{1/2}}s^{(1-b)/2}}{s-z}\, ds. \end{align*} $$
Now, if
$z\in G^{(+)}(\epsilon; \pi )$
, say,
$\epsilon <|z|<\epsilon _1$
, then using Cauchy’s residue theorem (along the curve obtained by considering a straight line segment going from a point on
$\gamma (\epsilon; \pi )$
radially to
$\gamma (\epsilon _1; \pi )$
which misses z), we see that [Reference Dzhrbashyan25, Equation (2.9)],
$$ \begin{align*} \frac{1}{4\pi i}\int_{\gamma(\epsilon_1; \pi)}\frac{e^{s^{1/2}}s^{(1-b)/2}}{s-z}\, ds-\frac{1}{4\pi i}\int_{\gamma(\epsilon; \pi)}\frac{e^{s^{1/2}}s^{(1-b)/2}}{s-z}\, ds=\frac{1}{2}z^{(1-b)/2}e^{z^{1/2}}, \end{align*} $$
and hence, this implies that, for
$z\in G^{(+)}(\epsilon; \pi )$
, we have [Reference Dzhrbashyan25, Equation (2.5)]
$$ \begin{align} E_{2, b}(z)=\frac{1}{2}z^{(1-b)/2}e^{z^{1/2}}+\frac{1}{4\pi i}\int_{\gamma(\epsilon; \pi)}\frac{e^{s^{1/2}}s^{(1-b)/2}}{s-z}\, ds. \end{align} $$
For more details, see [Reference Dzhrbashyan25, p. 129]. Now, in addition to Re
$(b)>0$
, if we assume Re
$(b)<3$
, then we can let
$\epsilon \to 0$
in (4.6), thereby obtaining
$$ \begin{align*} E_{2, b}(z)&=\frac{1}{2}z^{(1-b)/2}e^{z^{1/2}}+\frac{1}{4\pi i}\int_{\gamma(0; \pi)}\frac{e^{s^{1/2}}s^{(1-b)/2}}{s-z}\, ds. \end{align*} $$
Since the integral over the Hankel contour can be written as sum of two integrals from
$0$
to
$\infty $
, we can rewrite the above equation in the form
$$ \begin{align} \frac{1}{2}z^{(1-b)/2}e^{z^{1/2}}+\frac{1}{2\pi}\int_{0}^{\infty}\frac{\sin\left(\sqrt{t}+\frac{\pi}{2}(1-b)\right)}{t+z}t^{\frac{1-b}{2}}\, dt=E_{2, b}(z). \end{align} $$
This representation holds for any fixed z such that
$|\arg (z)|<\pi $
.
Next, we show that for
$|\arg (z)|<\pi $
, we have [Reference Dzhrbashyan25, Equation (2.15)]
$$ \begin{align} z^{(1-b)/2}e^{-z^{1/2}}+\frac{1}{2\pi i}\int_{\gamma(0; \pi)}\frac{e^{-s^{1/2}}s^{(1-b)/2}}{s-z}\, ds=0. \end{align} $$
Let
$\gamma _R(\epsilon; \pi )$
denote the portion of the contour
$\gamma (\epsilon; \pi )$
belonging to the disk
$|s|<R$
. By Cauchy’s residue theorem,
$$ \begin{align} \frac{1}{2\pi i}\int_{\gamma_R(\epsilon; \pi)}\frac{e^{-s^{1/2}}s^{(1-b)/2}}{s-z}\, ds+\frac{1}{2\pi i}\int_{|s|=R}\frac{e^{-s^{1/2}}s^{(1-b)/2}}{s-z}\, ds=-e^{-z^{1/2}}z^{(1-b)/2} \end{align} $$
if
$\epsilon <|z|<R$
and
$|\arg (z)|<\pi $
. Observe that the following estimate holds:
$$ \begin{align*} \left|\int_{|s|=R}\frac{e^{-s^{1/2}}s^{(1-b)/2}}{s-z}\, ds\right|\leq \frac{R^{\frac{3}{2}-\frac{\text{Re}(b)}{2}}}{R-|z|}\int_{-\pi}^{\pi}e^{-R^{1/2}\cos\left(\frac{\phi}{2}\right)+\frac{\phi}{2}\text{Im}(b)}\, d\phi<\frac{2\pi R}{R-|z|}R^{-\frac{1}{2}\text{Re}(b)}e^{\frac{\pi}{2}\text{Im}(b)}, \end{align*} $$
in the last step, we applied Jordan’s inequality, namely,
$\sin (u/2)\geq u/\pi $
for
$u\in [0, \pi ]$
after the change of variable
$\phi =\pi -u$
. Using the above estimate, and letting
$\epsilon \to 0$
,
$R\to \infty $
in (4.9) leads us to (4.8), since b is a fixed complex number with
$0<\text {Re}(b)<3$
.
Now, for
$z\neq 0$
, (4.8) can be rewritten in the form
$$ \begin{align*} z^{(1-b)/2}e^{-z^{1/2}}+\frac{1}{2\pi i}\int_{0}^{\infty}\frac{\exp{\left(-i\left(\sqrt{t}-\frac{\pi}{2}(1-b)\right)\right)}-\exp{\left(i\left(\sqrt{t}-\frac{\pi}{2}(1-b)\right)\right)}}{t+z}t^{\frac{1-b}{2}}\, dt=0. \end{align*} $$
Now, multiplying both sides of the above equation by
$\frac {1}{2}e^{-i\pi (1-b)}$
if
$0\leq \arg (z)<\pi $
, and by
$\frac {1}{2}e^{i\pi (1-b)}$
if
$-\pi <\arg (z)\leq 0$
, and then adding the corresponding sides of the respective resulting equations to those of (4.7), we arrive at (4.4).
We are now ready to prove our result on evaluating the second derivative of the Mittag-Leffler function
$E_{2,b}(z)$
with respect to the parameter b at
$b=1$
.
Theorem 4.4 Let
$1\leq b\leq 3/2$
and
$w>0$
. Let the two-variable Mittag-Leffler function
$E_{2,b}(z)$
be defined in (4.1). Then
$$ \begin{align} \left.\frac{\partial^2}{\partial b^2}E_{2, b}(w^2)\right|{}_{b=1}=\log^{2}(w)\cosh(w)+2\int_{0}^{\infty}\frac{u\cos(u)\log(u)\, du}{u^2+w^2}. \end{align} $$
Proof Assume
$z>0$
. We would like to differentiate (4.4) twice with respect to b. This, in turn, requires differentiating the integral in (4.4) under the integral sign twice with respect to b. (Note that since
$\arg (z)=0$
, we can take the plus sign in the exponent of the exponential function inside the integrand.) To justify this, one needs to invoke Theorem 2.3 twice. We justify this only for the first derivative with respect to b. The verification for the second derivative can be done similarly.
To that end, let
$$ \begin{align*} \mathcal{I}(b):=\int_{0}^{\infty}\frac{e^{ i\sqrt{t}}\hspace{1mm}t^{\frac{1}{2}(1-b)}}{t+z}\, dt. \end{align*} $$
Observe that the convergence of
$\mathcal {I}(b)$
for any
$b\in [1, 3/2]$
results from (4.4) itself. Thus, we can apply (2.4) provided, we show that
$$ \begin{align*} \mathcal{J}(b):= \int_{0}^{\infty}\frac{\partial}{\partial b}\frac{e^{ i\sqrt{t}}\hspace{1mm}t^{\frac{1}{2}(1-b)}}{t+z}\, dt= -\frac{1}{2}\int_{0}^{\infty}\frac{e^{ i\sqrt{t}}\hspace{1mm}t^{\frac{1}{2}(1-b)}\log(t)}{t+z}\, dt \end{align*} $$
converges uniformly in
$[1, 3/2]$
. Now, write the above integral as the sum of two integrals—one from
$0$
to
$1$
, and the second from
$1$
to
$\infty $
. Then in the first, replace t by
$1/t$
and in the second, employ the change of variable
$t=x^2$
to get
$$ \begin{align*} \mathcal{J}(b)&={1\over 2} \int_{1}^{\infty} \frac{e^{i\over \sqrt{t}}t^{{1\over2}(b-3)}\log(t)}{1+tz}\ dt-{ 2} \int_{1}^{\infty} \frac{e^{ix}x^{(2-b)}\log(x)}{x^2+z}\ dx\nonumber\\ &=:I_2+I_3. \end{align*} $$
We now show that both
$I_2$
and
$I_3$
converge uniformly in
$[1, 3/2]$
, whence we will be done. We first handle
$I_2$
. Let
$f(t,b)={t^{1/2}\over 1+zt}$
and
$g(t,b)=t^{{b\over 2}-2}e^{i/\sqrt {t}}\log (t)$
.
Suppose first
$z\in [1,\infty )$
. Then
$f(t, b)$
not only tends to zero as
$t\to \infty $
but is also decreasing on
$[1, \infty )$
. Further,
$$ \begin{align*} \left|\int_{1}^{X}t^{{b\over 2}-2}e^{i/\sqrt{t}}\log(t)\, dt\right|&\leq\int_{1}^{X}t^{\frac{b}{2}-2}\log(t)\, dt =\frac{X^{\frac{b}{2}-1}\log(X)}{\frac{b}{2}-1}-\frac{(X^{\frac{b}{2}-1}-1)}{(\frac{b}{2}-1)^2}\nonumber\\ &\leq16. \end{align*} $$
Hence, the hypotheses of Dirichlet’s test for uniform convergence given in Theorem 2.2 are satisfied, and
$I_2$
converges uniformly on
$[1, 3/2]$
.
Now, if
$z\in (0, 1)$
, then
$f(t, b)$
increases on
$[1,1/z]$
and decreases on
$[1/z,\infty )$
. Thus, in this case, one needs to further split
$I_2$
as
$$ \begin{align*} I_2=\int_{1}^{1/z}f(t, b)g(t, b)\, dt+\int_{1/z}^{\infty}f(t, b)g(t, b)\, dt. \end{align*} $$
The integral from
$1/z$
to
$\infty $
converges uniformly by Dirichlet’s test similarly as was just shown above. For the integral from
$1$
to
$1/z$
, we apply Weierstrass M-test [Reference Widder62, p. 289, Theorem 7*]. Together, we see that for any fixed
$z>0$
,
$I_2$
converges uniformly on
$[1, 3/2]$
.
We now focus on
$I_3$
and begin by rewriting it as
$$ \begin{align*} I_3=-{ 2} \int_{1}^{\infty} \frac{ x^{(2-b)}\cos x\log x}{x^2+z}\ dx-{ 2i} \int_{1}^{\infty} \frac{x^{(2-b)}\sin x\log x}{x^2+z}\ dx. \end{align*} $$
We show the uniform convergence of only the integral involving
$\cos (x)$
. That for the second integral can be shown similarly.
To that end, we again apply Dirichlet’s test (Theorem 2.2) with
$f(x,b)= \frac {x^{2-b}\log x}{x^2+z}$
and
$g(x,b)=\cos x$
. To verify that its hypotheses are satisfied, first observe that
$f(x,b)$
tends to zero as
$x\to \infty $
. However,
$f(x,b)$
is not decreasing throughout the interval
$[1, \infty )$
. But if we write
$f(x,b)=\frac {\log (x)}{\sqrt {x}}\frac {x^{\frac {5}{2}-b}}{x^2+z}$
, by elementary calculus, it is not difficult to see that if
$C_z:=\max \{e^2,\sqrt {3z}\}$
, then
$f(x, b)$
is decreasing in
$[C_z, \infty )$
, since
$\frac {\log (x)}{\sqrt {x}}$
is positive and decreasing in
$(e^2,\infty )$
and
$\frac {x^{\frac {5}{2}-b}}{x^2+z}$
is positive and decreasing in
$(\sqrt {3z},\infty )$
.
Hence, we write
$$ \begin{align*} \int_{1}^{\infty} \frac{ x^{(2-b)}\cos x\log x}{x^2+z}\ dx=\int_{1}^{C_{z}} \frac{ x^{(2-b)}\cos x\log x}{x^2+z}\ dx+\int_{C_{z}}^{\infty} \frac{ x^{(2-b)}\cos x\log x}{x^2+z}\ dx=J_2+J_3(\text{say}). \end{align*} $$
Using Weierstrass test for
$J_2$
with
$M(x)=\frac {2}{z}x\log x$
justifies its uniform convergence. Finally, for
$J_3$
, we have
$\left |\int _{C_{z}}^{X}\cos x \ dx\right |\leq 2$
. Hence, by another application of Dirichlet’s test,
$J_3$
converges uniformly. Therefore,
$I_3$
converges uniformly too. Combining all of the above facts, we conclude that
$\mathcal {J}(b)$
converges uniformly for all
$b\in [1,3/2]$
.
Differentiating (4.4) twice with respect to b and simplifying leads to
$$ \begin{align*} \frac{\partial^2}{\partial b^2}E_{2, b}(z)&=\frac{1}{2}\Bigg[-\frac{1}{2}\log(z)\left\{-\frac{1}{2}z^{\frac{1}{2}(1-b)}\log(z)\left(e^{\sqrt{z}}+e^{-i\pi(1-b)-\sqrt{z}}\right)+i\pi z^{\frac{1}{2}(1-b)}e^{i\pi(b-1)-\sqrt{z}}\right\}\nonumber\\ &\quad+i\pi\sqrt{z}e^{-\sqrt{z}}z^{-\frac{b}{2}}e^{i\pi(b-1)}\left(i\pi-\frac{1}{2}\log(z)\right)\Bigg]-\frac{\pi\sin(\pi b)}{2}\int_{0}^{\infty}\frac{e^{i\left(\sqrt{t}-\frac{\pi}{2}(1-b)\right)}}{t+z}t^{\frac{1}{2}(1-b)}\, dt\nonumber\\ &\quad+\frac{1}{2}\cos(\pi b)\int_{0}^{\infty}\frac{e^{i\left(\sqrt{t}-\frac{\pi}{2}(1-b)\right)}}{t+z}t^{\frac{1}{2}(1-b)}(i\pi-\log(t))\, dt\nonumber\\ &\quad+\frac{1}{8\pi}\sin(\pi b)\int_{0}^{\infty}\frac{e^{i\left(\sqrt{t}-\frac{\pi}{2}(1-b)\right)}}{t+z}t^{\frac{1}{2}(1-b)}(i\pi-\log(t))^{2}\, dt, \end{align*} $$
so that
$$ \begin{align} \left.\frac{\partial^2}{\partial b^2}E_{2, b}(z)\right|{}_{b=1}=\frac{1}{4}\log^{2}(z)\cosh(\sqrt{z})-\frac{i\pi}{2}e^{-\sqrt{z}}\log(z)-\frac{\pi^2}{2}e^{-\sqrt{z}}-\frac{1}{2}\int_{0}^{\infty}\frac{e^{i\sqrt{t}}(i\pi-\log(t))}{t+z}\, dt. \end{align} $$
Now, employing the change of variable
$t=u^2$
, we have
$$ \begin{align} \int_{0}^{\infty}\frac{e^{i\sqrt{t}}(i\pi-\log(t))}{t+z}\, dt&=2\int_{0}^{\infty}\frac{ue^{iu}(i\pi-2\log(u))}{u^2+z}\, du\nonumber\\ &=2\pi i\int_{0}^{\infty}\frac{u\cos(u)}{u^2+z}\, du-2\pi\int_{0}^{\infty}\frac{u\sin(u)}{u^2+z}\, du-4\int_{0}^{\infty}\frac{ue^{iu}\log(u)}{u^2+z}\, du. \end{align} $$
Next, from Lemma 4.1,
$$ \begin{align} \int_{0}^{\infty}\frac{u\cos(u)}{u^2+z}\, du=\left(\sinh\operatorname{Shi}-\cosh\operatorname{Chi}\right)(\sqrt{z}). \end{align} $$
Moreover,
$$ \begin{align} \int_{0}^{\infty}\frac{ue^{iu}\log(u)}{u^2+z}\, du&=\int_{0}^{\infty}\frac{u\cos(u)\log(u)}{u^2+z}\, du+i\int_{0}^{\infty}\frac{u\sin(u)\log(u)}{u^2+z}\, du, \end{align} $$
Now, from [Reference Prudnikov, Brychkov and Marichev50, p. 537, Formula 2.6.32.8],Footnote 8
$$ \begin{align} \int_{0}^{\infty}\frac{u\sin(u)\log(u)}{u^2+z}\, du=\frac{\pi}{2}\left\{e^{-\sqrt{z}}\log(\sqrt{z})-\frac{1}{2}\left(e^{\sqrt{z}}\text{Ei}(-\sqrt{z})+e^{-\sqrt{z}}\text{Ei}(\sqrt{z})\right)\right\}. \end{align} $$
Hence, along with Lemma 4.1, (3.30), and (4.15) imply
$$ \begin{align} \int_{0}^{\infty}\frac{u\sin(u)\log(u)}{u^2+z}\, du=\frac{\pi}{2}\left\{e^{-\sqrt{z}}\log(\sqrt{z})+\left(\sinh\operatorname{Shi}-\cosh\operatorname{Chi}\right)(\sqrt{z})\right\}. \end{align} $$
Therefore, from (4.12), (4.13), (3.36), (4.14), and (4.16), we arrive at
$$ \begin{align} \int_{0}^{\infty}\frac{e^{i\sqrt{t}}(i\pi-\log(t))}{t+z}\, dt&=-\pi^2e^{-\sqrt{z}}-2\pi i e^{-\sqrt{z}}\log(\sqrt{z})-4\int_{0}^{\infty}\frac{u\cos(u)\log(u)}{u^2+z}\, du. \end{align} $$
Finally, substituting (4.17) in (4.11), we arrive at
$$ \begin{align*} \left.\frac{\partial^2}{\partial b^2}E_{2, b}(z)\right|{}_{b=1}=\log^2(\sqrt{z})\cosh(\sqrt{z})+2\int_{0}^{\infty}\frac{u\cos(u)\log(u)}{u^2+z}\, du. \end{align*} $$
Now, let
$z=w^2$
to arrive at (4.10).
5 Proof of the main results
This section is devoted to proving the transformation for the Lambert series for logarithm given in Theorem 1.1, the asymptotic expansion of this series in Theorem 1.2, and a mean value theorem in Theorem 1.3.
5.1 Proof of Theorem 1.1
We first prove the result for
$y>0$
and then extend it to Re
$(y)>0$
by analytic continuation.
The idea is to differentiate both sides of (1.5) with respect to a and then let
$a\to 0$
. Define
$$ \begin{align} F_1(a,y)&:=\frac{d}{da}\sum_{n=1}^{\infty}\sigma_a(n)e^{-ny},\nonumber\\ F_2(a, y)&:=\frac{d}{da}\left\{\frac{1}{2}\left(\left(\frac{2\pi}{y}\right)^{1+a}\mathrm{cosec}\left(\frac{\pi a}{2}\right)+1\right)\zeta(-a)-\frac{1}{y}\zeta(1-a)\right\},\nonumber\\ F_3(a, y)&:=\frac{d}{da}\left\{\frac{2\pi}{y\sin\left(\frac{\pi a}{2}\right)}\sum_{n=1}^\infty \sigma_{a}(n)\Bigg(\tfrac{(2\pi n)^{-a}}{\Gamma(1-a)} {}_1F_2\left(1;\tfrac{1-a}{2},1-\tfrac{a}{2};\tfrac{4\pi^4n^2}{y^2} \right) -\left(\tfrac{2\pi}{y}\right)^{a}\hspace{-5pt}\cosh\left(\tfrac{4\pi^2n}{y}\right)\Bigg)\right\}, \end{align} $$
and let
$$ \begin{align} G_1(y)=\lim_{a\to0}F_1(a, y),\hspace{5mm}G_2(y)=\lim_{a\to0}F_2(a, y),\hspace{5mm}G_3(y)=\lim_{a\to0}F_3(a, y). \end{align} $$
Clearly, from (1.5),
$$ \begin{align} G_1(y)+G_2(y)=G_3(y). \end{align} $$
Using (1.3), it is readily seen that
$$ \begin{align} G_1(y)=\sum_{n=1}^{\infty}\frac{\log(n)}{e^{ny}-1}. \end{align} $$
By routine differentiation,
$$ \begin{align} F_2(a, y)&=\frac{1}{y}\zeta'(1-a)-\frac{1}{2}\zeta'(-a)-\frac{1}{2}\left(\frac{2\pi}{y}\right)^{1+a}\mathrm{cosec}\left(\frac{\pi a}{2}\right)\zeta'(-a)\nonumber\\ &\quad+\frac{1}{2}\zeta(-a)\left(\frac{2\pi}{y}\right)^{1+a}\mathrm{cosec}\left(\frac{\pi a}{2}\right)\left(\log\left(\frac{2\pi}{y}\right)-\frac{\pi}{2}\cot\left(\frac{\pi a}{2}\right)\right). \end{align} $$
Letting
$a\to 0$
in (5.5) leads to
$$ \begin{align} G_2(y)=\frac{1}{4}\log(2\pi)-\frac{1}{2y}\log^{2}(y)+\frac{\gamma^2}{2y}-\frac{\pi^2}{12y}, \end{align} $$
which is now proved. Note that
$$ \begin{align} G_2(y) &=\lim_{a\to 0} \left(-\frac{1}{2}\zeta'(-a)\right) \nonumber\\ &\quad+ \lim_{a\to 0} \left[\frac{1}{y}\zeta'(1-a)-\frac{\left(2\pi/y\right)^{1+a}}{2\sin\left(\frac{\pi a}{2}\right)}\left\{ \zeta'(-a)-\zeta(-a)\log\left(\frac{2\pi}{y}\right) + \frac{\pi}{2}\zeta(-a)\cot\left(\frac{\pi a}{2}\right)\right\} \right]. \end{align} $$
We make use of the following well-known Laurent series expansions around
$a=0$
:
$$ \begin{align} \zeta(-a) &= -\frac{1}{2} + \frac{1}{2} \log(2\pi)a + \left[\frac{\gamma^2}{4}-\frac{\pi^2}{48}- \frac{\log^2(2\pi)}{4}+ \frac{\gamma_1}{2} \right]a^2 + O(a^3),\nonumber\\ \zeta'(1-a)&= -\frac{1}{a^2}-\gamma_1-\gamma_2 a+ O(a^2),\nonumber\\ \left(\frac{2\pi}{y}\right)^{1+a}&= \frac{2\pi}{y}+\frac{2\pi}{y}\log\left(\frac{2\pi}{y}\right) a + \frac{\pi}{y} \log^2 \left(\frac{2\pi}{y}\right) a^2 + O(a^3),\nonumber\\ \text{cosec} \left(\frac{\pi a}{2}\right) &= \frac{2}{\pi a}+ \frac{\pi}{12}a + O(a^3),\nonumber\\ \cot \left(\frac{\pi a}{2}\right) &= \frac{2}{\pi a}- \frac{\pi}{6}a + O(a^3). \end{align} $$
Hence, substituting (5.8) in (5.7), we get
$$ \begin{align*} G_2(y)&=\tfrac{1}{4}\log(2\pi) + \lim_{a\to 0}\Big[-\tfrac{1}{ya^2}-\tfrac{\gamma_1}{y} + O(a)+ \left\{-\tfrac{2}{ya} -\tfrac{2}{y}\log\left(\tfrac{2\pi}{y}\right)+\left(-\tfrac{\pi^2}{12y}-\tfrac{1}{y}\log^2 \left(\tfrac{2\pi}{y}\right) \right)a + O(a^2) \right\}\nonumber\\ &\qquad \qquad \times \left\{-\tfrac{1}{2a}+ \tfrac{1}{2}\log\left(\tfrac{2\pi}{y}\right) + \left(-\tfrac{\gamma^2}{4}+\tfrac{\pi^2}{16}-\tfrac{\gamma_1}{2}+\tfrac{1}{4}\log^2(2\pi)-\tfrac{1}{2}\log(2\pi)\log\left(\tfrac{2\pi}{y}\right) \right)a + O(a^2) \right\} \Big]\nonumber\\ &= \frac{1}{4}\log(2\pi) + \lim_{a\to 0}\Bigg[\left(-\frac{1}{y}+ \frac{1}{y} \right)\frac{1}{a^2} + \left(-\frac{1}{y}\log\left(\frac{2\pi}{y}\right) + \frac{1}{y}\log\left(\frac{2\pi}{y}\right)\right)\frac{1}{a} \nonumber\\ &\qquad + \left(-\frac{\gamma_1}{y}+ \frac{\gamma^2}{2y}-\frac{\pi^2}{12y}+\frac{\gamma_1}{y}-\frac{1}{2y}\left\{\log^2(2\pi)-2\log(2\pi)\log\left(\frac{2\pi}{y}\right)+ \log^2\left(\frac{2\pi}{y}\right) \right\}\right)+ O(a) \Bigg]\nonumber\\ &= \frac{1}{4}\log(2\pi) + \frac{\gamma^2}{2y} -\frac{\pi^2}{12y} -\frac{\log^2y}{2y}. \end{align*} $$
Next, we apply the definitions of
$\sigma _a(n)$
,
${}_1F_{2}$
and simplify to obtain
$$ \begin{align*} F_3(a, y)&=\frac{d}{da}\left[\frac{2\pi}{y\sin\left(\frac{\pi a}{2}\right)}\sum_{m, n=1}^\infty\left\{(2\pi n)^{-a}\sum_{k=0}^{\infty}\frac{\left(4\pi^2mn/y\right)^{2k}}{\Gamma(1-a+2k)}-\left(\frac{2\pi m}{y}\right)^{a}\cosh\left(\frac{4\pi^2mn}{y}\right)\right\}\right]\notag\\ &=\frac{2\pi}{y}\sum_{m, n=1}^{\infty}\sum_{k=0}^{\infty}\left(\frac{4\pi^2mn}{y}\right)^{2k}\frac{1}{\sin^{2}\left(\frac{\pi a}{2}\right)}\Bigg[\frac{(2\pi n)^{-a}}{\Gamma(1-a+2k)}\bigg\{\left(\psi(1-a+2k)-\log(2\pi n)\right)\sin\left(\frac{\pi a}{2}\right)\nonumber\\ &\qquad\quad-\frac{\pi}{2}\cos\left(\frac{\pi a}{2}\right)\bigg\}-\frac{1}{\Gamma(2k+1)}\left(\frac{2\pi m}{y}\right)^{a}\left(\log\left(\frac{2\pi m}{y}\right)\sin\left(\frac{\pi a}{2}\right)-\frac{\pi}{2}\cos\left(\frac{\pi a}{2}\right)\right)\Bigg]\nonumber\\ &=\frac{2\pi}{y}\sum_{m, n=1}^{\infty}\sum_{k=0}^{\infty}\left(\frac{4\pi^2mn}{y}\right)^{2k}\frac{A_1(a)-A_2(a)}{\sin^{2}\left(\frac{\pi a}{2}\right)}, \end{align*} $$
where in the first step, we have interchanged the order of summation and differentiation using the fact [Reference Dixit, Kesarwani and Kumar23, p. 35] that the series in the definition of (5.1) converges uniformly as long as Re
$(a)>-1$
, and where
$$ \begin{align*} \hspace{-3mm}A_1(a)&=A_1(m, n, k; a):=\frac{(2\pi n)^{-a}}{\Gamma(1-a+2k)}\left\{\left(\psi(1-a+2k)-\log(2\pi n)\right)\sin\left(\frac{\pi a}{2}\right)-\frac{\pi}{2}\cos\left(\frac{\pi a}{2}\right)\right\},\\ \hspace{-3mm}A_2(a)&=A_2(m, n, k; a):=\frac{1}{\Gamma(2k+1)}\left(\frac{2\pi m}{y}\right)^{a}\left\{\log\left(\frac{2\pi m}{y}\right)\sin\left(\frac{\pi a}{2}\right)-\frac{\pi}{2}\cos\left(\frac{\pi a}{2}\right)\right\}. \end{align*} $$
We now show that
$$ \begin{align} \lim_{a\to0}\frac{A_1(a)-A_2(a)}{\sin^{2}\left(\frac{\pi a}{2}\right)} &=\frac{1}{\pi\Gamma(2k+1)}\bigg\{\log\left(\frac{4\pi^2mn}{y}\right)\log\left(\frac{ny}{m}\right)-2\log(2n\pi)\psi(2k+1)+\psi^{2}(2k+1)\nonumber\\ &\qquad\qquad\qquad\quad-\psi'(2k+1)\bigg\}. \end{align} $$
Let L denote the limit in the equation given above. The expression inside the limit is of the form
$0/0$
. By routine calculation, we find that
$$ \begin{align} A_1'(a)&=\frac{(2\pi n)^{-a}}{\Gamma(1-a+2k)}\left\{-\psi'(1-a+2k)+\frac{\pi^2}{4}+\left(\psi(1-a+2k)-\log(2\pi n)\right)^{2}\right\}\sin\left(\frac{\pi a}{2}\right), \end{align} $$
$$ \begin{align} A_2'(a)&=\frac{\left(2\pi m/y\right)^{a}}{\Gamma(2k+1)}\bigg\{\log\left(\frac{2\pi m}{y}\right)\left(\log\left(\frac{2\pi m}{y}\right)\sin\left(\frac{\pi a}{2}\right)-\frac{\pi}{2}\cos\left(\frac{\pi a}{2}\right)\right) \nonumber\\ &\qquad\qquad\qquad+\frac{\pi}{2}\log\left(\frac{2\pi m}{y}\right)\cos\left(\frac{\pi a}{2}\right)+\frac{\pi^2}{4}\sin\left(\frac{\pi a}{2}\right)\bigg\}, \end{align} $$
where
$'$
denotes differentiation with respect to a. Since
$A_1'(0)=A_2'(0)=0$
, using L’Hopital’s rule again, it is seen that
$$ \begin{align*} L=\frac{A_1"(0)-A_2"(0)}{\pi^2/2}, \end{align*} $$
Differentiating (5.10) and (5.11) with respect to a, we get
$$ \begin{align*} A_1"(0)&=\frac{\pi}{2\Gamma(2k+1)}\left\{-\psi'(2k+1)+\frac{\pi^2}{4}+\left(\psi(2k+1)-\log(2\pi n)\right)^{2}\right\},\\ A_2"(0)&=\frac{1}{\Gamma(2k+1)}\left\{\frac{\pi}{2}\log^{2}\left(\frac{2\pi m}{y}\right)+\frac{\pi^3}{8}\right\}, \end{align*} $$
whence we obtain (5.9) upon simplification. Therefore, from (5.2) and (5.9), we deduce that
$$ \begin{align*} G_3(y)&=\frac{2}{y}\sum_{m, n=1}^{\infty}\sum_{k=0}^{\infty}\frac{\left(4\pi^2mn/y\right)^{2k}}{(2k)!}\bigg\{\log\left(\frac{4\pi^2mn}{y}\right)\log\left(\frac{ny}{m}\right)-2\log(2n\pi)\psi(2k+1)\nonumber\\ &\qquad\qquad\qquad\qquad\qquad\qquad+\psi^{2}(2k+1)-\psi'(2k+1)\bigg\}\nonumber\\ &=\frac{2}{y}\sum_{m, n=1}^{\infty}\Bigg\{\log\left(\frac{4\pi^2mn}{y}\right)\log\left(\frac{ny}{m}\right)\cosh\left(\frac{4\pi^2mn}{y}\right)-2\log(2n\pi)\sum_{k=0}^{\infty}\frac{\psi(2k+1)}{\Gamma(2k+1)}\left(\frac{4\pi^2mn}{y}\right)^{2k}\nonumber\\ &\qquad\qquad\quad+\sum_{k=0}^{\infty}\frac{\psi^{2}(2k+1)-\psi'(2k+1)}{\Gamma(2k+1)}\left(\frac{4\pi^2mn}{y}\right)^{2k}\Bigg\}. \end{align*} $$
Therefore, invoking Lemma 4.2, using (4.2) and Theorem 4.4 with
$w=4\pi ^2mn/y$
, we are led to
$$ \begin{align*} G_3(y)&=\frac{2}{y}\sum_{m, n=1}^{\infty}\hspace{-4pt}\bigg\{\hspace{-3pt}\log\left(\frac{4\pi^2mn}{y}\right)\log\left(\frac{ny}{m}\right)\cosh\left(\frac{4\pi^2mn}{y}\right)-2\log(2n\pi)\bigg[\left(\sinh\operatorname{Shi}-\cosh\operatorname{Chi}\right)\left(\frac{4\pi^2mn}{y}\right)\nonumber\\ &\quad+\log\left(\frac{4\pi^2mn}{y}\right)\cosh\left(\frac{4\pi^2mn}{y}\right)\hspace{-4pt}\bigg]+\log^{2}\left(\frac{4\pi^2mn}{y}\right)\cosh\left(\frac{4\pi^2mn}{y}\right)+2\hspace{-3pt}\int_{0}^{\infty}\frac{u\cos(u)\log(u)\, du}{u^2+(4\pi^2mn/y)^2}\bigg\}\nonumber\\ &=\frac{4}{y}\sum_{n=1}^{\infty}\sum_{m=1}^{\infty}\int_{0}^{\infty}\frac{u\cos(u)\log(u/(2\pi n))}{u^2+(4\pi^2mn/y)^2}\, du, \end{align*} $$
where in the last step, we used Lemma 4.1 with
$w=4\pi ^2mn/y$
.
Next, an application of Theorem 3.4 with
$w=2\pi n/y$
and then of (2.2) with
$w=4\pi ^2n/y$
in the second step further yields
$$ \begin{align} G_3(y)&=\frac{4}{y}\sum_{n=1}^{\infty}\left\{\sum_{m=1}^{\infty}\int_{0}^{\infty}\frac{u\cos(u)\log(uy/(2\pi n))}{u^2+(4\pi^2mn/y)^2}\, du-\log(y)\sum_{m=1}^{\infty}\int_{0}^{\infty}\frac{u\cos(u)}{u^2+(4\pi^2mn/y)^2}\, du\right\}\nonumber\\ &=\frac{1}{y}\sum_{n=1}^{\infty}\Bigg\{\psi_1\left(\frac{2\pi in}{y}\right)-\frac{1}{2}\log^{2}\left(\frac{2\pi in}{y}\right)+\psi_1\left(-\frac{2\pi in}{y}\right)-\frac{1}{2}\log^{2}\left(-\frac{2\pi in}{y}\right)+\frac{y}{4n}\nonumber\\ &\quad+\left(\gamma+\log(y)\right)\left(\psi\left(\frac{2\pi in}{y}\right)+\psi\left(-\frac{2\pi in}{y}\right)-2\log\left(\frac{2\pi n}{y}\right)\right)\Bigg\}\nonumber\\ &=\frac{1}{y}\sum_{n=1}^{\infty}\Bigg\{\psi_1\left(\frac{2\pi in}{y}\right)-\frac{1}{2}\log^{2}\left(\frac{2\pi in}{y}\right)+\psi_1\left(-\frac{2\pi in}{y}\right)-\frac{1}{2}\log^{2}\left(-\frac{2\pi in}{y}\right)+\frac{y}{4n}\Bigg\}\nonumber\\ &\quad+\frac{\left(\gamma+\log(y)\right)}{y}\sum_{n=1}^{\infty}\Bigg\{\left(\psi\left(\frac{2\pi in}{y}\right)+\psi\left(-\frac{2\pi in}{y}\right)-2\log\left(\frac{2\pi n}{y}\right)\right)\Bigg\}, \end{align} $$
where the validity of the last step results from the fact that invoking Theorem 3.2, once with
$z=2\pi in/y$
, and again with
$z=-2\pi in/y$
, and adding the two expansions yields
$$ \begin{align} \psi_1\left(\frac{2\pi in}{y}\right)-\frac{1}{2}\log^{2}\left(\frac{2\pi in}{y}\right)+\psi_1\left(-\frac{2\pi in}{y}\right)-\frac{1}{2}\log^{2}\left(-\frac{2\pi in}{y}\right)+\frac{y}{4n}=O_y\left(\frac{\log(n)}{n^2}\right). \end{align} $$
Therefore, from (5.3), (5.4), (5.6), and (5.12), we arrive at
$$ \begin{align*} &\sum_{n=1}^{\infty}\frac{\log(n)}{e^{ny}-1}+\frac{1}{4}\log(2\pi)-\frac{1}{2y}\log^{2}(y)+\frac{\gamma^2}{2y}-\frac{\pi^2}{12y}\nonumber\\ &=\frac{1}{y}\sum_{n=1}^{\infty}\Bigg\{\psi_1\left(\frac{2\pi in}{y}\right)-\frac{1}{2}\log^{2}\left(\frac{2\pi in}{y}\right)+\psi_1\left(-\frac{2\pi in}{y}\right)-\frac{1}{2}\log^{2}\left(-\frac{2\pi in}{y}\right)+\frac{y}{4n}\Bigg\}\nonumber\\ &\quad+\frac{\left(\gamma+\log(y)\right)}{y}\sum_{n=1}^{\infty}\Bigg\{\left(\psi\left(\frac{2\pi in}{y}\right)+\psi\left(-\frac{2\pi in}{y}\right)-2\log\left(\frac{2\pi n}{y}\right)\right)\Bigg\}, \end{align*} $$
which, upon rearrangement, gives (1.13).
Now, (1.14) can be immediately derived from (1.13) by invoking (1.6) to transform the first series on the right-hand side of (1.13), multiplying both sides of the resulting identity by y followed by simplification and rearrangement. This completes the proof for
$y>0$
. Using Weierstrass’ theorem on analytic functions, it is not difficult to see that all of the infinite series are analytic in Re
$(y)>0$
. Since the other expressions in (1.14) are analytic in this region too, the result holds in Re
$(y)>0$
by analytic continuation.
The theorem just proved allows us to obtain the complete asymptotic expansion of
$\sum \limits _{n=1}^{\infty }d(n)\log (n)e^{-ny}$
as
$y\to 0$
. This is derived next.
5.2 Proof of Theorem 1.2
From (3.13), as
$y\to 0$
,
$$ \begin{align*} \psi\left(\pm\frac{2\pi i n}{y} \right) \hspace{-2pt}\sim \log\left(\pm\frac{2\pi i n}{y} \right) \mp \frac{y}{4\pi in}-\sum_{k=1}^\infty \frac{B_{2k}}{2k}\left(\pm\frac{2\pi i n}{y} \right)^{-2k} \end{align*} $$
Inserting the above asymptotics into the first sum of the right-hand side of (1.13), we obtain
$$ \begin{align} \sum_{n=1}^\infty \left\{\log\left(\frac{2\pi n}{y} \right) -\frac{1}{2}\left(\psi\left(\frac{2\pi i n}{y} \right) + \psi\left(-\frac{2\pi i n}{y} \right) \right) \right\} &\sim \sum_{n=1}^\infty \sum_{k=1}^\infty \frac{(-1)^k B_{2k}}{2k}\left(\frac{2\pi n}{y} \right)^{-2k}\nonumber\\ &= \sum_{k=1}^\infty \frac{(-1)^k B_{2k}\zeta(2k)}{2k}\left(\frac{2\pi}{y} \right)^{-2k} \nonumber\\ &=-\frac{1}{2} \sum_{k=1}^\infty \frac{B_{2k}^2 y^{2k}}{(2k)(2k)!}, \end{align} $$
where in the last step, we used Euler’s formula
$$ \begin{align} \zeta(2 m ) = (-1)^{m +1} \displaystyle\frac{(2\pi)^{2 m}B_{2 m }}{2 (2 m)!}\hspace{5mm} (m\geq0). \end{align} $$
Next, we need to find the asymptotic expansion of the second sum on the right-hand side of (1.13). Invoking Theorem 3.2 twice, once with
$z=2\pi in/y$
, and again, with
$z=-2\pi in/y$
, and inserting them into the second sum of the right-hand side of (1.13), we obtain
$$ \begin{align} &\sum_{n=1}^{\infty}\left\{\psi_1\left(\frac{2\pi in}{y}\right)+\psi_1\left(-\frac{2\pi in}{y}\right)-\frac{1}{2}\left(\log^{2}\left(\frac{2\pi in}{y}\right)+\log^{2}\left(-\frac{2\pi in}{y}\right)\right)+\frac{y}{4n}\right\}\nonumber\\ & \sim \sum_{n=1}^{\infty} \sum_{k=1}^{\infty} \frac{(-1)^k B_{2k}}{k}\left(\frac{y}{2\pi n}\right)^{2k}\left[\frac{1}{2k-1} + \sum_{j=1}^{2k-2}\frac{1}{j}- \log \left(\frac{2\pi n}{y} \right) \right]\nonumber\\ &= \sum_{n=1}^{\infty} \sum_{k=1}^{\infty} \frac{(-1)^k B_{2k}}{k}\left(\frac{y}{2\pi n}\right)^{2k}\left[\frac{1}{2k-1} + \left(\sum_{j=1}^{2k-2}\frac{1}{j}-\log \left(\frac{2\pi}{y} \right)\right) -\log n \right]\nonumber\\ &= \sum_{k=1}^{\infty} \frac{(-1)^k B_{2k}}{k}\left(\frac{y}{2\pi}\right)^{2k}\left[\zeta(2k)\left\{\frac{1}{2k-1} + \left(\sum_{j=1}^{2k-2}\frac{1}{j}-\log \left(\frac{2\pi}{y} \right)\right)\right\}+\zeta'(2k) \right] \nonumber\\ &= -\sum_{k=1}^\infty\left[ \frac{B_{2k}^2 y^{2k}}{(2k-1)(2k)(2k)!} + \frac{B_{2k}^2 y^{2k}}{2k(2k)!}\left(\sum_{j=1}^{2k-2}\frac{1}{j}-\log \left(\frac{2\pi}{y} \right)\right) + \frac{(-1)^{k+1} B_{2k}\zeta'(2k)}{k}\left(\frac{y}{2\pi}\right)^{2k}\right], \end{align} $$
where in the penultimate step, we used
$\zeta '(s)=-\sum _{n=1}^{\infty }\log (n)n^{-s}$
for Re
$(s)>1$
, and in the last step, we used (5.15). Substituting (5.14) and (5.16) in (1.13), we see that as
$y\to 0$
,
$$ \begin{align*} &\sum_{n=1}^{\infty}\frac{\log(n) }{e^{ny}-1} \nonumber\\ &\sim -\frac{1}{4}\log(2\pi)+\frac{1}{2y}\log^{2}(y)-\frac{\gamma^2}{2y}+\frac{\pi^2}{12y} -\frac{2}{y}(\gamma+\log(y))\left\{-\frac{1}{2} \sum_{k=1}^\infty \frac{B_{2k}^2 y^{2k}}{(2k)(2k)!}\right\}\nonumber\\ &\quad -\frac{1}{y}\sum_{k=1}^\infty\left[ \frac{B_{2k}^2 y^{2k}}{(2k-1)(2k)(2k)!} + \frac{B_{2k}^2 y^{2k}}{2k(2k)!}\left(\sum_{j=1}^{2k-2}\frac{1}{j}-\log \left(\frac{2\pi}{y} \right)\right) + \frac{(-1)^{k+1} B_{2k}\zeta'(2k)}{k}\left(\frac{y}{2\pi}\right)^{2k}\right]\nonumber\\ & = -\frac{1}{4}\log(2\pi)+\frac{1}{2y}\log^{2}(y)-\frac{\gamma^2}{2y}+\frac{\pi^2}{12y} +\hspace{-2pt} \sum_{k=1}^{\infty} \frac{B_{2k} y^{2k-1}}{k}\hspace{-2pt}\left\{\frac{B_{2k}}{2(2k)!}\left(\gamma -\hspace{-2pt} \sum_{j=1}^{2k-1}\frac{1}{j}+\log (2\pi)\right)\hspace{-4pt}+\hspace{-2pt} \frac{(-1)^k \zeta'(2k)}{(2\pi)^{2k}}\right\}\nonumber\\ &= -\frac{1}{4}\log(2\pi)+\frac{1}{2y}\log^{2}(y)-\frac{\gamma^2}{2y}+\frac{\pi^2}{12y} + \frac{y}{6}\bigg\{\frac{1}{24}(\gamma-1+\log(2\pi)) -\frac{1}{4\pi^2} \bigg[\frac{\pi^2}{6}(\gamma + \log(2\pi) \nonumber\\ &\quad- 12\log (A)) \bigg] \bigg\} +\sum_{k=2}^{\infty} \frac{B_{2k} y^{2k-1}}{k}\left\{\frac{B_{2k}}{2(2k)!}\left(\gamma - \sum_{j=1}^{2k-1}\frac{1}{j}+\log (2\pi)\right)+ \frac{(-1)^k \zeta'(2k)}{(2\pi)^{2k}}\right\}\nonumber\\ &= \frac{1}{2y}\log^{2}(y) + \frac{1}{y}\left(\frac{\pi^2}{12} - \frac{\gamma^2}{2} \right)-\frac{1}{4}\log(2\pi) +\frac{y}{12}\left(\log (A) - \frac{1}{12} \right) \nonumber\\ &\quad +\sum_{k=2}^{\infty} \frac{B_{2k} y^{2k-1}}{k}\left\{\frac{B_{2k}}{2(2k)!}\left(\gamma - \sum_{j=1}^{2k-1}\frac{1}{j}+\log (2\pi)\right)+ \frac{(-1)^k \zeta'(2k)}{(2\pi)^{2k}}\right\}. \end{align*} $$
This completes the proof.
An application of the result proved above in the theory of the moments of the Riemann zeta function is given next.
5.3 Proof of Theorem 1.3
Our goal is to link
$\int \limits _{0}^{\infty }\zeta \left (\frac {1}{2}-it\right )\zeta '\left (\frac {1}{2}+it\right )e^{-\delta t}\, dt$
with
$\sum \limits _{n=1}^{\infty }\frac {\log (n) }{\exp \left (2 \pi i n e^{-i{\delta }}\right )-1}$
and then invoke Theorem 1.2. Our treatment is similar to that of Atkinson [Reference Atkinson3].
First note that, for
$\text {Re}(y)>0$
,
$$ \begin{align} \sum_{n=1}^{\infty} d(n)\log(n) e^{-ny}=\sum_{n=1}^{\infty} d(n)\log( n) {1\over 2\pi i}\int\limits_{(c)}\Gamma(s)(ny)^{-s}ds, \end{align} $$
where
$c=\text {Re}(s)>1$
. Using
$(1*\log )(n)=\sum _{d|n}\log d=\frac {1}{2}d(n)\log ( n)$
and interchanging the order of summation and integration on the right-hand side of (5.17), we obtain
$$ \begin{align} \sum_{n=1}^{\infty} d(n)\log( n) e^{-ny}&={1\over 2\pi i}\int\limits_{(c)}\Gamma(s)\left( \sum_{n=1}^{\infty} {d(n)\log (n)\over n^s }\right) y^{-s}ds\nonumber\\ &={2\over 2\pi i}\int\limits_{(c)}\Gamma(s) \sum_{n=1}^{\infty} {(1*\log) (n)\over n^s } y^{-s}ds\nonumber\\ &=-{2\over 2\pi i}\int\limits_{(c)}\Gamma(s) \zeta(s)\zeta'(s) y^{-s}ds. \end{align} $$
Letting
$y=2 \pi i e^{-i{\delta }}$
so that
$0<\text {Re}({\delta })<\pi $
, we deduce that
$$ \begin{align} \sum_{n=1}^{\infty} d(n)\log( n) \exp\left(-2 \pi i n e^{-i{\delta}}\right)&=-{2\over 2\pi i}\int\limits_{(c)}\Gamma(s) \zeta(s)\zeta'(s) (2 \pi i e^{-i{\delta}})^{-s}ds. \end{align} $$
We would like to shift the line of integration from Re
$(s)=c$
to Re
$(s)=1/2$
. The integrand in (5.19) has a third-order pole at
$s=1$
. Therefore, using Cauchy’s residue theorem on the rectangular contour with sides
$\left [c -iT, c+iT \right ], \left [c+iT, {1\over 2} + iT \right ], \left [{1\over 2} + iT, {1\over 2}-iT \right ]$
, and
$ \left [{1\over 2}-iT, c-iT \right ] $
, where
$T>0$
, noting that (2.1) implies that the integrals along the horizontal line segments tend to zero as
$T \to \infty $
, we obtain
$$ \begin{align} &{1\over 2\pi i}\int\limits_{(c)}\Gamma(s) \zeta(s)\zeta'(s) (2 \pi i e^{-i{\delta}})^{-s}ds \nonumber\\ &={1\over 2\pi i}\int\limits_{({1\over 2})}\Gamma(s) \zeta(s)\zeta'(s) (2 \pi i e^{-i{\delta}})^{-s}ds+{\text{Res}_{s=1}}\Gamma(s) \zeta(s)\zeta'(s) (2 \pi i e^{-i{\delta}})^{-s} \nonumber \\ &= {1\over 4\pi i}\int\limits_{({1\over 2})}{\zeta(1-s) \zeta'(s) ( i e^{-i{\delta}})^{-s}\over \cos\left({\pi s\over 2} \right) }ds+{\frac{1}{2 \pi i e^{-i{\delta}}}}\left({\gamma^2 \over 2 }-{\pi^2\over 12}-\frac{1}{2}\log ^2(2 \pi i e^{-i{\delta}}) \right), \end{align} $$
where, in the last step, we used the functional equation (3.25) with s replaced by
$1-s$
. Hence, from (5.19) and (5.20), we arrive at
$$ \begin{align} {e^{-{i{\delta}\over 2}}\over 2 i}\int\limits_{(\frac{1}{2})}{\zeta(1-s) \zeta'(s) e^{-is\left({\pi\over 2}-{\delta} \right) }\over \cos\left({\pi s\over 2} \right) }ds&=-\pi e^{-{i{\delta}\over 2}}\sum_{n=1}^{\infty} d(n)\log( n) \exp\left(-2 \pi i n e^{-i{\delta}}\right)\nonumber\\ &\quad+{ie^{{i{\delta}\over 2}}\over 2}\left({\gamma^2 }-{\pi^2\over 6}-{\log ^2(2 \pi i e^{-i{\delta}})} \right). \end{align} $$
We next consider the difference of the integrals on the left-hand sides of (1.16) and (5.21) and employ the change of variable
$s={1\over 2}+it$
in the second integral in the first step below to see that
$$ \begin{align} \int_{0}^{\infty}&\zeta\left({1\over 2}-it\right)\zeta'\left({1\over 2}+it\right)e^{-{\delta} t}dt-{e^{-{i{\delta}\over 2}}\over i}\int_{\left( 1\over 2\right) }\frac{\zeta\left({1-s}\right)\zeta'\left(s\right)}{2\cos\left(\pi s \over 2 \right) }e^{-is \left({\pi\over 2}-{\delta} \right)}ds\nonumber \\ &=\int_{0}^{\infty}\zeta\left({1\over 2}-it\right)\zeta'\left({1\over 2}+it\right)e^{-{\delta} t}dt-{e^{-{i{\delta}\over 2}}}\int_{-\infty}^{\infty}\frac{\zeta\left({1\over 2}-it\right)\zeta'\left({1\over 2}+it\right)}{\left(e^{{i\pi \over 2 }\left({1\over 2}+it\right)} +e^{-{i\pi \over 2 }\left({1\over 2}+it\right)}\right) }e^{-i\left({1\over 2}+it \right) \left({\pi\over 2}-{\delta} \right)}dt\nonumber \\ &=\int_{0}^{\infty}\zeta\left({1\over 2}-it\right)\zeta'\left({1\over 2}+it\right)e^{-{\delta} t}dt-\int_{0}^{\infty}\frac{\zeta\left({1\over 2}+it\right)\zeta'\left({1\over 2}-it\right)}{\left( e^{{i\pi \over 4 }+{\pi t\over 2}} +e^{-{i\pi \over 4 }-{\pi t\over 2}} \right) }e^{-{i\pi \over 4 }-{\pi t\over 2}+{\delta} t}dt\nonumber \\ & \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad -\int_{0}^{\infty}\frac{\zeta\left({1\over 2}-it\right)\zeta'\left({1\over 2}+it\right)}{\left( e^{{i\pi \over 4 }-{\pi t\over 2}} +e^{-{i\pi \over 4 }+{\pi t\over 2}} \right) }e^{-{i\pi \over 4 }+{\pi t\over 2}-{\delta} t}dt\nonumber \\ &=\int_{0}^{\infty}\frac{\zeta\left({1\over 2}-it\right)\zeta'\left({1\over 2}+it\right)}{\left( e^{{i\pi \over 4 }-{\pi t\over 2}} +e^{-{i\pi \over 4 }+{\pi t\over 2}} \right) }e^{{i\pi \over 4 }-{\pi t\over 2}-{\delta} t}dt -\int_{0}^{\infty}\frac{\zeta\left({1\over 2}+it\right)\zeta'\left({1\over 2}-it\right)}{\left( e^{{i\pi \over 4 }+{\pi t\over 2}} +e^{-{i\pi \over 4 }-{\pi t\over 2}} \right) }e^{-{i\pi \over 4 }-{\pi t\over 2}+{\delta} t}dt. \end{align} $$
From [Reference Gonek29, p. 127, Equation (20)], we have
$$ \begin{align*} \zeta\left({1\over 2}-it\right)\ll |t|^{{1\over 4}+{\epsilon \over 2}}\hspace{10pt}\text{and} \hspace{10pt} \zeta'\left({1\over 2}+it\right)\ll |t|^{{1\over 4}+{\epsilon \over 2}}, \end{align*} $$
whence, by reverse triangle inequality, we have
$$ \begin{align*} \left|\frac{\zeta\left({1\over 2}-it\right)\zeta'\left({1\over 2}+it\right)}{\left( e^{{i\pi \over 4 }-{\pi t\over 2}} +e^{-{i\pi \over 4 }+{\pi t\over 2}} \right) }e^{{i\pi \over 4 }-{\pi t\over 2}-{\delta} t}\right|\ll\frac{|t|^{{1\over 2}+\epsilon}e^{-\text{Re}({\delta}) t-{\pi t \over 2}}}{e^{{\pi t \over 2}}-e^{-{\pi t \over 2}}}=\frac{|t|^{{1\over 2}+\epsilon}e^{(-\text{Re}({\delta})-\pi) t}}{1-e^{{-\pi t }}}. \end{align*} $$
This implies that the first integral is analytic for
$\text {Re}({\delta })>-\pi $
. Similarly, the second integral is analytic for
$\text {Re}({\delta }) <\pi $
. Consequently, both integrals of (5.22) are analytic in
${\delta }$
in
$|{\delta }|<\pi $
.
From (5.21) and above discussion, we can say that the expression
$$ \begin{align} \phi ({\delta})&:=\int_{0}^{\infty}\zeta\left({1\over 2}-it\right)\zeta'\left({1\over 2}+it\right)e^{-{\delta} t}dt+\pi e^{-{i{\delta}\over 2}}\sum_{n=1}^{\infty} d(n)\log( n) \exp\left(-2 \pi i n e^{-i{\delta}}\right)\nonumber\\ &\quad-ie^{{i{\delta}\over 2}}\left({\gamma^2 \over 2 }-{\pi^2\over 12}-{\log ^2(2 \pi i e^{-i{\delta}})\over 2} \right) \end{align} $$
is an analytic function of
${\delta }$
in
$|{\delta }|<\pi /2$
. Hence,
$\phi ({\delta })+ie^{{i{\delta }\over 2}}\left ({\gamma ^2 \over 2 }-{\pi ^2\over 12}-{\log ^2(2 \pi i e^{-i{\delta }})\over 2} \right )$
can be expressed as a power series in
${\delta }$
for
$|\delta |<\pi /2$
.
Letting
$y=2\pi i (e^{-i{\delta }}-1)$
in the asymptotic expansion of
$\sum _{n=1}^{\infty } d(n)\log (n) e^{-ny}$
in (1.15), we find that as
${\delta } \to 0$
(within the region
$0<\text {Re}(\delta )<\pi $
),
$$ \begin{align} &\pi e^{-{i{\delta}\over 2}}\sum_{n=1}^{\infty} d(n)\log( n) \exp\left(-2 \pi i n e^{-i{\delta}}\right)\nonumber \\ &=\pi e^{-{i{\delta}\over 2}}\sum_{n=1}^{\infty} d(n)\log( n) \exp\left(-2 \pi i n (e^{-i{\delta}}-1)\right)\nonumber\\ &= \pi e^{-{i{\delta}\over 2}}\left[ {1\over 2 \pi i (e^{-i{\delta}}-1)}\left(\log ^2(2 \pi i (e^{-i{\delta}}-1))+ {\pi^2\over 6}-{\gamma^2 }\right) -\frac{1}{2}\log(2\pi) \right. \nonumber \\ &\quad+\sum_{k=2}^{m-1}\frac{B_{2k}(2\pi i (e^{-i{\delta}}-1))^{2k-1}}{k}\left\lbrace {B_{2k}\over (2k)!}\left(\gamma-\sum_{j=1}^{2k-1}{1\over j}+\log(2\pi) \right)+\frac{2(-1)^k\zeta'(2k)}{(2\pi)^{2k}} \right\rbrace \nonumber \\ &\quad+\left. {2 \pi i (e^{-i{\delta}}-1)\over 6}\left(\log A -{1\over 12}\right) +O\left( (e^{-i{\delta}}-1)^{2m-1}\right)\right]. \end{align} $$
Now, observe that upon expanding
$e^{-i{\delta }}$
as a power series in
${\delta }$
and simplifying, we have
$$ \begin{align} \log ^2(2 \pi i (e^{-i{\delta}}-1))&=\log^{2}(2\pi{\delta})+2\log(2\pi{\delta})\log\left(1+\frac{i^3{\delta}}{2!}-\frac{i^4{\delta}^2}{3!}+\ldots\right)\nonumber\\ &\quad+\log^2\left(1+\frac{i^3{\delta}}{2!}-\frac{i^4{\delta}^2}{3!}+\ldots\right). \end{align} $$
As
${\delta }\to 0$
, the second expression on the above right-hand side simplifies to
$$ \begin{align} 2\log(2\pi{\delta})\log\left(1+\frac{i^3{\delta}}{2!}-\frac{i^4{\delta}^2}{3!}+\ldots\right)&=2\log(2\pi{\delta})\sum_{k=1}^{\infty}\frac{(-1)^{k+1}}{k}\left(\frac{i^3{\delta}}{2!}-\frac{i^4{\delta}^2}{3!}+\ldots\right)^k\nonumber\\ &=-2\log(2\pi{\delta})\sum_{k=1}^{2m-1}a_k{\delta}^k+O\left({\delta}^{2m}\log({\delta})\right), \end{align} $$
and, using the power series expansion of
$\log ^{2}(1+x)$
, we see that the third expression becomes
$$ \begin{align} \log^2\left(1+\frac{i^3{\delta}}{2!}-\frac{i^4{\delta}^2}{3!}+\ldots\right)=\sum_{k=2}^{2m-1}b_k{\delta}^k+O\left(\delta^{2m}\right), \end{align} $$
where
$a_k$
and
$b_k$
are effectively computable constants. Inserting (5.26) and (5.27) in (5.25), we find that
$$ \begin{align} \log ^2(2 \pi i (e^{-i{\delta}}-1)&=\log^{2}(2\pi{\delta})-2\log(2\pi{\delta})\sum_{k=1}^{2m-1}a_k{\delta}^k+\sum_{k=2}^{2m-1}b_k{\delta}^k+O\left({\delta}^{2m}\log({\delta})\right). \end{align} $$
Substitute the above estimate for
$\log ^2(2 \pi i (e^{-i{\delta }}-1)$
in (5.24) to find upon simplification that as
${\delta }\to 0$
,
$$ \begin{align} &\pi e^{-{i{\delta}\over 2}}\sum_{n=1}^{\infty} d(n)\log( n) \exp\left(-2 \pi i n e^{-i{\delta}}\right)\nonumber \\ &={1\over 4\sin\left({\delta}\over 2\right)}\left(\log^{2}(2\pi{\delta})-2\log(2\pi{\delta})\sum_{k=1}^{2m-1}a_k{\delta}^k+\sum_{k=2}^{2m-1}b_k{\delta}^k\right. \nonumber\\ &\qquad\quad \left. +O\left({\delta}^{2m}\log({\delta})\right)+ {\pi^2\over 6}-{\gamma^2 }\right)-\frac{\pi }{2} e^{-{i{\delta}\over 2}}\log (2\pi)\nonumber \\ &\quad +\sum_{k=1}^{m-1}\pi c'_ke^{-{i{\delta}\over 2}}( 2 \pi i (e^{-i{\delta}}-1))^{2k-1}+O\left( (e^{-i{\delta}}-1)^{2m-1}\right) \nonumber \\ &={1\over 4\sin\left({\delta}\over 2\right)}\left( \log^{2}(2\pi{\delta})-2\log(2\pi{\delta})\sum_{k=1}^{2m-1}a_k{\delta}^k+\sum_{k=2}^{2m-1}b_k{\delta}^k+ {\pi^2\over 6}-{\gamma^2 }\right)\nonumber\\ &\quad +\sum_{k=0}^{2m-2}c_k{\delta}^k +O\left({\delta}^{2m-1}\log({\delta})\right), \end{align} $$
where
$c_0=-(\pi /2)\log (2\pi )$
. In the last step, we used the fact that
$1/\sin \left ({\delta }\over 2\right )=O(1/\delta )$
.
Consequently, from (5.23) and (5.29), as
${\delta }\to 0$
in
$|\arg (\delta )|<\pi /2$
, we arrive at (1.16) upon simplification which involves the use of the estimate
$$ \begin{align*} \frac{1}{\sin(\frac{\delta}{2})}=\frac{2}{\delta}+\sum_{n=1}^{m-1}r_n\delta^{2n-1}+O\left(\delta^{2m-1}\right) \end{align*} $$
as
$\delta \to 0$
, where
$r_n$
are constants. This completes the proof.
6 Concluding remarks
The main highlight of this paper was to derive (1.13), that is, an exact transformation for the series
$\displaystyle \sum _{n=1}^{\infty }\frac {\log (n)}{e^{ny}-1}$
, or equivalently, for
$\sum _{n=1}^{\infty }d(n)\log (n)e^{-ny}$
, where
$\text {Re}(y)>0$
. Such a transformation was missing from the literature up to now. One of the reasons for this could be the lack of availability of the transformation in (1.5) until [Reference Dixit, Kesarwani and Kumar23] appeared, which, in turn, resulted from evaluating an integral with a combination of Bessel functions as its associated kernel. This underscores the importance of the applicability of integral transforms in number theory.
In addition, it is to be emphasized that in order to derive (1.13), several new intermediate results, interesting in themselves, had to be derived, for example, the ones given in Theorems 3.3, 3.4, and 4.4. This also shows how important
$\psi _1(z)$
, and, in general,
$\psi _k(z)$
, are in number theory, and further corroborates Ishibashi’s quote given in the introduction.
The transformation in (1.13) has a nice application in the study of moments of
$\zeta (s)$
, namely, to obtain the asymptotic expansion of
$ \int _{0}^{\infty }\zeta \left (\frac {1}{2}-it\right )\zeta '\left (\frac {1}{2}+it\right )e^{-\delta t}\, dt$
as
$\delta \to 0$
. However, considering the fact that (1.13) holds for any y with Re
$(y)>0$
, we expect further applications of it in the future, in particular, in the theory of modular forms.
A generalization of (1.13), equivalently, of (1.14), may be obtained for the series
$\sum _{n=1}^{\infty }d(n)\log ^{k}(n)e^{-ny}$
. This would require differentiating (1.5) k times with respect to a and then letting
$a\to 0$
. This would involve Ishibashi’s higher analogs of Deninger’s
$R(z)$
defined in (3.4). Ishibashi [Reference Ishibashi36, Theorem 1] gave a Plana-type formula for
$R_k(x), x>0$
, which is easily seen to hold for complex x in the right-half plane Re
$(x)>0$
. This formula involves a polynomial in
$\log (t)$
defined by
$S_k(t):=\sum _{j=0}^{k-1}a_{k, j}\log ^{j}(t)$
, where
$a_{k, j}$
are recursively defined by
$a_{k, j}=-\sum _{r=0}^{k-2}\binom {k-1}{r}\Gamma ^{(k-r-1)}(1)a_{r+1, j}, 0\leq j\leq k-2$
, with
$a_{1,0}=1$
and
$a_{k, k-1}=1$
.
Observe that
$S_1(t)=1$
and
$S_2(t)=\gamma +\log (t)$
, and so the numerators of the summands of the series on the left-hand sides of (1.6) and (1.14) are
$S_1(ny)$
and
$S_2(ny)$
respectively. In view of this, we speculate the left-hand side of (1.14) to generalize to
$\sum \limits _{n=1}^{\infty }\displaystyle \frac {S_{k+1}(ny)}{e^{ny}-1}$
and the right-hand side to involve
$\psi _k(z)$
.
Since (5.18) can be generalized to
$$ \begin{align*} \sum_{n=1}^{\infty}\frac{\log^{k}(n)}{e^{ny}-1}=-\frac{1}{2\pi i}\int_{(c)}\Gamma(s)\zeta(s)\zeta^{(k)}(s)y^{-s}\, ds\hspace{5mm}(c=\text{Re}(s)>1, \text{Re}(y)>0), \end{align*} $$
on account of the fact that
$\zeta ^{(k)}(s)=(-1)^k\sum \limits _{n=1}^{\infty }\log ^{k}(n)n^{-s}$
, once a generalization of (1.14) is obtained, it would possibly give us the complete asymptotic expansion of
$ \int _{0}^{\infty }\zeta \left (\frac {1}{2}-it\right )\zeta ^{(k)}\left (\frac {1}{2}+it\right )e^{-\delta t}\, dt$
as
$\delta \to 0$
. Details will appear elsewhere.
Acknowledgments
The authors sincerely thank the referee for his/her invaluable suggestions which enhanced the quality of the paper. They also thank Christopher Deninger, Nico M. Temme, Rahul Kumar, Shigeru Kanemitsu, and Alessandro Languasco for helpful discussions. Further, they thank Professor Alexander Yu. Solynin of Texas Tech University for his help in translating the relevant pages of [Reference Dzhrbashyan25] from Russian to English, Professor Inese Bula from University of Latvia for sending a copy of [Reference Riekstins54], and Amogh Parab of Ohio State University for informing us about [Reference Rogers55].
