Hostname: page-component-848d4c4894-p2v8j Total loading time: 0 Render date: 2024-06-08T17:59:05.257Z Has data issue: false hasContentIssue false
  • English
  • Français

An Algorithm for a Minimum Cover of an Abstract Complex

Published online by Cambridge University Press:  20 November 2018

D. K. Ray-Chaudhuri
D. K. Ray-Chaudhuri*
Affiliation:
University of North Carolina
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X = {x1, x2,...,xm} be a finite set of m points and 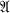= {A1, A2, . . . , An] be a class of n subsets of X. Such a system of points and sets is called a complex (X, 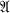). If every set of the class 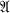contains two points, the complex is a graph with m points x1x2, . . . , xm and n edges A1, A2, . . . , An. A complex (X, 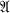) in which every set has the same number of points is called regular.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 15 , 1963 , pp. 11 - 24
Copyright
Copyright © Canadian Mathematical Society 1963

References

1. Berge, C., Two theorems in graph theory, Proc. Natl. Acad. Sci. U.S.A., 43 (1957), 842–844.Google Scholar
2. Fulkerson, D. R. and Ryser, H. J., Traces, term ranks, widths and heights, I.B.M. J. of Research and Development, 4 (1960), 455–459.Google Scholar
3. Norman, R. Z. and Rabin, M. O., An algorithm for a minimum cover of a graph, Proc. Amer. Math. Soc, 10 (1959), 315–319.Google Scholar
4. Petersen, J., Die Théorie der regulàren Graphen, Acta Math., 51 (1891), 193–220.Google Scholar
5. Roth, J. P., Algebraic topological methods for the synthesis of switching systems I, Trans. Amer. Math. Soc, 88 (1958), 302–326.Google Scholar