Hostname: page-component-848d4c4894-x5gtn Total loading time: 0 Render date: 2024-05-31T07:48:24.063Z Has data issue: false hasContentIssue false
  • English
  • Français

Annihilators of the Ideal Class Group of a Cyclic Extension of an Imaginary Quadratic Field

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  09 January 2019

Hugo Chapdelaine  and
Radan Kučera
Hugo Chapdelaine
Affiliation:
Faculty of Science and Engineering, Laval University, Québec G1V 0A6, Canada Email: hugo.chapdelaine@mat.ulaval.ca
Radan Kučera
Affiliation:
Faculty of Science, Masaryk University, 611 37 Brno, Czech Republic Email: kucera@math.muni.cz
Get access Rights & Permissions [Opens in a new window]

Abstract

The aim of this paper is to study the group of elliptic units of a cyclic extension 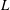$L$ of an imaginary quadratic field 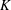$K$ such that the degree 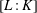$[L:K]$ is a power of an odd prime 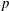$p$. We construct an explicit root of the usual top generator of this group, and we use it to obtain an annihilation result of the 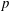$p$-Sylow subgroup of the ideal class group of 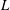$L$.

Keywords

annihilatorclass groupelliptic unit

MSC classification

Primary: 11R20: Other abelian and metabelian extensions
Secondary: 11R27: Units and factorization 11R29: Class numbers, class groups, discriminants
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 6 , December 2019 , pp. 1395 - 1419
Copyright
© Canadian Mathematical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The second author was supported under Project 15-15785S of the Czech Science Foundation.

References

Bley, W., Wild Euler systems of elliptic units and the equivariant Tamagawa number conjecture . J. Reine Angew. Math. 577(2004), 117–146. https://doi.org/10.1515/crll.2004.2004.577.117.Google Scholar
Bley, W., Equivariant Tamagawa number conjecture for abelian extensions of a quadratic imaginary field . Doc. Math. 11(2006), 73–118.Google Scholar
Burns, D., Congruences between derivatives of abelian L-functions at s = 0 . Invent. Math. 169(2007), 451–499. https://doi.org/10.1007/s00222-007-0052-3.Google Scholar
Gras, G., Class field theory. From theory to practice . Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
Greither, C. and Kučera, R., Annihilators for the class group of a cyclic field of prime power degree . Acta Arith. 112(2004), 177–198. https://doi.org/10.4064/aa112-2-6.Google Scholar
Greither, C. and Kučera, R., Annihilators for the class group of a cyclic field of prime power degree II . Canad. J. Math. 58(2006), 580–599. https://doi.org/10.4153/CJM-2006-024-2.Google Scholar
Greither, C. and Kučera, R., Linear forms on Sinnott’s module . J. Number Theory 141(2014), 324–342. https://doi.org/10.1016/j.jnt.2014.02.003.Google Scholar
Greither, C. and Kučera, R., Eigenspaces of the ideal class group . Ann. Inst. Fourier (Grenoble) 64(2014), 2165–2203. https://doi.org/10.5802/aif.2908.Google Scholar
Greither, C. and Kučera, R., Annihilators for the class group of a cyclic field of prime power degree III . Publ. Math. Debrecen 86(2015), no. 3–4, 401–421.Google Scholar
Ohshita, T., On higher Fitting ideals of Iwasawa modules of ideal class groups over imaginary quadratic fields and Euler systems of elliptic units . Kyoto J. Math. 53(2013), 845–887. https://doi.org/10.1215/21562261-2366118.Google Scholar
Oukhaba, H., Index formulas for ramified elliptic units . Compositio Math. 137(2003), 1–22. https://doi.org/10.1023/A:1023667807218.Google Scholar
Rubin, K., Global units and ideal class groups . Invent. Math. 89(1987), 511–526. https://doi.org/10.1007/BF01388983.Google Scholar
Rubin, K., Stark units and Kolyvagin’s “Euler systems” . J. Reine Angew. Math. 425(1992), 141–154. https://doi.org/10.1515/crll.1992.425.141.Google Scholar
Sinnott, W., On the Stickelberger ideal and the circular units of an abelian field . Invent. Math. 62(1980), 181–234. https://doi.org/10.1007/BF01389158.Google Scholar
Thaine, F., On the ideal class groups of real abelian number fields . Ann. of Math. (2) 128(1988), no. 1, 1–18. https://doi.org/10.2307/1971460.Google Scholar