Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-06-08T13:02:20.096Z Has data issue: false hasContentIssue false
  • English
  • Français

The Behaviour of Legendre And Ultraspherical Polynomials in Lp-Spaces

Published online by Cambridge University Press:  20 November 2018

N. J. Kalton  and
L. Tzafriri
N. J. Kalton
Affiliation:
Department of Mathematics, University of Missouri, Columbia, MO 65211, USA email: nigel@math.missouri.edu
L. Tzafriri
Affiliation:
Department of Mathematics, The Hebrew University, Jerusalem, Israel email: liortz@math.huji.ac.il
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the analogue of the 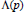$\wedge (p)$―problem for subsets of the Legendre polynomials or more general ultraspherical polynomials. We obtain the “best possible” result that if 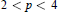$2\,<\,p\,<\,4$ then a random subset of $N$ Legendre polynomials of size 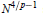${{N}^{4/p-1}}$ spans an Hilbertian subspace. We also answer a question of König concerning the structure of the space of polynomials of degree $n$ in various weighted 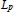${{L}_{p}}$-spaces.

Keywords

42C1033C4546B07
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 6 , 01 December 1998 , pp. 1236 - 1252
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Badkov, V.M., Convergence in mean and almost everywhere of Fourier series in polynomials orthogonal on an interval.. Math. USSR Sbornik 24(1974), 223–256.Google Scholar
2. Bourgain, J., Bounded orthogonal sets and the Λ(p)-problem. Acta Math. 162(1989), 227–246.Google Scholar
3. Garnett, J., Bounded analytic functions. Academic Press, Orlando, 1981.Google Scholar
4. Hunt, R.A., Muckenhaupt, B. and Wheeden, R.L.,Weighted norm inequalities for the conjugate function and the Hilbert transfrom.. Trans. Amer.Math. Soc. 176(1973), 227–251.Google Scholar
5. Kalton, N.J. and Verbitsky, I., Weighted norm inequalities and nonlinear equations. Trans. Amer.Math. Soc. (To appear.)Google Scholar
6. Muckenhaupt, B., Mean convergence of Jacobi series. Proc. Amer. Math. Soc. 24(1970), 288–292.Google Scholar
7. Muckenhaupt, B.,Weighted norm inequalities for theHardy maximal function. Trans. Amer.Math. Soc. 165(1972), 207–226.Google Scholar
8. Newman, D.J. and W, Rudin, Mean convergence of orthogonal series. Proc. Amer.Math. Soc. 3(1952), 219–222.Google Scholar
9. Pollard, H., The mean convergence of orthogonal series I. Trans. Amer.Math. Soc. 62(1947), 387–403.Google Scholar
10. Pollard, H., The mean convergence of orthogonal series II. Trans. Amer.Math. Soc. 63(1948), 355–367.Google Scholar
11. Pollard, H., The mean convergence of orthogonal series III. Duke Math. J. 16(1949), 189–191.Google Scholar
12. Rudin, W., Trigonometric series with gaps. J. Math. Mech. 9(1960), 203–227.Google Scholar
13. Sawyer, E.T., A two-weight weak type inequality for fractional integrals. Trans. Amer. Math. Soc. 281(1984), 339–345.Google Scholar
14. Szegö, G., Orthogonal polynomials. 4th edn, Amer. Math. Soc. Colloq. Publ. 23, Providence, 1975.Google Scholar
15. Talagrand, M., Sections of smooth convex bodies via majorizing measures. Acta Math. 175(1995), 273- 300.Google Scholar