No CrossRef data available.
Article contents
The blowup-polynomial of a metric space: connections to stable polynomials, graphs and their distance spectra
Published online by Cambridge University Press: 09 November 2023
Abstract
To every finite metric space X, including all connected unweighted graphs with the minimum edge-distance metric, we attach an invariant that we call its blowup-polynomial 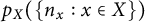 $p_X(\{ n_x : x \in X \})$. This is obtained from the blowup
$p_X(\{ n_x : x \in X \})$. This is obtained from the blowup 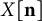 $X[\mathbf {n}]$ – which contains
$X[\mathbf {n}]$ – which contains 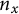 $n_x$ copies of each point x – by computing the determinant of the distance matrix of
$n_x$ copies of each point x – by computing the determinant of the distance matrix of 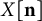 $X[\mathbf {n}]$ and removing an exponential factor. We prove that as a function of the sizes
$X[\mathbf {n}]$ and removing an exponential factor. We prove that as a function of the sizes 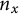 $n_x$,
$n_x$, 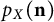 $p_X(\mathbf {n})$ is a polynomial, is multi-affine, and is real-stable. This naturally associates a hitherto unstudied delta-matroid to each metric space X; we produce another novel delta-matroid for each tree, which interestingly does not generalize to all graphs. We next specialize to the case of
$p_X(\mathbf {n})$ is a polynomial, is multi-affine, and is real-stable. This naturally associates a hitherto unstudied delta-matroid to each metric space X; we produce another novel delta-matroid for each tree, which interestingly does not generalize to all graphs. We next specialize to the case of 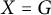 $X = G$ a connected unweighted graph – so
$X = G$ a connected unweighted graph – so 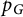 $p_G$ is “partially symmetric” in
$p_G$ is “partially symmetric” in 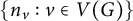 $\{ n_v : v \in V(G) \}$ – and show three further results: (a) We show that the polynomial
$\{ n_v : v \in V(G) \}$ – and show three further results: (a) We show that the polynomial 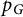 $p_G$ is indeed a graph invariant, in that
$p_G$ is indeed a graph invariant, in that 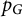 $p_G$ and its symmetries recover the graph G and its isometries, respectively. (b) We show that the univariate specialization
$p_G$ and its symmetries recover the graph G and its isometries, respectively. (b) We show that the univariate specialization 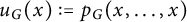 $u_G(x) := p_G(x,\dots ,x)$ is a transform of the characteristic polynomial of the distance matrix
$u_G(x) := p_G(x,\dots ,x)$ is a transform of the characteristic polynomial of the distance matrix 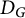 $D_G$; this connects the blowup-polynomial of G to the well-studied “distance spectrum” of G. (c) We obtain a novel characterization of complete multipartite graphs, as precisely those for which the “homogenization at
$D_G$; this connects the blowup-polynomial of G to the well-studied “distance spectrum” of G. (c) We obtain a novel characterization of complete multipartite graphs, as precisely those for which the “homogenization at 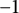 $-1$” of
$-1$” of 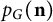 $p_G(\mathbf { n})$ is real-stable (equivalently, Lorentzian, or strongly/completely log-concave), if and only if the normalization of
$p_G(\mathbf { n})$ is real-stable (equivalently, Lorentzian, or strongly/completely log-concave), if and only if the normalization of 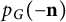 $p_G(-\mathbf { n})$ is strongly Rayleigh.
$p_G(-\mathbf { n})$ is strongly Rayleigh.
Keywords
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
Footnotes
P. N. Choudhury was partially supported by INSPIRE Faculty Fellowship research grant DST/INSPIRE/04/2021/002620 (DST, Govt. of India), IIT Gandhinagar Internal Project grant IP/IITGN/MATH/PNC/2223/25, C.V. Raman Postdoctoral Fellowship 80008664 (IISc), and National Post-Doctoral Fellowship (NPDF) PDF/2019/000275 from SERB (Govt. of India). A. Khare was partially supported by Ramanujan Fellowship grant SB/S2/RJN-121/2017, MATRICS grant MTR/2017/000295, and SwarnaJayanti Fellowship grants SB/SJF/2019-20/14 and DST/SJF/MS/2019/3 from SERB and DST (Govt. of India), by a Shanti Swarup Bhatnagar Award from CSIR (Govt. of India), by grant F.510/25/CAS-II/2018(SAP-I) from UGC (Govt. of India), and by the DST FIST program 2021 (TPN–700661).





